Импульс МТ. Импульс системы МТ и АТТ. Лекция 5

1. Лекция 5. Импульс МТ. Импульс системы МТ и АТТ.

2012

2.

Импульс материальной точки
Импульс – количество движения – векторная
величина равная произведению массы тела на его
скорость.
(Первое упоминание – Декарт, XVII в.; определение – И. Ньютон)
p m
[ p] кг м / с
2

3.

Импульс материальной точки
II закон Ньютона в импульсной (дифференциальной)
форме:
md dp
F ma
dt
dt
Импульс силы:
[ p] Н c
dp Fdt
p p2 p1 Fdt Fср t
t
3
0

4.

Импульс системы материальных точек
N
P pi
i 1
N – количество материальных точек, входящих в
систему
dP N dp i
dt i 1 dt
4
dpi
Fik (внутр.) Fвнешн.
dt k 1

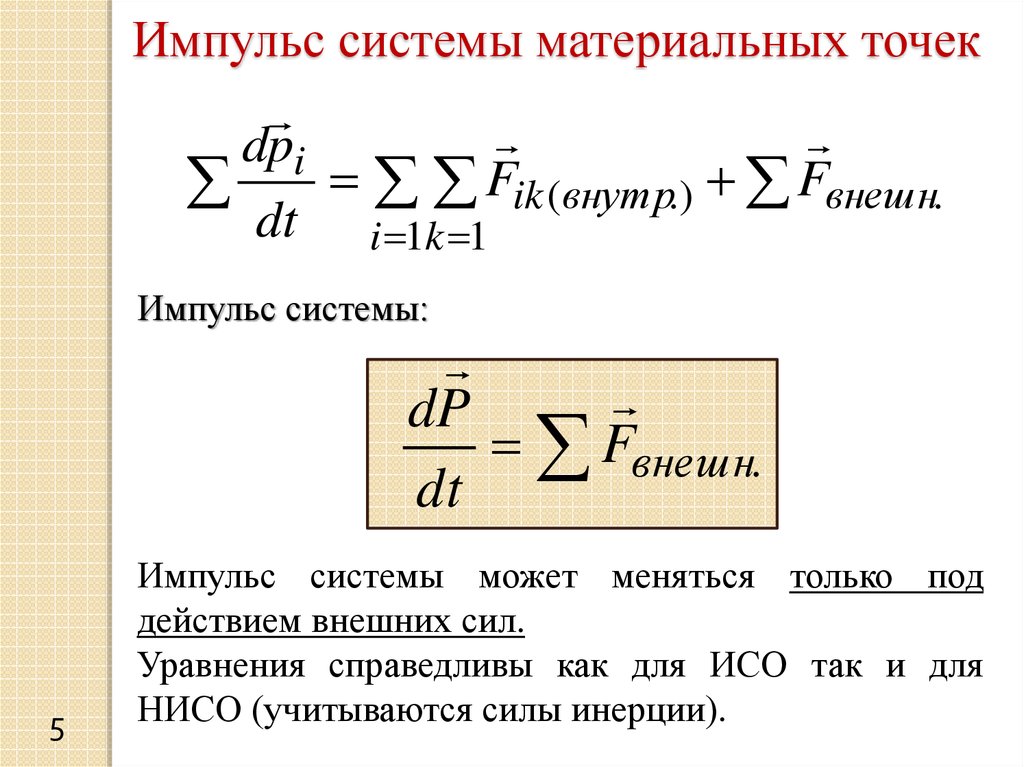
5.

Импульс системы материальных точек
dpi
Fik (внутр.) Fвнешн.
dt i 1k 1
Импульс системы:
dP
Fвнешн.
dt
5
Импульс системы может меняться только под
действием внешних сил.
Уравнения справедливы как для ИСО так и для
НИСО (учитываются силы инерции).

6.

Закон сохранения импульса
dP
Fвнешн.
dt
Замкнутая система – система частиц, на которую не
действуют внешние силы (или их воздействие
пренебрежимо мало). (ИСО)
Закон сохранения импульса – фундаментальный
закон природы:
Импульс замкнутой системы остается постоянной
величиной
P const
6

7.

Закон сохранения импульса выполняется
в случаях:
1. Система является замкнутой.
2. В незамкнутой системе сумма всех внешних сил
равна нулю
Fвнешн. 0
3.
4.
7
Fx, внешн. 0, px const
При условии, что кратковременные силы
взаимодействия в системе во много раз больше
внешних сил.

8.

Законы сохранения в механике
- фундаментальные законы природы, связанные со
свойствами пространства и времени
1. Закон сохранения импульса (однородность
пространства)
2. Закон сохранения энергии (однородность
времени)
3. Закон сохранения момента импульса
(изотропность пространства)
8

9.

Центр масс. Ц-система
Положение центра масс системы материальных точек
определяется радиус-вектором:
mi ri
rc
mi
Скорость центра масс системы:
mi i
с
mi
Импульс системы:
9
P
mi
P m c

10.

Центр масс
Уравнение движения центра масс:
d с dP
m
Fвнешн
dt
dt
Центр масс любой системы движется так, как если
бы вся масса системы была сосредоточена в одной
точке и к ней были бы приложены все внешние
силы.
10

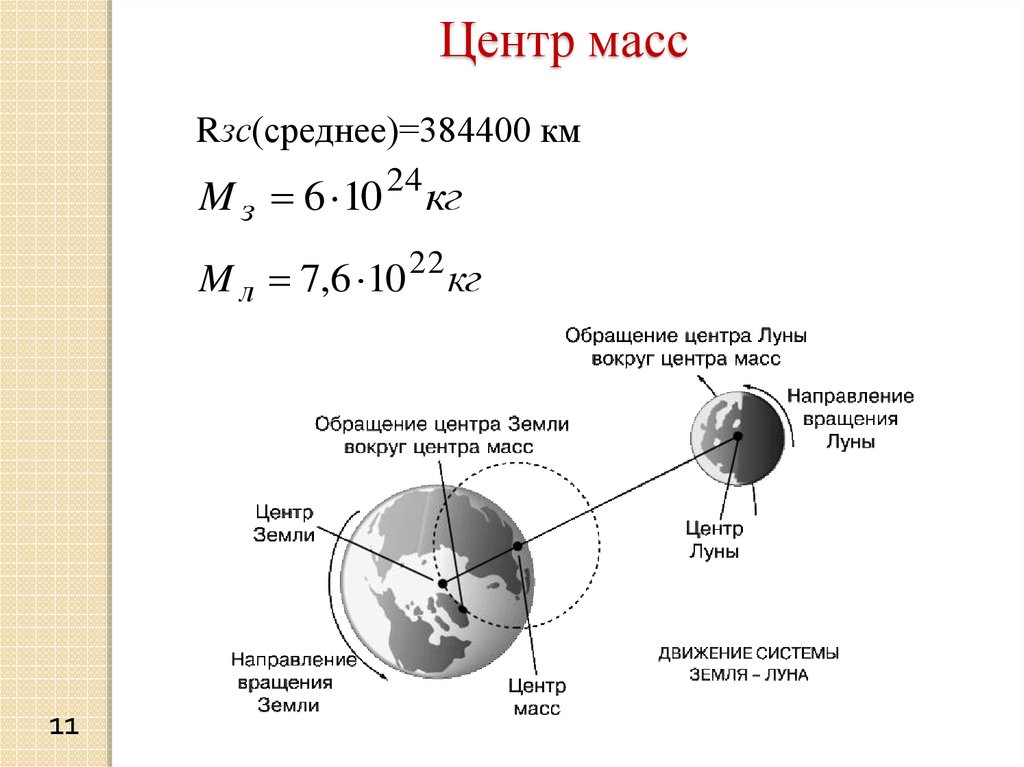
11.

Центр масс
Rзс(среднее)=384400 км
M з 6 10
24
кг
M л 7,6 10 22 кг
11

12.

Ц-система
- Система отсчета, жестко связанная с центром масс
системы и перемещающаяся поступательно по
отношению к инерциальным системам (центр масс
неподвижен).
Полный импульс частиц, входящих в Ц-систему,
всегда равен нулю
с 0 P 0
12

13.

Реактивное движение
- движение тела, возникающее при отделении некоторой
его части с определенной скоростью относительно тела.
При этом возникает т.н. реактивная сила, сообщающая
телу ускорение.
Из истории: первые пороховые фейерверочные и
сигнальные ракеты были применены в Китае в 10 веке.
Живые «ракеты»: осьминоги, кальмары, каракатицы,
медузы используют для плавания отдачу выбрасываемой
струи воды.
13

14.

Реактивное движение. Движение тела
переменной массы.
Уравнение Мещерского:
d
dm
m
F
u
dt
dt
u
14
– скорость отделяемого или присоединяемого вещества
относительно рассматриваемого тела;
dm/dt – скорость изменения массы тела;
dm
u – реактивная сила;
dt
F – сумма сил, действующих на тело со стороны других
тел или силового поля.

15.

Уравнение Мещерского.
d
dm
m
F
u
dt
dt
1) u=0, R=0. Масса присоединяется или отсоединяется
без скорости относительно тела (движение платформы,
из которой высыпается песок).
d
m(t )
F
dt
...
15
F
m0
(t ) ln
m0 t

16.

Уравнение Мещерского.
d
dm
m
F
u
dt
dt
2) u = -υ. Присоединяемая или отсоединяемая масса
неподвижна в выбранной системе отсчета. (Движение
платформы, нагружаемой песком)
d (mv )
F
dt
...
16
Ft
(t )
m0 t

17.

Движение ракеты
Ракета движется в отсутствии внешнего силового поля
так, что скорость отделяемого горючего относительно
ракеты равна u. Найти зависимость скорости ракеты от ее
массы. Масса ракеты в начальный момент времени m0.
d
dm
m
F
u
dt
dt
F 0
...
17
m0
u ln
m
Формула Циолковского

18.

Движение ракеты
Ракета движется во внешнем силовом поле так, что
скорость отделяемого горючего относительно ракеты
равна u. Найти зависимость скорости ракеты от ее массы.
Масса ракеты в начальный момент времени m0.
d
dm
m
F
u
dt
dt
F mg
...
18
m0
u ln
gt
m