Теорема об изменении импульса механической системы

1. ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ. ДИНАМИКА

ЛЕКЦИЯ №8
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
ИМПУЛЬСА МЕХАНИЧЕСКОЙ
СИСТЕМЫ

2. ПЛАН ЛЕКЦИИ

Понятие импульса механической системы
Теорема об изменении импульса системы
Закон сохранения импульса системы
ЦЕЛЬ ЛЕКЦИИ
Ознакомиться с теоремой изменения
импульса МС и примерами ее практического
применения.
2
План и цель лекции.

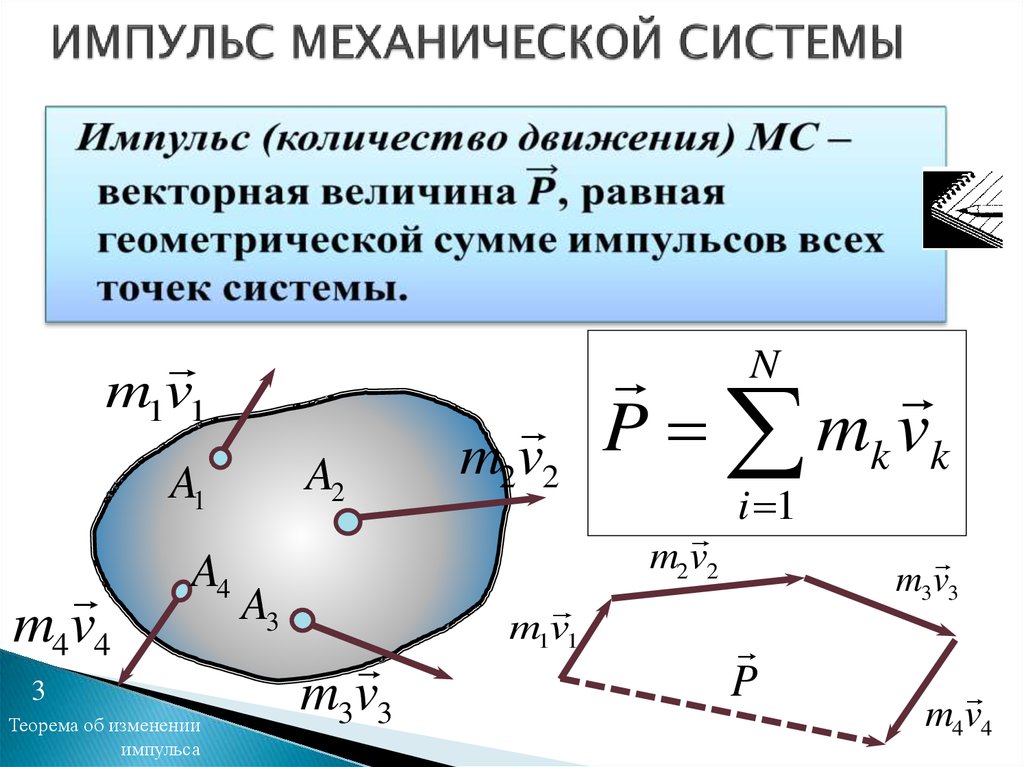
3. ИМПУЛЬС МЕХАНИЧЕСКОЙ СИСТЕМЫ

Понятие импульса механической
системы (МС)
m1v1
A2
A1
m4v4
A4
3
Теорема об изменении
импульса
m2v2
N
P mk vk
m2v2
A3
m3v3
m1v1
i 1
m3v3
P
m4v4

4. ФОРМУЛА ИМПУЛЬСА МС

По определению можно
вывести формулу, по которой значительно легче
вычислить величину P
P mk vk ,
1
rc
M
mk rk
mk rk Mrc
От этого выражения возьмем производную по времени
drk
drc
mk dt M dt
Следовательно, P Mvc
, или
mk vk Mvc
то есть
Количество движения системы равно произведению
массы всей системы на скорость её центра масс.
4
Из этого следует, что если центр масс при движении
системы остаётся неподвижным, то импульс системы
равен нулю.
Теорема об изменении
импульса

5. ПРИМЕР

Дано:
M
ω
R
С
P ?
R
Решение:
P Mv M R
P 0
5
Теорема об изменении
импульса.
В каком случае выражение
является
P M R
ответом данной задачи?

6. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ИМПУЛЬСА МС

Теорема об изменении импульса МС
Производная по времени вектора количества
движения МС равна главному вектору всех
внешних сил, действующих на систему.
dv1
dv n e i
e
i
m1
F1 F1 , ..., mn
Fn Fn
dt
dt
n
n
n
dvk
e
i
m
F
F
k
k
k
dt
k 1
k 1
k 1
e
d
mk vk F , или
dt k 1
n
6
Теорема об изменении
импульса.
dP e
F , что доказывает теорему.
dt

7. В ИНТЕГРАЛЬНОЙ ФОРМЕ:

Изменение импульса МС за некоторый
промежуток времени равно сумме импульсов
действующих на систему внешних сил за тот же
промежуток времени.
e
dP
Fk dP
dt
e
Fk dt
e
e
e
S S k Fk dt ;
t1
t1
e
dP Fk dt;
P1
P0
t0
7
Теорема об изменении
импульса.
e
P1 P0 S
t0

8. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ

Закон сохранения импульса
1. Если сумма импульсов внешних сил, действующих на
систему за некоторый промежуток времени равна нулю,
то вектор импульса системы не изменится за этот
промежуток времени.
e
Sk 0 P t1 P t0
2. Если сумма проекций импульсов внешних сил,
действующих на систему, на какую-нибудь ось равна
нулю, то проекция вектора импульса системы не
изменится за этот промежуток времени.
S
8
Теорема об изменении
импульса.
e
kx
0 Px t1 Px t0

9. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ

Следствия из дифференциальной формы
– закон
сохранения импульса:
1. Если главный вектор всех внешних сил, действующих
на систему, равен нулю, то вектор импульса системы
остаётся постоянным по величине и направлению.
e
Fk 0
P const
2. Если проекция главного вектора всех внешних сил,
приложенных к системе, на некоторую неподвижную
ось равна нулю, то проекция импульса системы на эту
ось остаётся постоянной.
F
e
kx
9
Теорема об изменении
импульса.
0
Px const

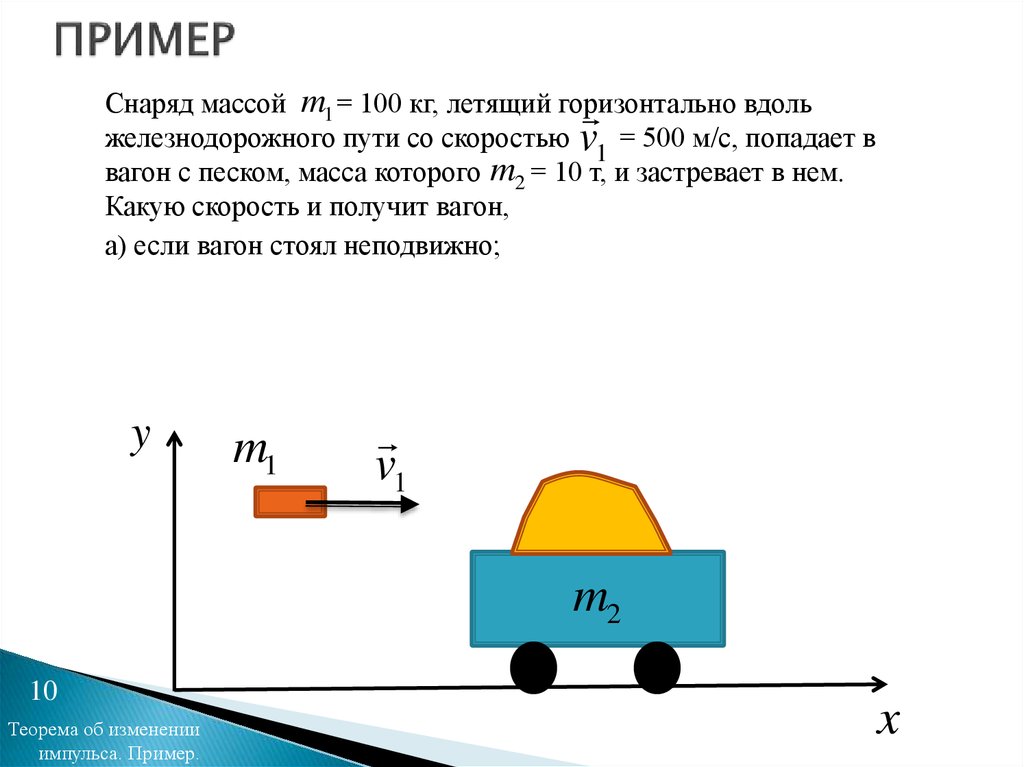
10. ПРИМЕР

Снаряд массой m1 = 100 кг, летящий горизонтально
вдоль
железнодорожного пути со скоростью v1 = 500 м/с, попадает в
вагон с песком, масса которого m2 = 10 т, и застревает в нем.
Какую скорость и получит вагон,
а) если вагон стоял неподвижно;
y
m1
v1
m2
10
Теорема об изменении
импульса. Пример.
x

11. ПРИМЕР

Закон сохранения импульса в данном случае имеет вид
m1v1 m2v2 (m1 m2 )u
а) Будем считать удар абсолютно неупругим, тогда в проекции на
горизонтальную ось по закону сохранения импульса:
m1v1
500 *100
u
4,95( м / с)
(m1 m2 ) 10000 100
y
m1
v1
u
m2
11
Теорема об изменении
импульса. Пример.
x

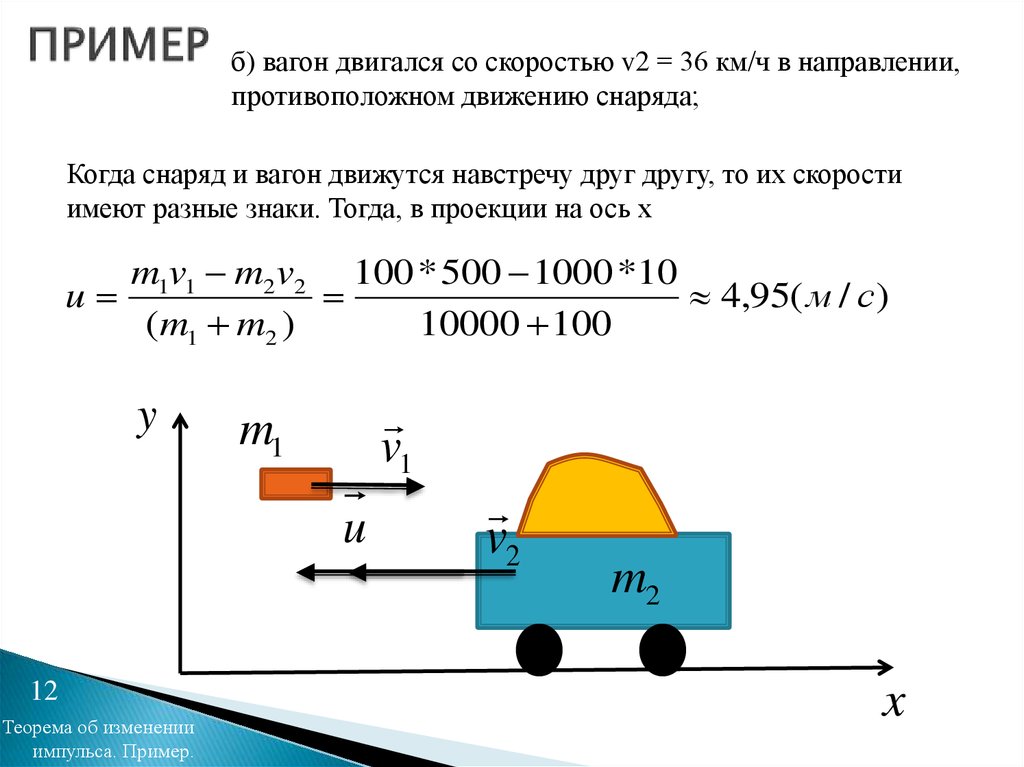
12. ПРИМЕР

б) вагон двигался со скоростью v2 = 36 км/ч в направлении,
противоположном движению снаряда;
Когда снаряд и вагон движутся навстречу друг другу, то их скорости
имеют разные знаки. Тогда, в проекции на ось х
m1v1 m2 v2 100 * 500 1000 *10
u
4,95( м / с)
(m1 m2 )
10000 100
y
v1
m1
u
12
Теорема об изменении
импульса. Пример.
v2
m2
x

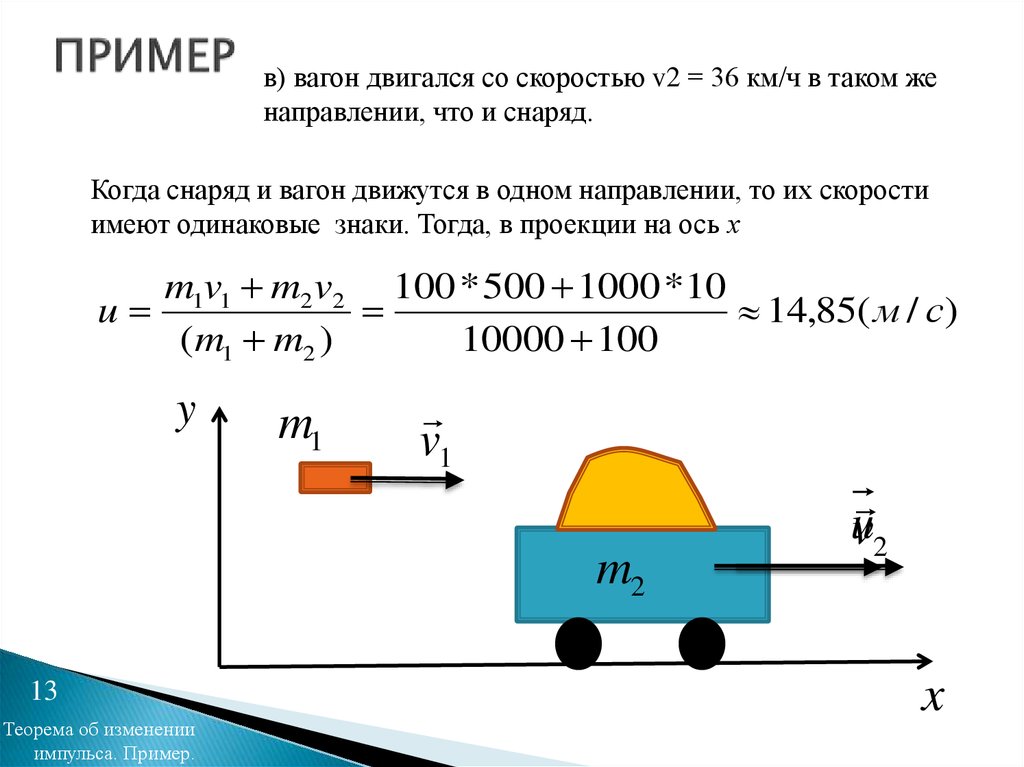
13. ПРИМЕР

в) вагон двигался со скоростью v2 = 36 км/ч в таком же
направлении, что и снаряд.
Когда снаряд и вагон движутся в одном направлении, то их скорости
имеют одинаковые знаки. Тогда, в проекции на ось х
m1v1 m2 v2 100 * 500 1000 *10
u
14,85( м / с)
(m1 m2 )
10000 100
y
m1
v1
m2
13
Теорема об изменении
импульса. Пример.
uv2
x

14. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ТЕОРЕМЫ.

14
Применение теоремы об
изменении импульса

15. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ТЕОРЕМЫ

Пример: тело переменной массы
Почему двигается
самолет?
15
Реактивное движение
От чего оттолкнуться в
космосе?

16. РЕАКТИВНОЕ ДВИЖЕНИЕ

Реактивное движение
«Земля — это колыбель разума, но нельзя вечно
жить в колыбели.»
К.Э.Циолковский
Движение тела, возникающее вследствие
отделения от него части его массы с некоторой
скоростью, называют реактивным.
16
Реактивное движение

17. ПРИМЕРЫ РЕАКТИВНОГО ДВИЖЕНИЯ

Устройство ракеты
17
Реактивное движение

18. ЗАПУСК РАКЕТЫ

18
Реактивное движение

19. ДВИЖЕНИЕ РАКЕТЫ

Уравнение движения ракеты
U
M
dm
dP Mdv UdM
19
e dM
dv
M
Fk U
dt
dt
Движение ракеты
e
dP
Fk
dt
dP Mdv Udm
e
dP
dv
dM
M
U
Fk
dt
dt
dt
dM
FR U
dt

20. ФОРМУЛА МЕЩЕРСКОГО

Уравнение движения ракеты
e
dv
M
Fk FR
dt
FR - реактивная сила
20
Формула мещерского
Иван Всеволодович
Константин Эдуардович
Мещерский
Циолковский

21. ФОРМУЛА ЦИОЛКОВСКОГО

Уравнение движения ракеты
dM
dv
dM
M
U
U
U
dt
dt
dt
dv
M
FR
dt
Mdv UdM
vk
dM
dv U
M
MK
dM
v dv U M M
0
0
vk v0 U ln( M K ) ln( M 0 )
21
Формула Циолковского
U
M
dm
vk v0 U ln( M 0 / M K )