Теорема об изменении кинетической энергии системы

1.

Новосибирский Государственный Архитектурно-Строительный
Университет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
ДИНАМИКА
ЛЕКЦИЯ №10
ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КИНЕТИЧЕСКОЙ ЭНЕРГИИ
СИСТЕМЫ
Кафедра теоретической механики

2.

План лекции:
•Введение
•Теорема об изменении кинетической
энергии для механической системы
•Кинетическая энергия системы. Теорема
Кёнига
•Кинетическая энергия твердого тела
•Закон сохранения полной механической
энергии материальной системы
•Пример решения задачи

3. Цель лекции:

Ознакомиться с теоремой об изменении
кинетической энергии системы.
Научится считать кинетическую энергии и
работу для ряда специальных случаев.

4.

Теорема об изменении кинетической энергии
для точки
F
T2 T1 A12
1
2
T mv2 / 2 - кинетическая энергия точки
A12 A12 Fi , A12 Fi A Fi – работа силы Fi
i
S12
на перемещении S12
A F(s) ds F(s) ds cos – элементарная работа

5.

Запишем теорему об изменении кинетической энергии
для каждой точки системы состоящей из n точек
Tk 2 Tk1 Ake12 Aki 12 , k 1...n
Tk1 , Tk 2 – кинетическая энергия k-й точки в начальном и в
конечном положениях системы
Ake12 – работа внешних сил системы, приложенных к точке
системы с номером k
Aki 12 – работа внутренних сил системы, приложенных к той же
точке
Складывая между собой правые и левые части этих равенств,
имеем
T2 T1 A A
e
12
i
12

6.

Теорема об изменении кинетической энергии
для системы точек
T2 T1 A A
e
12
mk vk2
T
2
k 1
i
12
n
- кинетическая энергия системы
A12e - работа внешних сил системы
A12i - работа внутренних сил системы
Изменение кинетической энергии системы
точек на некотором перемещении равно
сумме работ внешних и внутренних сил
системы на этом же перемещении

7.

Кинетическая энергия системы. Теорема Кёнига
z1
O1
x1
Mk
z2
rk O
r x2
k
y2
O
y1
Пусть Mk одна из точек материальной
системы
Введем подвижную систему координат
Ox2y2z2 перемещающуюся поступательно
относительно неподвижной системы
координат O1x1y1z1
Для произвольной k-й точки нашей
системы
rk rO k
vk vO vkr
n
2
1 n
1
2
T mk vk mk vk
2 k 1
2 k 1
n
2 1 n
1 n
1 n
2
T mk vO vkr mk vO mk vO vkr mk vkr2
2 k 1
2 k 1
2 k 1
k 1
n
1 2 n
1 n
vO mk vO mk vkr mk vkr2
2 k 1
2 k 1
k 1

8.

n
1 2 n
1 n
2
T vO mk vO mk vkr mk vkr
2 k 1
2 k 1
k 1
n
M mk
- масса системы
k 1
1
vCr
M
- скорость центра масс С относительно
mk vkr
n
k 1
подвижной системы отсчета Ox2y2z2
1 n
TOr mk vkr2 - кинетическая энергия относительного
2 k 1
движения
1
2
T MvO MvO vCr TOr
2

9.

1
2
T MvO MvO vCr Tr
2
Если начало подвижных осей О совпадает с центром масс С
системы, то vO vC , vCr 0
1
T MvC2 TCr
2
Теорема Кёнига: кинетическая энергия системы
материальных точек равна сумме кинетической
энергии поступательного движения системы
вместе с центром масс, и кинетической энергии
движения системы относительно центра масс

10.

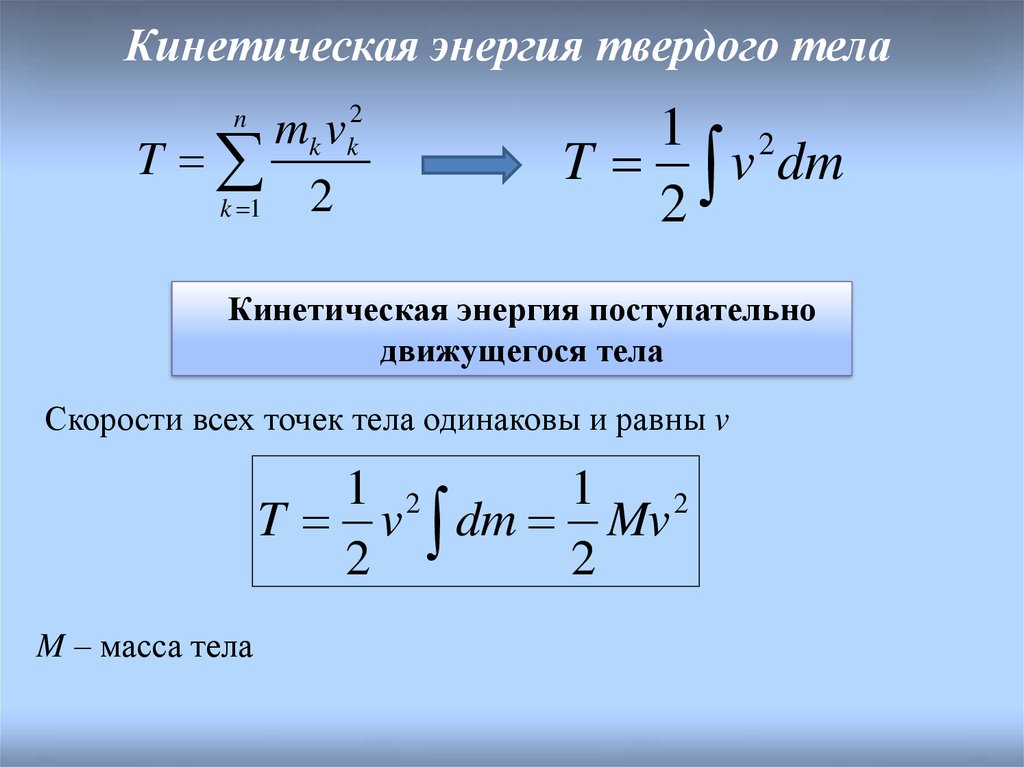
Кинетическая энергия твердого тела
n
mk v
T
2
k 1
2
k
1 2
T v dm
2
Кинетическая энергия поступательно
движущегося тела
Скорости всех точек тела одинаковы и равны v
1 2
1
2
T v dm Mv
2
2
M – масса тела

11.

Кинетическая энергия при вращении относительно
неподвижной оси
Модуль скорости точки твердого тела
Z
h
v h
1 2
1 2 2
1
T v dm h dm I z 2
2
2
2
O
v
I z – момент инерции тела
относительно оси вращения z

12.

Кинетическая энергия твердого тела
движущегося плоскопараллельно
z1
O1
x1
Введем поступательно движущуюся
систему координат Сx2y2z2 с началом в
центре масс C тела. По теореме Кёнига
z2
C
x2
y2
y1
1
T MvC2 TCr
2
Движение тела относительно подвижной
системы координат – вращение с угловой
скоростью ω и поэтому
1
2
TCr
IC
1
1
2
T MvC I C 2
2
2
2
I C

13.

Работа силы тяжести
z
h
mg
n
n
n
k 1
k 1
k 1
e
A
k mk ghk g mk hk gMhC
hC – изменение высоты центра масс системы
Работа сил тяжести равна произведению модуля силы
тяжести, действующей на систему, на вертикальное
перемещение ее центра тяжести, взятому со знаком плюс
или минус

14.

Работа внутренних сил твердого тела
B
i
F1
i D
F2
i i
F1 и F2 – внутренние силы взаимодействия
точек B и D твердого тела
i
i
F1 F2
Теорема о проекциях:
vB cos vD cos
vB x vD x
i
i
i
i
dA
F
d
s
F
d
s
F
ds
cos
F
1
B
2
D
1
B
2 ds D cos
i
i
A
0
Сумма работ всех внутренних сил абсолютно твердого тела
на любом его перемещении равна нулю

15.

Работа силы, приложенной к твердому телу,
вращающемуся вокруг неподвижной оси
A F ds
S2
2
A M z ( F )d
1
S1
2
A M z ( F ) d
1
Если
M const , то A M 0
e
z
e
e
z

16.

Закон сохранения полной механической энергии
материальной системы
Пусть все силы (внешние и внутренние), действующие на
систему, потенциальные. Тогда работа сил при переходе из
начального положения в текущее
A Ae Ai Пн Пк
Tк Tн Ae Ai П н П к
П н Tн П к Tк
Если система движется под действием одних
консервативных сил, то сумма кинетической и
потенциальной энергий сохраняет постоянное значение

17. Пример

R
2
1
Fтр
C
P1
N
B
P2
3
P3
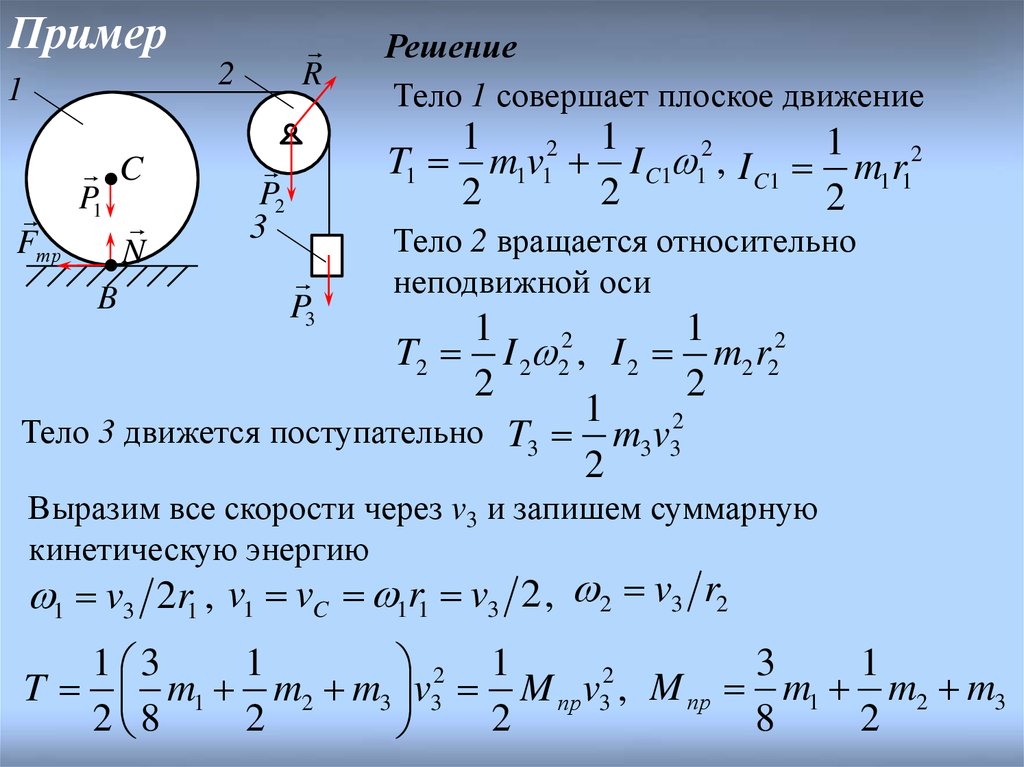
Материальная система состоит из трех тел.
Груз 3 под действием силы тяжести
опускается вниз из состояния покоя.
Определить скорость груза 3 при
опускании его на высоту h.
Массы тел m1, m2, m3. Тела 1 и 2 считать
однородными дисками с радиусами r1 и r2.
Решение
Расставим внешние силы, действующие на систему. Внутренние
силы учитывать не нужно, так как сумма их работ равна нулю.
Запишем теорему об изменении кинетической энергии системы
T T0 Ae Ai
T0 = 0 так как движение начинается из состояния покоя
T T1 T2 T3

18. Пример

R
2
1
Fтр
C
P1
N
B
Решение
Тело 1 совершает плоское движение
1
1
2
T1 m1v1 I C1 12 , I C1 1 m1r12
2
2
2
P2
3
P3
Тело 2 вращается относительно
неподвижной оси
1
1
2
T2 I 2 2 , I 2 m2 r22
2
2
1
Тело 3 движется поступательно T3 m3v32
2
Выразим все скорости через v3 и запишем суммарную
кинетическую энергию
1 v3 2r1 , v1 vC 1r1 v3 2 , 2 v3 r2
3
1
1 3
1
2 1
2
T m1 m2 m3 v3 M прv3 , M пр m1 m2 m3
8
2
2 8
2
2

19. Пример

R
2
1
Fтр
P2
3
C
P1
N
B
P3
Решение
Вычислим работы всех сил
Работа сил P2 , R равна нулю, так как
точка их приложения неподвижна
Работа силы P1 равна нулю, так как эта
сила перпендикулярна к перемещению
точки ее приложения C
Работа сил Fтр , N равна нулю, так как эти силы приложены в
мгновенном центре скоростей B катка 1
Тогда A A A( P3 ) P3h m3 gh,
e
i
v3 2m3 gh M пр
1
M прv32 m3 gh
2
2m3 gh
3
1
m1 m2 m3
8
2

20. Тема следующей лекции

Уравнения движения
твердого тела, физический
маятник