Математика на английском языке

1. Analysis

Sets
The individual objects of the set are called members or elements. Any part of a
set is called a subset of the given set. The set consisting of no elements is called
the empty set or null set.
Отдельные объекты множества называются членами или элементами.
Любая часть множества называется подмножеством данного множества.
Множество, не содержащее элементов, называется пустым множеством.
object
member
element
subset
given
empty
null
объект
член
элемент
подмножество
данный
пустой
нуль
1

2. Real Numbers

The number system based on the symbols 1, 2, 3, 4, 5, 6, 7, 8, 9, 0 is called a base
ten system.
357 7 10 5 10 3 10
0
1
2
9
7
2
.972 1 2 3
10 10 10
Система счисления, основанная на символах, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0
называется десятичной системой счисления.
real
based
symbol
base
real
based
symbol
действительный
основанный
символ
основание
действительный
основанный
символ
2

3. Natural numbers

1. Natural numbers 1, 2, 3, 4, . . . , also called positive integers, are used in counting
members of a set. The sum a + b and product a・b or ab of any two natural numbers a and b
is also a natural number. The set of natural numbers is closed under the operations of addition
and multiplication, or satisfies the closure property with respect to these operations.
1. Натуральные числа 1, 2, 3, 4,..., называемые также положительными целыми,
используются при подсчете членов множества. Сумма а + b и произведение а · b или аb
любых двух натуральных чисел а и b также натуральное число. Множество
натуральных чисел замкнуто относительно операций сложения и умножения, или
удовлетворяет свойству замкнутости относительно этих операций.
natural
positive
integer
count
operation
closure
property
with respect to
натуральный
положительный
целый
считать
операция
замкнуьый
свойство
по отношению к
3

4. Integer numbers

2. Negative integers and zero, denoted by –1, –2, –3, . . . , and 0, respectively, arose to
permit solutions of equations such as x + b = a, where a and b are any natural numbers. This
leads to the operation of subtraction, or inverse of addition, and we write x = a – b. The set of
positive and negative integers and zero is called the set of integers.
2. Отрицательные числа и ноль, обозначаемые -1, -2, -3,..., , и 0, соответственно,
возникли для обеспечения решения уравнений, таких как x + b = a, где а и b – любые
натуральные числа. Это приводит к операции вычитания или обращению сложения, и
мы пишем x = a – b. Множество положительных и отрицательных чисел и нуля,
называется множеством целых чисел.
.
negative
arose
permit
lead
subtraction
отрицательный
возникать
позволять
вести
вычитание
4

5. Rational numbers

3. Rational numbers or fractions such as 2/3 , 5/4, . . . arose to permit solutions of equations such as bx
= a for all integers a and b, where b _ 0. This leads to the operation of division, or inverse of
multiplication, and we write x = a/b or a ÷ b, where a is the numerator and b the denominator. The set of
integers is a subset of the rational numbers, since integers correspond to rational numbers where b = 1.
3. Рациональные числа или дроби, такие как 2/3 , 5/4, . . ., возникли, чтобы позволить решения
уравнений, таких как bx = a для всех целых чисел а и b, где b _ 0. Это приводит к операции
деления, или обращения умножения, и мы пишем x = a/b или a ÷ b, где a, где а – числитель и b –
знаменатель. Множество целых чисел есть подмножество рациональных чисел, так как целые
числа соответствуют рациональным числам, в которых b = 1.
.
rational
fractions
division
numerator
denominator
рациональный
дробь
деление
числитель
знаменатель
5

6. Irrational numbers

and π are numbers which are not rational; i.e.,
they cannot be expressed as a/b (called the quotient of a and b), where a and b are
integers and b 0. The set of rational and irrational numbers is called the set of real
numbers.
4. Irrational numbers such as
2
4. Иррациональные числа, такие как
и π – числа, которые не являются
рациональными; т.е. они не могут быть выражены в виде a/ b (называемому
частным а и b), где а и b целые и b 0. Множество рациональных и
иррациональных чисел называется множеством действительных чисел
.
irrational
express
quotient
2
иррациональный
выражать
частное
6

7.

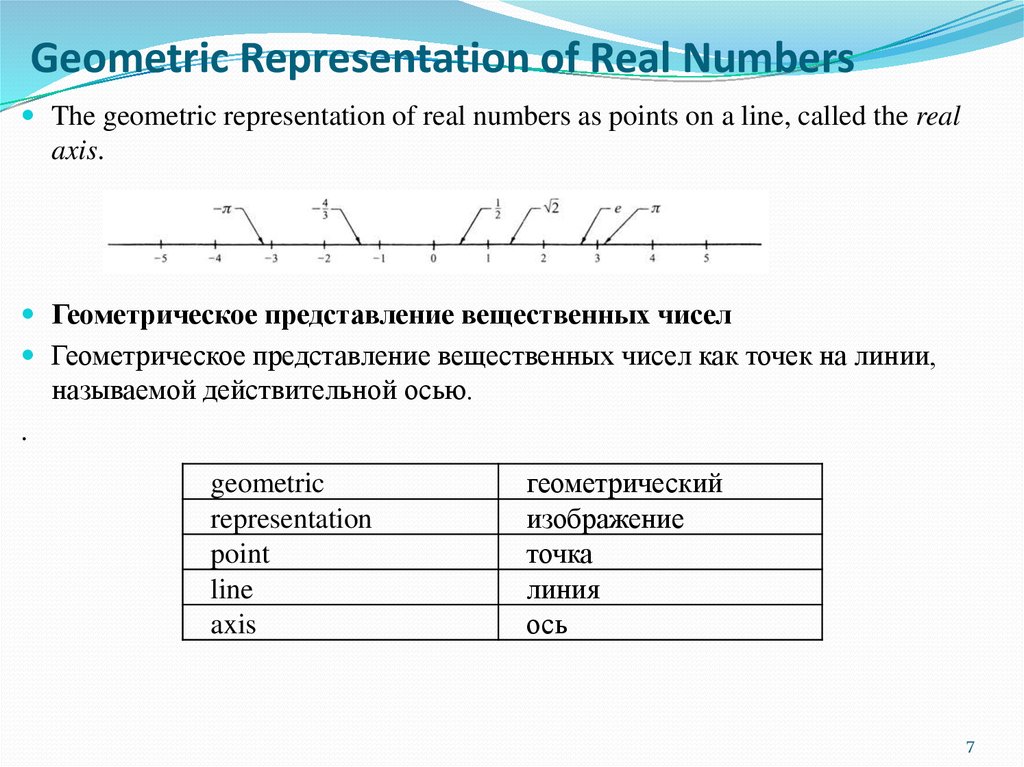
Geometric Representation of Real Numbers
The geometric representation of real numbers as points on a line, called the real
axis.
Геометрическое представление вещественных чисел
Геометрическое представление вещественных чисел как точек на линии,
называемой действительной осью.
.
geometric
representation
point
line
axis
геометрический
изображение
точка
линия
ось
7

8.

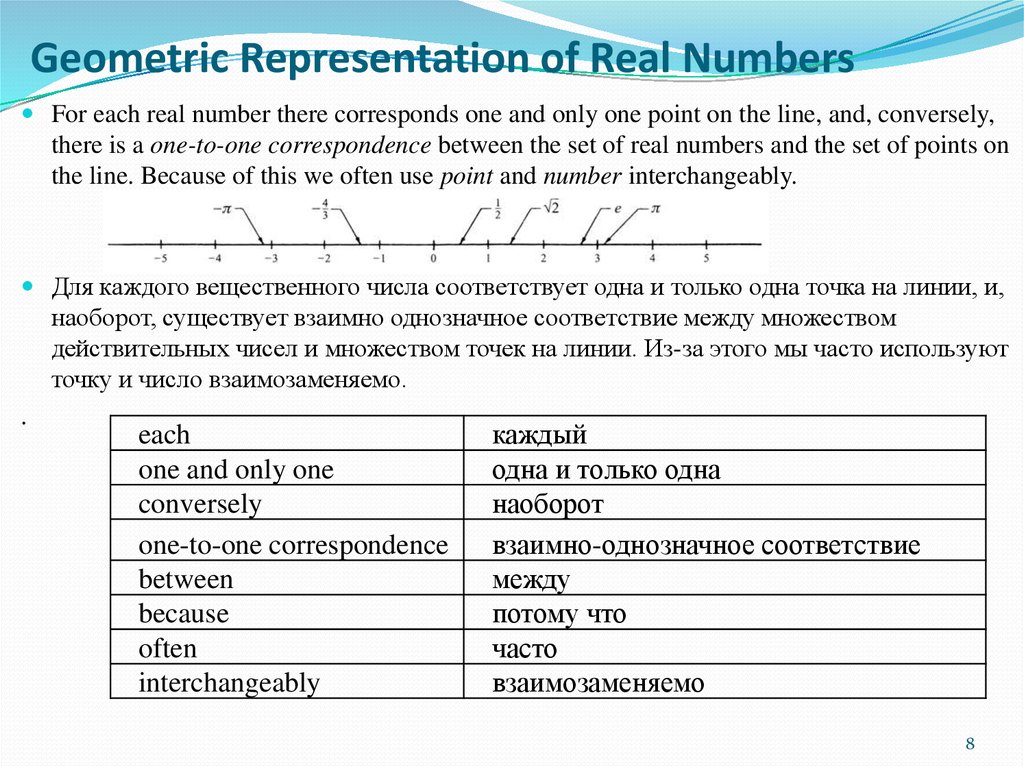
Geometric Representation of Real Numbers
For each real number there corresponds one and only one point on the line, and, conversely,
there is a one-to-one correspondence between the set of real numbers and the set of points on
the line. Because of this we often use point and number interchangeably.
Для каждого вещественного числа соответствует одна и только одна точка на линии, и,
наоборот, существует взаимно однозначное соответствие между множеством
действительных чисел и множеством точек на линии. Из-за этого мы часто используют
точку и число взаимозаменяемо.
.
each
one and only one
conversely
one-to-one correspondence
between
because
often
interchangeably
каждый
одна и только одна
наоборот
взаимно-однозначное соответствие
между
потому что
часто
взаимозаменяемо
8

9.

Geometric Representation of Real Numbers
The set of real numbers to the right of 0 is called the set of positive numbers, the set
to the left of 0 is the set of negative numbers, while 0 itself is neither positive nor
negative.
Множество действительных чисел справа от 0 называется множеством
положительных чисел, множество слева от 0 – множеством отрицательных
чисел, в то время как 0 само по себе не является ни положительным, ни
отрицательным
.
to the right of …
to the left of …
neither … nor
справа от …
слева от …
ни … ни…
9

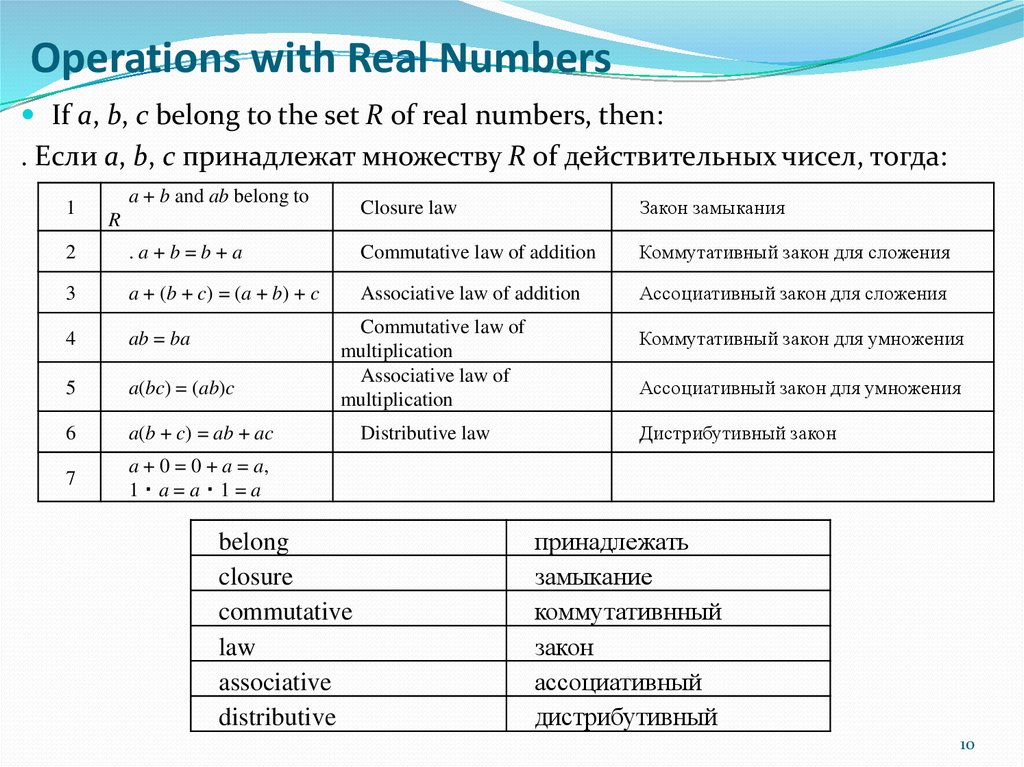
10. Operations with Real Numbers

If a, b, c belong to the set R of real numbers, then:
. Если a, b, c принадлежат множеству R of действительных чисел, тогда:
1
a + b and ab belong to
R
Closure law
Закон замыкания
2
.a+b=b+a
Commutative law of addition
Коммутативный закон для сложения
3
a + (b + c) = (a + b) + c
Associative law of addition
Ассоциативный закон для сложения
4
ab = ba
5
a(bc) = (ab)c
6
a(b + c) = ab + ac
7
a + 0 = 0 + a = a,
1・a = a・1 = a
Commutative law of
multiplication
Associative law of
multiplication
belong
closure
commutative
law
associative
distributive
Distributive law
Коммутативный закон для умножения
Ассоциативный закон для умножения
Дистрибутивный закон
принадлежать
замыкание
коммутативнный
закон
ассоциативный
дистрибутивный
10

11. Inequalities

If a – b is a nonnegative number, we say that a is greater than or equal to b or b is less than
or equal to a, and write, respectively, a > b or b < a. If there is no possibility that a = b, we
write a > b or b < a. Geometrically, a > b if the point on the real axis corresponding to a lies
to the right of the point corresponding to b.
Неравенства
Если a – b неотрицательное число, мы говорим, что a больше или равно b или b is
меньше или равно a, и пишем, соответственно, a > b или b < a. Если невозможно, что a
= b, мы пишем a > b или b < a. Геометрически, a > b если точка на действительной оси,
соответствующая a лежит справа от точки, соответствующей b.
inequality
nonnegative
great
greater than or equal
less than or equal
lie
inequality
неравенство
неотрицательный
большой
больше или равно
меньше или равно
лежать
неравенство
11

12. Absolute Value of Real Numbers

The absolute value of a real number a, denoted by |a|, is defined as a if a > 0, – a if a < 0, and
0 if a = 0.
The distance between any two points (real numbers) a and b on the real axis is |a–b| = |b–a|.
Абсолютное значение действительных чисел
Абсолютное значение действительного числа a, обозначаемое |a|, определяется как a
если a > 0, – a если a < 0, и 0 если a = 0.
Расстояние между двумя точками (действительными числами) a и b на действительной
оси есть |a–b| = |b–a|.
absolute
distance
абсолютный
расстояние
12

13. Exponents and Roots

The product a・ a . . . a of a real number a by itself p times is denoted by ap, where p is
called the exponent and a is called the base.
If ap = N, where p is a positive integer, we call a a pth root of N, written
p
If p and q are positive integers, we define a p / q
.
q
a
p
N
Показатели и корни
Произведение a・ a . . . a действительного числа a на себя p обозначают ap, где p
называют показателем и a называют основанием.
Если ap = N, где p положительное число, мы называем a a p-ым корнем из N, пишется
p
N
Если p и q положительные целые, мы определяем a p / q
exponent
root
itself
base
q
ap .
показатель
корень
себя
основание
13

14. Logarithms

If ap = N, p is called the logarithm of N to the base a, written p = loga N. If a and N
are positive and a 1, there is only one real value for p.
Логарифмы
Если ap = N, p называют логарифмом N по основанию a, пишется p = loga N.
Если a и N положительны и a 1, существует только одно действительное
значение для p.
.
logarithm
логарифм
14

15. Logarithms

In practice, two bases are used: base a = 10, and the natural base a = e = 2.71828. . . . The
logarithmic systems associated with these bases are called common and natural, respectively.
The common logarithm system is signified by log N; i.e., the subscript 10 is not used. For
natural logarithms, the usual notation is ln N.
На практике два основания применяют: основание a = 10, и натуральное основание a =
e = 2,71828. . . . Логарифмические системы, связанные с этими основаниями, называют
обыкновенной и натуральной, соответственно. Десятичная логарифмическая система
обозначается signified log N; то есть, нижний индекс 10 не используется. Для
натуральных логарифмов обычная запись – ln N.
.
common
общий
common logarithm
signify
natural logarithm
use
usual
notation
десятичный логарифм
обозначать
натуральный логарифм
использовать
обычный
запись
15