Similar presentations:
Геометрические характеристики плоских сечений
1.
ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»Инженерно-технический институт
Кафедра прикладной механики
Решение задач
по дисциплине «Техническая механика»
270800 - Строительство
2. Геометрические характеристики плоских сечений
3.
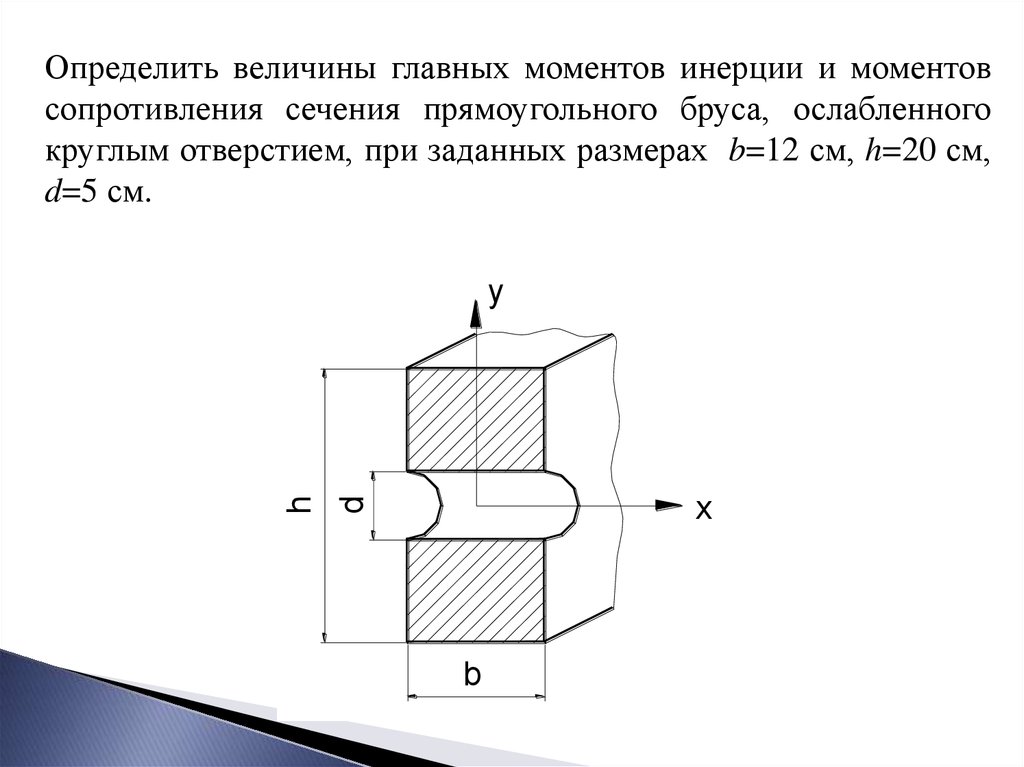
Определить величины главных моментов инерции и моментовсопротивления сечения прямоугольного бруса, ослабленного
круглым отверстием, при заданных размерах b=12 см, h=20 см,
d=5 см.
x
d
h
y
b
4.
Решение:Центральные оси x и y являются главными, так как они
являются осями симметрии сечения.
Моменты инерции относительно осей:
bh3 bd 3 12 203 12 53
I X I X1 I X 2
7875см4
12
12
12
12
bh3 db3 20 123 5 123
IY IY1 IY2
2160см4
12
12
12
12
Соответственно, моменты сопротивления:
Ix
IX
7875
Wx
787,5см3 ;
ymax h / 2
10
WY
Iy
xmax
IY
2160
360см3 .
b/2
6
5.
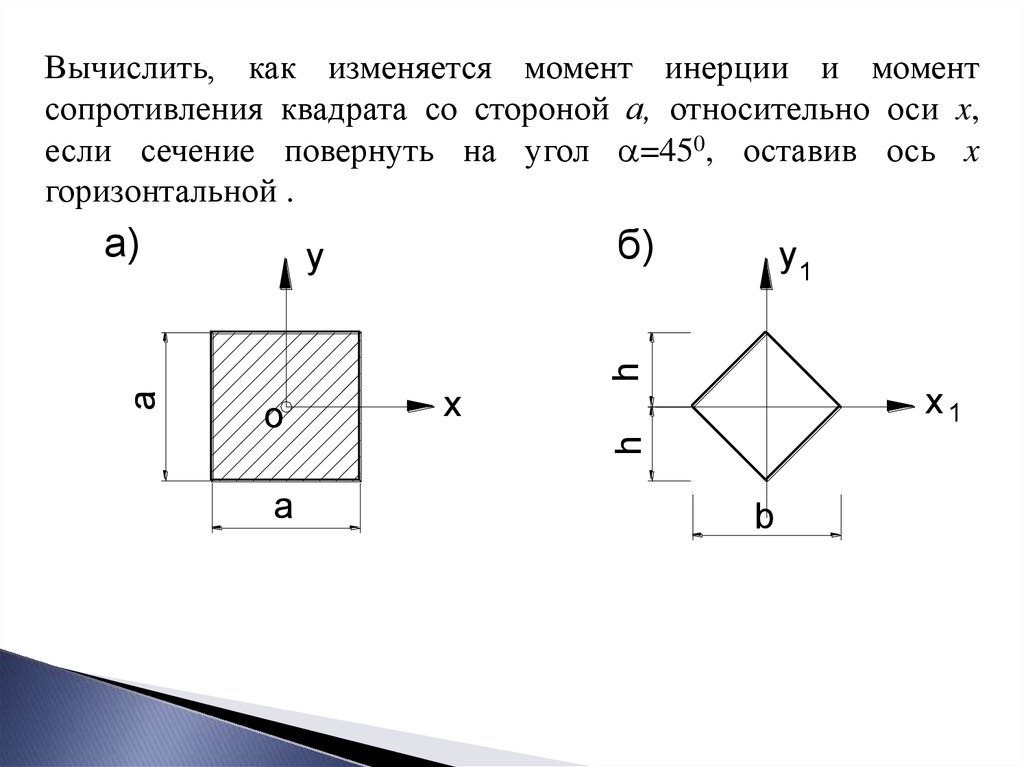
Вычислить, как изменяется момент инерции и моментсопротивления квадрата со стороной а, относительно оси x,
если сечение повернуть на угол =450, оставив ось x
горизонтальной .
а)
б)
y1
o
a
x1
x
h
a
h
y
b
6.
РешениеОсевой момент инерции и момент сопротивления
квадрата относительно оси x в положении а) будут равны:
bh 3 a a 3 a 4
IX
0,0833a 4
12
12
12
IX
a3
WX
0,16667a 3
a/2 6
Осевой момент инерции и момент сопротивления повернутого
на 450 квадрата (рис.б) относительно горизонтальной оси x1
будут равны:
3
3
bh
1,414a (0,707a)
I X1 2
2
0,0833a 4
12
12
h 0,707a.
где b 2 a Cos450 a 2 0,707 1,414a;
W X1
I X1
0,0833a 4
0,11787a 3
h
0,707a
Моменты инерции IX и IХ1 равны, т.е. не изменяются,
момент сопротивления WX1 уменьшается на 29,3%.
7.
Сравнить величины моментов инерции относительноцентральной оси x сечений прямоугольника, квадрата и круга
при условии, что площади А всех трех сечений одинаковы.
б)
x
a
в)
x
x
b
2a
a)
b
d
8.
РешениеДля сравнения величин моментов инерции, выражаем
.
их через площади сечения, так как у всех сечений площади
одинаковые.
d 2
A A( a ) a 2a 2a 2 , A A( б ) b b b 2 , A A(b )
Моменты инерции сечений относительно оси x:
I X(a)
I X (б )
I X (b)
4
a ( 2a ) 3
8 4 2 ( 2a 2 ) ( 2a 2 )
a
0,1667 Aa2 0,1667 A 2 ;
12
12
12
b b3 b4 b2 b2
0,08333 Aб2 0,08333 A 2 ;
12
12
12
d 4 d 2 d 2
1
Ab2 0,0796 A 2 .
64
4 4 4
4
Момент инерции прямоугольника больше, чем квадрата в 2
раза, а круглого сечения - в 2,1 раза. Момент инерции
квадратного сечения больше, чем круглого в 1,05 раза.
9.
Для сечений, показанных на рис., определить:•положение центра тяжести;
•вычислить осевые моменты инерции IX и IY ;
•осевые моменты сопротивления
•вычислить
осевые и центробежный момент инерции
относительно осей, повернутых на угол α а) =300
б)
=-450
в) =600 г) =-600.
5a
б)
3a
г)
в)
4a
3a
2a
1,
5a
8a
9a
9a
8a
2a
а)
5a
4a
9a
10.
РешениеСечение
а
.
Положение центра тяжести фигуры относительно оси x1:
1,5a 2
0,424. 1,5a
S x1 5a 8a 4a
2
yC
4,326a
2
A
1,5a
y0
5a 8a
y2
2
Моменты инерции фигуры относительно
2
центральных осей x0, y0:
x
5a (8a)
2
I x0
4,326a 4a (5a 8a)
12
2
3
I y0
x0
1,
5a
8a
(1,5a) 2
4
2
0,11 (1,5a)
(4,326a 0,424 1,5a )
2
168,929a 4 ;
8a (5a) 3 (1,5a) 4
81,346a 4
12
8
=30 0
1
1
3a
5a
x1
11.
Моменты сопротивлениясоответствующих точках 1 и 2.
W
(1)
x
сечения
относительно
оси
x0
в
I x0 168,929a 4
168,929a 4
( 2)
3
45,98a 3
39,05a Wx
y2
3,674a
y1
4,326a
I x0
где y1=4,326a, y2=h-y1=3,674а.
В сечении ось y0 является осью симметрии, следовательно,
.
центробежный момент инерции I x у 0
0 0
Осевые моменты инерции относительно осей x2 и y2 , повернутых на
угол =300:
I x2 I x0 Cos 2 300 I y0 Sin 2 300
168,929a 4 Cos 2 300 81,346a 4 Sin 2 300 147,033a 4
I y2 I x0 Sin 2 300 I y0 Cos 2 300
168,929a 4 Sin 2 300 81,346a 4 Cos 2 300 103,242a 4
Центробежный момент инерции относительно осей x2 и y2:
I x2 y 2
I x0 I y0
2
168,929a 4 81,346a 4
Sin 2
Sin 60 0 37,923a 4
2
12.
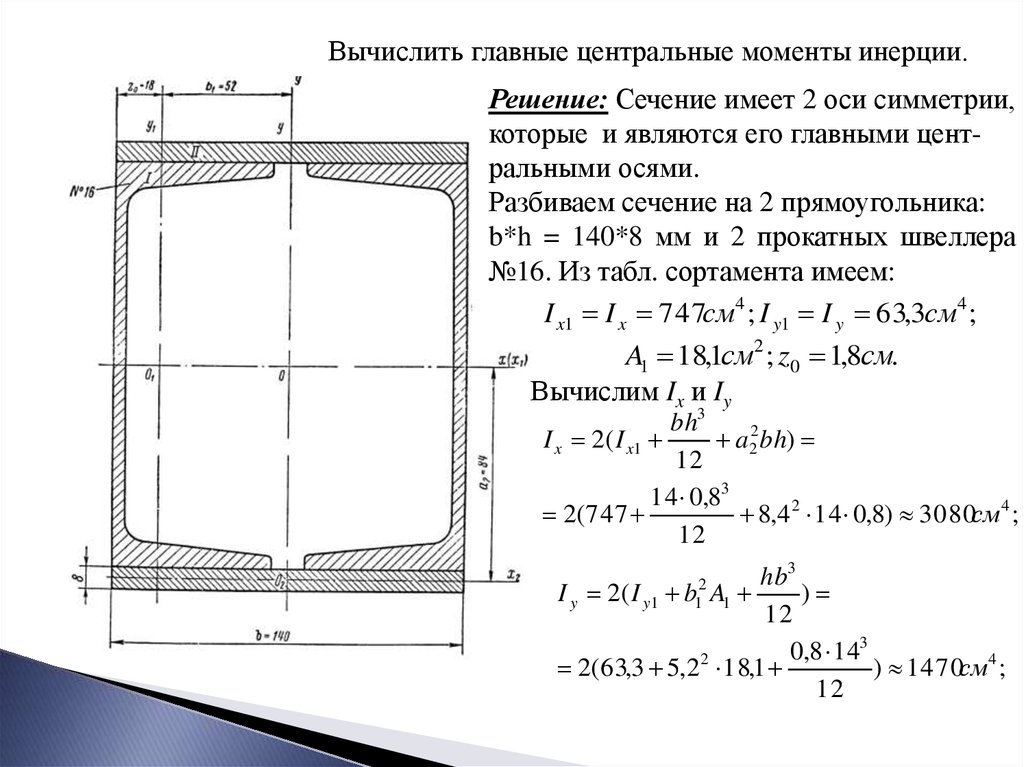
Вычислить главные центральные моменты инерции.Решение: Сечение имеет 2 оси симметрии,
которые и являются его главными центральными осями.
Разбиваем сечение на 2 прямоугольника:
b*h = 140*8 мм и 2 прокатных швеллера
№16. Из табл. сортамента имеем:
I x1 I x 747см4 ; I y1 I y 63,3см4 ;
A1 18,1см2 ; z0 1,8см.
Вычислим Ix и Iy
bh3
I x 2( I x1
a22bh)
12
14 0,83
2(747
8,4 2 14 0,8) 3080см4 ;
12
hb3
I y 2( I y1 b A
)
12
0,8 143
2
2(63,3 5,2 18,1
) 1470см4 ;
12
2
1 1
13.
Определить на каком расстоянии друг от друга нужнорасположить два швеллера №14, чтобы осевые моменты
инерции сечения были равны между собой.
у
х
а-?
а) 4,63 см
б) 20,4 см
в) 7,35 см
г) 16,0 см
14.
Определить на каком расстоянии друг от друга нужнорасположить два двутавра №20, чтобы осевые моменты
инерции сечения были равны между собой.
у
А) 20,2 см ;
В) 12,24см;
Б) 16,04см;
Г) 32,24см;
х
а-?
15.
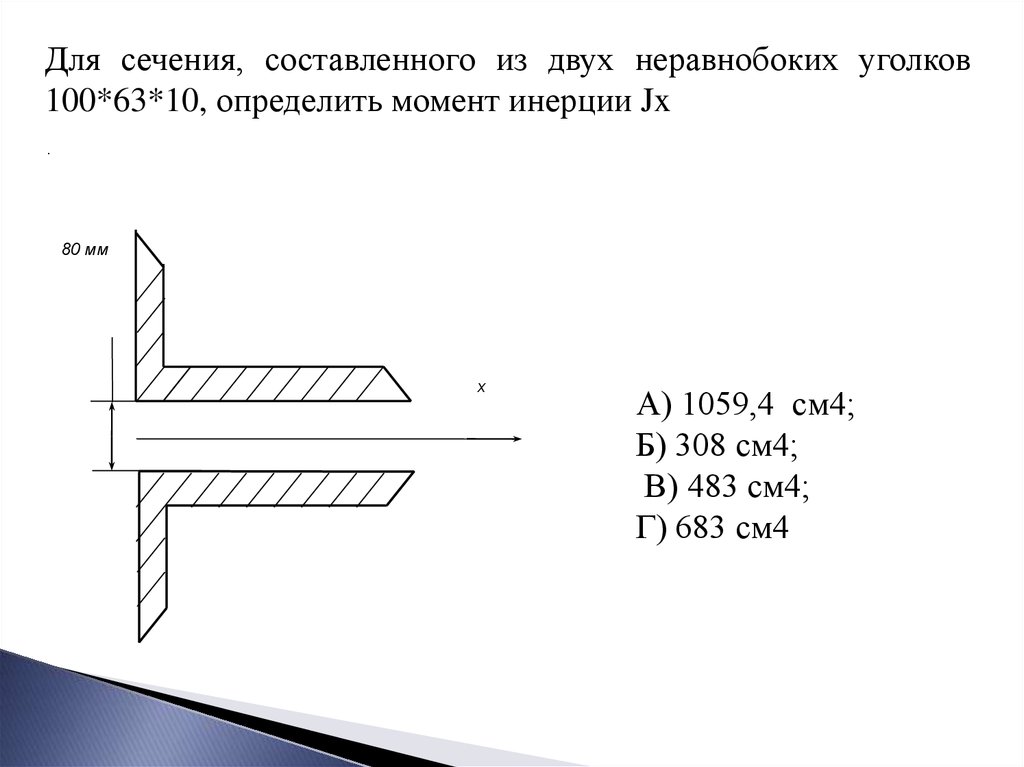
Для сечения, составленного из двух неравнобоких уголков100*63*10, определить момент инерции Jx
.
80 мм
x
А) 1059,4 см4;
Б) 308 см4;
В) 483 см4;
Г) 683 см4











 mechanics
mechanics








