Similar presentations:
Сопротивление материалов
1.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВОбзорная лекция
Тихонкин Игорь Васильевич, доцент, к.т.н.
Кафедра Теоретической и прикладной механики
Инженерного института ФГБОУ ВО Новосибирский ГАУ
2.
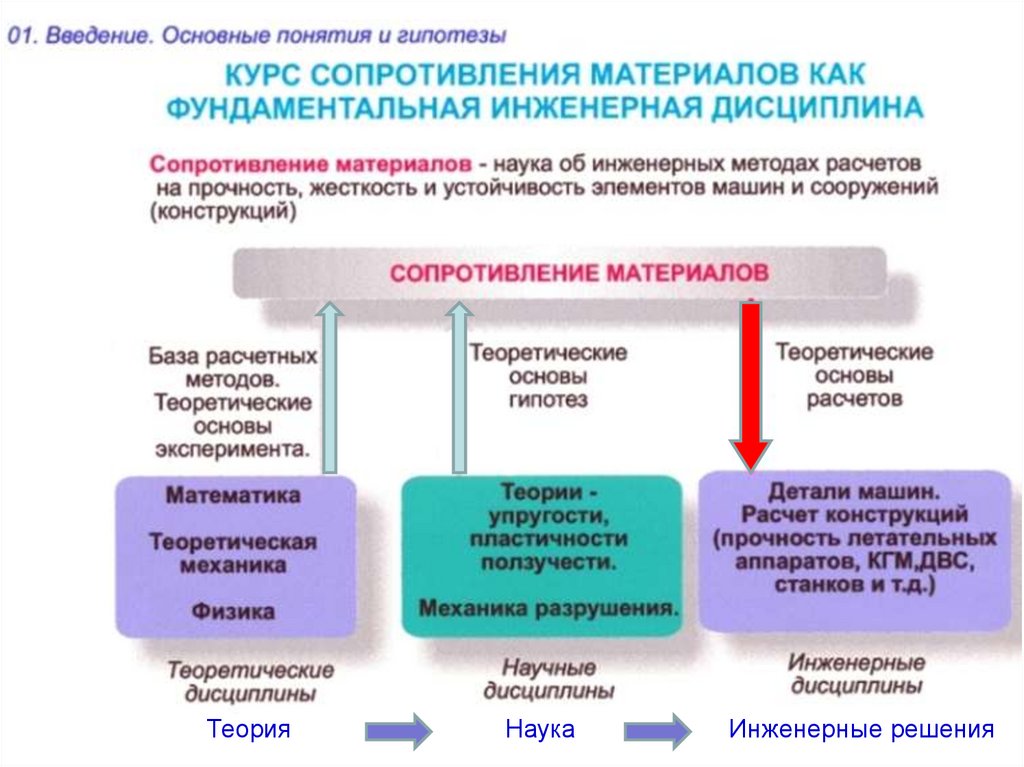
ТеорияНаука
Инженерные решения
3. Дачные домики
4. Турники
5. Грузовые эвакуаторы
6.
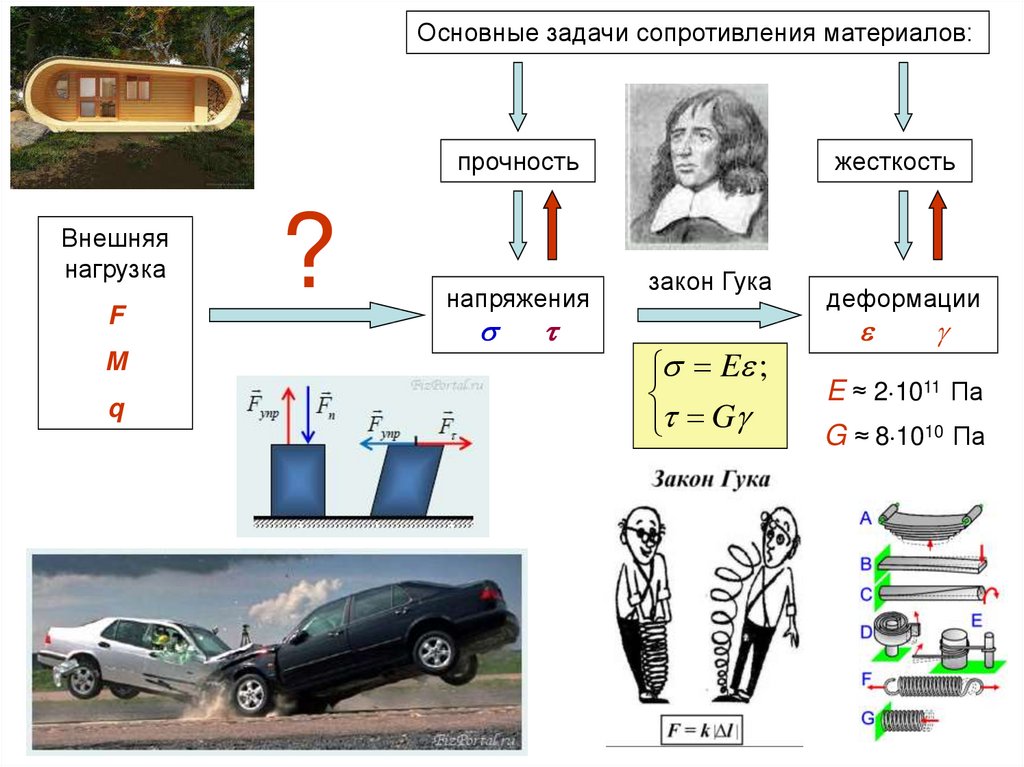
Основные задачи сопротивления материалов:прочность
Внешняя
нагрузка
F
M
q
?
напряжения
жесткость
закон Гука
E ;
G
деформации
E ≈ 2 1011 Па
G ≈ 8 1010 Па
7.
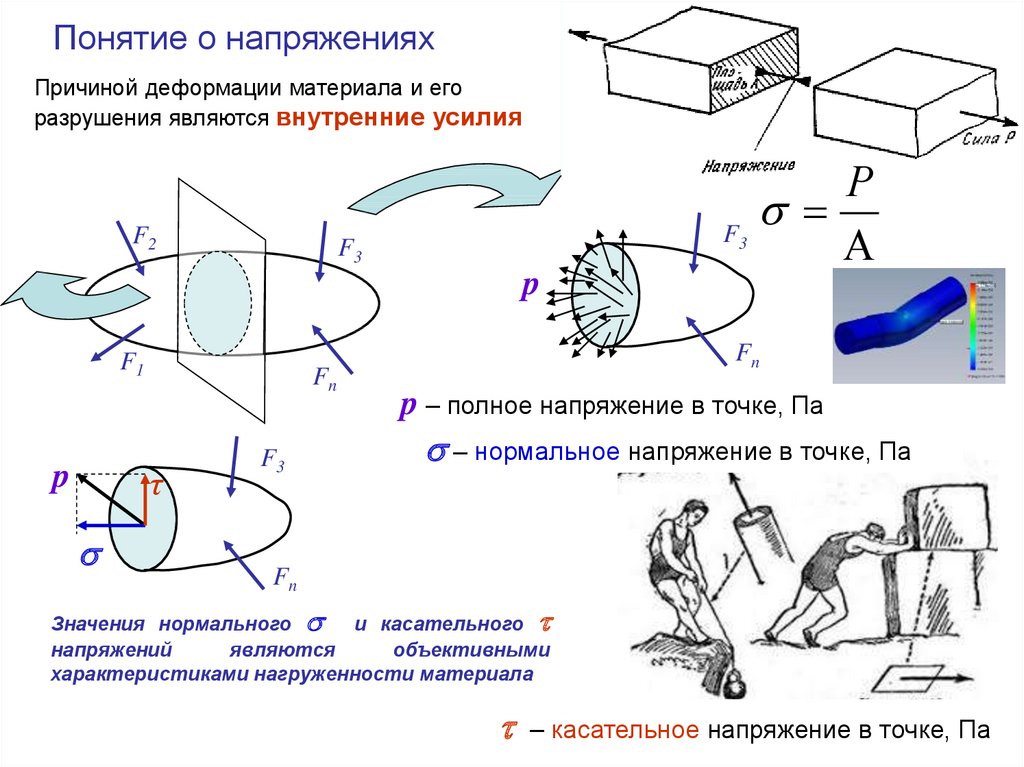
Понятие о напряженияхПричиной деформации материала и его
разрушения являются внутренние усилия
F2
F3
F3
Р
А
p
F1
p
Fn
τ
F3
Fn
p – полное напряжение в точке, Па
– нормальное напряжение в точке, Па
Fn
Значения нормального
и касательного
напряжений
являются
объективными
характеристиками нагруженности материала
– касательное напряжение в точке, Па
8.
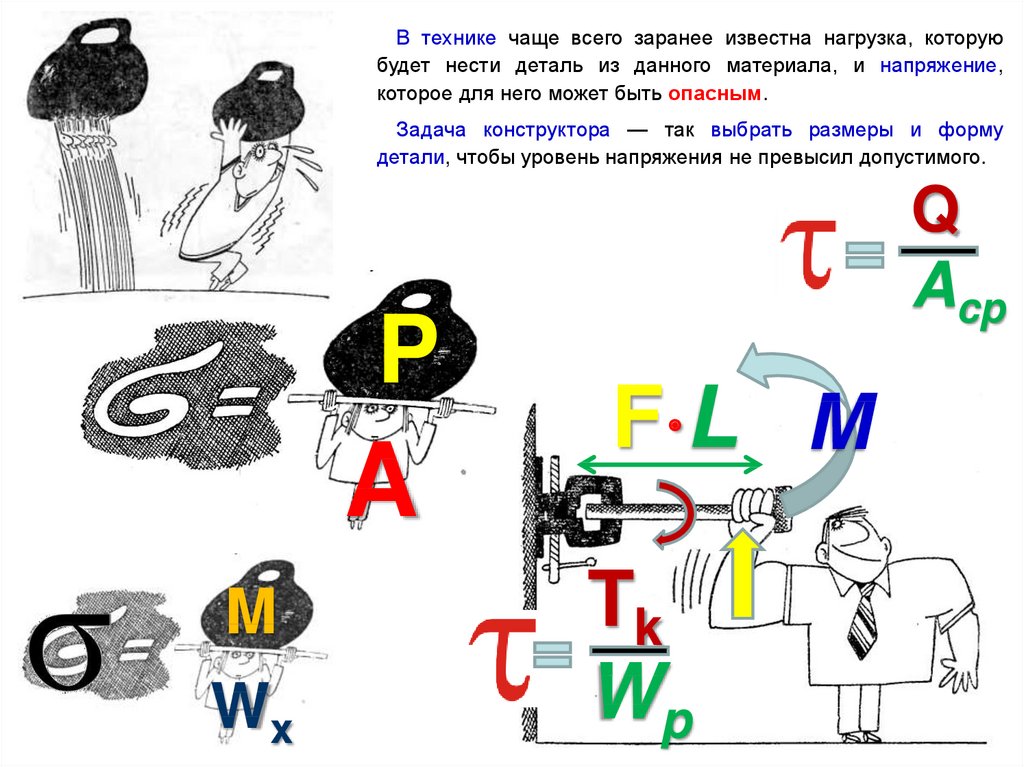
В технике чаще всего заранее известна нагрузка, которуюбудет нести деталь из данного материала, и напряжение,
которое для него может быть опасным.
Задача конструктора — так выбрать размеры и форму
детали, чтобы уровень напряжения не превысил допустимого.
P
A
M
Wx
Q
Acp
F L M
Tk
Wp
9.
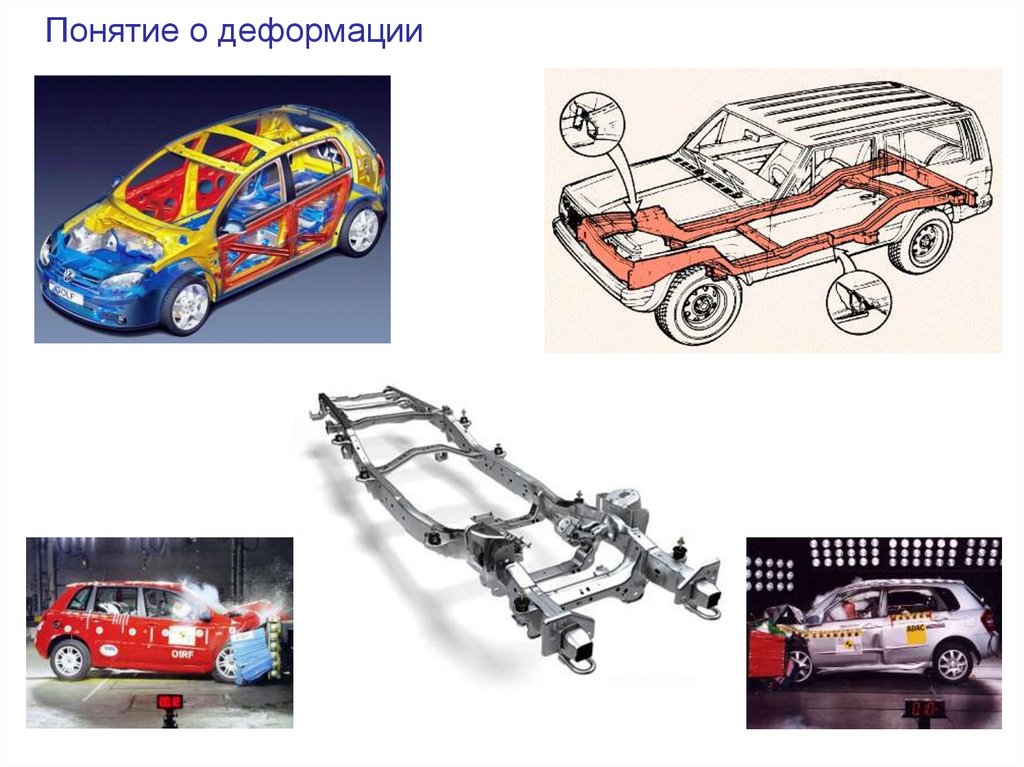
Понятие о деформации10.
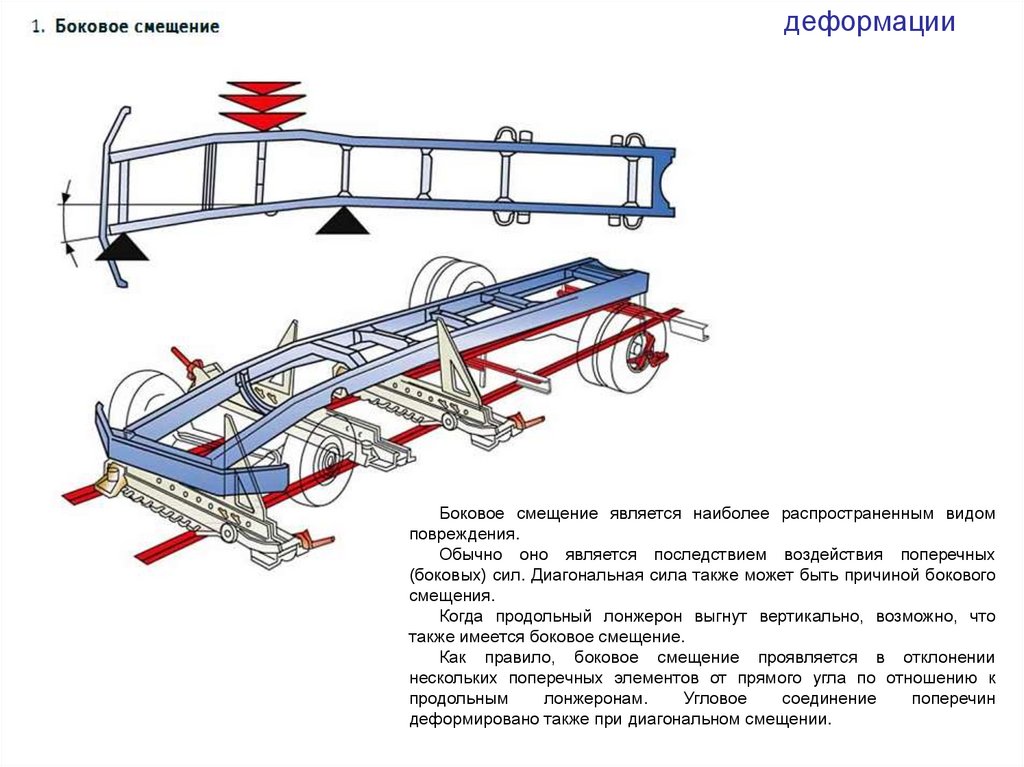
деформацииБоковое смещение является наиболее распространенным видом
повреждения.
Обычно оно является последствием воздействия поперечных
(боковых) сил. Диагональная сила также может быть причиной бокового
смещения.
Когда продольный лонжерон выгнут вертикально, возможно, что
также имеется боковое смещение.
Как правило, боковое смещение проявляется в отклонении
нескольких поперечных элементов от прямого угла по отношению к
продольным
лонжеронам.
Угловое
соединение
поперечин
деформировано также при диагональном смещении.
11.
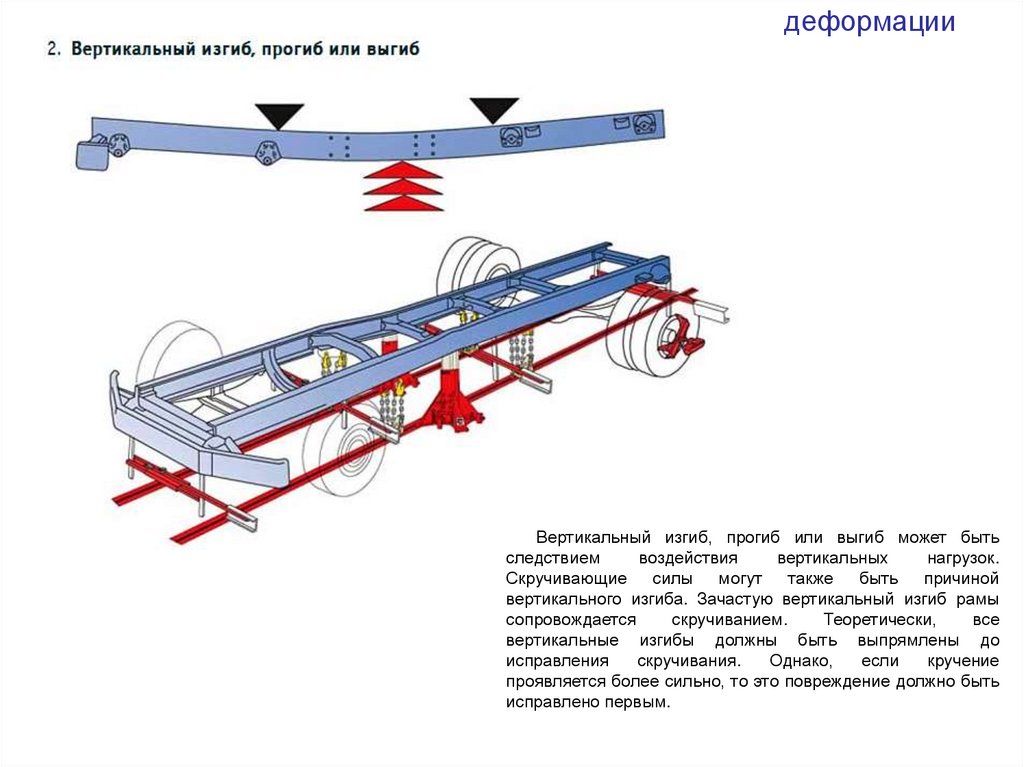
деформацииВертикальный изгиб, прогиб или выгиб может быть
следствием
воздействия
вертикальных
нагрузок.
Скручивающие
силы
могут
также быть
причиной
вертикального изгиба. Зачастую вертикальный изгиб рамы
сопровождается
скручиванием.
Теоретически,
все
вертикальные изгибы должны быть выпрямлены до
исправления
скручивания.
Однако,
если
кручение
проявляется более сильно, то это повреждение должно быть
исправлено первым.
12.
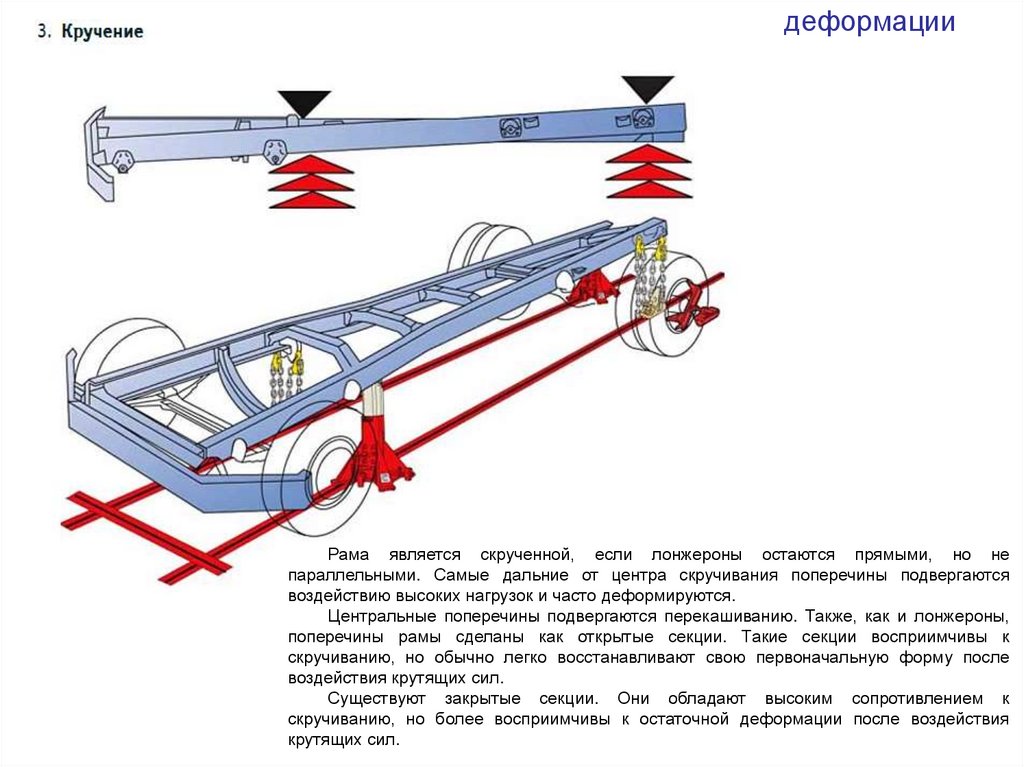
деформацииРама является скрученной, если лонжероны остаются прямыми, но не
параллельными. Самые дальние от центра скручивания поперечины подвергаются
воздействию высоких нагрузок и часто деформируются.
Центральные поперечины подвергаются перекашиванию. Также, как и лонжероны,
поперечины рамы сделаны как открытые секции. Такие секции восприимчивы к
скручиванию, но обычно легко восстанавливают свою первоначальную форму после
воздействия крутящих сил.
Существуют закрытые секции. Они обладают высоким сопротивлением к
скручиванию, но более восприимчивы к остаточной деформации после воздействия
крутящих сил.
13.
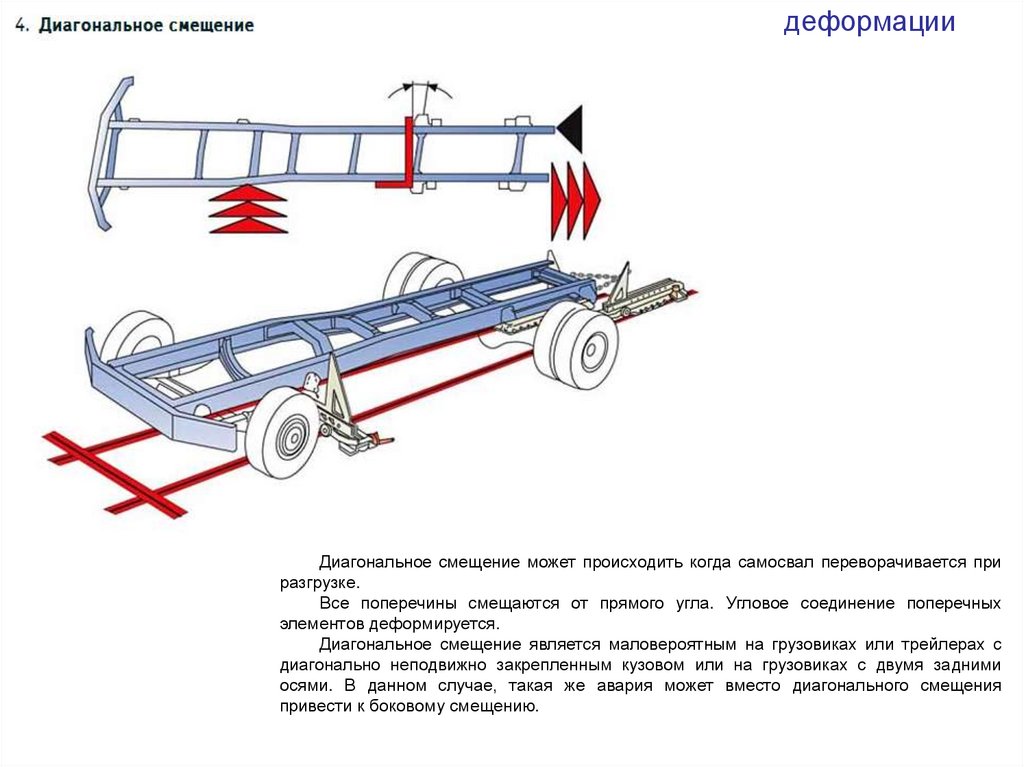
деформацииДиагональное смещение может происходить когда самосвал переворачивается при
разгрузке.
Все поперечины смещаются от прямого угла. Угловое соединение поперечных
элементов деформируется.
Диагональное смещение является маловероятным на грузовиках или трейлерах с
диагонально неподвижно закрепленным кузовом или на грузовиках с двумя задними
осями. В данном случае, такая же авария может вместо диагонального смещения
привести к боковому смещению.
14.
F 4m 2
d k ср
lшв
m
F
dt см
F
10 мм
1,4h Э
15.
16.
Варианты расчетов6
8
1
7
6
7
8
3
4
2
8
8
6
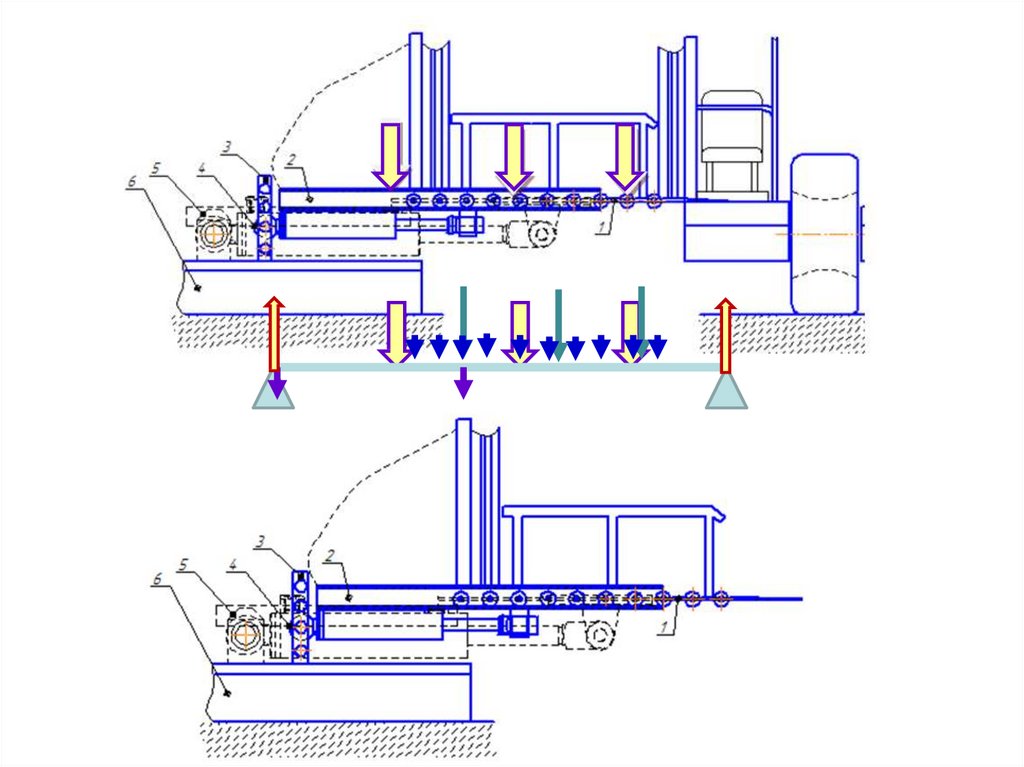
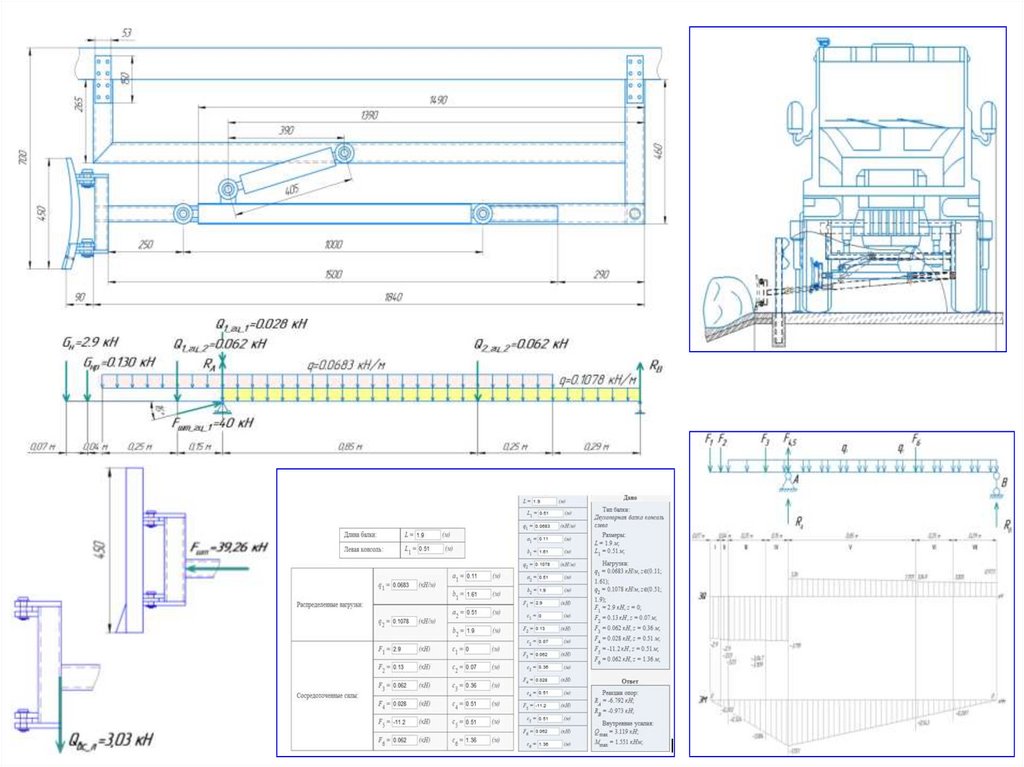
1.Расчет двухопорной балки переносного
козлового крана на изгиб (подбор
профиля сечения, сортамента балки)
2. Расчет устойчивости опор крана
(максимальные нагрузки на опоры при
сжатии, подбор профиля опор)
3.Определение
максимального
крутящего момента телескопического
вала
(определение
диаметров
составного сечения вала)
4.Расчет троса переносного козлового
крана на растяжение (подбор профиля
сечения)
5. Расчет узла цепной передачи
5
6
8
6
2
6
8
9
8
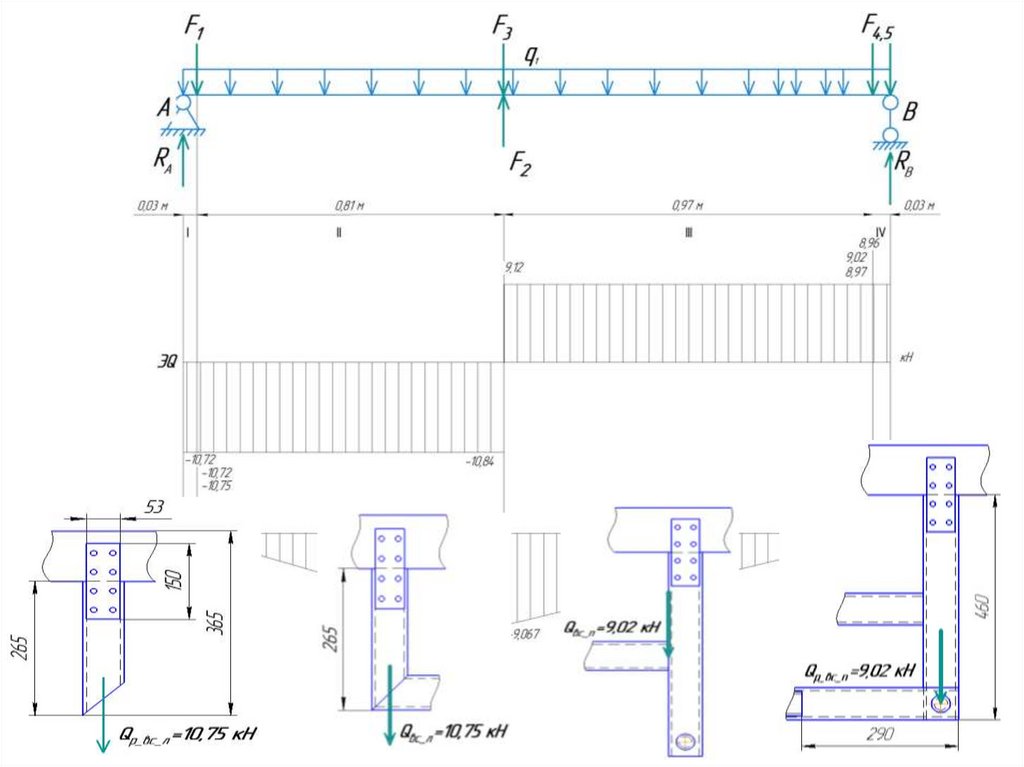
6.Расчет сварочных соединений (длины сварных швов,
определение катета шва, прочности сварных швов на срез)
7. Расчет
разъемных
соединений
(определение
диаметров болтовых соединений)
8.Расчет соединительных элементов на смятие, срез.
9. Расчет предельных углов отклонения крана от
вертикального положения
17.
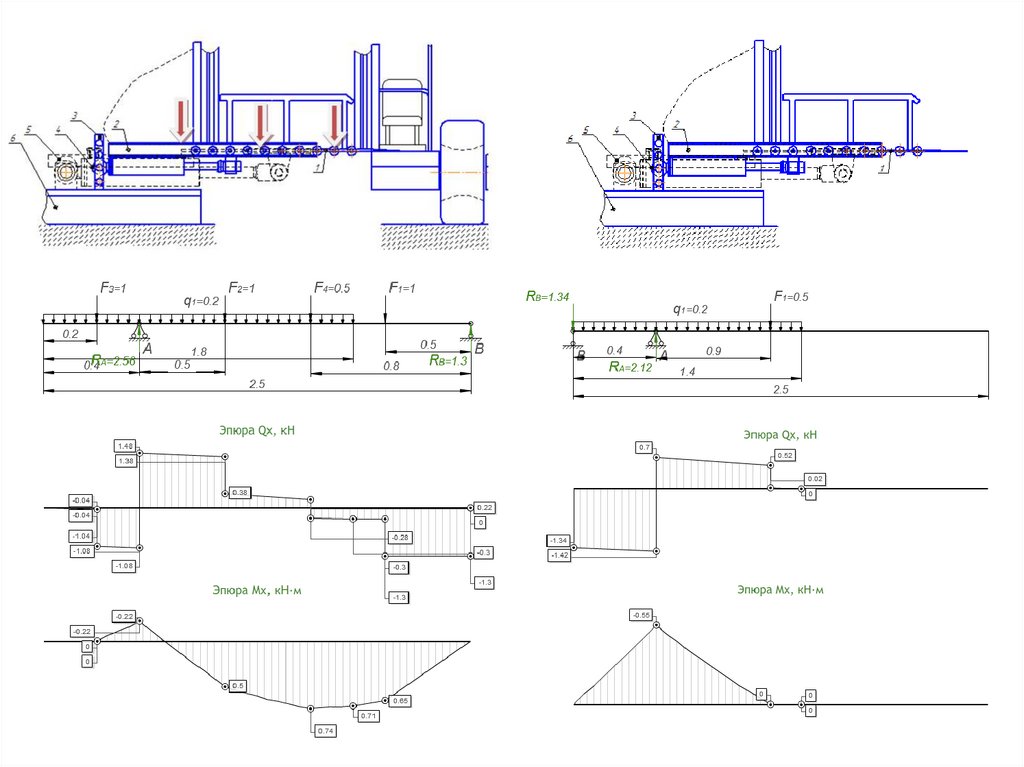
Расчет балки на изгиб (определение прогиба)Нагрузка приложена в центре
(максимальный прогиб)
18.
19.
20.
21.
22.
ˣВнешняя
нагрузка
F
напряжения
M
внутренние силовые факторы
q
Qx ; Qy ; N ; Mx ; My ; Tk
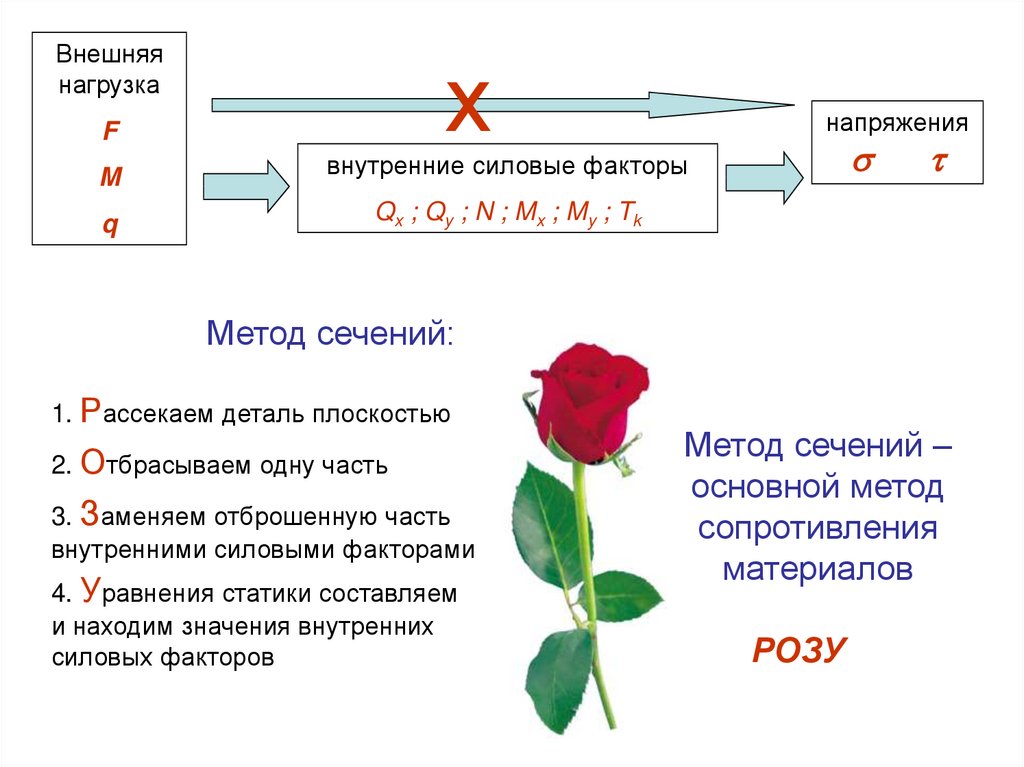
Метод сечений:
1. Рассекаем деталь плоскостью
2. Отбрасываем одну часть
3. Заменяем отброшенную часть
внутренними силовыми факторами
4. Уравнения статики составляем
и находим значения внутренних
силовых факторов
Метод сечений –
основной метод
сопротивления
материалов
РОЗУ
23.
Основные характеристики прочности и жесткостиФактор
влияния
Поперечное
сечение
детали
Нагрузка
Материал
Характеристики
прочности
Площадь сечения А – при
растяжении, сжатии, сдвиге
Полярный момент
сопротивления WP – при
кручении
Осевые моменты
сопротивления сечения
WX WY – при изгибе
жесткости
Площадь сечения А – при
растяжении, сжатии, сдвиге
Полярный момент инерции
IP – при кручении
Осевые моменты инерции
сечения
IX IY – при изгибе
Внутренние силовые факторы:
Продольная сила N – при растяжении и сжатии
Поперечные силы QX QY – при сдвиге (срезе)
Крутящий момент TK – при кручении
Изгибающие моменты MX MY – при изгибе
Допускаемые напряжения:
нормальные - [σ]
касательные - [τ]
Модуль упругости материала – Е
при действии нормальных
напряжений
Модуль сдвига материала - G при
действии касательных напряжений
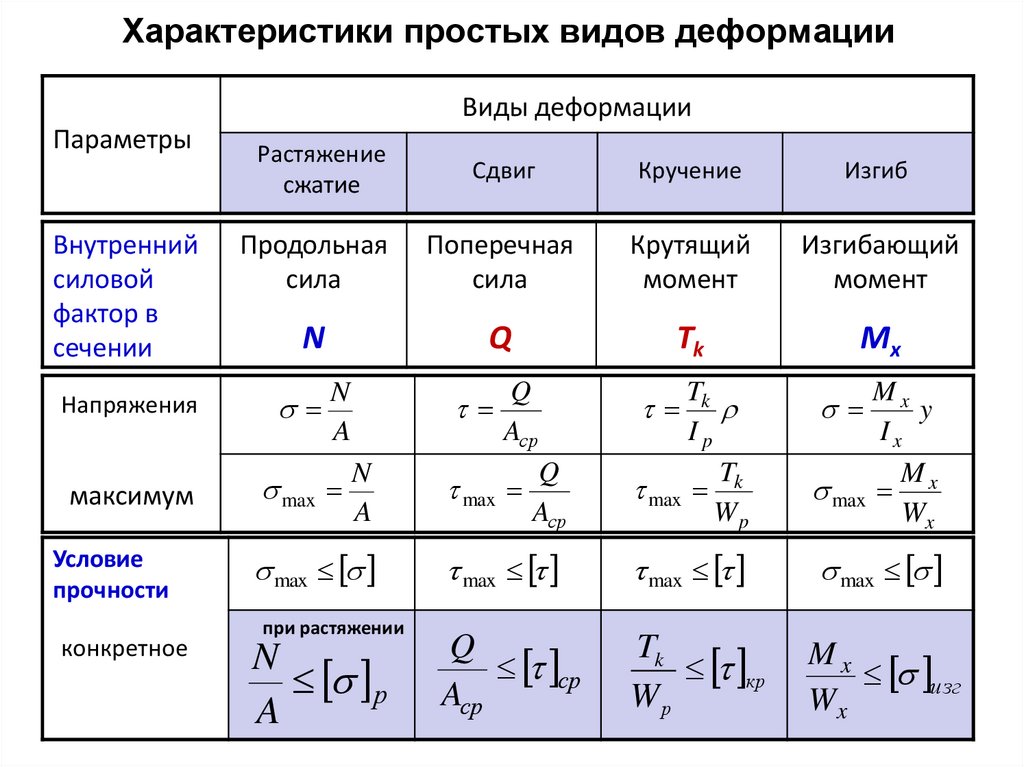
24. Характеристики простых видов деформации
Виды деформацииПараметры
Внутренний
силовой
фактор в
сечении
Растяжение
сжатие
Сдвиг
Кручение
Изгиб
Продольная
сила
Поперечная
сила
Крутящий
момент
Изгибающий
момент
N
Q
Tk
Mx
Q
Aср
Tk
Ip
T
max k
Wp
Mx
y
Ix
M
max x
Wx
max
max
max
Q
ср
Aср
Tk
кр
Wр
Mx
изг
Wx
N
A
Напряжения
максимум
max
Условие
прочности
конкретное
N
A
max
при растяжении
N
р
A
Q
Aср
max
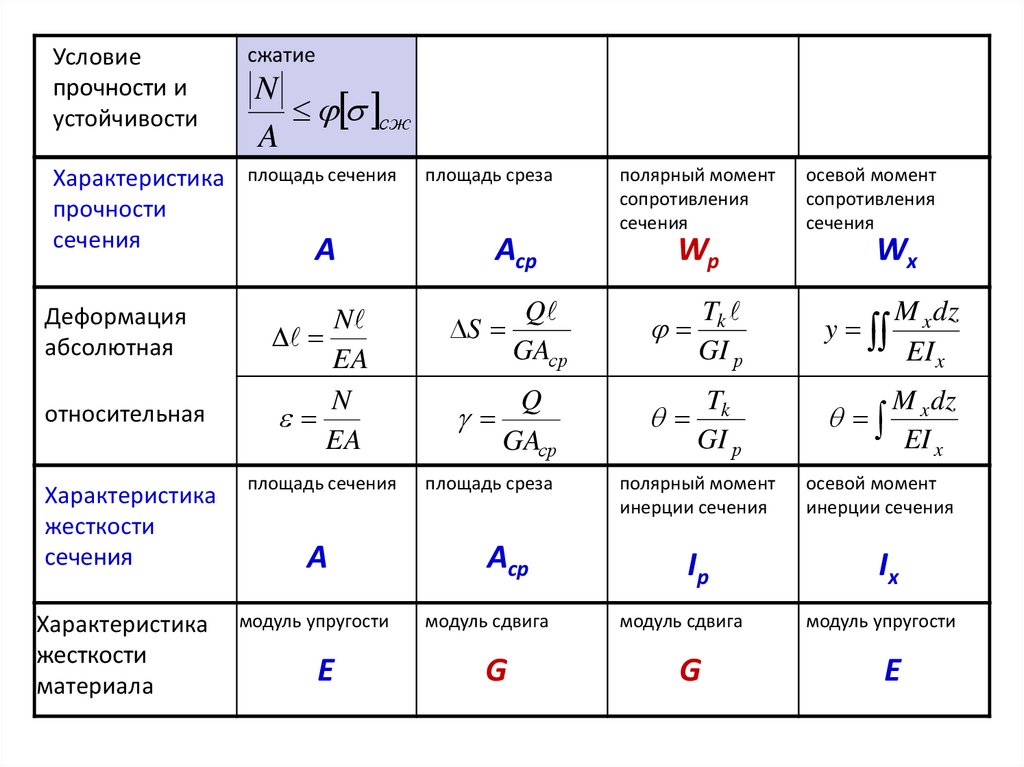
25.
Условиепрочности и
устойчивости
сжатие
Характеристика
прочности
сечения
площадь сечения
Деформация
абсолютная
относительная
Характеристика
жесткости
сечения
Характеристика
жесткости
материала
N
сж
A
А
N
EA
N
EA
площадь сечения
А
модуль упругости
E
площадь среза
Аср
S
Q
GAср
Q
GAср
площадь среза
Аср
модуль сдвига
G
полярный момент
сопротивления
сечения
Wp
Tk
GI р
Tk
GI р
полярный момент
инерции сечения
Ip
модуль сдвига
G
осевой момент
сопротивления
сечения
Wx
y
M x dz
EI x
M x dz
EI x
осевой момент
инерции сечения
Ix
модуль упругости
E
26.
2.7 Типы расчетов на прочность- расчет проектировочный
N
р
A
цель расчета – определение необходимых размеров сечения детали
- определить нагрузку N, действующую на деталь;
- выбрать материал (по прототипам) и найти в справочных таблицах значение
допускаемого напряжения
- выбрать рациональную форму сечения детали, подставить в условие прочности
выражение площади через размеры сечения и из полученного неравенства вычислить
размеры сечения
- расчет поверочный
(производится при известных размерах, нагрузке и материале)
цель расчета – проверить выполнение неравенства условия прочности
оптимальным считается отклонение от равенства в пределах ± 5%
- расчет несущей способности конструкции
цель расчета – определение допускаемой нагрузки
27. Тема 1
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВТема 1
Геометрические характеристики
плоских сечений
Тихонкин Игорь Васильевич, доцент, к.т.н.
Кафедра Теоретической и прикладной механики
Инженерного института ФГБОУ ВО Новосибирский ГАУ
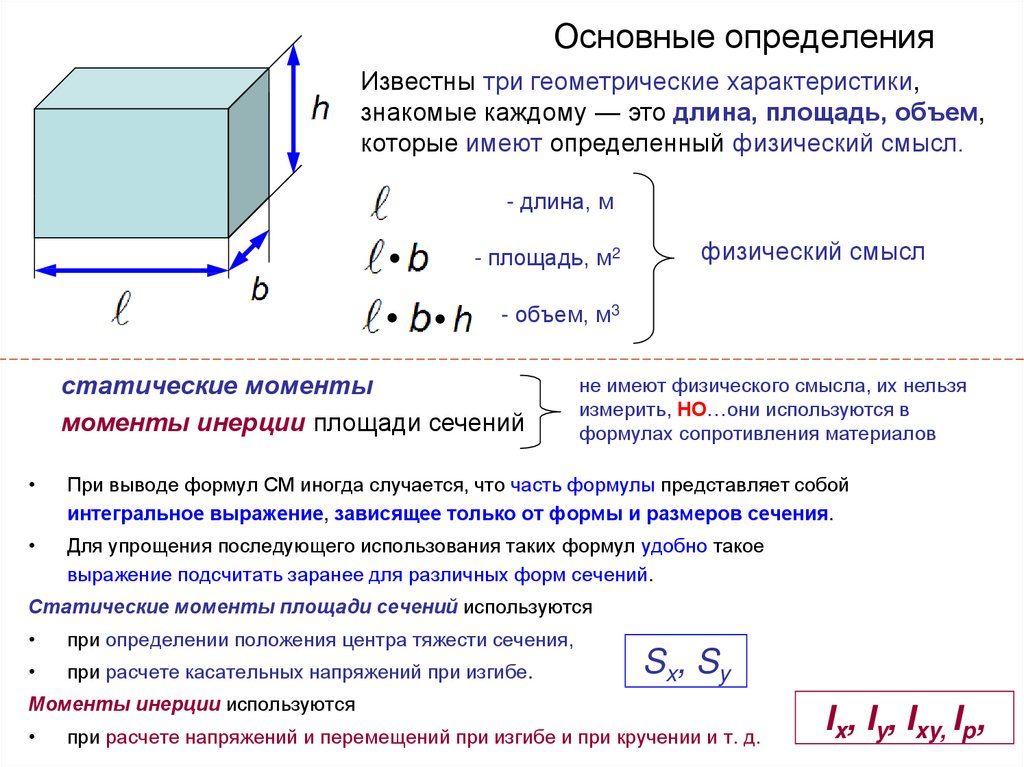
28. Основные определения
Известны три геометрические характеристики,знакомые каждому — это длина, площадь, объем,
которые имеют определенный физический смысл.
- длина, м
- площадь, м2
физический смысл
- объем, м3
статические моменты
моменты инерции площади сечений
не имеют физического смысла, их нельзя
измерить, НО…они используются в
формулах сопротивления материалов
При выводе формул СМ иногда случается, что часть формулы представляет собой
интегральное выражение, зависящее только от формы и размеров сечения.
Для упрощения последующего использования таких формул удобно такое
выражение подсчитать заранее для различных форм сечений.
Статические моменты площади сечений используются
при определении положения центра тяжести сечения,
при расчете касательных напряжений при изгибе.
Sx, Sy
Моменты инерции используются
при расчете напряжений и перемещений при изгибе и при кручении и т. д.
Ix, Iy, Ixy, Ip,
29.
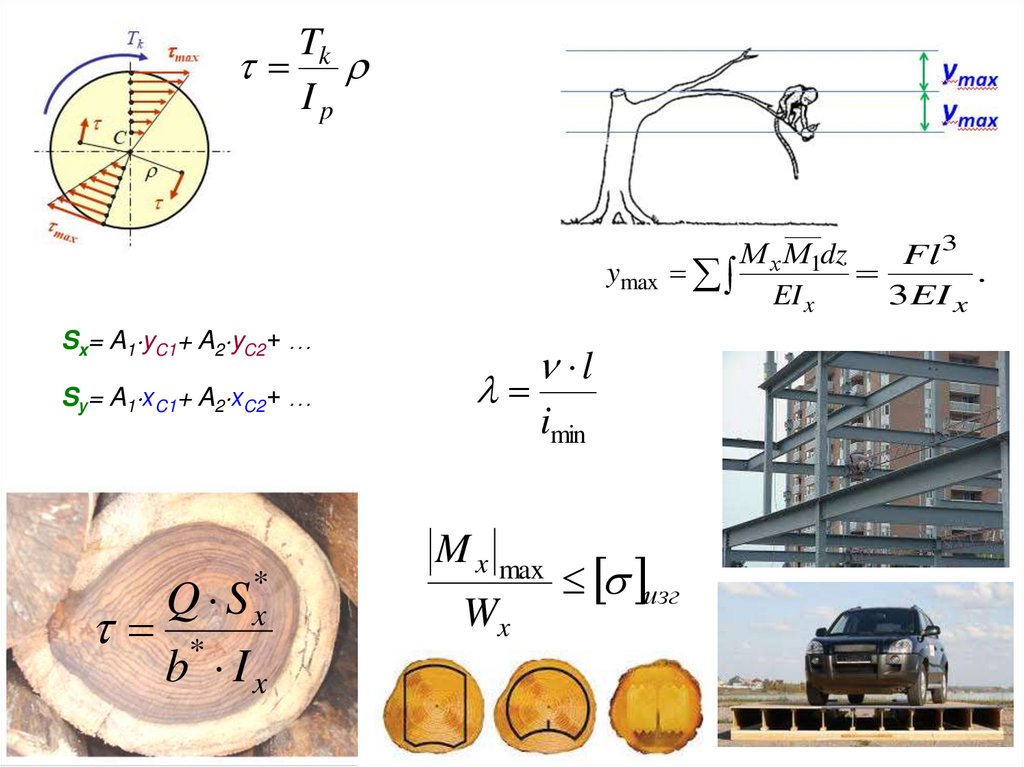
TkIp
ymax
Sx= A1 yC1+ A2 yC2+ …
Sу= A1 хC1+ A2 хC2+ …
Q S x*
*
b Ix
l
imin
M x max
Wx
М х М1dz
Fl 3
.
3EI x
EI x
изг
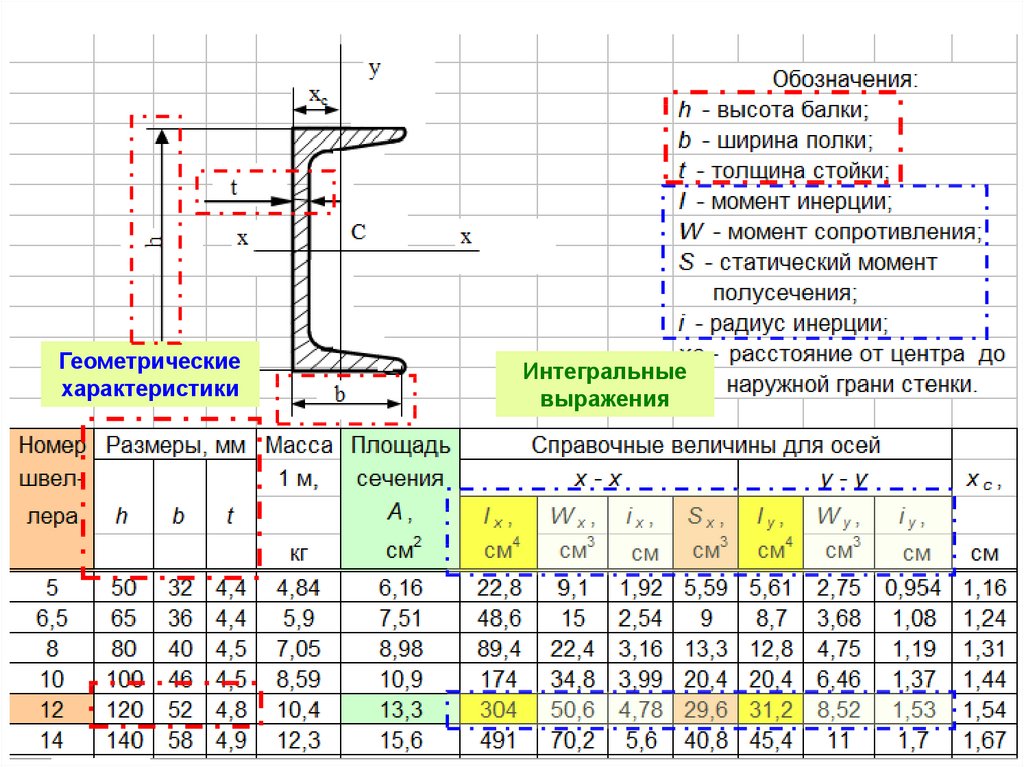
30.
Геометрическиехарактеристики
Интегральные
выражения
31.
1. ПОПЕРЕЧНОЕ СЕЧЕНИЕ ДЕТАЛИГеометрические характеристики:
Площадь сечения
y
А=
dA
А
A
Статические моменты площади
dA
S y х dA
x
S х у dA
А
А
Моменты инерции сечения
I x y 2 dA
y
А
- осевые
ρ
I y x 2 dA
х
Моменты сопротивления сечения
- осевые
Ix
Wx
ymax
Wy
Iy
xmax
- полярный
Wp
А
A
- полярный
I p dA
2
A
Ip
max
I xy x y dA
- центробежный
Радиусы инерции
сечения
ix
iy
Ix
A
Iy
A
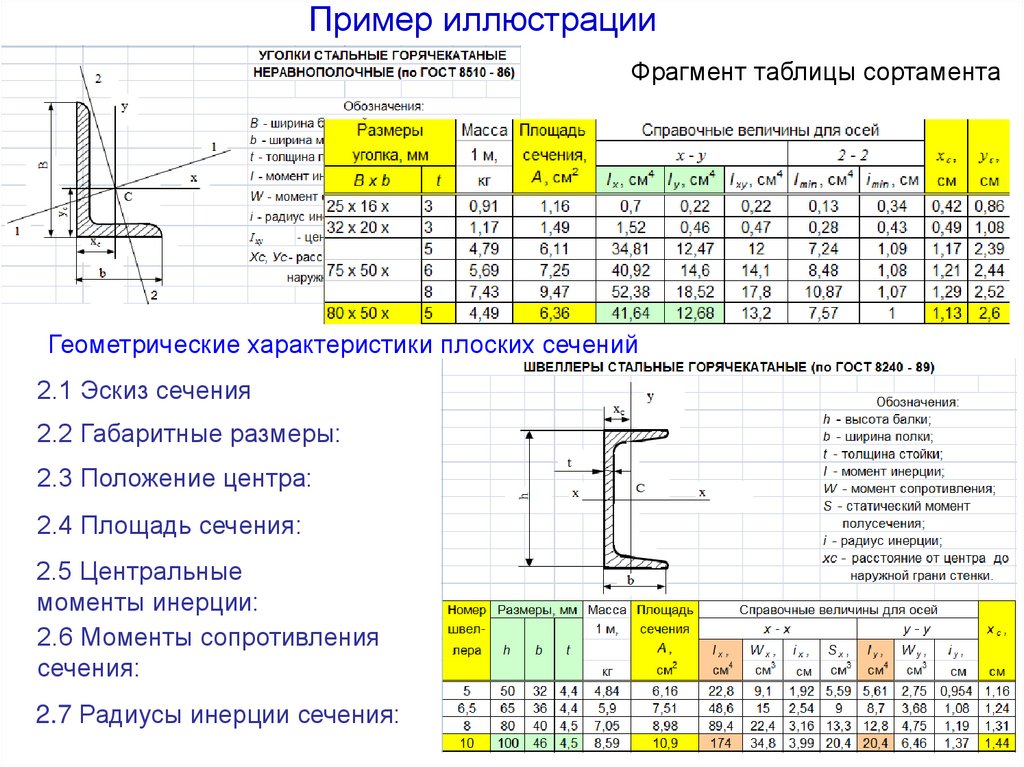
32. Пример иллюстрации
Фрагмент таблицы сортаментаГеометрические характеристики плоских сечений
2.1 Эскиз сечения
2.2 Габаритные размеры:
2.3 Положение центра:
2.4 Площадь сечения:
2.5 Центральные
моменты инерции:
2.6 Моменты сопротивления
сечения:
2.7 Радиусы инерции сечения:
33.
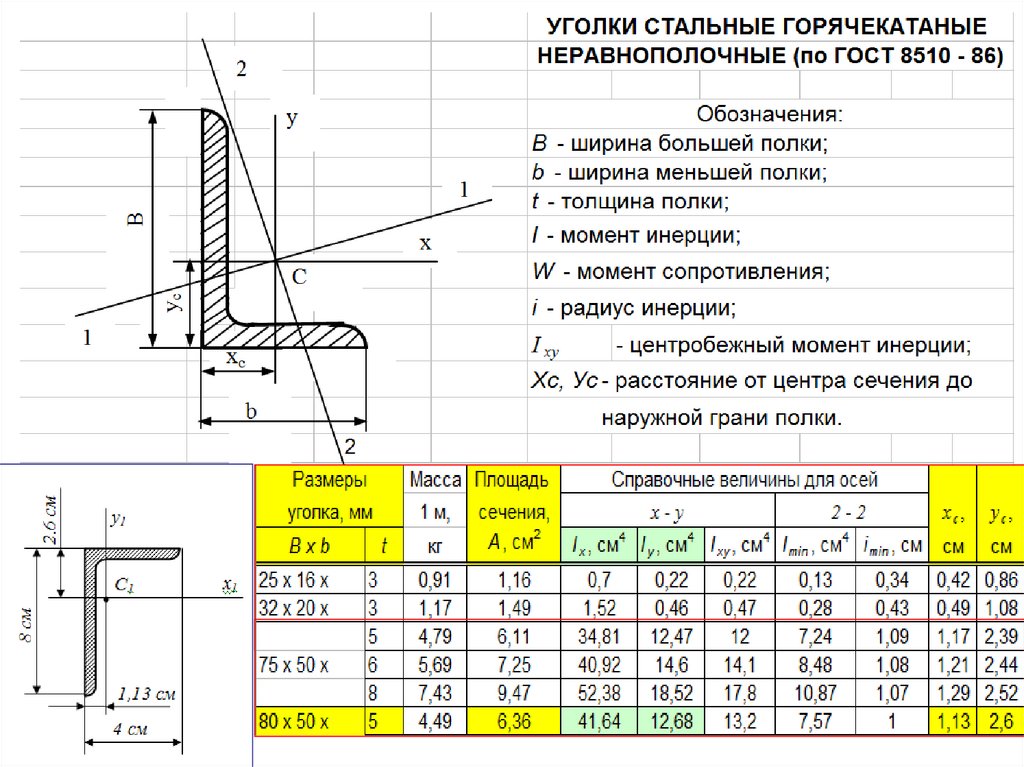
Определить геометрические характеристики сечениястержня, сваренного из двух неравнополочных уголков
80×50×5 и швеллера №10 (см. табл. сортамента)
п.1, п.2. - Уголок 80 50 5мм (ГОСТ 8510–86):
– габаритные размеры:
8 5 см;
– координаты центра уголка относительно его полок С1(1,13; 2,6);
– площадь сечения уголка
А1=6,36 см2;
– осевые моменты инерции относительно центральных осей
Ixc1=41,64 см4 , Iyc1=12,68 см4.
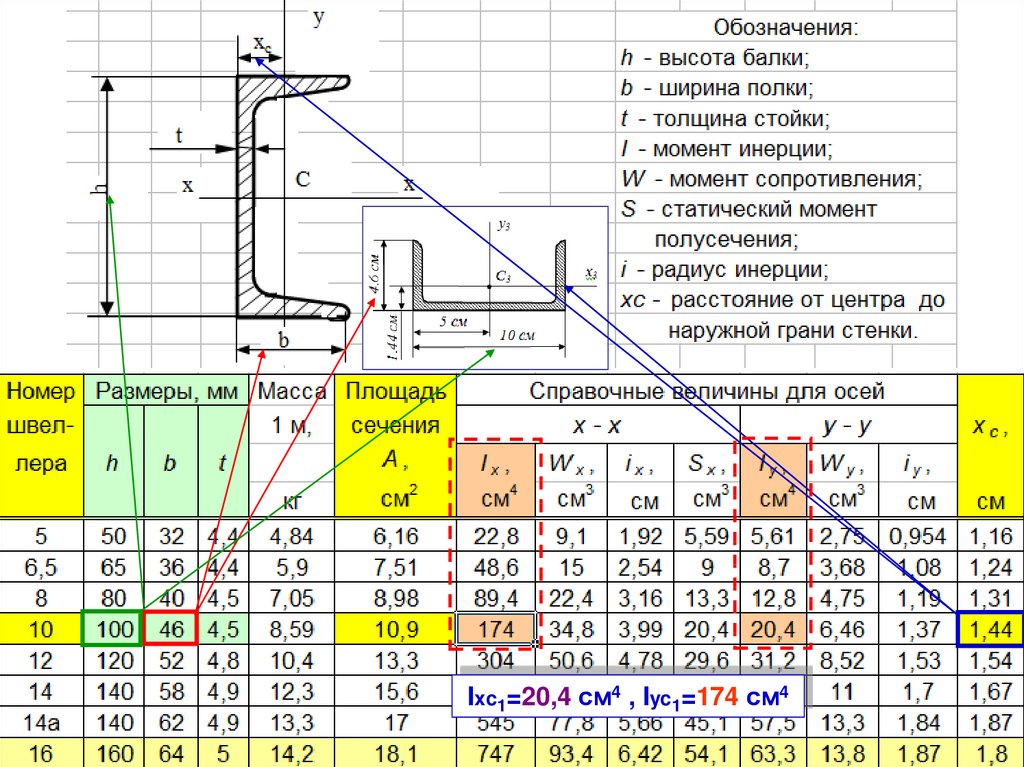
п.3. - Швеллер №10 (ГОСТ 8240–89):
– габаритные размеры
10 4,6 см;
– координаты центра швеллера С2 (5; 1,44);
– площадь сечения
А3 =10,9 см2;
– табличные значения моментов инерции швеллера необходимо
согласовать с принятыми нами обозначениями осей (в таблице сортамента
швеллер изображен вертикально Ixc1=174 см4 , Iyc1=20,4 см4):
Ixc1=20,4 см4 , Iyc1=174 см4.
34.
35.
Ixc1=20,4 см4 , Iyc1=174 см436.
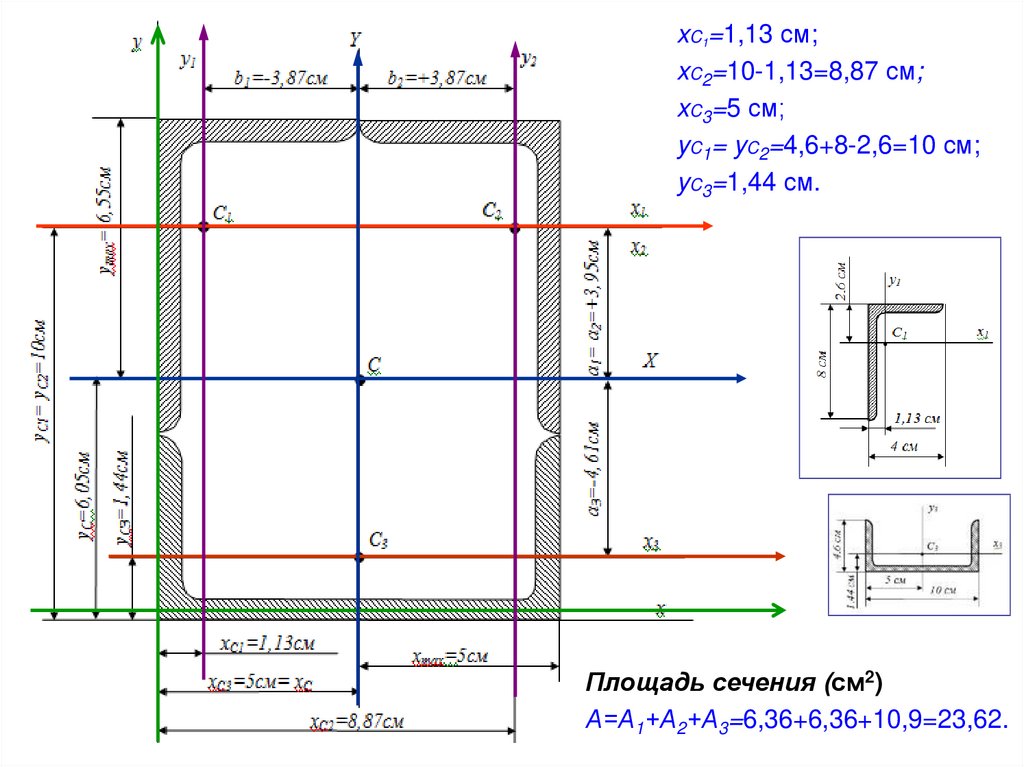
xC1=1,13 см;xC2=10-1,13=8,87 см;
xC3=5 см;
yC1= yC2=4,6+8-2,6=10 см;
yC3=1,44 см.
Площадь сечения (см2)
А=А1+А2+А3=6,36+6,36+10,9=23,62.
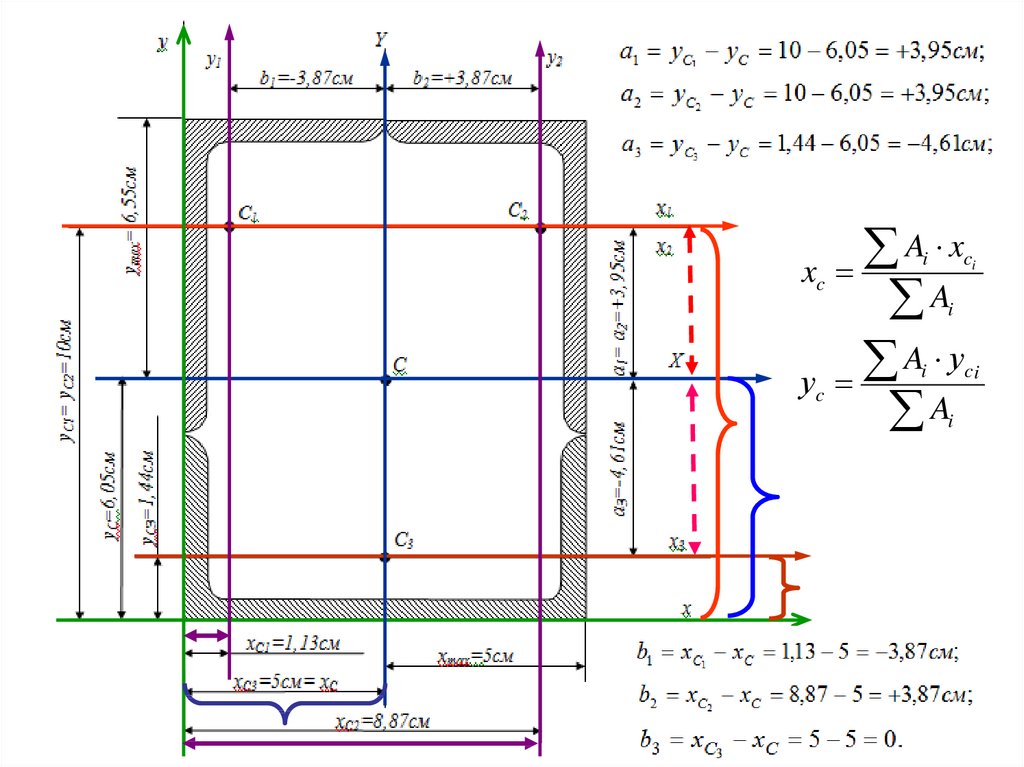
37.
xcA x
A
A у
A
i
ci
i
уc
i
ci
i
38.
J xc J ixi Ai (ai )2J yc J iyi Ai (bi )2
J xc yc J ixyi Ai ai bi
39.
40.
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВСложные виды
Тихонкин Игорь Васильевич, доцент, к.т.н.
Кафедра Теоретической и прикладной механики
Инженерного института ФГБОУ ВО Новосибирский ГАУ
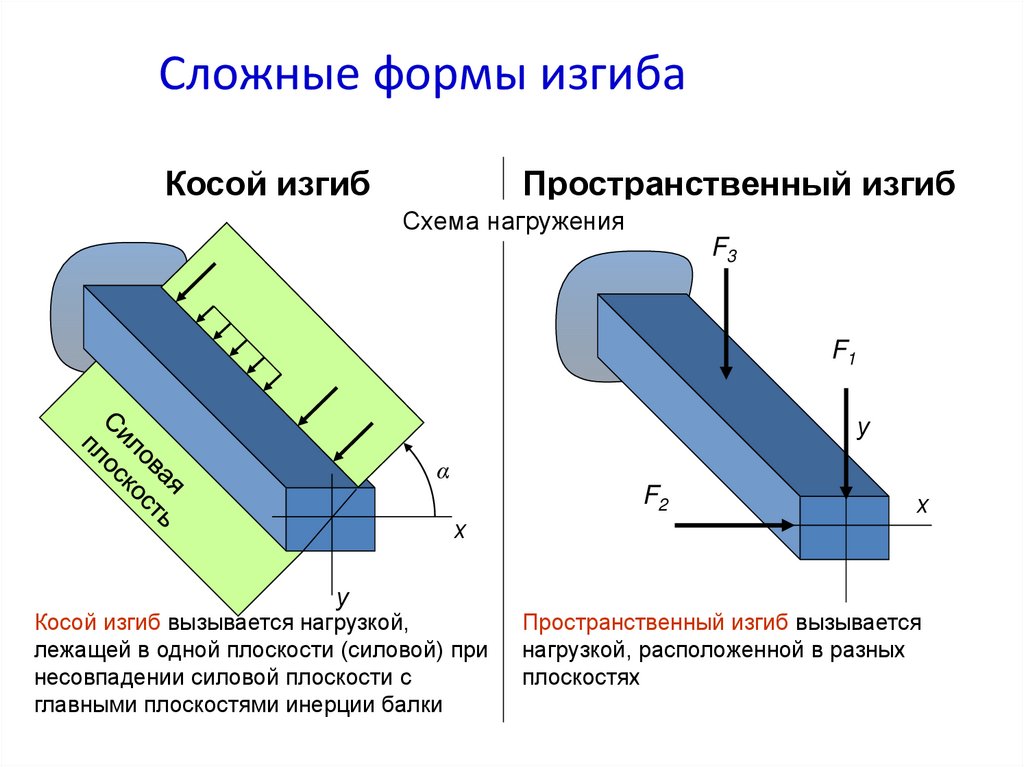
41. Сложные формы изгиба
Косой изгибПространственный изгиб
Схема нагружения
F3
F1
у
α
F2
х
у
Косой изгиб вызывается нагрузкой,
лежащей в одной плоскости (силовой) при
несовпадении силовой плоскости с
главными плоскостями инерции балки
х
Пространственный изгиб вызывается
нагрузкой, расположенной в разных
плоскостях
42.
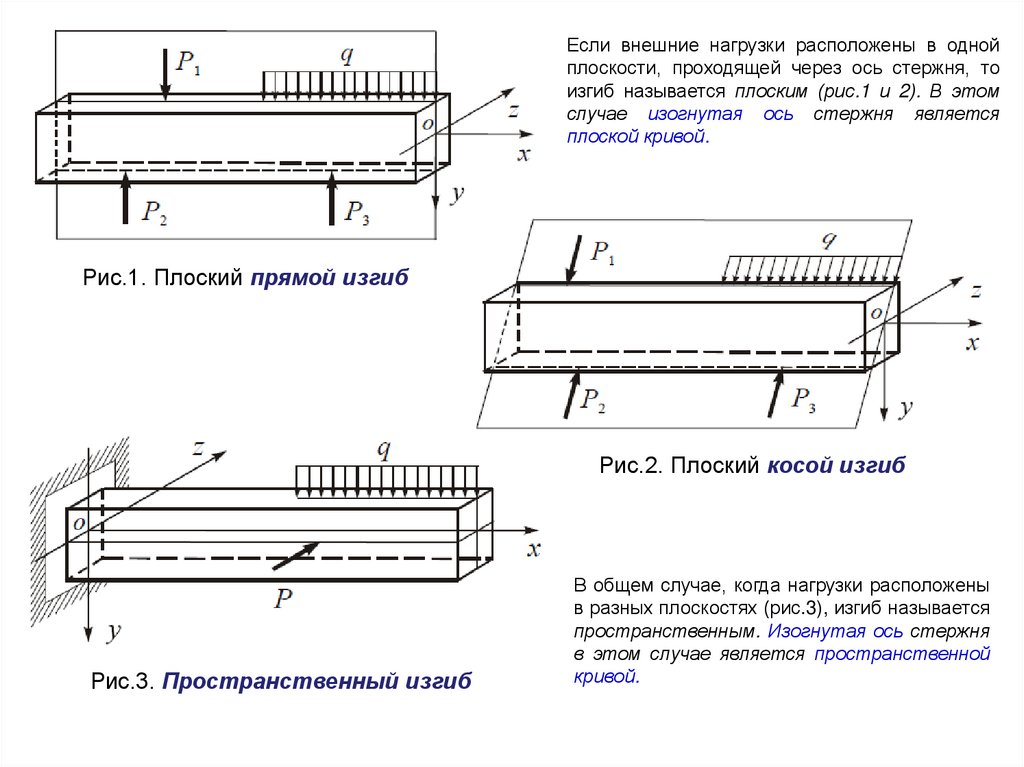
Если внешние нагрузки расположены в однойплоскости, проходящей через ось стержня, то
изгиб называется плоским (рис.1 и 2). В этом
случае изогнутая ось стержня является
плоской кривой.
Рис.1. Плоский прямой изгиб
Рис.2. Плоский косой изгиб
Рис.3. Пространственный изгиб
В общем случае, когда нагрузки расположены
в разных плоскостях (рис.3), изгиб называется
пространственным. Изогнутая ось стержня
в этом случае является пространственной
кривой.
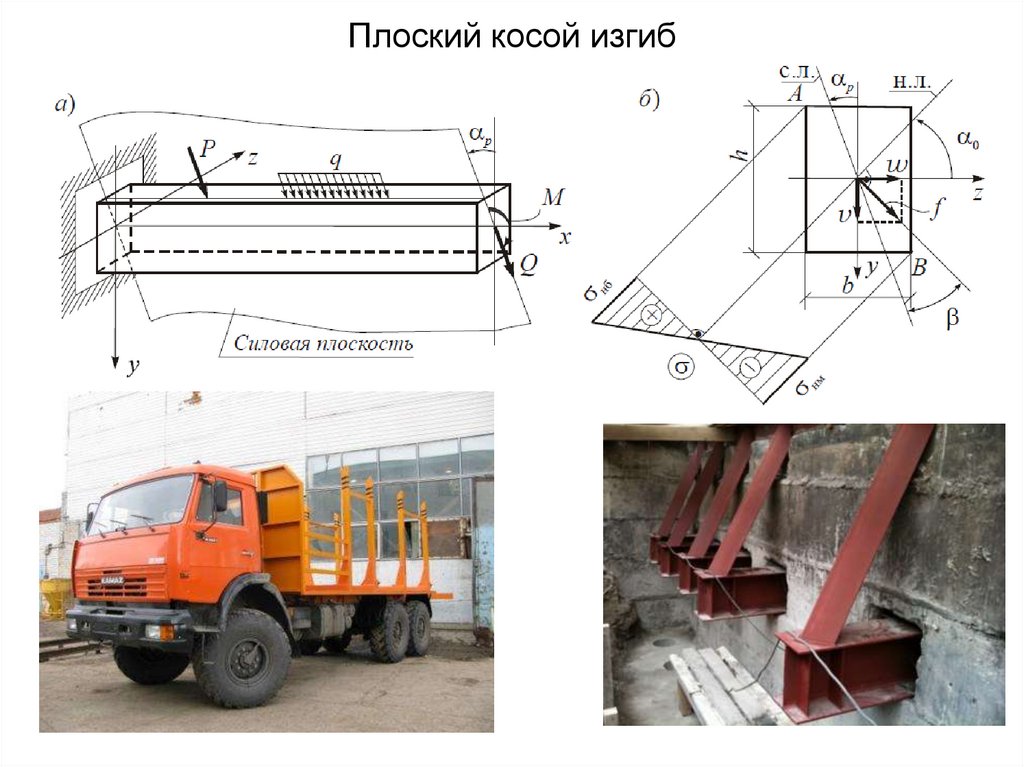
43. Плоский косой изгиб
44.
косой изгибпространственный изгиб
Максимальные напряжения в опасном сечении при xmax и ymax
max М
max Sin
изг
Wx
Cos
W y
max
Mx My
Wx
W y
max
Положение опасного сечения не очевидно.
Поэтому его приходится находить,
сравнивая напряжения в двух
потенциально опасных сечениях
Положение опасного сечения
определяется эпюрой Мизг
Условие прочности
σmax≤[σ]
или в более удобном для расчета виде
М изг
Sin Wx Cos изг
Wx
Wy
max
(67)
Wx
1
Mx
My
изг
Wx
Wy
max
(68)
45.
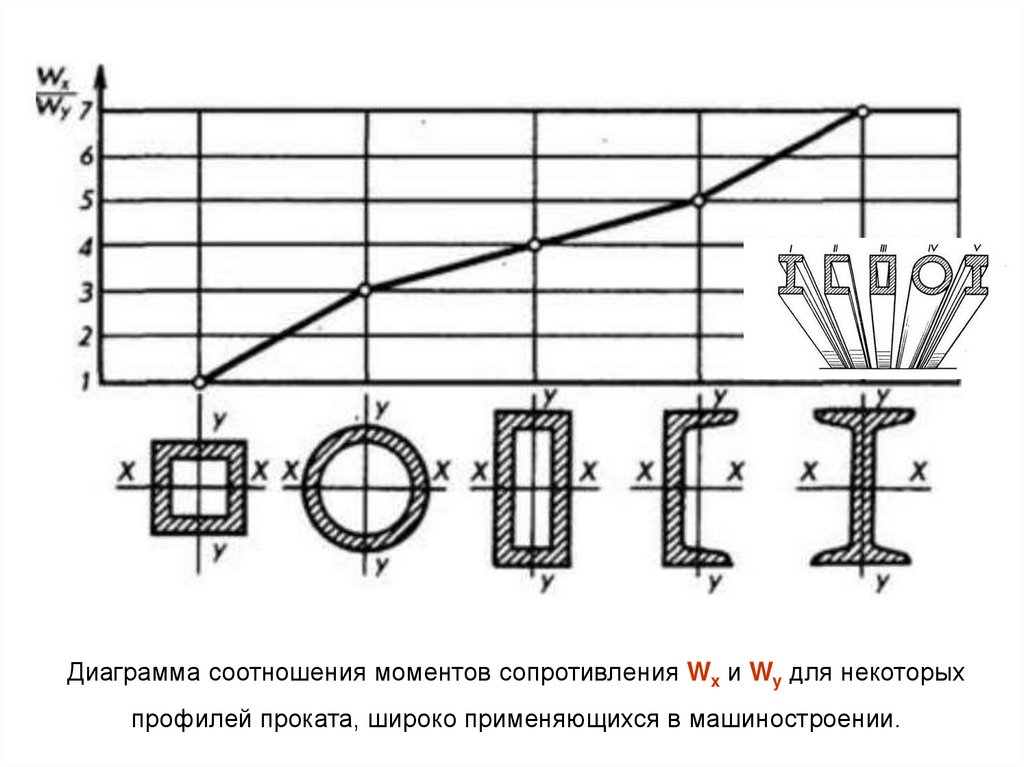
В обоих условиях прочности по 2 неизвестных: Wx и WyДля осуществления практического расчета на прочность соотношением моментов
сопротивления сечения приходится задаваться хотя бы ориентировочно
Для прямоугольного сечения
Wx bh 2 6
h
задать!
2
Wy
6 hb
b
При расчете стандартных профилей (двутавра, швеллера) задается ориентировочное
соотношение:
для двутавра
для швеллера
Wx
8
Wy
Wx
6
Wy
После определения номера профиля необходимо
провести поверочный расчет по истинным значениям
моментов сопротивления
Для прокатных двутавров k изменяется в пределах 6 -14.
46.
Диаграмма соотношения моментов сопротивления Wx и Wy для некоторыхпрофилей проката, широко применяющихся в машиностроении.
47.
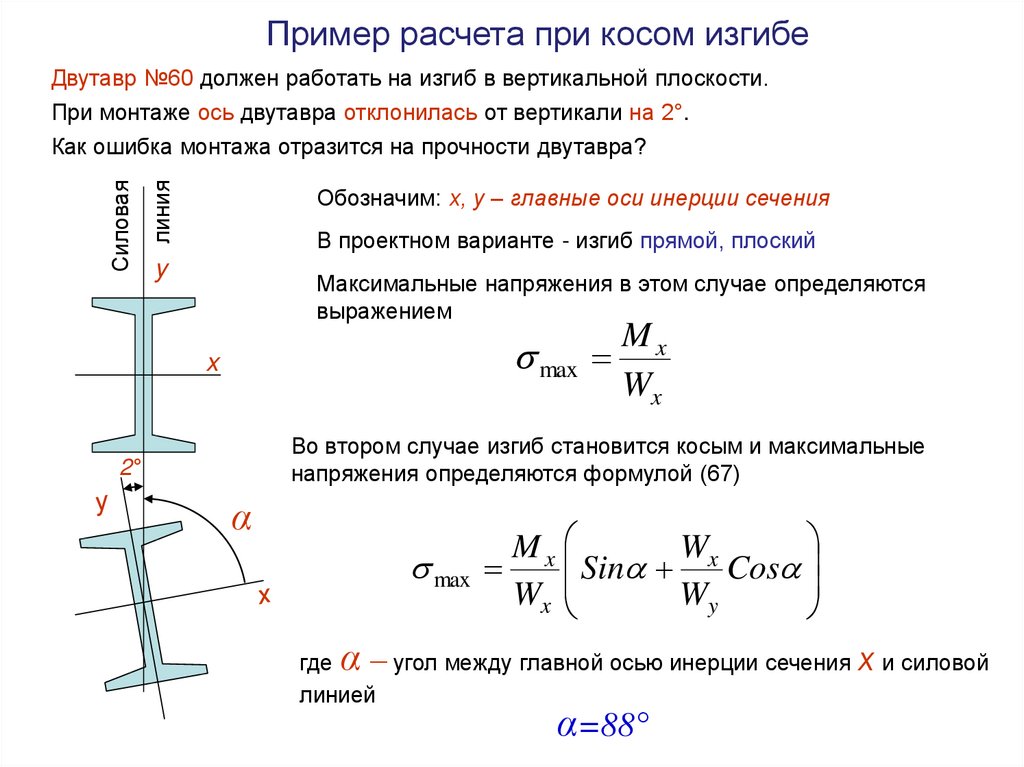
Пример расчета при косом изгибеДвутавр №60 должен работать на изгиб в вертикальной плоскости.
При монтаже ось двутавра отклонилась от вертикали на 2°.
линия
Силовая
Как ошибка монтажа отразится на прочности двутавра?
Обозначим: х, у – главные оси инерции сечения
В проектном варианте - изгиб прямой, плоский
y
Максимальные напряжения в этом случае определяются
выражением
max
x
Mx
Wx
Во втором случае изгиб становится косым и максимальные
напряжения определяются формулой (67)
2°
α
max
M x
Wx
Sin
Cos
Wx
Wy
α
где
– угол между главной осью инерции сечения
линией
α=88°
х и силовой
48.
49.
Значения:Sin 88°=0,9994
Cos 88°=0,0349
Табличные значения моментов сопротивления двутавра №60:
Wx =2560 см3
Wy =182 см3
их соотношение
Wx 2560
14,07
Wy 182
Полученные значения подставляем в формулу для напряжений
max
Mx
M x
Wx
M
Sin
Cos
0,9994 14,07 0,0349 1,49 x
W
Wx
Wy
Wx
x
Отсюда следует, что ошибка при установке двутавра в 2° приведет к
увеличению напряжений в 1,49 раза.
50.
Плоский косой изгиб опасен для балок с поперечными сечениями, моментыинерции которых значительно отличаются друг от друга. Например, для
двутавровых балок даже незначительное отклонение силовой линии от оси Оу
приводит к существенному отклонению плоскости изгиба от силовой
плоскости и к увеличению нормальных напряжений и перемещений.
51.
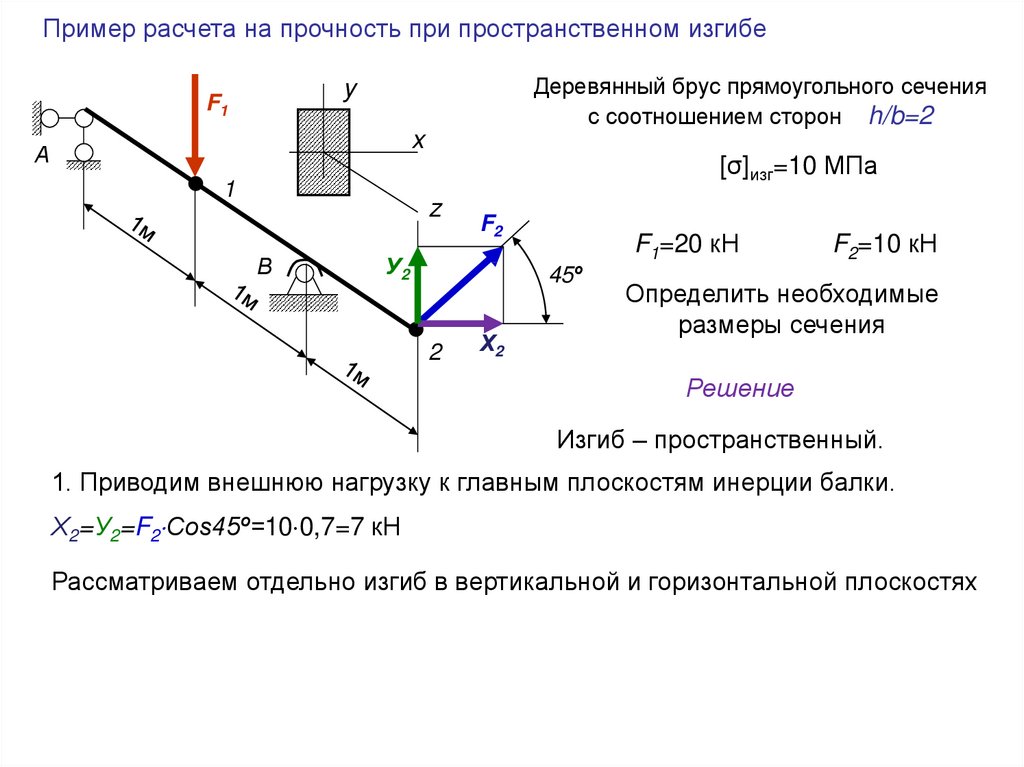
Пример расчета на прочность при пространственном изгибеДеревянный брус прямоугольного сечения
с соотношением сторон h/b=2
y
F1
x
А
1
[σ]изг=10 МПа
z
В
F2
У2
F1=20 кН
45º
2
Х2
F2=10 кН
Определить необходимые
размеры сечения
Решение
Изгиб – пространственный.
1. Приводим внешнюю нагрузку к главным плоскостям инерции балки.
Х2=У2=F2 Cos45º=10 0,7=7 кН
Рассматриваем отдельно изгиб в вертикальной и горизонтальной плоскостях
52.
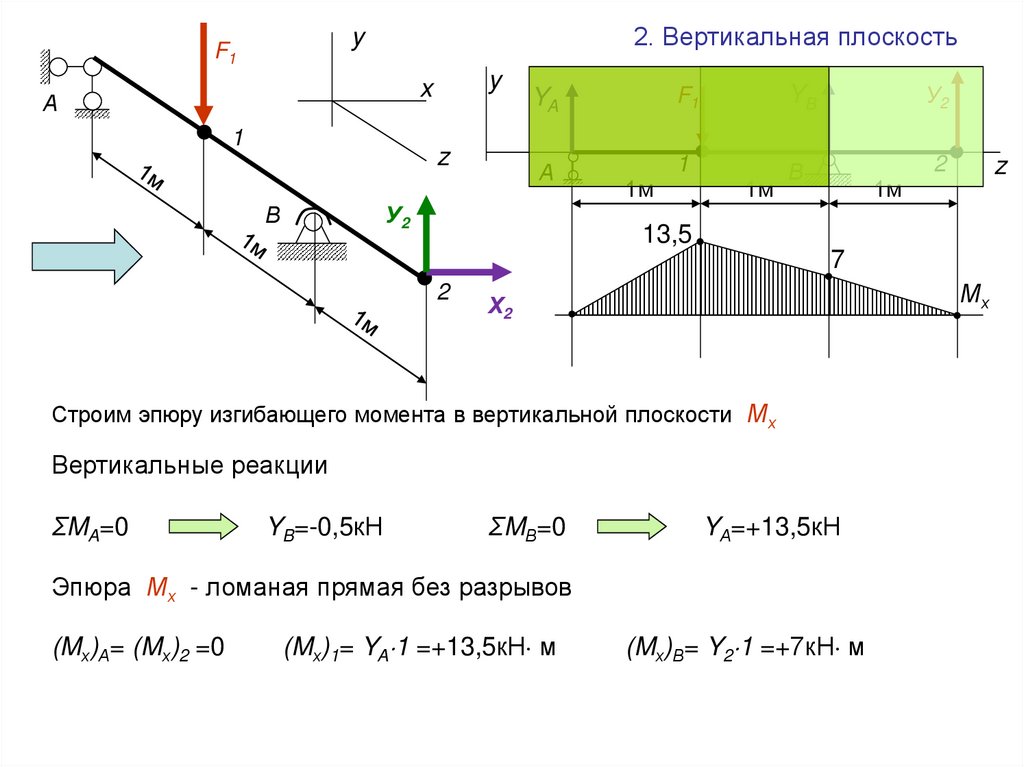
2. Вертикальная плоскостьy
F1
y
x
А
1
z
В
YA
F1
YB
У2
А
1
В
2
У2
1м
1м
z
1м
13,5
7
2
Мх
Х2
Строим эпюру изгибающего момента в вертикальной плоскости Мх
Вертикальные реакции
ΣMA=0
YB=-0,5кН
ΣMВ=0
YА=+13,5кН
Эпюра Мх - ломаная прямая без разрывов
(Mх)А= (Mх)2 =0
(Mх)1= YA 1 =+13,5кН м
(Mх)В= Y2 1 =+7кН м
53.
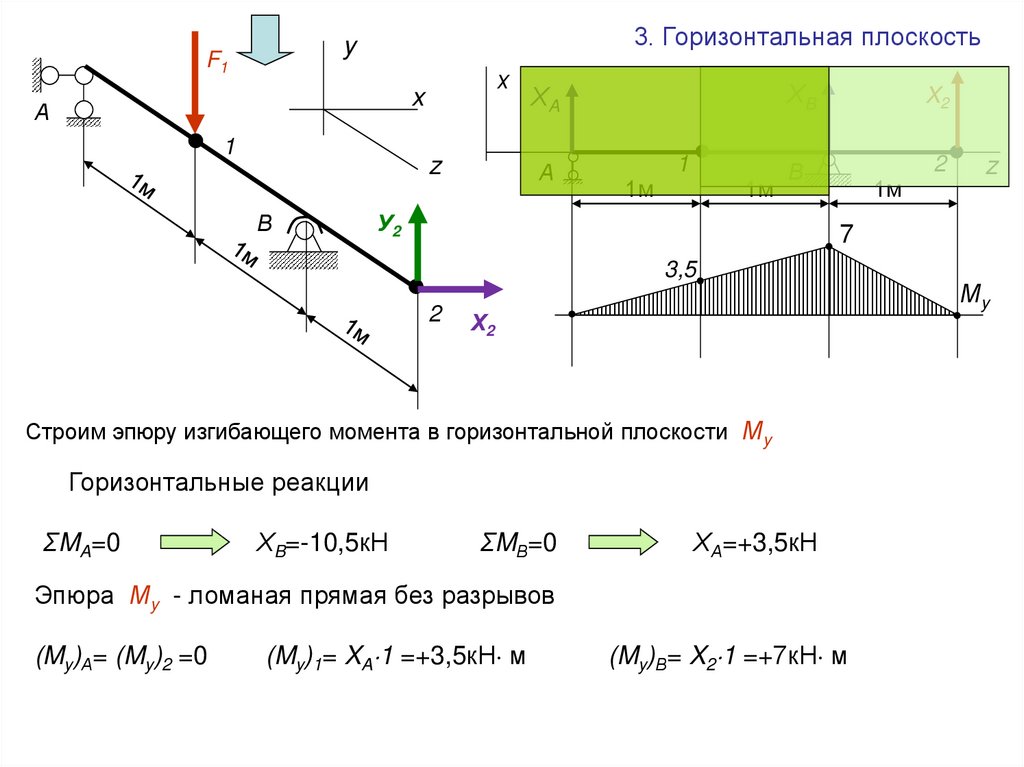
3. Горизонтальная плоскостьy
F1
х
x
А
1
z
В
ХA
А
1
1м
1м
ХB
X2
В
2
У2
1м
7
3,5
2
Х2
Строим эпюру изгибающего момента в горизонтальной плоскости Мy
Горизонтальные реакции
ΣMA=0
ХB=-10,5кН
ΣMВ=0
ХА=+3,5кН
Эпюра Мy - ломаная прямая без разрывов
(My)А= (My)2 =0
z
(My)1= XA 1 =+3,5кН м
(My)В= X2 1 =+7кН м
Мy
54.
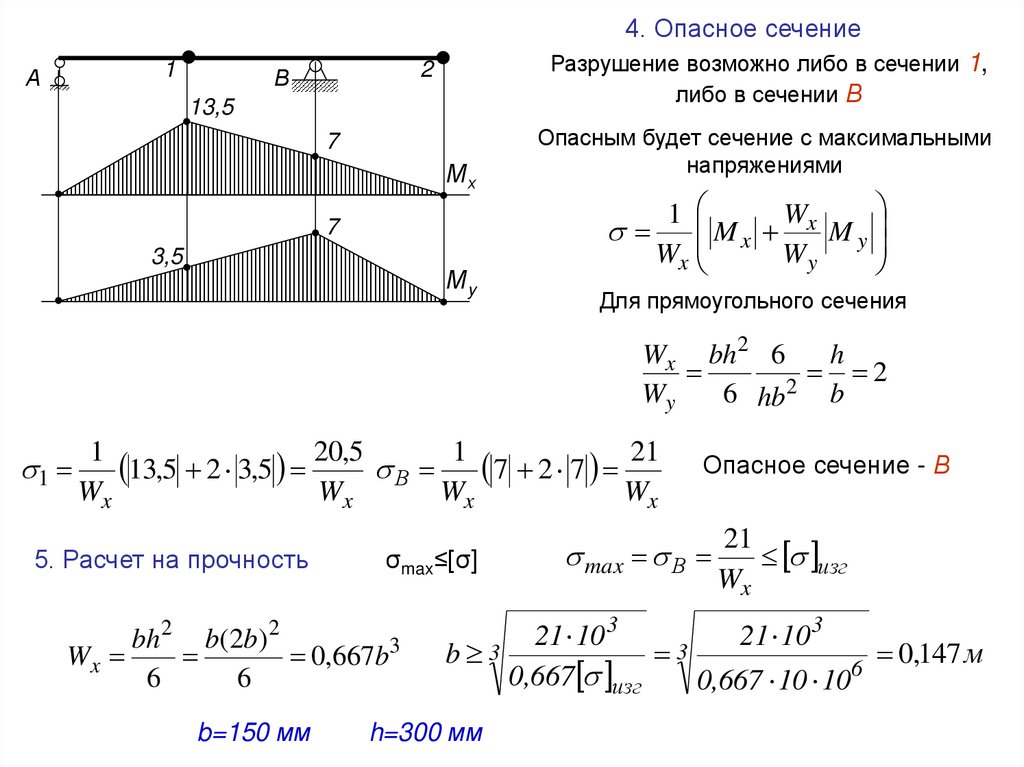
4. Опасное сечениеА
1
Разрушение возможно либо в сечении 1,
либо в сечении В
2
В
13,5
7
Мх
7
3,5
Мy
Опасным будет сечение с максимальными
напряжениями
1
Wx
Mx
My
Wx
Wy
Для прямоугольного сечения
Wx bh2 6
h
2
Wy
6 hb2 b
1
20,5
1
21
13,5 2 3,5
7 2 7
1
В
Wx
Wx
Wx
Wx
5. Расчет на прочность
σmax≤[σ]
bh 2 b(2b) 2
Wx
0,667b3
6
6
b=150 мм
Опасное сечение - В
max В
21
изг
Wx
3
21 10 3
21
10
b 3
3
0,147 м
6
0,667 изг
0,667 10 10
h=300 мм
55.
Изгиб с кручениемиспытывают оси
редукторов, валы
двигателя
«Квант-Л-II»
–
это
усовершенствованная, адаптированная
к российским условиям измерительная
система для центровки горизонтальных
валов (центровка насоса, центровка
механизмов,
центровка
валов
редукторов,
центровка
турбин,
центровка
двигателя,
лазерная
центровка
валов
вентиляторов,
выверка гребных валопроводов и пр.),
с точностью до 0, 01 мм.
В ней используется два лазерных
луча и два приемника.
56.
Пример расчета валаВал условно рассчитывается на изгиб
экв
Mp
W
изг
(86)
Величина расчетного момента определяется по одной из формул гипотез
прочности
2
2
М
T
по третьей гипотезе прочности ;
изг
k
2
М р М изг
0,75Tk2 по четвертой гипотезе прочности ; (87)
1 k
1 k
2
2
М
М
T
по гипотезе прочности Мора .
изг
изг
k
2
2
Третья и четвертая гипотеза – только для пластичных материалов,
Гипотеза Мора – универсальна для любого материала
57.
0,2мБ
A
0,3м
2
0,4м
3
Б
0,2м
y
1
B
1
x
t 2 2
1 t
1
T2
T1
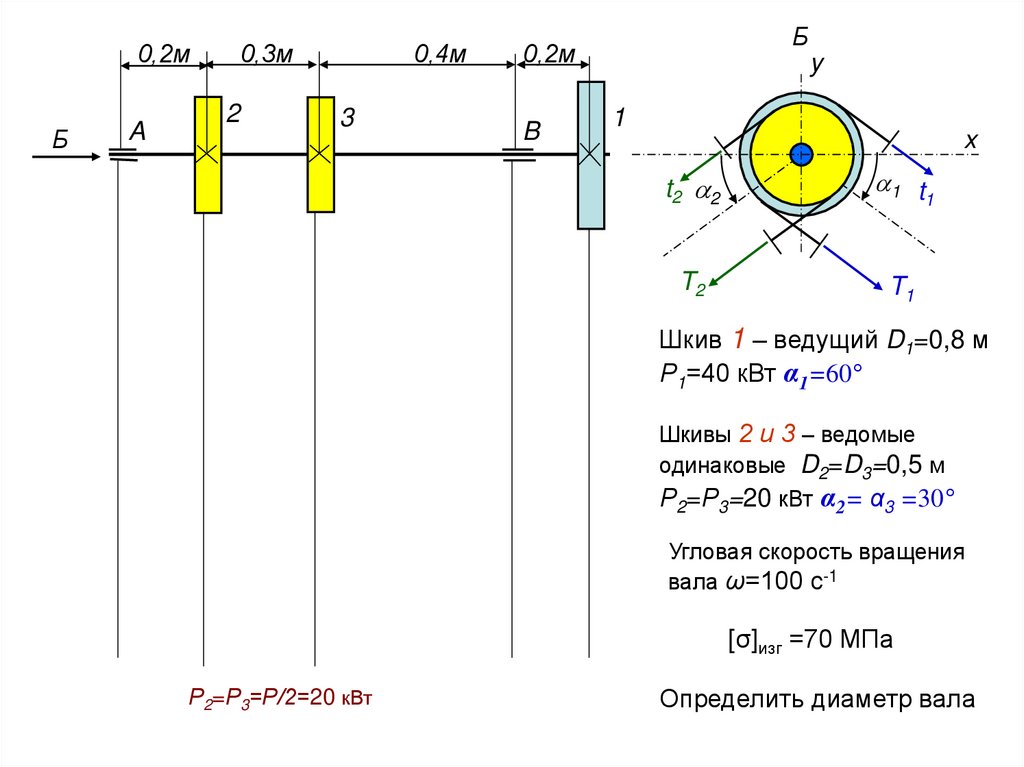
Шкив 1 – ведущий D1=0,8 м
Р1=40 кВт α1=60°
Шкивы 2 и 3 – ведомые
одинаковые D2=D3=0,5 м
Р2=Р3=20 кВт α2= α3 =30°
Угловая скорость вращения
вала ω=100 с-1
[σ]изг =70 МПа
Р2=Р3=Р/2=20 кВт
Определить диаметр вала
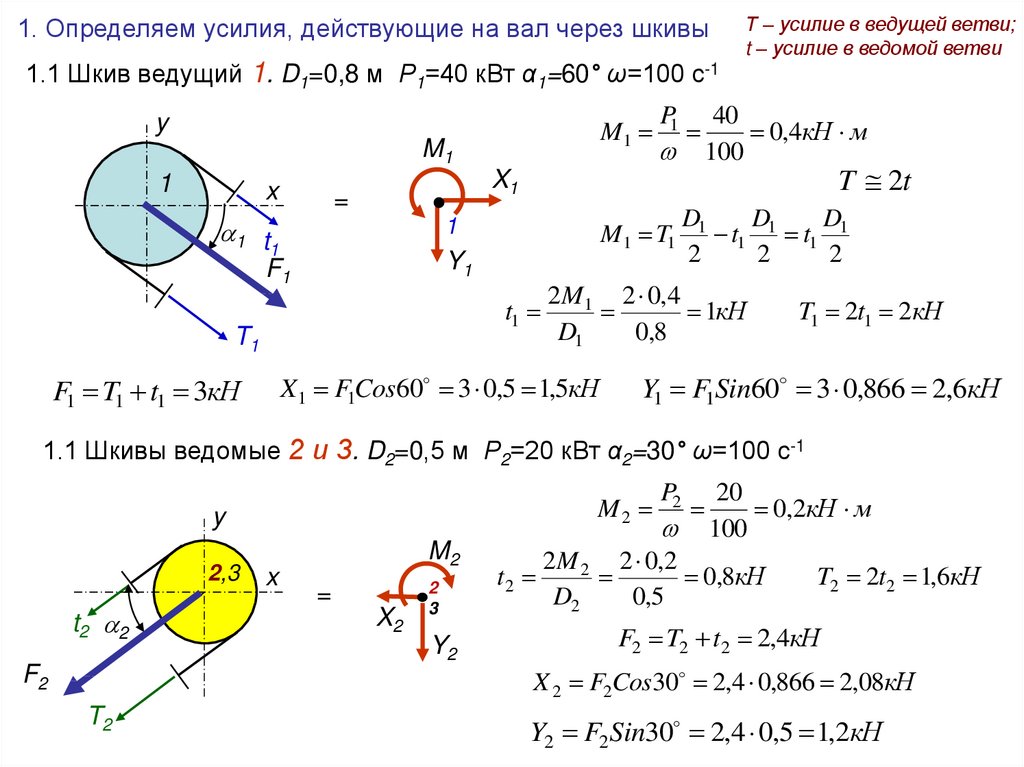
58.
1. Определяем усилия, действующие на вал через шкивы1.1 Шкив ведущий 1. D1=0,8 м Р1=40 кВт α1=60° ω=100 с-1
y
M1
M1
1
x
40
0,4кН м
100
T 2t
X1
=
1 t
1
M1 T1
1
Y1
F1
t1
T1
D1
D
D
t1 1 t1 1
2
2
2
2M1 2 0,4
1кН
D1
0,8
X1 F1Cos60 3 0,5 1,5кН
F1 T1 t1 3кН
P1
Т – усилие в ведущей ветви;
t – усилие в ведомой ветви
T1 2t1 2кН
Y1 F1Sin60 3 0,866 2,6кН
1.1 Шкивы ведомые 2 и 3. D2=0,5 м Р2=20 кВт α2=30° ω=100 с-1
M2
y
2,3
t2 2
F2
x
M2
=
X2
2
3
Y2
t2
P2
20
0,2кН м
100
2M 2 2 0,2
0,8кН
D2
0,5
T2 2t2 1,6кН
F2 T2 t2 2,4кН
X 2 F2Cos30 2,4 0,866 2,08кН
T2
Y2 F2 Sin30 2,4 0,5 1,2кН
59.
0,2м2
A
Б
0,3м
0,4м
0,2м
3
M1
1
B
X1
1
Y1
1
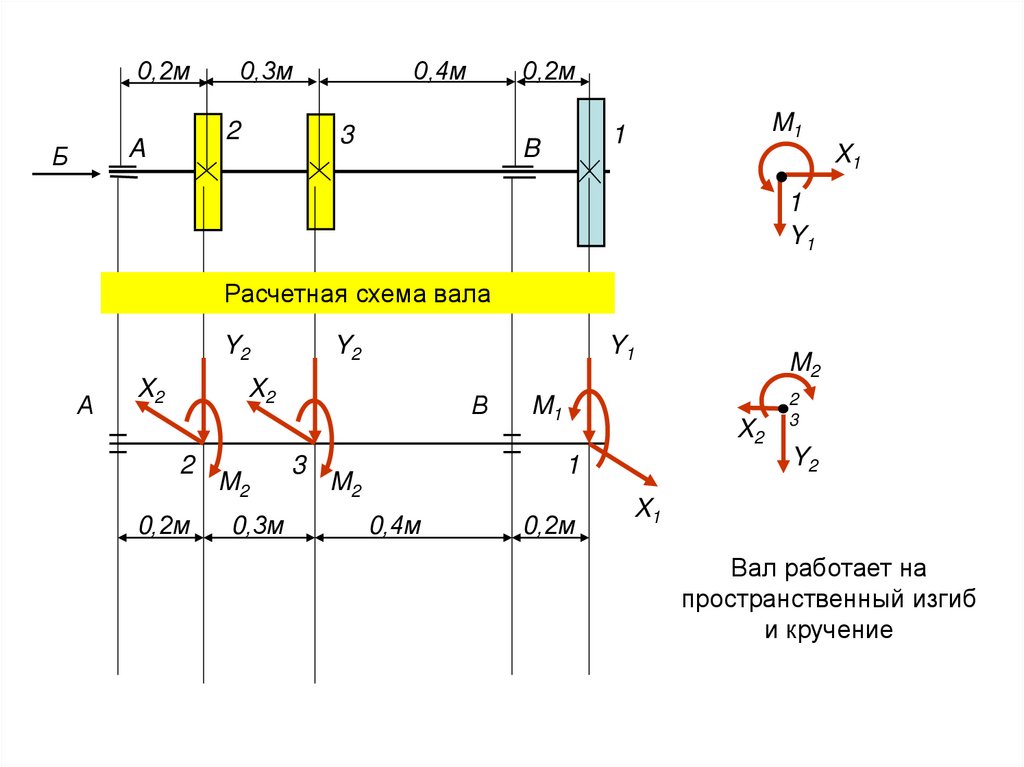
Расчетная схема вала
Y2
А
X2
Y2
Y1
X2
2
0,2м
M2
0,3м
В
3
M1
X2
1
M2
0,4м
M2
0,2м
2
3
Y2
X1
Вал работает на
пространственный изгиб
и кручение
60.
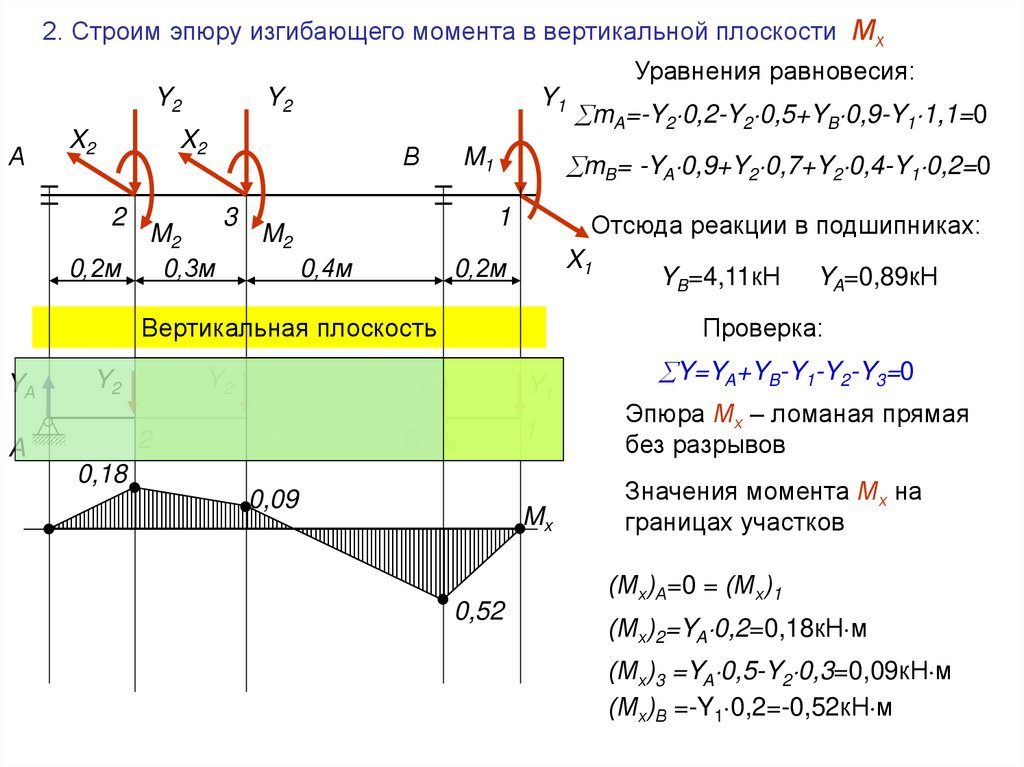
2. Строим эпюру изгибающего момента в вертикальной плоскости МхУравнения равновесия:
Y2
А
X2
Y2
Y1
X2
2
0,2м
M2
0,3м
В
3
mB= -YA 0,9+Y2 0,7+Y2 0,4-Y1 0,2=0
M1
1
M2
0,4м
Отсюда реакции в подшипниках:
X1
0,2м
Вертикальная плоскость
YА
Y2
Y2
2
A
3
mA=-Y2 0,2-Y2 0,5+YB 0,9-Y1 1,1=0
YB=4,11кН
YA=0,89кН
Проверка:
YB
Y1
B
1
0,18
0,09
Mx
0,52
Y=YA+YB-Y1-Y2-Y3=0
Эпюра Мх – ломаная прямая
без разрывов
Значения момента Мх на
границах участков
(Мх)А=0 = (Мх)1
(Мх)2=YA 0,2=0,18кН м
(Мх)3 =YA 0,5-Y2 0,3=0,09кН м
(Мх)В =-Y1 0,2=-0,52кН м
61.
3. Строим эпюру изгибающего момента в горизонтальной плоскости МуY2
А
X2
Y2
Y1
X2
2
0,2м
M2
0,3м
В
3
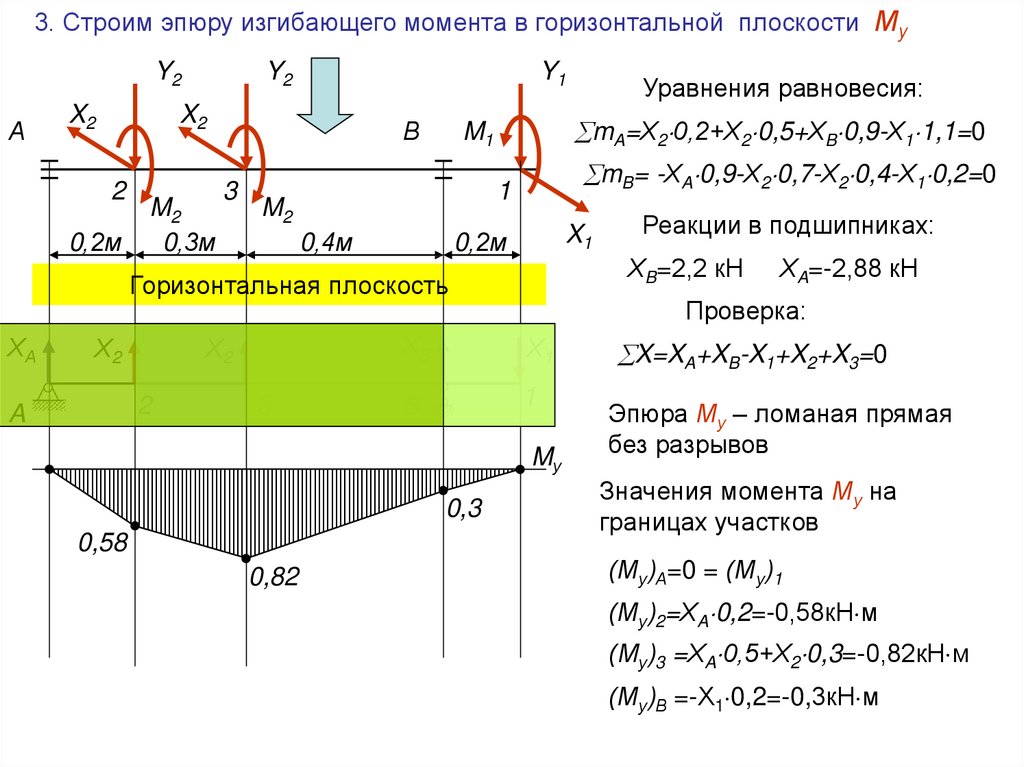
mA=Х2 0,2+Х2 0,5+ХB 0,9-Х1 1,1=0
M1
mB= -ХA 0,9-Х2 0,7-Х2 0,4-Х1 0,2=0
1
M2
0,4м
X1
0,2м
Х2
Х2
2
A
3
Х1
B
1
Mу
0,58
0,82
ХA=-2,88 кН
Проверка:
ХB
0,3
Реакции в подшипниках:
ХB=2,2 кН
Горизонтальная плоскость
ХА
Уравнения равновесия:
X=XA+XB-X1+X2+X3=0
Эпюра Му – ломаная прямая
без разрывов
Значения момента Му на
границах участков
(Му)А=0 = (Му)1
(Му)2=ХA 0,2=-0,58кН м
(Му)3 =ХA 0,5+Х2 0,3=-0,82кН м
(Му)В =-Х1 0,2=-0,3кН м
62.
4. Строим эпюру результирующего изгибающего момента МизгМх
0,18
0,09
Мизг
Mx
Му
0,52
Mу
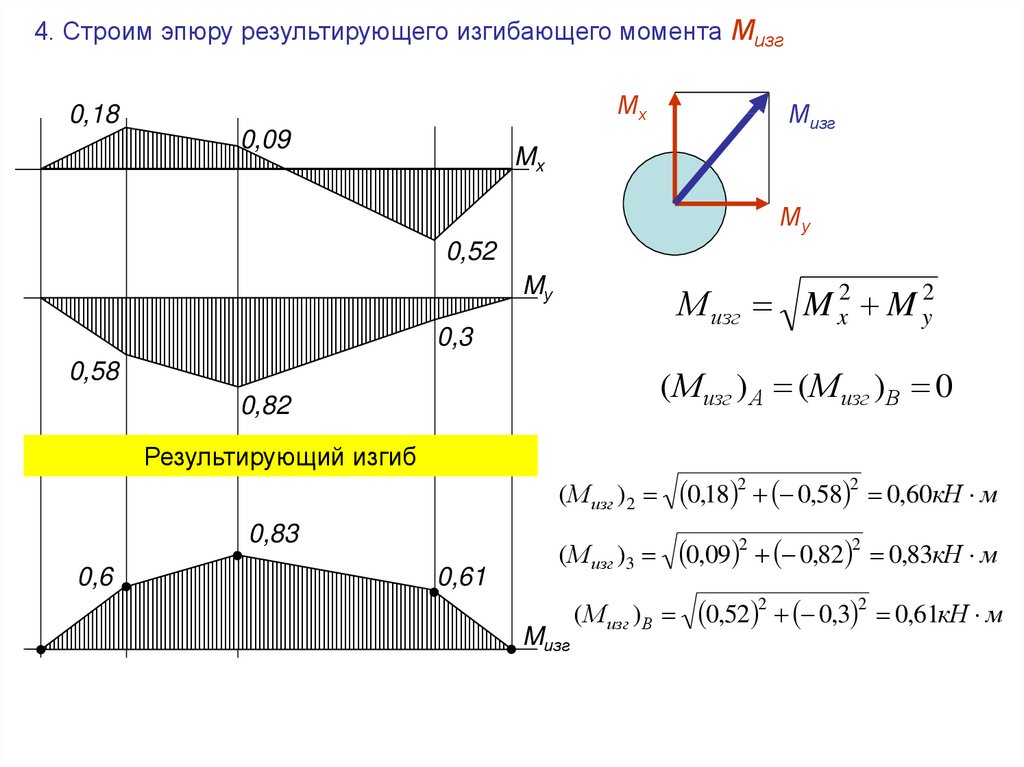
М изг M x2 M y2
0,3
0,58
(М изг ) А (М изг ) В 0
0,82
Результирующий изгиб
0,83
0,6
0,61
( М изг )2
0,18 2 0,58 2 0,60кН м
( М изг )3
0,09 2 0,82 2 0,83кН м
Mизг
( М изг ) В
0,52 2 0,3 2 0,61кН м
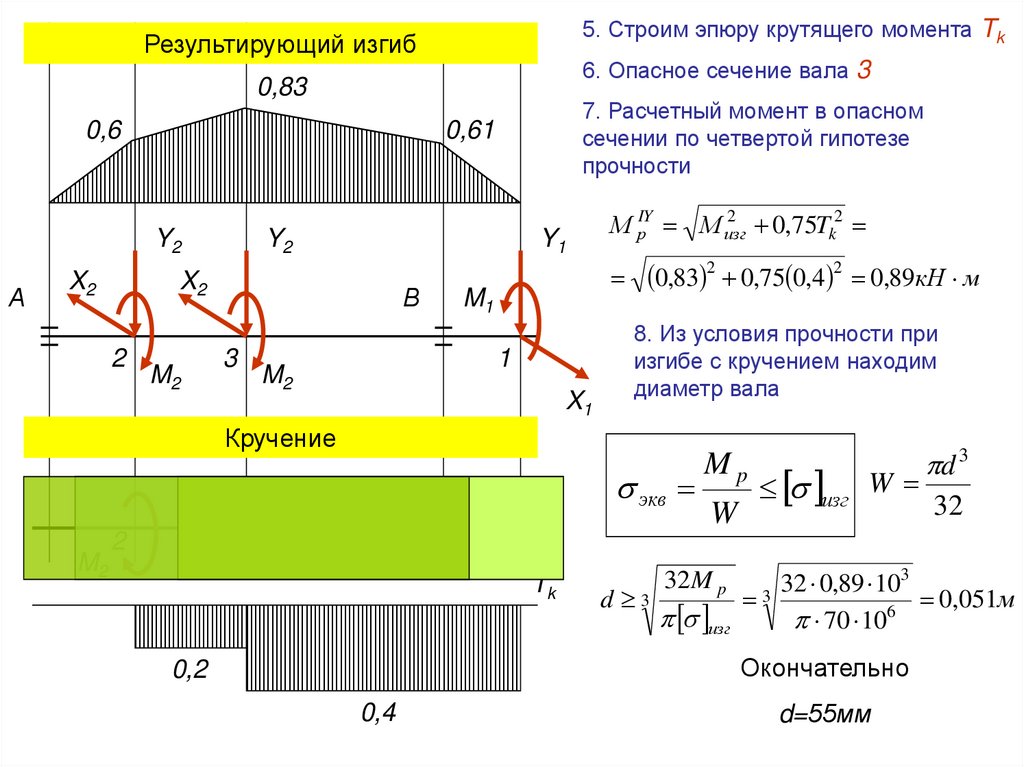
63.
5. Строим эпюру крутящего момента TkРезультирующий изгиб
6. Опасное сечение вала 3
0,83
0,6
Y2
А
X2
Y2
Y1
X2
2
7. Расчетный момент в опасном
сечении по четвертой гипотезе
прочности
0,61
В
3
M2
M1
1
M2
2
М рIY М изг
0,75Tk2
X1
0,83 2 0,75 0,4 2 0,89кН м
8. Из условия прочности при
изгибе с кручением находим
диаметр вала
Кручение
экв
M1
M2
2
M2
3
Mp
W
изг W
d 3
32
1
Tk
d 3
32 M p
изг
3
32
0
,
89
10
3
0,051м
6
70 10
Окончательно
0,2
0,4
d=55мм
64.
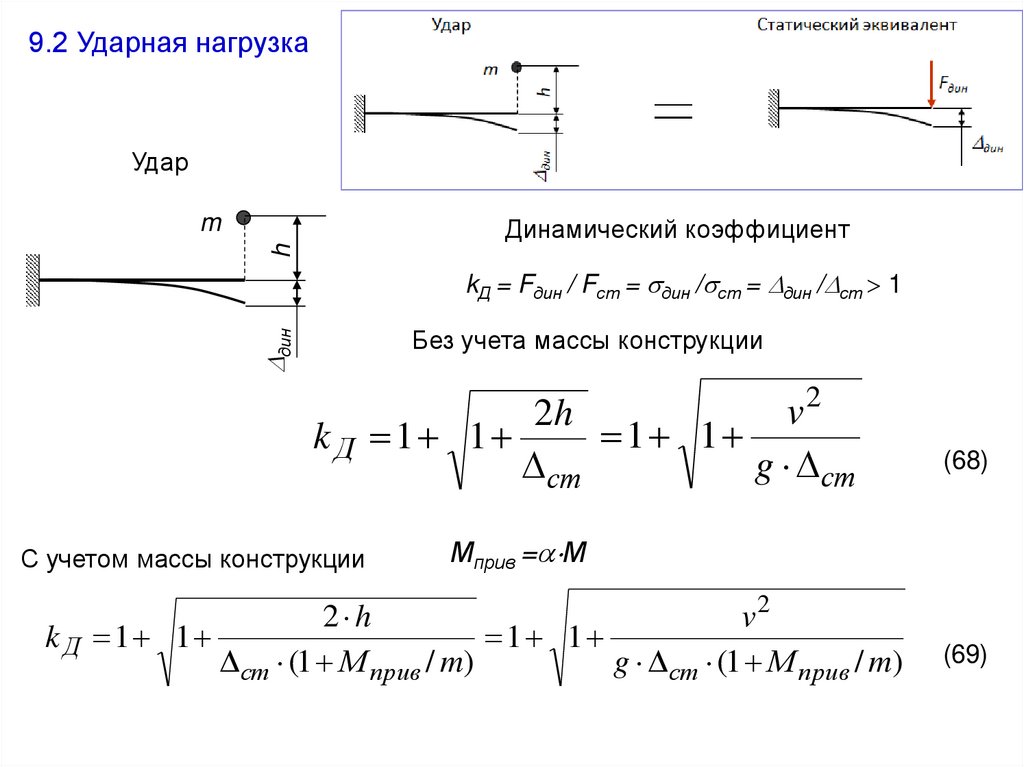
9.2 Ударная нагрузкаУдар
m
h
Динамический коэффициент
kД = Fдин / Fст = дин / ст = дин / ст 1
дин
Без учета массы конструкции
kД
С учетом массы конструкции
kД
v2
2h
1 1
1 1
g ст
ст
(68)
Мприв = М
2 h
v2
1 1
1 1
ст (1 М прив / m)
g ст (1 М прив / m)
(69)
65.
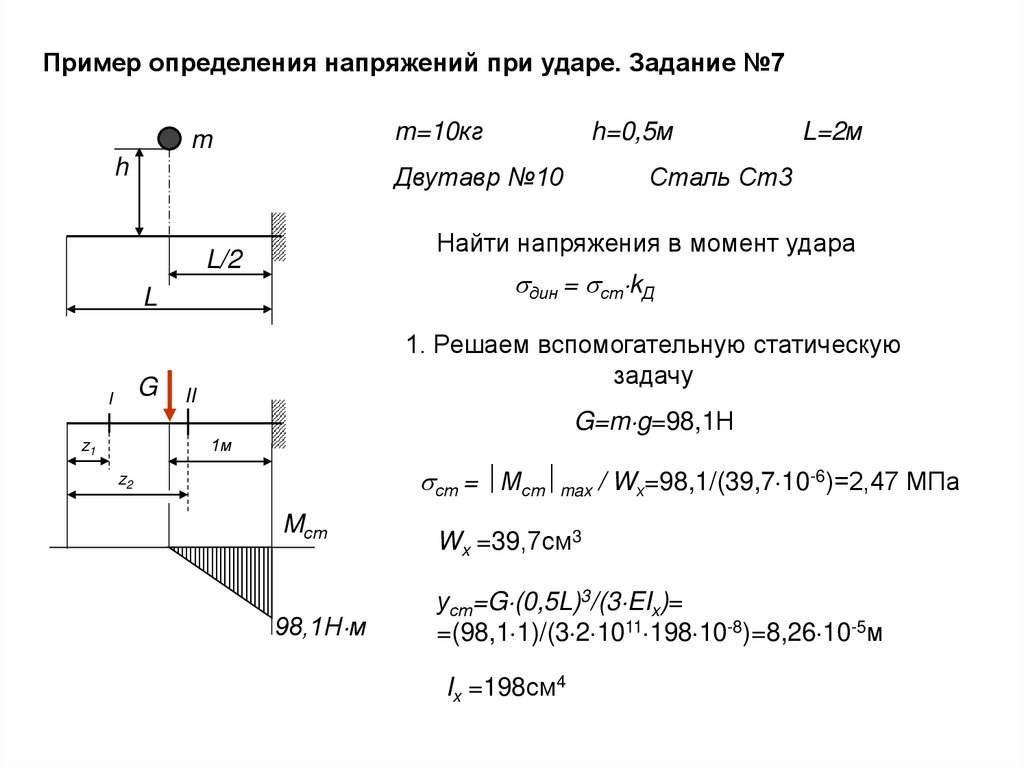
Пример определения напряжений при ударе. Задание №7m=10кг
m
h
Двутавр №10
1. Решаем вспомогательную статическую
задачу
II
G=m g=98,1Н
1м
z1
Сталь Ст3
дин = ст kД
L
G
L=2м
Найти напряжения в момент удара
L/2
I
h=0,5м
ст = Мст max / Wх=98,1/(39,7 10-6)=2,47 МПа
z2
Mст
98,1Н м
Wx =39,7см3
уст=G (0,5L)3/(3 EIx)=
=(98,1 1)/(3 2 1011 198 10-8)=8,26 10-5м
Ix =198см4
66.
2. Динамический коэффициент без учета массы балкиk Д 1 1
2 h
2 0,5
1 1
111
5
yст
8,26 10
3. Динамические напряжения без учета массы балки
дин = ст kД=2,47 111=274,2 МПа
Т = 240 МПа
4. Уточненный расчет с учетом массы балки
Мприв
L/2
L
Мприв = Мб
mб = 9,46кг/м
с=0,5
k Д 1 1
Мб = mб L = 9,46 2=18,92кг
105 105c 35c 2 2c3
140c
2
1,74
Мприв= МБ=1,74 18,92=32,97кг
2 h
2 0,5
1 1
54
5
yст (1 М прив / m)
8,26 10 (1 32,97 / 10)
дин = ст kД=2,47 54=133,4 МПа
67.
Ударная нагрузкаkД=Fдин/Fст = дин/ ст = дин/ ст 1
Удар
Статический эквивалент
m
h
Fдин
дин
дин
Энергия удара
Энергия деформации
U=П=mg(h+ дин)=Fст(h+ ст kД)
U=(1/2)Fдин дин = (1/2)Fст ст kД2
kД2+2kД -2h/ ст=0
kД
2h
1 1
ст
v2
1 1
g ст
68.
69.
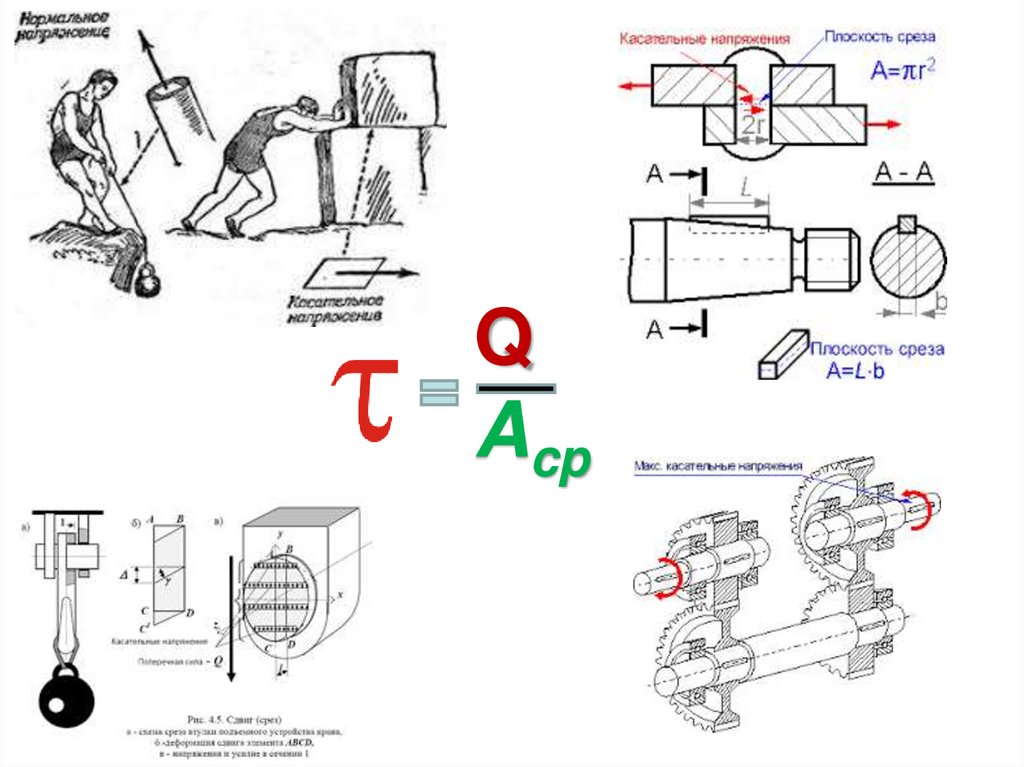
QAcp

























 mechanics
mechanics








