Similar presentations:
Сопротивление материалов
1.
Сопротивлениематериалов
2.
Курс «Сопротивление материалов» являетсячастью общей науки механики.
Теоретическая механика изучает
материальную точку и абсолютно твердое
тело.
Теория упругости изучает твердые тела.
Гидравлика – жидкости.
Аэрогазодинамика – газообразные
вещества.
3.
В курсе «Сопротивление материалов» изучаюттвердые деформируемые тела, т.е. меняющие размеры
и форму под действием нагрузок.
Сопротивление материалов –
наука о прочности, жесткости,
устойчивости и надежности
инженерных конструкций.
Целью курса является разработка инженерных
методов расчета конструкций и их деталей, а
также методов изучения свойств материалов.
4.
Прочность –свойство деталей и конструкций
выдерживать рабочие нагрузки без
разрушения или пластических
деформаций.
5.
Жесткость –свойство конструкций или деталей
выдерживать рабочие нагрузки без
значительных деформаций, нарушающих
их нормальную работу.
6.
Кроме прочности и жесткости конструкции и деталидолжны быть:
вибростойкими
вибропрочными
устойчивыми
технологичными
иметь современный дизайн.
7.
Физическая и математическаямодель.
8.
Физическая модель – упрощенноепредставление объекта или явления,
сохраняющая основные его черты.
Применительно к расчетам на прочность
и жесткость физическая модель должна
отражать:
геометрические свойства детали,
свойства материала детали,
действующие на деталь нагрузки.
9.
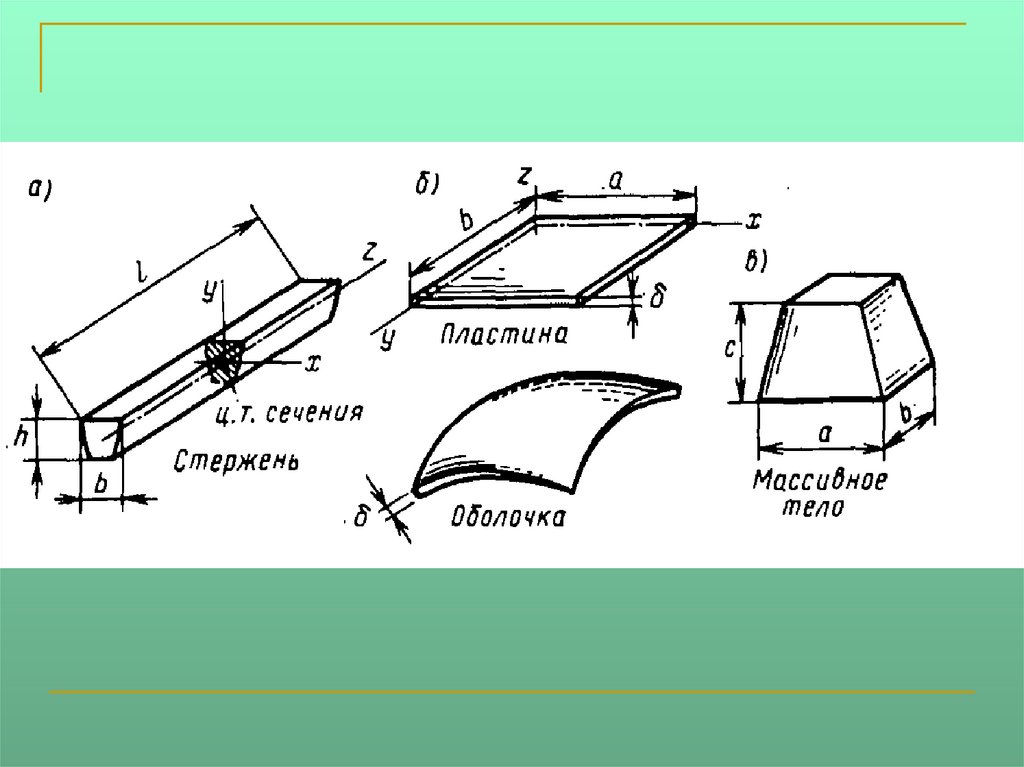
По геометрическим признакам все тела делятсяна три группы:
стержни
пластины и оболочки
массивы
10.
Стержни (брус) –тела, у которых одно измерение
существенно больше двух других (ширина,
высота).
Характеризуются поперечным сечением и
формой оси.
11.
Пластины и оболочки –тела, у которых одно измерение
существенно меньше двух других.
Характеризуются толщиной и формой
серединной поверхности.
12.
Массивы –тела, у которых все три измерения
соизмеримы.
13.
14.
Реальные конструкционные материалы(стали, чугуны, цветные материалы)
имеют кристаллическое строение,
кристаллы малы и расположены хаотично.
Сложность реального строения и
возникающая трудность при
математическом его описании явились
причиной разработки модели твердого
тела.
15.
Эта модель должна сохранитьосновные свойства материалов и в тоже
время сделать простым их аналитическое
описание. Поэтому в расчетах на
прочность и жесткость принимается ряд
основных гипотез и допущений:
16.
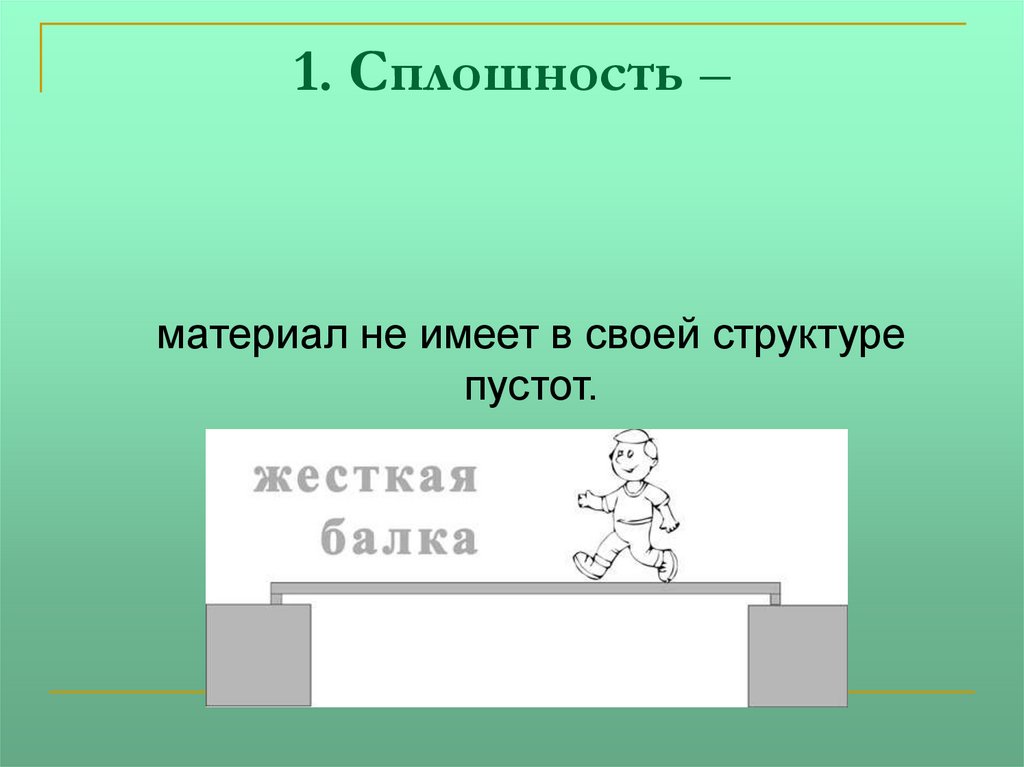
1. Сплошность –материал не имеет в своей структуре
пустот.
17.
2. Однородность –одинаковые свойства материала в любой
точке детали.
18.
3. Изотропность –одинаковые свойства материала в
различных направлениях.
19.
4. Идеальная упругостьУпругость – свойство тела
восстанавливать форму и размеры после
снятия нагрузки.
Пластичность – свойство тела получать
большие остаточные деформации после
снятия нагрузки.
20.
5. Отсутствие первоначальныхвнутренних напряжений.
21.
6.Принцип малых перемещений –перемещения конструкции малы по
сравнению с размерами конструкции.
22.
7. Линейная деформируемостьматериала –
в зоне действия упругих деформаций
зависимость между силой и
приращением размера линейная.
23.
8. Гипотеза плоских сечений –плоское до нагружения сечение остается
плоским и после нагружения.
24.
Все свойства физической модели,описанные уравнениями, составляют
математическую модель
деформированного тела.
25.
Математическая модель должнасодержать три группы уравнений:
статические – включающие нагрузки и
условия равновесия;
физические – отражающие связь между
нагрузками и деформациями;
геометрические – отражающие
изменение формы и размеров под
нагрузкой.
26.
Схематизация (внешних) нагрузок(сил):
по типу контакта
– сосредоточенная нагрузка
– распределенная (погонная) нагрузка
– массовые силы
по закону изменения во времени
– статическая
– динамическая
27.
Сосредоточенная нагрузка:приложена к части внешней поверхности
тела, размеры которой малы в сравнении
с размерами тела.
На схеме изображается как вектор (стрелка).
Задаётся в [Н]
Р
28.
Распределенная (погонная) нагрузкаприложена к части поверхности тела или ко всей
поверхности. Для распределённой нагрузки
задается её интенсивность, т.е. количество
нагрузки приходящейся на определенный участок
поверхности нагружаемого тела.
Интенсивность постоянной нагрузки,
распределенной по длине бруса задается в [кН/м].
q
29.
Принцип Сен-Венанав сечениях, достаточно удалённых от мест
приложения нагрузки, деформация тела
не зависит от конкретного способа
нагрузки и определяется лишь
статическим эквивалентом нагрузки.
30.
Геометрические характеристикиплоских фигур.
31.
При решении задач возникаетнеобходимость оперировать некоторыми
геометрическими (интегральными)
характеристиками плоских сечений
(ИХС).
Эти характеристики имеют применение, в
основном, при решении задач на
прочность и жесткость, в силу узкого
прикладного значения их рассматривают
в курсе «Сопротивления материалов».
32.
Деформация –изменение формы и/или размеров тела,
вызванное изменением взаимного
положения частиц (атомов, молекул) этого
тела под влиянием внешней нагрузки или
изменения температуры.
33.
Для бруса различают деформации:растяжение-сжатие (увеличение-
уменьшение продольного и поперечного
размера)
изгиб (изменение кривизны продольной
оси)
кручение (взаимный поворот поперечных
сечений относительно продольной оси)
34.
Рассматривая элементарный объём тела dV =dx dy dz различают:
3 линейные деформации (соответственно вдоль
осей X,Y,Z)
3 угловые деформации (изменение первоначально
прямых углов между координатными осями X,Y,Z).
Линейные деформации:
– абсолютные, т.е. приращение длины отрезка
(разность между конечным и начальным размером);
– относительные, т.е. отношение абсолютных
деформаций (приращений длины) к первоначальной
величине деформированного отрезка.
35.
Линейные деформации обозначаютсях, у, z - соответственно вдоль X,Y, Z.
Угловые деформации обозначаются ху,
хz, zу – соответственно изменение
прямых углов в плоскостях XY, XZ, ZY.
Для изучения внутренних сил в теле
используется метод сечений.
36.
Метод сечений.Внутренние силы.
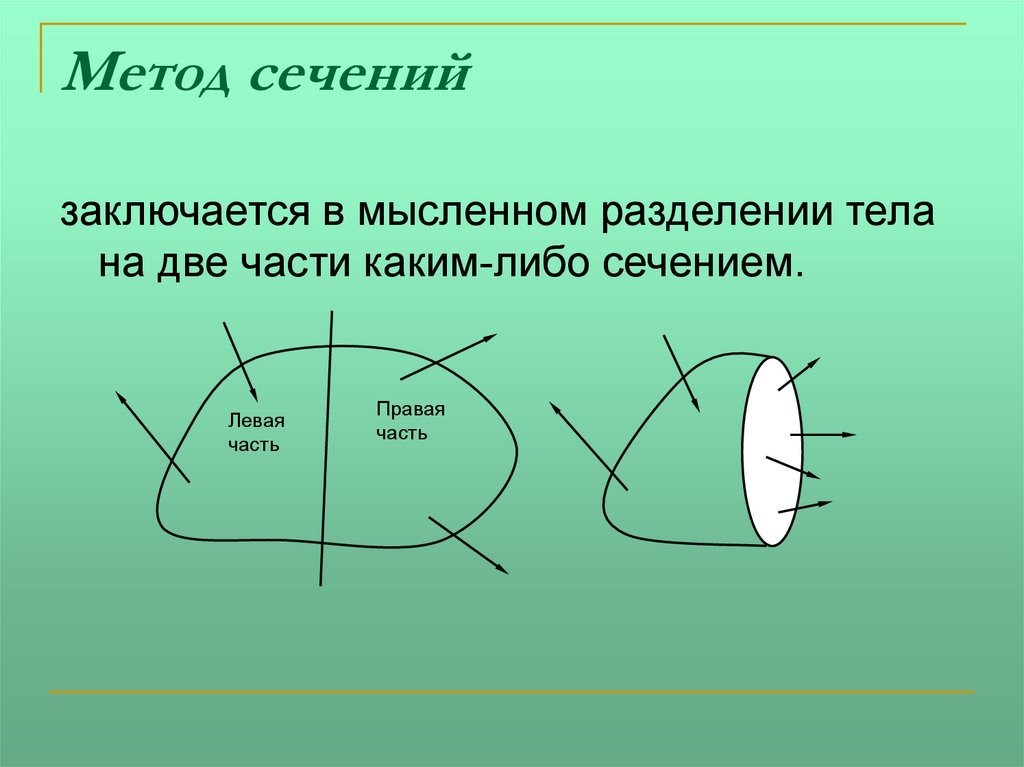
37.
Метод сеченийзаключается в мысленном разделении тела
на две части каким-либо сечением.
Левая
часть
Правая
часть
38.
Все тело находится в равновесии.После мысленного рассечения и отбрасывания
правой части, её действие должно быть
заменено системой сил в сечении,
сохраняющих равновесие левой части.
Такие же силы, но противоположного
направления, действуют на правую часть.
39.
При этом внутренние силывзаимодействия между частицами,
расположенными вблизи друг от друга, но
разделенными сечением, можно
рассматривать как внешние – для каждой
из частей тела.
Так как обычно в сопротивлении материалов
рассматриваются покоящиеся элементы
конструкций, то система внешних сил
(включая силы, приложенные со стороны
другой части тела), приложенных к каждой
из частей тела является
уравновешенной.
40.
Для удобства приводим все силы, действующиев сечении, к центру тяжести.
Q
Левая
часть
Левая
часть
М
41.
Эпюры внутренних силовыхфакторов
График зависимости величины какого-либо
внутреннего силового фактора от координаты
z поперечного сечения, в котором действует
этот внутренний силовой фактор, называется
эпюрой.
Эпюры имеют большое значение в расчетах на
прочность, так как позволяют легко
определить сечение, в котором брус
максимально нагружен.
Такое сечение называется опасным сечением.
42.
Грузовой участок –часть бруса, для которой эпюра есть
непрерывная линия, выражаемая единой
формулой.
Практически сначала определяются
границы грузовых участков, а грузовой
участок – часть бруса между границами.
43.
Границей грузового участка являетсясечение:
являющееся началом/концом бруса или местом
излома продольной оси;
в котором приложена сосредоточенная нагрузка
или пара сил;
начинается /заканчивается/ изменяется
интенсивность распределенной нагрузки;
в котором имеется опора (это частный случай
приложения сосредоточенной силы, т.к. опора
создает реакцию).
44.
Граничное условие (Г.У.)– это информация об известных
интегральных характеристиках
напряжённого состояния в начале или
конце стержня.
Различают:
левое Г.У. (с противоположным знаком)
правое Г.У. (с естественным знаком)
45.
Напряжение.Напряженное состояние в точке
тела.
46.
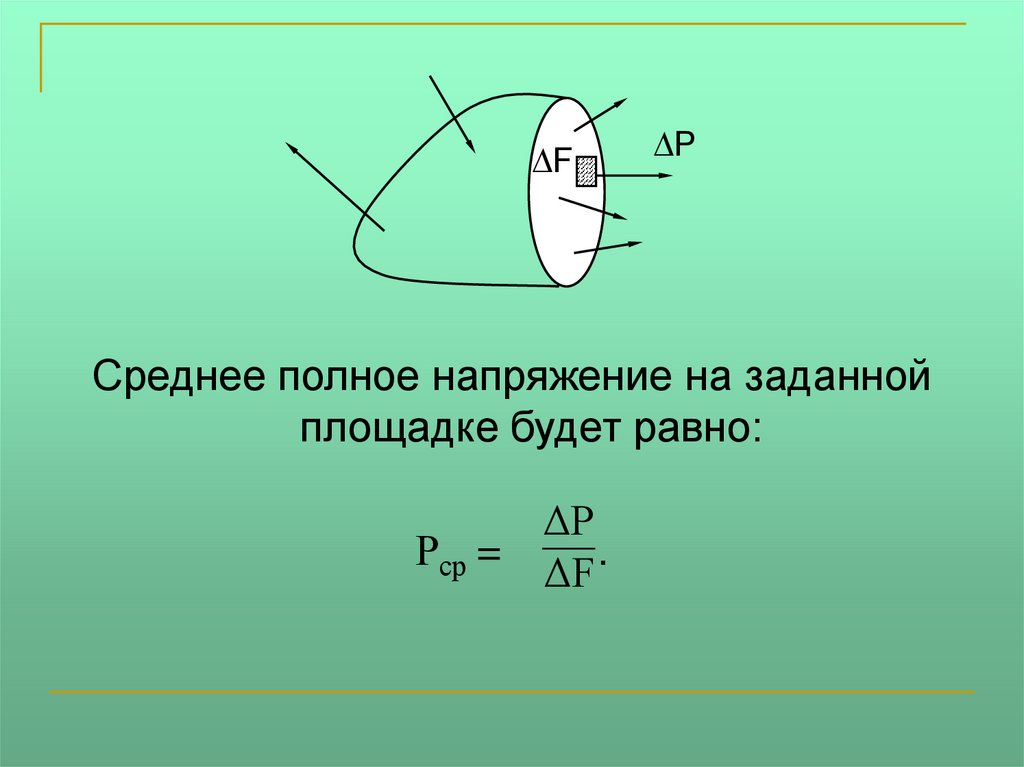
Нагруженное тело мысленно рассечемплоскостью, и действие отброшенной
части заменим действием внутренних сил.
В сечении выберем произвольную точку, а в
её окрестности элементарную площадку
F.
Равнодействующую сил, действующих на
площадку, обозначим Р.
47.
FР
Среднее полное напряжение на заданной
площадке будет равно:
ΔР
Рср =
.
ΔF
48.
Если площадку уменьшать, то в пределе онаобратится в точку.
Напряжение – это предел отношения
внутренней силы к площади, на которой
она действует, при условии, что площадь
стремится к нулю.
Р – полное напряжение [Н/м2=Па].
P = lim F 0 ΔР
ΔF
49.
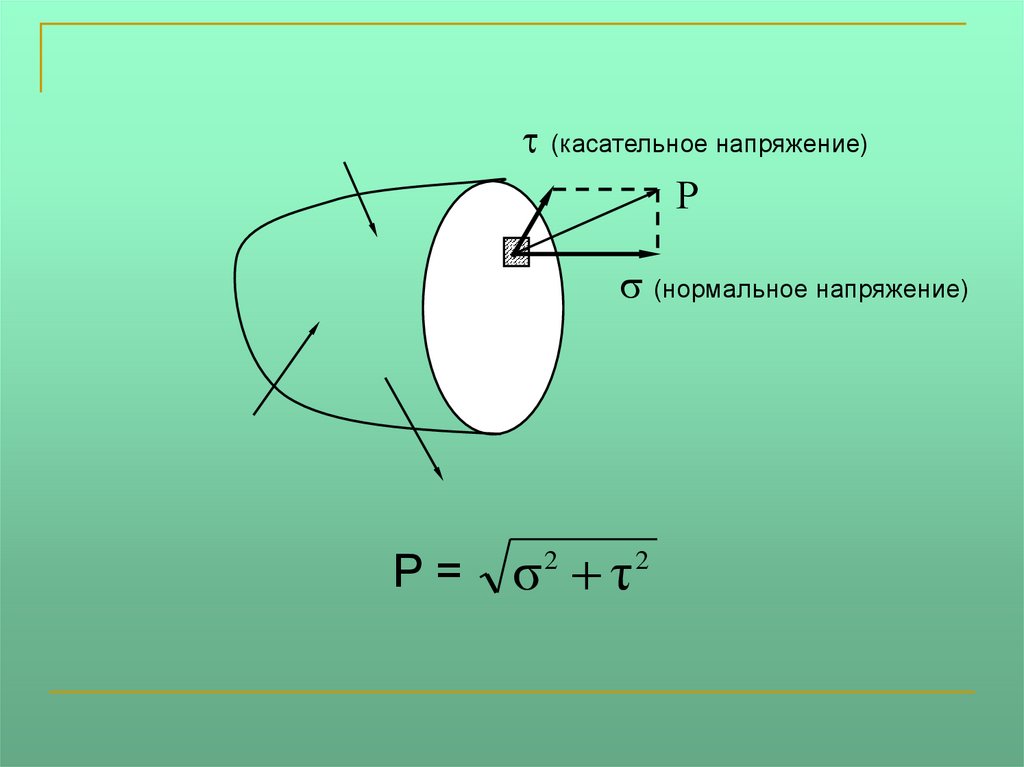
Вектор полного напряжения можно разложитьна проекции
Проекцию полного напряжения на
нормаль к плоскости сечения будем
называть нормальным
напряжением (обозначается ),
а проекцию полного напряжения на
плоскость сечения – касательным
напряжением (обозначается ).
50.
(касательное напряжение)Р
(нормальное напряжение)
Р=
σ2 τ2
51.
Индекс нормального напряжения (σi)соответствует оси, перпендикулярной
плоскости сечения.
Индексы касательного напряжения (τij)
проставляются следующим образом:
первый индекс соответствует оси,
перпендикулярной плоскости сечения, в
котором лежит касательное напряжение,
второй индекс соответствует оси, которой
параллельно касательное напряжение.
52.
Проводя другие плоскости, будем получатьдругие значения напряжений.
Совокупность напряжений по всем
плоскостям, проходящим через заданную
точку, называется напряженным
состоянием в точке тела.
53.
Формула нормальных напряжений поплоскости поперечного сечения:
My
N Mx
y
x
F Jx
Jy
где – нормальное напряжение в точке сечения;
N – продольная сила в сечении;
Мх, Му – изгибающие моменты в сечении;
F – площадь поперечного сечения;
Jх, Jу – главные осевые моменты инерции сечения;
х, у – координаты точки, в которой вычисляется
напряжение относительно главных центральных
осей.
54.
Растяжение-сжатиеMy
N Mx
y
x
F Jx
Jy
N
F
55.
Поперечный изгиб(в вертикальной плоскости)
My
N Mx
y
x
F Jx
Jy
Mx
y
Jx
56.
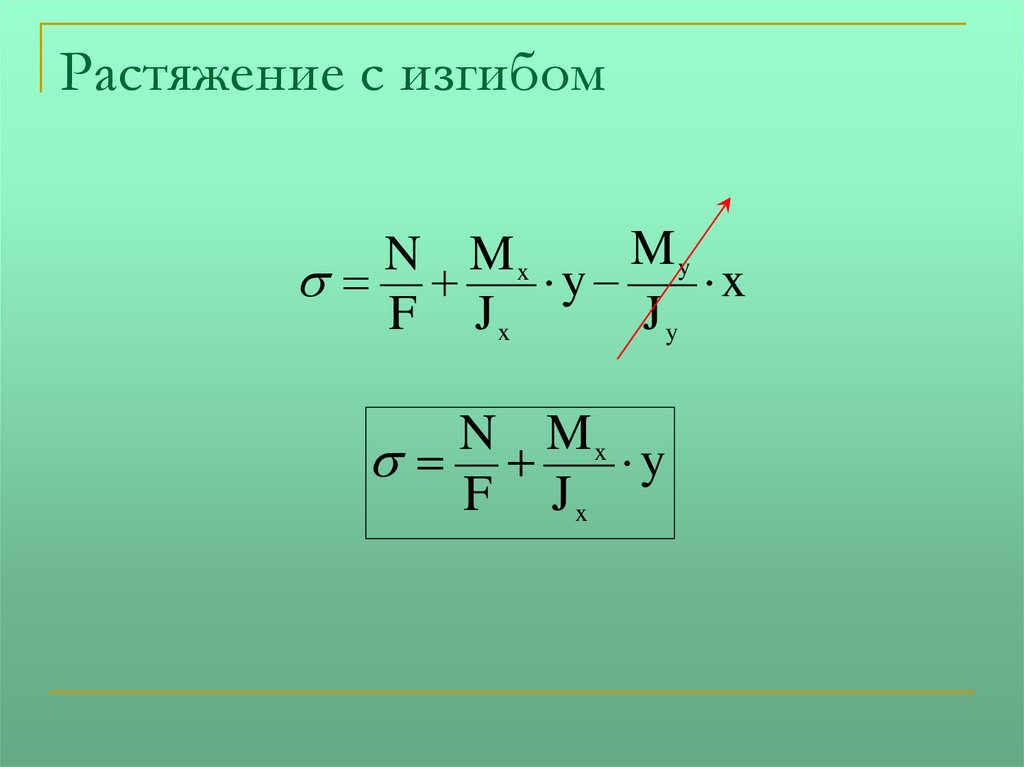
Растяжение с изгибомMy
N Mx
y
x
F Jx
Jy
N Mx
y
F Jx
57.
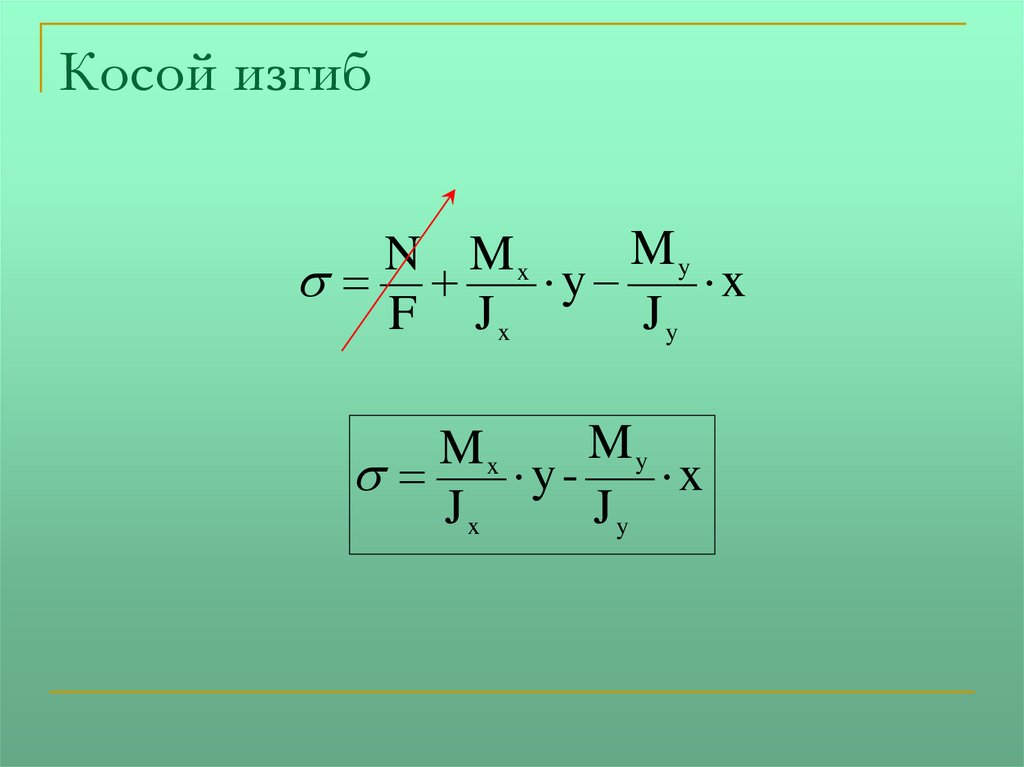
Косой изгибMy
N Mx
y
x
F Jx
Jy
My
Mx
y x
Jx
Jy
58.
Касательные напряжения в плоскости поперечногосечения при кручении вычисляются по формуле:
Mк
J
max
Mк
W
где – касательное напряжение в точке сечения;
Мк – крутящий момент в сечении;
J – полярный момент инерции сечения;
– расстояние от центра тяжести сечения до
точки, в которой вычисляется касательное
напряжение;
Wρ – полярный момент сопротивления.
59.
Касательное напряжение в плоскости поперечногосечения при изгибе вычисляются по формуле
Журавского:
Q y S*x
Jxb
где – касательное напряжение в точке сечения;
Qу – поперечная сила в сечении;
S*x – статический момент части сечения отсеченной
по уровню на котором вычисляются напряжения
относительно главной оси Х;
Jх – осевой момент инерции относительно главной
оси Х;
b – ширина сечения на том уровне, где вычисляются
напряжения.
60.
Испытания материалов нарастяжение.
Диаграмма растяжения.
61.
При проектировании строительныхконструкций, машин и механизмов инженеру
необходимо знать значения величин,
характеризующих прочностные и
деформационные свойства материалов. Их
можно получить путем механических испытаний,
проводимых в экспериментальных лабораториях
на соответствующих испытательных машинах.
Наибольшую информацию о механических
свойствах металлов можно получить из
статических испытаний на растяжение.
Испытания проводятся в соответствии с ГОСТом.
62.
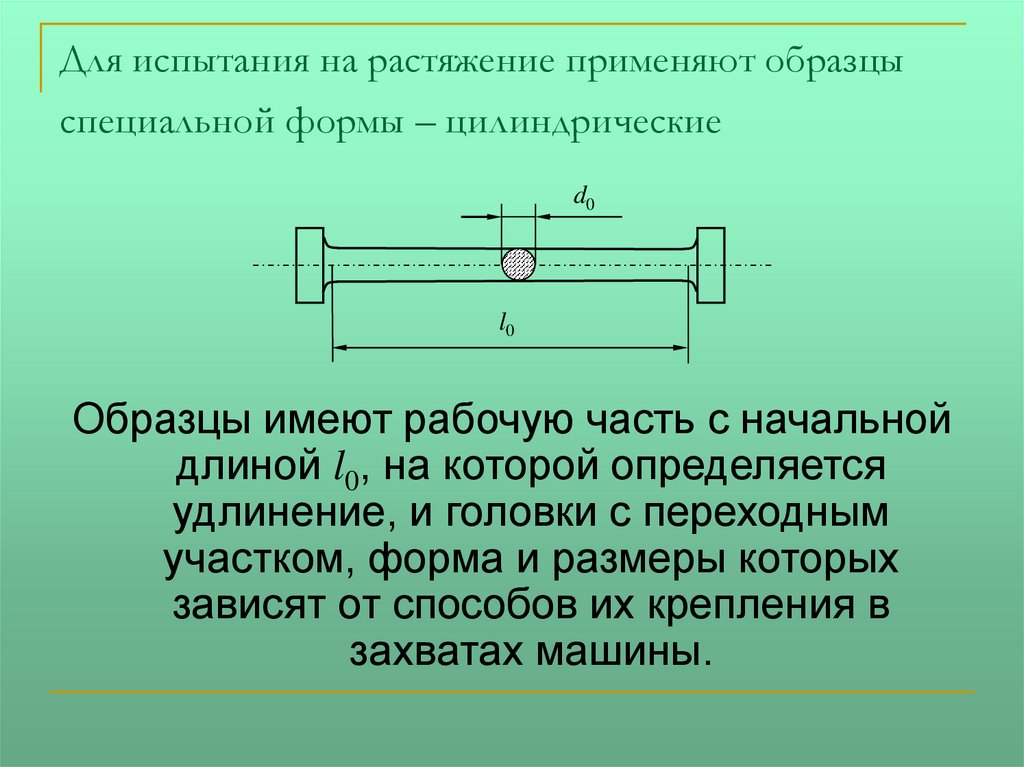
Для испытания на растяжение применяют образцыспециальной формы – цилиндрические
d0
l0
Образцы имеют рабочую часть с начальной
длиной l0, на которой определяется
удлинение, и головки с переходным
участком, форма и размеры которых
зависят от способов их крепления в
захватах машины.
63.
Испытания проводят на разрывных илиуниверсальных машинах.
Разрывная машина снабжена устройством
для автоматической записи в
определенном масштабе диаграммы
растяжения, т.е. графика зависимости
между растягивающей силой Р и
удлинением образца l.
Рассмотрим диаграмму растяжения
образца из низкоуглеродистой стали.
64.
Диаграмма растяженияP
D
К
В
С
А
О
Δl
65.
ОА – зона упругостиАВ – зона пропорциональности
ВС – зона общей текучести (площадка
текучести)
СD – зона упрочнения
DK – зона местной текучести
66.
Механические характеристики материала:σу – предел упругости
σпц – предел пропорциональности
σт – предел текучести
σв – предел прочности (временное
сопротивление отрыву)
tg E
E – закон Гука
Е – модуль Юнга
67.
Допускаемые напряженияопределяются по формуле:
Т ( В )
n
n – коэффициент запаса (1,5 … 17)
Помимо характеристик прочности
диаграмма напряжений позволяет
определять характеристики пластичности.
68.
Относительное удлинение послеразрыва ( )
– это отношение приращения расчетной
длины образца после разрыва к ее
первоначальному значению, вычисляемое
по формуле:
lк lo
δ
100%
lo
69.
Относительное сужение послеразрыва ( )
– это отношение уменьшения площади
поперечного сечения образца в месте
разрыва к начальной площади
поперечного сечения образца:
Fк Fo
ψ
100%
Fo
70.
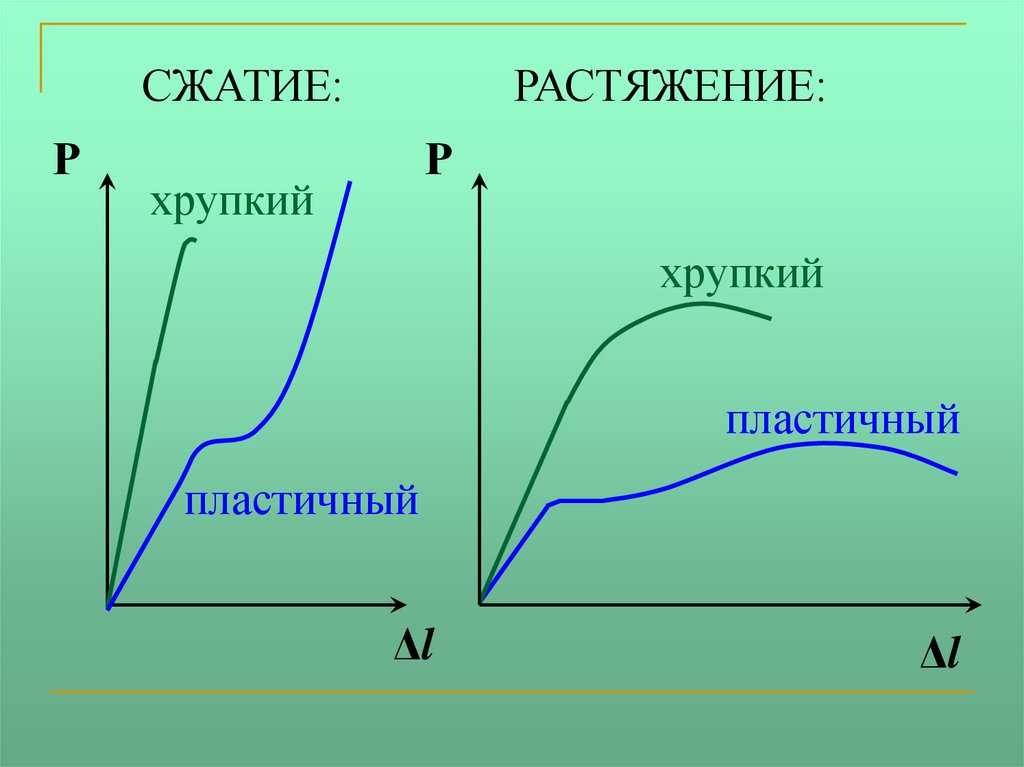
СЖАТИЕ:Р
РАСТЯЖЕНИЕ:
Р
хрупкий
хрупкий
пластичный
пластичный
Δl
Δl
71.
Перемещения.72.
Растяжение-сжатиеW – линейное (горизонтальное)
перемещение;
Кручение
Θ – угол закрутки (угловое перемещение);
Изгиб
– угол поворота сечения;
V – прогиб (вертикальное перемещение);
73.
Статически определимойназывается система, у которой число наложенных
связей равно числу степеней свободы.
Если же число наложенных связей будет больше,
то такая система называется статически
неопределимой, а разница между ними
определяет
степень
статической
неопределимости плоской рамы:
n = m – 3,
где n – степень статической неопределимости,
m – число наложенных связей.
74.
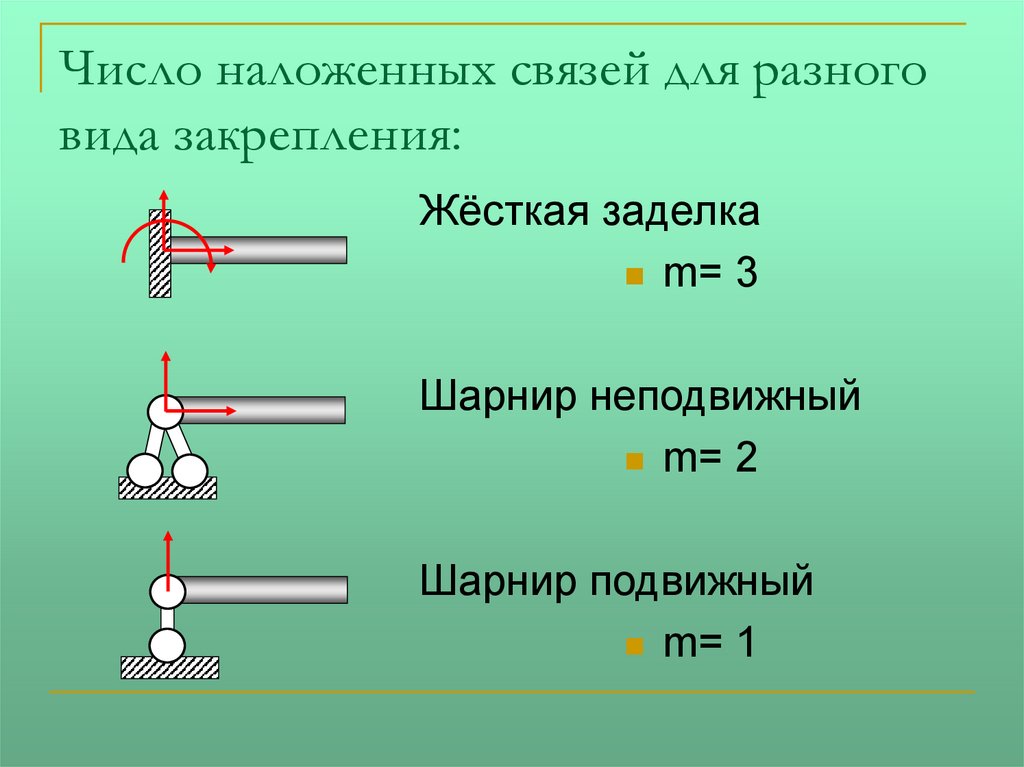
Число наложенных связей для разноговида закрепления:
Жёсткая заделка
m= 3
Шарнир неподвижный
m= 2
Шарнир подвижный
m= 1
75.
Интеграл Мора:Растяжение-сжатие
Кручение
Изгиб
N ( z) N ( z)
0
EF
dz
М к ( z) M ( z)
dz
GJ
0
к
М х ( z) M ( z)
dz
EJ x
0
x
76.
Формула Эйлера.Коэффициент приведения длины.
77.
Формула Эйлера имеет вид:EJ min
Fкр
2
( l )
2
где Fкр – критическая сила сжатого стержня;
Е – модуль упругости;
Jmin – минимальный момент инерции сечения;
l – приведённая длина стержня.
78.
Коэффициент приведения длины:Схема нагружения
µ=0,5
µ=0,5
µ=0,7
µ=1
µ=2
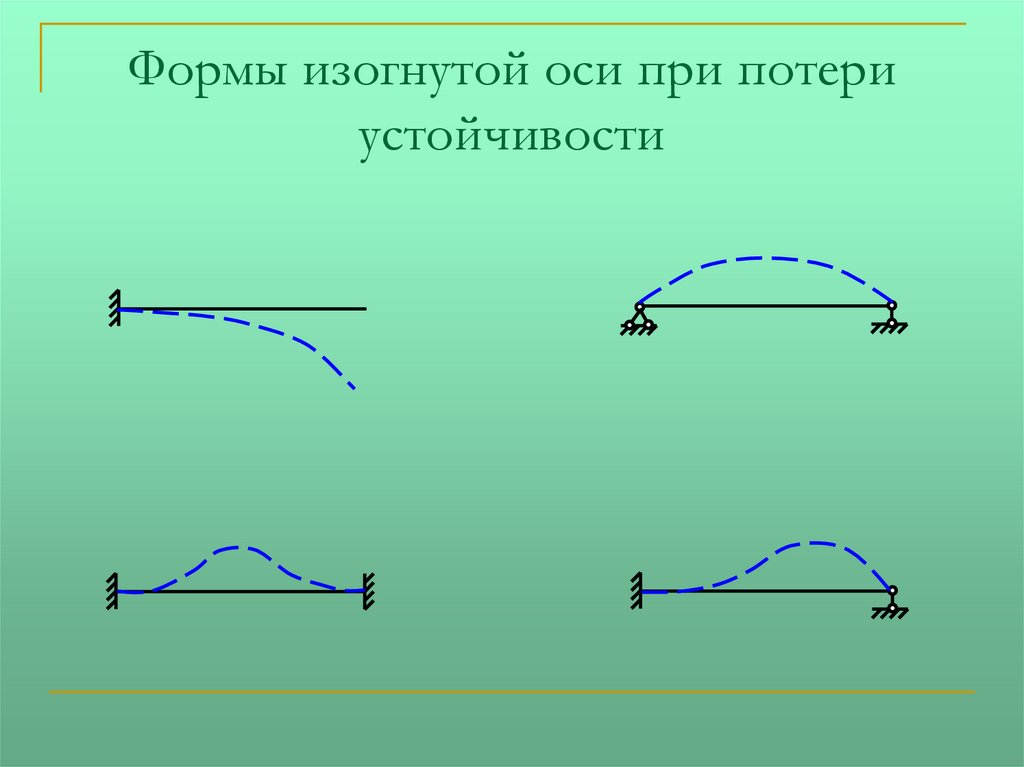
79.
Формы изогнутой оси при потериустойчивости




































































 mechanics
mechanics