Similar presentations:
Расчет на прочность по нормальным напряжениям при изгибе
1. Расчет на прочность по нормальным напряжениям при изгибе
Цель: изучить условия прочности по нормальным напряжениямпри прямом поперечном изгибе и виды расчетов на прочность
Опорные знания
Прочностные характеристики материала
Нормальные напряжения в любой точке
поперечного сечения
Механические характеристики
Пластичный материал
σ
σт
Т
п
n =1,4 …2
ε
σb
ε
σт- предел текучести
σв- предел временно-
в
п
го сопротивления
[σ]- допускаемое нап-
h
x
C
R
-нормальное
сопротивление
Устанавливается
соответствующими
ГОСТами
y
+
b
нейтральная линия
n =2,5…5
ряжение для материала
σ-напряжение в любой
Сопротивление строительных материалов
Н
Эпюра σ
y
Хрупкий материал
σ
R- расчетное
сопротивление
R R
н
m
γm- коэффициент безопасности
γm=1,05…1,15
точке поперечного сечения;
Mx
y
Jx
Мх - изгибающий момент
в сечении;
Jх - осевой момент инерции
сечения;
y- расстояние от нейтрального слоя до точки в которой
определяется напряжение
2.
Максимальные нормальные напряженияС
h
max M max ymax
max
-
Y
Jx
Х
+
min
в
Геометрическая
характеристика
прочности
сечения балок
Wx – осевой момент сопротивления
Круг
Y
Y
С
Х
С
ymax h
Wx вh
2
6
12
2
W y hв
6
d
Единицы измерения,
cм3, м3
2
Прокатные
профили
Y
Х
2
3 в
3 h
hв
вh
W
:
y
Wx
: ;
2
Wx
Квадрат
ymax d
2
в
12
max M х max
для элементарных плоских сечений
Прямоугольник
h
max M xmax
J x ymax
Wx J x ymax
d4 :d
Wx Wy 64
2
3
Wx Wy d
32
a
С
Х
ymax a
2
a
4
Wx W y a12 : a2
3
Wx Wy a
6
Сортамент
прокатной
стали
ГОСТ 8509-86
ГОСТ 8510-86
ГОСТ 8239-89
ГОСТ 8240-89
3.
Условие прочностиПо предельным состояниям
p
max M xmax mR
Wx
M xpmax -максимальный изгибающий
момент в сечении от расчетной
нагрузки
Wx
-осевой момент сопротивления
R
-расчетное сопротивление
заданного материала
m
-коэффициент условий работы
m c к
с -оценивает условия эксплуатации
к -оценивает степень
ответственности и капитальности
Принимаем с эпюры моментов Мх
Зависит от геометрических размеров и
формы поперечного сечения
Зависит от материала. Принимаем по
справочным таблицам
m =1 для нормальных условий
эксплуатации, в остальных случаях
принимается заданием на проектирование
4.
Три вида расчетов по нормальным напряжениямp
M
x
max max mR
Wx
Проверочный расчет Проектировочный расчет
Проверка прочности
p
max M xmax mR
Wx
Подбор сечения
p
WхТР M xmax
mR
Определение
эксплуатационной
способности
Определение предельной
нагрузки
М хmax mR Wx
5. Пример №1
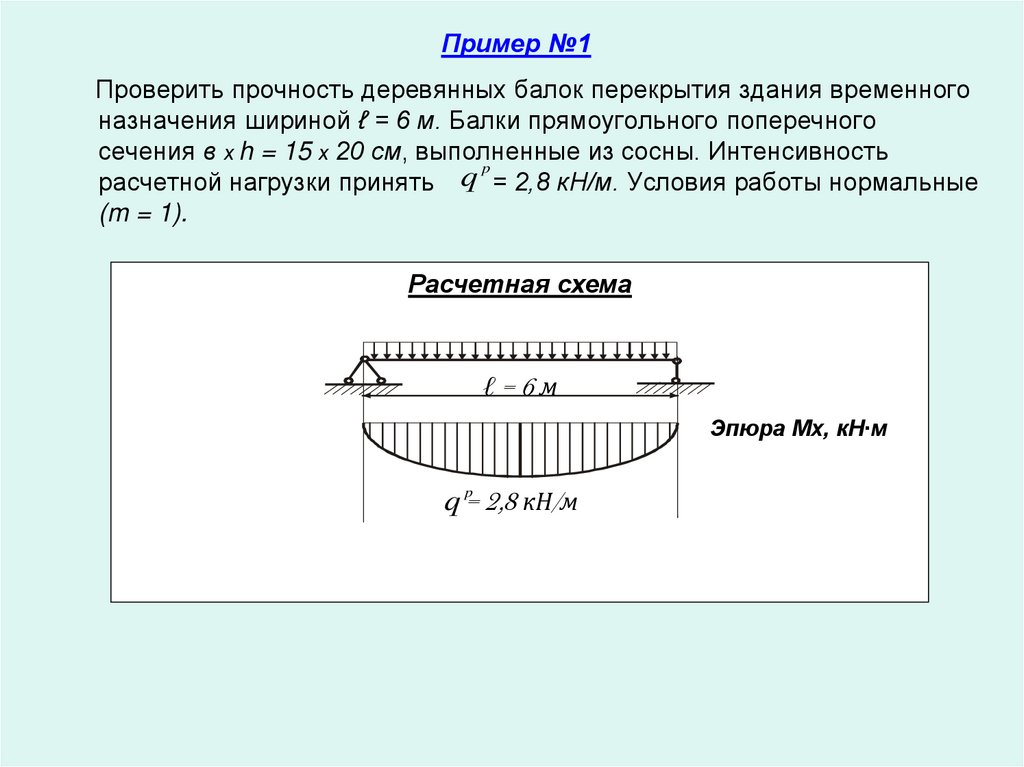
Проверить прочность деревянных балок перекрытия здания временногоназначения шириной ℓ = 6 м. Балки прямоугольного поперечного
сечения в х h = 15 х 20 см, выполненные из сосны. Интенсивность
p
расчетной нагрузки принять q = 2,8 кН/м. Условия работы нормальные
(m = 1).
Расчетная схема
ℓ=6м
Эпюра Мх, кН∙м
q p= 2,8 кН/м
6.
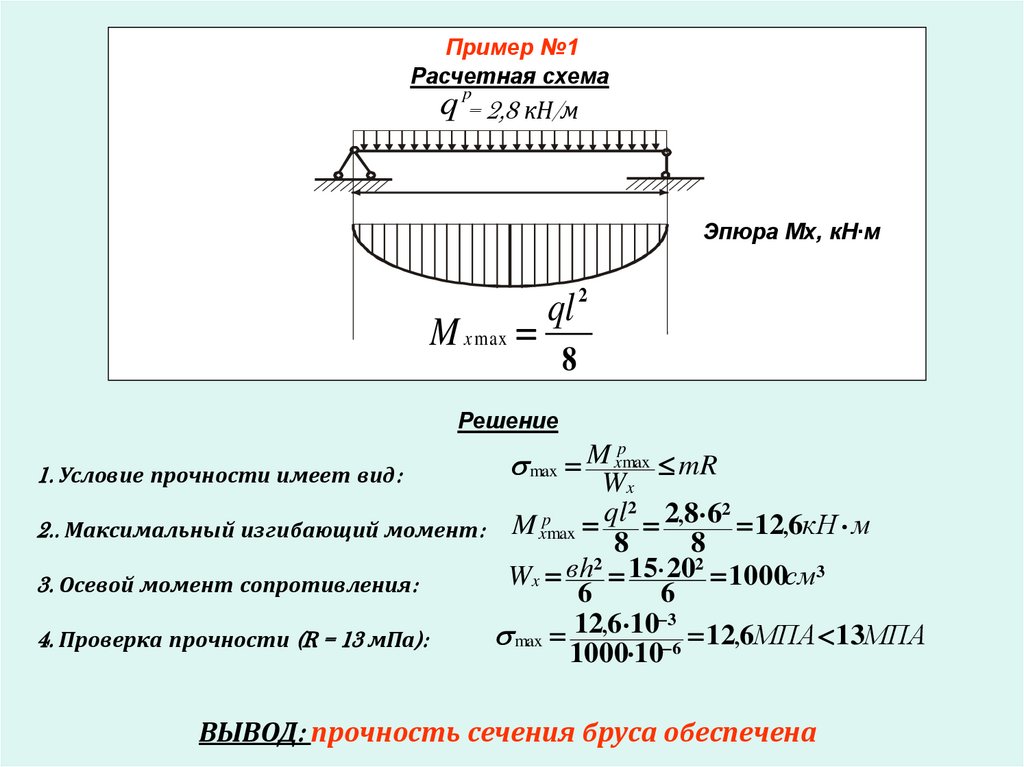
Пример №1Расчетная схема
q p= 2,8 кН/м
ℓ=6м
Эпюра Мх, кН∙м
M x max
ql 2
8
Решение
p
M
x
max max mR
1. Условие прочности имеет вид:
Wx
ql 2 2,8 62 12,6кН м
p
M
2.. Максимальный изгибающий момент:
x max
8
8
вh2 15 202 1000см3
W
x
3. Осевой момент сопротивления:
6
6
3
12
,
6
10
max
12,6МПА 13МПА
4. Проверка прочности (R = 13 мПа):
1000 10 6
ВЫВОД: прочность сечения бруса обеспечена
7. Пример №2
Для заданной схемы загружения подобрать сечение стальной двутавровой балки изусловия прочности по нормальным напряжениям. Расчетное сопротивление стали R =
210 МПа. Нагрузку считать расчетной. Условия работы нормальные.
Р=16 кН
l 4м
Эпюра Мх, кН
∙ м
pl 16
4
Решение
1. Условие прочности имеет вид:
xmax М xmax mR
p
W
x
2. Максимальный изгибающий момент
:
M xmax pl 16 4 16кН м
4
4
3. Из условия прочности выражаем требуемый момент
сопротивления:
3
WxТР M x max 16 10 0,076 10 3 м3 76см3
R
210
8.
4. По сортаменту прокатной стали WТР ≥ 76 см³ (ГОСТ 8239 – 89)принимаем двутавр №14, Wч = 81,7 см ³
Двутавры стальные горячекатаные (ГОСТ 8239-89)
h – высота швеллера
b – ширина полки
s – толщина стенки
l – cредняя толщина полки
А – площадь поперечного сечения
J – момент инерции
W – момент сопротивления
S – статический момент полусечения
i – радиус инерции
9.
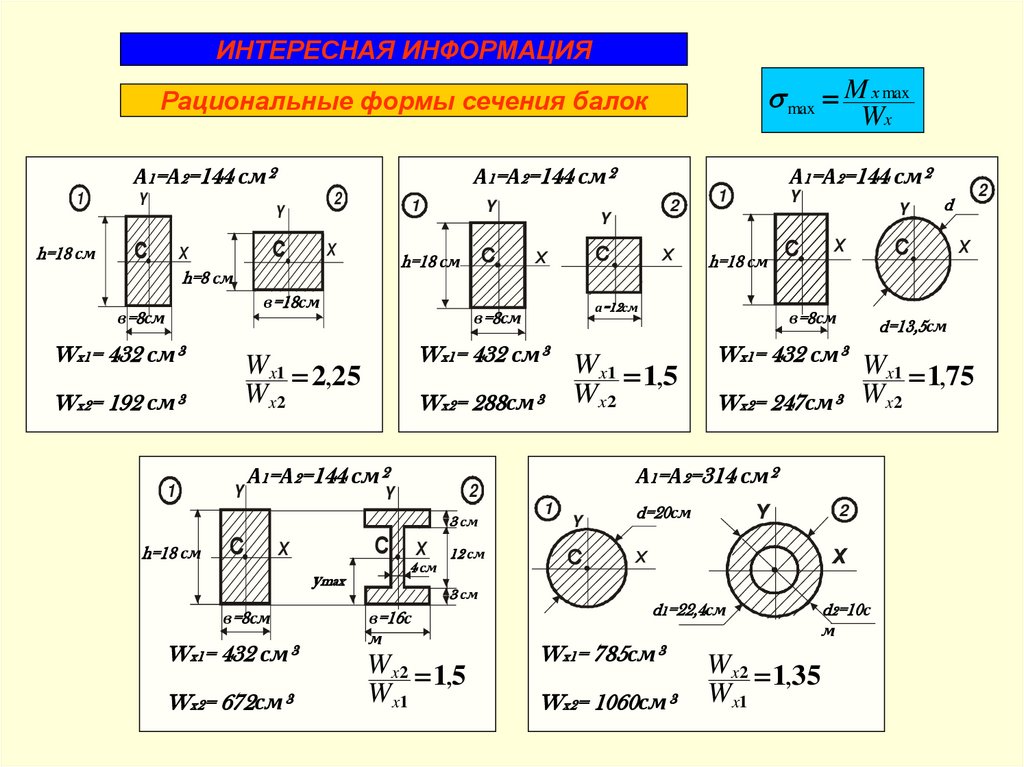
ИНТЕРЕСНАЯ ИНФОРМАЦИЯmax M х max
Рациональные формы сечения балок
А1=А2=144 см²
1
h=18 см
Y
А1=А2=144 см²
2
Y
С
С
Х
h=8 см
1
Х
Y
Wx1= 432 см³
1
Y
h=18 см
С
С
Х
ymax
в=8см
Wx1= 432 см³
Wx2= 672см³
Х
4 см
12 см
3 см
в=16с
м
Wx2 1,5
Wx1
h=18 см
Y
С
Х
Y
С
Wx1= 432 см³ W
x1
Wx2= 247см³ Wx2
d=20см
2
Х
d1=22,4см
Wx1= 785см³
Wx2= 1060см³
С
d2=10с
м
Wx2 1,35
Wx1
Х
d=13,5см
А1=А2=314 см²
1
2
d
Y
в=8см
Wx1 1,5
Wx 2
2
3 см
Х
1
а=12см
Wx2= 288см³
Y
2
С
Х
Wx1= 432 см³
А1=А2=144 см²
А1=А2=144 см²
Y
в=8см
Wx1 2,25
Wx 2
Wx2= 192 см³
С
h=18 см
в=18см
в=8см
Wx
1,75
10. Задача Парана (1666-1716)
Как следует опилить круглое бревно, чтобы получился брус прямоугольногосечения, обладающий наибольшей прочностью при изгибе.
Практическое решение задачи
e
a
b
c
f
D/3 D/3 D/3
d
11.
БЛОК- КОНСПЕКТРасчет на прочность по нормальным напряжениям при прямом поперечном изгибе
Опорные знания
Прочностная характеристика материала
Нормальные напряжения в любой точке поперечного сечения
Mx y
Сопротивление строительных материалов
Rн
– нормативное сопротивление (устанавливается ГОСТом)
R н -расчетное сопротивление
R
σ- напряжение в любой точке поперечного
сечения; J x
Мх- изгибающий момент в сечении;
Jx- осевой момент инерции сечения;
m
у- расстояние от нейтрального слоя до точки в которой определяется
напряжение
γm – коэффициент безопасности
γm =1,05…1,15
Осевой момент сопротивления Wx [ м3] –геометрическая
характеристика прочности сечения балок
Максимальные нормальные напряжения
прямоугольник
max M x max
max M x max y max
J x y max
Wx J x y max
Jx
Wx вh ;Wy hв
6
6
2
max M x max
квадрат
3
Wx W y a
2
6
круг
прокатные профили
сортамент прокатной
стали
3
Wx Wy d
Wx
32
M xpmax
max
mR
Wx
Условие прочности по нормальным
напряжениям
σmax-максимальное нормальное
напряжение в сечении;
Мpхmax – максимальный изгибающий момент в сечении от расчетной нагрузки (принимается
с эпюры моментов Мх);
Wх – осевой момент сопротивления(зависит от геометрических размеров и формы поперечного
сечения)
R – расчетное сопротивление материалов (зависит от материала);
m – коэффициент условий работы (m=1 для нормальных условий).
Три вида расчетов по нормальным напряжениям
Проверка прочности
(Проверочный расчет)
max
M xpmax
mR
Wx
Подбор сечения
(Проектировочный расчет)
WхТР
M xpmax
mR
Определение предельной
нагрузки
(эксплуатационной способности)
M x max mRWx
Рациональные формы сечений балок (при одинаковой площади сечения)
1. Двутавровое сечение рациональнее прямоугольного;
2. Прямоугольное сечение рациональнее квадратного и круглого;
3. Кольцевое сечение рациональнее круглого.








 mechanics
mechanics








