Расчёты на прочность стержней при простых видах нагружения

1.

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «Прикладная механика, динамика и прочность машин»
РАСЧЁТЫ НА ПРОЧНОСТЬ
СТЕРЖНЕЙ ПРИ ПРОСТЫХ
ВИДАХ НАГРУЖЕНИЯ
Курс лекций по дисциплинам: «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»;
«ТЕХНИЧЕСКАЯ МЕХАНИКА»;
«ПРИКЛАДНАЯ МЕХАНИКА»
Автор: доцент кафедры «ПМ и ДПМ» к.т.н. КОЛОСОВА О.П.

2.

2
ПОРЯДОК РЕШЕНИЯ ЗАДАЧ
УСЛОВИЕ ЗАДАЧИ
1. РАСЧЁТНАЯ СХЕМА
2. АНАЛИЗ НАГРУЖЕННОСТИ
Построить ЭПЮРЫ внутренних силовых факторов
3. АНАЛИЗ НАПРЯЖЕНИЙ
Найти наибольшее действующее напряжение в стержне
4. УСЛОВИЕ ПРОЧНОСТИ
Наибольшее действующее напряжение в стержне
не превышает допускаемое напряжение

3.

3
ИЗГИБ
— это вид нагружения стержня, при котором в его поперечном сечении возникает
изгибающий момент Мх (и/или Му)
один или в комбинации с поперечной силой Qу (и/или Qх).
Стержень, работающий на изгиб, носит название балка
ВИДЫ ИЗГИБА
Чистый изгиб
M
только изгибающий момент
Мх (и/или Му)
Mx
M
Поперечный изгиб
поперечная сила + изгибающий момент:
Qу, Мх (и/или Qх, Му)
изгиб в одной плоскости — Мх ИЛИ Му
изгиб в двух плоскостях — Мх И Му
F
Qy
Mx
F
Прямой изгиб
Косой изгиб

4.

4
ИЗГИБ
— это вид нагружения стержня, при котором в его поперечном сечении возникает
изгибающий момент Мх (и/или Му)
один или в комбинации с поперечной силой Qх (и/или Qу).
Стержень, работающий на изгиб, носит название балка
ВИДЫ ИЗГИБА
Чистый прямой изгиб
1 ВСФ: Мх или Му
Чистый косой изгиб
2 ВСФ: Мх и Му
Поперечный прямой изгиб
2 ВСФ: Qу, Мх или Qх, Му
Поперечный косой изгиб
4 ВСФ: Qу, Мх и Qх, Му

5.

5
ИЗГИБ
1. РАСЧЁТНАЯ СХЕМА
1.1. Консольная балка
F1 M
ℓ1
ℓ2
F2
ℓ3
1.2. Шарнирная балка
М
А
ℓ1
ℓ2
В
F
ℓ3
Необходимо найти реакции
шарнирных опор балки из
условий её равновесия:
MАFk = 0
MВFk = 0
Проверка: ∑Fkу = 0
2. АНАЛИЗ НАГРУЖЕННОСТИ
Построить ЭПЮРЫ поперечной силы и изгибающего момента:
ЭQу и ЭМх
2.1. Эпюра поперечной силы — ЭQу
2.1.1. Метод сечений: поперечная сила Qу в произвольном сечении балки равна
сумме всех СИЛ, приложенных по одну сторону от сечения
и взятых со знаком сопротивления материалов

6.

6
ИЗГИБ
2. АНАЛИЗ НАГРУЖЕННОСТИ
2.1. Эпюра поперечной силы — ЭQу
2.1.1. Метод сечений: поперечная сила Qу в произвольном сечении балки равна
сумме всех СИЛ, приложенных по одну сторону от сечения
и взятых со знаком сопротивления материалов
2.1.2. Правило знаков:
Положительная поперечная сила поворачивает
вырезанный участок балки ПО часовой стрелке,
отрицательная — против часовой стрелки!!!
2.1.3. Сколько сечений на участке?
dQу
│
│= q
dz
Qу
Qу
Qу
— Дифференциальная зависимость
поперечной силы от распределённой
внешней поперечной нагрузки:
q = 0 Qу = const
1 сечение на участке
q = const Qу(z) ~ z
2 сечения на участке
Достаточно провести 2 сечения на участке — в начале и в конце участка
ПРОВЕРКА: 1. Поперечные силы для правой и левой отсечённой части одинаковы.
2. В точках приложения сосредоточенных СИЛ — скачки на ЭQу.
Qу

7.

7
ИЗГИБ
2. АНАЛИЗ НАГРУЖЕННОСТИ
2.2. Эпюра изгибающего момента — ЭМх
2.2.1. Метод сечений: изгибающий момент Мх в сечении балки равен сумме
МОМЕНТОВ всех нагрузок, приложенных по одну сторону
от сечения и взятых со знаком сопротивления материалов
2.2.2. Правило знаков:
сжатые волокна сверху
Положительный изгибающий момент сообщает
участку балки положительную кривизну:
вогнутые сжатые волокна балки — сверху.
Mх
Для отрицательного момента — снизу!!!
ЭМх строится на сжатом волокне без указания знака!!!
Mх
Mх
Mх
сжатые волокна снизу
— Дифференциальная зависимость
изгибающего момента от поперечной силы:
Qу = 0 Мх = const
1 сечение на участке
2.2.3. Сколько сечений на участке?
dМх
│
│= Qу
dz
Qу = const Мх(z) ~ z
2 сечения на участке
Достаточно провести 2 сечения на участке — в начале и в конце участка
ПРОВЕРКА: 1. Изгибающие моменты для правой и левой отсечённой части одинаковы.
2. В точках приложения сосредоточенных МОМЕНТОВ — скачки на ЭМх.

8.

8
ИЗГИБ
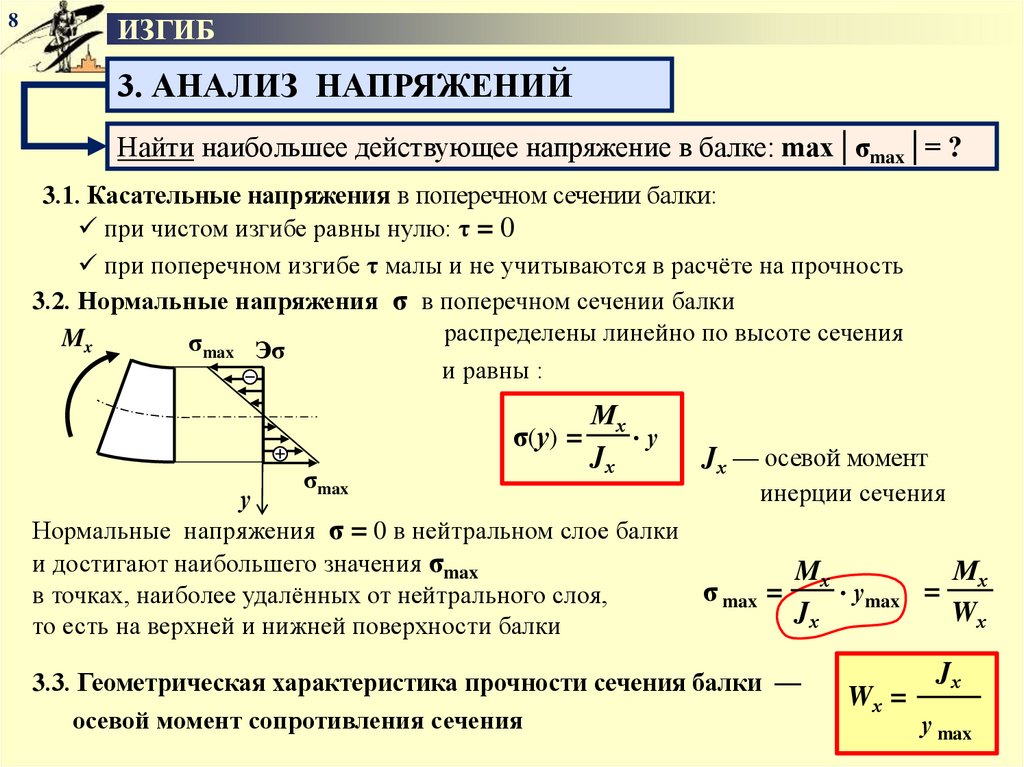
3. АНАЛИЗ НАПРЯЖЕНИЙ
Найти наибольшее действующее напряжение в балке: max│σmax│= ?
3.1. Касательные напряжения в поперечном сечении балки:
при чистом изгибе равны нулю: τ = 0
при поперечном изгибе τ малы и не учитываются в расчёте на прочность
3.2. Нормальные напряжения σ в поперечном сечении балки
распределены линейно по высоте сечения
Mx
σmax Эσ
и равны :
σmax
Мх
σ(у) =
у
Jх
Jх — осевой момент
инерции сечения
у
Нормальные напряжения σ = 0 в нейтральном слое балки
и достигают наибольшего значения σmax
Mх
Мх
σ max =
уmax =
в точках, наиболее удалённых от нейтрального слоя,
Jх
Wх
то есть на верхней и нижней поверхности балки
3.3. Геометрическая характеристика прочности сечения балки —
осевой момент сопротивления сечения
Wх =
Jх
у max

9.

9
ИЗГИБ
3. АНАЛИЗ НАПРЯЖЕНИЙ
Найти наибольшее действующее напряжение в балке: max│σmax│= ?
3.3. Геометрическая характеристика прочности сечения балки —
осевой момент сопротивления сечения
Wх =
Прямоугольное поперечное сечение:
h
b
bh 3
Jх =
12
h
ymax =
2
bh 2
Wx =
6
а
a4
Jх =
12
a
ymax =
2
Jх
уmax
a3
Wx =
6
Круглое поперечное сечение:
d
dО
d
πd 4
Jx =
64
d
ymax =
2
πd 3
≈ 0,098 d 3
Wx =
32
Кольцевое поперечное сечение:
d
с= O
d
πd 4
Jx =
(1– c 4 )
64
Для пустотелых сечений:
d
ymax =
2
πd 3
Wx =
(1– c 4 ) ≈ 0,098 d 3(1– c 4 )
32
Wх ≠ Wхвнешнего контура − Wхотверстия
Jх = Jхвнешнего контура − Jхотверстия
Wх =
Jх
уmax
!

10.

10
ИЗГИБ
3. АНАЛИЗ НАПРЯЖЕНИЙ
Найти наибольшее действующее напряжение в балке: max│σmax│= ?
3.4. Наибольшее нормальное напряжение в сечении балки:
действующее напряжение =
σ max =
Мх
Wх
внутренний силовой фактор
геометрическая характеристика прочности сечения
3.5. Наибольшее действующее напряжение в балке постоянного сечения:
max│Мх│
Wх = const max│σmax│=
Wх
4. УСЛОВИЕ ПРОЧНОСТИ
Наибольшее действующее напряжение в балке
не превышает допускаемое напряжение
max│σmax │ [ σ ]
Допускаемое напряжение для пластичного материала (например, стали):
[σ]=
σт
[ nт ]
σт — предел текучести материала
[ nт ] — нормированный коэффициент запаса прочности

11.

11
ИЗГИБ
ПРИМЕР 1
Проектировочный расчёт консольной балки
3Pℓ
F1
F2
F3
ℓ1
ℓ2
ℓ3
1,5ℓ
d
3P
P
ℓ
dО
2P
2ℓ
Дано:
ℓ1 = 1,5ℓ; ℓ2 = ℓ; ℓ3 = 2ℓ; dO = 0,80d;
F1 = P; F2 = – 3Р; F3 = 2Р.
Принять ℓ = 40 см; Р = 550 Н.
Материал — сталь 65,
σт = 420 МПа; [nт] = 1,45.
Определить из расчёта на прочность
размер поперечного сечения балки
РЕШЕНИЕ
1) Расчётная схема
Проведём размерные линии
Проставим длины участков
Изобразим балку и заделку
Покажем нагрузку
Найдём реакции заделки
MЗFk = – 2Р 4,5ℓ + 3Р 2,5ℓ – Р 1,5ℓ = – 3Рℓ
МЗ = + 3Рℓ

12.

12
ИЗГИБ
3Pℓ
3P
P
6
1,5ℓ
ПРИМЕР 1
2P
5 4 3 2
ℓ
1
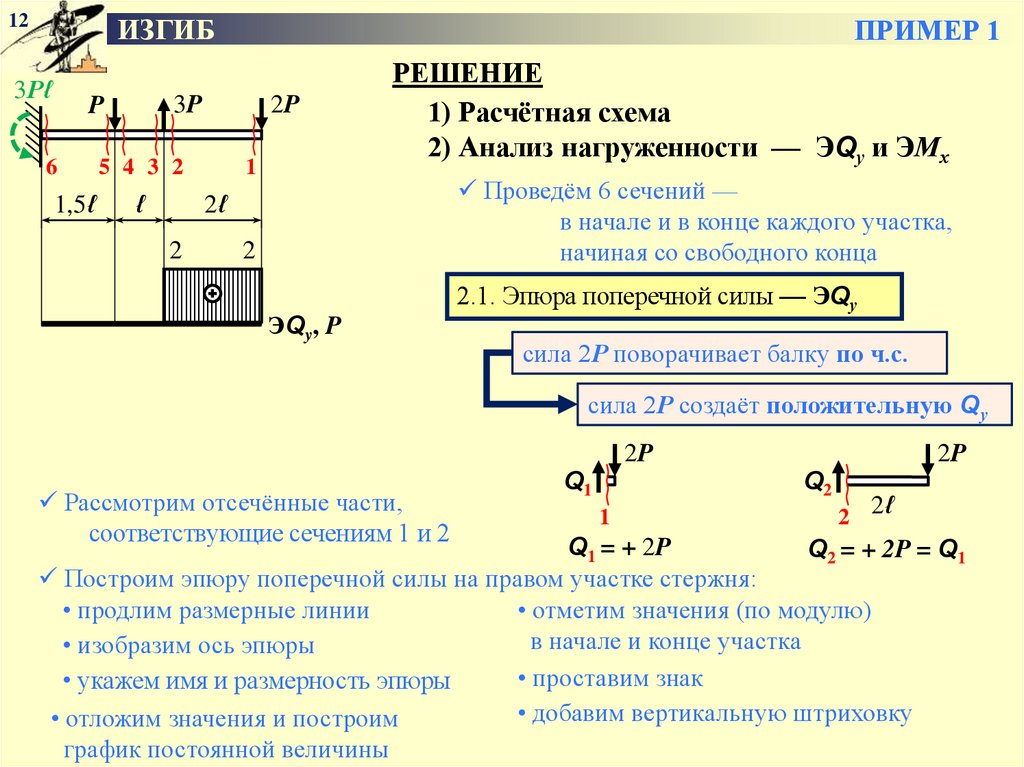
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
Проведём 6 сечений —
в начале и в конце каждого участка,
начиная со свободного конца
2ℓ
2
2
ЭQy, P
2.1. Эпюра поперечной силы — ЭQу
сила 2Р поворачивает балку по ч.с.
сила 2Р создаёт положительную Qу
2P
Рассмотрим отсечённые части,
соответствующие сечениям 1 и 2
Q1
2P
Q2
1
2 2ℓ
Q1 = + 2P
Q2 = + 2P = Q1
Построим эпюру поперечной силы на правом участке стержня:
• продлим размерные линии
• отметим значения (по модулю)
в начале и конце участка
• изобразим ось эпюры
• проставим знак
• укажем имя и размерность эпюры
• добавим вертикальную штриховку
• отложим значения и построим
график постоянной величины

13.

13
ИЗГИБ
3Pℓ
P
6
3P
ℓ
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2P
5 4 3 2
1,5ℓ
ПРИМЕР 1
1
2.1. Эпюра поперечной силы — ЭQу
2ℓ
2
Рассмотрим отсечённые части,
соответствующие сечениям 3, 4, 5 и 6
Q 3 = + 2P – 3P = – P = Q 4
2
ЭQy, P
1
Q 5 = + 2P – 3P + P = 0 = Q 6
1
Строим ЭQy параллельно с вычислениями!
ПРОВЕРКА ЭQy:
• справа и слева — одно и то же: Q6→ = 0 = Q6←
• скачки соответствуют силам !!!
2.2. Эпюра изгибающего момента — ЭMх
момент силы = (знак + или –) (модуль силы) ∙ (плечо силы)
сила 2Р прогибает балку вниз
сжатые волокна балки — снизу
сила 2Р создаёт отрицательный Mх

14.

14
ИЗГИБ
3Pℓ
P
6
3P
2P
5 4 3 2
1,5ℓ
ПРИМЕР 1
ℓ
1
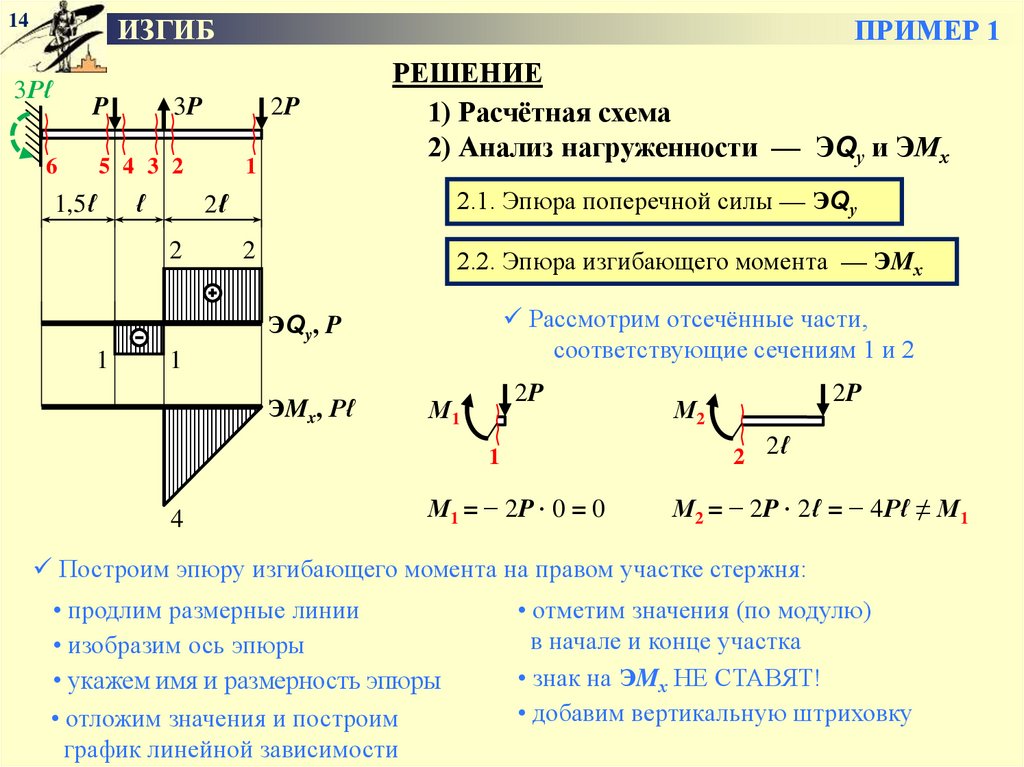
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2.1. Эпюра поперечной силы — ЭQу
2ℓ
2
2
2.2. Эпюра изгибающего момента — ЭMх
Рассмотрим отсечённые части,
соответствующие сечениям 1 и 2
ЭQy, P
1
1
ЭMx, Pℓ
2P
М1
2 2ℓ
1
4
2P
М2
М1 = − 2P ∙ 0 = 0
М2 = − 2P ∙ 2ℓ = − 4Рℓ ≠ М1
Построим эпюру изгибающего момента на правом участке стержня:
• продлим размерные линии
• изобразим ось эпюры
• укажем имя и размерность эпюры
• отложим значения и построим
график линейной зависимости
• отметим значения (по модулю)
в начале и конце участка
• знак на ЭMх НЕ СТАВЯТ!
• добавим вертикальную штриховку

15.

15
ИЗГИБ
3Pℓ
P
6
3P
2P
5 4 3 2
ℓ
1,5ℓ
ПРИМЕР 1
1
2.1. Эпюра поперечной силы — ЭQу
2ℓ
2
2
2.2. Эпюра изгибающего момента — ЭMх
ЭQy, P
1
1
ЭMx, Pℓ
3
3
4
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
Рассмотрим отсечённые части,
соответствующие сечениям 3, 4, 5 и 6
М3 = − 2P ∙ 2ℓ + 3P ∙ 0 = − 4Рℓ = М2
М4 = − 2P ∙ 3ℓ + 3P ∙ ℓ = − 3Рℓ ≠ М3
М5 = − 2P ∙ 3ℓ + 3P ∙ ℓ − P ∙ 0 = − 3Рℓ = М4
М6 = − 2P ∙ 4,5ℓ + 3P ∙ 2,5ℓ − P ∙1,5ℓ = − 3Рℓ
Строим ЭМх параллельно с вычислениями!
ПРОВЕРКА ЭМy:
• справа и слева — одно и то же: М6→ = − 3Рℓ = М6←
• скачок там, где заделка (опорный момент) !!!
Опасные сечения балки — сечения 2 и 3:
max│Мх│ = 4Рℓ

16.

16
ИЗГИБ
3Pℓ
P
6
3P
ℓ
dО РЕШЕНИЕ
2P
5 4 3 2
1,5ℓ
ПРИМЕР 1
1
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
d
3) Анализ напряжений — max│σmax │= ?
2ℓ
2
Для балки постоянного кольцевого сечения:
d
с = O = 0,80
d
2
ЭQy, P
1
πd 3
Wх =
(1– c 4 ) ≈ 0,098 d 3(1– 0,80 4 ) =
32
1
ЭMx, Pℓ
3
3
= 0,0579 d 3 = const
max│σmax│=
4
max│Мх│
Wх
4) Условие прочности
[σ]=
σт
[ nт ]
Рℓ
69,1 3 [ σ ] d ≥
d
3
Рℓ
69,1
[σ]
d ≈ 38 мм
3
=
69,1
=
4Рℓ
Рℓ
=
0,0579d 3 = 69,1 d 3
max│σmax │ [ σ ]
420 МПа
= 290 МПа
1,45
550 H ∙ 0,4м
= 0,0374 м = 37,4 мм
290∙106 Па
по ГОСТ 6636-69

17.

17
ИЗГИБ
ПРИМЕР 2
Расчёт на грузоподъёмность консольной балки
F1
M
F2
Дано: ℓ1 = 2ℓ; ℓ2 = 1,5ℓ; ℓ3 = ℓ; F1 = P; F2 = – 3Р; М = 2Рℓ.
d h
ℓ1
ℓ2
ℓ3
b
2Pℓ 3P 0,5Pℓ
P
2ℓ
1,5ℓ
ℓ
2P
Принять ℓ = 90 см;
h = 95 мм; b = 75 мм; d = 67 мм.
Материал — сталь 20ХН,
σт = 600 МПа; [nт] = 2,35.
Определить из расчёта на прочность
допускаемое значение параметра нагрузки
РЕШЕНИЕ
1) Расчётная схема
Размерные линии
Балка с заделкой
Длины участков
Реакции заделки:
Нагрузка
MЗFk = + Р 4,5ℓ – 2Рℓ – 3Р ℓ = – 0,5Рℓ
МЗ = + 0,5Рℓ
Параметр размера сечения: а = 100 мм
h = 0,95а; b = 0,75а; d = 0,67а.

18.

18
ИЗГИБ
ПРИМЕР 2
2Pℓ 3P 0,5Pℓ
P
1
23
2ℓ
45 6
ℓ
1,5ℓ
2
2P
2
ЭQy, P
1
1
1
• размерные линии
• ось эпюры
• имя и размерность эпюры
• график
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
Проведём 6 сечений —
в начале и в конце каждого участка
Эпюра поперечной силы — ЭQу
сила Р поворачивает балку против ч.с.
сила Р создаёт отрицательную Qу
Q1 = – P
Q2 = – P = Q1
Q3 = – P = Q1 = Q2
Q4 = – P = Q1 = Q2 = Q3
Q5 = – P + 3P = + 2P
Q6 = – P + 3P = + 2P = Q5
• значения (по модулю)
Строим ЭQy параллельно с вычислениями!
в начале и конце участка
ПРОВЕРКА ЭQy:
• справа и слева — одно и то же: Q6← = + 2P = Q6→
• скачки соответствуют силам !!!
• знак
• штриховка

19.

19
ИЗГИБ
ПРИМЕР 2
2Pℓ 3P 0,5Pℓ
P
1
23
2ℓ
45 6
ℓ
1,5ℓ
2
2P
Эпюра поперечной силы — ЭQу
2
Эпюра изгибающего момента — ЭMх
ЭQy, P
1
1
1
0,5
ЭMx, Pℓ
2,0
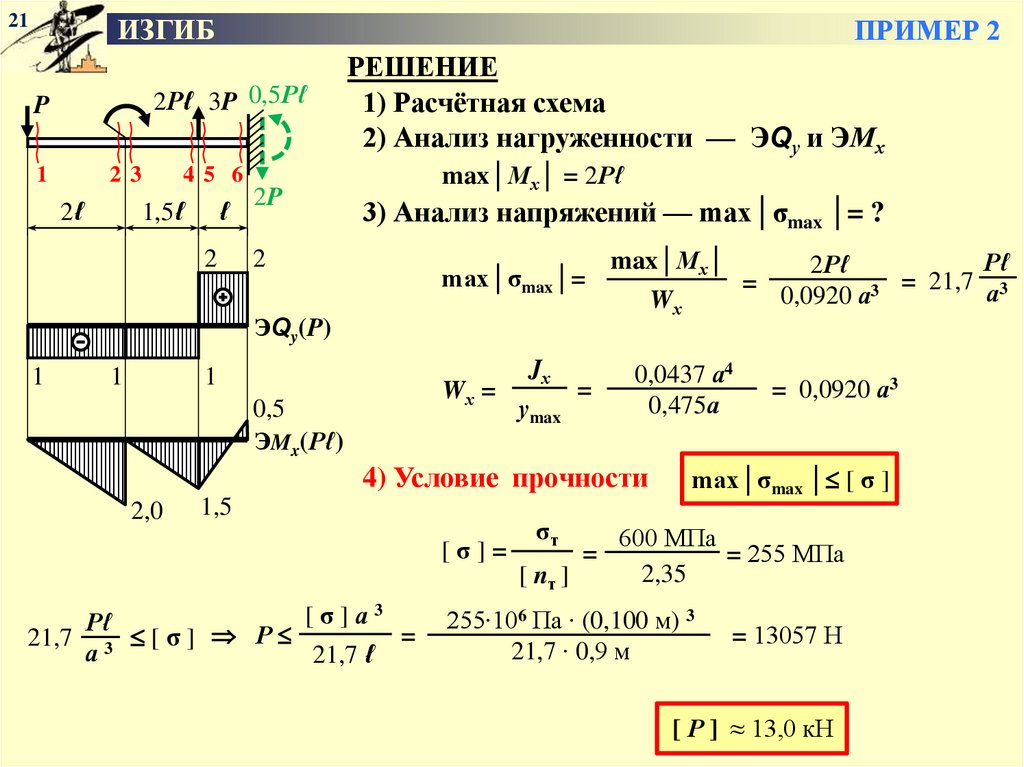
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
1,5
Строим ЭМх параллельно
с вычислениями!
сила Р прогибает балку вниз
сжатые волокна балки — снизу
сила Р создаёт отрицательный Mх
М1 = − P ∙ 0 = 0
М2 = − P ∙ 2ℓ = − 2Рℓ ≠ М1
М3 = − P ∙ 2ℓ + 2Pℓ = 0 ≠ М2
М4 = − P ∙ 3,5ℓ + 2Pℓ = − 1,5Рℓ ≠ М3
М5 = − P ∙ 3,5ℓ + 2Pℓ + 3P ∙ 0 = − 1,5Рℓ = М4
М6 = − P ∙ 4,5ℓ + 2Pℓ + 3P ∙ ℓ = + 0,5Рℓ ≠ М5
ПРОВЕРКА ЭМy:
• справа и слева — одно и то же: М6← = + 0,5Рℓ = М6→
max│Мх│ = 2Рℓ
• скачки соответствуют моментам !!!

20.

20
ИЗГИБ
ПРИМЕР 2
2Pℓ 3P 0,5Pℓ
P
1
23
2ℓ
45 6
ℓ
1,5ℓ
2
2P
2
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
max│Мх│ = 2Рℓ
3) Анализ напряжений — max│σmax │= ?
max│σmax│=
max│Мх│
Wх
ЭQy(P)
1
1
1
0,5
ЭMx(Pℓ)
2,0
1,5
Wх =
Jх
уmax
=
0,0437 а4
0,475а
Рℓ
2Рℓ
= 21,7 а3
=
0,0920 а3
= 0,0920 а3
bh 3 πd 4
Jх = Jхвнешнего контура − Jхотверстия = 12 – 64 =
0,75а ∙ (0,95а) 3
π ∙ (0,67а) 4
=
–
=
12
64
= (0,0536 – 0,0099) а4 = 0,0437 а4
d h
b
ymax =
h
= 0,475а
2
4) Условие прочности
max│σmax │ [ σ ]

21.

21
ИЗГИБ
ПРИМЕР 2
2Pℓ 3P 0,5Pℓ
P
1
23
2ℓ
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
max│Мх│ = 2Рℓ
45 6
ℓ
1,5ℓ
2
2P
3) Анализ напряжений — max│σmax │= ?
2
max│σmax│=
max│Мх│
Wх
ЭQy(P)
1
1
1
Wх =
0,5
ЭMx(Pℓ)
Jх
уmax
=
0,0437 а4
0,475а
4) Условие прочности
2,0
1,5
[σ]=
σт
[ nт ]
[σ]а
Рℓ
=
21,7 3 [ σ ] Р
а
21,7 ℓ
3
=
Рℓ
2Рℓ
= 21,7 а3
=
0,0920 а3
= 0,0920 а3
max│σmax │ [ σ ]
600 МПа
= 255 МПа
2,35
255∙106 Па ∙ (0,100 м) 3
21,7 ∙ 0,9 м
= 13057 Н
[ Р ] ≈ 13,0 кН

22.

22
ИЗГИБ
ПРИМЕР 3
Проектировочный расчёт шарнирной балки
М1 F
b
М2
h
ℓ1
YA
Рℓ
ℓ2
ℓ3
2Pℓ YB
2P
2ℓ
ℓ
2P
Рℓ
□а
2ℓ
Дано: ℓ1 = 2ℓ; ℓ2 = ℓ; ℓ3 = 2ℓ; b = 0,8а; h = 0,6а;
F = –2P; М1 = –Рℓ; М2 = 2Рℓ.
Принять ℓ = 40 см; P = 1,5 кН.
Материал — сталь 10, σт = 210 МПа; [nт] = 2,5.
Определить из расчёта на прочность
размер поперечного сечения балки
РЕШЕНИЕ
1) Расчётная схема
Размеры участков, балка, нагрузка
Реакции опор балки из условий равновесия:
MАFk = 0 = + 2Р 2ℓ + Рℓ – 2Рℓ + YB 5ℓ
2Pℓ
MВFk = 0 = – 2Р 3ℓ + Рℓ – 2Рℓ – YА 5ℓ
1,4P
0,6P
YB = (− 4Р − Р + 2Р)/5 = − 0,6Р
YА = (− 6Р + Р − 2Р)/5 = − 1,4Р
Проверка:
Fkу = 0 = + YА + 2Р + YB = − 1,4Р + 2Р − 0,6Р = 0

23.

23
ИЗГИБ
YA
Рℓ
2Pℓ YB
2P
ℓ
2ℓ
2P
Рℓ
1,4P 1
ПРИМЕР 3
2 34 5
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2ℓ
Проведём 6 сечений —
в начале и в конце каждого участка
2Pℓ
Эпюра поперечной силы — ЭQу — строим слева
6 0,6P
0,6
0,6
ЭQy, P
1,4
1,4
• размерные линии
• ось эпюры
• имя и размерность эпюры
• график
• значения (по модулю)
в начале и конце участка
• знак
• штриховка
сила 1,4Р поворачивает балку против ч.с.
сила 1,4Р создаёт отрицательную Qу
Q1 = – 1,4 P
Q2 = – 1,4 P = Q1
Q3 = – 1,4 P + 2P = + 0,6 P
Q4 = – 1,4 P + 2P = + 0,6 P = Q3
Q5 = – 1,4 P + 2P = + 0,6 P = Q4 = Q3
Q6 = – 1,4 P + 2P = + 0,6 P = Q5 = Q4 = Q3
Строим ЭQy параллельно с вычислениями!
ПРОВЕРКА ЭQy:
• справа и слева — одно и то же: Q6 ← = +0,6P = Q6 →
• скачки соответствуют силам !!!

24.

24
ИЗГИБ
YA
Рℓ
2Pℓ YB
2P
ℓ
2ℓ
2P
Рℓ
1,4P 1
ПРИМЕР 3
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2ℓ
Эпюра поперечной силы — ЭQу
2Pℓ
Эпюра изгибающего момента — ЭMх
2 34 5
0,6
6 0,6P
0,6
ЭQy, P
1,4
1,4
ЭMx, Pℓ
1
3,8
1,2
3,2
сила 1,4Р создаёт отрицательный Mх
момент Рℓ создаёт отрицательный Mх
• Сечения 1…5 — левая отсечённая часть:
М1 = − Pℓ − 1,4P ∙ 0 = − Pℓ
М2 = − Pℓ − 1,4P ∙ 2ℓ = − 3,8Рℓ ≠ М1
М3 = − Pℓ − 1,4P ∙ 2ℓ + 2P ∙ 0 = − 3,8Рℓ = М2
М4 = − Pℓ − 1,4P ∙ 3ℓ + 2P ∙ ℓ = − 3,2Рℓ ≠ М3
М5 = − Pℓ − 1,4P ∙ 3ℓ + 2P ∙ ℓ + 2Pℓ = − 1,2Рℓ ≠ М4
• Сечения 5 и 6 — правая отсечённая часть:
Строим ЭМх параллельно
М5← = − 0,6P ∙ 2ℓ = − 1,2Рℓ = М5→ — ПРОВЕРКА!
с вычислениями!
М6 = − 0,6P ∙ 0 = 0
ПРОВЕРКА ЭМх — скачки соответствуют моментам !!!
max│Мх│ = 3,8Рℓ

25.

25
ИЗГИБ
YA
Рℓ
2Pℓ YB
2P
ℓ
2ℓ
1,4P 1
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
max│Мх│ = 3,8Рℓ
2ℓ
2P
Рℓ
ПРИМЕР 3
3) Анализ напряжений — max│σmax │= ?
2Pℓ
2 34 5
0,6
max│σmax│=
6 0,6P
0,6
Wх =
ЭQy, P
1,4
уmax
=
Wх
0,0689 а4
0,5 а
=
3,8Рℓ
Рℓ
=
27,5
0,138 а3
а3
= 0,138 а3
а4
bh3
Jх = Jхвнешнего контура − Jхотверстия = 12 – 12 =
1,4
ЭMx, Pℓ
1
1,2
3,2
3,8
4
3
а
0,8а
∙
(0,6а)
=
–
= 0,0689 а4
12
12
ymax =
b
h
□а
Jх
max│Мх│
а
2
4) Условие прочности
max│σmax │ [ σ ]

26.

26
ИЗГИБ
YA
Рℓ
2Pℓ YB
2P
ℓ
2ℓ
1,4P 1
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
max│Мх│ = 3,8Рℓ
2ℓ
2P
Рℓ
ПРИМЕР 3
3) Анализ напряжений — max│σmax │= ?
2Pℓ
2 34 5
0,6
6 0,6P
0,6
ЭQy, P
1,4
ЭMx, Pℓ
1,2
3,2
3,8
σт
[ nт ]
=
Рℓ
27,5 3 [ σ ]
а
=
h
□а
[σ]=
3
b
Wх
4) Условие прочности
1,4
1
max│Мх│
max│σmax│=
27,5
=
3,8Рℓ
Рℓ
=
27,5
0,138 а3
а3
max│σmax │ [ σ ]
210 МПа
= 84 МПа
2,5
3
а≥
27,5
Рℓ
[σ]
=
1500 H ∙ 0,4 м
= 0,0582 м = 58,2 мм
84∙106 Па
а ≈ 60 мм
по ГОСТ 6636-69

27.

27
ИЗГИБ
ПРИМЕР 4
Проектировочный расчёт консольной балки
F1
F2
F3
h
ℓ1
ℓ2
ℓ3
b
Дано: ℓ1 = 1,5ℓ; ℓ2 = ℓ; ℓ3 = 2ℓ; b = 0,80h;
F1 = P; F2 = – 2P; F3 = 3P.
Принять ℓ = 80 см; P = 5,5 кН.
Материал – сталь Ст.2,
σт = 220 МПа; [nт] = 1,15.
Определить из расчёта на прочность
размер поперечного сечения балки
2P
P
2P
1,5ℓ
3P
ℓ
2ℓ
4,5Pℓ
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

28.

28
ИЗГИБ
ПРИМЕР 4
РЕШЕНИЕ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2P
2P
P
1
3P
2 3 4 5
ℓ
1,5ℓ
1
6
2ℓ
4,5Pℓ
3) Анализ напряжений — max│σmax │= ?
Для балки постоянного прямоугольного сечения:
1
ЭQy, P
1
1
2
Wх =
6
= 0,133 h 3 = const
2
max│σmax│=
ЭMx, Pℓ
1,5
bh2
max│Мх│
Wх
=
4,5 Рℓ
Рℓ
0,133 h3 = 33,8 h3
0,5
4) Условие прочности
4,5
[σ]=
σт
[ nт ]
3
Рℓ
33,8 3 [ σ ] h ≥
h
Рℓ
33,8
[σ]
h ≈ 95 мм
3
=
33,8
=
max│σmax │ [ σ ]
220 МПа
= 191 МПа
1,15
5500 H ∙ 0,8 м
= 0,0920 м = 92,0 мм
191∙106 Па
по ГОСТ 6636-69

29.

29
ИЗГИБ
ПРИМЕР 5
Расчёт на грузоподъёмность шарнирной балки
F1
ℓ1
F2
ℓ2
ℓ3
d
Дано: ℓ1 = ℓ; ℓ2 = ℓ; ℓ3 = 2ℓ; a = 0,6 d;
F1 = P; F2 = 1,5P.
□a
Принять ℓ = 80 см; d = 75 мм.
Материал – сталь 45Г,
σт = 380 МПа; [nт] = 1,75.
Определить из расчёта на прочность
допускаемое значение параметра нагрузки
YA
P
P
YB
ℓ ℓ
2ℓ
P
3,5P
1,5P
РЕШЕНИЕ
1) Расчётная схема — реакции опор
2) Анализ нагруженности — ЭQу и ЭМх
1,5P
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

30.

30
ИЗГИБ
YA
P
P
ПРИМЕР 5
РЕШЕНИЕ
1) Расчётная схема
1,5P
2) Анализ нагруженности — ЭQу и ЭМх
YB
ℓ ℓ
2ℓ
P
3,5P
3) Анализ напряжений — max│σmax │= ?
1,5P
6
1 2 3 4 5
1,5
1,5
ЭQy, P
1
max│Мх│
max│σmax│=
=
3 Рℓ
Рℓ
=
39,2
0,0765 d 3
d3
Wх
Jх
0,0383 d 4
=
= 0,0765 d 3
Wх =
0,5 d
уmax
πd
Jх = Jхвнеш. − Jхотв. =
4
a4
–
= 0,0383 d 4
64
12
1
2
4) Условие прочности
2
ЭMx, Pℓ
1
[σ]=
σт
[ nт ]
=
max│σmax │ [ σ ]
380 МПа
= 217 МПа
1,75
3
[σ]d
Рℓ
=
39,2 3 [ σ ] Р
d
39,2 ℓ
3
□a
d
[ Р ] ≈ 2,91 кН
217∙106 Па ∙ (0,075 м) 3
39,2 ∙ 0,8 м
= 2919 Н

31.

31
ИЗГИБ
ЗАДАЧА 1
Проектировочный расчёт консольной балки
F1
F2
ℓ1
F3
ℓ2
dO
ℓ3
d
Дано: ℓ1 = 2ℓ; ℓ2 = ℓ; ℓ3 = 1,5ℓ; dO = 0,70d;
F1 = – 2P; F2 = 4P; F3 = P.
Принять ℓ = 75 см; P = 3,5 кН.
Материал – сталь Ст.5,
σт = 280 МПа; [nт] = 1,45.
Определить из расчёта на прочность
размер поперечного сечения балки
РЕШЕНИЕ
2P
4P
P
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2ℓ
ℓ
1,5ℓ
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

32.

32
ИЗГИБ
ЗАДАЧА 1
РЕШЕНИЕ
1) Расчётная схема
2P
4P
3P
P
0,7d
Реакции заделки:
MЗFk = –2Р 4,5ℓ +4Р 2,5ℓ +Р 1,5ℓ = +2,5Рℓ МЗ = –2,5Рℓ
2) Анализ нагруженности — ЭQу и ЭМх
1
2ℓ
2
ЭQ у: Q1 = +2P = Q2
2 3 4 5
6 2,5Pℓ d
ℓ 1,5ℓ
М4 = +2P ∙3ℓ – 4Р ∙ℓ = +2Рℓ = М5
М6 = +2P ∙4,5ℓ – 4Р ∙2,5ℓ – Р ∙1,5ℓ = –2,5Рℓ
max│Мх│ = 4Рℓ
ЭQy , P
4
2
3
3) Анализ напряжений — max│σmax │= ?
3
ЭMx , Pℓ
max│σmax│=
2,5
max│Мх│
Wх
4) Условие прочности
Допускаемое напряжение:
Рℓ
[σ] d≥
d3
[σ]=
3
53,6
dO
= 0,70
Для балки постоянного кольцевого сечения: с =
d
πd 3
Wх = 32 (1– c 4 ) ≈ 0,098 d 3(1– 0,70 4 ) = 0,0746 d 3
2
53,6
Q5 = –3P = Q6
ЭM x: М1 = 0 М2 = +2P ∙2ℓ = +4Рℓ = М3
2
2
Q3 = –2P = Q4
Рℓ
[σ]
σт
[ nт ]
4Рℓ
Рℓ
= 53,6 3
3
0,0746d
d
max│σmax │ [ σ ]
=
280 МПа
= 193 МПа
1,45
53,6
3500 H ∙ 0,75м
= 0,0900 м = 90,0 мм ≈ 90 мм
193∙106 Па
по ГОСТ 6636-69
3
=
=

33.

33
ИЗГИБ
ЗАДАЧА 2
Расчёт консольной балки на грузоподъёмность
M
F2
F1
h
ℓ1
ℓ2
ℓ3
b
Дано: ℓ1 = 2ℓ; ℓ2 = 1,5ℓ; ℓ3 = ℓ;
F1 = P; F2 = – 2P; М = – 2Pℓ.
Принять ℓ = 120 см; b = 60 мм; h = 90 мм.
Материал – сталь 45,
σт = 360 МПа; [nт] = 1,65.
Определить из расчёта на прочность
допускаемое значение параметра нагрузки
РЕШЕНИЕ
2Pℓ
P
2P
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
2ℓ
1,5ℓ
ℓ
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

34.

34
ИЗГИБ
ЗАДАЧА 2
РЕШЕНИЕ
3,5Pℓ
2Pℓ
P
2P
P
54
2ℓ
3 2 1
3,5
1
1,5
1
2
Параметр размера сечения: а = 100 мм; h = 0,9а; b = 0,6а;
ЭQ у: Q1 = – 2P = Q2
Q3 = – P = Q4 = Q5 = Q6
ЭM x: М1 = 0 М2 = +2P ∙ ℓ = +2Рℓ = М3
ЭQy , P
1
МЗ = –3,5Рℓ
2) Анализ нагруженности — ЭQу и ЭМх
0,6a
ℓ
1,5ℓ
Реакции заделки:
MЗFk = +2Р 4,5ℓ – Р 3,5ℓ – 2Рℓ = +3,5Рℓ
0,9a
6
1) Расчётная схема
М4 = + 2P ∙ 2,5ℓ – Р ∙ 1,5ℓ = +3,5Рℓ
М5 = + 2P ∙ 2,5ℓ – Р ∙ 1,5ℓ – 2Рℓ = +1,5Рℓ
2
М6 = + 2P ∙ 4,5ℓ – Р ∙ 3,5ℓ – 2Рℓ = +3,5Рℓ
max│Мх│ = 3,5Рℓ
3,5
2,0
3) Анализ напряжений — max│σmax │= ?
ЭMx , Pℓ
Для балки постоянного прямоугольного сечения:
bh2
0,6а ∙ (0,9а)2
Wх =
=
= 0,081 а 3
6
6
max│Мх│
3,5Рℓ
Рℓ
=
= 43,2 3
max│σmax│=
3
0,081а
а
W
х
4) Условие прочности
max│σmax │ [ σ ]
[σ]а
Рℓ
43,2 3 [ σ ] Р
а
43,2 ℓ
3
=
[σ]=
218∙106 Па ∙ (0,100 м) 3
43,2 ∙ 1,2 м
σт
[ nт ]
=
360 МПа
= 218 МПа
1,65
= 4205 Н
[ Р ] ≈ 4,20 кН

35.

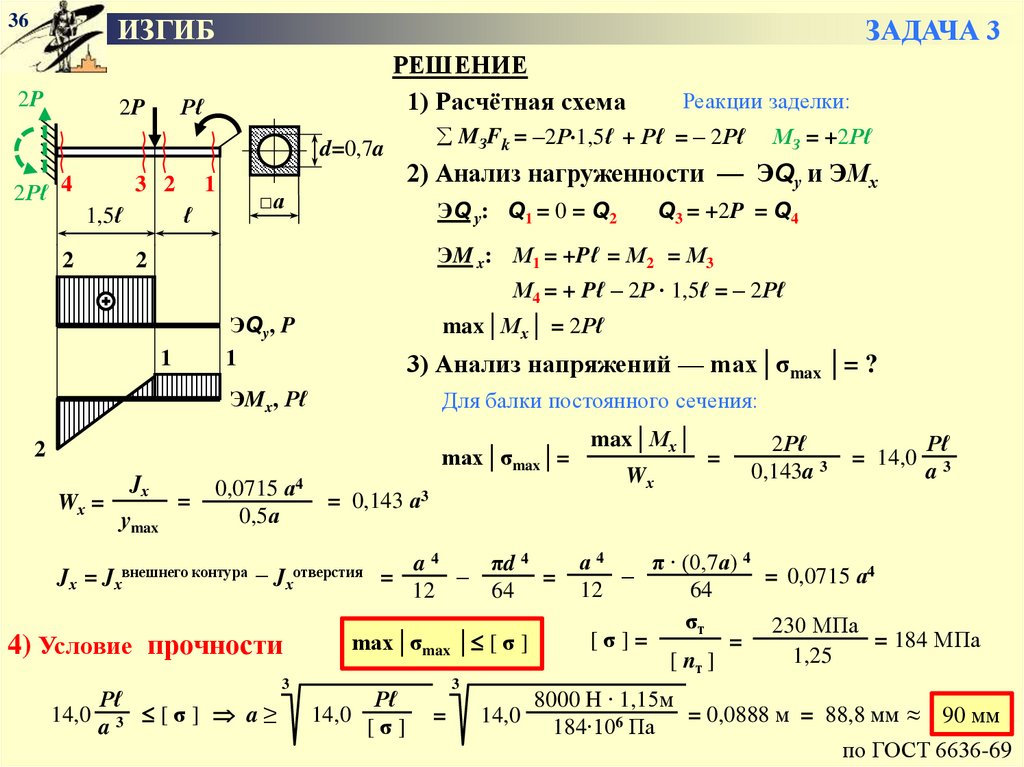
35
ИЗГИБ
ЗАДАЧА 3
Проектировочный расчёт консольной балки
M
F
d
ℓ1
ℓ2
□а
Дано: ℓ1 = 1,5ℓ; ℓ2 = ℓ; d = 0,7a;
F = 2P; М = – Pℓ.
Принять ℓ = 115 см; P = 8 кН.
Материал – сталь 15,
σт = 230 МПа; [nт] = 1,25.
Определить из расчёта на прочность
размер поперечного сечения балки
РЕШЕНИЕ
2P
Pℓ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
1,5ℓ
ℓ
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

36.

36
ИЗГИБ
2P
ЗАДАЧА 3
РЕШЕНИЕ
1) Расчётная схема
Pℓ
2P
d=0,7a
2Pℓ 4
3 2
ℓ
1,5ℓ
2
1
□а
Реакции заделки:
MЗFk = –2Р 1,5ℓ + Рℓ = – 2Рℓ
МЗ = +2Рℓ
2) Анализ нагруженности — ЭQу и ЭМх
ЭQ у: Q1 = 0 = Q2
Q3 = +2P = Q4
ЭM x: М1 = +Pℓ = М2 = М3
2
М4 = + Pℓ – 2Р ∙ 1,5ℓ = – 2Рℓ
ЭQy, P
1
1
max│Мх│ = 2Рℓ
3) Анализ напряжений — max│σmax │= ?
ЭMx, Pℓ
Для балки постоянного сечения:
2
max│σmax│=
Wх =
Jх
уmax
=
0,0715 а4
0,5а
= 0,143 а3
Jх = Jхвнешнего контура − Jхотверстия
4) Условие прочности
14,0
Рℓ
[σ] a≥
a3
a4
πd 4
=
–
=
12
64
max│σmax │ [ σ ]
3
14,0
Рℓ
[σ]
3
=
14,0
max│Мх│
Wх
=
2Рℓ
0,143a 3
= 14,0
Рℓ
a3
а4
π ∙ (0,7а) 4
–
= 0,0715 а4
12
64
σт
230 МПа
[σ]=
= 184 МПа
=
1,25
[ nт ]
8000 H ∙ 1,15м
= 0,0888 м = 88,8 мм ≈ 90 мм
184∙106 Па
по ГОСТ 6636-69

37.

37
ИЗГИБ
ЗАДАЧА 4
Расчёт шарнирной балки на грузоподъёмность
F1
F2
h
ℓ1
ℓ2
ℓ3
b
Дано: ℓ1 = 2ℓ; ℓ2 = ℓ; ℓ3 = 2ℓ;
F1 = – 2P; F2 = P.
Принять ℓ = 70 см; b = 40 мм; h = 60 мм.
Материал – сталь Ст. 3,
σт = 240 МПа; [nт] = 2,15.
Определить из расчёта на прочность
допускаемое значение параметра нагрузки
РЕШЕНИЕ
P
2P
2ℓ
ℓ
1) Расчётная схема
2ℓ
2) Анализ нагруженности — ЭQу и ЭМх
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

38.

38
ИЗГИБ
ЗАДАЧА 4
РЕШЕНИЕ
YA
YB
P
2P
A
B
2ℓ
2P
0,8P
1
ℓ
2ℓ
3a
2a
P
23 4 5
1,2
1,2
0,2
0,8
Реакции опор:
MАFk = 0 = +2Р 2ℓ – Р 3ℓ + YB 5ℓ = + Рℓ + YB 5ℓ
MВFk = 0 = – 2Р 3ℓ + Р 2ℓ – YА 5ℓ = – 4Рℓ – YА 5ℓ
YB = – 0,2Р
YА = – 0,8Р
Проверка: Fkу = 0
Параметр размера сечения: а = 20мм h = 3а; b = 2а
2) Анализ нагруженности — ЭQу и ЭМх
6
0,2P
0,2
ЭQy, P
0,8
1) Расчётная схема
ЭMx, Pℓ
ЭQ у: Q1 = – 0,8P = Q2
Q3 = – 0,8P + 2P = +1,2P = Q4
Q5 = – 0,8P + 2P – P = +0,2P = Q6 = Q6← – проверка
ЭM x: М1→ = 0 М2→ = – 0,8P ∙ 2ℓ = –1,6Рℓ = М3→
М4→ = – 0,8P ∙ 3ℓ + 2P ∙ ℓ = – 0,4Рℓ = М5→
М6← = 0
М5← = – 0,2P ∙ 2ℓ = – 0,4Рℓ = М5→ – проверка
max│Мх│ = 1,6Рℓ
3) Анализ напряжений — max│σmax │= ?
0,4
max│σmax│=
1,6
4) Условие прочности
max│Мх│
Wх
=
1,6Рℓ
Рℓ
=
0,178
9а3
а3
bh2
2а ∙ (3а)2
Wх =
=
= 9,00 а 3
6
6
σт
240 МПа
max│σmax │ [ σ ]
[σ]=
=
= 112 МПа
2,15
[ nт ]
[σ]а3
Рℓ
=
0,178 3 [ σ ] Р
а
0,178 ℓ
112∙106 Па ∙ (0,020 м) 3
0,178 ∙ 0,70 м
= 7191 Н
[ Р ] ≈ 7,19 кН

39.

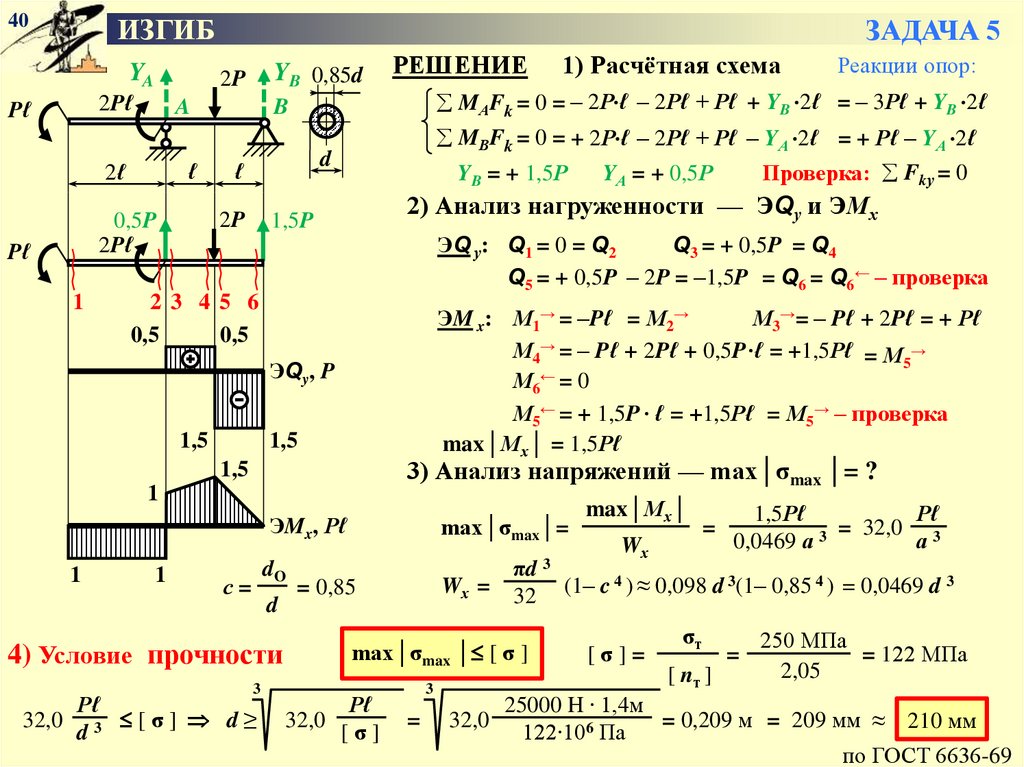
39
ИЗГИБ
ЗАДАЧА 5
Проектировочный расчёт шарнирной балки
М1
М2
F
ℓ1
ℓ2
ℓ3
dO
d
Дано: ℓ1 = 2ℓ; ℓ2 = ℓ; ℓ3 = ℓ; dO = 0,85d;
М1 = –Pℓ; М2 = 2Pℓ; F = 2P.
Принять ℓ = 140 см; P = 25 кН.
Материал – сталь 15Г,
σт = 250 МПа; [nт] = 2,05.
Определить из расчёта на прочность
размер поперечного сечения балки
РЕШЕНИЕ
2P
Pℓ
2Pℓ
2ℓ
ℓ
ℓ
1) Расчётная схема
2) Анализ нагруженности — ЭQу и ЭМх
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

40.

40
ИЗГИБ
YA
A
ℓ
2ℓ
1
РЕШЕНИЕ
YB = + 1,5Р
ЭQ у: Q1 = 0 = Q2
Q3 = + 0,5P = Q4
Q5 = + 0,5P – 2P = –1,5P = Q6 = Q6← – проверка
23 4 5 6
0,5
0,5
ЭM x: М1→ = –Pℓ = М2→
М3→= – Pℓ + 2Pℓ = + Рℓ
М4→ = – Pℓ + 2Pℓ + 0,5P ∙ℓ = +1,5Рℓ = М5→
М6← = 0
М5← = + 1,5P ∙ ℓ = +1,5Рℓ = М5→ – проверка
max│Мх│ = 1,5Рℓ
ЭQy, P
1,5
3) Анализ напряжений — max│σmax │= ?
1,5
1
ЭMx, Pℓ
1
1
dO
с=
d
Wх =
πd 3
32
max│σmax │ [ σ ]
3
Рℓ
[σ] d≥
d3
max│σmax│=
= 0,85
4) Условие прочности
32,0
Проверка: Fkу = 0
YА = + 0,5Р
2) Анализ нагруженности — ЭQу и ЭМх
1,5P
1,5
Реакции опор:
MВFk = 0 = + 2Р ℓ – 2Рℓ + Рℓ – YА 2ℓ = + Рℓ – YА 2ℓ
d
ℓ
1) Расчётная схема
MАFk = 0 = – 2Р ℓ – 2Рℓ + Рℓ + YB 2ℓ = – 3Рℓ + YB 2ℓ
B
2P
0,5P
2Pℓ
Pℓ
YB 0,85d
2P
2Pℓ
Pℓ
ЗАДАЧА 5
32,0
Рℓ
[σ]
3
=
32,0
max│Мх│
Wх
=
1,5Рℓ
Рℓ
=
32,0
0,0469 а 3
а3
(1– c 4 ) ≈ 0,098 d 3(1– 0,85 4 ) = 0,0469 d 3
[σ]=
σт
[ nт ]
=
250 МПа
= 122 МПа
2,05
25000 H ∙ 1,4м
= 0,209 м = 209 мм ≈ 210 мм
122∙106 Па
по ГОСТ 6636-69

41.

41
ИЗГИБ
ЗАДАЧА 6
Расчёт шарнирной балки на грузоподъёмность
□а
М1 М2
ℓ1
ℓ2
b
Дано: ℓ1 = 2ℓ; ℓ2 = ℓ; M1 = 2Pℓ; M2 = – Pℓ.
Принять ℓ = 40 см; b = 28 мм;
h
h = 42 мм ; a = 24 мм.
Материал – сталь 20,
σт = 250 МПа; [nт] = 2,25.
Определить из расчёта на прочность
допускаемое значение параметра нагрузки
РЕШЕНИЕ
1) Расчётная схема
Pℓ
2Pℓ
2ℓ
ℓ
2) Анализ нагруженности — ЭQу и ЭМх
3) Анализ напряжений — max│σmax │= ?
4) Условие прочности
max│σmax │ [ σ ]

42.

42
ИЗГИБ
ЗАДАЧА 6
YA
YB
Pℓ
B
2Pℓ
A
ℓ
2ℓ
0,333P
2Pℓ
1
0,333P
Pℓ
23
0,333
0,333
2,8t
1) Расчётная схема
Реакции опор:
MАFk = 0 = + 2Рℓ – Рℓ + YB 3ℓ = + Рℓ + YB 3ℓ
MВFk = 0 = + 2Рℓ – Рℓ – YА 3ℓ = + Рℓ – YА 3ℓ
4,2t
YB = –0,333Р
YА = +0,333Р Проверка: Fkу = 0
□2,4t Параметр размера сечения: t = 10 мм
h = 4,2t
b = 2,8t
a = 2,4t
2) Анализ нагруженности — ЭQу и ЭМх
4
0,333
ЭQy, P
0,67
ЭMx, Pℓ
Wх =
РЕШЕНИЕ
ЭQ у: Q1 = +0,333P = Q2 = Q3 = Q4 = Q4← – проверка
ЭM x: М1 = 0
М2 = + 0,333P ∙ 2ℓ = +0,67Рℓ
М3 = +0,333P ∙ 2ℓ – 2P ℓ = – 1,33Рℓ
М4 = +0,333P ∙ 3ℓ – 2P ℓ = – Рℓ = М4← – проверка
max│Мх│ = 1,33Рℓ
1,33
1
3) Анализ напряжений — max│σmax │= ?
=
14,52 t 4
= 6,91 t 3
2,1t
max│Мх│
Jх
уmax
max│σmax│=
Wх
=
1,33Рℓ
Рℓ
=
0,192
6,91 t 3
t3
bh 3
a4
2,8t ∙ (4,2t ) 3
(2,4t ) 4
h
=
–
=
–
= 14,52 t 4
ymax =
= 2,1t
12
12
12
12
2
σт
250 МПа
max│σ
│
[
σ
]
[σ]=
=
= 111 МПа
4) Условие прочности
max
2,25
[ nт ]
[σ]t3
111∙106 Па ∙ (0,010 м) 3
Рℓ
= 1445 Н
[ Р ] ≈ 1,44 кН
=
0,192 3 [ σ ] Р
0,193
∙
0,40
м
t
0,192 ℓ
Jх = Jхвнеш. − Jхотв.