Similar presentations:
Геометрические характеристики плоских сечений
1. Геометрические характеристики плоских сечений
Различают следующие характеристики сечений: площадь А, статическиймомент площади (SX, или SY ), момент инерции площади (IX, или IY),
центробежный момент инерции площади (IXY).
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
SY ZdA
Sz YdA
A
A
Y
Оси, проходящие через центр тяжести,
называются центральными осями.
z
dА
Моменты площади фигуры относительно
центральных осей равны нулю
А
Y
z
Координаты центра тяжести
SY
ZC ;
A
SZ
YC
A
2.
Геометрические характеристики плоских сеченийМоментом инерции площади относительно оси называется сумма
произведений площадей элементарных площадок на квадрат расстояний
от их центра тяжести до соответствующей оси.
I Z Y 2 dA
I Y Z dA
2
A
A
Центробежным моментом инерции называется сумма произведений
площадей элементарных площадок на расстояния от центра тяжести до осей
IYZ ZYdA
A
Полярным моментом инерции называется сумма произведения площадей
элементарных площадок на квадрат расстояния от центра тяжести до начала
координат
I 2dA Z 2 Y 2 dA Z 2dA Y 2dA IY I Z
I dA
2
A
A
Z Y
2
2
2
A
A
A
Полярный момент инерции равен сумме осевых моментов
инерции относительно взаимно перпендикулярных осей.
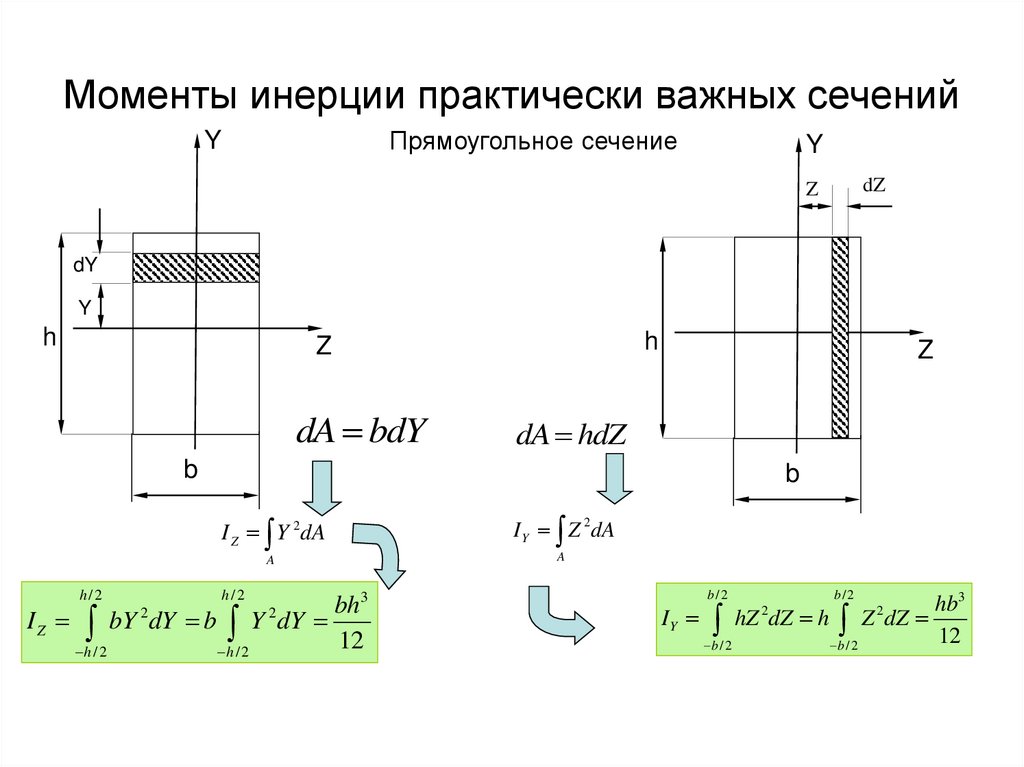
3. Моменты инерции практически важных сечений
Прямоугольное сечениеY
Y
dZ
Z
dY
Y
h
h
Z
dA bdY
Z
dA hdZ
b
b
I Z Y 2 dA
A
h/2
h/2
bh3
I Z bY dY b Y dY
12
h / 2
h / 2
2
2
I Y Z 2 dA
A
b/2
b/2
hb3
IY hZ dZ h Z dZ
12
b / 2
b / 2
2
2
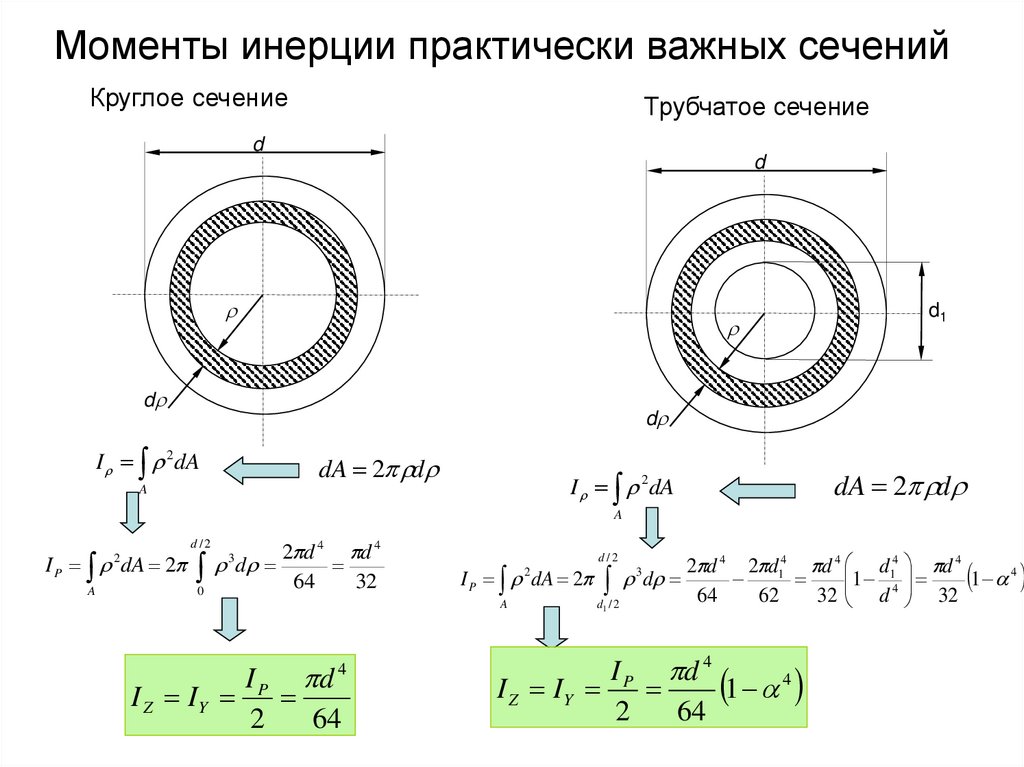
4. Моменты инерции практически важных сечений
Круглое сечениеТрубчатое сечение
d
d
d
d1
d
I 2dA
dA 2 d
I 2dA
A
dA 2 d
A
2 d 4 d 4
I P dA 2 d
64
32
A
0
d /2
2
3
I P d 4
I Z IY
2
64
2 d 4 2 d14 d 4 d14 d 4
1 4
I P dA 2 d
1 4
64
62
32 d 32
A
d1 / 2
d /2
2
3
I P d 4
I Z IY
1 4
2
64
5. Расчетные формы и их классификация
Брусом называется расчетный элемент, длина которого значительно большеразмеров его поперечного сечения.
Брусья классифицируются по форме поперечного сечения и форме оси.
По форме поперечного сечения различают брусья постоянного сечения и
переменного сечения. По форме оси – прямолинейные и криволинейные
брусья.
Примерами прямых брусьев являются балки и стержни мостовых и козловых
кранов, валы редукторов и коробок передач, оси транспортных средств.
Примерами кривых брусьев служат грузоподъёмные крюки, звенья сварных
цепей, струбцины, коленчатые валы, станины станков.
6.
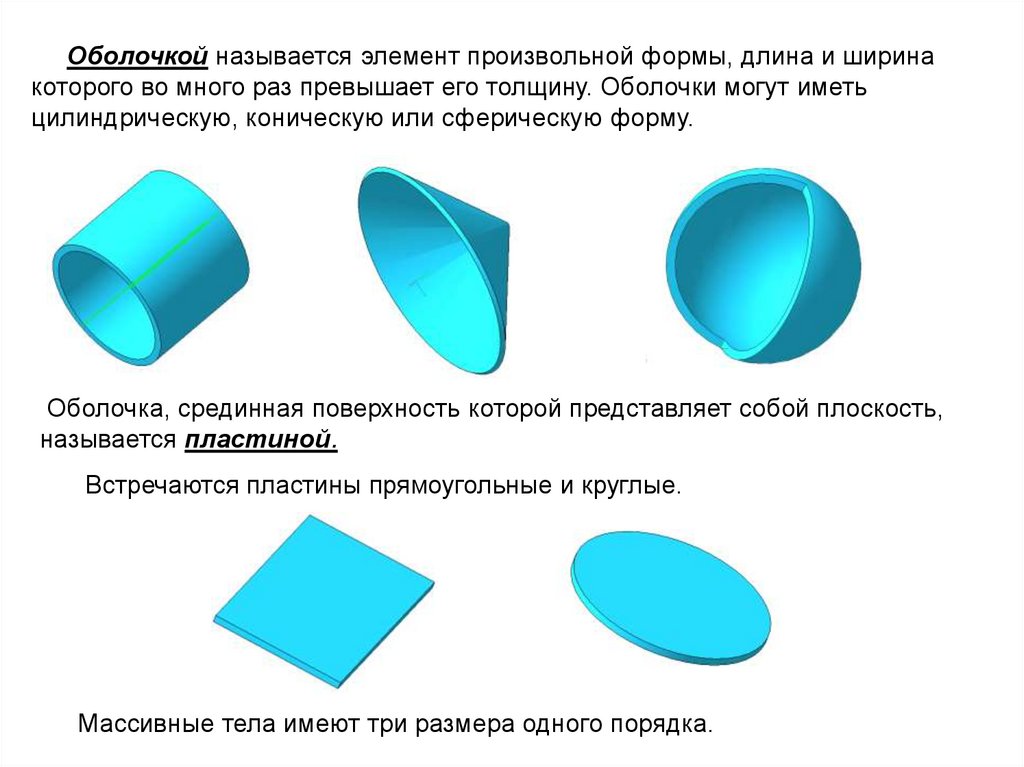
Оболочкой называется элемент произвольной формы, длина и ширинакоторого во много раз превышает его толщину. Оболочки могут иметь
цилиндрическую, коническую или сферическую форму.
Оболочка, срединная поверхность которой представляет собой плоскость,
называется пластиной.
Встречаются пластины прямоугольные и круглые.
Массивные тела имеют три размера одного порядка.
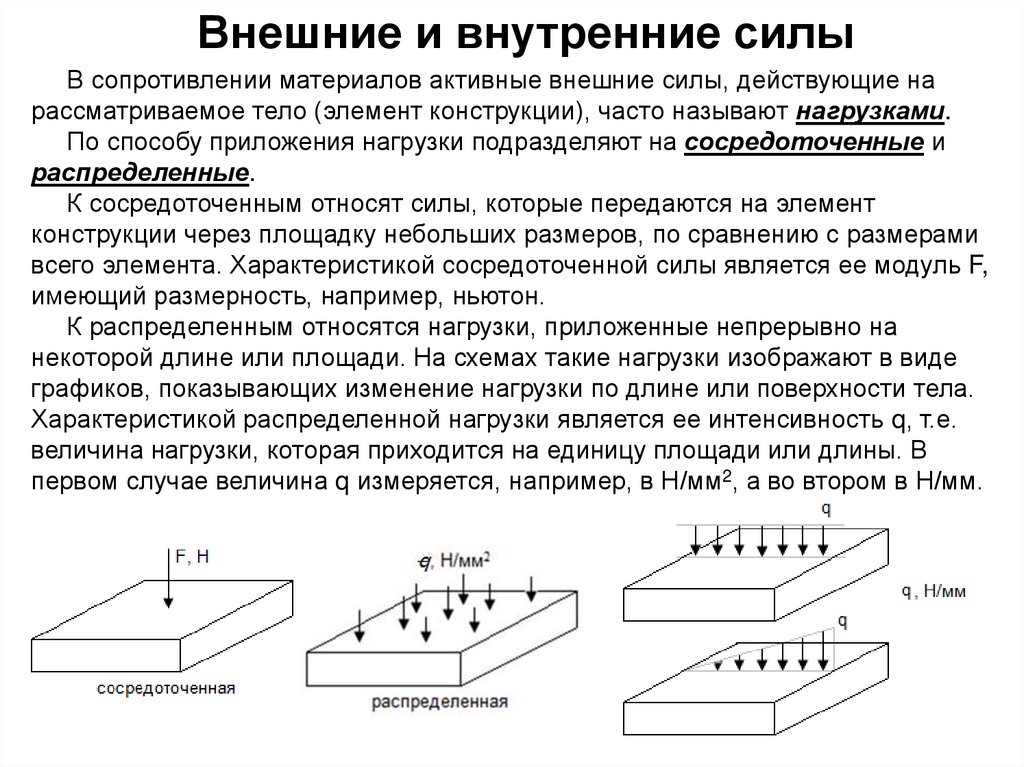
7. Внешние и внутренние силы
В сопротивлении материалов активные внешние силы, действующие нарассматриваемое тело (элемент конструкции), часто называют нагрузками.
По способу приложения нагрузки подразделяют на сосредоточенные и
распределенные.
К сосредоточенным относят силы, которые передаются на элемент
конструкции через площадку небольших размеров, по сравнению с размерами
всего элемента. Характеристикой сосредоточенной силы является ее модуль F,
имеющий размерность, например, ньютон.
К распределенным относятся нагрузки, приложенные непрерывно на
некоторой длине или площади. На схемах такие нагрузки изображают в виде
графиков, показывающих изменение нагрузки по длине или поверхности тела.
Характеристикой распределенной нагрузки является ее интенсивность q, т.е.
величина нагрузки, которая приходится на единицу площади или длины. В
первом случае величина q измеряется, например, в Н/мм2, а во втором в Н/мм.
8.
Различные виды нагрузокНагрузки подразделяют на статические и динамические.
Статическими называют нагрузки, которые прикладываются к
телу, постепенно возрастая от нуля до своей конечной величины и
оставаясь в дальнейшем практически постоянными.
Динамическими называют нагрузки, которые сопровождаются
значительными ускорениями как деформированного тела (или его
частей), так и взаимодействующих с ним тел. Возникающими при
этом силами инерции пренебречь нельзя.
Сопротивление тел, оказываемое действующим на них нагрузкам,
обуславливается наличием в этих телах особых внутренних сил,
природа которых объясняется теорией молекулярного строения
материи.
При действии на тело внешних сил изменяются внутренние
силы.




 mechanics
mechanics








