Геометрические характеристики сечений

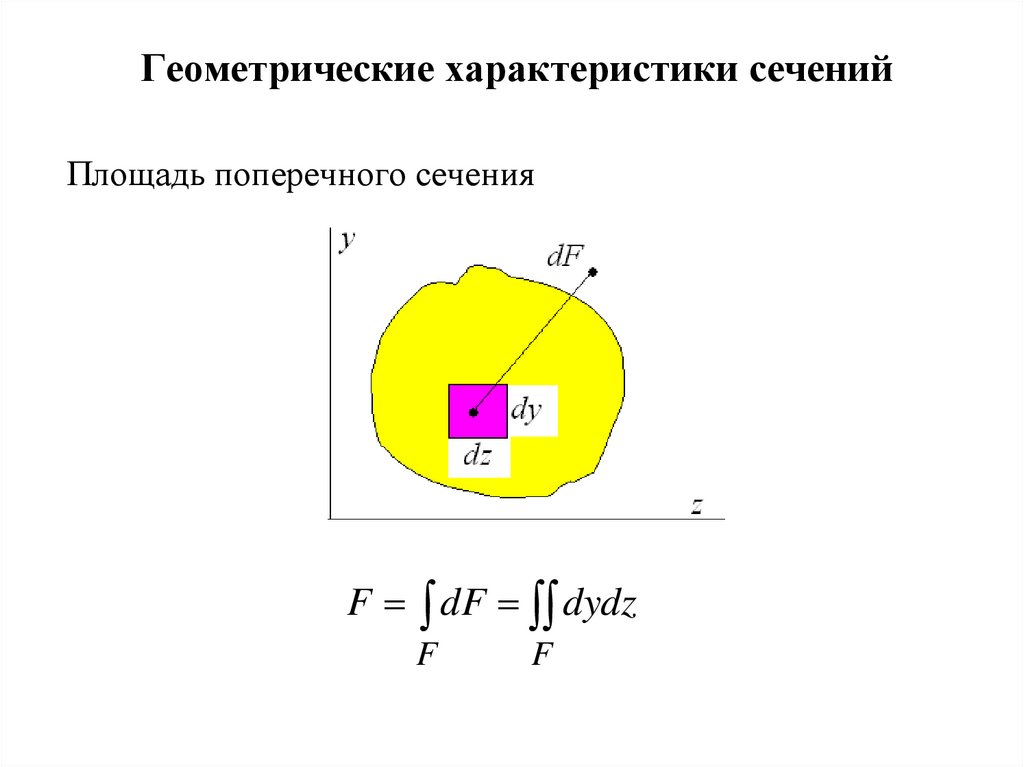
1. Геометрические характеристики сечений

Площадь поперечного сечения
F dF dydz
F
F

2. Статические моменты сечения

S z ydF
S y zdF
F
F
y1 y b
S z1 y1dF y b dF ydF bdF S z bF
F
F
F
S z1 0
F
S z bF
Ось z1 , относительно которой
статический момент сечения S z1
равен нулю, называется центральной

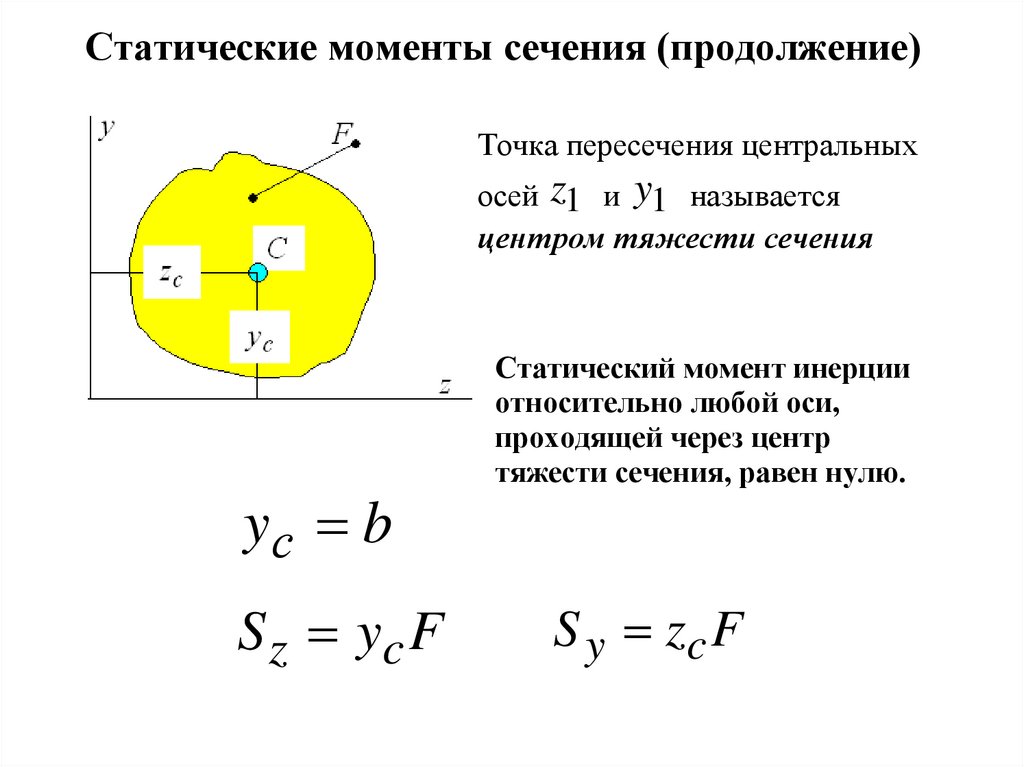
3. Статические моменты сечения (продолжение)

Точка пересечения центральных
осей z1 и y1 называется
центром тяжести сечения
yс b
S z yc F
Статический момент инерции
относительно любой оси,
проходящей через центр
тяжести сечения, равен нулю.
S y zc F

4. Статические моменты сечения (продолжение)

Определить статический момент полукруга
радиусом R относительно оси z, совпадающей с
диаметром, и координату центра тяжести yc.

5. Статические моменты сечения (продолжение)

6. Осевые моменты инерции сечения

I z y 2dF
F
I y z 2dF
F
y1 y b
I z1 y12dF y b 2 dF y 2dF 2 bydF b2 dF
F
F
F
F
F
I z1 I z 2bS z b 2 F

7. Осевые моменты инерции (продолжение)

Допустим, что ось z – центральная.
S z 0 , b yс
2
I z1 I z yc F
Осевой момент инерции относительно центральной оси имеет
минимальное значение среди всех моментов относительно осей,
параллельной данной центральной.

8. Полярный момент инерции

I p 2dF
F
z y
2
2
2
I p z 2 y 2 dF I z I y
F

9. Полярные моменты инерции сечения

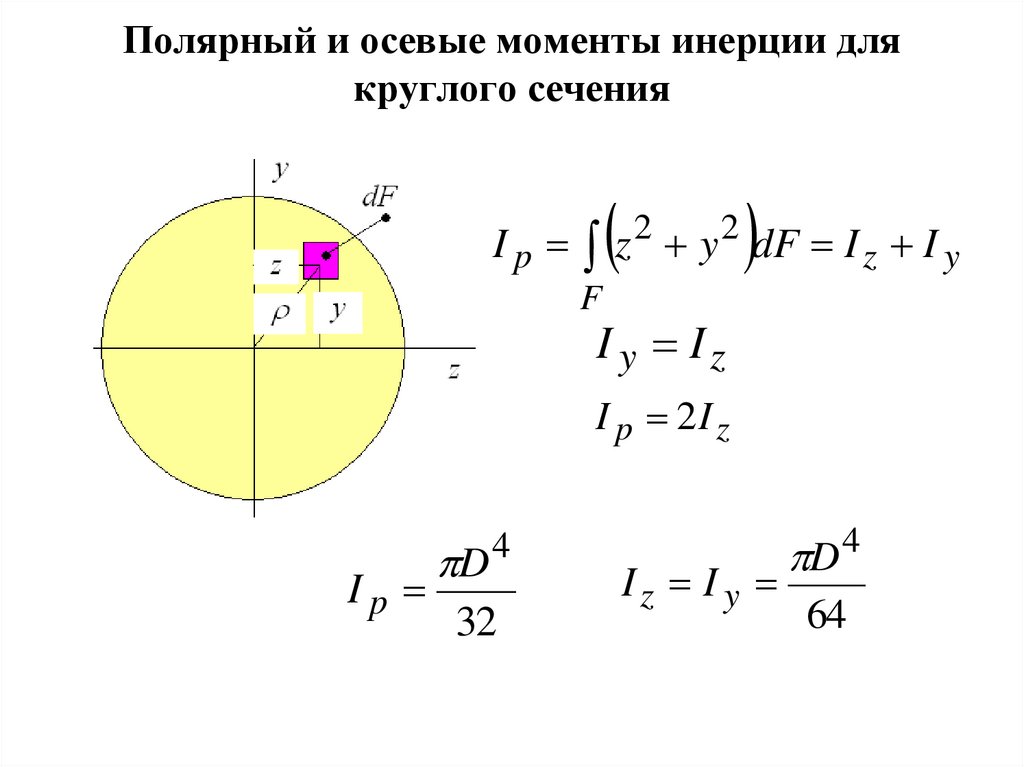
• Если оси y и z – центральные, тогда

10. Полярный и осевые моменты инерции для круглого сечения

I p z 2 y 2 dF I z I y
F
I y Iz
I p 2I z
Ip
D
4
32
Iz I y
D
4
64

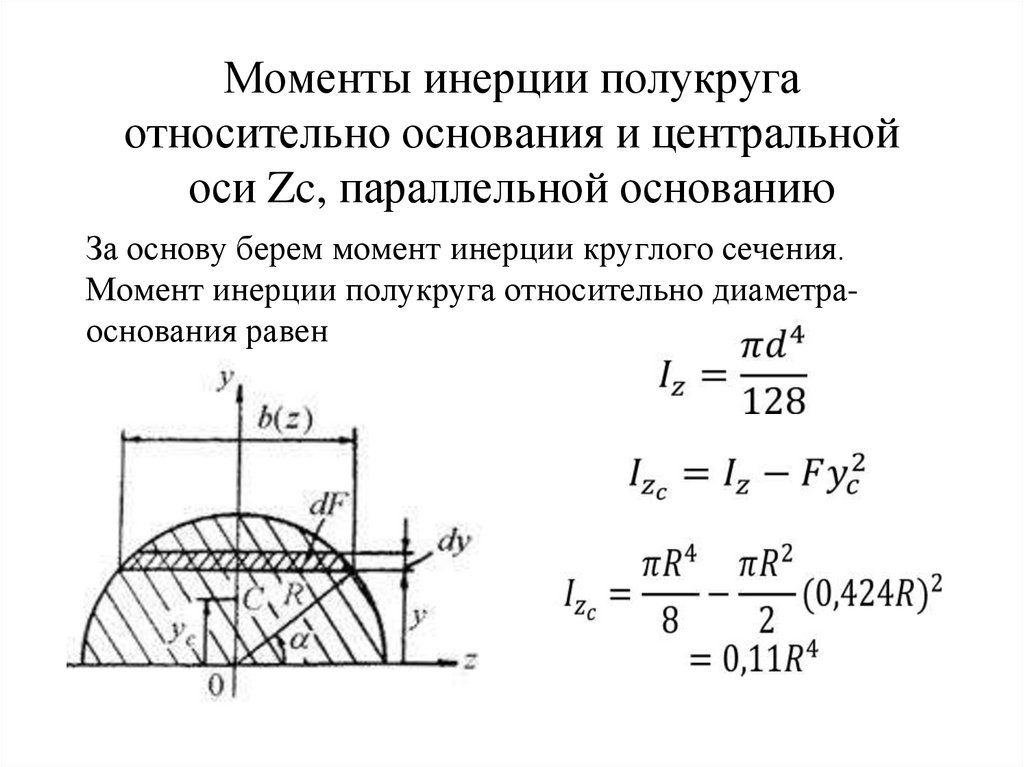
11. Моменты инерции полукруга относительно основания и центральной оси Zc, параллельной основанию

За основу берем момент инерции круглого сечения.
Момент инерции полукруга относительно диаметраоснования равен

12. Осевые моменты инерции для треугольного сечения

3
bh
Iz
36
3
bh
I z1
12
3
b
h
3
hb
2
Iy 2
12
48

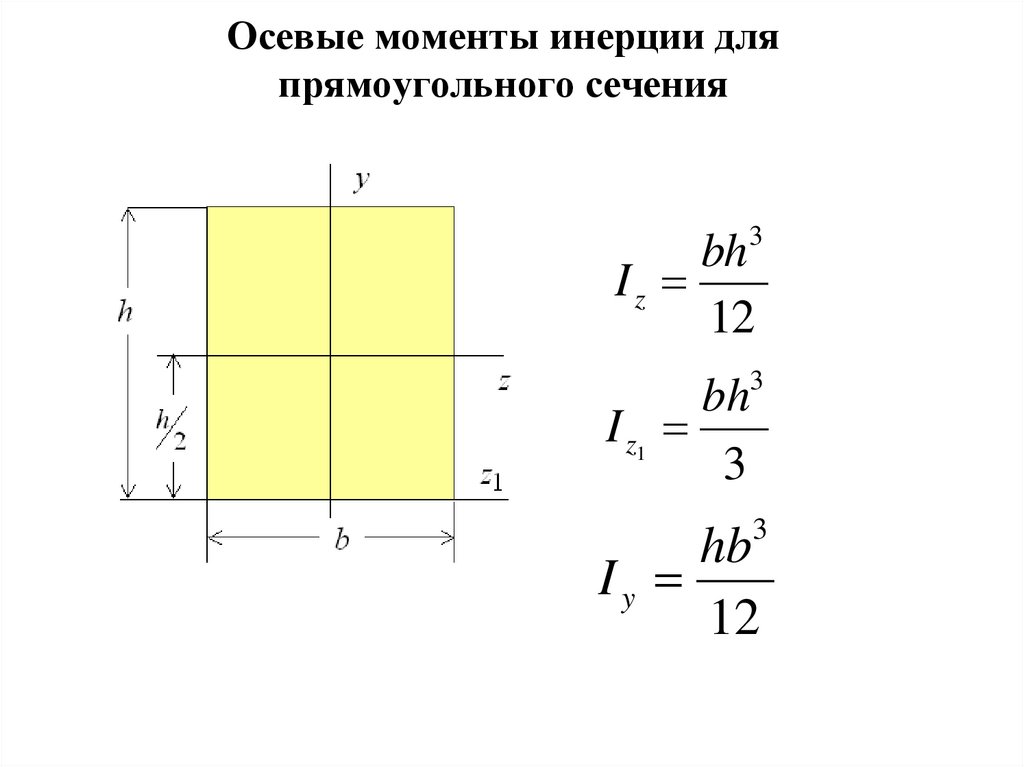
13. Осевые моменты инерции для прямоугольного сечения

bh3
Iz
12
3
bh
I z1
3
3
hb
Iy
12

14.

Определение момента инерции и момента сопротивления
относительно оси Z составного сечения

15. Центробежный момент инерции

I zy zydF
F
Координатные оси, относительно которых I zy 0 , называются
главными осями инерции.
Если главные оси проходят через центр тяжести сечения, то они
называются главными центральными осями. Начало координат в этом
случае находится в центре тяжести сечения.
Осевые моменты инерции относительно главных осей называются
главными моментами инерции. Главные моменты инерции экстремальны
относительно всех осей, проходящих через центр тяжести.
Оси симметрии – всегда главные оси.

16.

Определение положения главных центральных осей для
прямоугольного треугольника

17.

vu