Similar presentations:
Геометрические характеристики плоских сечений
1. Лекция
Геометрические характеристикиплоских сечений
1
2. 1. Геометрические характеристики поперечных сечений
АСопротивление бруса внешним силам зависит не только от его размеров и
материала, но и от формы поперечного сечения, геометрические свойства
которого выражаются численно посредством геометрических характеристик.
1.1. Площадь поперечного сечения - A
Y
∫∫ dxdy = ∫dA=А
dA = dx∙dy
A
A
dy
dx
Размерность А: [A] = [длина 2] = [ м2]
X
Y
2
dy
3
2
3
0
0
A = ∫∫dxdy = ∫dx ∫dy = x| y| = 6 (ед2 ).
dx
2
3
А
X
0
0
2
3. Геометрические характеристики
АГеометрические характеристики
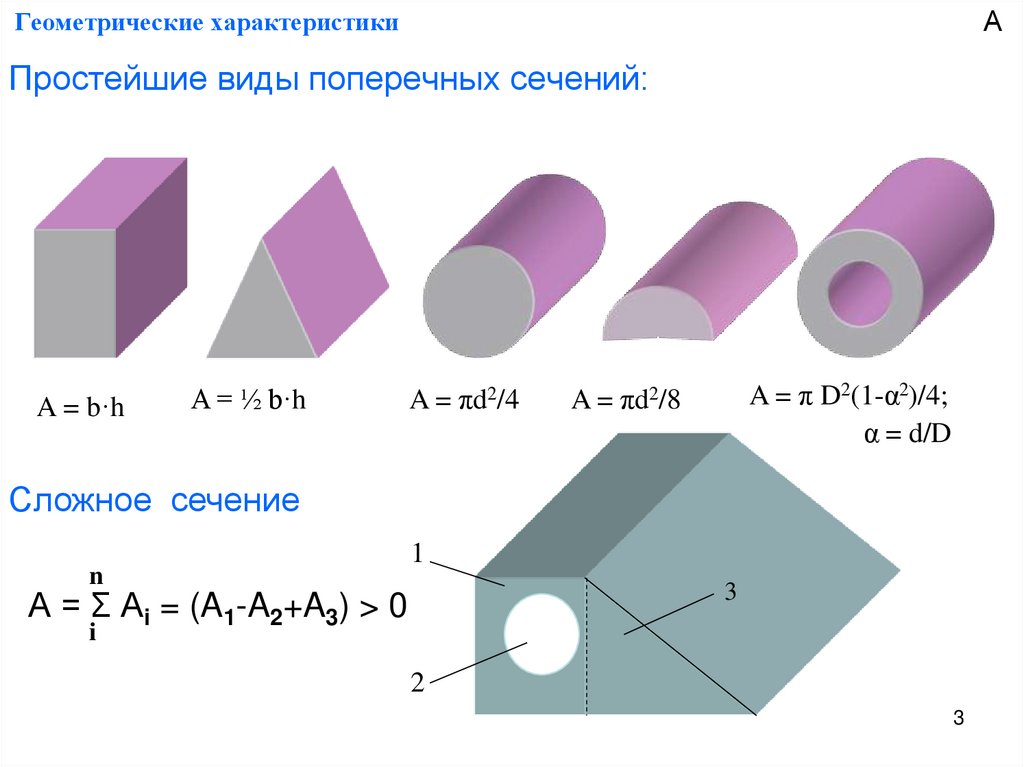
Простейшие виды поперечных сечений:
A = b·h
A = ½ b·h
A = πd2/4
A = π D2(1-α2)/4;
α = d/D
A = πd2/8
Сложное сечение
n
1
3
А = Σ Аi = (A1-A2+A3) > 0
i
2
3
4. Геометрические характеристики
А1.2. Статические моменты поперечного сечения – Sx , Sy
Y
Y
dA
x
x
xc
.C
xc
dA y
y
yc
.c
A yc
X
SX = ∫ y∙dA,
SY = ∫ x∙dA.
>0
< 0 (1)
=0
SX = ∫ y∙dA = A∙ yC
SY = ∫ x∙dA = A∙ xC
dA ·y = dMx
dA ·x =
dMy
X
yC = SX / A
xC = Sy / A (2)
[S] = [длина3]
Оси, проходящие через центр тяжести, называются центральными.
Центральных осей – бесконечное множество.
4
Из (2)
S y, x = 0 для центральных осей
5. Геометрические характеристики
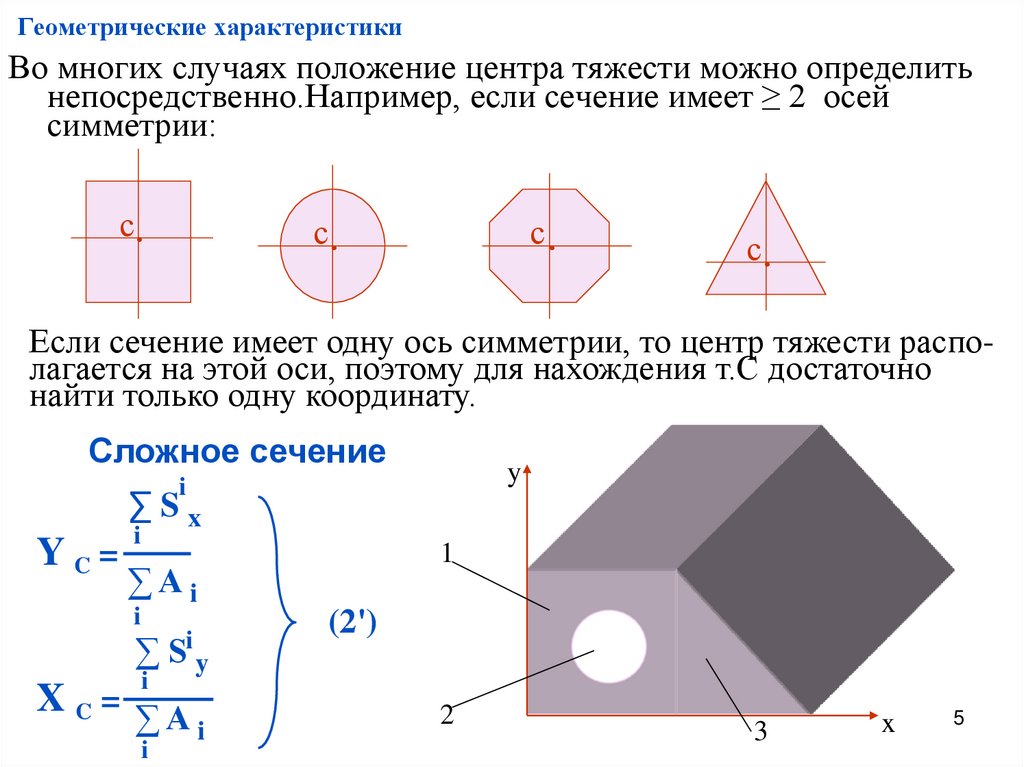
Во многих случаях положение центра тяжести можно определитьнепосредственно.Например, если сечение имеет ≥ 2 осей
симметрии:
с·
с·
с·
с·
Если сечение имеет одну ось симметрии, то центр тяжести располагается на этой оси, поэтому для нахождения т.С достаточно
найти только одну координату.
Сложное сечение
y
i
∑Sx
YC=
i
1
∑Ai
i
i
∑Sy
(2')
i
X C= ∑A
i
i
2
3
x
5
6. Геометрические характеристики
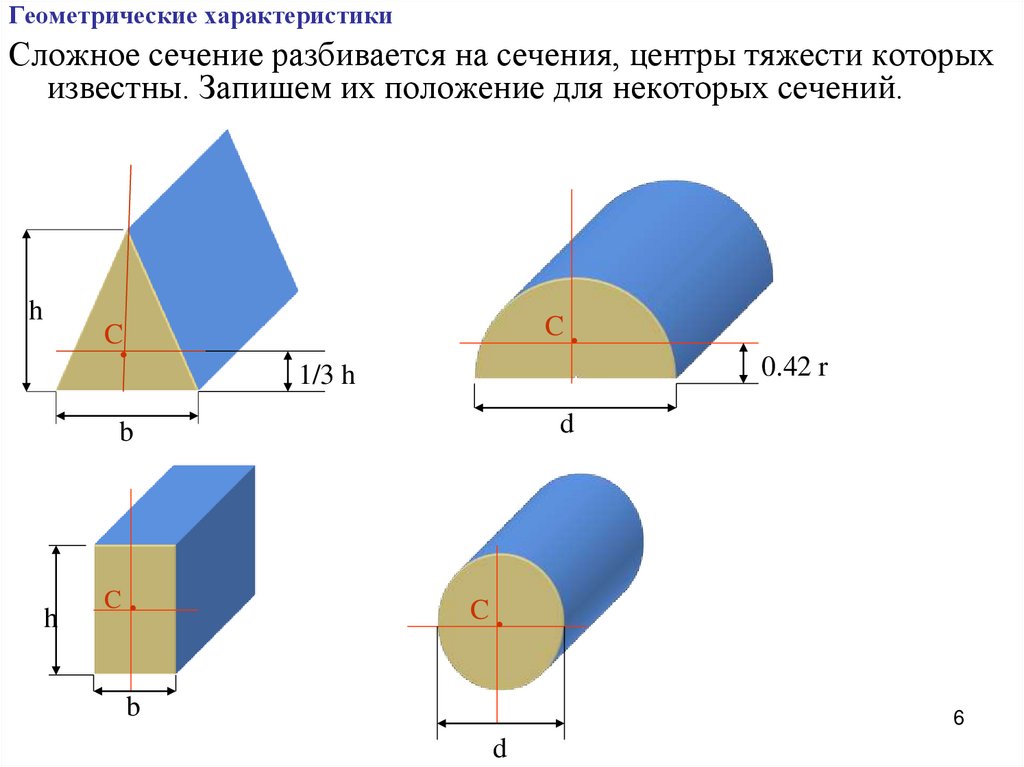
Сложное сечение разбивается на сечения, центры тяжести которыхизвестны. Запишем их положение для некоторых сечений.
h
C
C.
·
1/3 h
d
b
h
C
·
0.42 r
C
·
b
6
d
7. Геометрические характеристики
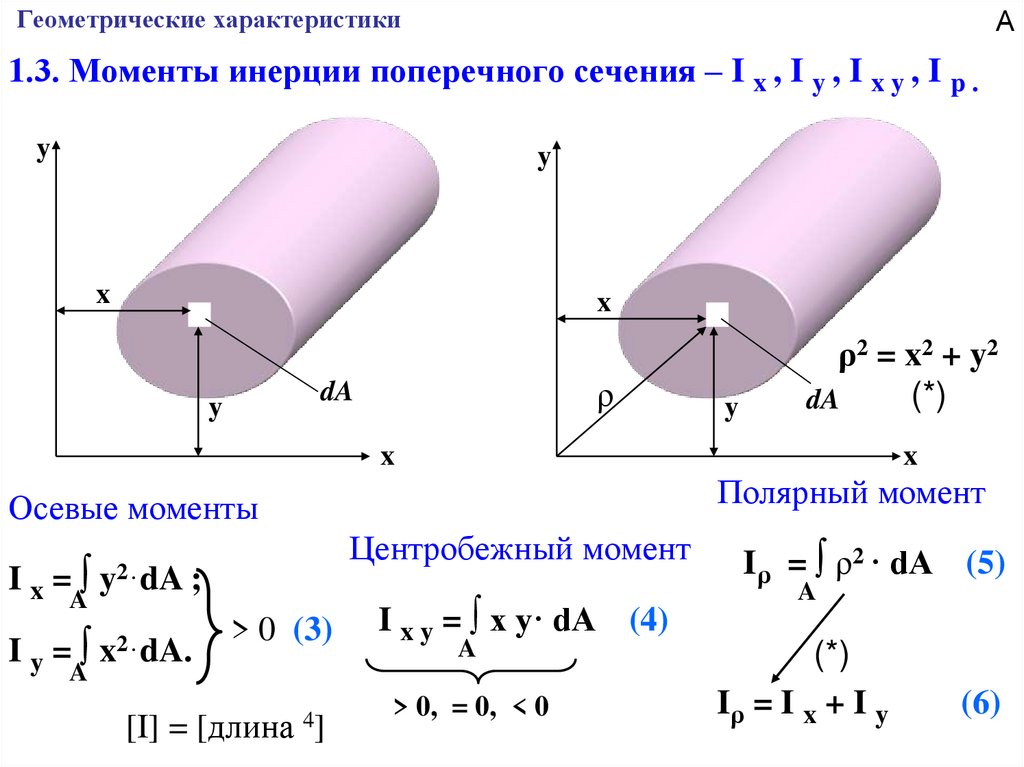
А1.3. Моменты инерции поперечного сечения – I x , I y , I x y , I p .
y
y
x
x
ρ
dA
y
y
ρ2 = x2 + y2
(*)
dA
x
x
Полярный момент
Осевые моменты
Ix=∫
A
Центробежный момент
y2·dA ;
I y = ∫ x2·dA.
> 0 (3)
I x y = ∫ x y· dA (4)
A
A
[I] = [длина 4]
> 0, = 0, < 0
Iρ = ∫ ρ2 · dA (5)
A
(*)
Iρ = I x + I y
(6)
8. Геометрические характеристики
АГеометрические характеристики
y
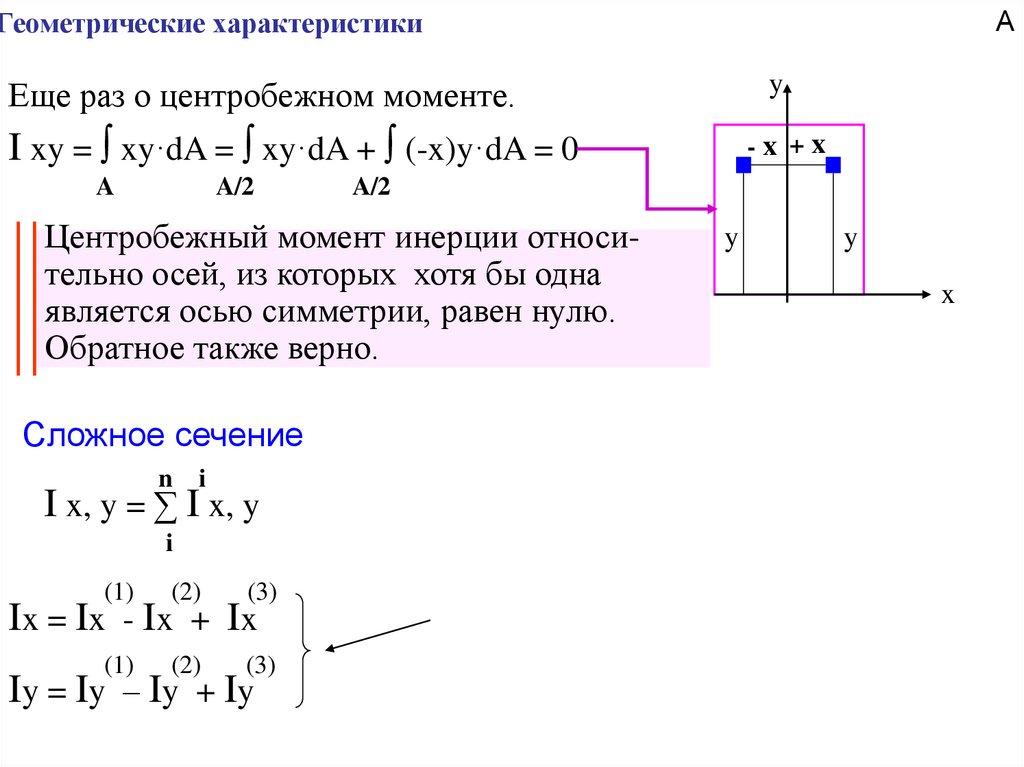
Еще раз о центробежном моменте.
I xy = ∫ xy·dA = ∫ xy·dA + ∫ (-x)y·dA = 0
A
A/2
A/2
Центробежный момент инерции относительно осей, из которых хотя бы одна
является осью симметрии, равен нулю.
Обратное также верно.
Сложное сечение
n
-x +x
y
y
x
y
i
I x, y = ∑ I x, y
i
(1)
(2)
(3)
(1)
(2)
(3)
1
Ix = Ix - Ix + Ix
2
Iy = Iy – Iy + Iy
z
3
8
9. Геометрические характеристики
Центральные моменты инерции – моменты относительноцентральных осей. Поскольку центральных осей –
бесконечное множество, центральных моментов также –
бесконечное множество
9
10. Геометрические характеристики
А1.4. Моменты инерции простейших сечений
1.5. Изменение моментов инерции при преобразовании осей
Параллельный перенос
Y
YC
x
xc
dA
yc
b c.
y
Поворот осей
Yα
XC
a
X
x = xC + b ; (*) y= yC + a; (**)
Дано: Ixc , Iyc, Ixcyc. Ix, Iy, Ixy = ?
c.
dA
xc
Xα
α
yc
Xc
xα = x cos α + y sin α
yα = - x sin α + y cos α
Дано: Ixc , Iyc, Ixcyc.
Ix = ∫
Ixc
A
(7) Ixα = ? Iyα = ? Ixαyα=? (8)
Iy =A∫ x2∙dA = (*) = Iyc + b2∙A
10
Ixy =A∫xy∙dA =(*),(**)=Ixcyc + ab∙A
y2∙dA = (**) =
+ a2∙A
Yc
11. Геометрические характеристики
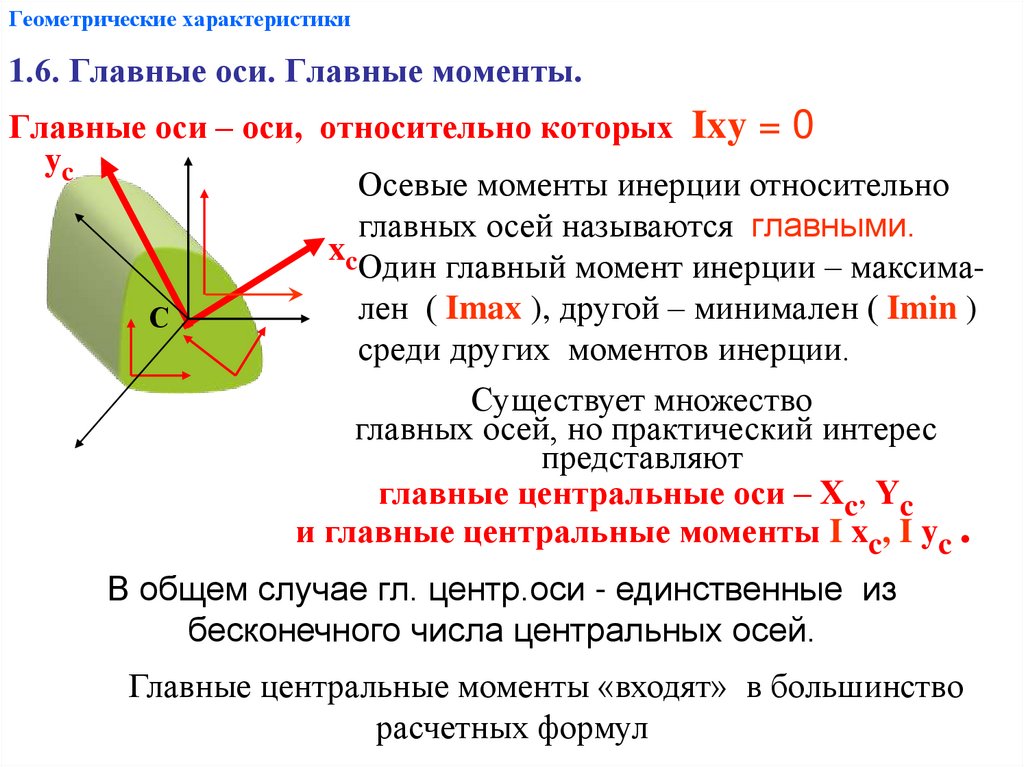
1.6. Главные оси. Главные моменты.Главные оси – оси, относительно которых Ixy = 0
yc
Осевые моменты инерции относительно
главных осей называются главными.
xc
Один главный момент инерции – максимален ( Imax ), другой – минимален ( Imin )
С
среди других моментов инерции.
Существует множество
главных осей, но практический интерес
представляют
главные центральные оси – Xc, Yc
и главные центральные моменты I xc, I yc .
В общем случае гл. центр.оси - единственные из
бесконечного числа центральных осей.
Главные центральные моменты «входят» в большинство
расчетных формул
12. Геометрические характеристики
АОси симметрии всегда являются главными
центральными осями !
Поэтому, если тело имеет хотя бы одну ось симметрии, нахождение главных центральных осей не представляет трудностей.
В случае отсутствия осей симметрии, нужно провести любые
центральные оси, определить для них центральные моменты
(осевые и центробежный), и затем повернуть эти оси на угол:
у
v
u
С
α)
2Ixy
tg 2α =
Iy - Ix
,
х
и получим оси u,v – главные центральные оси.
12
13. СИЛОВАЯ ПЛОСКОСТЬ
АГеометрические характеристики
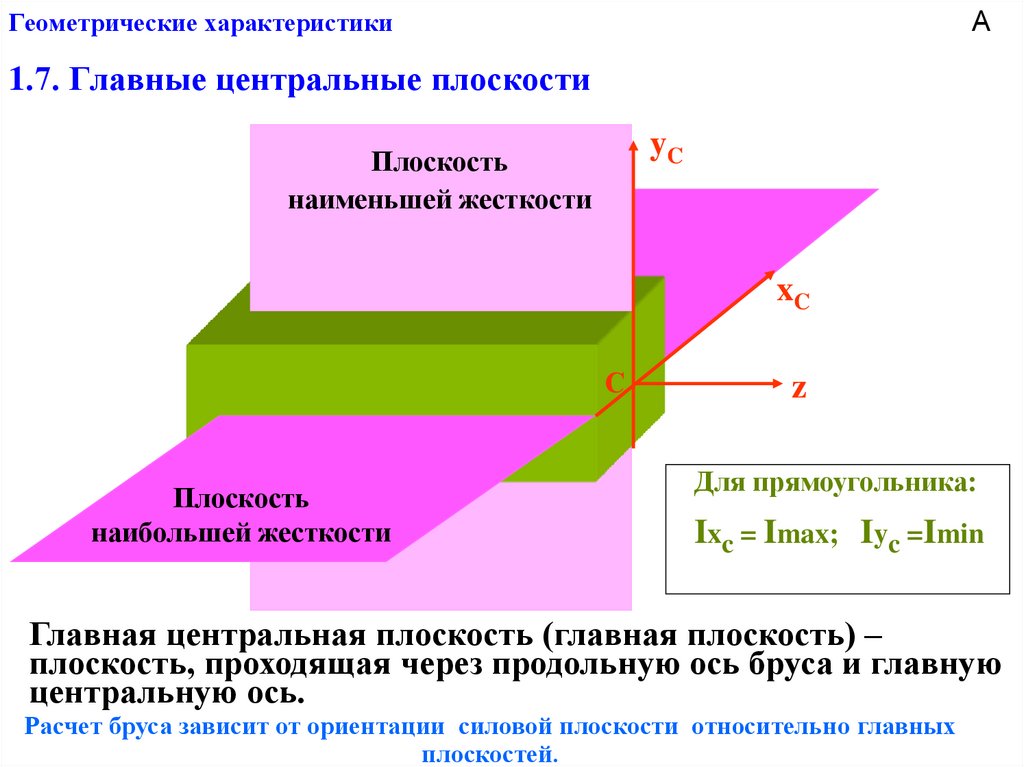
1.7. Главные центральные плоскости
yC
Плоскость
наименьшей жесткости
xC
С
Плоскость
наибольшей жесткости
z
Для прямоугольника:
Ixc = Imax; Iyc =Imin
Главная центральная плоскость (главная плоскость) –
плоскость, проходящая через продольную ось бруса и главную
центральную ось.
Расчет бруса зависит от ориентации силовой плоскости относительно главных
плоскостей.
14. Геометрические характеристики
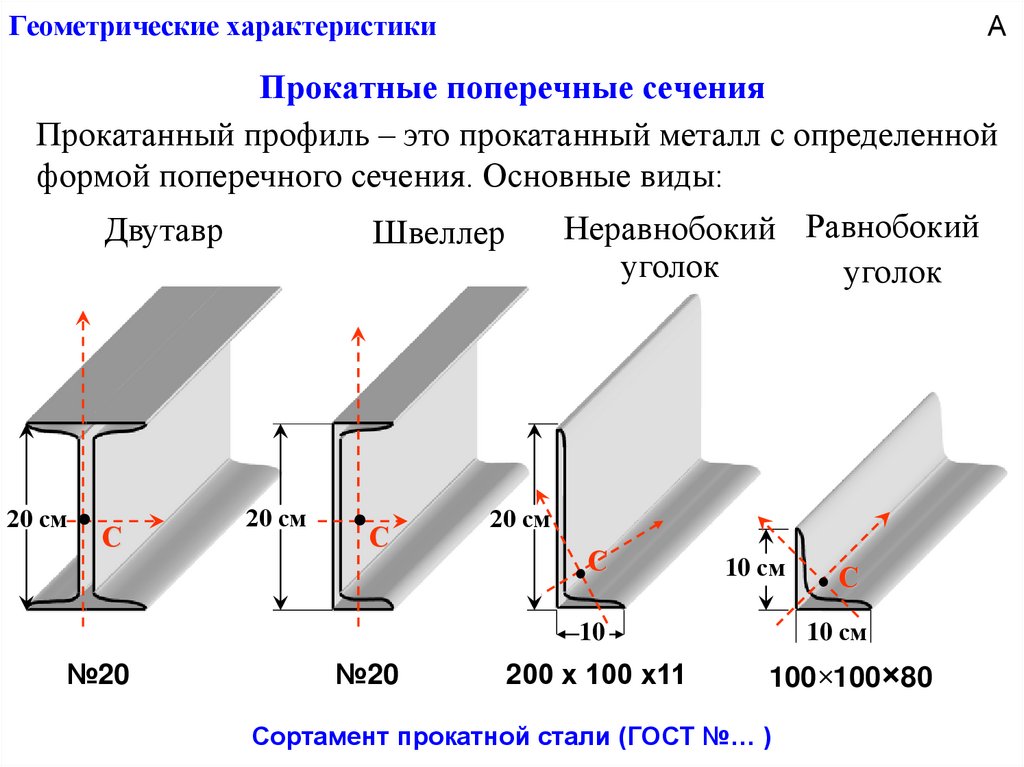
АПрокатные поперечные сечения
Прокатанный профиль – это прокатанный металл с определенной
формой поперечного сечения. Основные виды:
Неравнобокий Равнобокий
Двутавр
Швеллер
уголок
уголок
20 см
С
№20
20 см
С
№20
20 см
С
10 см
С
10
10 см
200 х 100 х11
100×100×80
Сортамент прокатной стали (ГОСТ №… )
15. Геометрические характеристики
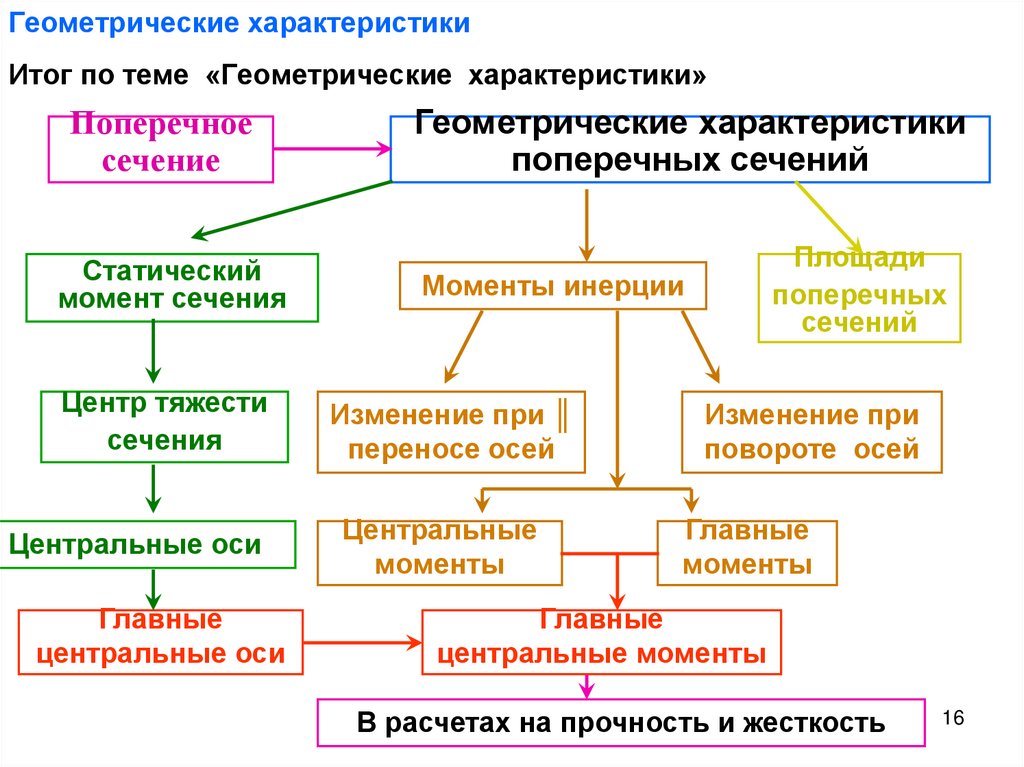
Итог по теме «Геометрические характеристики»Поперечное
сечение
Статический
момент сечения
Центр тяжести
сечения
Центральные оси
Главные
центральные оси
Геометрические характеристики
поперечных сечений
Площади
поперечных
сечений
Моменты инерции
Изменение при ║
переносе осей
Центральные
моменты
Изменение при
повороте осей
Главные
моменты
Главные
центральные моменты
В расчетах на прочность и жесткость
16






 mechanics
mechanics








