Геометрические характеристики плоских сечений

1.

Геометрические характеристики
плоских сечений

2.

Статический момент сечения и положение
центра тяжести
• Найти положения центра тяжести сечения, имеющего
форму тавра. Сечение разбиваем на 2 части 1 и 2.
Вычисляем статический момент
сечения
сечения относительно оси z2.
Находим координату центра тяжести.

3.

Статический момент сечения и положение
центра тяжести
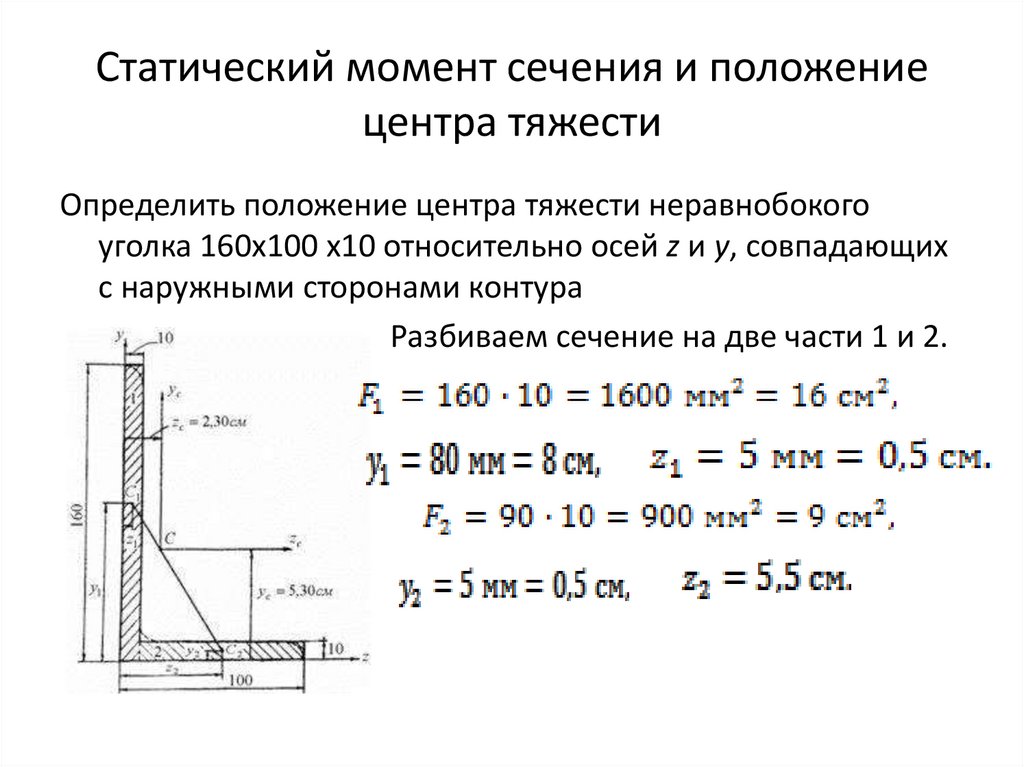
Определить положение центра тяжести неравнобокого
уголка 160х100 х10 относительно осей z и y, совпадающих
с наружными сторонами контура
Разбиваем сечение на две части 1 и 2.

4.

Статический момент сечения и положение
центра тяжести
Координаты центра тяжести сечения определяем по
формулам:
По данным сортамента с учетом закруглений координаты
центра тяжести равны zc=2,28см; yc=5,23см.
Графическая проверка: точка С должна находиться на
отрезке С1С2.

5.

Моменты инерции сложных сечений
Для вычисления момента инерции сложной фигуры надо
разбить ее на ряд простых фигур, вычислить моменты
инерции этих фигур, а затем просуммировать их.

6.

Моменты инерции сложных сечений
Определить момент инерции сечения относительно оси
симметрии, a=10 см.
Разбиваем заданное сечение на простейшие элементы: I равнобедренный треугольник, II - прямоугольник, III - круг.
Окончательно получим:
Iz= 4,0a4 + 10,67a4 - 0,0491a4 = 14,6a4 = 14,6·104 см4.

7.

Моменты инерции сложных сечений
Какая из фигур имеет больший момент инерции
относительно оси z, если их площади равны A=400 см2?
Диаметр круглого сечения:
Сторона квадрата:

8.

Осевые и центробежный моменты инерции
Найти осевые и центробежный моменты инерции
прямоугольника относительно осей y1 и z1.