Similar presentations:
Кинематические характеристики движения точки
1.
КИНЕМАТИКАТема 1.3. Кинематические характеристики
движения точки
Тема 1.4. Частные случаи движения точки
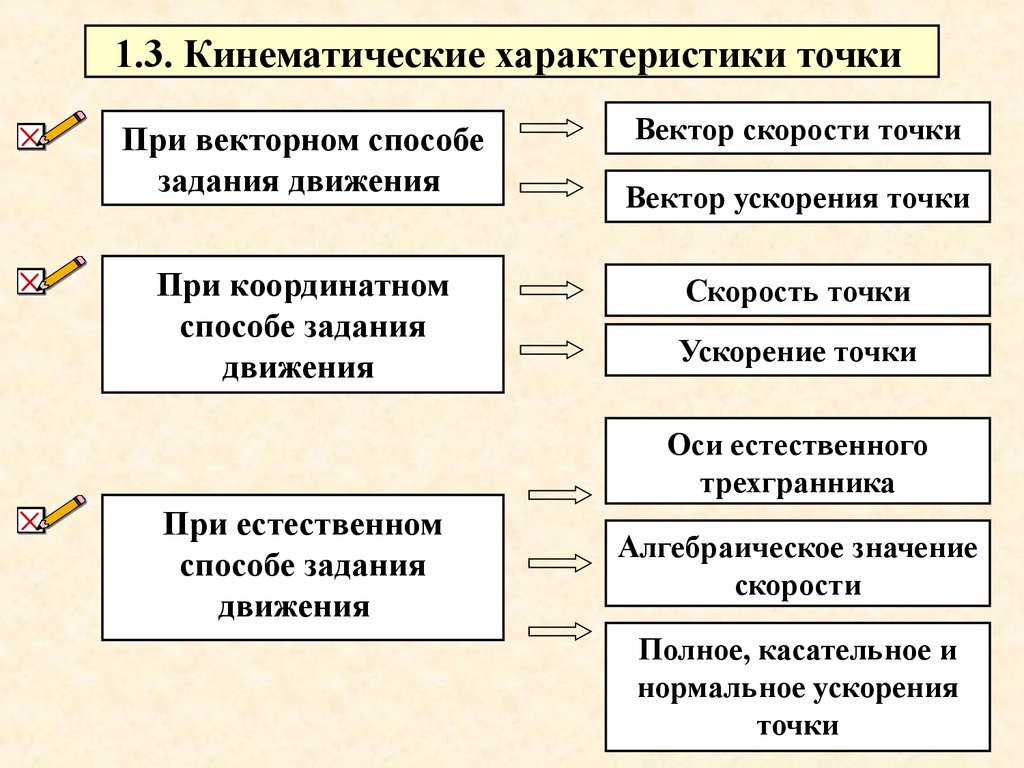
2. 1.3. Кинематические характеристики точки
При векторном способезадания движения
При координатном
способе задания
движения
Вектор скорости точки
Вектор ускорения точки
Скорость точки
Ускорение точки
Оси естественного
трехгранника
При естественном
способе задания
движения
Алгебраическое значение
скорости
Полное, касательное и
нормальное ускорения
точки
3.
Кинематические характеристики точки при еевекторном способе задания движения
z
V ср
Вектор скорости точки
M1
r
r1
V
Средняя скорость точки
Пусть положение точки в момент
времени t определяется
радиусом –
вектором r .
r
О
у
В момент времени
t1 – радиусом –
вектором r1 .
х
За t = t1 – t радиус – вектор
точки получат приращение
M
r r1 r .
Опр. Средней скоростью точки называется отношение V
СР
r
t .
Опр. Мгновенной скоростью точки называется вектор
V
lim
t 0
r
t
d
r
dt
.
4.
Вывод. Вектор скорости точки в момент времени t равенпервой производной по времени от радиуса вектора точки
V
dr .
dt
(*)
Вектор мгновенной скорости точки направлен по
касательной к ее траектории.
Вектор ускорения точки
Опр. Ускорением точки называется векторная величина,
характеризующая изменение с течением времени модуля и
направления скорости точки.
5.
V,Пусть при t точка занимает положение
М и имеет скорость
а в момент времени t1 – скорость V1 . За промежуток времени
t = t1 – t скорость точки получит приращение V V1 V .
Вектор V всегда направлен в сторону
М
V
вогнутости траектории.
М1
V
Опр. Средним ускорением точки
а
V1
называется вектор, который
аср
определяется по формуле аср V t .
V1
Опр. Ускорением точки в данный
момент времени
называется вектор а lim V t .
t
или с учетом того, что V
0
dr
dt
,
переходя к приделу, получим
2
а dV dt d r / dt 2 .
(**)
Вывод. Вектор ускорения точки определяется по формуле (**),
направлен в сторону вогнутости траектории и лежит в
соприкасающейся плоскости.
6.
Задание 1.Движение материальной точки
М задано
уравнением
r 5t i cost j 11 k .
Вектор скорости точки направлен …
Варианты ответа
1) параллельно плоскости xOz
(не параллельно осям)
2) перпендикулярно плоскости xOy
3) параллельно оси Оz
4) перпендикулярно оси Оz
dr d(5t i cost j 11 k ) d(5t i ) d(cost j ) d(11 k )
V
dt
dt
dt
dt
dt
d(5t) d(cost) d(11)
i
j
k 5 i sint j .
dt
dt
dt
7.
Задание 2.Движение материальной точки М задано уравнением
r 4 i sint j 3t k .
Вектор ускорения точки направлен …
Варианты ответа
1) перпендикулярно оси Oу
2) параллельно плоскости xOz
3) параллельно оси Оу
4) перпендикулярно плоскости уОz
(непараллельно осям)
2
2
2
2
2
d r d (4 i sint j 3t k ) d (4 i ) d (sint j ) d (3t k )
а 2
2
2
2
2
dt
dt
dt
dt
dt
sint j .
8.
Кинематические характеристики точки при ее координатномспособе задания движения
Теорема. Проекция производной от вектора на ось,
неподвижную в данной системе отчета, равна производной
от проекции дифференцируемого вектора на ту же ось, т. е:
d
p
d pх
d pz
d pу
,
.
q ,
, qz
если
то q х
qу
(1)
dt
dt
d
t
dt
Определение скорости точки
Вектор скорости точки V
d r
d t
z
.
Отсюда, учитывая, что
rх = х , rу = у, rz = z , найдем
Vх
d х
d у
d z
х, V у
у, V z
z .
d t
d t
d t
M
k
О
i
(2)
j
r
rу = у
х
rz = z
rx = х у
9.
Вывод. Проекции скорости точек на координатные осиравны первым производным от соответствующих
координат точки по времени.
Модуль и направление скорости точки определяются по
формулам:
z
А) пространственный случай:
соs Vx / | V |,
| V | V x 2 V 2у V z 2 , сos V у / | V |, (3)
cos Vz / | V | .
Vz
х
Vу
у
у
В) плоский случай:
| V | V x 2 V 2у ,
Vx
А
V
соs Vx / | V | . (4)
Vу
О
V
Vх
х
10.
Определение ускорения точкиВектор ускорения точки а dV dt .
Тогда на основании формулы (1) получаем:
d Vx
ах d t
d Vу
ау d t
dVz
аz d t
d x
d t
2
2
d 2у
d t2
d 2z
d t2
V x
x
,
V у
у
,
V z
z .
(5)
Вывод. Проекции ускорения точек на координатные оси
равны первым производным от проекций скорости или
вторым производным от соответствующих координат точки
по времени.
11.
Модуль и направление ускорения точки найдутся из формул:| а | а x 2 а 2у а z 2 ,
(6)
соs 1 а x / | а |, сos 1 а у / | а |, cos 1 а z / | а |,
где 1, 1, 1 – углы, образуемые вектором ускорения с
координатными осями.
Вывод. Если движение точки задано координатным способом,
т. е. заданы уравнения движения: х = f 1 (t), у = f 2 (t), z = f 3 (t),
то скорость точки определяется по формулам (3) и (4), а
ускорение - по формулам (5) и (6).
При прямолинейном движении
dх
Vх d t
х
,
d Vx
ах d t
d x
d t
2
2
V x
x .
12.
Кинематические характеристики точки при ееестественном способе задания движения
Оси естественного трехгранника
V
n
Скорости и ускорения точки при ее
естественном способе задания
движения определяются с помощью
подвижных осей М nb.
–О +
Эти оси называются осями
естественного трехгранника .
х
z
s
/
М
b
О
у
Ось М - направлена по касательной к траектории в сторону
положительного отсчета координаты s;
Ось Мn - (главная нормаль) – направлена по нормали к
траектории, лежащей в соприкасающейся плоскости.
Ось Мb (бинормаль) – направлена перпендикулярно к
первым двум осям.
13.
Определение скорости точкиВектор скорости точки всегда
направлен по касательной к ее
траектории, поэтому проектируется
только на ось М , то есть | V | = |V |.
z
V
s
М
–О +
/
О
у
х
Алгебраическое значение скорости точки (проекция скорости
точки на касательную М : V = V ) в данный момент времени
равно первой производной от координаты s этой точки по
времени, т. е.
ds
V
s .
dt
(1)
14.
Вывод. Вектор скорости точки в данный момент временинаправлен по касательной к траектории точки, а
алгебраическое значение скорости точки при ее естественном
способе задания определяется по формуле (1).
Если V 0, то скорость направлена
в сторону возрастания дуговой
координаты s, если V 0, то в
сторону убывания.
z
–О +
/
О
х
s
V<0
V>0
М
у
15.
Определение ускорения точкиУскорение точки при естественном способе
задания ее движения равно геометрической
сумме двух векторов а аn а τ .
(2)
n
а
аn
М
Вектор аn направлен по главной нормали и называется
аτ
нормальным ускорением.
Вектор а τ направлен по касательной и называется
касательным ускорением.
Модуль нормального ускорения определяется по формуле
а n = V 2/ ,
(3)
где - радиус кривизны траектории в точке М.
Алгебраическое значение касательного ускорения находится
по формуле
2
dV
d
s V s .
аτ
dt
dt 2
(4)
16.
Если а 0, то оно направлено в сторонувозрастания дуговой координаты s,
если а < 0, то – в сторону убывания s.
Модуль полного ускорения определиться
в виде
2
2
| а | а n а τ ,
а
аn
s
а > 0
М
– О /+ а
< 0
(5)
а направление - по формуле
tg | a | / аn .
(6)
Вывод. Если движение точки задано естественным способом,
то, зная траекторию и закон движения, т. е. зависимость
s = s (t), можно по формулам (1) - (6) определить модуль и
направление векторов скорости и ускорения точки в любой
момент времени.
17.
1.4. Некоторые частные случаи движения точкиГармонические
колебания
Равнопеременное
криволинейное
движение
Ускоренное и
замедленное
движения
Равномерное
криволинейное
движение
Прямолинейное
движение
Равноускоренное и
равнозамедленное
движения
Равномерное
прямолинейное
движение
18.
Прямолинейное движение точкиОпр. Движение точки называется прямолинейным, если ее
траекторией является прямая линия.
При прямолинейном движении = и аn= V 2/ = 0, то есть
ускорение точки равно только одному касательному
dV .
ускорению: а = а = dt
Вывод. Физический смысл нормального ускорения
заключается в том, что оно характеризует изменение
скорости точки по направлению.
19.
Равномерное криволинейное движение точкиОпр. Равномерным называется такое криволинейное
движение точки, в котором числовое значение скорости все
время остается постоянным: V = const.
При равномерном криволинейном движение а = dV 0,
dt
то есть ускорение точки равно только одному нормальному
ускорению: а = аn .
Закон равномерного движения точки имеет вид: s = sО + V . t.
Вывод. Физический смысл касательного ускорения
заключается в том, что оно характеризует изменение
числового значения (величины) скорости.
20.
Равномерное прямолинейное движение точкиОпр. Движение точки называется равномерным
прямолинейным, если ее траекторией является прямая
линия, и в котором числовое значение скорости все время
остается постоянным: V = const.
Так как движение прямолинейное, то = и аn= V 2/ = 0, и
так как движение равномерное, то а =
полное ускорение точки а = 0.
dV 0 ,
dt
то есть
Вывод. Равномерное прямолинейное движение точки - это
единственный вид движения, в котором полное ускорение
точки все время равно нулю.
21.
Равнопеременное криволинейное движение точкиОпр. Равнопеременным называется такое криволинейное
движение точки, в котором касательное ускорение всё время
остается постоянным: а = const.
Вывод. При равнопеременном криволинейном движении
точки ее скорость изменяется по закону: V = VО + а · t, а
закон движения точки имеет вид:
s = s 0 + V0 · t + а ·
t2
.
2
22.
Ускоренное и замедленное движение точкиОпр. Движение точки называется ускоренным, если модуль
скорости возрастает, и замедленным, если убывает.
Вывод. Движение будет ускоренным,
если знаки V и а совпадают (Рис.а)),
и замедленным, если знаки
противоположные (Рис. б) и в)).
V
Рис б)
s
– О / +
аτ
М
а < 0
V>0
Рис а)
s
– О /+
М
а < 0
V<0
аτ
Рис в)
s
– О /+
а > 0
V>0
М
а > 0
V<0
V
Равноускоренное и равнозамедленное движение точки
Опр. Равноускоренным движением точки называется ее
ускоренное равнопеременное движение, а равнозамедленным
– замедленное равнопеременное движение.
23.
Гармонические колебания точкиА1
Опр. Движения точки, происходящие по закону: x=А· cos (kt),
называются гармоническими
колебаниями.
М0
Т
М2
А
0
1
М1
М
-1
-А
Опр. Величина А, равная наибольшему отклонению точки от
центра колебаний О, называется амплитудой колебаний.
Опр. Промежуток Т = 2 / k, в течение которого точка совершает одно полное колебание, называется периодом колебаний.
Вывод. Скорость и ускорение точки при гармонических
колебаниях изменяются по гармоническим законам:
V = Vx= - А · k · sin (kt),
a = ах = - А · k2 · cos (kt).
Аналогичные колебания происходят и при законе x = А· sin(kt),
только движение в этом случае начинается из точки О.
24.
Пример выполнения задачи К1По заданным уравнениям движения точки М
х = 4 t см;
у
= 16 t 2 – 1 см; установить вид ее траектории и для момента
времени t1 = ½ с найти положение точки на траектории, ее
скорость, полное, касательное и нормальное ускорения, а
также радиус кривизны траектории в соответствующей точке.
Решение.
1. Определим траекторию точки
Исключим время t из уравнений движения, тогда: у = х 2 – 1.
Это выражение есть уравнение параболы.
2. Определим скорость точки
Найдем проекции скорости на оси координат:
Vx x 4 см / с; V у у 32 t см / с.
Модуль скорости точки
При t1 = 1/2с
| V | V 2х V 2у 4 2 1024 t 2 .
V1 = V |t = 0,5 = 16, 5см/c .
25.
3. Определим ускорение точкиНайдем проекции ускорения на оси координат:
а х х 0;
а у у 32 см / с 2 .
Модуль ускорения точки
| а | a x2 a у2 32 см / с 2 .
4. Определим касательное ускорение точки
dV |
посредством дифференцирования скорости a |
dt
2 V x V x 2 V у V у V x а x V у а у
dV
.
dt
V
2 V 2x V 2у
При t1 = 1/2с
dV
dt
4 0 16 32
16,5
= 31 см/с2.
Следовательно, модуль касательного ускорения а = 31 см/с2.
Знак «+» при а показывает, что движение точки ускоренное
и, следовательно, направления а и V совпадают.
26.
5. Определим нормальное ускорение точки и радиускривизны траектории при t1 = 1/2 с .
Из формулы для полного ускорения | а | а
аn =
2
а а = 7,94 см/с2 и
2
2
n
а
2
τ
получим:
= V 2/ а n= 16,5 2 / 7,94 = 34,3 см.
Полученные данные представим в виде таблицы
Координаты,
см
Скорость,
см/с
х
у
Vx Vу
2
3
4
V
16 16,5
Ускорение,
см/с2
ах ау
0
а
a
Радиус
кривизны, см
an
32 32 31 7,94
34,3
27.
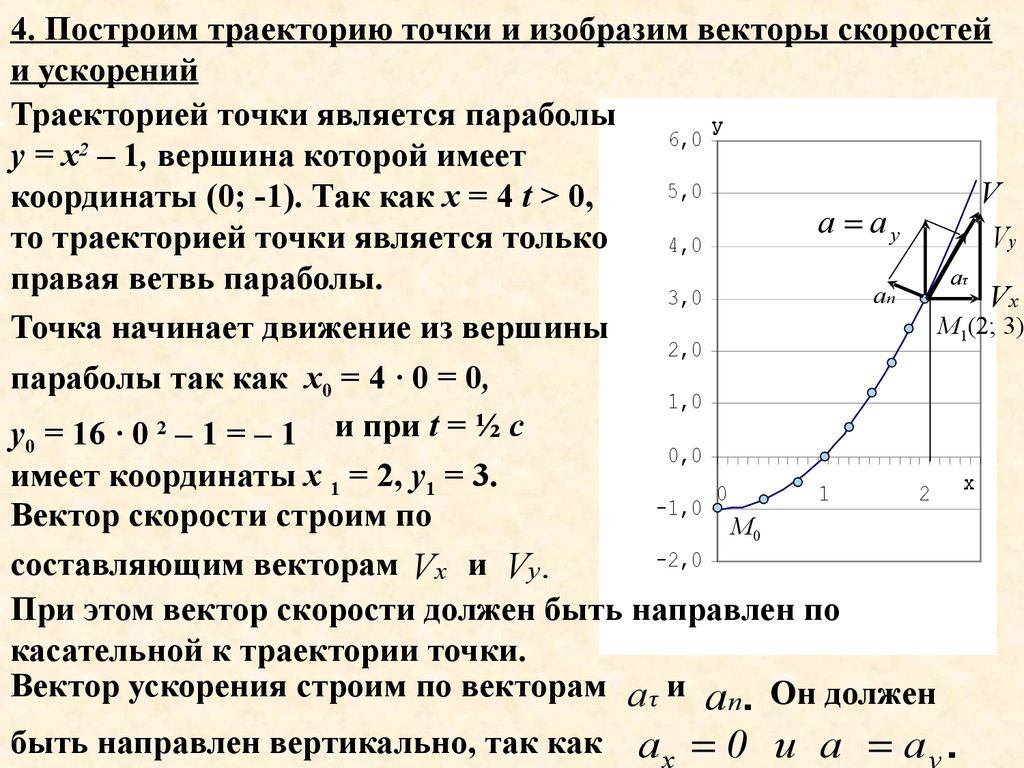
4. Построим траекторию точки и изобразим векторы скоростейи ускорений
Траекторией точки является параболы
у
6,0
у = х2 – 1, вершина которой имеет
5,0
V
координаты (0; -1). Так как х = 4 t > 0,
а
а
у
Vу
то траекторией точки является только
4,0
аτ
правая ветвь параболы.
аn
3,0
Vх
М1(2; 3)
Точка начинает движение из вершины
2,0
параболы так как х0 = 4 · 0 = 0,
1,0
у0 = 16 · 0 2 – 1 = – 1 и при t = ½ с
0,0
имеет координаты х 1 = 2, у1 = 3.
0
1
2 х
-1,0
Вектор скорости строим по
М0
-2,0
составляющим векторам Vх и Vу .
При этом вектор скорости должен быть направлен по
касательной к траектории точки.
Он должен
Вектор ускорения строим по векторам а τ и а
n.
быть направлен вертикально, так как а х 0 и а а у .

























 physics
physics








