Similar presentations:
Кинематика точки. Естественный способ описания движения точки. Лекция 10
1. Лекция 10 Кинематика точки. Естественный способ описания движения точки
2. При естественном способе задания движения задаются: -траектория -закон движения точки вдоль траектории
3. При естественном способе задания движения задаются: -траектория -закон движения точки вдоль траектории
4. При естественном способе задания движения задаются: -траектория -закон движения точки вдоль траектории
s f (t )5. От задания движения в декартовых координатах можно перейти к его заданию естественным способом
x f1 t , y f 2 t , z f3 t .ds dx dy dz
2
s
t
o
2
dx dy dz
2
2
2
2
t
o
f t f t f t ,dt
'
1
2
'
2
2
'
3
2
6. Скорость точки при естественном способе задания движения
7.
8.
9.
10.
11.
Геометрические понятия.Дифференцирование единичного вектора.
Радиус кривизны и соприкасающаяся плоскость
12.
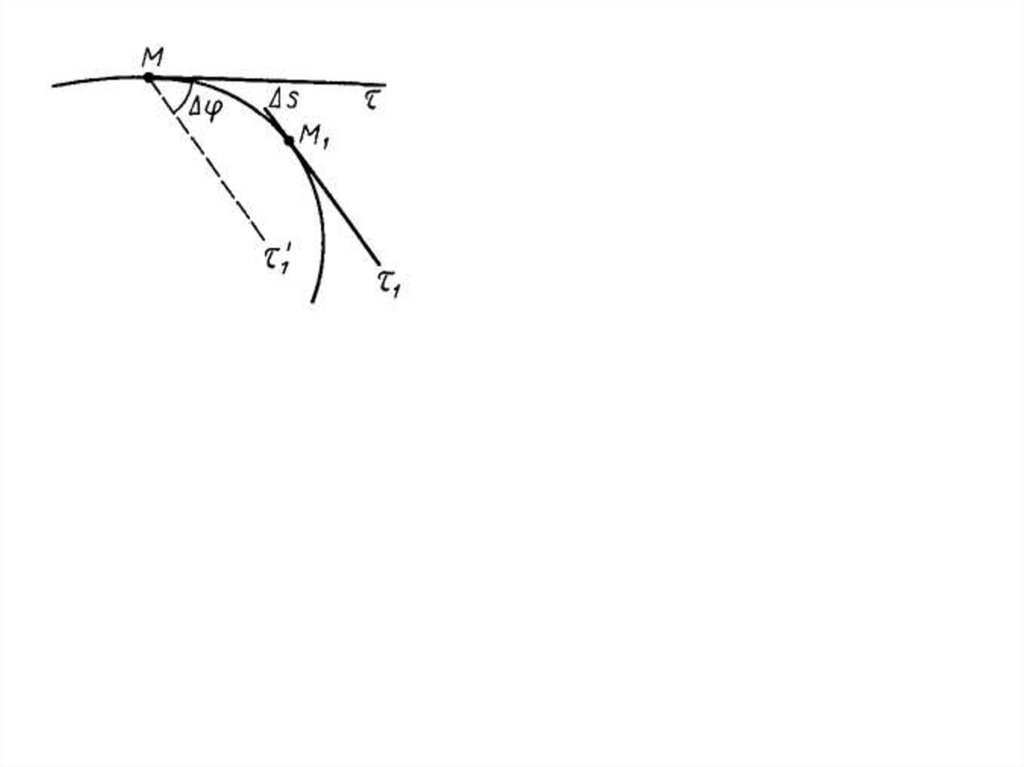
13. - угол смежности
- угол смежности14. - угол смежности k – кривизна
- угол смежностиk – кривизна
d
k lim
.
s 0 s
ds
15. - радиус кривизны
1ds
.
k d
- радиус кривизны
16. Пример
s = Rds d R
R.
d
d
17. Соприкасающаяся плоскость
18. Соприкасающаяся плоскость
19.
Естественный трехгранник20.
21.
M22.
MMn
23.
MMn
Mb
24. - естественный трехгранник
M , Mn, Mb- естественные оси, n, b
- естественный трехгранник
25.
Дифференцирование единичного вектора26.
ddt
27.
ddt
1.
d
d
d
0 2
0.
dt
dt
dt
28.
dd
n.
dt
dt
29.
dd
n.
dt
dt
d
lim
.
t 0 t
dt
30.
dd
n.
dt
dt
d
lim
.
t 0 t
dt
1 ,
31.
dd
n.
dt
dt
d
lim
.
t 0 t
dt
1 ,
d
d
lim
lim
.
t 0 t
t 0 t
dt
dt
32.
dd
n.
dt
dt
d
lim
.
t 0 t
dt
1 ,
d
d
lim
lim
.
t 0 t
t 0 t
dt
dt
s
d
d
d ds
n
n n.
dt
dt
ds dt
33.
dbd
b
n,
dt
dt
db
b,
dt
34.
Ускорение точки при естественном способезадания движения
35.
v s v ,36.
v s v ,dv d
d
v
a
s s s
s n,
dt dt
dt
2
37.
v s v ,dv d
d
v
a
s s s
s n,
dt dt
dt
2
dv
a s
dt
v2
s2
an n n
- касательная (тангенциальная)
составляющая ускорения
- нормальная составляющая
ускорения
38.
a a an .a s , an
v
2
, ab 0.
a a a , tg
2
2
n
a
an
.
39.
Kасательное ускорение характеризуетизменение вектора скорости по величине,
нормальное - по направлению
40.
a v a v cos a v,41.
a v a v cos a v,a v vx a x v y a y vz a z
42.
a v a v cos a v,a v vx a x v y a y vz a z
a
v x a x v y a y vz a z
v
.

































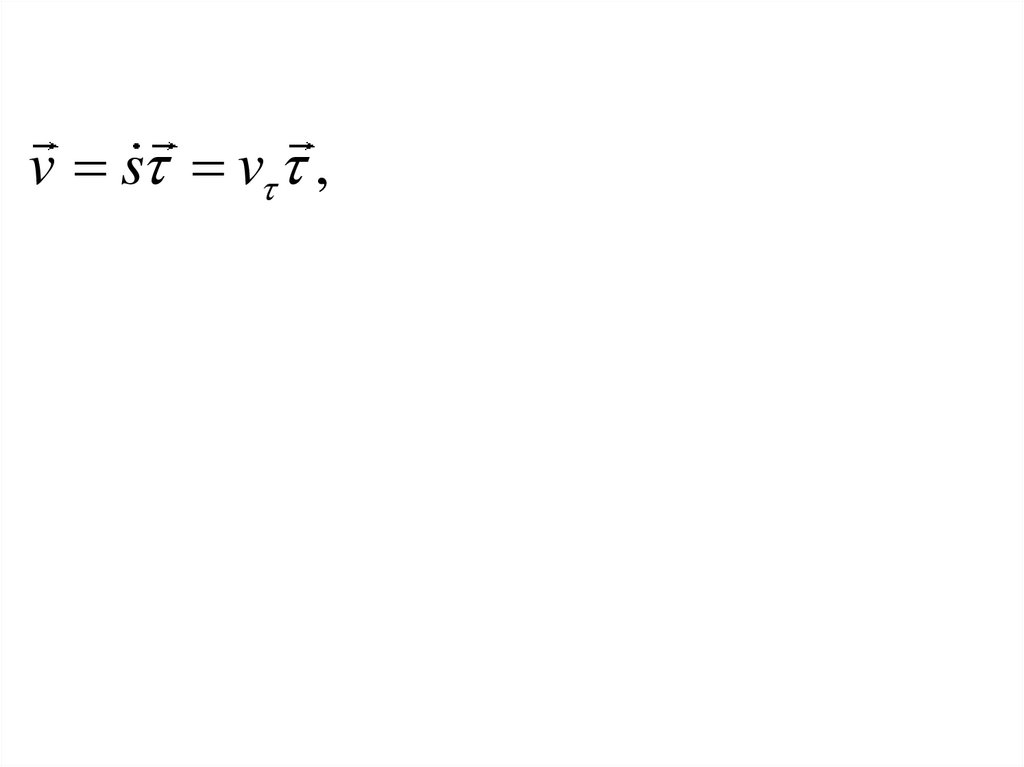











 physics
physics








