Similar presentations:
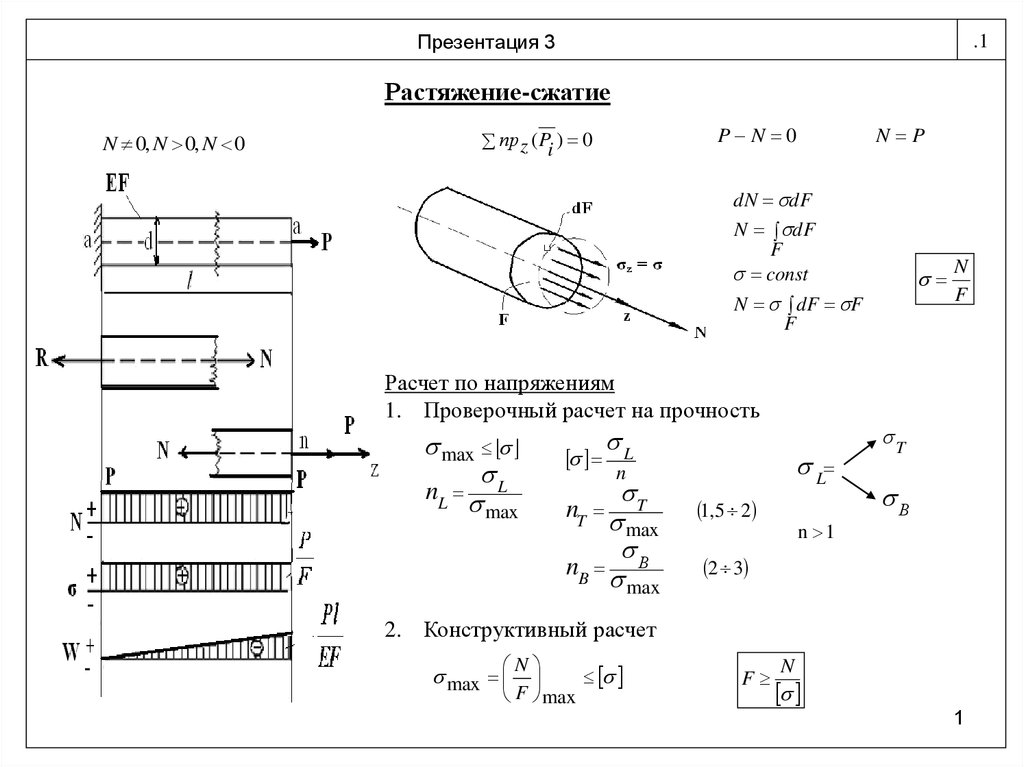
Растяжение-сжатие
1. Презентация 3
.1Растяжение-сжатие
N 0, N 0, N 0
P N 0
пр z ( Pi ) 0
N P
dN dF
N dF
F
const
N dF F
F
N
F
Расчет по напряжениям
1. Проверочный расчет на прочность
max
nL L
max
L
L
n
T
max
nB В
max
nT
1,5 2
n 1
T
В
2 3
2. Конструктивный расчет
N
F
max
max
F
N
1
2.
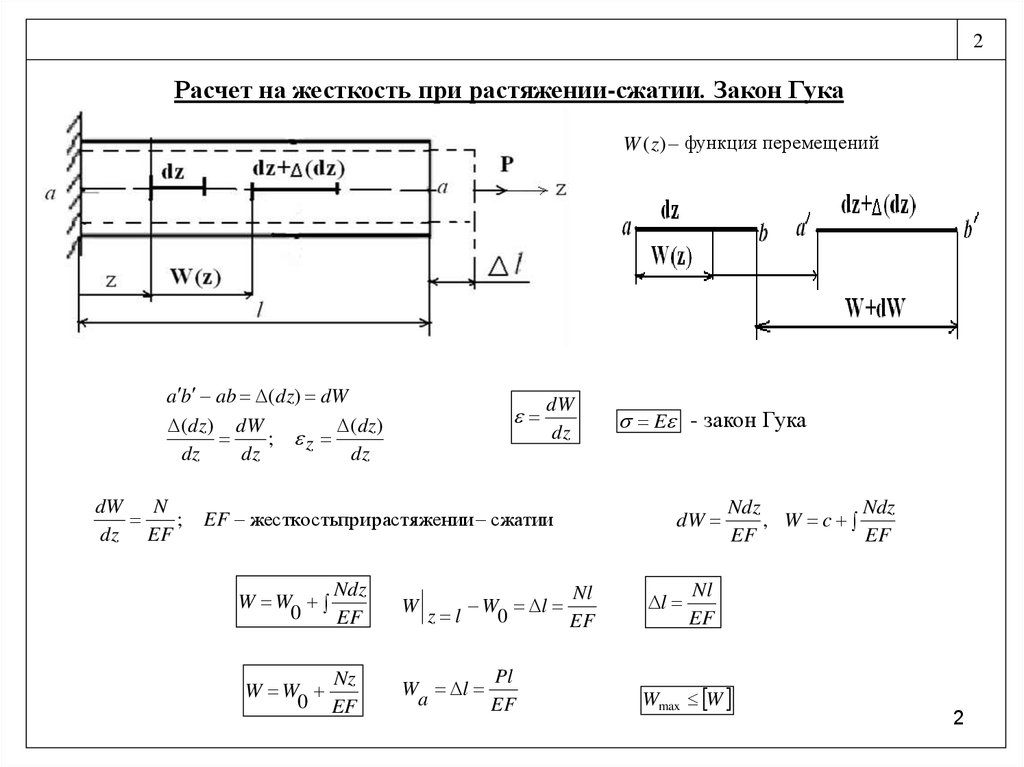
2Расчет на жесткость при растяжении-сжатии. Закон Гука
W (z ) функция перемещений
a b ab (dz) dW
(dz) dW
;
dz
dz
dW
N
;
dz EF
z
(dz)
dz
dW
dz
EF жесткостьпри растяжении сжатии
Ndz
W W
0
EF
Nz
W W
0 EF
W
Nl
W l
z l
0
EF
Pl
W l
a
EF
E - закон Гука
dW
l
Ndz
Ndz
, W c
EF
EF
Nl
EF
Wmax W
2
3.
3Деформации
до нагружения
Линейные деформации
после нагружения
перемещение
x
∆y1
∆y
∆x
∆z
ср
x1 x
x
(средняя относительная деформация)
∆z1
∆x1
- истинная (относительная)
линейная деформация по оси x
компоненты
деформации
3
4.
4Учет температуры в перемещениях
Ndz
W W
t ( z )dz
0
EF
Nl
l
l t
EF
коэффициент линейного расширения
t ( z ) Tк Т н , ( t )
Tк конечная (рабочая) температура
Т н Начальная температура (температура монтажа)
Поперечная деформация при растяжении-сжатии
Закон Пуассона
поп
(dz) l
-закон Пуассона
0
прод
dz
l
d
поп
0
поп пр
d
0 0,5
0,25 0,33 металлы
пр
поп
d
N
пр d d пр d d
d
E
EF
4
5.
5Учет температуры в перемещениях
Ndz
W W
t ( z )dz
0
EF
Nl
l
l t
EF
коэффициент линейного расширения
t ( z ) Tк Т н , ( t )
Tк конечная (рабочая) температура
Т н Начальная температура (температура монтажа)
Поперечная деформация при растяжении-сжатии
Закон Пуассона
поп
(dz) l
-закон Пуассона
0
прод
dz
l
d
поп
0
поп пр
d
0 0,5
0,25 0,33 металлы
пр
поп
d
N
пр d d пр d d
d
E
EF
5
6.
Геометрические характеристики плоских сечений [Моменты инерции поперечных сечений бруса]Общие понятия и определения
F – площадь поперечного сечения
0.1 S x ydF >
0[ м3 ] - статический момент
<
F
сечения плоской фигуры относительно
оси x,
S y xdF >
0[ м3 ].
<
F
0.2 I x y 2 dF 0[ м4 ] - осевой или экваториальный момент инерции пл. фигуры относительно оси x,
F
I y x2dF 0[ м4 ].
F
0.3 I xy xydF >
0[ м4 ] - центробежный момент инерции плоской фигуры относительно осей x и y.
<
F
0.4 I 0 I p r 2 dF 0[ м4 ] - полярный момент инерции плоской фигуры относительно выбранного
F
полюса O.
I
0.5 ix x 0[ м] - радиус инерции плоской фигуры относительно оси x,
F
iy
Iy
F
0[ м].
6
7.
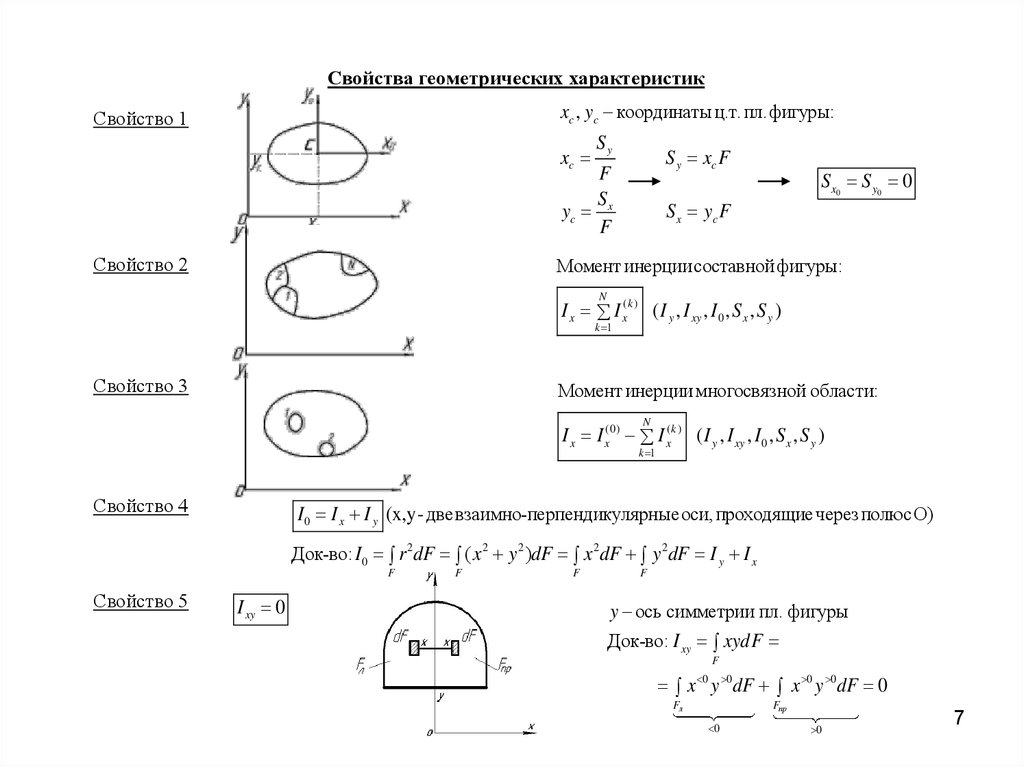
Свойства геометрических характеристикxc , yc координаты ц.т.пл.фигуры:
Свойство 1
xc
Sy
S y xc F
F
S
yc x
F
Свойство 2
S x0 S y0 0
S x yc F
Момент инерции составной фигуры:
N
I x I x( k ) ( I y , I xy , I 0 , S x , S y )
k 1
Свойство 3
Момент инерции многосвязной области:
N
I x I x(0) I x( k ) ( I y , I xy , I 0 , S x , S y )
k 1
Свойство 4
I 0 I x I y (x,y- две взаимно-перпендикулярные оси,проходящие через полюсO)
Док-во: I 0 r 2 dF ( x 2 y 2 )dF x 2 dF y 2dF I y I x
F
Свойство 5
I xy 0
F
F
F
y ось симметрии пл. фигуры
Док-во: I xy xydF
F
0
x y 0dF x 0 y 0 dF 0
Fл
Fпр
0
0
7
8.
Геометрические характеристики плоских сечений [Моменты инерции поперечных сечений бруса]Определение центра тяжести пл. фигуры
xc
Sy
i
Fi
i
Fi xi
i
Fi
yc
,
i
Sx
i
Fi
i
Fi yi
i
Fi
i
Преобразование моментов инерции при
параллельном переносе осей
Дано: I x0 , I y0 , I x0 y0 ; xc , yc координаты
ц.т. пл. фигуры в новой системе xOy
I x , I y , I xy ?
x xc x0 a x0
y y c y0 b y 0
формулы преобразования
координат при переходе
к новой системе
I x y 2dF (b y0 )2dF b2 dF 2b y0dF y02dF b2 F 2b S x0 I x0 I x I x0 b2 F
F
F
F
F
F
0 (св-во 1)
Аналогично:
I y I y0 a 2 F
I xy I x0 y0 abF
8
9.
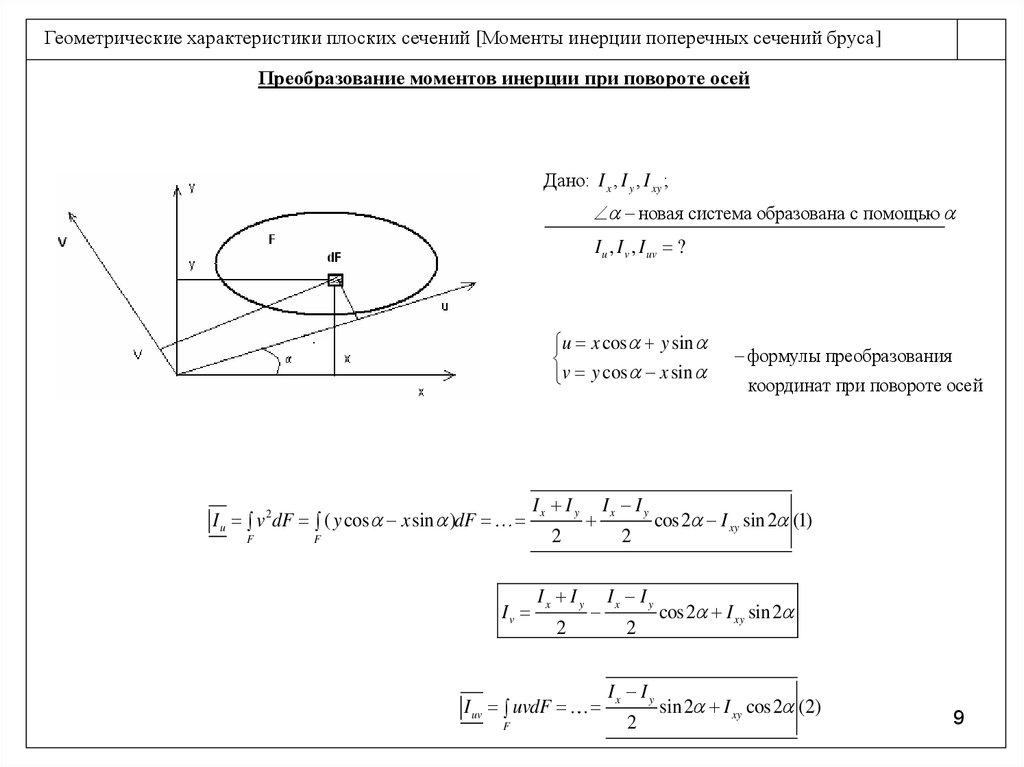
Геометрические характеристики плоских сечений [Моменты инерции поперечных сечений бруса]Преобразование моментов инерции при повороте осей
Дано: I x , I y , I xy ;
новая система образована с помощью
I u , I v , I uv ?
u x cos y sin
v y cos x sin
I u v 2 dF ( y cos x sin )dF
F
F
Iv
Ix I y
2
Ix I y
2
I uv uvdF
F
Ix I y
2
Ix I y
2
Ix I y
2
формулы преобразования
координат при повороте осей
cos2 I xy sin 2 (1)
cos2 I xy sin 2
sin 2 I xy cos2 (2)
9
10.
Геометрические характеристики плоских сечений [Моменты инерции поперечных сечений бруса]Главные оси и главные моменты инерции
(1)
I u f ( )
dI u
0
d
I1 , I 2
(2)
I uv ( )
(1)
Ix I y
dI uv
0
d
2
(2)
tg 2
2 I xy
Ix I y
(3)
I I
x y I xy2 (4) главные моменты инерции
2
2
tg 2 1
Ix I y
2 I xy
(5)
I I
max I uv , min I uv x y I xy 2 (6) экстрем.значения ц. б. момента инерции I uv
2
2
Из (4) и (6):
I1 I 2
2
I1 I 2 I x I y const инвариантная величина
I1 I 2 2 max I uv max I uv
Свойство гл. оси инерции: I uv 0
10
11.
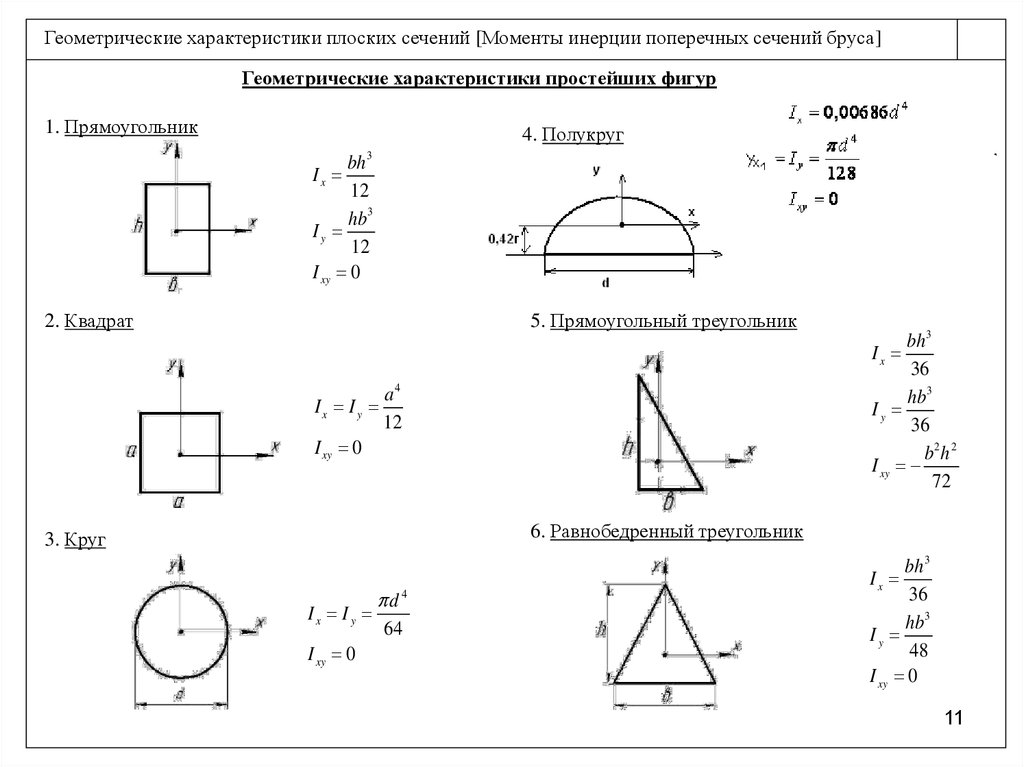
Геометрические характеристики плоских сечений [Моменты инерции поперечных сечений бруса]Геометрические характеристики простейших фигур
1. Прямоугольник
4. Полукруг
3
bh
12
hb3
Iy
12
I xy 0
Ix
2. Квадрат
5. Прямоугольный треугольник
a4
Ix I y
12
I xy 0
bh 3
Ix
36
hb3
Iy
36
b2 h 2
I xy
72
6. Равнобедренный треугольник
3. Круг
Ix Iy
I xy 0
d4
64
bh 3
Ix
36
hb3
Iy
48
I xy 0
11






 mechanics
mechanics








