Similar presentations:
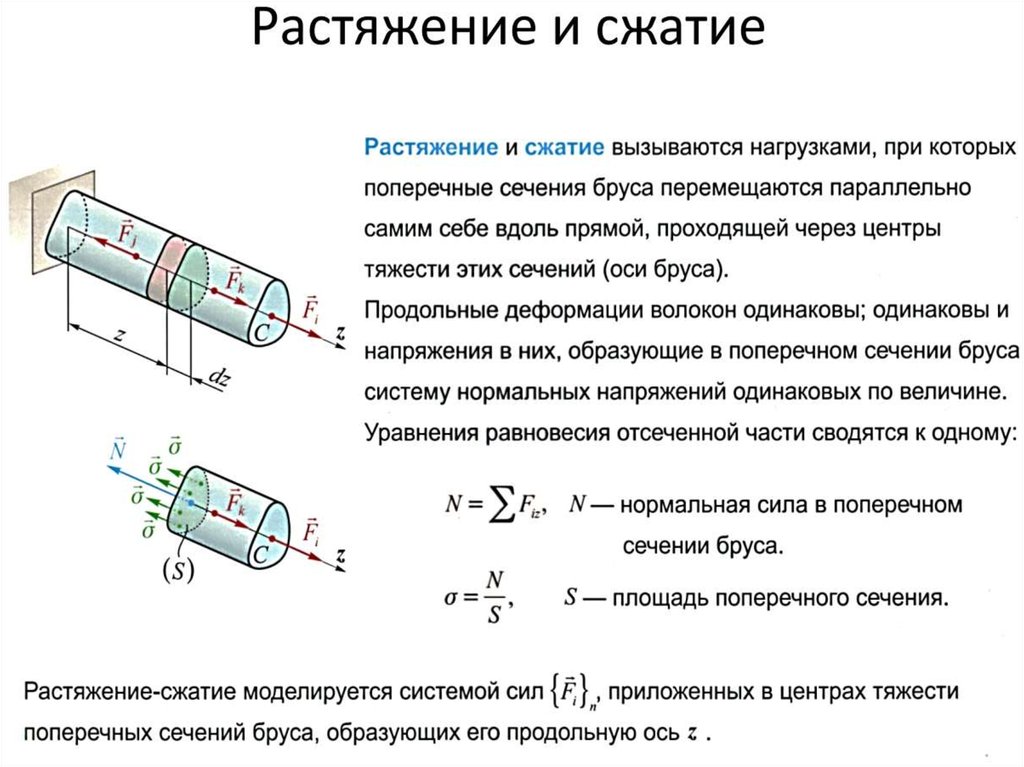
Растяжение и сжатие
1.
2.
3. Лекция 5
Определение перемещений при растяжении-сжатии – Рассмотрим стержень, нагруженный растягивающей силой F. Выделим на расстоянии z участокдлиной dz. Удлинение этого участка dz равно перемещению второй его границы относительно первой dw.
Деформация на этом участке определяется выражением,
w(z) w(z)+dw
dz w( z ) dw w( z ) dw
z
.
представляющим собой дифференциальное уравнение:
F z
dz
dz
dz
Разделим переменные и сведем решение этого уравнения
z
w
z
w
к интегрированию левой и правой частей:
w
z dz.
dw
dz
.
z
dw
dz
.
z
w0
z
dz
z
w
z
z
Подставим пределы и выражение для деформации,
следующего из закона Гука:
N
z
,
E
EA
0
z
0
0
N
w w0
dz.
z0 EA
z
N
w w0
dz.
z0 EA
Здесь w0 – перемещение левой границы рассматриваемого участка на расстоянии z0, EA – жесткость стержня при растяжении-сжатии,
N – продольное усилие.
N
В случае постоянства продольного усилия и площади поперечного сечения имеем:
w w0
( z z 0 ).
EA
Отсюда, как частный случай, получается выражение для абсолютного удлинения стержня (w0 = 0, z0 = 0, z = l):
w l
Nl
.
EA
Общая формула вычисления перемещений показывает, что перемещения исчисляются нарастающим итогом, т.е. к перемещению, вычисляемому
Таким образом,
учет равномерно
распределенной
продольной левой
нагрузки
(собственный
веса) может быть
на рассматриваемом участке [z0 ,z] (второе слагаемое),
добавляется
перемещение
сечения, соответствующего
границе,
и представляющего
выполнен
непосредственным
интегрированием
по
рассматриваемому
участку
или
использованием
перемещение всего участка, как жесткого целого (твердого тела). Если на каждом из участков продольное усилие и площадь поперечного сечения постоянны,
подобного
абсолютному
удлинению
стержня
при постоянной
то определение перемещения любого сечениявыражения,
или конца стержня
сводится
к простому
суммированию
удлинений
каждого продольной силе,
в
котором
сила
уменьшена
вдвое!
(см.
результат
определения
перемещения
конца стержня).
из участков от неподвижного сечения до рассматриваемого.
Например,
второй результат
(перемещение
сечения
посредине
длины стержня)
можетстержня
быть получен,
Учет собственного веса – Рассмотрим стержень,
нагруженный
собственным
весом (длина
стержня
l, объемный
вес материала
).
как сумма перемещений рассматриваемого сечения стержня от действия собственного веса верхней
Продольное усилие от собственного веса в произвольном сечении на расстоянии z равно весу нижерасположенной части стержня
N A(l z )
части, учитываемого как распределенная нагрузка, и перемещения его от веса нижней части,
и линейно зависит от координаты. Эпюры продольной силы и нормальных напряжений имеют вид треугольников:
действующего на верхнюю часть как внешняя сила:
G l зависимость
G l от координаты:
Перемещение произвольного сечения на расстоянии z имеет квадратичную
σ
N
w
z
z
N
A(l z )
A (l z ) 2
dz 0
dz
EA
EA 2
z0 EA
0
z
w w0
+
z
+
0
G
A 2 2 2 2 A2 2 3 A
w 2(lEA
z ) EA l
(l2.l z ) z.
4
2
EA
2 EA
2 EA
2 EA
Определим перемещения конца стержня и сечения на расстоянии половины длины:
+
w
A
2 EA
(2l z ) z
z l
Здесь G – вес стержня.
A
2 EA
l2
G
l,
2 EA
w
A
2 EA
(2l z ) z
z
l
2
3 A 2 3 G
l
l.
4 2 EA
4 2EA
13
z
4. Лекция 5 (продолжение – 5.2)
Статически неопределимые системы при растяжении-сжатии – В статически неопределимых системах число наложенных связей больше числанезависимых уравнений равновесия. Как указывалось выше, такие задачи решаются последовательным рассмотрением статической,
геометрической и физической сторон, в результате чего получается полная система уравнений, позволяющая найти искомые усилия. Общий порядок
решения определяется вышесказанным, конкретные шаги и особенности рассмотрим на примерах:
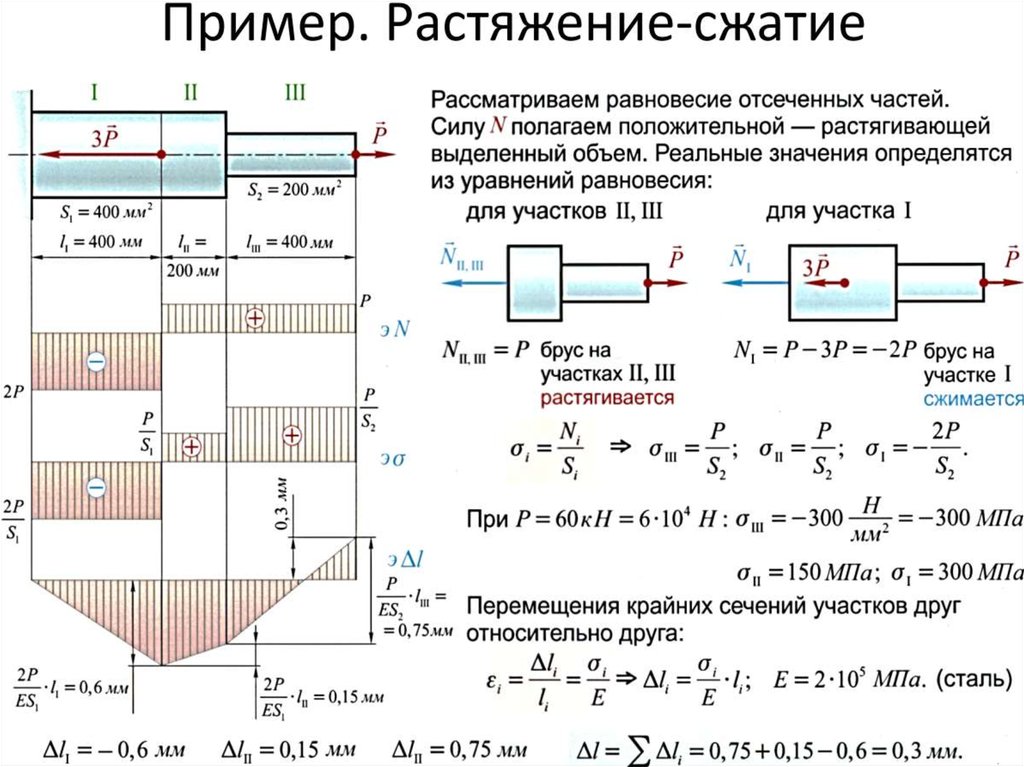
Пример 1. Стержень переменного сечения (2A и A) жестко заделан с двух сторон и нагружен продольной силой. Построить эпюры N и σ.
RA
F
A
a
F
A
a
z
B RB
Это единственное уравнение равновесия, которое можно составить для линейной системы сил.
Следовательно система один раз статически неопределима.
3. Геометрия:
l 0; l1 l 2 l3
z Составляем уравнение совместности деформаций:
a
a
l1
0,75F
+
N
0,375F/A
0,25F
+
-
RB 0.
0.
Это уравнение устанавливает неизменность общей длины стержня при любых воздействиях, которую
обеспечивали связи (жесткие заделки) до их удаления.
4. Физика: Записываем соотношения связи деформаций с усилиями:
a
a
1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:
2. Статика : Составляем уравнение равновесия:
Z i 0; -R A F
B RB
0,25F/A
N1l1 R A a
;
EA1 E 2 A
l 2
N 2 l 2 RB a
;
EA2
E2 A
l3
N 3 l 2 RB a
.
EA3
EA
Получили полную систему уравнений, решающую данную задачу (5 уравнений и 5 неизвестных – 2
реакции и 3 перемещения) .
Подставляем соотношения упругости в уравнения совместности:
R A a RB a RB a
0.
E 2 A E 2 A EA
RA 3RB 0.
RA 3RB .
F
3F
Подставим полученное соотношение
RB ; R A
.
3RB F RB 0
4
4
в уравнение равновесия:
Такой же результат можно получить с использованием статически определимой
Составляем уравнение совместности деформаций:
После определения
опорных
реакций
можно построить
системы,
образованной
из заданной
статически
неопределимой отбрасыванием
l R l F .
l 0; l F l R 0. или
эпюру продольных
сил вычисление
значений
по участкам:
“лишней”
связи, и принципа
независимости
действия
сил:
N1 = RA = 3F/4,
Это уравнение устанавливает неизменность общей длины стержня, которую обеспечивала “лишняя” связь (правая жесткая заделка) до ее удаления, или
N2 = N3 = RB = F/4.
Если имелся первоначальный зазор, например между правым концом
равенство
перемещений и их противоположное направление при отдельном действии внешней нагрузки и реакции этой связи.
В сечении, в котором приложена сосредоточенная сила,
стержня и заделкой, или напротив натяг (первоначальный размер стержня
Fa
получился скачок, равный
величине
этой силы.
превышает расстояние
лишьN ( R )l
N i ( RB )liмежду
RB опорами),
2a RB aто это
2Rучитывается
Записываем
соотношения
связи деформаций
Ba
l F i F i
;
l
;
R
в
уравнениях
совместности
деформаций:
(перемещений)
с
усилиями:
Эпюра нормальных напряжений также строится
EAi
E2 A
EAi
E2 A
EA
EA
l1 l 2 l3 . или lF lR . ( >0 зазор, <0 натяг)
вычислением значений напряжений по участкам:
Получили полную систему уравнений, решающую данную задачу
σ1 = N1 / A1= 3F/8A,
Если вместо силового нагружения, или дополнительно
к нему, действует
Подставим полученное
соотношение
(4 уравнения
и 4 неизвестных – 2 реакции и 2 перемещения) .
F учитывается
2 RB a
Faнагрузка (нагрев), то это
σ2 = N2 / A2= F/8A,
температурная
введением
в
уравнение
равновесия
и получим
R
.
;
перемещения в уравнения совместности:
B
σ3 = N3 / Подставляем
A3= F/4A.
14
температурных
удлинений в уравнения
деформаций.
величину второй
реакции (RB).
4 совместности
EA
E2 A
В сечении резкого изменения площади получился скачок.
0,125F/A
-
σ
5. Лекция 5 (продолжение – 5.3)
Расчет статически неопределимых систем на действие температуры – В статически неопределимых системах нагрев (охлаждение) элементоввызывает дополнительные внутренние усилия (напряжения), которые могут значительно превышать усилия от действия силового нагружения. Общий
порядок решения задачи сохраняется, но уравнения совместности деформаций (удлинений) содержат удлинения от действия разности температур t
:
-коэффициент линейного расширения
материала,
lt
l t l – длина стержня.
Пример 2. Стержень переменного сечения (2A и A), рассмотренный в примере 1, дополнительно нагревается на t градусов.
t
1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:
B RB
RA
F
A
2. Статика : Составляем уравнение равновесия:
z
Z i 0; -R A F RB 0.
3. Геометрия:
Составляем уравнение совместности деформаций:
l 0;
l1 l2 l3 lt 0.
a
a
a
Это уравнение устанавливает неизменность общей длины стержня при любых воздействиях, в том
числе от нагрева, которую обеспечивали связи (жесткие заделки) до их удаления.
4. Физика: Записываем соотношения связи деформаций с усилиями и температурным
воздействием:
Nl
R a
l1
N l
R a
N1l1 R A a
; l 2 2 2 B ; l3 3 2 B ; lt 3a t.
EA3
EA
EA2
E2 A
EA1 E 2 A
Подставляем соотношения упругости и температурного удлинения в уравнения совместности:
RA a RB a RB a
3a t 0.
E 2 A E 2 A EA
Подставим полученное соотношение
в уравнение равновесия:
3RB 6 tEA F RB 0
RA 3RB 6 tEA.
RA 3RB 6 tEA.
F 6 tEA
;
4
F 6 tEA
F 2 tEA
RA 3
6 tEA 3
.
4
4
RB
Теперь, при температурном воздействии, в выражения для реакций входят абсолютные значения
модуля упругости E и площади A. Вычислим величины реакций для конкретных данных: F = 10 кН,
A = 1 см2, t = 10o, E = 2*105 МПа, =10-5 (сталь):
10 103 6 10 5 10 2 1011 1 10 4
5.5 103 5.5 кН; При отсутствии нагрева
4
реакции получаются равными
10 103 2 10 5 10 2 1011 1 10 4
3
RA 3
4.5 10 4.5 кН. -2.5 кН и 7.5 кН соответственно.
4
RB
Эпюру продольных сил строим вычислением значений по участкам:
N1 = RA = 4.5 кН, N2 = N3 = RB = -5.5 кН. В сечении, в котором приложена сосредоточенная сила,
получился скачок, равный величине этой силы.
Эпюра нормальных напряжений также строится вычислением значений напряжений по участкам:
σ1 = N1 / A1= 22.5 МПа, σ2 = N2 / A2= - 27.5 МПа,
σ3 = N3 / A3= - 55 МПа.
При отсутствии нагрева значения напряжений
получаются равными
37.5 МПа, - 12.5 МПа, и -25 МПа
соответственно (вид эпюры напряжений см. в
примере 1).
Таким образом, нагрев всего на 10о привел к
увеличению сжимающей силы
и максимальных сжимающих напряжений
больше, чем в 2 раза.
Статически неопределимые системы всегда
реагируют на изменение температуры
изменением внутренних усилий.
Это же происходит при взаимных смещениях
опор (неравномерная осадка опор).
15
6. Лекция 5 (продолжение – 5.4)
Расчет статически неопределимых систем на неточность сборки – В статически неопределимых системах несоответствие длин изготовленных элементовпроектным вызывает дополнительные внутренние усилия, которые могут заметно влиять на результат определения усилий от действия внешних сил. Более
того, даже при отсутствии внешних сил, при сборке могут возникать начальные (монтажные) усилия. Общий порядок решения задачи сохраняется, но
уравнения совместности деформаций (удлинений) содержат дополнительные удлинения (укорочения) необходимые для осуществления сборки неточно
изготовленных элементов.
Пример 2. Абсолютно жесткая балка подвешивается на двух медных и одном стальном (Eм/Eс=1/2) стержнях одинаковой длины. Стальной стержень при
изготовлении был сделан длиннее на величину . Определить монтажные усилия после сборки и усилия при нагружении силой F.
1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:
Z
2. Статика : Составляем уравнение равновесия:
i
Реакции от медных
стержней равны из-за
симметрии системы.
0; 2Rм Rс 0.
3. Геометрия: Задаем промежуточное положение балки и составляем
уравнение совместности деформаций:
l
lм lс .
4. Физика: Записываем соотношения связи деформаций с усилиями:
l м
N мl
Rl
м ;
Eм A E м A
lc
N сl
Rl
с .
Eс A
Eс A
a
a
медь
медь
сталь
Rм
Rс
lм
Знак минус присваивается, поскольку стальной
стержень должен укоротиться и внутреннее усилие
должно быть отрицательным (сжатие).
Rм
lс
Подставляем соотношения упругости в уравнения совместности:
Rмl Rсl
.
Eм A Eс A
Rl E A
Rм с м .
Eс A l
Подставим полученное соотношение
в уравнение равновесия:
Rм
E A
2 м
l AE .
Rс
м
2
l
1
E A
2 м Rс Rс 0
l
2
Из этого же уравнения равновесия
следует:
Rм
Rс
AEм .
2 2l
В выражения для реакций входят абсолютные значения модуля упругости Eм , длины и площади стержней.
Вычислим величины реакций для конкретных данных: l = 2 м, A = 20 см2, = 0.5 мм, Eм = 105 МПа :
Rс
0,5 10 3
20 10 4 2 1011 5 10 4 50 кН ;
2
Rм
50
25 кН.
2
При нагружении балки силой F посередине балка получает дополнительное перемещение б:
Уравнения равновесия, совместности
деформаций и соотношения упругости
принимают вид:
Z
i
0; 2Rм Rс F 0.
l м
N мl
Rl
м ;
Eм A E м A
lc
F
Eм A
E
E A
1
Rс м м Rс .
l
Eс
l
2
lм lс .
N сl
Rl
с .
Eс A Eс A
Из выражения
Rм=Rм(Rс) :
Rм
Подстановка соотношений
упругости в уравнения
совместности приводит
к ранее полученному
выражению для Rм=Rм(Rс).
Подстановка в уравнение
равновесия дает:
Rс
Eм A
l F AEм .
2
2
l
F 2
Eм A F
AEм
l
l
2
AEм
1 F
.
2l
2 4
После подстановки значений силы F =500 кН получаем
16
Rс = 200 кН и Rм= 150 кН.
7. Лекция 5 (продолжение 5.5 – дополнительный материал )
Пример 3. В предыдущем примере рассматриваемая система была симметричной. Если система несимметричная по геометрии, нагружению, материаламстержней, то перемещение жесткой балки при деформации будет не поступательное, а плоское (с поворотом вокруг некоторого центра). Рассмотрим
решение такой задачи, подобной предыдущей, но со следующими данными: Левый медный стержень изготовлен короче остальных на величину , сила F
приложена на расстоянии c > a от левого стержня. Найти усилия в стержнях.
1. Выбираем объект равновесия, отбрасываем связи и заменяем их действие реакциями:
Z i 0; R1м Rс R2м F 0.
M Ai 0; Rс a R2м 2a Fc 0.
2. Статика : Составляем уравнение равновесия:
3. Геометрия: Задаем произвольное наклонное положение балки и составляем
уравнения совместности деформаций:
l ; l a;
с
1м
a
a
с
медь
l
l 2м 2a.
медь
R1м
сталь
4. Физика: Записываем соотношения связи деформаций с усилиями:
l1м
N l R l
1м 1м ;
Eм A Eм A
N l
Rl
lc с с .
Eс A Eс A
l 2м
Rс
N l R l
2м 2м ;
Eм A Eм A
l1мА
R1м
б
lс
φ
Получили полную систему уравнений, решающую данную задачу (8 уравнений и 8 неизвестных – 3 реакции
и 5 перемещений, два из которых поступательное перемещение балки, угловое перемещение - поворот).
Последние неизвестные можно исключить, составляя одно, но более сложное, уравнение совместности из подобия
треугольников в виде:
Поскольку решать вручную 5 уравнений тоже достаточно сложно можно
l2м
F
lс ( l1м ) 1
. оставить первоначальную систему из 8 уравнений и решить ее численно, например, в системе
l 2м ( l1м ) 2 MathCAD, в которой не требуются какие-либо подстановки и преобразования (посмотреть).
Если направления одного или двух стержней отличны от вертикального, то эта задача становится
статически определимой (для плоской произвольной системы сил можно составить 3 независимых
Удлинения наклонных стержней определяются отрезками,
уравнений равновесия) и несоответствие одного или двух размеров проектным не будут вызывать
отсекаемые перпендикулярами, опущенными из нового
начальных (монтажных) усилий (балка лишь изменит свое положение при сборке).
положения узла (конца стержня) на старое направление
Пример 4. Пусть к такой системе добавлен еще
один “лишний” стержень).
стержня.
Система становится статически неопределимой, для которой можно составить 3 уравнения равновесия
и 4 уравнения совместности деформаций (вместе с 4 соотношениями упругости получается система 11
уравнений):
X 0; R sin R sin 0.
i
2м
2
3м
с
l 2 l / cos 2 ; l3 l / cos 3
сталь
А
l1м ; lс a; l 2м ( 2a) cos 2 - x sin 2 ; l3м ( 2a) cos 3 - x sin 3 .
Теперь в соотношениях упругости длины 2-го и 3-го медных стержней:
медь φ2
R1м
l1м
медь
медь
l
3
Z i 0; R1м Rс R2м cos 2 R3м cos 3 F 0.
M Ai 0; Rс a R2м cos 2 2a R3м cos 3 2a Fc 0.
a
a
lс
R2м
Rс
l2м
φ
φ3 медь
RR2м
3м
B
l3м б
B1
F
(Посмотреть решение этой
задачи в системе MathCAD)
бx
17





 mechanics
mechanics








