Similar presentations:
Центральное растяжение и сжатие. Закон Гука (лекция № 2)
1.
ЛЕКЦИЯ №21
Центральное растяжение и сжатие
Закон Гука
2.
РАСТЯЖЕНИЕ – СЖАТИЕ2
Под растяжением понимается такой вид нагружения, при котором в
поперечных сечениях стержня возникают только нормальные силы N, а все
прочие внутренние силовые факторы (поперечные силы Qx, Qy крутящий
момент Mz и изгибающий моменты Mx, My) равны нулю.
Если N действует от сечения, то она вызывает растяжение (увеличение
длины бруса) и считается положительной (N > 0 – растяжение).
Если N действует к сечению, то она вызывает сжатие (уменьшение
бруса) и считается отрицательной (N < 0 – сжатие).
Брусья, в основном работающие на растяжение-сжатие, называются
стержнями.
3.
РАСТЯЖЕНИЕ – СЖАТИЕ3
N
l
a - ∆a
N
a
y
x
b - ∆b
b
l+ l
Δl
ε
l
Δb
εx
b
относительная продольная деформация;
Δa
εy
a
относительная поперечная деформация;
4.
РАСТЯЖЕНИЕ – СЖАТИЕ4
Экспериментально доказано, что при центральном растяжении-сжатии
горизонтальная и вертикальная относительные поперечные деформации
равны, т.е.
ε x ε y ε
Отношение поперечной деформации к продольной деформации –
величина постоянная для любого материала и её абсолютное значение
называется коэффициентом Пуассона.
5.
РАСТЯЖЕНИЕ – СЖАТИЕ5
Эта величина безразмерна и определяется экспериментально. В
зависимости от пластических свойств, для изотропных материалов имеем:
0 ≤ μ ≤ 0,5
Пример:
μ пробки = 0;
μчугуна = 0,23 ÷ 0,27;
μстали = 0,29 ÷ 0,33;
μмеди = 0,31 ÷ 0,33;
каучука = 0,47.
Чем выше пластичность материала, тем
больше его коэффициент Пуассона.
Для большинства металлов в области
действия закона Гука коэффициент Пуассона
лежит в пределах
0,25 0,35
6.
ЗАКОН ГУКА6
Для большинства материалов с достаточной точностью можно сказать,
что в упругой области нагружения существует прямая пропорциональная
зависимость
между
относительной
линейной
деформацией
и
нормальным напряжением. Это положение называется законом Гука и
выражается формулой:
σ Еε
где: Е – модуль продольной упругости (модуль упругости первого рода,
модуль Юнга), справочная величина, для каждого материала своя и
неизменная.
H
E 2 Па
м
7.
ЗАКОН ГУКА7
Пример:
σ
1
Материал
E, МПа
Сталь
(1,8-2,2) 105
0,25-0,33
Медь
105
0,31-0,34
Алюминий
0,7 105
0,33
1 – сталь;
2
2 – алюминий.
Чем пластичнее материал, тем меньше угол .
α1
0,002
α2
Экспериментально показано, что стали = 0,002.
ε
8.
ФОРМУЛА ГУКА8
Выведем формулу Гука из одноименного закона.
q
N (z)
dz
∆(dz)
l
На участка длиной dz имеем:
z
N (z)
dz
∆l
N z
σ
F
ε
Δ dz
dz
∆(dz)
9.
ФОРМУЛА ГУКА9
Подставим эти соотношения в закон Гука:
N z
Δ dz
E
F
dz
N z
dz
dz
EF
0
0
l
l
N z
l
dz
EF
z
формула Гука для стержня с
распределенной нормальной нагрузкой
Nl
l
EF
формула Гука для стержня с постоянной
нормальной нагрузкой
Для стержня, имеющего n различных участков, получаем:
N zi
l
dzi
Ei Fi
i 1
n
EF – жесткость при растяжении-сжатии
10.
ПРИМЕР10
Определить удлинение стержня l, вызываемое действием собственного веса q.
N
ql
z
+
l
q
ql 2
2 EF
z
0 z l
N(z) = qz ,
N(0) = 0 ,
N(l) = ql .
0 z l
N(z ) = ql-qz ,
N(0) = ql ,
N(l) = 0 .
l
N( z )
ql qz
ql 2 ql 2
ql 2
l
dz
.
dz
EF
EF
EF 2 EF 2 EF
0
0
l
2
ql
Ответ : l
.
2 EF
11.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИСТЕРЖНЯ ПРИ РАСТЯЖЕНИИ-СЖАТИИ
11
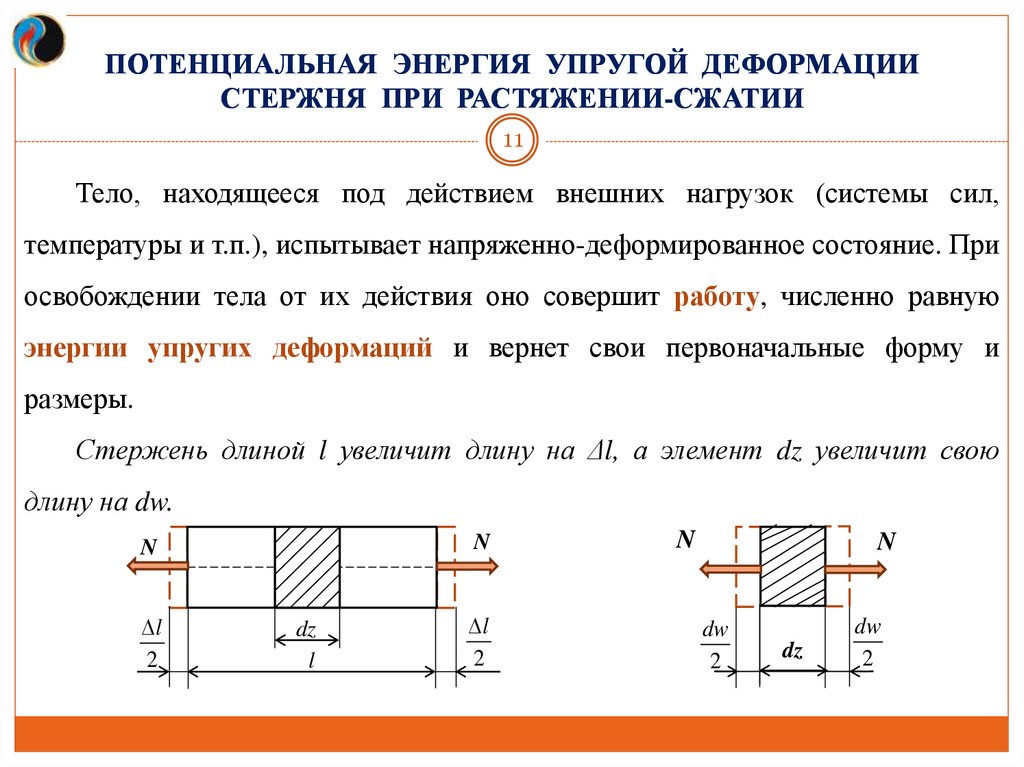
Тело, находящееся под действием внешних нагрузок (системы сил,
температуры и т.п.), испытывает напряженно-деформированное состояние. При
освобождении тела от их действия оно совершит работу, численно равную
энергии упругих деформаций и вернет свои первоначальные форму и
размеры.
Стержень длиной l увеличит длину на Δl, а элемент dz увеличит свою
длину на dw.
N
N
l
2
dz
l
l
2
N
N
dw
2
dz
dw
2
12.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГОЙ ДЕФОРМАЦИИСТЕРЖНЯ ПРИ РАСТЯЖЕНИИ-СЖАТИИ
12
Поскольку связь между напряжением и деформацией линейна (согласно
закону Гука), то, очевидно, что связь между силой N и изменением длины dw
тоже будет линейна.
1
dU Ndw
2
N
dU – площадь
треугольника
dw
(1)
По аналогии с формулой Гука для
постоянной нагрузки N, имеем:
Ndz
dw
EF
(2)
13.
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ13
Подставив (2) в (1), получаем:
2
1
Ndz N dz
dU N
2
EF
2 EF
l
Следовательно
U
0
N2
N 2l
dz
2 EF
2 EF
Итак, получена формула для определения потенциальной энергии
упругой деформации стержня при растяжении-сжатии постоянной
нормальной силой:
N 2l
U
2 EF
Если нормальная сила не постоянна по длине стержня, то есть N =
N(z) ≠ const, то работа, а следовательно, и потенциальная энергия
определяются по формуле:
2
N z dz
A U
2 EF
z
14.
НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИРАСТЯЖЕНИИ-СЖАТИИ
14
Рассмотрим стержень, нагруженный
растягивающей
силой
N,
в
наклонном сечении n1 – n1.
Согласно методу сечений, отбросим
верхнюю часть стержня, заменив ее
действие усилием p, равномерно
распределенным
по
площади
наклонного сечения.
0 против хода
часовой стрелки
р
n1
n
n0
n1
N
0
n0
n1
n1
n0
N
Площадь наклонного сечения n – n определим по формуле: F
1
1
F
cos
где F – площадь сечения n0 – n0.
Нормальная сила N определяется по формуле: N pF
Тогда
N N cos
p
cos
F
F
15.
НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИРАСТЯЖЕНИИ-СЖАТИИ
15
Определим нормальные σα и касательные τα напряжения в наклонном
сечении n1 – n1 :
р
σα = p cos cos cos cos
2
sin 2
τα = p sin sin cos
2
т.к. 2 sin cos sin 2
Итак, получено:
cos
2
С
внутренняя
нормаль
sin 2
2
16.
НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИРАСТЯЖЕНИИ-СЖАТИИ
16
Правила знаков
σα > 0, если действует от сечения (при растяжении);
σα < 0, если действует к сечению (при сжатии);
τα > 0, если поворачивается относительно точки С,
лежащей на внутренней нормали, по часовой стрелке;
τα < 0, если поворачивается относительно точки С,
лежащей на внутренней нормали, против часовой
стрелки.
17.
НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ ПРИРАСТЯЖЕНИИ-СЖАТИИ
17
Следствие:
σα = max при = 0 , т.к. сos0 = 1 ;
τα = max при = 45 , т.к. sin90 = 1.
Вывод:
максимальные касательные напряжения возникают
на площадках, расположенных под углом 45 к
нормали поперечного сечения стержня.
Пример: разрушение чугунного образца происходит по
площадкам
максимальных
касательных
напряжений.
18.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫПРИ РАСТЯЖЕНИИ-СЖАТИИ
18
Статически определимая система – это система, в которой
количество неизвестных усилий не превышает количества
независимых уравнений статики.
Статически неопределимая система – это система, в
которой усилия не могут быть определены из уравнений
статики.
19.
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫПРИ РАСТЯЖЕНИИ-СЖАТИИ
19
Степень статической неопределимости определяется разностью
между числом неизвестных (реакций опор или заделок) и числом
основных уравнений равновесия. Для плоской системы таких
независимых
уравнений
может
быть
не
более
3-х,
для
пространственной – не более 6-ти.
Для решения статически неопределимых задач необходимо
составить столько дополнительных уравнений, сколько раз система
статически неопределима. Эти уравнения называются уравнениями
совместности деформаций.
20.
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ20
Основными
механическими
характеристиками
материала
являются:
прочность, пластичность, упругость и твёрдость.
П РОЧН О СТЬ
–
способность
материалов
воспринимать
внешние
механические (и температурные) воздействия, не разрушаясь.
П Л А С Т И Ч Н О С Т Ь – способность материалов получать значительные
остаточные деформации, не разрушаясь.
УПРУГОСТЬ – способность материалов восстанавливать первоначальные
форму и размеры после снятия действия нагрузки (и температуры).
ТВЁРДОСТЬ – способность материалов сопротивляться проникновению в
него другого тела, практически не получающего остаточные деформации.
21.
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ21
При проектировании конструкций, машин и механизмов необходимо знать
прочностные и деформационные свойства материалов. Их определяют
экспериментально путем испытания стандартных образцов на растяжение,
сжатие, кручение, изгиб, смятие и т.д..
Основными являются сопротивления на растяжение и сжатие, дающие
наибольшую и важнейшую информацию о механических свойствах
металлов.
22.
ИСПЫТАНИЕ НА РАСТЯЖЕНИЕ22
Испытание на растяжение проводят на разрывных или универсальных
машинах, имеющих специальные захваты для передачи усилия.
Используются стандартные образцы специальной формы
(l0 – длина рабочей части, l0/ a0 = 5 – короткие, l0/ a0 = 10 – длинные):
a0
d
b0
l0
l0
Все машины снабжены устройством для автоматической записи в
определенном масштабе диаграммы-графика зависимости величины
растягивающей силы от удлинения образца.
23.
ПЕРВИЧНАЯ ДИАГРАММА РАСТЯЖЕНИЯ23
1.
Р
E
Рmax
Рр
Рт
Ру
Рпц
2.
K
С D
3.
B
A
4.
O
Типичная диаграмма растяжения образца из l 5.
малоуглеродистой стали (< 0,25% С)
6.
В начальной стадии (OA, до Pпц) нагружения
удлинение
растет
прямопропорционально
величине нагрузки (на этой стадии справедлив
закон Гука)
Далее (AB, до Pу) деформации начинают расти
чуть быстрее и не линейно, но остаются малыми
и упругими (исчезающими после снятия
нагрузки).
При дальнейшем нагружении (BС, до Pт)
криволинейная часть переходит в
горизонтальную площадку CD, на которой
деформации растут без увеличения нагрузки
(текучесть). Зона BCD – зона общей текучести.
При дальнейшем нагружении (DE, до Pmax)
изменяется структура металла и материал вновь
может воспринимать возрастание нагрузки
(упрочнение) вплоть до максимальной.
Далее (EK, до Pp) в наиболее слабом месте
возникает и развивается локальное уменьшение
поперечного сечения (шейка). Зона EK – зона
местной текучести.
В точке K образец внезапно разрушается с
резким ударным звуком
24.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ24
Для удобства дальнейшей обработки первичную диаграмму растяжения
перестраивают в координатах . Для этого используют следующие
соотношения:
где:
P
F0
l
l0
F0 – первоначальная площадь образца.
Получаемый график называется условной диаграммой растяжения (т.к. при
его построении не учитывается изменение площади поперечного сечения
образца, и величины напряжений носят условный характер).
25.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ25
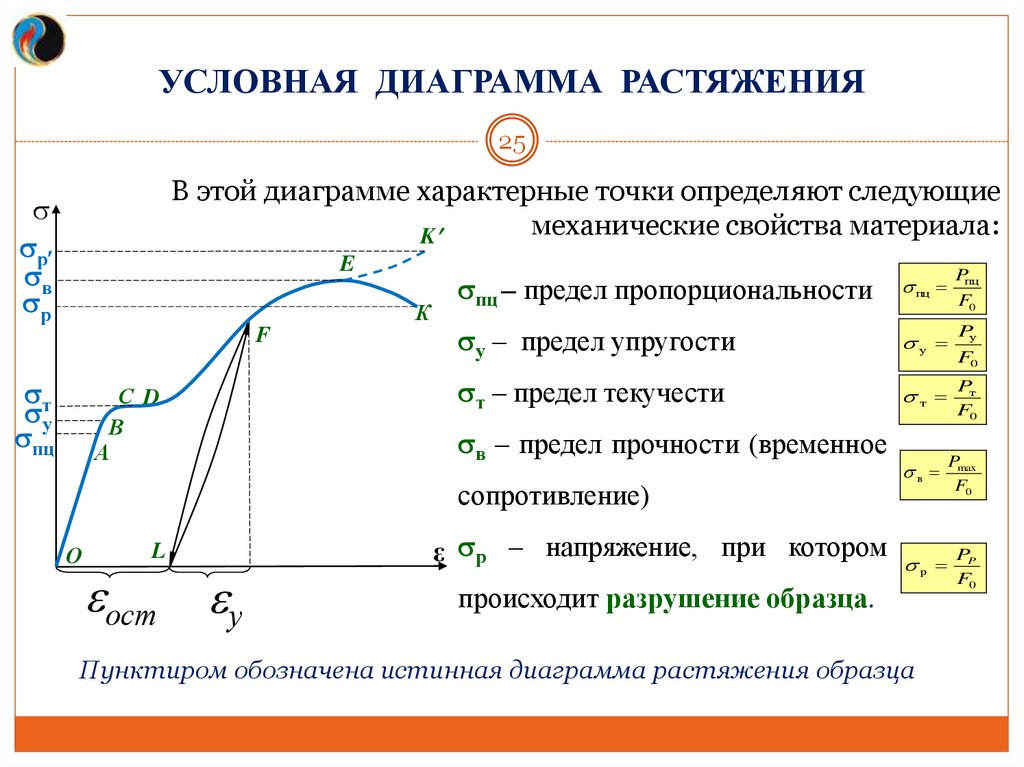
В этой диаграмме характерные точки определяют следующие
механические свойства материала:
K
р
в
р
E
К
F
т
у
пц
С D
В
А
пц – предел пропорциональности
пц
Pпц
F0
у – предел упругости
у
Pу
т – предел текучести
т
Pт
F0
в
Pmax
F0
в – предел прочности (временное
сопротивление)
О
L
ост
у
F0
ε р – напряжение, при котором P
р
происходит разрушение образца.
Пунктиром обозначена истинная диаграмма растяжения образца
P
F0
26.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ26
Предел пропорциональности σпц – наибольшее напряжение, до которого существует
пропорциональная зависимость между нагрузкой и деформацией
(для Ст3 σпц = 195-200МПа).
Предел упругости σу – наибольшее напряжение, при котором в материале не
обнаруживается признаков пластической (остаточной) деформации
(для Ст3 σу = 205-210МПа).
Предел текучести σт – наименьшее напряжение, при котором образец деформируется без
заметного увеличения растягивающей нагрузки
(для Ст3 σт = 220-250МПа).
Предел прочности, или временное сопротивление, σв – напряжение, соответствующее
наибольшей нагрузке, предшествующей разрушению образца
(для Ст3 σв =370-470МПа).
Истинный предел прочности, или истинное сопротивление разрыву, σр – напряжение,
соответствующее разрушающей силе FK, вычисленное для площади поперечного сечения
образца в месте разрыва A1 (для Ст3 σр =900-1000МПа). Поскольку на участке EK
образуется шейка и площадь поперечного сечения быстро уменьшается, напряжение
увеличивается (EK1) при регистрируемом падении усилия.
27.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ27
Рассмотрим характерные точки и участки условной диаграммы:
ОА – участок прямой линейной пропорциональности между и ;
В – точка, соответствующая пределу упругости;
ОВ – область упругих (обратимых) деформаций;
С – точка, соответствующая наступлению предела текучести;
СD – площадка текучести;
DE – зона упрочнения (пологий криволинейный участок).
Если на этом участке произвести разгрузку образца, например, из точки F, то
диаграмма разгрузки будет линейна и прямая разгрузки FL параллельна
участку ОА.
28.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ28
Если затем произвести повторную нагрузку образца, то он покажет значение
предела текучести выше первоначального. При повторном нагружении
площадка текучести исчезает, исчерпывается пластичность материала, и он
становится более хрупким. Это явление называется наклепом (или
нагартовкой), оно связано с изменением микроструктуры кристаллической
решетки стали. Явление наклепа используют в технике для повышения
прочностных характеристик материалов. Если наклеп нежелателен, его
устраняют отжигом.
29.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ29
FLF – петля гистерезиса (разгрузка и повторная нагрузка образца).
Е – наивысшая точка диаграммы, соответствующая пределу прочности.
ВСDE – участок общей текучести.
ЕK – зона местной текучести (образование «шейки»). Площадь поперечного
сечения локально уменьшается, происходит утонение образца.
K – точка разрушения образца.
Полная деформация образца будет складываться из остаточной и упругой
деформаций:
ост у
30.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ30
Экспериментально
показано,
что
при образовании шейки
площадь
поперечного сечения образца уменьшается, происходит падение нагрузки.
Если учитывать это явление, то можно определить истинное напряжение в
момент разрыва образца:
р
Pр
Fш
где Fш – площадь «шейки».
ЕK – участок диаграммы, построенный с учетом изменения площади
поперечного сечения образца.
31.
УСЛОВНАЯ ДИАГРАММА РАСТЯЖЕНИЯ31
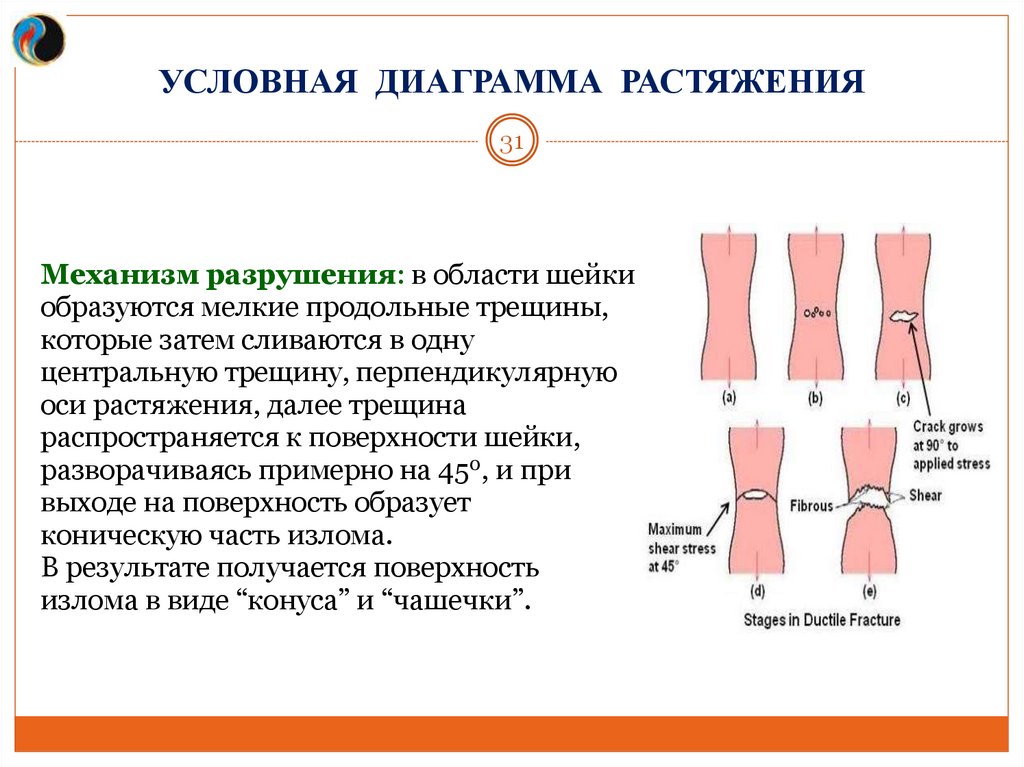
Механизм разрушения: в области шейки
образуются мелкие продольные трещины,
которые затем сливаются в одну
центральную трещину, перпендикулярную
оси растяжения, далее трещина
распространяется к поверхности шейки,
разворачиваясь примерно на 450, и при
выходе на поверхность образует
коническую часть излома.
В результате получается поверхность
излома в виде “конуса” и “чашечки”.
32.
ХАРАКТЕРИСТИКИ ПЛАСТИЧНОСТИ32
Относительное удлинение после разрыва (%) – отношение приращения расчетной
длины образца после разрыва к ее первоначальному значению (для Ст3 = 25-27 %).
l l
l K
100% K 0 100%
l0
l0
Относительное сужение после разрыва ψ (%) – отношение уменьшения площади
поперечного сечения образца в месте разрыва к начальной площади поперечного
сечения (для Ст3 ψ =60-70 %).
A A0
AK
100% K
100%
A0
A0
33.
ИСПЫТАНИЕ НА СЖАТИЕ33
При испытаниях на сжатие применяются
цилиндрические образцы с отношением
высоты к диаметру h/d = 1,5 – 3. Образцы
устанавливаются на опорную поверхность с
использованием смазки для ослабления
влияния сил трения.
При испытаниях на сжатие хрупкие материалы не образуют площадки
текучести и разрушаются по достижении предела прочности
34.
СЖАТИЕ НИЗКОУГЛЕРОДИСТОЙ СТАЛИ34
Р
PТ
Pпц
O
Диаграмма низкоуглеродистой стали – начальный
B
A
l
участок диаграммы является прямолинейным (до точки A) и
совпадает с аналогичным участком диаграммы растяжения.
Это свидетельствует о том, что модуль упругости у стали
можно принимать одинаковым при растяжении и сжатии.
Нелинейный участок до площадки текучести также
совпадает с подобным участком на диаграмме растяжения.
Значения предела пропорциональности и предела текучести
при растяжении и сжатии практически одинаковы. Площадка
текучести при сжатии выражена очень слабо и после нее
кривая уходит все более круто вверх вследствие развития
значительных пластических деформаций, приводящих к
увеличению площади поперечного сечения. Образец
сплющивается, принимая бочкообразную форму. На этом
испытания заканчивают, т.к. образец разрушить не удастся,
не удается определить и предел прочности.
35.
СЖАТИЕ ЧУГУНА35
P
Диаграмма чугуна – начальный участок диаграммы
Pmax
имеет почти линейную зависимость, на этом участке
форма и размеры образца меняются незначительно. При
приближении к максимальной нагрузке кривая становится
более пологой и образец принимает слегка бочкообразную
форму. При достижении нагрузкой наибольшего значения
появляются трещины под углом примерно 450 и наступает
разрушение по площадкам с наибольшими касательными
напряжениями (хрупкое разрушение).
l
Другие хрупкие материалы (камень, бетон) имеют
подобную диаграмму и такой характер разрушения.
Хрупкие материалы сопротивляются сжатию значительно
лучше, чем растяжению, например, предел прочности
серого чугуна на сжатие 560-900МПа, а на растяжение –
120-190 МПа.
36.
СЖАТИЕ ДРЕВЕСИНЫ36
F
Рmax
Диаграмма древесины
A
O
B
l
Древесина – анизотропный материал. Сопротивляемость при сжатии
зависит от расположения волокон относительно направления
сжимающей силы. При сжатии вдоль волокон на участке OA
древесина
работает
почти
упруго,
деформации
растут
пропорционально
увеличению
сжимающей
силы.
Далее
деформации начинают расти более быстро, чем усилие, вследствие
возникновения пластических деформаций в отдельных волокнах.
Разрушение происходит при максимальной нагрузке в результате
потери местной устойчивости ряда волокон, сопровождаемой
сдвигом с образованием продольных трещин. При сжатии поперек
волокон на участке OB древесина работает почти упруго,
деформации растут пропорционально увеличению сжимающей
силы. Далее деформации начинают расти очень быстро при малом
увеличении силы, вследствие уплотнения (спрессовывания)
отдельных волокон. При наличии сучков и других пороков (трещин)
образец может разрушиться раскалыванием. Разрушающая нагрузка
определяется условно при достижении деформации сжатия, при
которой высота образца уменьшается на треть исходной высоты.
37.
ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ МАТЕРИАЛОВ37
Косвенным методом определения предела прочности является измерение
твердости.
Для определения твердости в поверхность материала с определенной
силой вдавливается другое тело (индентор) и замеряется полученный
отпечаток.
В справочниках твердость указывается как безразмерная величина.
Способы определения твердости
По Бринеллю
По Виккерсу
По Роквеллу
38.
СПОСОБ БРИНЕЛЛЯ38
Вдавливание стального закаленного шарика
Твердость по Бринеллю обозначается НВ.
HB
Р
2P
D( D D 2 d 2 )
Р – сила вдавливания индентора (Р = 2500Н);
d
D – диаметр индентора;
d – диаметр отпечатка.
Способ применяется для материалов малой твердости (НВ 4000).
39.
СПОСОБ ВИККЕРСА39
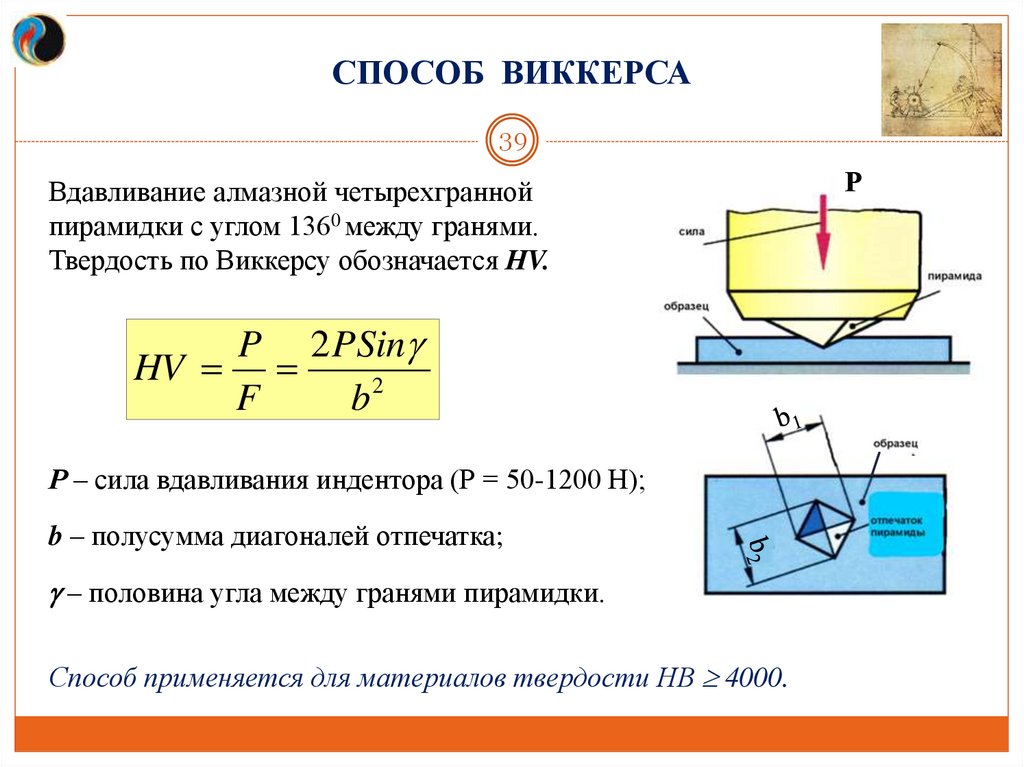
Вдавливание алмазной четырехгранной
пирамидки с углом 1360 между гранями.
Твердость по Виккерсу обозначается НV.
P 2 PSin
HV
F
b2
Р – сила вдавливания индентора (Р = 50-1200 Н);
b – полусумма диагоналей отпечатка;
– половина угла между гранями пирамидки.
Способ применяется для материалов твердости НВ 4000.
Р
40.
СПОСОБ РОКВЕЛЛА40
Вдавливание алмазного конуса с углом при
вершине 1200.
Твердость по Роквеллу обозначается НRC.
4P
HRC 2
d
Р
1200
1200
d
Р – сила вдавливания индентора;
d – диаметр отпечатка.
Способ применяется для материалов твердости НВ 4000.
41.
МАЯТНИКОВЫЙ КОПР41
Еще одним способом определения твердости является разрушение
прямоугольных образцов с помощью маятникового копра.
∆h
h1
h2
42.
МАЯТНИКОВЫЙ КОПР42
Стандартные образцы для испытаний на копре (поперечное сечение равносторонний прямоугольник) имеют U- и V-образные поперечные надрезы,
соответственно, их твердость обозначается как KCU и KCV.
2 KCU - надрез
2 KCV - надрез
10
10
50
50
По высоте отскока бойка копра при ударе образца судят об энергии
(численно равной работе), затраченной на его разрушение:
где: А – работа, затраченная на разрушение образца;
А
ан
F
А mg h
m – масса маятника копра;
Δh = (h1 – h2) – разность высот;
F – площадь нетто-сечения образца.






































 physics
physics mechanics
mechanics








