Тема 2.1. Закон Гука при центральном растяжении (сжатии). Занятие 2.1.3

1.

Кафедра Механики и Инженерной графики
Прикладная механика
Тема 2.1. Основные понятия и определения
сопротивления материалов
Занятие 2.1.3. Закон Гука при центральном
растяжении (сжатии)

2.

Кафедра Механики и Инженерной графики
Учебные вопросы:
1. Построение эпюр продольных сил.
2. Абсолютная и относительная продольная деформация.
Коэффициент Пуассона.
3. Закон Гука для абсолютных деформаций.
4. Закон Гука для нормальных напряжений.

3. Построение эпюр продольных сил

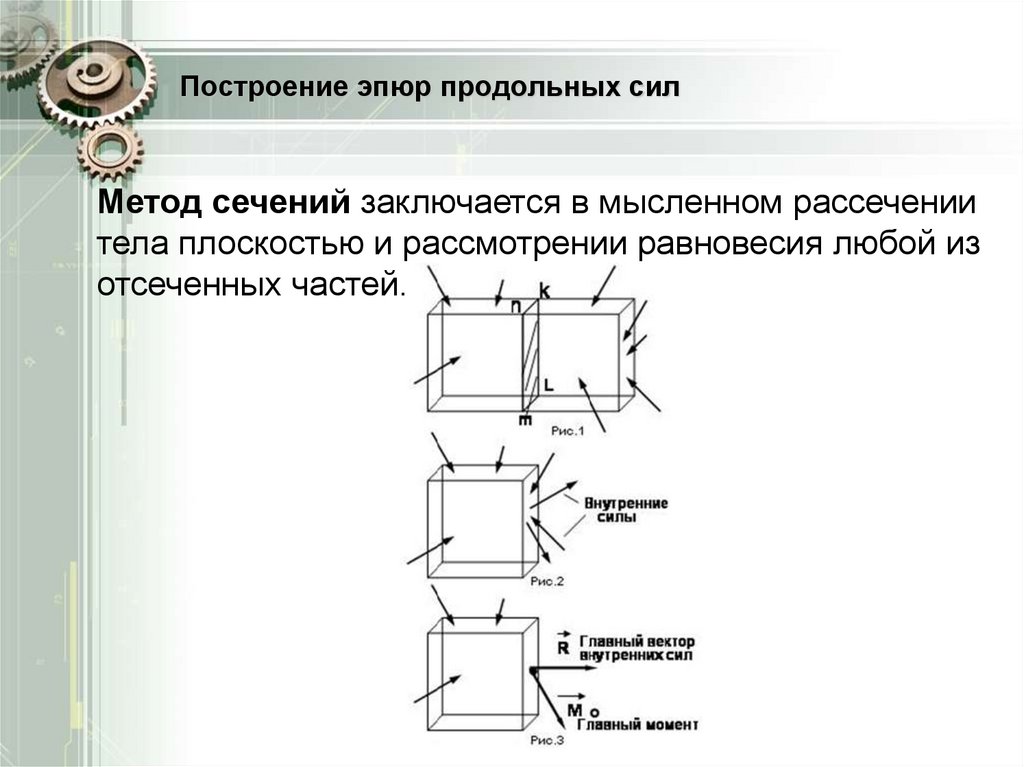
Метод сечений заключается в мысленном рассечении
тела плоскостью и рассмотрении равновесия любой из
отсеченных частей.

4. Построение эпюр продольных сил

5. Построение эпюр продольных сил

Q x , Q y , Qz , M x, M y , M к
Составляющие
называются
внутренними силовыми факторами.
Pix , Piy , Piz – суммы проекций всех
Здесь
i
i
i
внешних сил;
M , M , M – суммы проекций внешних моментов;
ix
i
iz
iy
i
i
N – продольная сила;
Qx , Qy - поперечные силы;
Mк
- крутящий момент;
M x , M y - изгибающие моменты.

6. Построение эпюр продольных сил

Деформированные состояния, при которых
возникают данные силовые факторы:
1. Растяжение-сжатие (продольные силы N);
2. Сдвиг (поперечные силы Qx , Qy );
3. Кручение (крутящий момент M к );
4. Изгиб (изгибающие моменты M x , M y );
5. Сложные деформации (несколько усилий,
например, изгибающий и крутящий
моменты).

7. Построение эпюр продольных сил

Правило знаков для продольной силы:
растягивающие продольные силы (направленные от сечения) считаются положительными,
сжимающие (направленные к сечению) –
отрицательными.
Эпюрой продольной силы называется график,
показывающий изменение продольной силы по
оси стержня.

8.

Кафедра Механики и Инженерной графики
Общий порядок построения эпюр внутренних усилий:
1. Если необходимо, то определяются опорные реакции так, как это
делается в курсе теоретической механики (выбрать объект, отбросить
связи, заменить отброшенные связи реакциями, составить уравнения
равновесия). Реакции можно не находить, если они не входят в число
внешних сил, приложенных по одну сторону от рассматриваемых
сечений.
2. Определяется число участков по длине бруса, на которых нагрузка
или геометрия бруса не изменяется. Границей участка является
любой фактор, влияющий на резкое (скачкообразное) изменение
рассматриваемого внутреннего усилия (начало или конец бруса,
перелом оси бруса, место расположения опоры, точка приложения
внешней сосредоточенной силы или другого фактора, например,
сосредоточенного момента, начало или конец распределенной
нагрузки).

9.

Кафедра Механики и Инженерной графики
3. На каждом из участков проводится сечение, отстоящее от начала
участка на некотором произвольном (переменном) расстоянии. Для
каждого сечения указывается текущая координата (z) от начала участка
или от начала бруса и записываются пределы изменения координаты. При
выборе начала локальных координат в начале участка нижний предел
всегда равен нулю.
4. Для
рассматриваемого сечения определяется выражение внутреннего
усилия в функции от координаты z рассмотрением равновесия
оставленной части или используя установленные определения для
вычисления внутреннего усилия по внешним силам, расположенным по
одну сторону от сечения.
По полученным выражениям строится эпюра изменения усилия
подстановкой верхнего и нижнего пределов, и если необходимо, других
значений координат в разрешенном интервале, обычно в середине
интервала.
5.

10. Построение эпюр продольных сил

Построить эпюру продольных сил для бруса, если:
F1=F, F2=2F, F3=4F
Проводя произвольно сечение а-а на участке I,
составляем уравнение равновесия:
F - NI = 0
Z = 0
N I = F (растяжение)

11. Построение эпюр продольных сил

Проводим сечение b-b на участке II:
Z = F - F - N
1
2
II
= F - 2F - N II = 0
N II = - F (сжатие)

12. Построение эпюр продольных сил

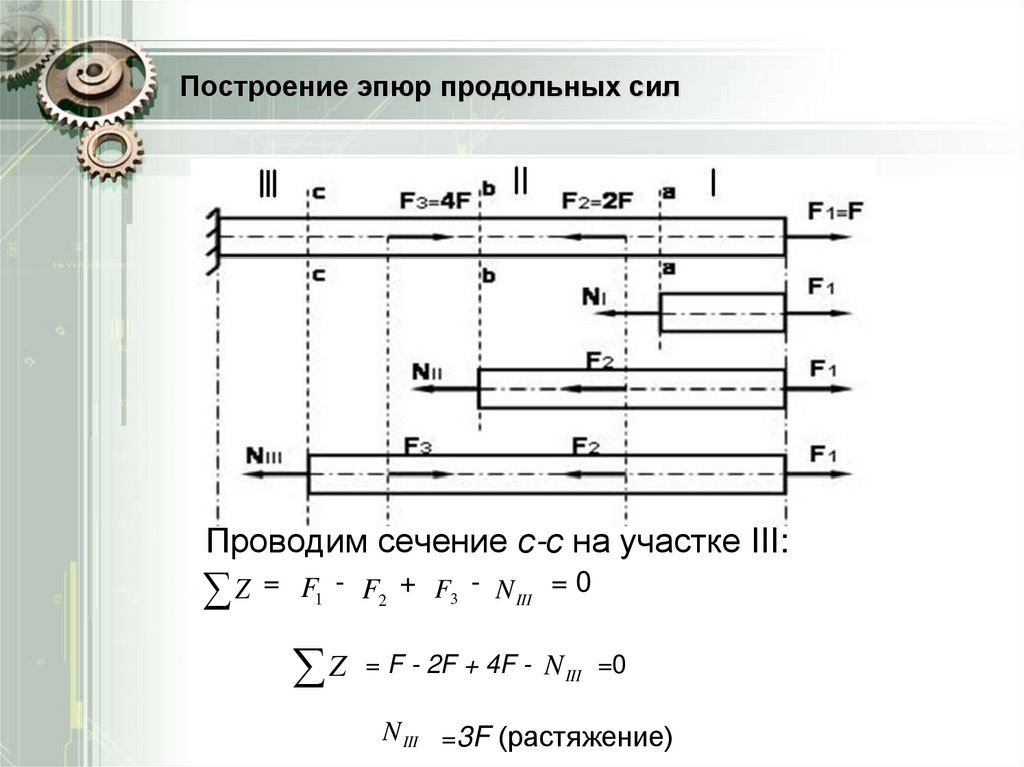
Проводим сечение с-с на участке III:
Z = F - F + F - N
1
2
3
III
=0
Z = F - 2F + 4F - N
III
=0
N III =3F (растяжение)

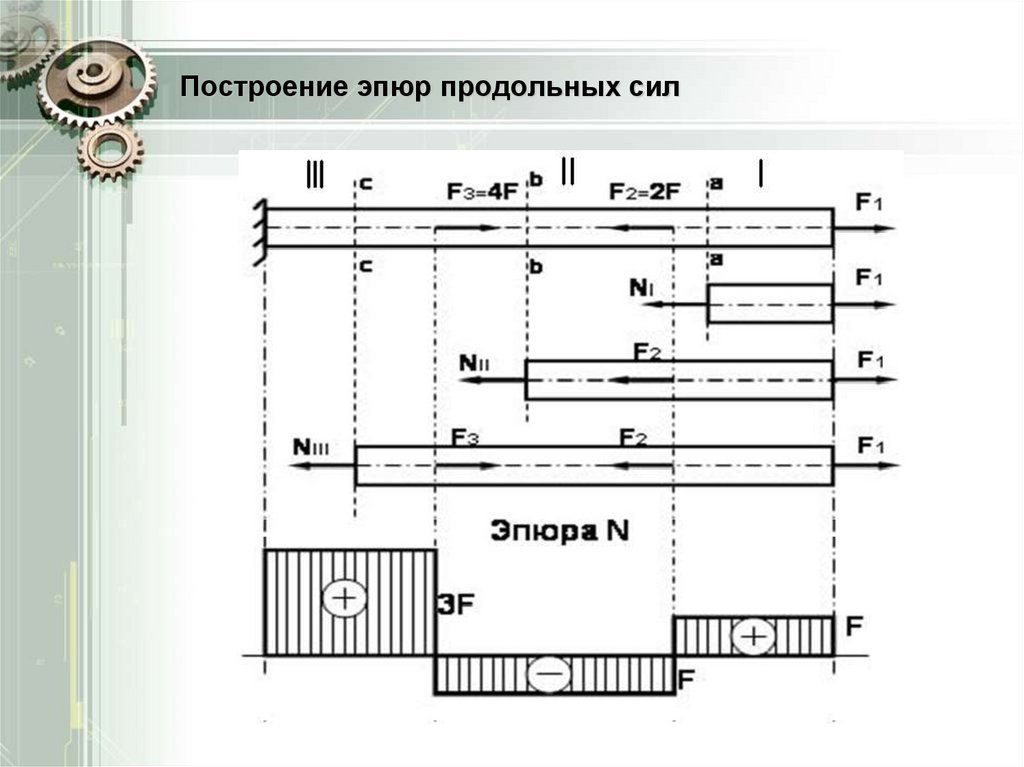
13. Построение эпюр продольных сил

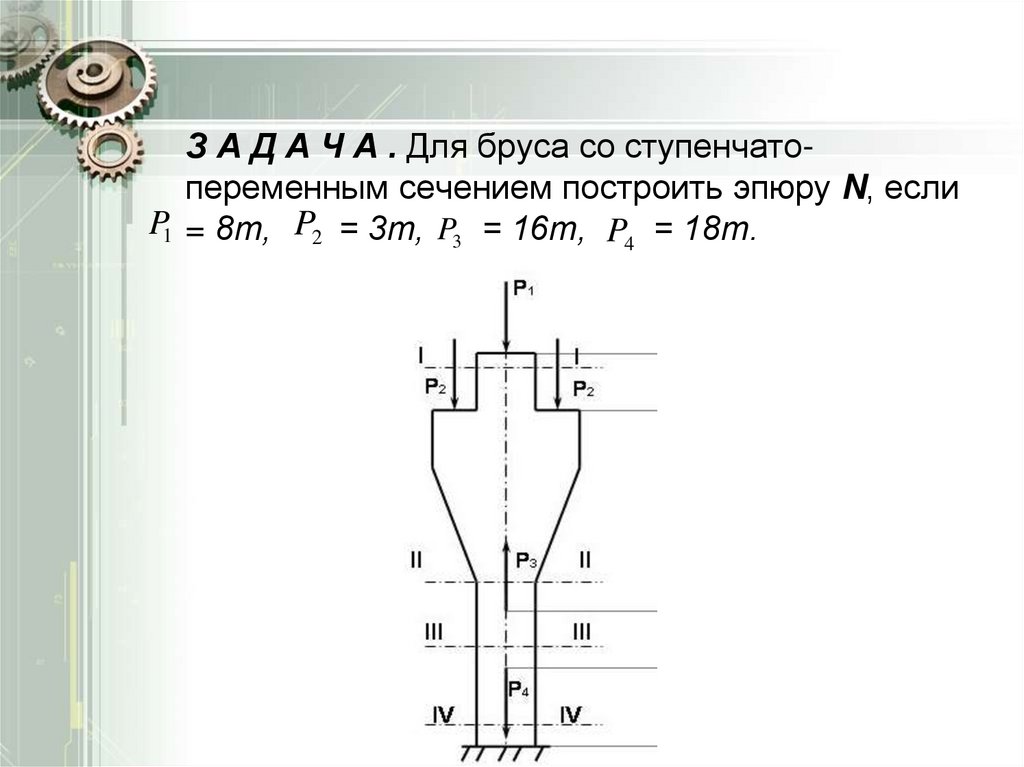
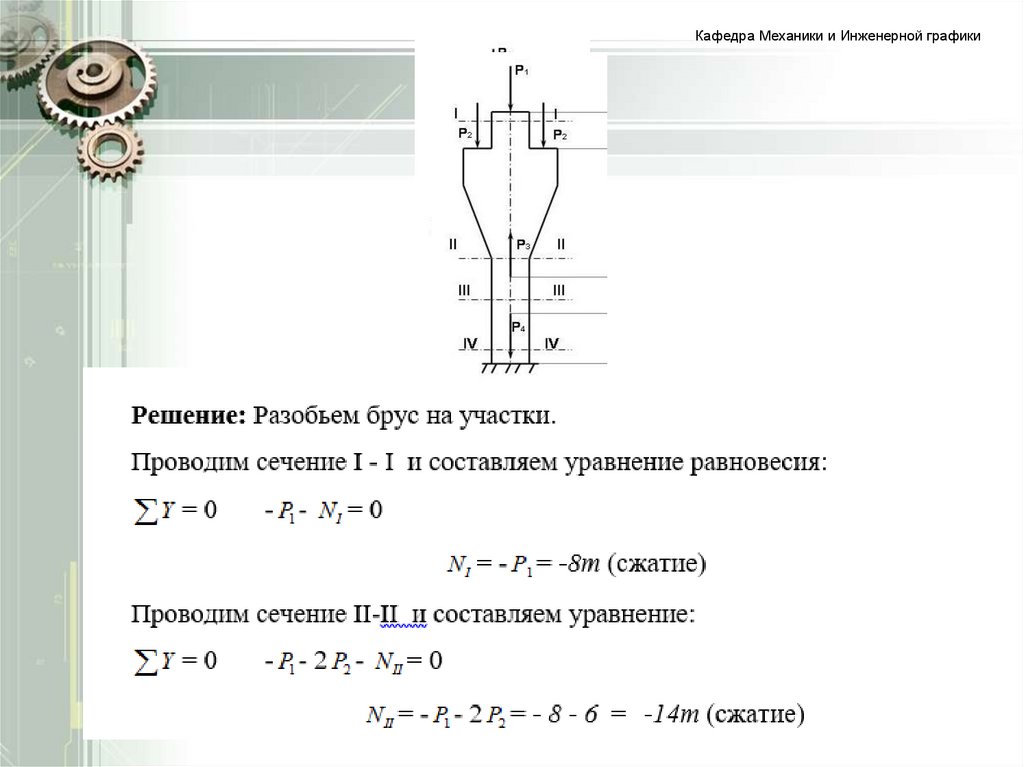
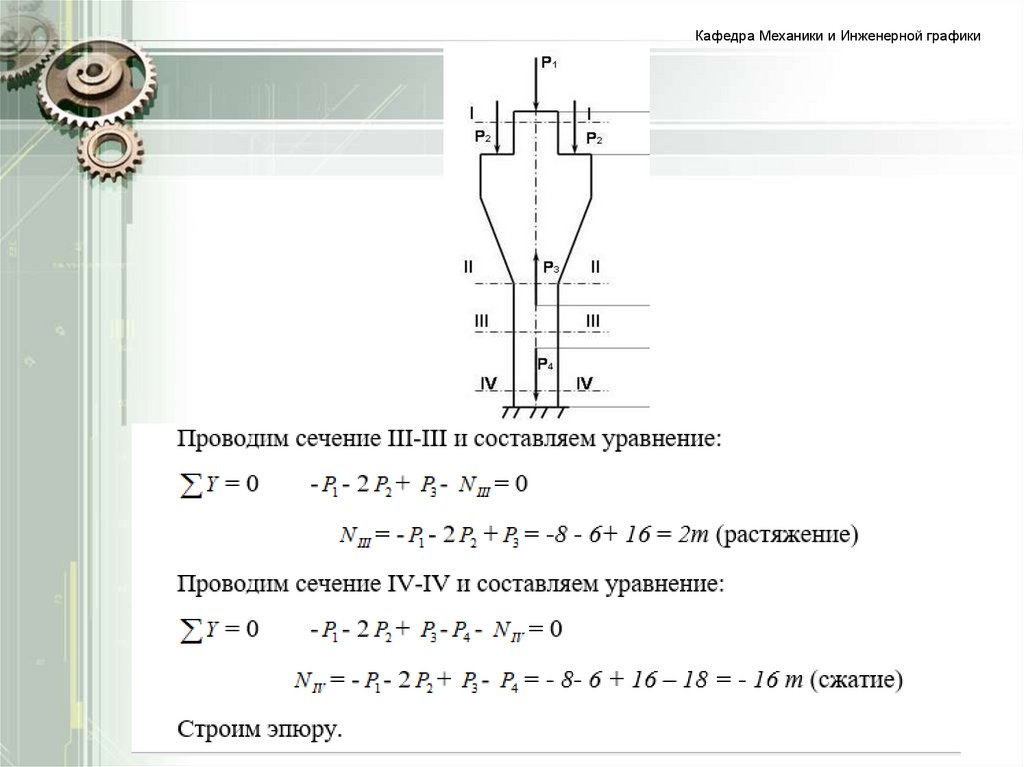
14. З А Д А Ч А . Для бруса со ступенчато-переменным сечением построить эпюру N, если = 8т, = 3т, = 16т, = 18т.

З А Д А Ч А . Для бруса со ступенчатопеременным сечением построить эпюру N, если
P1 = 8т, P2 = 3т, P3 = 16т, P4 = 18т.

15.

Кафедра Механики и Инженерной графики

16.

Кафедра Механики и Инженерной графики

17.

Кафедра Механики и Инженерной графики

18. Абсолютная и относительная продольная деформация. Коэффициент Пуассона

Напряжение – это внутренняя сила, приходящаяся на
единицу площади:
P
= F
Единицы измерения напряжения:
1 Па = 1 Н/м2 ; 1 МПа = 106Па =1 Н/мм2
Допускаемые напряжения ( и – нормальные и
касательные) – это такие максимальные напряжения,
при которых не происходит разрушение данной
конкретной детали, и она работает в условиях
упругих деформаций.

19. Абсолютная и относительная продольная деформация. Коэффициент Пуассона

При растяжении (сжатии) в поперечном сечении
стержня
P
N
= F = F
При растяжении нормальные напряжения –
положительные, при сжатии – отрицательные.
Изменение длины стержня l l1 l называют
линейной продольной деформацией (абсолютным
удлинением);
изменение поперечного сечения a a1 a - линейной
поперечной деформацией.

20.

Кафедра Механики и Инженерной графики
Абсолютная и относительная продольная деформация.
Коэффициент Пуассона
Интенсивность деформирования оценивают
деформациями, приходящимися на единицу длинны
стержня: относительной продольной и
относительной поперечной :
l
l
a
a
Отношение поперечной деформации к продольной
называется коэффициентом Пуассона :
0,2
0,5.

21.

Кафедра Механики и Инженерной графики
Закон Гука
ЗАКОН ГУКА (открыт в 1660):
где
N l
l
E F
l - абсолютная продольная деформация;
N – продольная сила;
F – площадь поперечного сечения;
E – модуль продольной упругости (модуль Юнга).
Закон Гука можно преобразовать, учитывая определения
N
внутреннего напряжения ( ) и относительной
F
деформации (
l
l
):
= E·

22.

Кафедра Механики и Инженерной графики
Закон Гука
Максимальные напряжения при растяжении (сжатии):
max = N max
F
Условие прочности: max
Условие жесткости: max
Условие жесткости при растяжении (сжатии) можно
записать и в другом виде:
lmax = N max l l
E F

23.

Кафедра Механики и Инженерной графики
Закон Гука
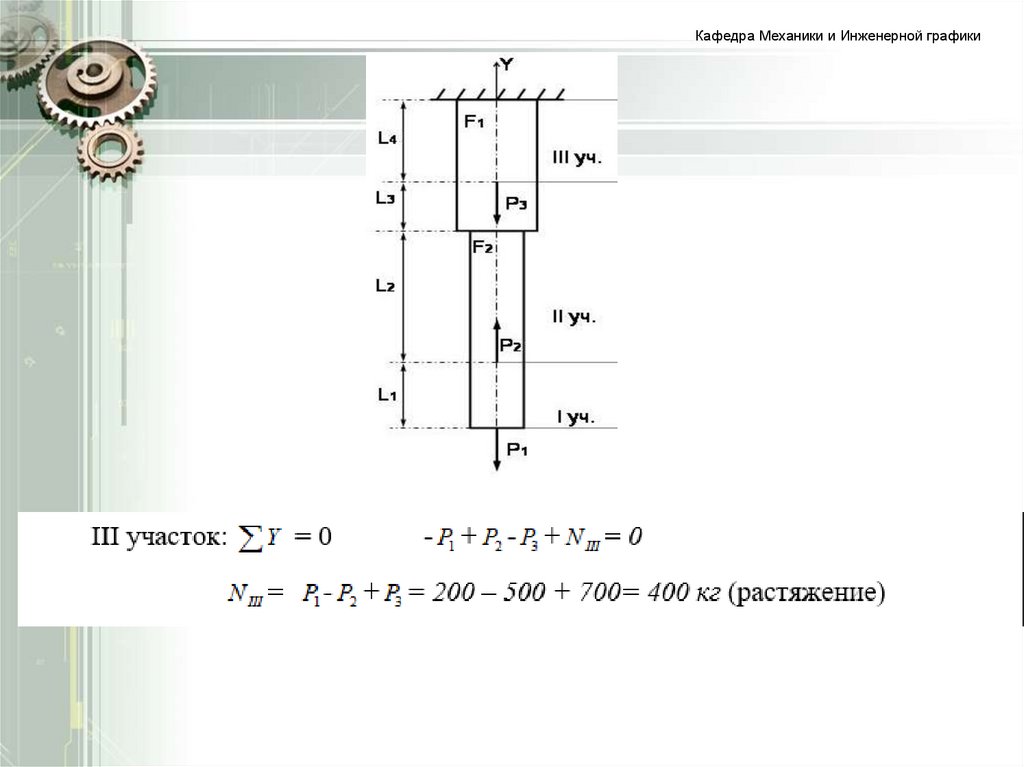
З А Д А Ч А . Вычислить
приращение длины стального
стержня ступенчатого сечения,
если l1 = 50 см, l 2 = 80 см,
l 3 = 40 см, l 4 = 60 см,
E 2 106 кг/см2 , F1 20 см2 ,
F2 10 см2 , P1 200 кг ,
P2 500 кг , P3 700 кг .

24.

Кафедра Механики и Инженерной графики

25.

Кафедра Механики и Инженерной графики

26.

Кафедра Механики и Инженерной графики
Закон Гука
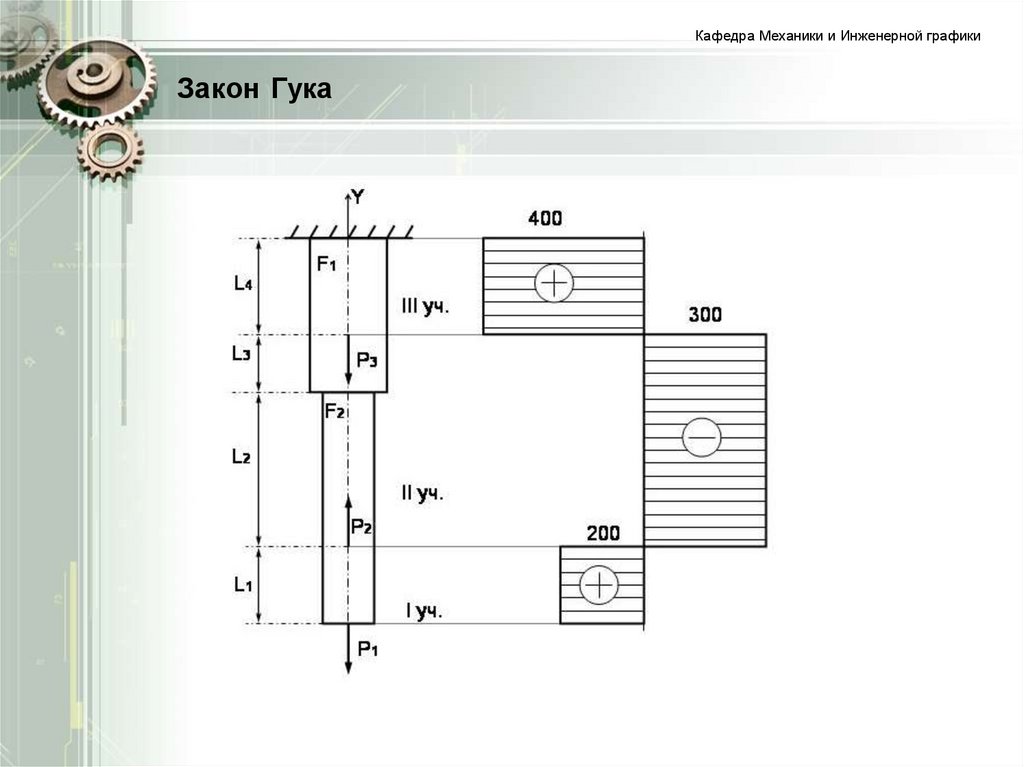
Полное удлинение стержня определяем как сумму
удлинений отдельных участков:
l = N1 l 1 +
E F2
N 2 l 2
E F2
N 2 l 3
+
E F1
N 3 l 4
+
E F1

27.

Кафедра Механики и Инженерной графики
Закон Гука

28.

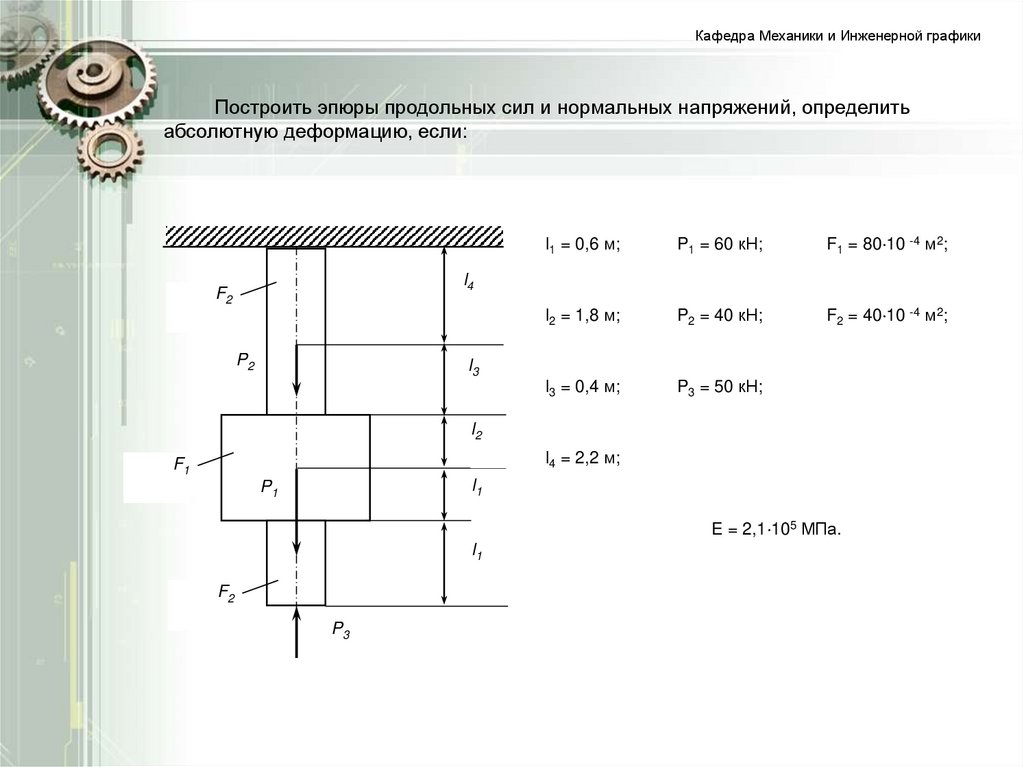
Кафедра Механики и Инженерной графики
Построить эпюры продольных сил и нормальных напряжений, определить
абсолютную деформацию, если:
l1 = 0,6 м;
P1 = 60 кН;
F1 = 80 10 -4 м2;
l2 = 1,8 м;
P2 = 40 кН;
F2 = 40 10 -4 м2;
l3 = 0,4 м;
P3 = 50 кН;
l4
F2
P2
l3
l2
l4 = 2,2 м;
F1
l1
P1
E = 2,1 105 МПа.
l1
F2
P3