Осевое растяжение и сжатие стержней

1.

2. ОСЕВОЕ РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
2.1. Осевое растяжение и сжатие призматических стержней
Растяжением или сжатием называют такой
вид деформации стержня, при котором в
поперечных сечениях его возникает лишь одно из
внутренних усилий
Nx N
Усилие
N
будем
положительным,
если
оно
растяжение стержня.
считать
вызывает
Величину N в произвольном сечении стержня определяют из условия
равновесия его отсеченной части. При этом, согласно закону Ньютона
(аксиоме) о равенстве действия и противодействия, не важно равновесие какой
из двух частей стержня рассматривать.
осевое растяжение-сжатие стержней
1

2.

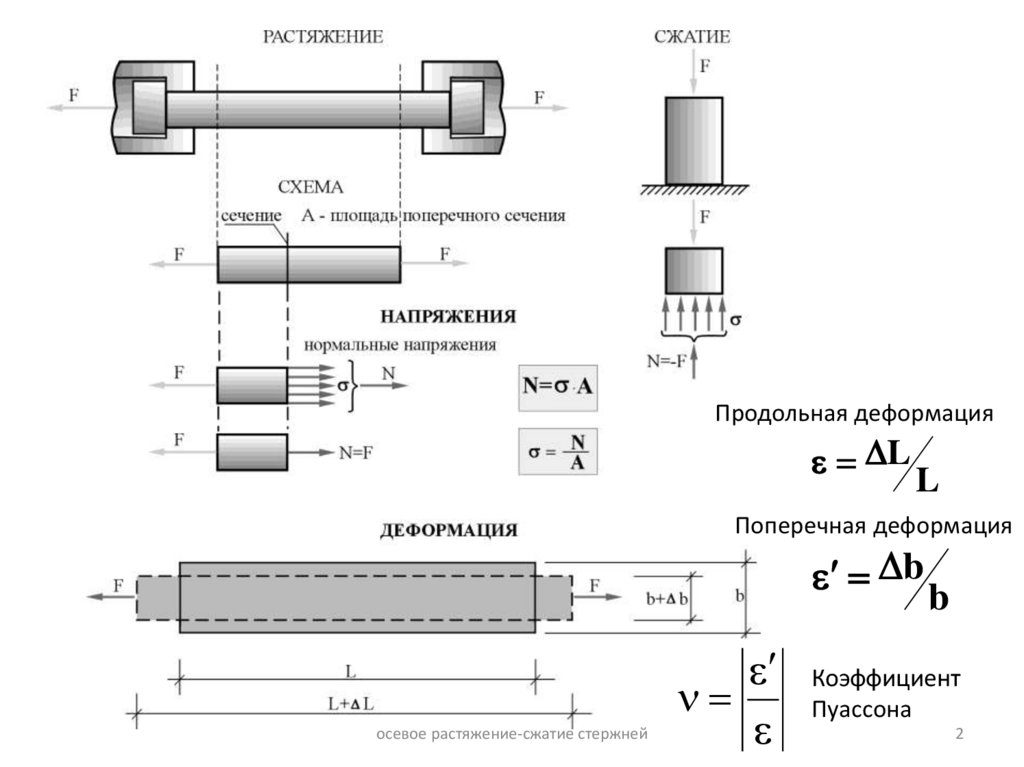
Продольная деформация
L
L
Поперечная деформация
b
осевое растяжение-сжатие стержней
b
Коэффициент
Пуассона
2

3.

2.2. Закон Гука
Между и (двумя разнородными факторами одного явления) существует связь,
называемая законом Гука, который является экспериментальным фактом и на
современном языке может быть сформулирован так: малые упругие деформации
материала, не зависящие от времени деформирования, пропорциональны
соответствующим им напряжениям. В случае линейного напряженного
состояния закон Гука определен зависимостью
E
E – модуль упругости (модуль Юнга, жесткость)
Е,
материала
физические характеристики материала
С учетом
L , N
L
A
закон Гука можно представить в виде
NL
L
EAрастяжении или сжатии
ЕА – жесткость стержня при осевом
осевое растяжение-сжатие стержней
3

4.

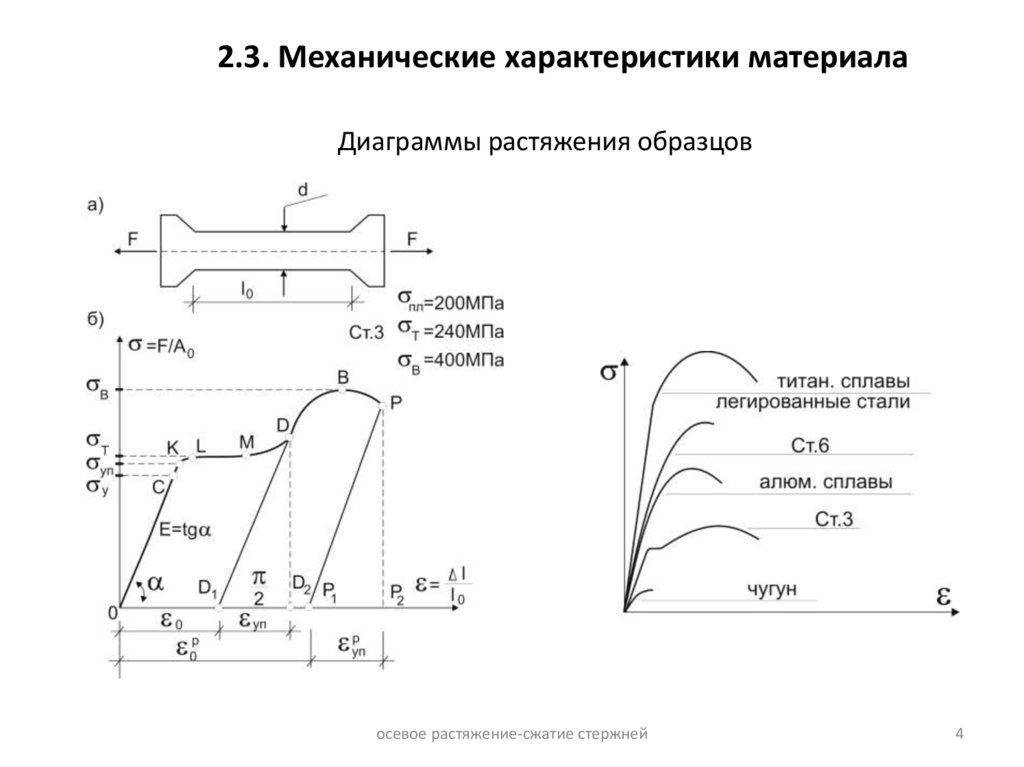
2.3. Механические характеристики материала
Диаграммы растяжения образцов
осевое растяжение-сжатие стержней
4

5.

2.4. Расчеты на прочность при растяжении или сжатии
Условие прочности при растяжении стержня
расч R
R – расчетное сопротивление материала
R Rн / k
Rн – нормативное сопротивление материала, устанавливаемое нормами
проектирования с учетом условий контроля и статистической изменчивости.
k – коэффициент безопасности (запаса прочности). В частности, может быть:
-- для пластичных материалов
– для
хрупких
R н т
R н в
осевое растяжение-сжатие стержней
5

6.

В зависимости от постановки задачи различают три вида расчета на прочность,
которые для случая растяжения или сжатия стержня сводятся к необходимости
удовлетворения следующих неравенств:
1) проверочный, когда известны нагрузки на стержень, его материал
(расчетное сопротивление) и размеры поперечного сечения:
расч N / A R
2) подбор сечения, когда известны нагрузки и материал:
A N/R
3) определение допускаемой нагрузки, когда известны размеры стержня и
го материал, а определению подлежит нагрузка. Из условия прочности
стержня определяют [N] – допускаемое значение усилия N:
N AR [ N]
По [N] находят соответствующее ему допускаемое значение внешних усилий.
осевое растяжение-сжатие стержней
6

7.

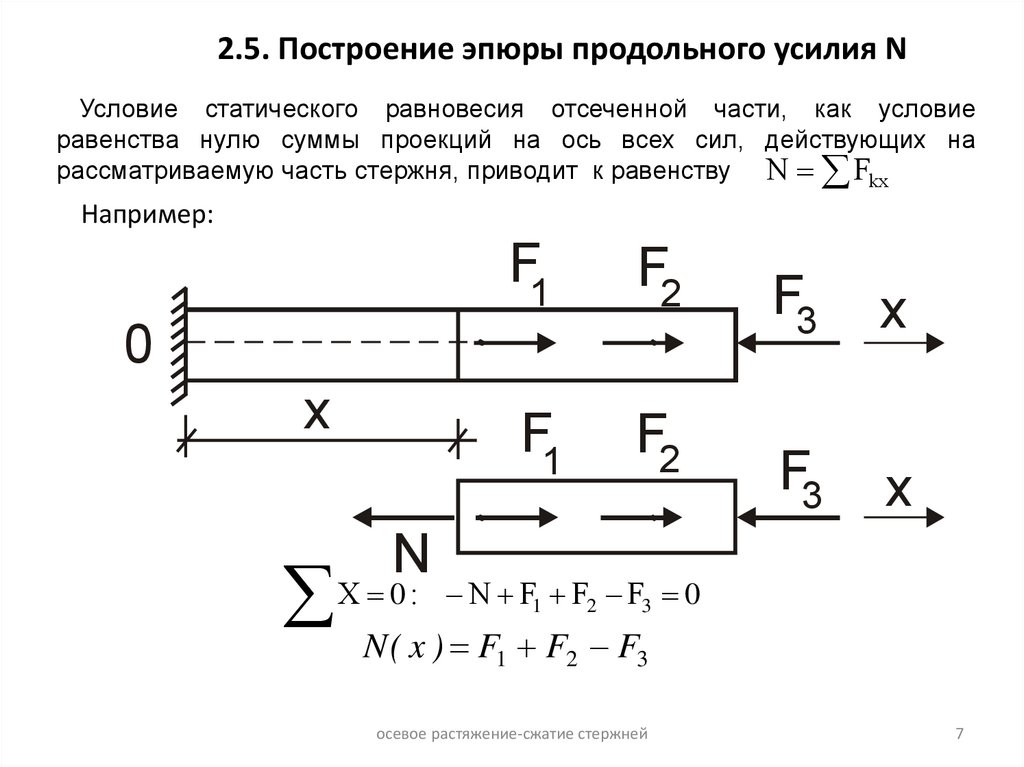
2.5. Построение эпюры продольного усилия N
Условие статического равновесия отсеченной части, как условие
равенства нулю суммы проекций на ось всех сил, действующих на
рассматриваемую часть стержня, приводит к равенству N Fkx
Например:
0
x
N
X 0 :
F1
F2
F1
F2
F3
x
F3
x
N F1 F2 F3 0
N ( x ) F1 F2 F3
осевое растяжение-сжатие стержней
7

8.

При исследовании прочности стержня возникает необходимость в
знании законов изменения N по его длине. Графические изображения
этого закона называют эпюрой продольного усилия.
Закон изменения какого-либо усилия по длине стержня в виде графика называют
эпюрой этого усилия. Грузовым участком стержня называют его часть, в пределах
которой характер действующей нагрузки и его геометрия не меняются. Функциональная
зависимость N(x), меняясь от одного грузового участка к другому, на каждом из них
сохраняет свой вид.
Величину N в произвольном сечении стержня определяют из условия
равновесия его отсеченной части. При этом, согласно закону Ньютона
(аксиоме) о равенстве действия и противодействия, не важно равновесие какой
из двух частей стержня рассматривать.
N в произвольном сечении стержня численно равно алгебраической
сумме проекций на его ось всех внешних сил, приложенных к
рассматриваемой (любой из двух) отсеченной части.
осевое растяжение-сжатие стержней
8

9.

Пример построения эпюры N
Для каждого из 4-х грузовых участков запишем выражения
для продольного усилия N(х).
осевое растяжение-сжатие стержней
9

10.

:
0 х 2:
2 х 6:
6 х 9:
9 х 11:
N F1 40;
N F1 q1( x 2 ) 40 10( x 2 );
N F1 q1 4 F2 40 40 60 20;
N F1 q1 4 F2 F3 q2 ( x 9 )
20 30 30( x 9) 10 30( x 9).
осевое растяжение-сжатие стержней
10

11.

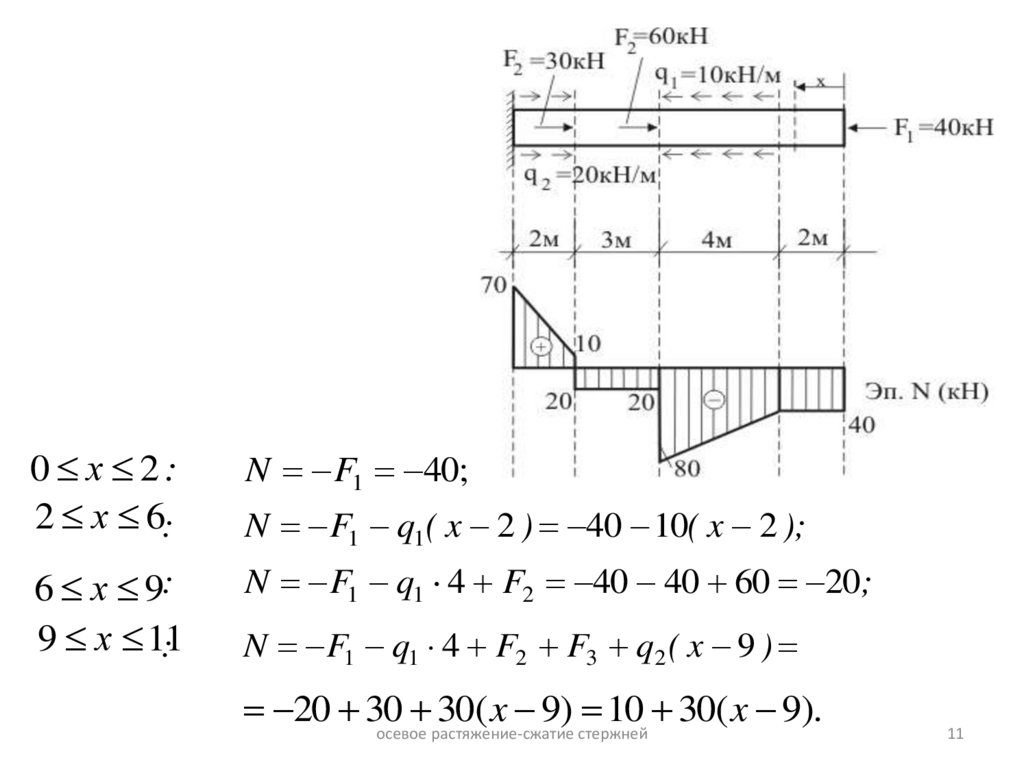
0 х 2:
2 х 6:
6 х 9:
9 х 11
:
N F1 40;
N F1 q1( x 2 ) 40 10( x 2 );
N F1 q1 4 F2 40 40 60 20;
N F1 q1 4 F2 F3 q2 ( x 9 )
20 30
30( x 9) 10 30( x 9).
осевое растяжение-сжатие стержней
11

12.

осевое растяжение-сжатие стержней
12

13.

5.6. Пример расчета стержня на прочность и жесткость
Задача:
1. Построить эпюру N
2. Подобрать сечение (RP=20МПа, RC=60МПа)
3. Определить l стержня
Е 3 103 МПа
4. Построить эпюру
осевое растяжение-сжатие стержней
13

14.

1. Построение эпюры N.
0 х 4
4 х 8
8 х 10
N F1 20кН
N F1 q( x 4) 20 25( x 4)
N F1 q 4 F2 20 25 4 30 50кН
осевое растяжение-сжатие стержней
14

15.

Построение эпюры N.
0 х 4
4 х 8
8 х 10
N F1 20кН
N F1 q( x 4) 20 25( x 4)
N F1 q 4 F2 20 25 4 30 50кН
осевое растяжение-сжатие стержней
15

16.

2. Подбор сечения: (1МПа =10-1 кН/см2)
Из условий прочности для опасных сечений стержня следует:
max N P
max N P 20
RP A
10(см2 ) A 1
A
RP
2
max N C
max N C 80
max C
RC A
13,3 см2 A 2
A
RC
6
max P
A max( A1 , A2 ) A2
Примем ( в запас прочности !)
А=13,4см2
осевое растяжение-сжатие стержней

17.

3. Определение
l
Е 3 10 3 МПа 3 10 2 кН / см 2
3
N i ,ср li
i 1
EA
l
1
20 80
20
400
400
30
200
2
2
( 3 10 ) 13.4
1
(80 120 60) 2.48(cм)
40.2
осевое растяжение-сжатие стержней
17

18.

:
4. Построение эпюры
х=0:
20( кН )
кН
1
.
49
14.9МПа
13,4( см 2 )
см 2
x 8 :
80
кН
5.97 2 59.7 МПа
13,4
см
x 8 :
50
кН
3.73 2 37.3МПа
13,4
см
N
A
осевое растяжение-сжатие стержней
18