Растяжение и сжатие стержней

1.

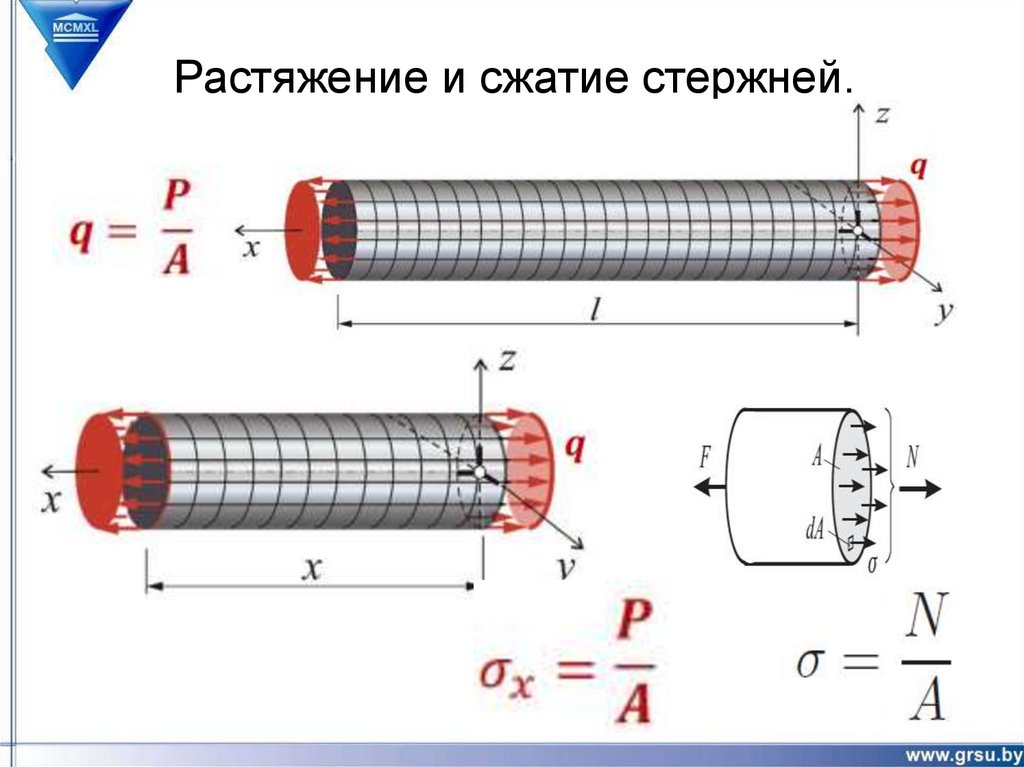
Растяжение и сжатие стержней.

2. Растяжение и сжатие стержней.

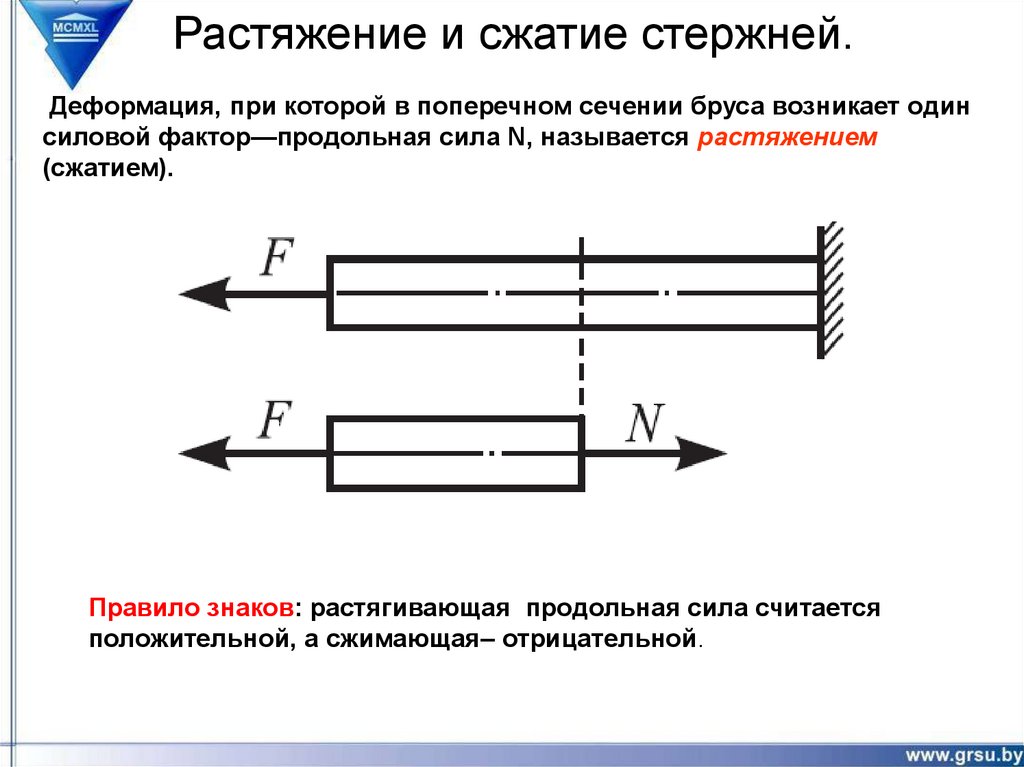
Деформация, при которой в поперечном сечении бруса возникает один
силовой фактор—продольная сила N, называется растяжением
(сжатием).
Правило знаков: растягивающая продольная сила считается
положительной, а сжимающая– отрицательной.

3.

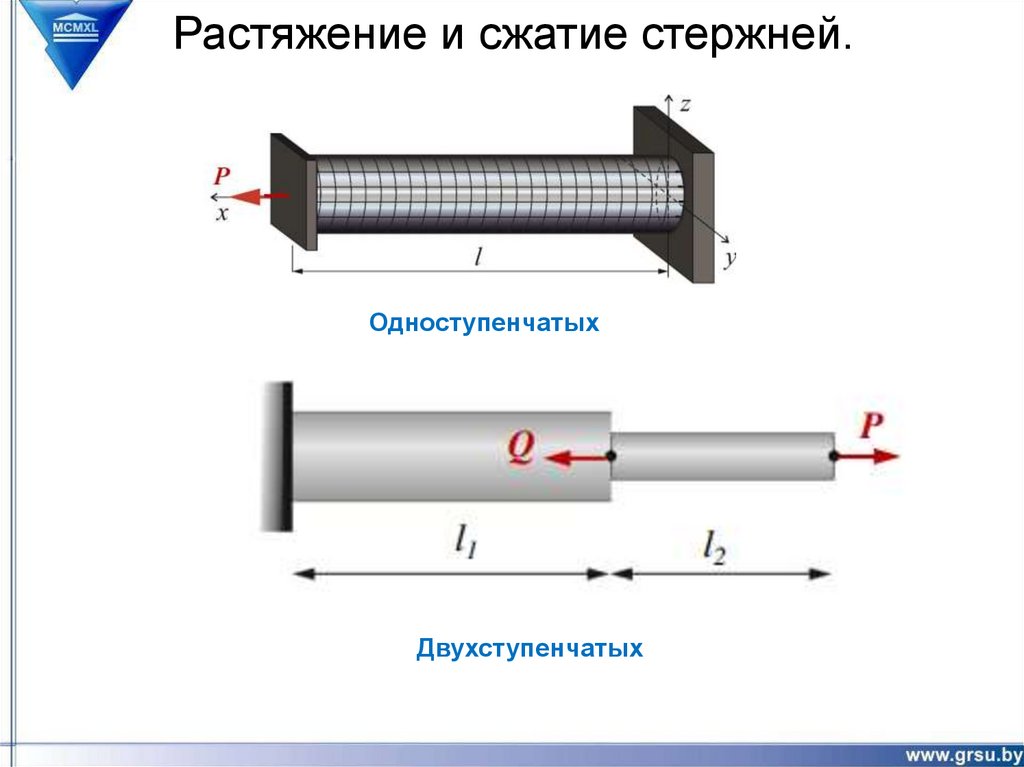
Растяжение и сжатие стержней.
Одноступенчатых
Двухступенчатых

4. Принципы построения эпюры продольных сил.

Растяжение и сжатие стержней.
Принципы построения эпюры продольных сил.
1. Определить опорные реакции так, как это делается в курсе
теоретической механики. (Реакции можно не находить, если они
не входят в число внешних сил, приложенных по одну сторону
от рассматриваемых сечений).
2. Выделить характерные сечения стержня.
Характерными называются сечения стержня где:
1) приложены внешние продольные силы;
2) происходит ступенчатое, или начинается участок постепенного
изменения площади поперечного сечения бруса.
3. Рассмотреть равновесие отсеченных частей стержня, составив
уравнения проекций сил на ось, проходящую вдоль стержня.
Рассчитать величину продольной силы.
4. По полученным данным построить эпюра продольных сил.

5.

Растяжение и сжатие стержней.
Правила контроля эпюры продольных сил
1. В сечении, где приложена сосредоточенная сила F,
эпюра продольных сил делает скачок на величину
этой силы и с ее знаком.
2. Изменение площади поперечного сечения стержня
влияния на эпюру продольных сил не оказывает,
независимо от характера этого изменения
(ступенчатое или постепенное).
3. На
участке,
где
приложена
равномерно
распределенная нагрузка эпюра продольных сил
имеет вид прямой наклонной линии.

6. Растяжение и сжатие стержней.

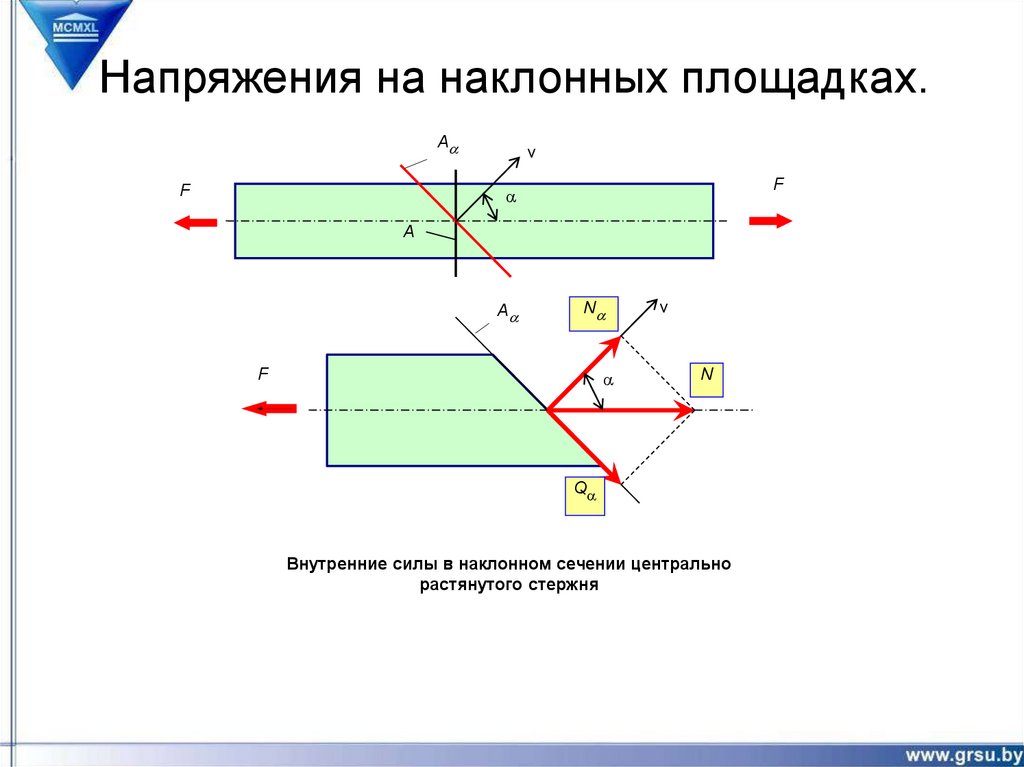
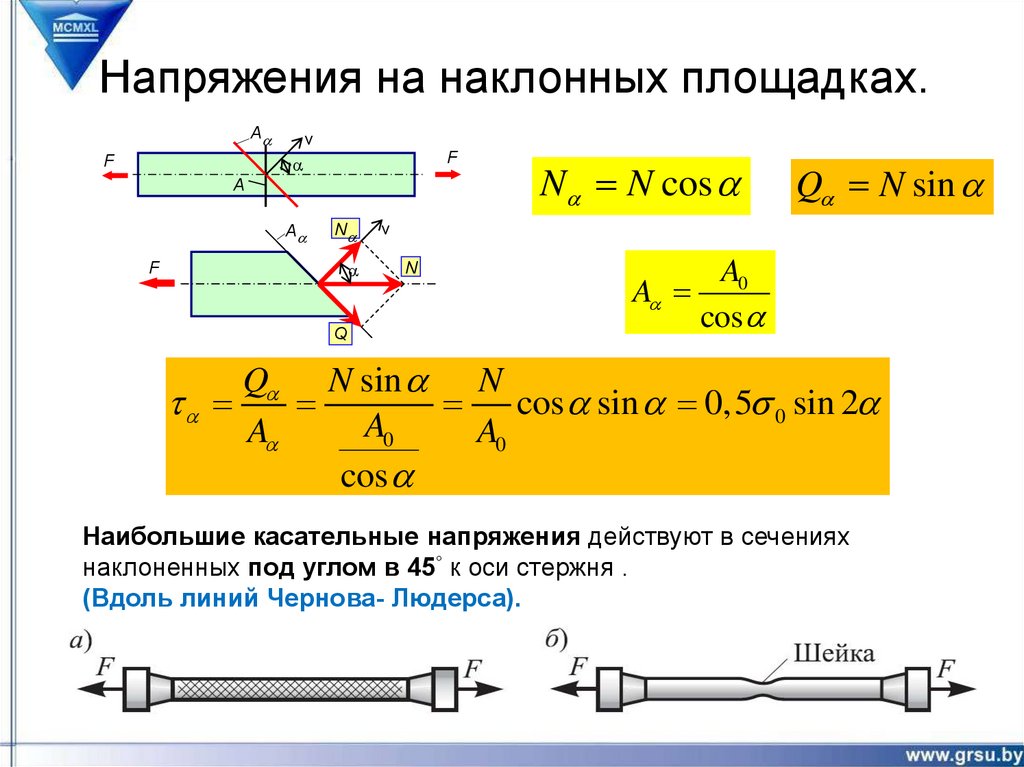
7. Напряжения на наклонных площадках.

A
F
ν
F
A
A
N
F
ν
N
Q
Внутренние силы в наклонном сечении центрально
растянутого стержня

8. Напряжения на наклонных площадках.

A
ν
F
F
A
A
N
F
N N cos
ν
N
Q N sin
Q
A0
A
cos
N N cos N
cos 2 0 cos 2 ,
A0
A
A0
cos
Наибольшие нормальные напряжения (по абсолютной величине)
действуют в поперечном сечении стержня.

9. Напряжения на наклонных площадках.

A
ν
F
F
A
A
N
F
Q
N N cos
Q N sin
ν
N
A0
A
cos
Q N sin N
cos sin 0,5 0 sin 2
A0
A
A0
cos
Наибольшие касательные напряжения действуют в сечениях
наклоненных под углом в 45° к оси стержня .
(Вдоль линий Чернова- Людерса).

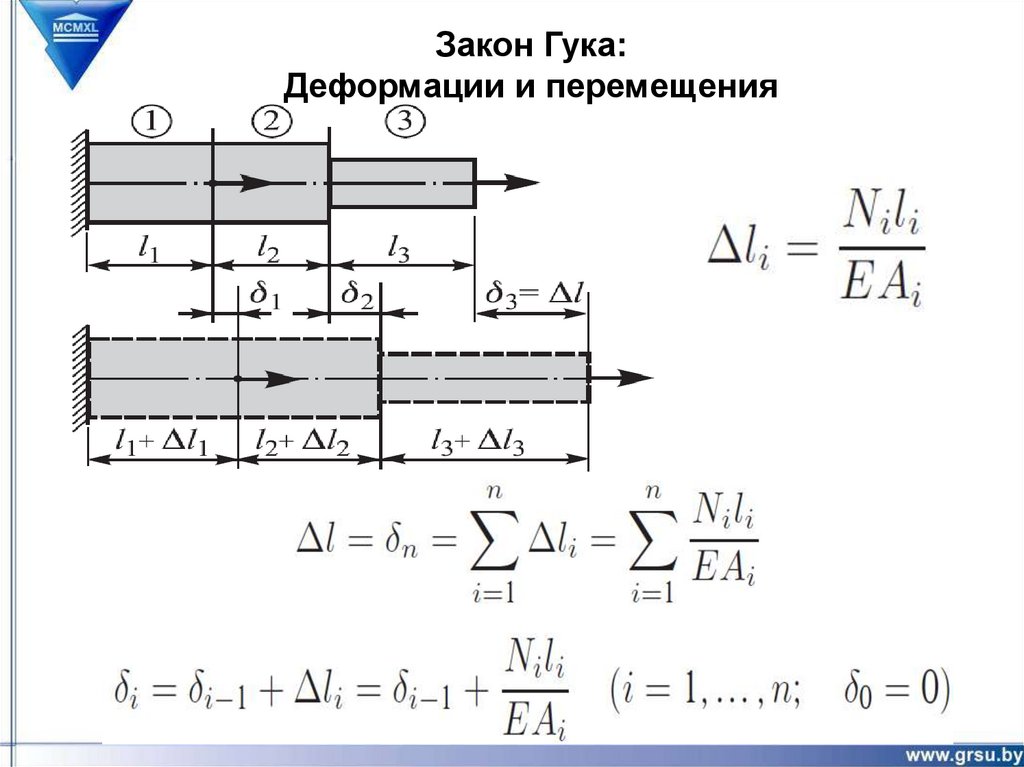
10. Закон Гука при растяжении – сжатии.

Растяжение и сжатие стержней.
Закон Гука при растяжении – сжатии.
Закон Гука имеет два аналитических выражения— через относительные, и
через абсолютные величины
В абсолютных величинах
В относительных величинах
Nl
l
EA
E
Жесткостью поперечного сечения стержня называют произведение
площади поперечного сечения А на модуль продольной упругости материала Е.
Способность стержня сопротивляться деформированию оценивают величиной
относительной жесткости стержня, которая равна отношению жесткости
поперечного сечения ЕА к длине стержня l:
АЕ
С
l

11. Диаграммы растяжения стали

Растяжение и сжатие стержней.
Диаграммы растяжения стали

12. Диаграммы растяжения

Растяжение и сжатие стержней.
Диаграммы растяжения

13.

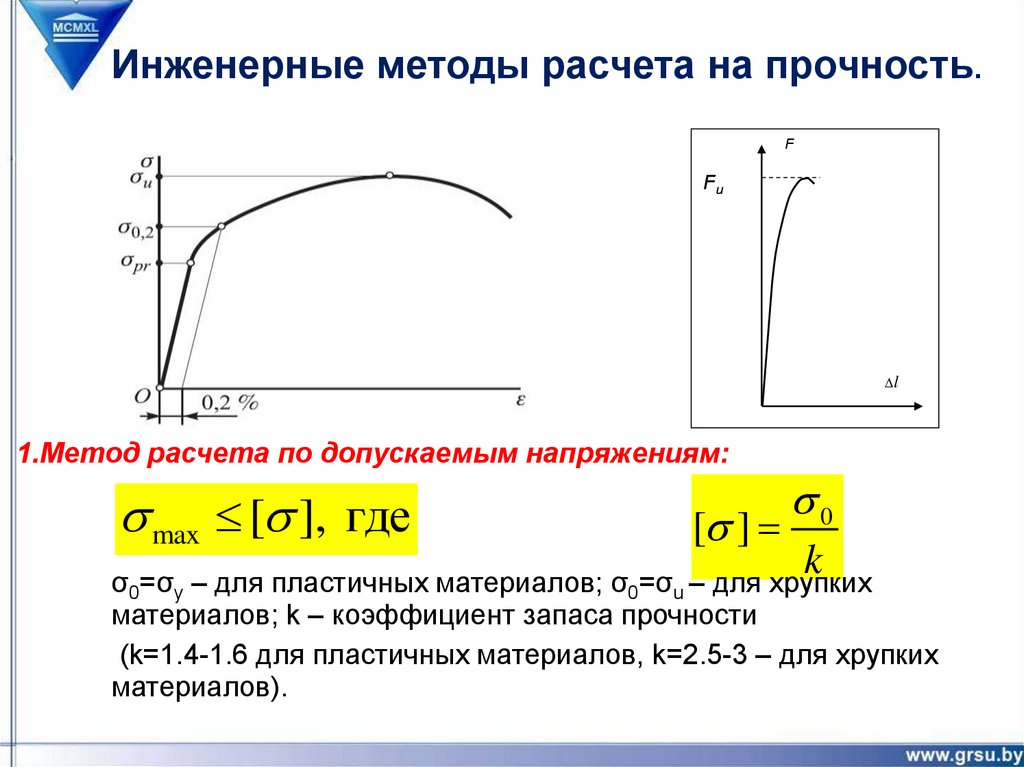
Инженерные методы расчета на прочность.
F
Fu
l
1.Метод расчета по допускаемым напряжениям:
max [ ], где
[ ]
0
k
σ0=σy – для пластичных материалов; σ0=σu – для хрупких
материалов; k – коэффициент запаса прочности
(k=1.4-1.6 для пластичных материалов, k=2.5-3 – для хрупких
материалов).

14.

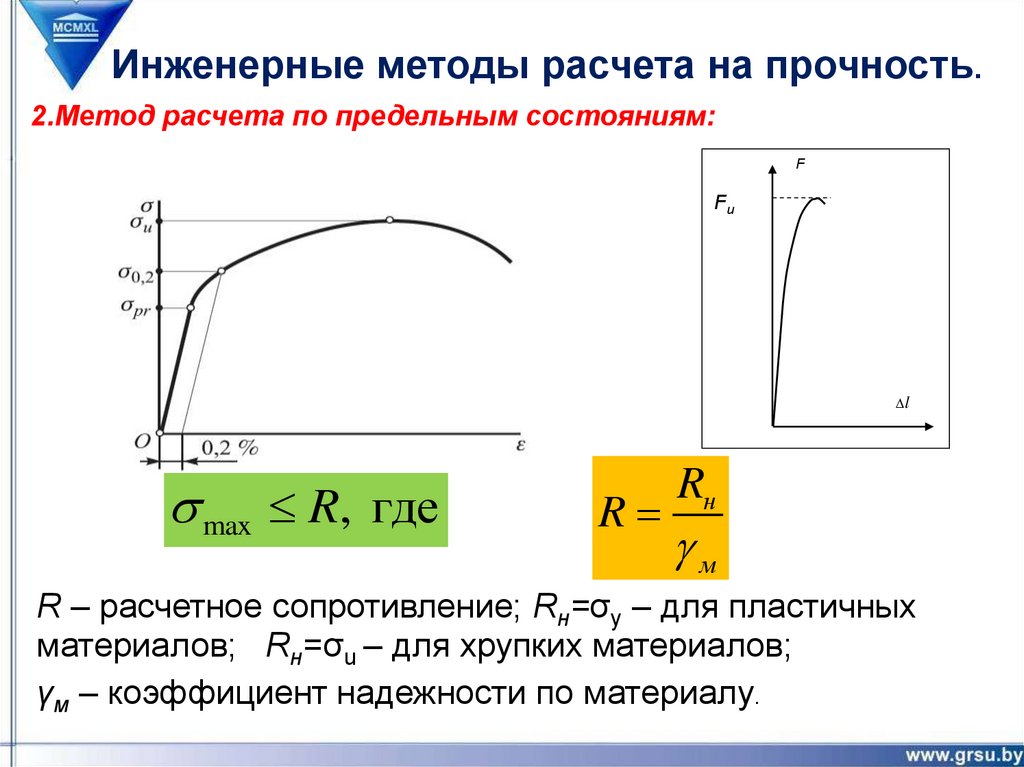
Инженерные методы расчета на прочность.
2.Метод расчета по предельным состояниям:
F
Fu
l
max R, где
R
Rн
м
R – расчетное сопротивление; Rн=σy – для пластичных
материалов; Rн=σu – для хрупких материалов;
γм – коэффициент надежности по материалу.

15.

Растяжение и сжатие стержней.
Деформации
Nl
l
EA

16.

Растяжение и сжатие стержней.
Деформации
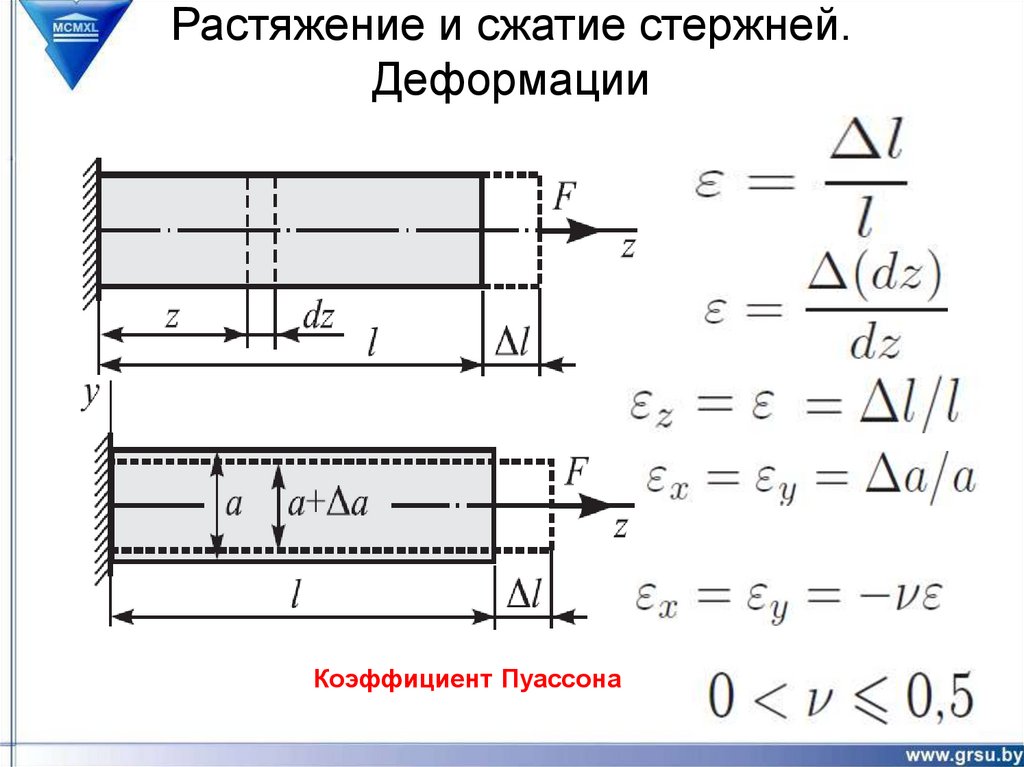
Коэффициент Пуассона

17.

Коэффициент Пуассона
Отношение относительной поперечной деформации ε / к
относительной продольной деформации ε, взятое по
модулю, называется коэффициентом Пуассона:
/
Коэффициент Пуассона принимает значения в пределах
от 0 до 0,5 и определяется экспериментально. Меньшее
значение коэффициента имеют бетон – 0,16…0,18,
стекло – 0,25, большие значения каучук – 0,48, свинец –
0,42, целлулоид – 0,38. У большинства материалов
используемых в машиностроении =0,24…0,36.

18.

Коэффициент изменения объёма
Коэффициентом
изменения
объёма
называется
безразмерная величина представляющая собой отношение
величины, на которую изменяется объём бруса при
деформации V=Vк-V0 к его первоначальному объёму V0
/
/
/
/
kV a b 2 1 2 1 2 .
Коэффициент изменения объема принимает следующие
значения: при сжатии объём бруса уменьшается и kV<0,
при растяжении объём увеличивается и kV>0.
Для
материалов с коэффициентом Пуассона 0,5 изменение
объёма не происходит и kV 0

19. Деформации и перемещения

Растяжение и сжатие стержней.
Деформации и перемещения
Величина, на которую изменится длина бруса (или
одного из его участков) под действием продольных сил,
называется продольной деформацией.
l lк l0 ,
Относительной продольной деформацией
называется отношение абсолютной продольной
деформации l к первоначальной длине стержня l0:
l l0
Величина а ( b), на которую изменится размер
поперечного сечения бруса а0 (b0) под действием
продольной силы, называется поперечной
деформацией.
Отношение абсолютной поперечной деформации, а ( b) к первоначальному
размеру сечения бруса а0 (b0), называется относительной поперечной
деформаций:
а/
a
,
a0
b/
b
b0

20.

Закон Гука:
Деформации и перемещения
Закон Гука:
Е- модуль упругости
(модуль Юнга (Янга))
T.Yong
С учетом температурных
деформаций
Для стали
Для дюралюминия
Для стали

21.

Закон Гука:
Деформации и перемещения

22.

Закон Гука:
Деформации и перемещения

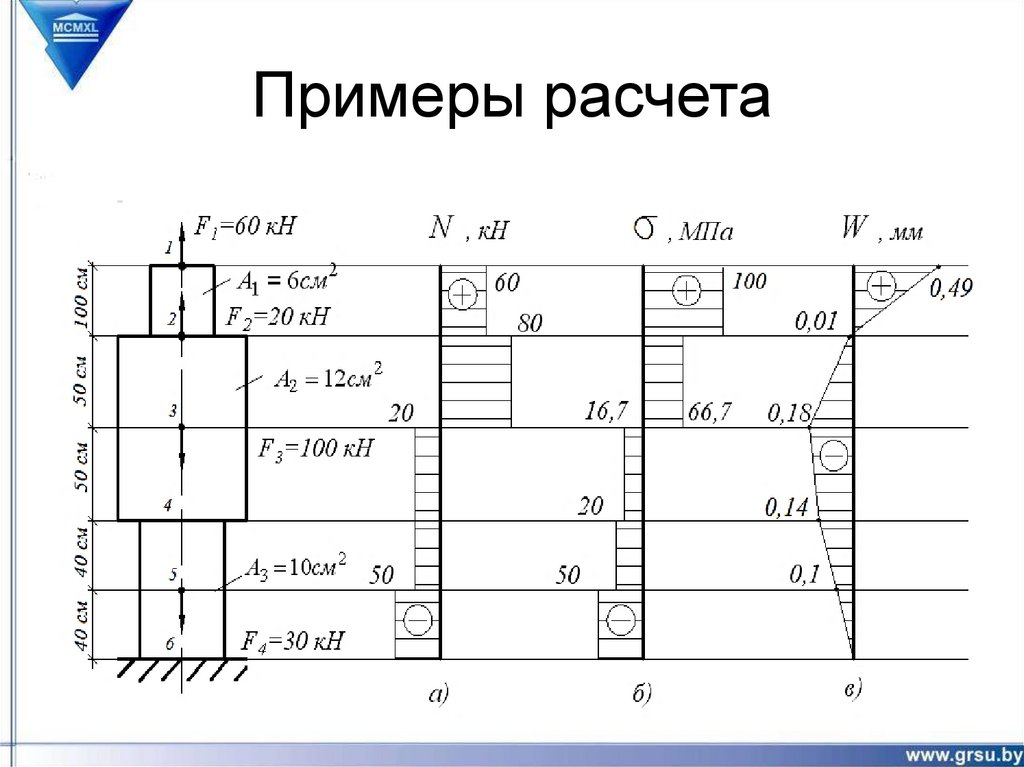
23. Примеры расчета

Ступенчатый стержень находится под действием внешних сил F (рис.1).
Материал стержня – сталь с модулем продольной упругости E = 200 ГПа.
Требуется: построить эпюры продольных сил, напряжений и перемещений.
Собственный вес стержня не учитывать.
F1 = 60 кН,
F2 = 20 кН,
F3 = 100 кН,
F4 = 30 кН,
А1 = 6 см2,
А2 = 12 см2,
А3 = 10 см2,
a = 80 см,
b = 100 см,
c = 100 см.

24. Примеры расчета

Решение.
Для определения внутренних усилий разбиваем стержень на участки.
Границами участков являются точки продольной оси, соответствующие
изменению площади поперечного сечения и местам приложения
сосредоточенных сил. Определяем, что стержень необходимо разбить на пять
участков

25. Примеры расчета

26.

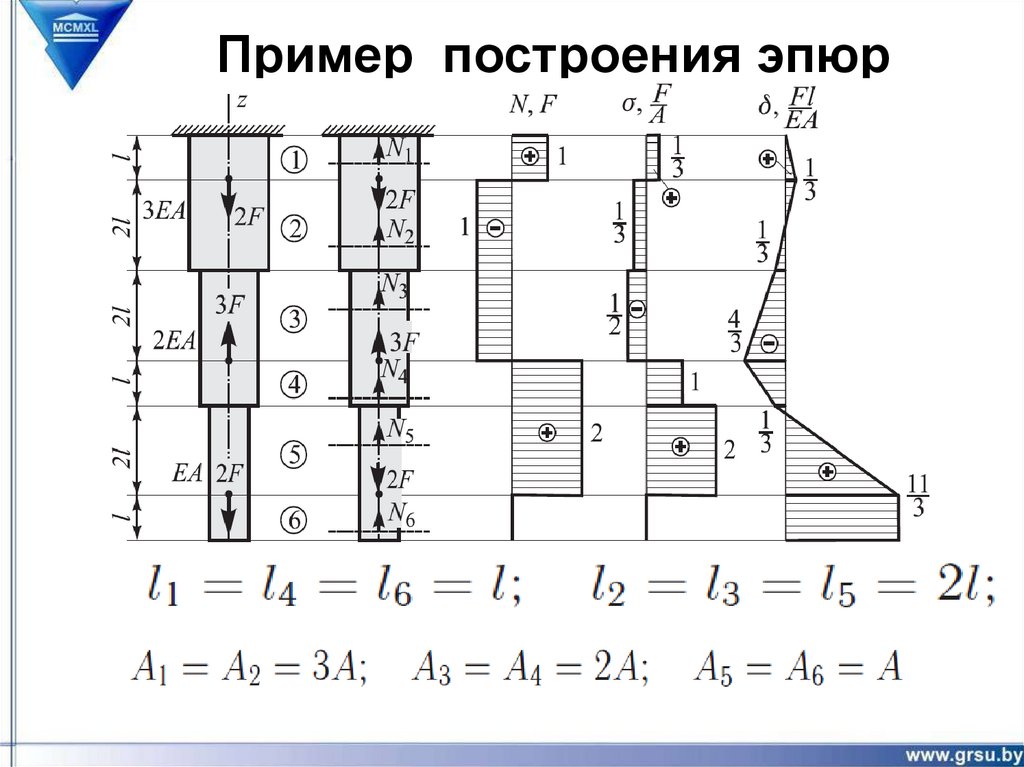
Пример построения эпюр

27.

Пример построения эпюр:
внутренние усилия и напряжения

28.

Пример построения эпюр:
удлинения и перемещения

29.

Пример построения эпюр:
удлинения и перемещения

30. 2.Примеры расчетов на растяжение- сжатие