Similar presentations:
Линейная алгебра. Матрица
1. Высшая математика
ВЫСШАЯ МАТЕМАТИКА2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
Линейная алгебра и аналитическаягеометрия:
1. Матрицы
2. Определители
3. Системы линейных уравнений
4. Аналитическая геометрия
Математический анализ:
1. Предел функции
2. Дифференциальное исчисление
3. Интегральное исчисление
4. Дифференциальные уравнения
5. Ряды
3.
Линейная алгебра4.
5.
Матрица – это прямоугольная таблица чисел.Аm*n – матрица размера m*n (m строк, n
столбцов)
bi j – элемент матрицы, стоящий на
пересечении iтой строки и jтого столбца.
6. Виды матриц:
ВИДЫ МАТРИЦ:Матрица-строка (вектор-строка) – матрица, состоящая из одной
строки.
Матрица-столбец – матрица, состоящая из одного столбца.
Квадратная матрица – матица, у которой число строк равно
числу столбцов (m=n)
Квадратная матрица 2-го порядка
Элементы квадратной матрицы, у которых i=j, называются
элементами главной диагонали.
с11, с22 – элементы главной диагонали
Диагональная матрица – матрица, у которой все элементы,
кроме элементов главной диагонали, равны нулю.
Единичная матрица – это диагональная матрица, у
которой элементы главной диагонали равны единице.
Нулевая матрица – матрица, у которой все элементы равны
нулю.
7.
8.
9.
10.
11. Операции над матрицами:
ОПЕРАЦИИ НАД МАТРИЦАМИ:Сложение – выполняется только для матриц
одинакового размера.
Умножение матрицы на число
Транспонирование матрицы –
осуществляется в результате замены строк
матрицы на соответствующие столбцы с
сохранением порядка элементов.
12. Свойства операций над матрицами:
СВОЙСТВАОПЕРАЦИЙ НАД МАТРИЦАМИ:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
переместительное свойство
сочетательное свойство
13.
Элементарные преобразованияПриведение матрицы к ступенчатому виду
1) можно менять строки (столбцы) местами;
2) можно умножать элементы строки на одно и то же число, отличное от
нуля;
3) можно складывать (вычитать) строки друг с другом.
Верхнетреугольная матрица, у которой под главной диагональю все
элементы равны нулю, называется приведенной к ступенчатому виду. При
этом элементы, стоящие на главной диагонали называются угловыми
элементами.
Ранг матрицы А – это максимальное число линейно независимых строк этой
матрицы.
Утверждение. В ступенчатой матрице строки, содержащие ненулевые
угловые элементы, линейно независимы. Отсюда следует, что ранг
ступенчатой матрицы равен числу ее угловых элементов.
14. Определители
ОПРЕДЕЛИТЕЛИОпределитель – это число, характеризующее
квадратную матрицу.
Обозначение:
Правила вычисления:
15.
16.
17.
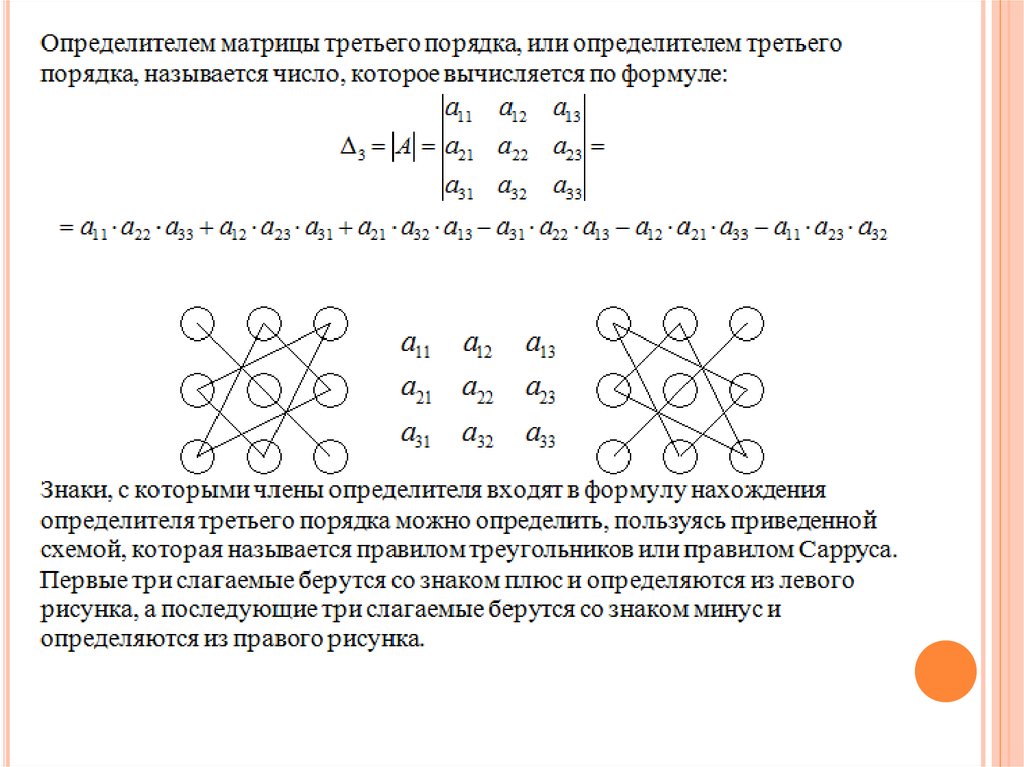
18. Правила вычисления определителя любого порядка
ПРАВИЛА ВЫЧИСЛЕНИЯОПРЕДЕЛИТЕЛЯ ЛЮБОГО ПОРЯДКА
Теорема Лапласа:
Определитель квадратной матрицы равен сумме
произведений элементов любой его строки
(столбца) на их алгебраические дополнения.
Вычислим определитель А разложением по i-той
строке:
Вычислим определитель разложением по j-тому
столбцу:
19.
20.
21.
22.
23. Обратная матрица
ОБРАТНАЯ МАТРИЦАМатрица А-1 называется обратной матрицей,
если
Алгоритм вычисления обратной матрицы А:
Вычисляем определить матрицы :
Вычисляем алгебраические дополнения всех
элементов матрицы А и составляем из них
присоединенную матрицу:
Транспонируем присоединенную матрицу:
Вычисляем обратную матрицу по формуле:
24. Решение систем линейных уравнений
РЕШЕНИЕ СИСТЕМЛИНЕЙНЫХ
УРАВНЕНИЙ
- переменные
- коэффициенты при переменных
- свободные коэффициенты
Решить систему уравнений – это значит найти значения переменных, при которых
каждое уравнение системы превращается в верное числовое равенство.
Если система имеет решение, то она называется совместной.
Если не имеет решений, то – несовместной.
Если совместная система имеет единственное решение, то она называется
определенной.
Если бесконечно много, то – неопределенной.
25.
26.
Метод Крамера27. 2 способ. Способ обратной матрицы
2 СПОСОБ. СПОСОБ ОБРАТНОЙМАТРИЦЫ
Систему линейных уравнений можно
представить в виде матричного уравнения
где
28. Аналитическая геометрия Векторы на плоскости и в пространстве
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯВЕКТОРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
Линейные операции над векторами
1. Суммой векторов a и b называется такой вектор с , начало которого
совпадает с началом вектора a , а конец – с концом вектора b (правило
треугольника).
2. Разностью векторов a и b называется такой вектор с , для которого
с b a.
3. Произведением вектора а на число (скаляр) называется вектор, длина
которого равна а , сонаправленный с вектором а , если >0, и
противоположено направленный, если <0.
4. Скалярным произведением вектора а на вектор b называется число,
равное произведению их длин (модулей) на косинус угла между ними:
(a , b ) a b cos .
Утверждение. Скалярное произведение ненулевых векторов a и b равно
нулю, если векторы перпендикулярны (ортогональны), и наоборот.
29. Операции над векторами, заданными в координатной форме
ОПЕРАЦИИ НАД ВЕКТОРАМИ, ЗАДАННЫМИ ВКООРДИНАТНОЙ ФОРМЕ
1. Два вектора равны, если их координаты равны.
2. При сложении векторов, заданных в координатной форме, их
координаты складываются.
3. При вычитании векторов, заданных в координатной форме, их
координаты вычитаются.
4. При умножении вектора на число надо все его координаты умножить
на это число.
5. Скалярное произведение векторов a и b , заданных в координатной
форме, определяется числом вида
(а , b ) x1 x2 y1 y2 z1 z 2 .
30. Уравнение прямой на плоскости
УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИУравнение прямой в общем виде
Где А, В, С – числа.
Уравнение прямой, проходящей через данную точку
Уравнение прямой, проходящей через две точки
Угол между двумя прямыми
Где k2 , k1 – угловые коэффициенты прямых
Формула берётся со знаком «+», если угол между прямыми
острый, т.к. тангенс острого угла – число положительное;
Формула берётся со знаком «-», если угол между прямыми тупой,
т.к. тангенс тупого угла – число отрицательное.
31.
Условия параллельности и перпендикулярностипрямых
а, в – прямые
k1, k2 – угловые коэффициенты прямых
а II в, если k2 = k1
а в, если k2 = -
Расстояние от точки до прямой
Точка пересечения двух прямых
32. Аналитическая геометрия в пространстве
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ВПРОСТРАНСТВЕ
Уравнение плоскости в пространстве,
проходящей через точку M0 (x0 ; y0 ; z0),
перпендикулярно вектору n=(A; B;C):
Общее уравнение плоскости:
Уравнение плоскости, проходящей через три
точки:
Уравнение плоскости в отрезках
A (a; 0; 0), B (0; b; 0), C (0; 0; c)
33. Уравнение прямой в пространстве
УРАВНЕНИЕ ПРЯМОЙ В ПРОСТРАНСТВЕo Параметрическое:
o Каноническое: S (m; n; p) – направляющий
вектор, M0 (x0 ; y0 ; z0)
o Уравнение прямой, проходящей через две
точки:
o Общее уравнение (пересечение двух
плоскостей)
34. Кривые второго порядка
КРИВЫЕ ВТОРОГО ПОРЯДКАОбщее уравнение второго порядка относительно х и у члены второй степени
( х 2 , ху, у 2 ), первой степени ( х, у ) и нулевой степени (свободный член), имеет
вид:
Ax 2 2Bxy Cy 2 2Dx 2Ey F 0 .
Хотя бы один из коэффициентов А, В, С должен быть отличен от нуля.
Данной уравнение является уравнением второй степени, а линии, уравнения
которых описываются этими уравнениями, называются кривыми второго
порядка на плоскости.
1. Окружность
Окружность – геометрическое место точек, равноудаленных от точки С (а, b)
на расстояние R.
Точка С называется центром окружности, R – радиус данной окружности.
Уравнение окружности с центром в точке С (а, b) и с радиусом R имеет вид:
( х а) 2 ( у b) 2 R 2 .
35.
2. ЭллипсЭллипс – это геометрическое место точек, сумма расстояний которых до двух
данных точек, называемых фокусами, есть величина постоянная.
Каноническое уравнение эллипса в выбранной системе координат имеет вид:
х2
у2
1,
а2 b2
где b 2 а 2 с 2 (с а) .
Вершины эллипса имеют следующие координаты:
А1 (а,0), А2 ( а,0), В1 (0, b), B2 (0, b) .
Отрезок A1 A2 2a - большая ось эллипса, отрезок B1 B2 2b - малая ось
эллипса, соответственно a и b - большая и малая полуоси эллипса.
Фокуса эллипса имеют следующие координаты:
F1 (c,0), F2 ( c,0) . Ось симметрии эллипса, на которой находятся фокусы,
называется фокальной осью.
Замечание 1. Если а b (c 0) , тогда каноническое уравнение эллипса примет
вид x 2 y 2 a 2 и определяет окружность, а значит, окружность можно
рассматривать как частный случай эллипса с равными полуосями.
Замечание 2. Число
с
называется эксцентриситетом эллипса.
а
Замечание 3. Если фокусы эллипса расположены на оси OY, то эллипс
«вытягивается» вдоль оси OY, тогда фокусы имеют координаты
F1 (0, с), F2 (0, с) , с 2 b 2 a 2 ;
c
.
b
36.
3. ГиперболаГиперболой называется геометрическое место точек на плоскости, разность
расстояний которых до двух данных точек, называемых фокусами, есть
величина постоянная.
Каноническое уравнение гиперболы в выбранной системе координат имеет
вид:
х2
у2
1,
а2
b2
где b 2 с 2 а 2 (с а) .
Вершины эллипса имеют следующие координаты:
А1 (а,0), А2 ( а,0) .
Отрезок A1 A2 2a - большая ось эллипса, отрезок B1 B2 2b - малая ось
эллипса, соответственно a и b - большая и малая полуоси эллипса.
Фокуса эллипса имеют следующие координаты:
F1 (c,0), F2 ( c,0) .
Асимптоты гиперболы – это прямые y
b
b
x и y x.
a
a
При а b гипербола называется равносторонней.
Замечание 1. Если мнимая ось гиперболы равна 2а и расположена на оси ОХ,
а действительная ось равна 2b и расположена на оси ОY, то уравнение такой
гиперболы имеет вид:
х2
у2
1.
а2
b2
Замечание 2. Эксцентриситетом гиперболы называется отношение фокусного
расстояния к действительной оси:
с
.
а
37.
4. ПараболаПарабола есть геометрическое место точек на плоскости, равноотстоящих от
данной точки, называемой фокусом, и данной прямой, называемой
директрисой.
Каноническое уравнений параболы в выбранной системе координат имеет
вид:
y 2 2 px .
Уравнение директрисы имеет вид:
х
p
.
2
p
2
Замечание 1. Уравнение y 2 2 px определяет параболу, область определения
Фокус имеет координаты F ( ,0) .
которой х<0.
Замечание 2. Парабола x 2 2 py имеет вершину в начале координат, фокус
p
p
F (0, ) , директрису y , ветви параболы направлены в положительную
2
2
сторону оси ОY, и ветви направлены в отрицательную сторону оси OY, если
уравнение параболы x 2 2 py .
38.
Математический анализ39. Функции
ФУНКЦИИФункцией (числовой функцией) называется
отображение числового множества D в числовое
множество Е.
Функцию записывают так: y=f(x).
Множество D называется областью определения
функции, а его элемент - аргументом. Множество
Е называется областью значений функции, а его
элемент - функцией (значением функции,
зависимой переменной).
Графиком функции y=f(x) называют множество
точек на плоскости, у которых абсциссы являются
допустимыми значениями аргумента , а ординаты
– соответствующими значениями функции.
40. Предел переменной величины
ПРЕДЕЛ ПЕРЕМЕННОЙ ВЕЛИЧИНЫПредел – одно из основных понятий математического
анализа. Понятие предела использовалось еще Ньютоном во
второй половине XVII века и математиками XVIII века, такими
как Эйлер и Лагранж, однако они понимали предел
интуитивно. Первые строгие
определения предела дали
Больцано в 1816 году и Коши в 1821 году.
Пусть переменная величина x в процессе своего изменения
неограниченно приближается к числу 5, принимая при этом
следующие значения: 4,9; 4,99;4,999;…или 5,1; 5,01; 5,001;… В
этих случаях модуль разности стремится к нулю: = 0,1; 0,01;
0,001;…
Число 5 в приведенном примере называют пределом
переменной величины x и пишут lim x = 5.
Определение. Постоянная величина a называется пределом
переменной x, если модуль разности при изменении x
становится и остается меньше любого как угодно малого
положительного числа e.
41. Предел функции в точке
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕОпределение. Число b называется
пределом функции в точке a, если для
всех значений x, достаточно близких к
a и отличных от a, значения функции
сколь угодно мало отличаются от
числа b.
42. Основные свойства пределов
ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛОВ1. Предел алгебраической суммы конченного числа
переменных величин равен алгебраической сумме пределов
слагаемых:
lim(x + y + … + t) = lim x + lim y + … + lim t.
2. Предел произведения конечного числа переменных
величин равен произведению их пределов:
lim(x·y…t) = lim x · lim y…lim t.
3. Постоянный множитель можно выносить за знак
предела:
lim(cx) = lim c · lim x = c lim x.
Например, lim(5x + 3) = lim 5x + lim 3 = 5 lim x + 3.
4. Предел отношения двух переменных величин равен
отношению пределов, если предел знаменателя не равен нулю
5. Предел целой положительной степени переменной
величины равен той же степени предела этой же переменной:
43. Замечательные пределы
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫВ математике
важную
роль играют два
специальных предела, которые ввиду их важности
названы «замечательными»:
sin x
lim
1 - первый замечательный предел
x 0
x
1 x
lim (1 ) e
x
x
- второй замечательный предел
Пример 1.
sin 5 x
5 sin 5 x
sin 5 x
sin y
lim
lim
5 lim
5 lim
5
x 0
x
0
x
0
y
0
x
5x
5x
y
1 x
x y, при х , у
lim
(
1
)
Пример 2. x
x
1
1
1
1
lim (1 ) y lim
y
y
1
1
y
e
(1 ) y
lim (1 ) y
y
y
y
44. Раскрытие неопределенностей
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙИногда правила предельного перехода непосредственно
неприменимы.
f ( x)
lim
Например, при отыскании
( x)
когда f(х)→0, φ(х) →0 или f(х)→∞, φ(х) → ∞.
В этом случае надо проделать над дробью некоторые
преобразования. Чтобы обозначить такие ситуации,
говорят, что имеем дело с неопределенностью 0
0
или
Пример 3.
x2 1 0
( x 1)( x 1)
x 1
2
lim 3
lim
lim 2
2
x 1 x 1
x
1
x
1
( x 1)( x x 1)
x x 1 3
0
45.
Пример 4.x 4 2 0
( x 4 2)( x 4 2)
x 4 4
lim
lim
lim
x 0
x 0
x
x( x 4 2)
x( x 4 2)
0 x 0
x 4 2 0
( x 4 2)( x 4 2)
x 4 4
lim
lim
lim
x 0
x
0
x 0
x
x( x 4 2)
x( x 4 2)
0
Пример 5.
x2
lim
x x 3
1
1
3
1
0
x
x
lim
0
x
3
1
3
1
x3
46. Дифференциальное исчисление
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕПроизводной функции y=f (x) называется
скорость изменения функции в данный момент
времени (мгновенная скорость)
Таблица производных
47. Правила дифференцирования
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ48.
Пример. Вычислите производную функцииy x (1 x) ln( 1 x)
1 x
y 1 (1 x) ln( 1 x) (1 x)(ln( 1 x)) 1 ln( 1 x)
( 1) ln( 1 x)
1 x
49. Применение производной к построению графика функции. Возрастание и убывание функции. Экстремумы.
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ПОСТРОЕНИЮГРАФИКА ФУНКЦИИ.
ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ. ЭКСТРЕМУМЫ.
Функция y=f(x) возрастает на некотором интервале [a;b],
если производная функции на этом интервале больше
нуля f’(x)>0.
Если f’(x)<0, то функция убывает.
Точка x0 называется точкой экстремума функции, если:
1) f’(x) в этой точке равна нулю или не существует
2) функция в этой точке должна существовать
3) f’(x) при переходе через точку меняет свой знак:
с «+» на «–» точка максимума max
с «–» на «+» точка минимума min
50. Промежутки выпуклости функции. Точки перегиба
ПРОМЕЖУТКИ ВЫПУКЛОСТИ ФУНКЦИИ. ТОЧКИПЕРЕГИБА
Функция y=f(x) на промежутке [a; b]
Если вторая производная f”(x)>0, то функция на
промежутке [a; b] является выпуклой вниз.
Если f”(x)<0, то функция выпукла вверх.
Точка x0 является точкой перегиба функции, если:
1)
f”(x)=0 или f”(x) не существует;
2)
f(x) в этой точке существует;
3)
f”(x) при переходе через эту точку меняет свой
знак.
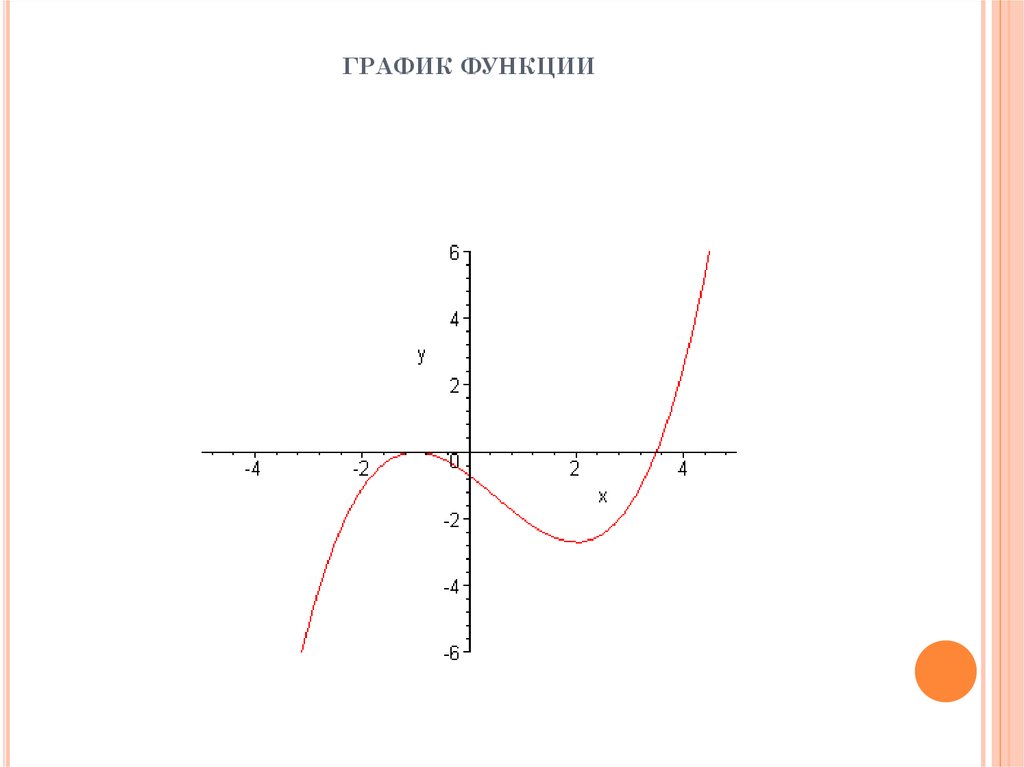
51. Пример. Исследовать функцию f(x) и построить ее график
f ( x)1
(2 x 3 3x 2 12 x 7)
10
1) Область определения R.
2) Функция непериодическая.
3) Четность/нечетность - функция общего вида.
f ( x)
1
( 2 x 3 3x 2 12 x 7) f ( x) f ( x)
10
52. 4) Точки пересечения с осью ОХ: y = 0
4) Точки пересечения с осью ОХ:y=0
2 x 3 3 x 2 12 x 7 0
2 x3 2 x 2 5x 2 5x 7 x 7 0
2 x 2 ( x 1) 5 x( x 1) 7( x 1) 0
x1 1;
2 x 2 5 x 7 0 D 25 56 81
x2 , 3
5 9 7
; 1;
4
2
7
A( 1; 0), B ; 0
2
53. c осью OY: х = 0 ; у = -7\10
y 0 при7
x ;
2
y 0 при
7
x ( ; 1) 1;
2
2
( x 1) 2 ( x 3,5)
10
lim f ( x )
f ( x)
x
lim f ( x )
x
54. 5) Экстремумы, возрастание, убывание
12
6 x 6 x 12 0
y
10
x2 x 2 0
D 1 8 9
x1, 2
1 3
1; 2
2
55.
x maxx min
1
1; y max
( 2 3 12 7) 0
10
1
27
2; y min
(16 12 24 7)
2,7
10
10
x
( ; 1]
y’
+
-
+
y
возрастание
убывание
возрастание
[ 1; 2]
[ 2; )
56. 6) Выпуклость/вогнутость
6y (2 x 1) 0
10
1
x точка перегиба
2
x ( ; 0,5) y 0 выпуклость
x ( 0,5; ) y 0 вогнутость
57. ГРАФИК ФУНКЦИИ
58. Первообразная и неопределенный интеграл
ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙИНТЕГРАЛ
Функция F x называется
первообразной функции f x , определенной на
некотором промежутке, если F x f x для
каждого x из этого промежутка.
Например, функция cos x является
Определение.
первообразной функции sin x , так как
cos x sin x .
59.
Очевидно, если F x - первообразнаяфункции f x , то F x C , где C некоторая постоянная, также является
первообразной функции f x .
Если F x есть какая-либо первообразная
функции f x , то всякая функция вида
Ф x F x C также является
первообразной функции f x и всякая
первообразная представима в таком виде.
60.
Определение. Совокупность всехпервообразных
функции
f x ,
определенных
на
некотором
промежутке,
называется
неопределенным
интегралом
от
функции f x на этом промежутке и
обозначается f x dx .
61.
Производная неопределенногоинтеграла равна подынтегральной
функции, а его дифференциалподынтегральному выражению.
Действительно:
1.( f ( x)dx) ( F ( x) C ) F ( x) f ( x);
2.d f ( x)dx ( f ( x)dx) dx f ( x)dx.
62. Таблица неопределенных интегралов
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХИНТЕГРАЛОВ
1. dx x C .
a 1
x
2. x a dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx
C .
ln a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
63. Таблица неопределенных интегралов
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХИНТЕГРАЛОВ
11.
dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
a x
2
arcsin
2
x
C ..
a
x2 a
ln x x 2 a C .
17. shxdx chx C .
18. chxdx shx C .
dx
1
x a
ln
C
2
2
2a x a
x a
19.
dx
1
a x
ln
a 2 x 2 2a a x C .
20.
14.
15.
dx
dx
16.
dx
ch 2 x thx C .
dx
cthx C .
2
sh x
64. Метод замены переменной
МЕТОД ЗАМЕНЫ ПЕРЕМЕННОЙПусть
требуется найти
f x dx , причем
непосредственно подобрать первообразную для
f x мы не можем, но нам известно, что она
существует. Часто удается найти первообразную,
введя новую переменную, по формуле
f x dx f t t dt , где x t , а t - новая
переменная
65. Примеры
ПРИМЕРЫПример . Вычислить cos 5xdx .
Решение. В таблице интегралов найдем
cos xdx sin x C .
Преобразуем данный интеграл к табличному,
воспользовавшись тем, что d ax adx .
Тогда:
d 5 x 1
= cos 5 xd 5 x =
cos 5xdx cos 5 x
5
5
1
= sin 5 x C .
5
66. Интегрирование по частям
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМЭтот метод основан на формуле udv uv vdu .
Методом интегрирования по частям берут такие интегралы:
а) x n sin xdx , где n 1,2...k ;
б) x n e x dx , где n 1,2...k ;
в) x n arctgxdx , где n 0, 1, 2,... k . ;
г) x n ln xdx , где n 0, 1, 2,... k .
При вычислении интегралов а) и б) вводят
n 1
обозначения: x n u , тогда du nx dx , а, например
sin xdx dv ,тогда v cos x .
При вычислении интегралов в), г) обозначают за u функцию
arctgx , ln x , а за dv берут x n dx .
67. Примеры
ПРИМЕРЫПример. Вычислить x cos xdx .
Решение.
u x, du dx
=
x cos xdx
dv cos xdx, v sin x
x sin x sin xdx x sin x cos x C .
68. Определенный интеграл
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛС геометрической точки зрения
b
при f x 0 f x dx равен
a
площади криволинейной
трапеции
69. Свойства определенного интеграла
СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛА
a
1. f x dx 0 ;
a
b
2. dx b a ;
a
b
a
3. f x dx f x dx ;
a
b
b
4. f1 x f 2 x dx f1 x dx f 2 x dx ;
a
b
b
a
a
70. Свойства определенного интеграла
СВОЙСТВА ОПРЕДЕЛЕННОГОИНТЕГРАЛА
b
b
a
b
a
5. Kf x dx K f x dx ;
c
b
a
c
6. f x dx f x dx f x dx ;
a
b
7. f x dx 0 , если f x 0 .
a
71. Вычисление определенного интеграла
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГОИНТЕГРАЛА
Теорема.
Пусть F x - первообразная функции f x .
b
Тогда f x dx F b F a .
a
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.
72. Пример
ПРИМЕР3
Вычислить
x
3
e 3 dx
e
0
1
3 x
e 3 dx
0
0
x
3 dx
.
1
x
3e 3
3
0
3 e
1
1
1 3
0
3 e 3 e 3
1 e
1
1 3 1 3
e
e
73. Вычисление интеграла
ВЫЧИСЛЕНИЕ ИНТЕГРАЛАТеорема (Замена переменной в
определенном интеграле).
Пусть f x непрерывна на a, b , а
функция x t непрерывна вместе
со своей производной t на
отрезке , , причем a ,
b . Тогда
b
a
f x dx f t t dt .
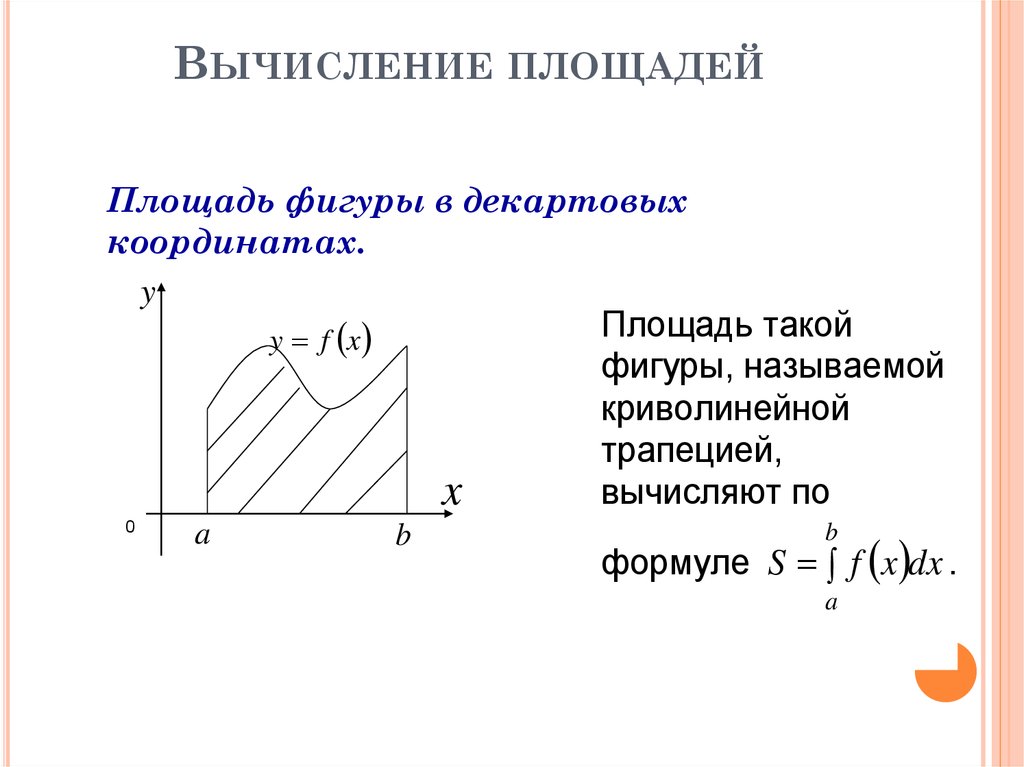
74. Вычисление площадей
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙПлощадь фигуры в декартовых
координатах.
y
y f x
x
0
a
b
Площадь такой
фигуры, называемой
криволинейной
трапецией,
вычисляют по
b
формуле S f x dx .
a
75. Вычисление площадей
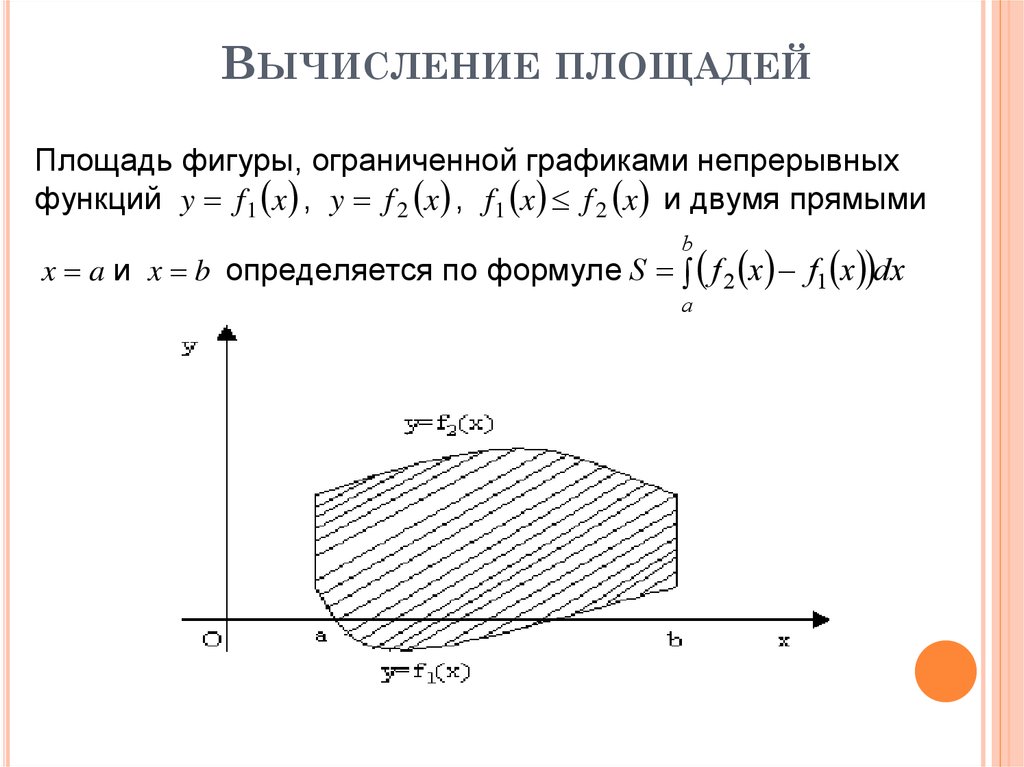
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙПлощадь фигуры, ограниченной графиками непрерывных
функций y f 1 x , y f 2 x , f1 x f 2 x и двумя прямыми
b
x a и x b определяется по формуле S f 2 x f1 x dx
a



















































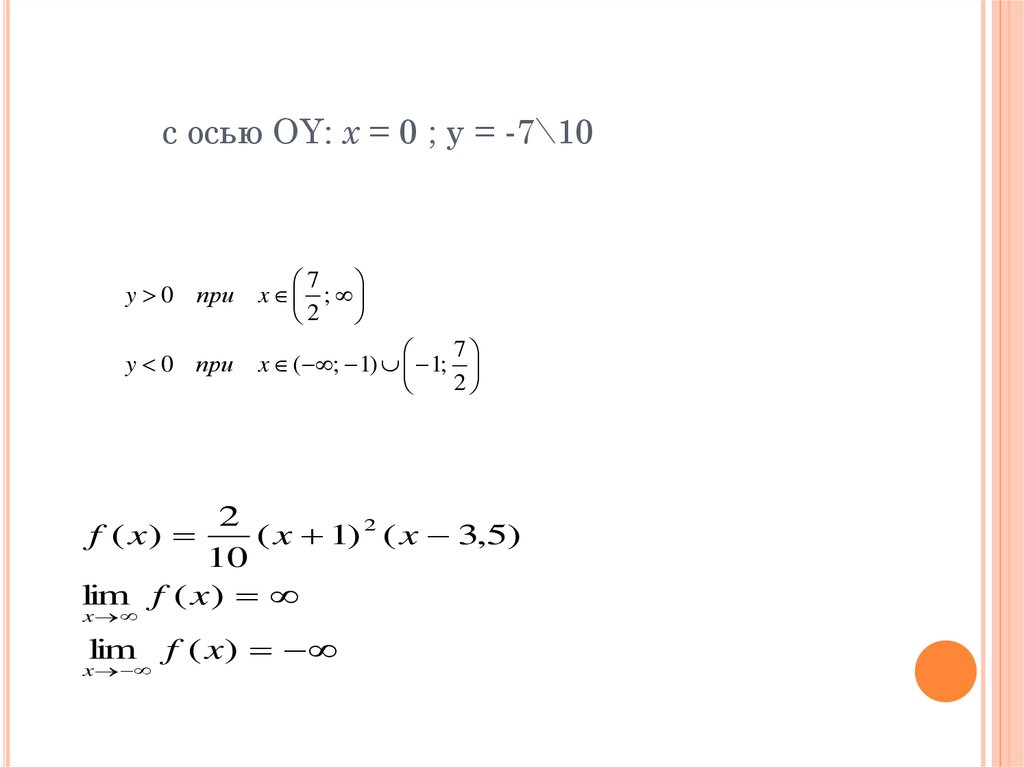



















 mathematics
mathematics








