Similar presentations:
Неопределенный и определенный интеграл
1. Неопределенный и определенный интеграл
Разработанопреподавателем
математики
Кольтиновой С.В.
2. Цели и задачи урока:
1. Дать понятие неопределенногоинтеграла
2. Изучить основные свойства
неопределенного интеграла
3. Научить находить неопределенный
интеграл
4. Дать понятие определенного интеграла
5. Формула Ньютона-Лейбница
6. Изучить основные свойства
определенного интеграла
7. Геометрический смысл определённого
интеграла
3.
Определение:Функция
F(x)
называется
первообразной для функции f(x) на
некотором промежутке, если для
всех x из этого промежутка
F ( x) f ( x)
4. Основное свойство первообразных
• Если F(x) – первообразная функции f(x),то и функция F(x)+C, где C –
произвольная постоянная, также
является первообразной функции f(x).
Геометрическая интерпретация
Графики всех первообразных
y
данной функции f(x) получаются
из графика какой-либо одной
первообразной параллельными
переносами вдоль оси y.
x
5. Неопределенный интеграл
• Совокупность всех первообразных даннойфункции f(x) называется ее неопределенным
интегралом и обозначается
f ( x)dx
f
(
x
)
dx
F
(
x
)
C
где C – произвольная постоянная
• Символ - знак неопределенного интеграла, означает
операцию интегрирования заданной функции, которая
называется подынтегральной функцией
- подынтегральное выражение
x - переменная интегрирования
6. Немного истории
• «Интеграл» - латинское словоintegro «восстанавливать» или
integer – «целый».
Одно из основных понятий
математического анализа,
возникшее в связи потребностью
измерять площади, объемы,
отыскивать функции по их
производным.
Впервые это слово употребил в
печати шведский ученый Якоб
Бернулли (1690 г.).
7.
• Операции интегрирования идифференцирования взаимно обратны и
последовательное выполнение над
некоторой функцией интегрирования и
дифференцирования восстанавливает
исходную функцию.
8.
• Символ ⨜ былвведен Лейбницем
(1675г.).
• Этот знак является
изменением
• латинской буквы S
– первой буквы
слова summa.
9. В развитии интегрального исчисления приняли участие русские математики:
В.Я. Буняковский(1804 – 1889)
П.Л. Чебышев
(1821 – 1894)
М.В. Остроградский
(1801 – 1862)
10. Свойства неопределенного интеграла
cf(
x
)
dx
c
f
(
x
)
dx
,
c
const
(
f
(
x
)
g
(
x
))
dx
f
(
x
)
dx
g
(
x
)
dx
1
f (ax b)dx a F (ax b) C , a 0
11. Таблица неопределенных интегралов
1. dx x C .x a 1
2. x dx
C, (a 1) .
a 1
dx
3. ln x C .
x
ax
x
4. a dx
C .
ln a
a
5. e x dx e x C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
ctgx C .
2
sin x
dx
9. 2 tgx C .
cos x
dx
arctgx C .
10.
2
1 x
8.
12. Пример
Вычислить x 2 3x 3 x 1 dx .3
2
3
2
x 3 x x 1 dx x dx 3 x dx xdx dx .
3
x
3
3
4
x
4
2
x
2
x C
13. Пример
14. Пример
Вычислим1
6
(2 3x) dx 3 6 (2 3x) C.
5
15. Определенный интеграл.
Используя геометрические методы, мы можем лишь найтиприблизительное значение площади нашей фигуры.
1. Давайте разобьем наш отрезок на n равных частей, отметим внутри
отрезка [а;b] точки a x0 x1 x2 ... xn b и
через
каждую
точку
проведем прямую параллельную оси ординат. Тогда наша фигура
разобьется на n столбиков. Площадь трапеции будет равна сумме
площадей столбиков.
16.
y f (x)y
x1 x2
0
xi
x n
a = x0c x1c x2 … xi 1c xi xn c1 xn = b
1
2
i
В результате получим промежутки:
n
x1, x2 ,..., xi ,..., xn
2. На каждом xi выберем произвольную точку c
3. Найдем
n
i
f (c1 ) x1 f (c2 ) x2 ... f (cn ) xn f (ci ) xi
i 1
формула интегральной суммы
x
17.
Опр: Если при любом разбиении отрезка[a, b] на части и при любом выборе
точек ci на каждой части
интегральная сумма стремится к
одному и тому же пределу, то его
называют определенным интегралом
и обозначают:
b
f
(
x
)
dx
lim
f
(
c
)
x
i
i
a
xi 0
i 1
18. Определенный интеграл.
Такой предел на самом деле существует, и для него было введеноспециальное обозначение и название – определенный интеграл. Важно!
Определенный интеграл существует только в случае непрерывной или
кусочно-непрерывной функции.
Определенный интеграл от непрерывной функции y=f(x) на
отрезке [a;b] обозначается как
Читается как определенный интеграл от a до бэ эф от икс дэ икс.
Числа a и b – пределы интегрирования. (Нижний и верхний
пределы).
19.
Теорема: Если функция f (x ) непрерывна наотрезке [a, b], а функция F (x )
является первообразной для f (x )
на этом отрезке, то справедлива
формула:
b
f ( x)dx F ( x) F (b) F (a)
b
a
a
формула Ньютона-Лейбница
20.
21. Основные свойства определенного интеграла
af
(
x
)
dx
0
a
b
1.
11.
.1
dx
b
a
a
b
a
a
b
f
(
x
)
dx
f
(
x
)
dx
22. Основные свойства определенного интеграла
bc
b
a
a
c
f
(
x
)
dx
f
(
x
)
dx
f
(
x
)
dx
b
b
a
a
cf
(
x
)
dx
c
f
(
x
)
dx
,
c
const
b
b
b
a
a
a
(
f
(
x
)
g
(
x
))
dx
f
(
x
)
dx
g
(
x
)
dx
23. Определенный интеграл.
Пример. Вычислить определенный интегралРешение. Первообразной для
,
служит
Воспользуемся формулой Ньютона – Лейбница
Ответ: 31/5
24.
bf ( x)dx F ( x) F (b) F (a)
b
a
a
Пример:
4
4
4
4 4
2 4
4 4
x
x
x
2 4
1 ( x 2 x)dx 1 x dx 1 2xdx 4 1 2 2 1 4 1 x 1
3
3
256 1
255
4 4 14
2
2
) (16 1)
15 78,75
( ) (4 1 ) (
4
4
4
4 4
25. Геометрический смысл определенного интеграла
• Площадь криволинейной трапеции,ограниченной графиком непрерывной
положительной на промежутке [a;b]
функции f(x), осью x и прямыми x=a и x=b:
b
S f ( x)dx
a
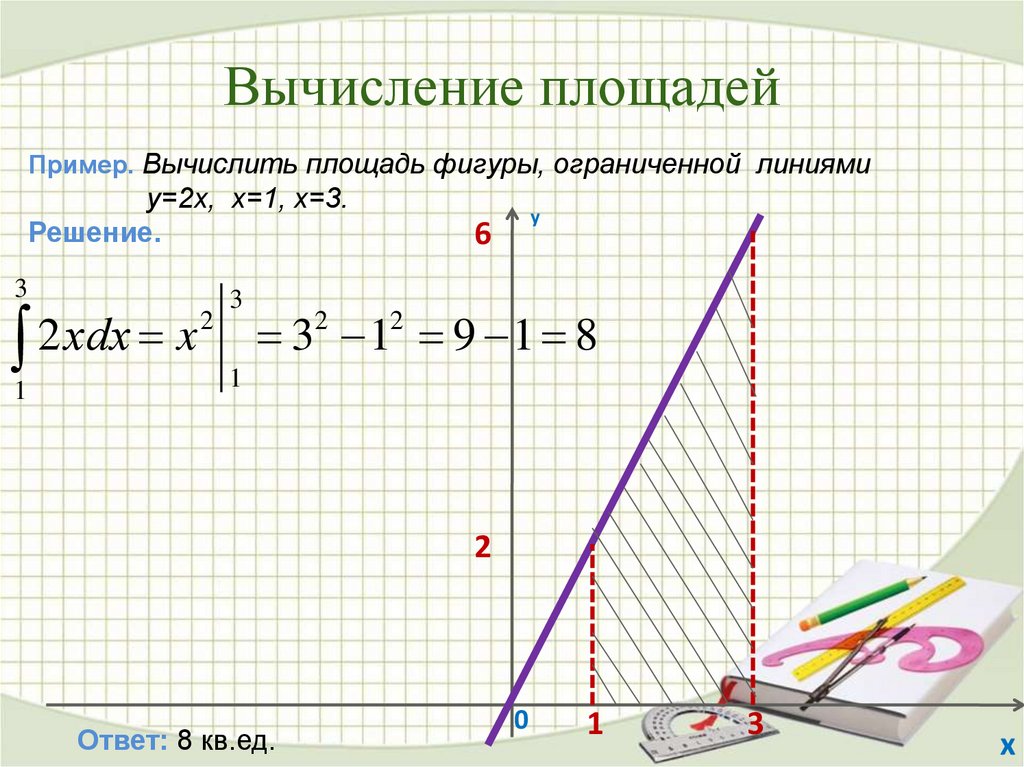
26. Вычисление площадей
Пример. Вычислить площадь фигуры, ограниченной линиямиy=2x, x=1, x=3.
Решение.
3
2 хdx x
1
2
3
у
6
3 1 9 1 8
2
2
1
2
Ответ: 8 кв.ед.
0
1
3
х
27. Пример. Вычислить площадь фигуры, ограниченной графиком функции y=cos(x) на отрезке [0;π/2].
Решение. Давайте построим график косинуса на нашем отрезкеПлощадь полученной фигуры вычисляется с помощью определенного
интеграла, гда a=0, b= π/2, f(x)=cos(x)
Ответ: 1
28.
00
sin хdx cos x cos ( cos 0) 1 1 2
y
1
-π
2
0
-1
Ответ: 2 кв.ед
2
x
π
29.
Задачи для самостоятельного решения.Найдите неопределенный интеграл
1.
5х dx
2. (4 x5)dx
3.
8.
(6 3sin x)dx
4 8x 5)dx. 9.
1 cos x dx
7dx
х
4. (3x
7.
x 4 dx
x3
x e x 1)dx
(
3
5.
(2 x) dx
6.
x
30. Определенный интеграл.
1.Вычислить определенный интеграл2. Вычислить площадь фигуры, ограниченной функцией y=sin(x)
на отрезке [2 π;3π].
3. Вычислить площадь фигуры, ограниченной линиями

























![Пример. Вычислить площадь фигуры, ограниченной графиком функции y=cos(x) на отрезке [0;π/2]. Пример. Вычислить площадь фигуры, ограниченной графиком функции y=cos(x) на отрезке [0;π/2].](https://cf4.ppt-online.org/files4/slide/6/6gfGU3hOFodcv5JRm9XLTYusV0tKIzNPlAix8y/slide-26.jpg)



 mathematics
mathematics








