2.26M

Category: $mathematics$ mathematics

Графики квадратичных функций

1.

С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек.

Сейчас появятся шесть графиков квадратичных функций и
значения старшего коэффициента (а) и дискриминанта
квадратного трёхчлена (D). Выберите график,
соответствующий указанным значениям, для этого
сделайте клик на прямоугольнике с цифрой или на слове
«нет», если такие значения отсутствуют. При правильном
ответе открывается часть картинки, при неправильном возникает слово «ошибка», чтобы вернуться к заданиям
нужно нажать на управляющую кнопку «назад». После
верного выполнения всех заданий картинка откроется
полностью.

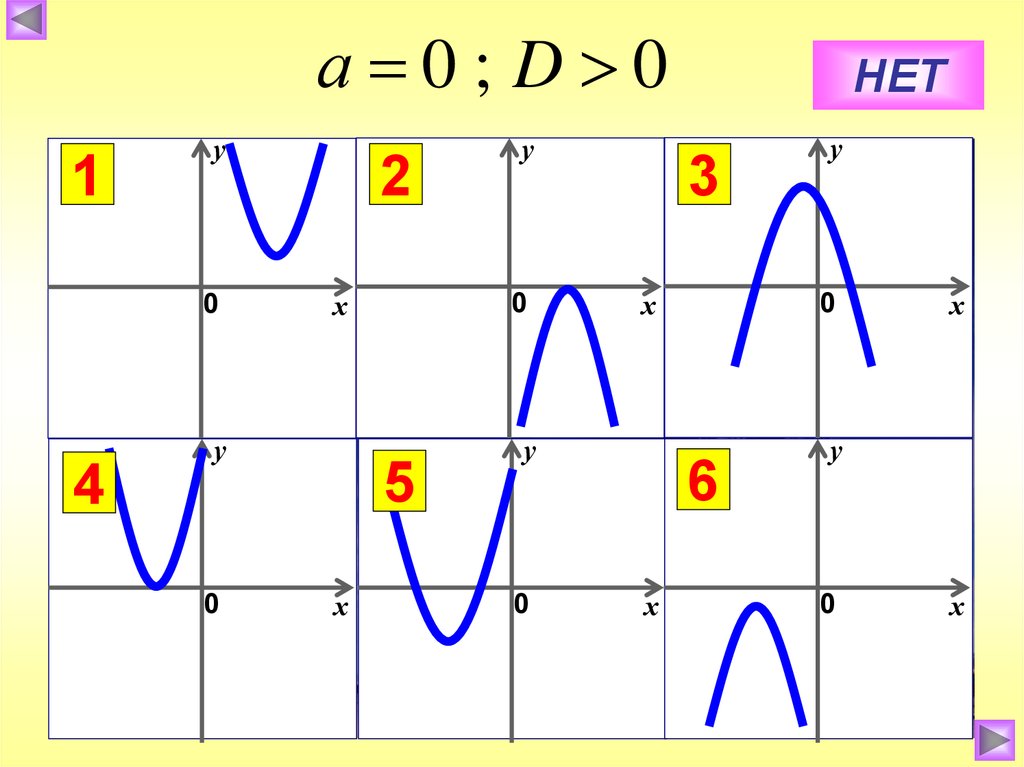
3.

а 0; D 0
1
у
0
4
2
х
у
0
0
5
х
у
3
х
у
0
НЕТ
0
6
х
у
х
у
0
х

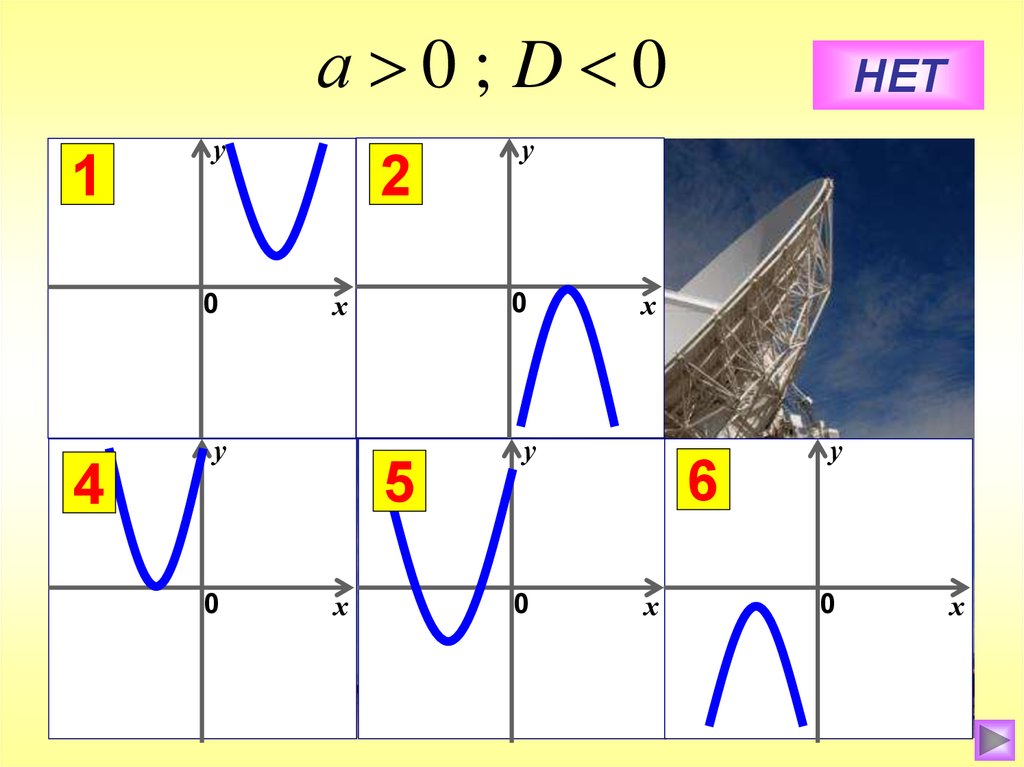
4.

а 0; D 0
1
у
0
4
2
х
у
0
0
5
х
у
3
х
у
0
НЕТ
0
6
х
у
х
у
0
х

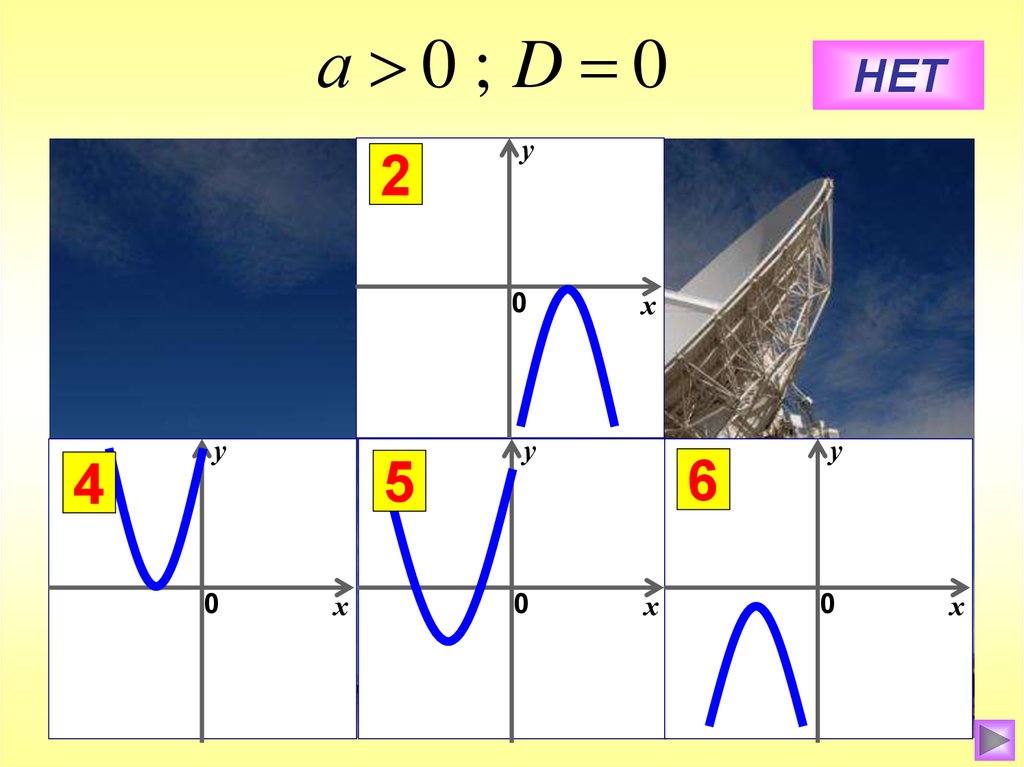
5.

6.

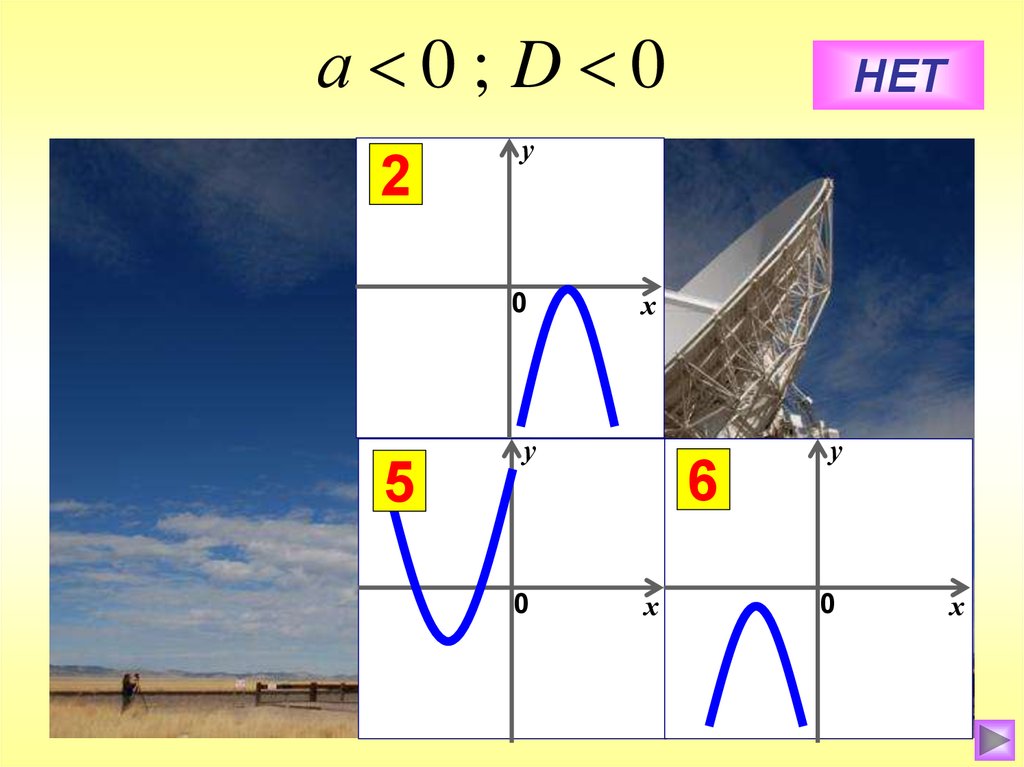
а 0; D 0
1
у
0
4
2
х
у
0
х
у
0
5
НЕТ
х
у
0
6
х
у
0
х

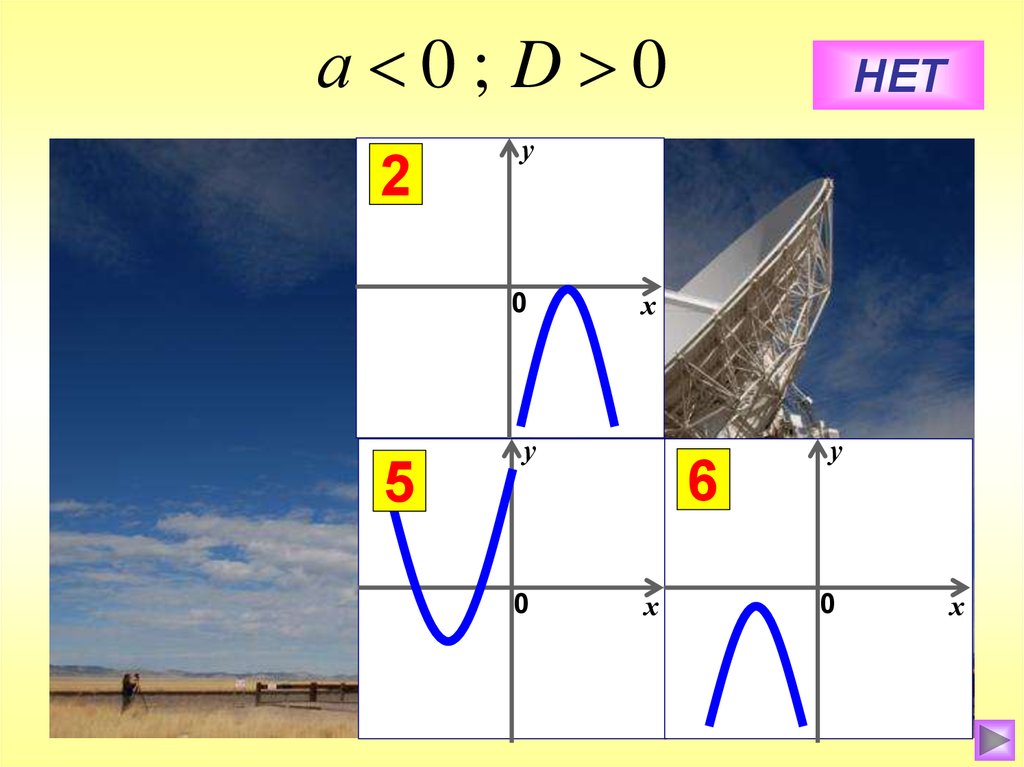
7.

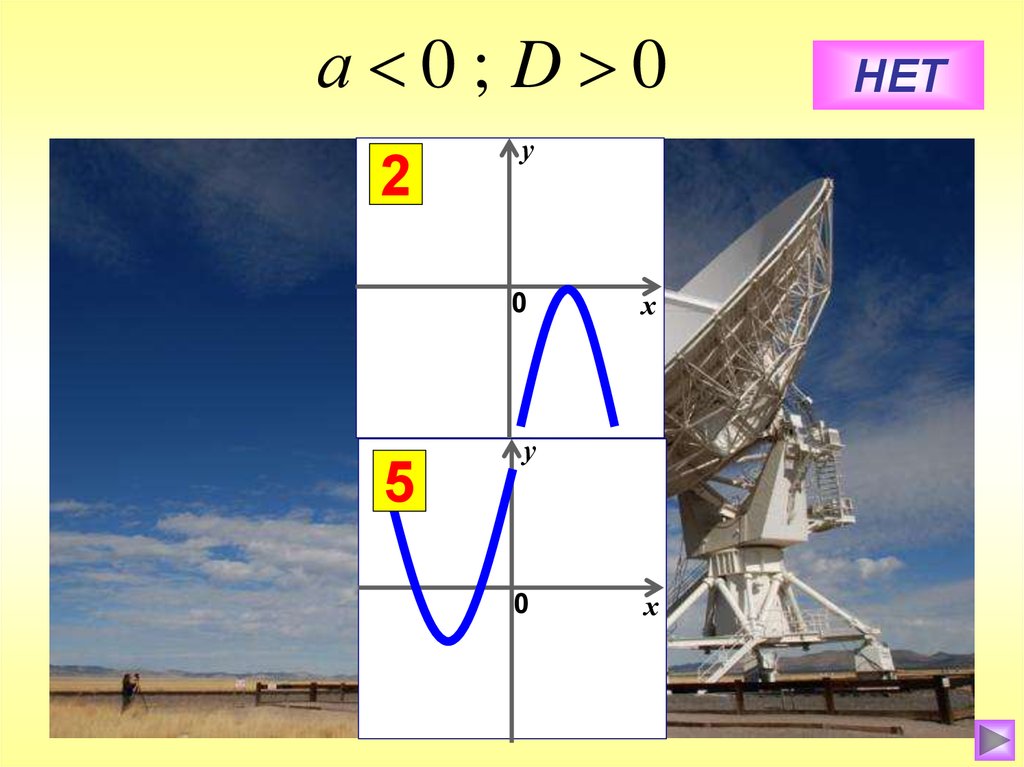
а 0; D 0
2
у
0
4
у
0
5
х
НЕТ
х
у
0
6
х
у
0
х

8.

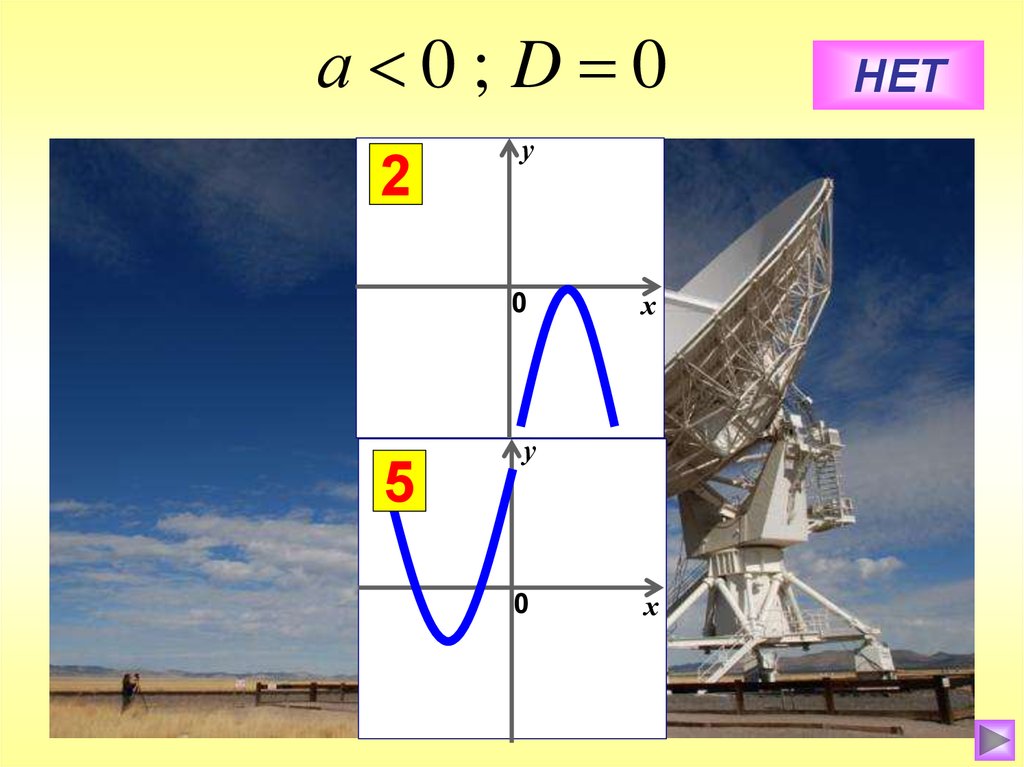
а 0; D 0
2
у
0
5
НЕТ
х
у
0
6
х
у
0
х

9.

а 0; D 0
2
у
0
5
НЕТ
х
у
0
6
х
у
0
х

10.

а 0; D 0
2
у
0
5
х
у
0
х
НЕТ

11.

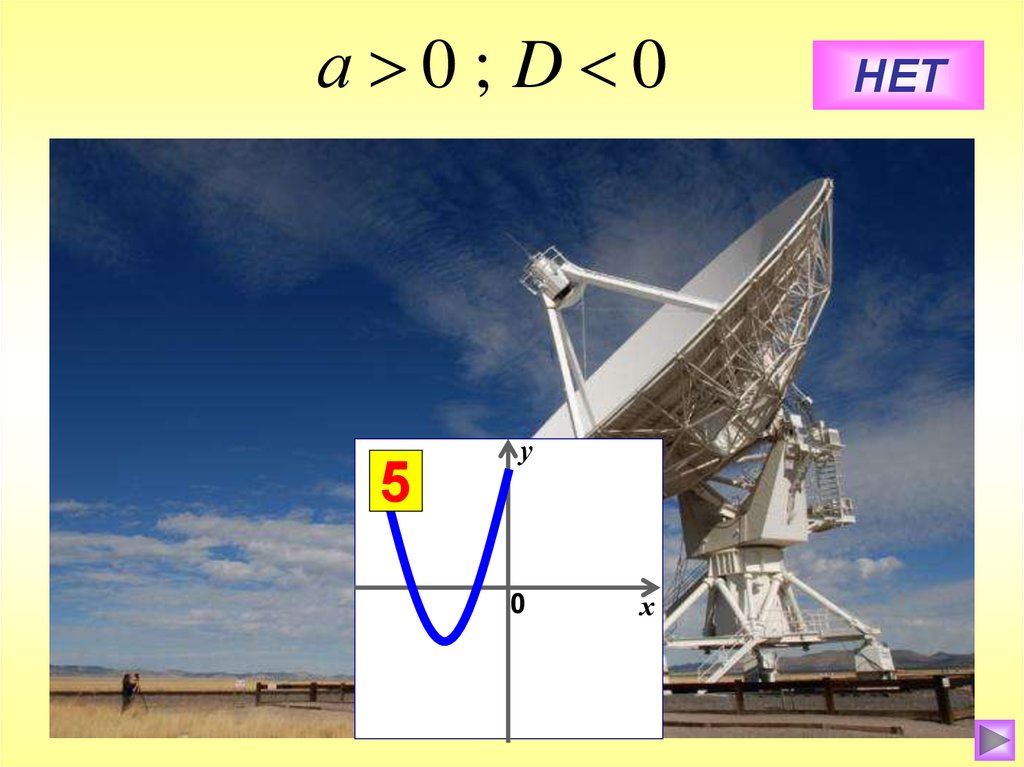
а 0; D 0
2
у
0
5
х
у
0
х
НЕТ

12.

а 0; D 0
5
у
0
х
НЕТ

13.

а 0; D 0
5
у
0
х
НЕТ

14.

15.

Найдите корни квадратного трехчлена:
Ι вариант.
а) х2+х-12
б) х2+6х+9.
ΙΙ вариант.
а) 2х2-7х+5;
б) 4х2-4х+1.

16.

Найдите корни квадратного трехчлена:
Ι вариант.
а) х2+х-12;
б) х2+6х+9;
ΙΙ вариант.
x1=-4; x2=3
x1,2=-3
а) 2х2-7х+5;
б) 4х2-4х+1;
x1=1; x2=2,5
x1,2=0,5

17.

у=ах²+bх+с
а>0
D=0
а>0
D<0
у
а<0
D>0
а>0
D>0
х
0
а<0
D=0
а<0
D<0

18.

По графику квадратичной функции укажите все
значения аргумента, при которых у ≥ 0. Сделайте клик
на прямоугольнике с цифрой.
у
1 -2 < х < 2
4
3
2
1
ВЕРНО!
2 х≤ -2 , х ≥2
3 -2 ≤ х ≤ 2
4 х<-2 , х >2
-3 -2 -1
01 2 3 4 х
-2
-3
-4

19.

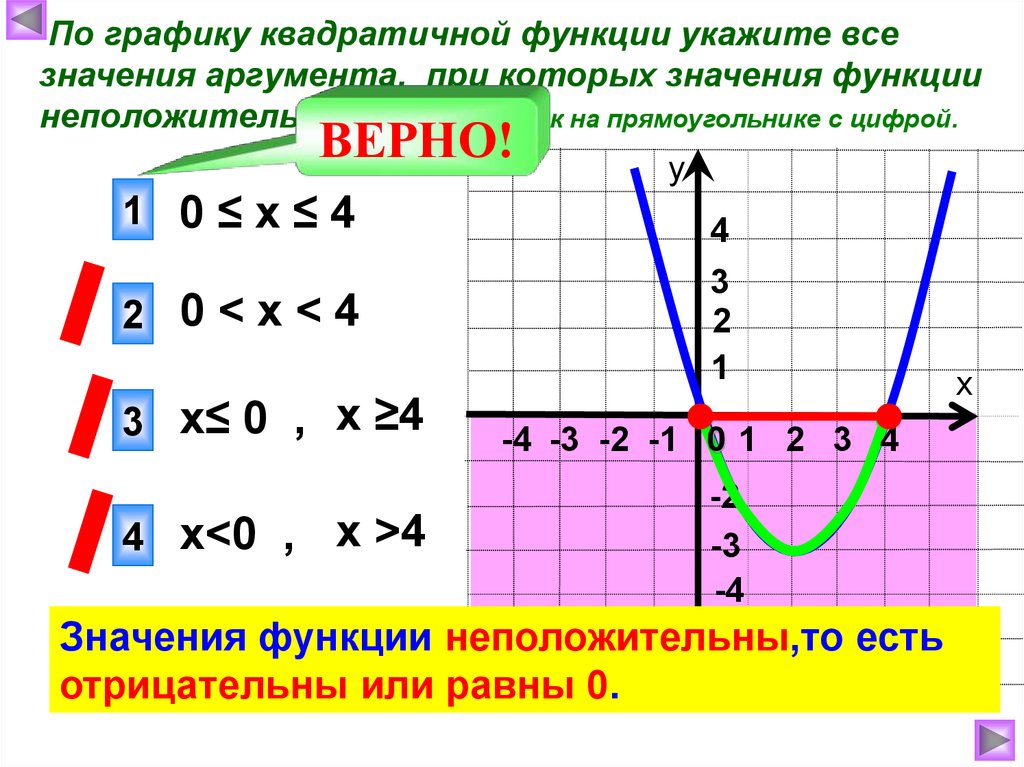
По графику квадратичной функции укажите все
значения аргумента, при которых значения функции
неположительны. Сделайте клик на прямоугольнике с цифрой.
ВЕРНО!
1 0≤х≤4
2 0<х<4
3 х≤ 0 , х ≥4
4 х<0 ,
х >4
у
4
3
2
1
-4 -3 -2 -1 0 1 2 3 4
-2
-3
-4
Значения функции неположительны,то есть
отрицательны или равны 0.
х

20.

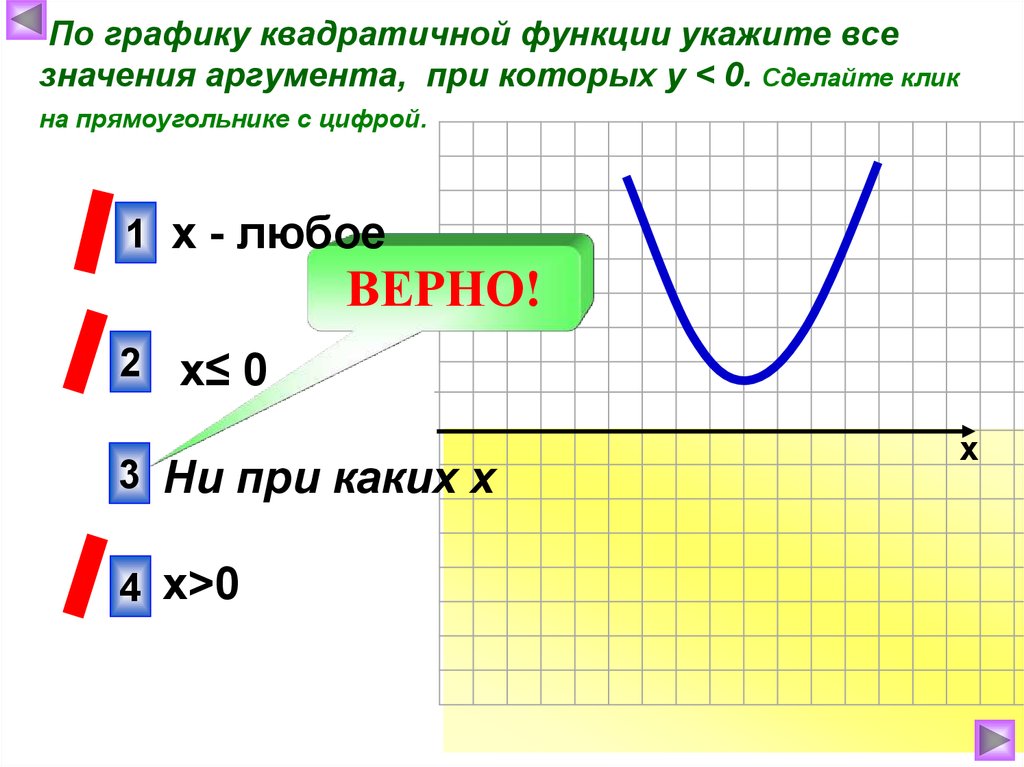
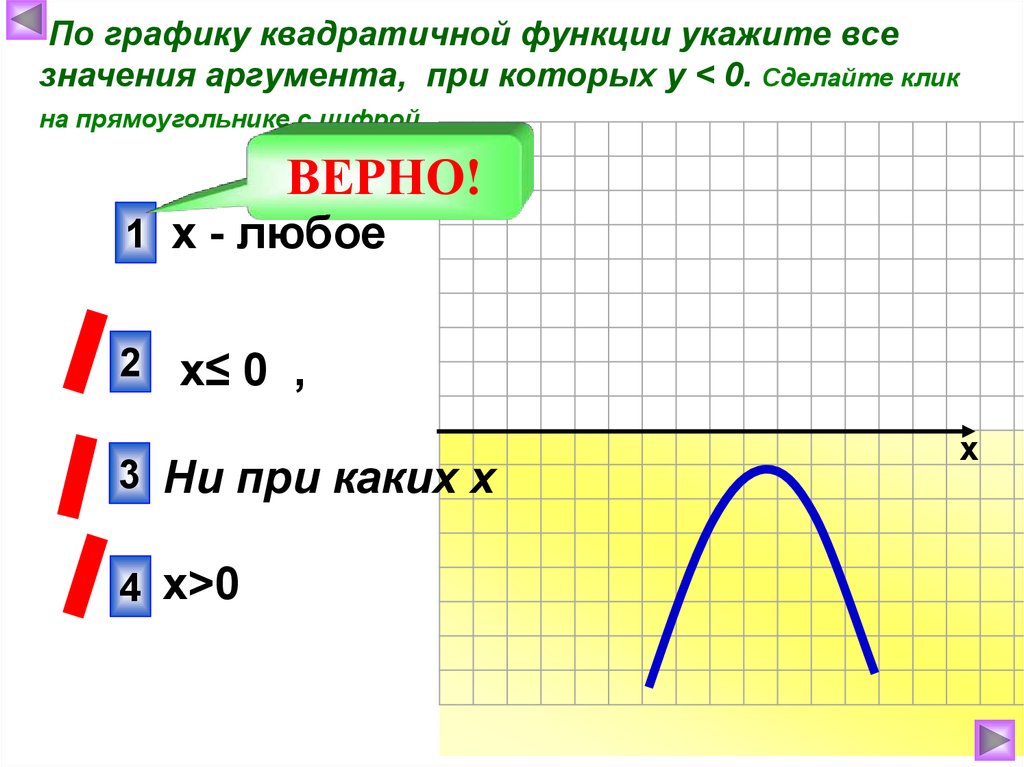
По графику квадратичной функции укажите все
значения аргумента, при которых у < 0. Сделайте клик
на прямоугольнике с цифрой.
1 х - любое
ВЕРНО!
2 х≤ 0 ,
3 Ни при каких х
4 х>0
х

21.

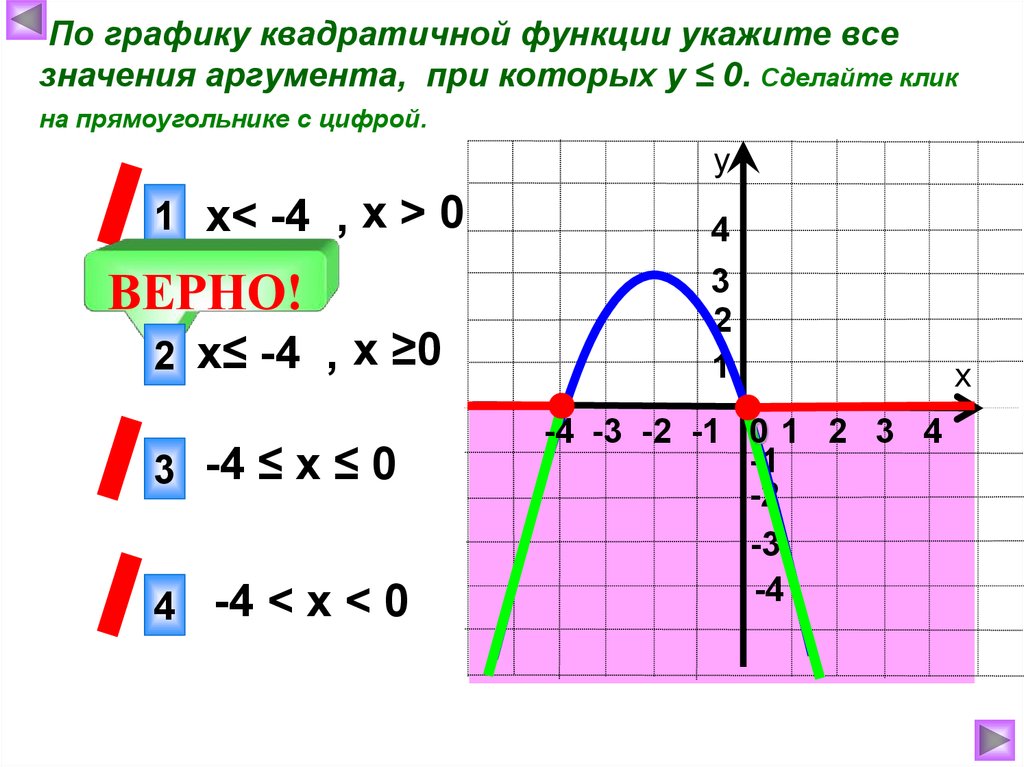
По графику квадратичной функции укажите все
значения аргумента, при которых у ≤ 0. Сделайте клик
на прямоугольнике с цифрой.
у
1 х< -4 , х > 0
ВЕРНО!
2 х≤ -4 , х ≥0
3 -4 ≤ х ≤ 0
4 -4 < х < 0
4
3
2
1
-4 -3 -2 -1 0 1 2 3 4
-1
-2
-3
-4
х

22.

По графику квадратичной функции укажите все
значения аргумента, при которых значения функции
неотрицательны. Сделайте клик на прямоугольнике с цифрой.
у
1 0<х<4
4
3
2
1
ВЕРНО!
2 х≤ 0 , х ≥4
3 0≤х≤4
4 х<0 ,
х >4
-3 -2 -1
01 2 3 4 х
-2
-3
-4
Значения функции неотрицательны,то есть
положительны или равны 0.

23.

По графику квадратичной функции укажите все
значения аргумента, при которых у < 0. Сделайте клик
на прямоугольнике с цифрой.
ВЕРНО!
1 х - любое
2 х≤ 0 ,
3 Ни при каких х
4 х>0
х

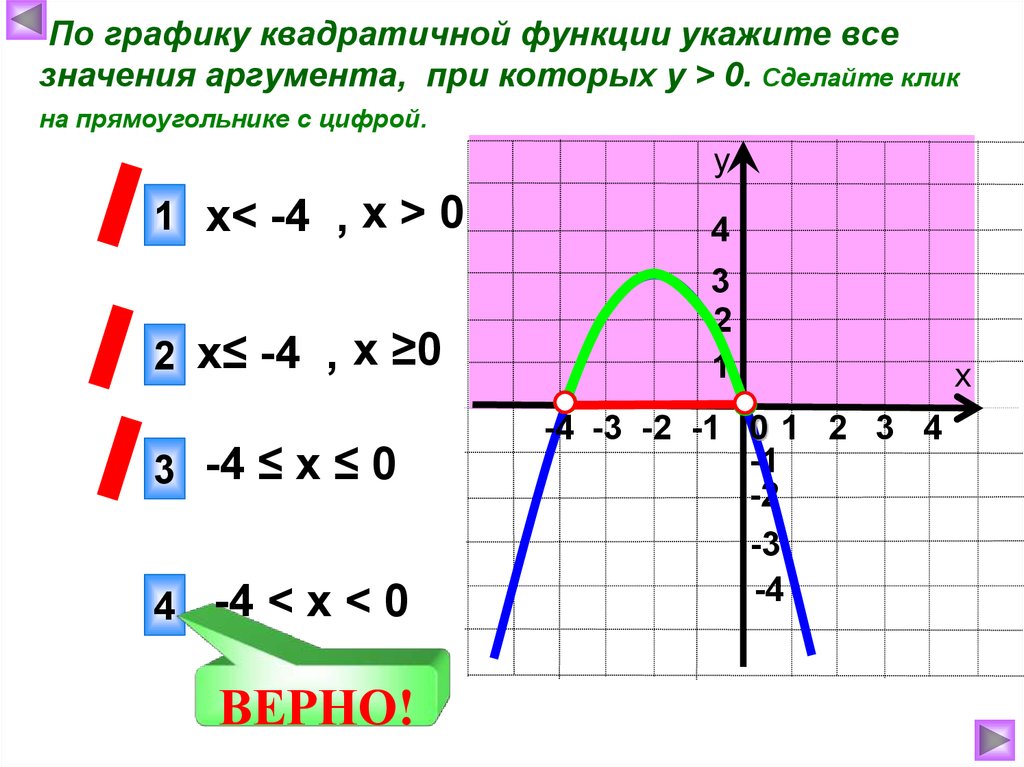
24.

По графику квадратичной функции укажите все
значения аргумента, при которых у > 0. Сделайте клик
на прямоугольнике с цифрой.
у
1 х< -4 , х > 0
4
2 х≤ -4 , х ≥0
3
2
1
3 -4 ≤ х ≤ 0
4 -4 < х < 0
ВЕРНО!
-4 -3 -2 -1 0 1 2 3 4
-1
-2
-3
-4
х

25.

По графику квадратичной функции укажите все
значения аргумента, при которых у < 0. Сделайте клик
на прямоугольнике с цифрой.
у
1 -2 < х < 2
4
3
2
1
2 х≤ -2 , х ≥2
3 -2 ≤ х ≤ 2
4 х<-2 , х >2
ВЕРНО!
-3 -2 -1
01 2 3 4 х
-2
-3
-4

26.

Решение квадратных
неравенств.

27.

Квадратным называется неравенство, левая часть
которого − квадратный трёхчлен, а правая часть
равна нулю.
ах²+bх+с>0
ах²+bх+с<0
ах²+bх+с≥0
ах²+bх+с≤0
Решением неравенства с одним неизвестным
называется то значение неизвестного, при котором
это неравенство обращается в верное числовое
неравенство.
Решить неравенство − это значит найти все его
решения или установить, что их нет.

28.

Являются ли следующие
неравенства квадратными?
2x2 4x 6
a)
0;
2
г)4 y 2 5 y 7 0;
б )4 x 2 x 0;
д)5x 6 x 4 0;
в )2 x 4 0;
е)3 y 5 y 2 7 0.
2
2

29.

Решите неравенство
х²+7х-8 < 0.
Алгоритм решения
квадратных неравенств:
1. Приведите неравенство к виду
ах²+bх+с>0 (≥0) , ах²+bх+с>0 (≤0) .
2. Рассмотрим функцию
у=х²+7х-8 .
2. Рассмотрите функцию
у=ах²+bх+с .
3. Определите направления
ветвей.
4. Найдите точки пересечения
параболы с осью абсцисс (для них
у=0; х1 и х2 найдите, решая
уравнение ах²+bх+с=0 ).
5. Схематически постройте
график функции у=ах²+bх+с .
6. Выделите часть параболы для
которой у>0 (≥0) или у<0 (≤0).
7. На оси абсцисс выделите те
значения х, для которых у>0 (≥0)
или у<0 (≤0).
8. Запишите ответ.
3. Графиком функции является
парабола, ветви которой
направлены вверх.
4. х²+7х-8=0 .
По теореме Виета
х 1+х 2=-7
х 1·х 2=-8
5.
−8
х 1= -8
х 2=1
//////////////////////
1
6 -7.
8. Ответ:
8;1
х

30.

Решите неравенство
х2 – 3х 0
у = х2 – 3х
-7 -6 -5 -4 -3 -2 -1
о
х2 – 3х = 0
х(х-3)=0
х=0 или х-3=0
х=3
1
2
3
4
5
6
7
х
Ответ : ( ;0] [3; )

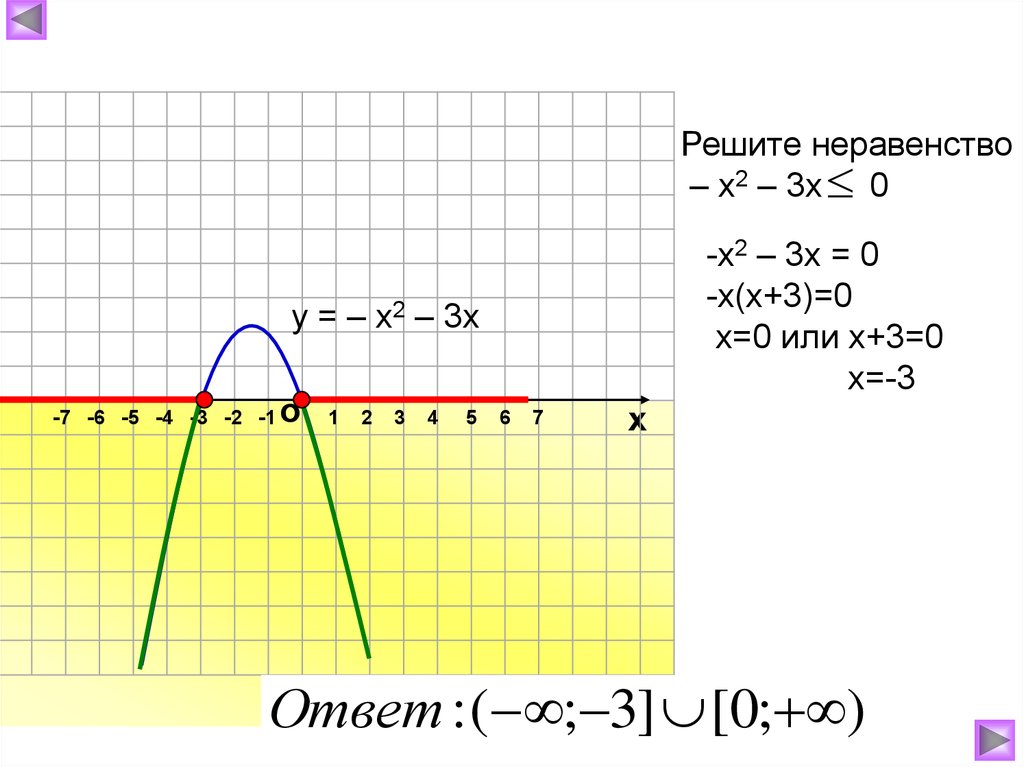
31.

Решите неравенство
– х2 – 3х 0
-х2 – 3х = 0
-х(х+3)=0
х=0 или х+3=0
х=-3
у = – х2 – 3х
-7 -6 -5 -4 -3 -2 -1
о
1
2
3
4
5
6
7
х
Ответ : ( ; 3] [0; )

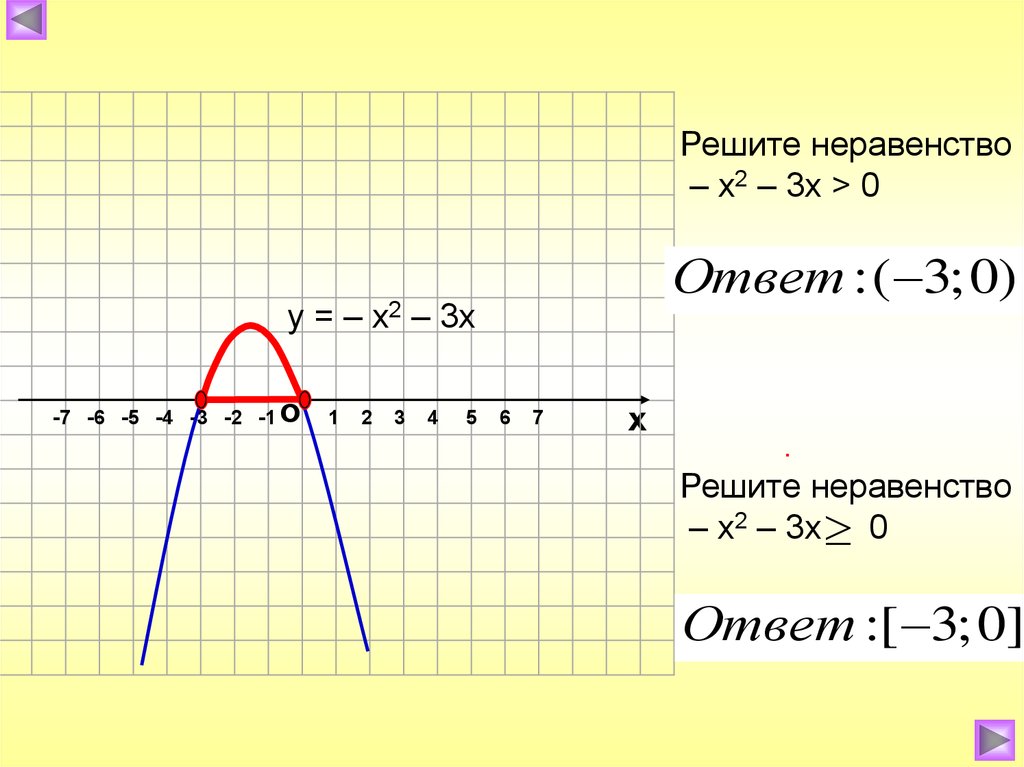
32.

Решите неравенство
– х2 – 3х > 0
Ответ : ( 3; 0)
у = – х2 – 3х
-7 -6 -5 -4 -3 -2 -1
о
1
2
3
4
5
6
7
х
.
Решите неравенство
– х2 – 3х 0
Ответ :[ 3; 0]

33.

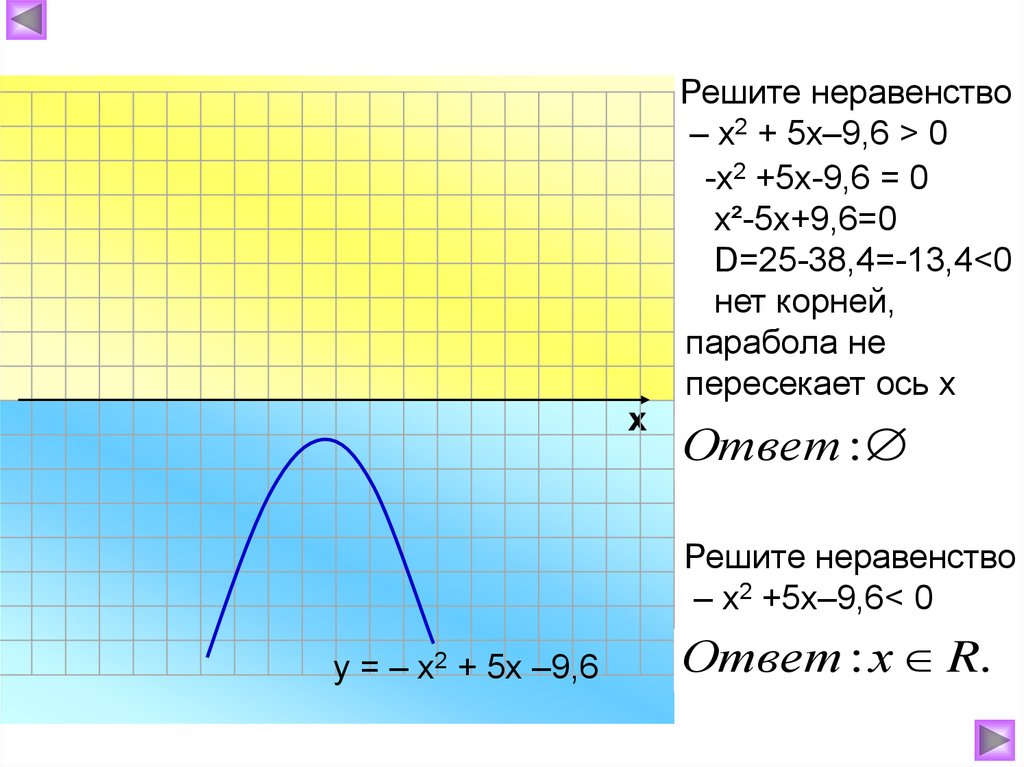
х
Решите неравенство
– х2 + 5х–9,6 > 0
-х2 +5х-9,6 = 0
х²-5х+9,6=0
D=25-38,4=-13,4<0
нет корней,
парабола не
пересекает ось х
Ответ :
Решите неравенство
– х2 +5х–9,6< 0
у = – х2 + 5х –9,6
Ответ : х R.

34.

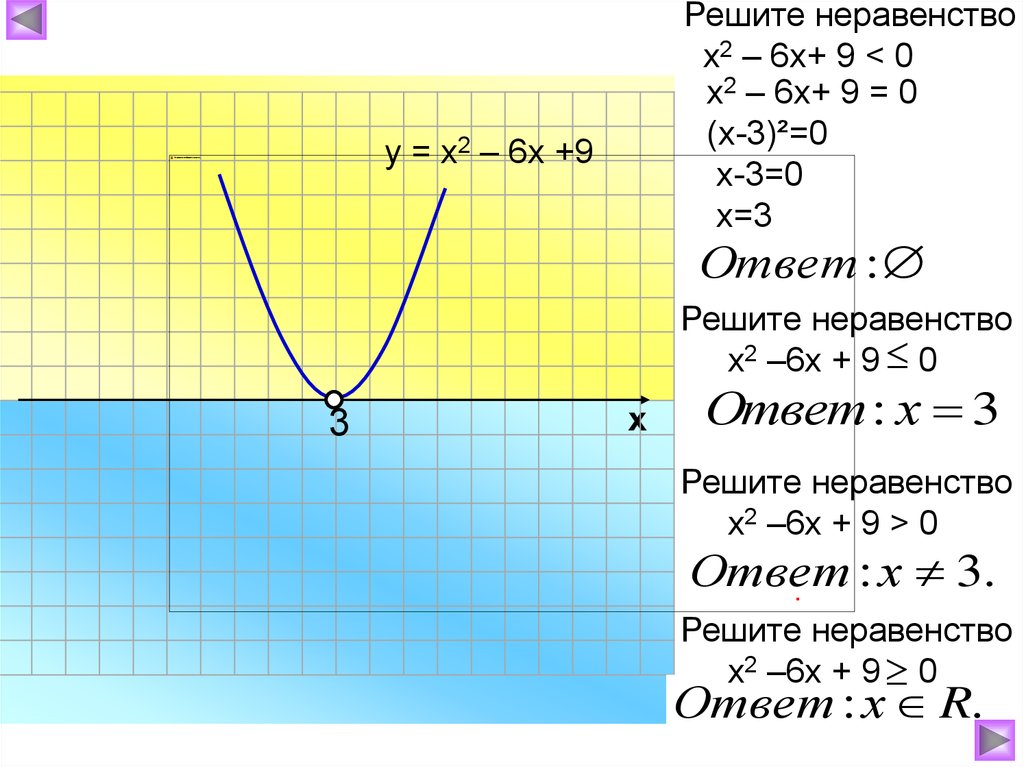
Решите неравенство
х2 – 6х+ 9 < 0
х2 – 6х+ 9 = 0
(х-3)²=0
х-3=0
х=3
у = х2 – 6х +9
Ответ :
Решите неравенство
х2 –6х + 9 0
3
х
Ответ : х 3
Решите неравенство
х2 –6х + 9 > 0
Ответ
: х 3.
.
Решите неравенство
х2 –6х + 9 0
Ответ : х R.

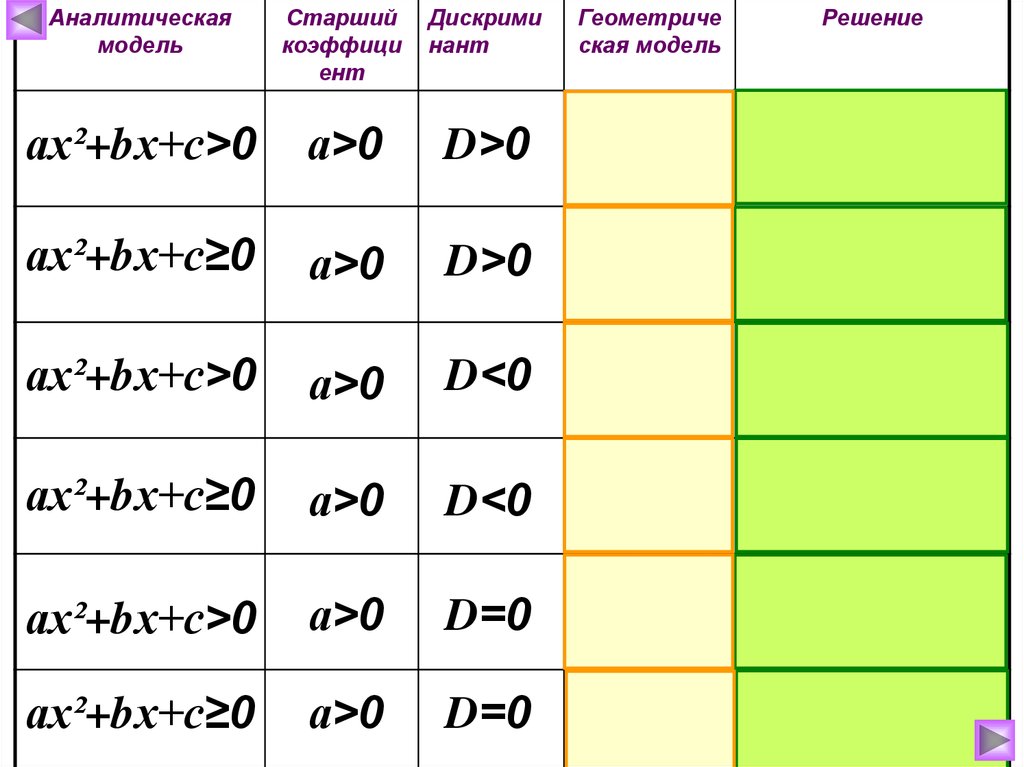
35.

Аналитическая
модель
Старший
коэффици
ент
Дискрими
нант
Геометриче
ская модель
у
ах²+bх+с>0
а>0
D>0
х1
х2 0
у
ах²+bх+с≥0
а>0
D>0
х1
х2 0
; х1
х
х2 ;
; х1
х
х2 ;
у
ах²+bх+с>0
а>0
D<0
0
х
0
х
0
х
0
х
у
ах²+bх+с≥0
а>0
D<0
у
ах²+bх+с>0
ах²+bх+с≥0
а>0
а>0
D=0
у
Решение
D=0
;
;
; хо
хо ;
;

36.

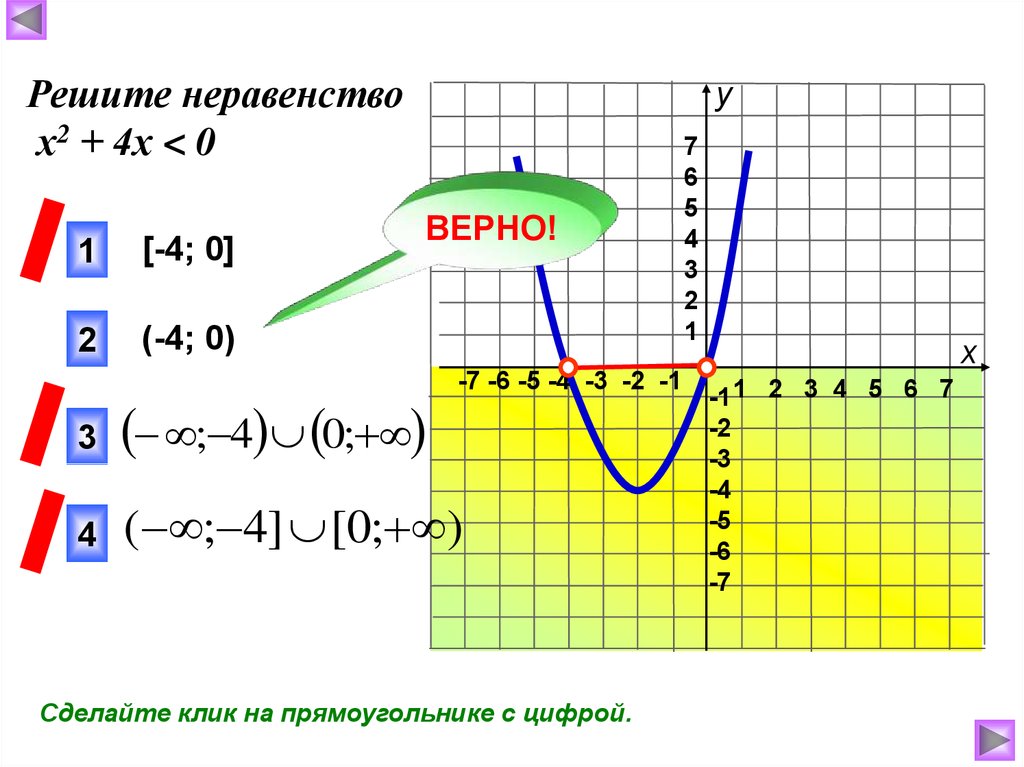
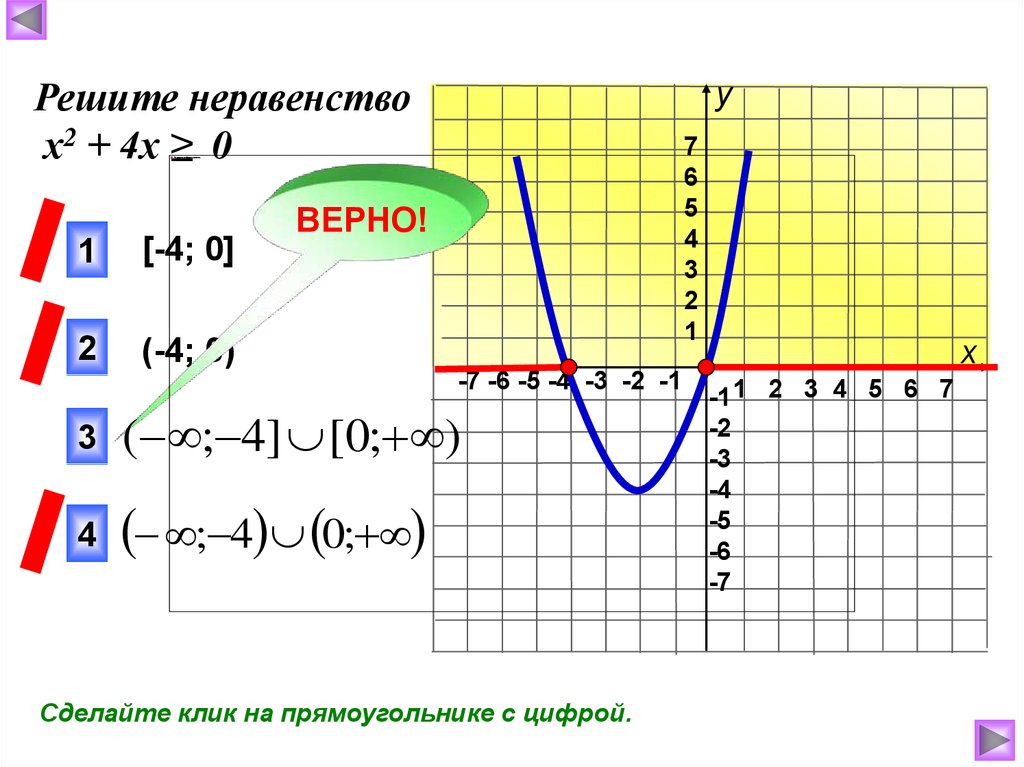
Решите неравенство
х2 + 4х < 0
1
[-4; 0]
2
(-4; 0)
у
ВЕРНО!
-7 -6 -5 -4 -3 -2 -1
3
; 4 0;
4
( ; 4] [0; )
Сделайте клик на прямоугольнике с цифрой.
7
6
5
4
3
2
1
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

37.

у
Решите неравенство
х2 + 4х ≥ 0
1
[-4; 0]
2
(-4; 0)
7
6
5
4
3
2
1
ВЕРНО!
-7 -6 -5 -4 -3 -2 -1
3
( ; 4] [0; )
4
; 4 0;
Сделайте клик на прямоугольнике с цифрой.
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

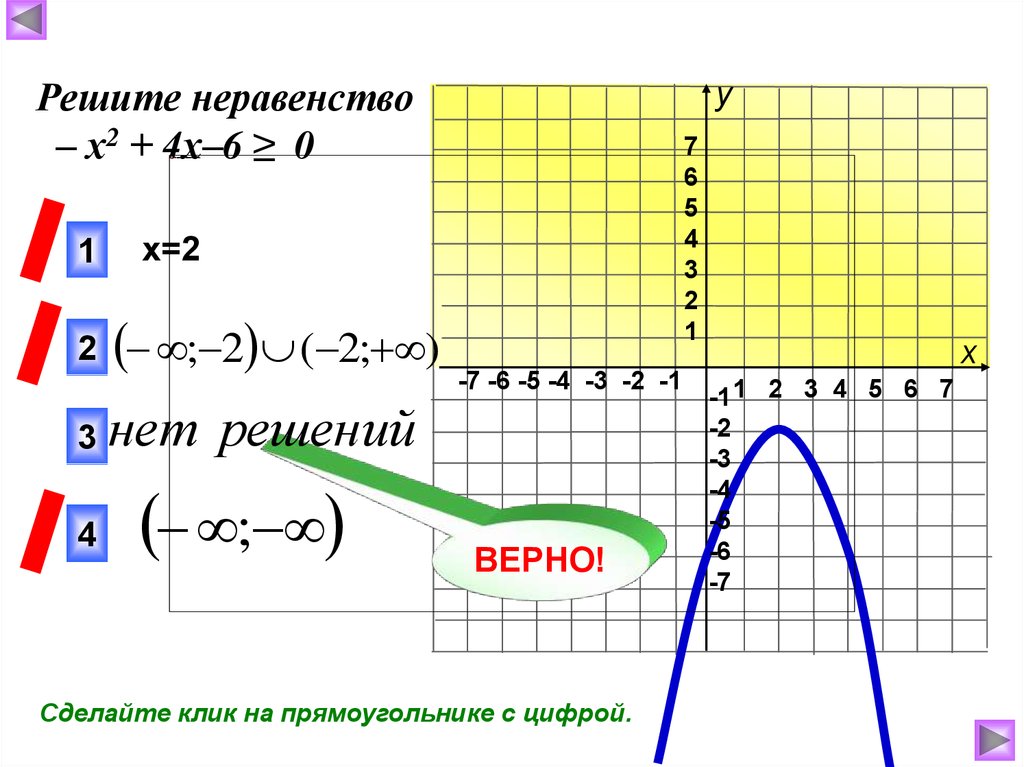
38.

у
Решите неравенство
– х2 + 4х–6 ≥ 0
1
2
3
4
7
6
5
4
3
2
1
x=2
; 2 ( 2; )
-7 -6 -5 -4 -3 -2 -1
нет решений
;
ВЕРНО!
Сделайте клик на прямоугольнике с цифрой.
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

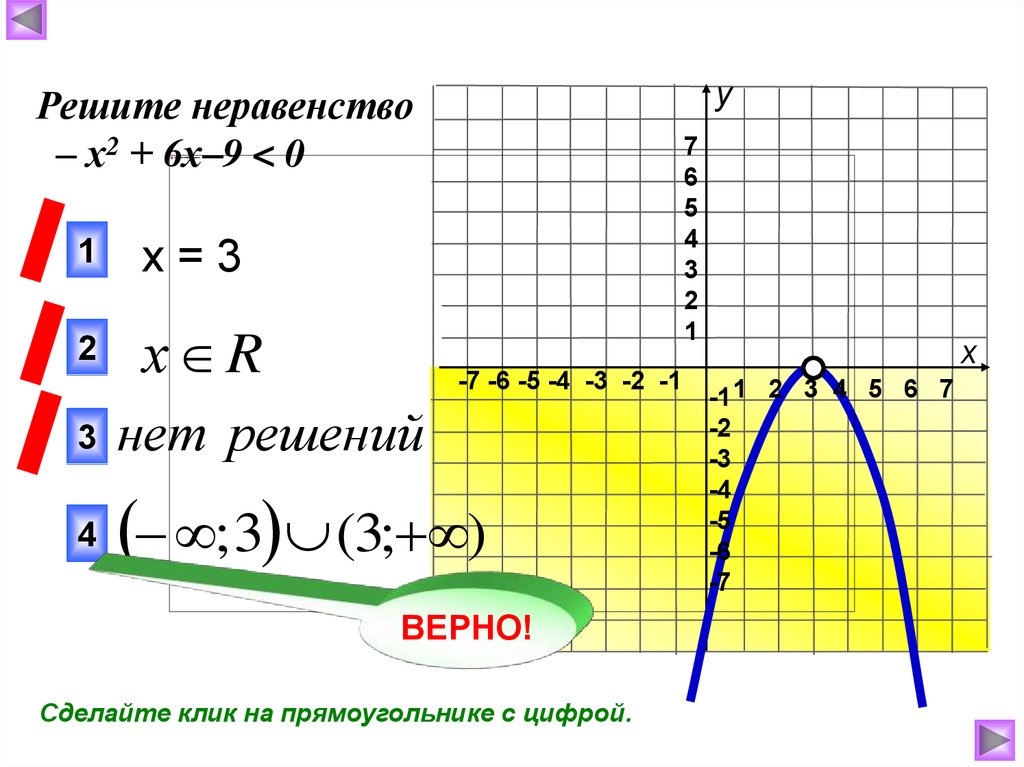
39.

у
Решите неравенство
– х2 + 6х–9 < 0
1
x=3
2
х R
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
3
нет решений
4
; 3 (3; )
ВЕРНО!
Сделайте клик на прямоугольнике с цифрой.
х
-1 1 2 3 4 5 6 7
-2
-3
-4
-5
-6
-7

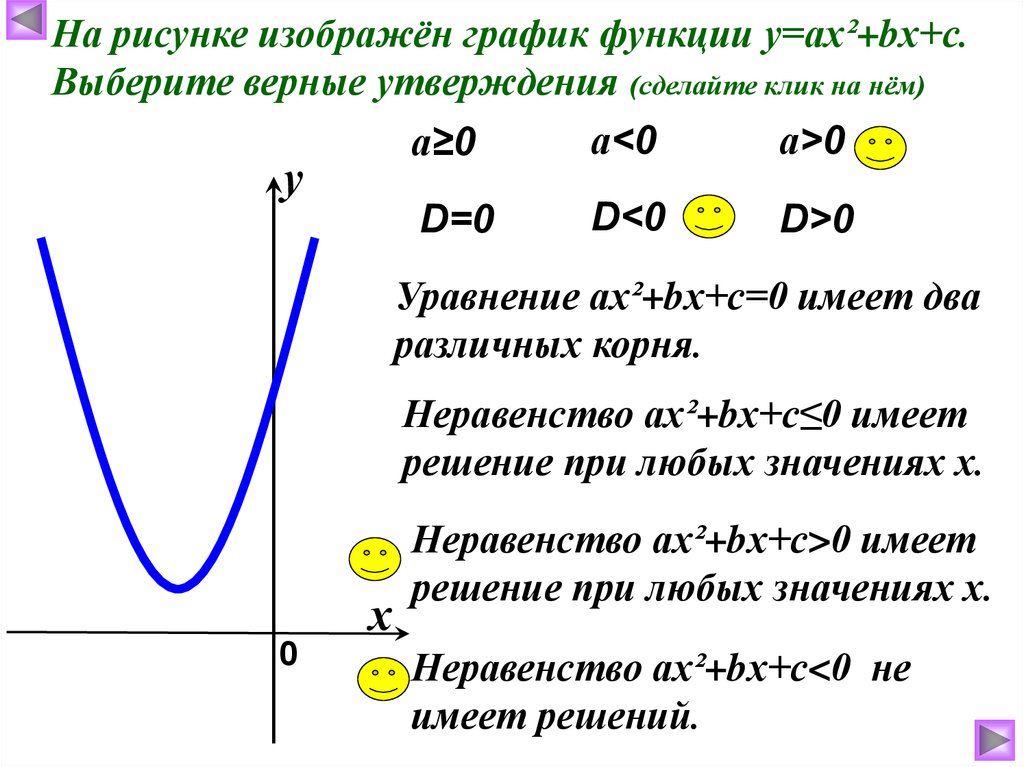
40.

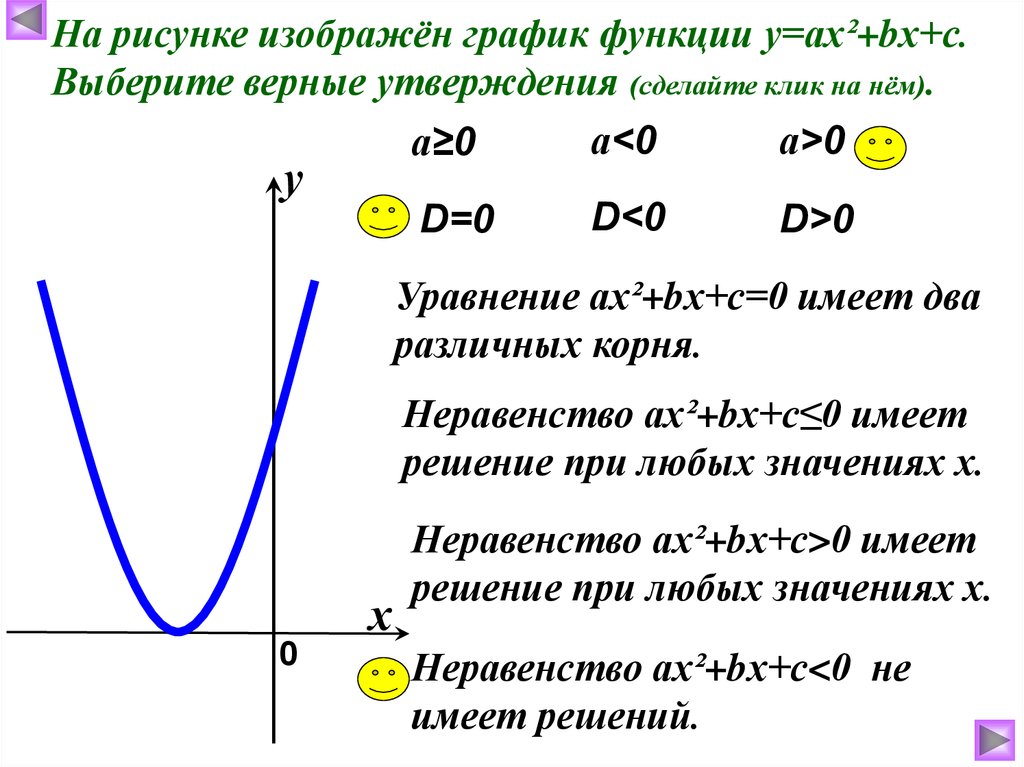
На рисунке изображён график функции у=ах²+bх+с.
Выберите верные утверждения (сделайте клик на нём)
а<0
а>0
а≥0
у
D=0
D<0
D>0
Уравнение ах²+bх+с=0 имеет два
различных корня.
Неравенство ах²+bх+с≤0 имеет
решение при любых значениях х.
х
0
Неравенство ах²+bх+с>0 имеет
решение при любых значениях х.
Неравенство ах²+bх+с<0 не
имеет решений.

41.

На рисунке изображён график функции у=ах²+bх+с.
Выберите верные утверждения (сделайте клик на нём).
а<0
а>0
а≥0
у
D=0
D<0
D>0
Уравнение ах²+bх+с=0 имеет два
различных корня.
Неравенство ах²+bх+с≤0 имеет
решение при любых значениях х.
х
0
Неравенство ах²+bх+с>0 имеет
решение при любых значениях х.
Неравенство ах²+bх+с<0 не
имеет решений.

42.

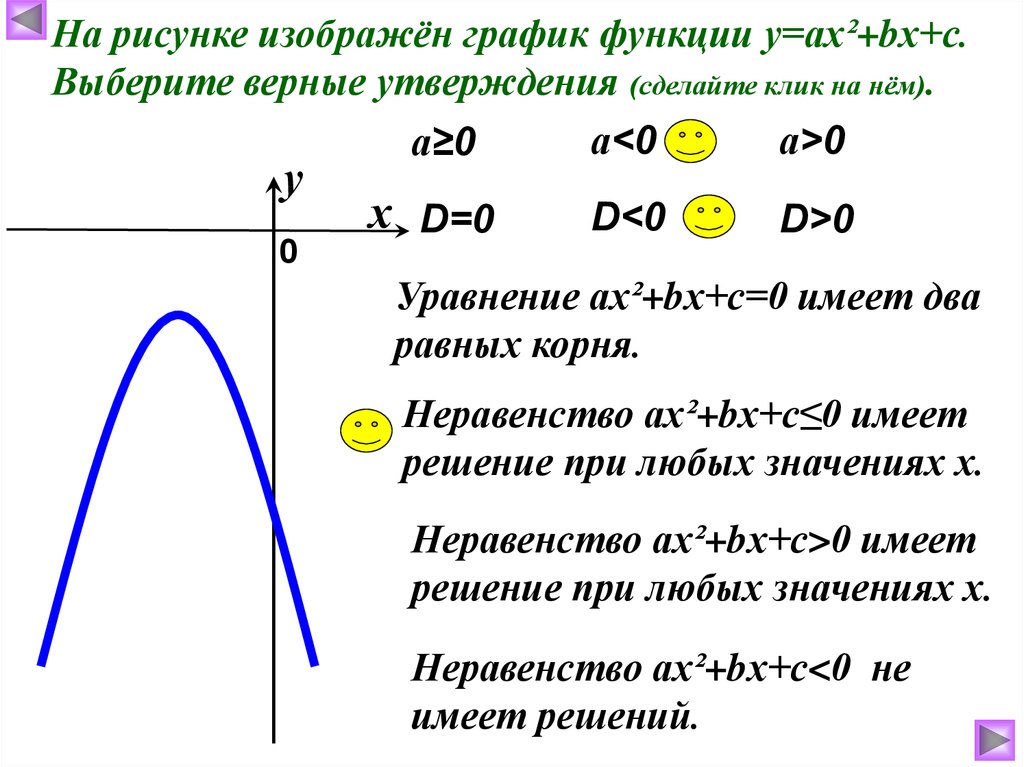
На рисунке изображён график функции у=ах²+bх+с.
Выберите верные утверждения (сделайте клик на нём).
а<0
а>0
а≥0
у
0
х D=0
D<0
D>0
Уравнение ах²+bх+с=0 имеет два
равных корня.
Неравенство ах²+bх+с≤0 имеет
решение при любых значениях х.
Неравенство ах²+bх+с>0 имеет
решение при любых значениях х.
Неравенство ах²+bх+с<0 не
имеет решений.

43.

44.

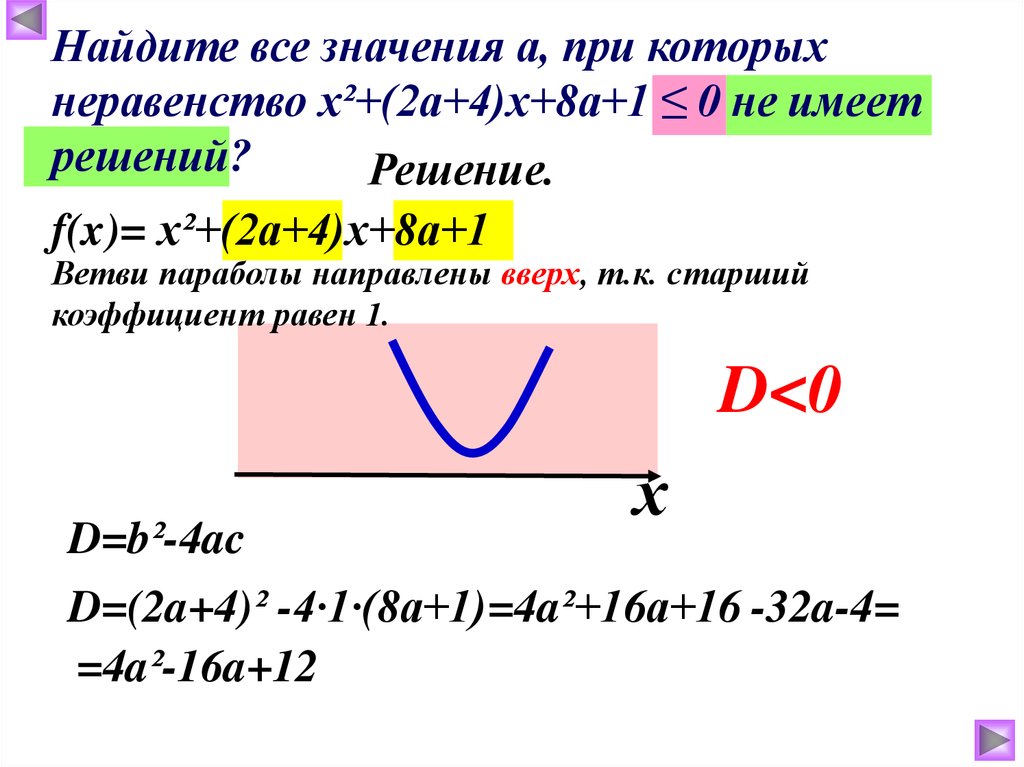
Найдите все значения а, при которых
неравенство х²+(2а+4)х+8а+1 ≤ 0 не имеет
решений?
Решение.
f(x)= х²+(2а+4)х+8а+1
Ветви параболы направлены вверх, т.к. старший
коэффициент равен 1.
D<0
х
D=b²-4ac
D=(2a+4)² -4·1·(8a+1)=4a²+16a+16 -32a-4=
=4a²-16a+12

45.

4a²-16a+12< 0
a²-4a+3< 0
g(a)= a²-4а+3
g(a)= 0
a²-4а+3=0
По теореме Виета
a 1+а 2=4
а 1=1
a 1·а 2=3
а 2=3
1
//////////
3
а
а 1; 3
Ответ: при а 1; 3
неравенство х²+(2а+4)х+8а+1 ≤ 0
не имеет решений.

46.

ТЕСТИРАВОНИЕ
2 вариант
1 вариант
;2 4;
2. ; 1 3; 2. ; 1 3;
1. 3;2
Б
4. А
3.
5. 2;3
1.
3.
Б
4.
В
5.
3;5

English Русский Rules