Символический метод. Цепи с магнитосвязанными элементами

1.

Символический метод
2003г
Цепи с магнитосвязанными элементами

2.

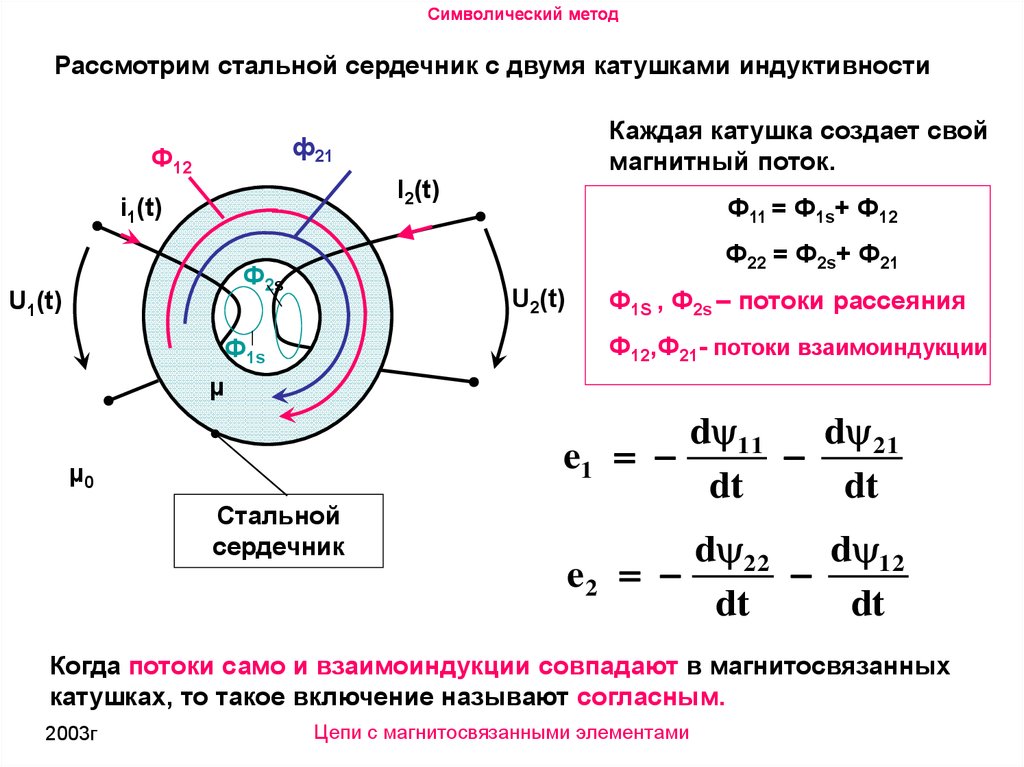
Символический метод
Рассмотрим стальной сердечник с двумя катушками индуктивности
Ф12
I2(t)
i1(t)
Ф11 = Ф1s+ Ф12
Ф22 = Ф2s+ Ф21
Ф2s
U1(t)
Каждая катушка создает свой
магнитный поток.
ф21
U2(t)
Ф1S , Ф2s – потоки рассеяния
Ф12,Ф21- потоки взаимоиндукции
Ф1s
μ
μ0
Стальной
сердечник
d 11
d 21
e1
dt
dt
d 22
d 12
e2
dt
dt
Когда потоки само и взаимоиндукции совпадают в магнитосвязанных
катушках, то такое включение называют согласным.
2003г
Цепи с магнитосвязанными элементами

3.

Символический метод
Таким образом при согласном включении напряжение на катушках
uk 1
d 11
d 21
dt
dt
uk 2
d 22
d 12
dt
dt
Так как ψ11 =L1i1 , ψ22= L2i2 , ψ12= Mi1 , ψ21= Mi2 , то
uk 1
di1
di 2
L1
M
dt
dt
uk 2
di 2
di1
L2
M
dt
dt
Или в комплексном виде
U k1= I 1 jωL1+ I 2jωM
2003г
U k2= I 2 jωL2+ I 1jωM
Цепи с магнитосвязанными элементами

4.

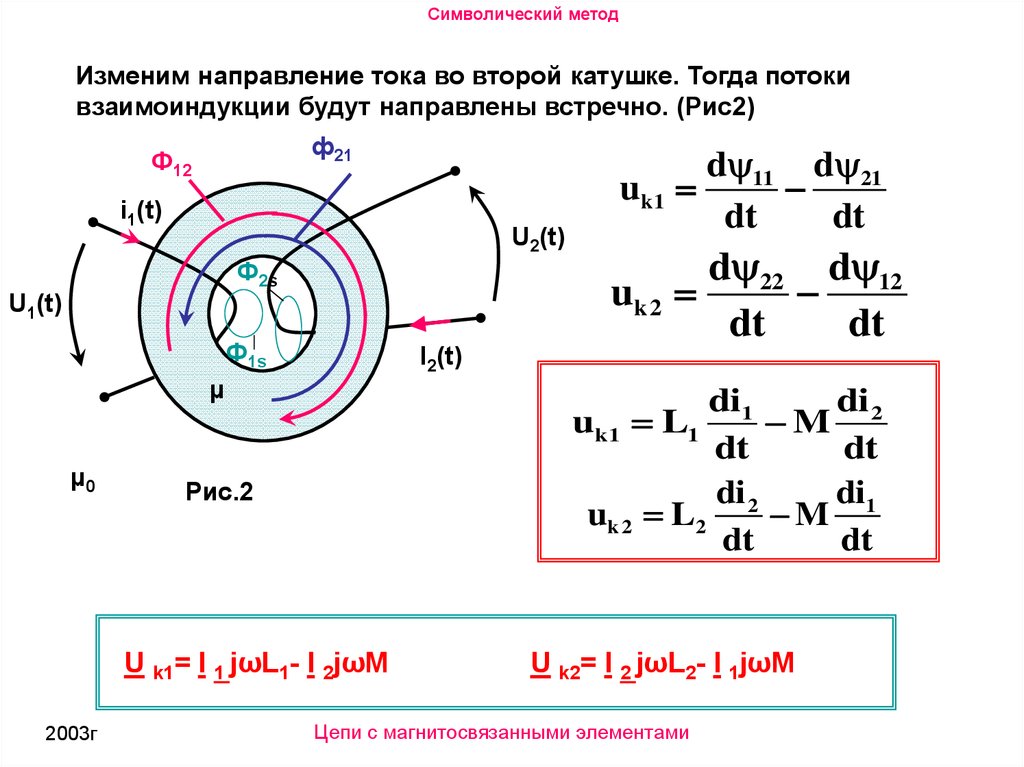
Символический метод
Изменим направление тока во второй катушке. Тогда потоки
взаимоиндукции будут направлены встречно. (Рис2)
ф21
Ф12
i1(t)
U2(t)
Ф2s
uk 2
U1(t)
Ф1s
di1
di 2
uk1 L1
M
dt
dt
di 2
di1
uk 2 L 2
M
dt
dt
Рис.2
U k1= I 1 jωL1- I 2jωM
2003г
d 22 d 12
dt
dt
I2(t)
μ
μ0
d 11 d 21
uk1
dt
dt
U k2= I 2 jωL2- I 1jωM
Цепи с магнитосвязанными элементами

5.

Символический метод
Если потоки само и взаимоиндукции в магнитосвязанных катушках
направлены навстречу друг другу, то такое включение катушек
называется встречным.
На электрической схеме способ включения катушек обозначается
звездочками,
причем
если
токи
одинаково
ориентированы
относительно помеченных
зажимов, то включение катушек
называется согласным, если токи ориентированы
по-разному то
включение катушек называется встречным.
М
Ik(t)
Lk
*
Ls
Is(t)
*
Согласное
включение
2003г
Цепи с магнитосвязанными элементами

6.

Символический метод
М
Ik(t)
Ls
Is(t)
Lk
*
*
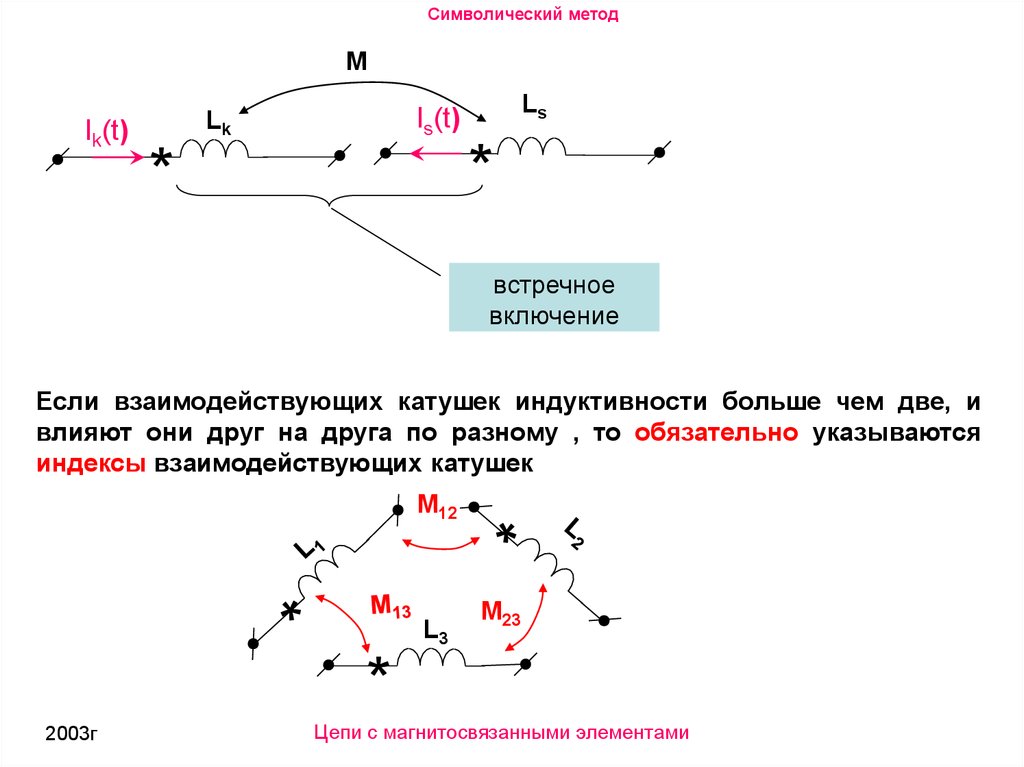
встречное
включение
Если взаимодействующих катушек индуктивности больше чем две, и
влияют они друг на друга по разному , то обязательно указываются
индексы взаимодействующих катушек
М12
L3
М23
*
2003г
Цепи с магнитосвязанными элементами

7.

Символический метод
Правило знаков при записи законов Кирхгофа
1.Если в электрической цепи две магнитосвязанных катушки
включены согласно, то в законах Кирхгофа напряжение
самоиндукции и взаимоиндукции записываются с одинаковыми
знаками,если встречно-то с противоположными знаками.
Замечание.
Напряжение, обусловленное потоком самоиндукции (Ф11,Ф22)
называется напряжением самоиндукции, а потоками (Ф12,Ф21)
напряжением взаимоиндукции.
U1=I1jωL1 , U2= I2jωL2-напряжения самоиндукции
U12=I2 jωM - напряжение взаимоиндукции( напряжение на первой
катушке обусловленное током второй катушки.)
U21=I1 jωM - напряжение взаимоиндукции( напряжение на второй
катушке обусловленное током первой катушки.)
2003г
Цепи с магнитосвязанными элементами

8.

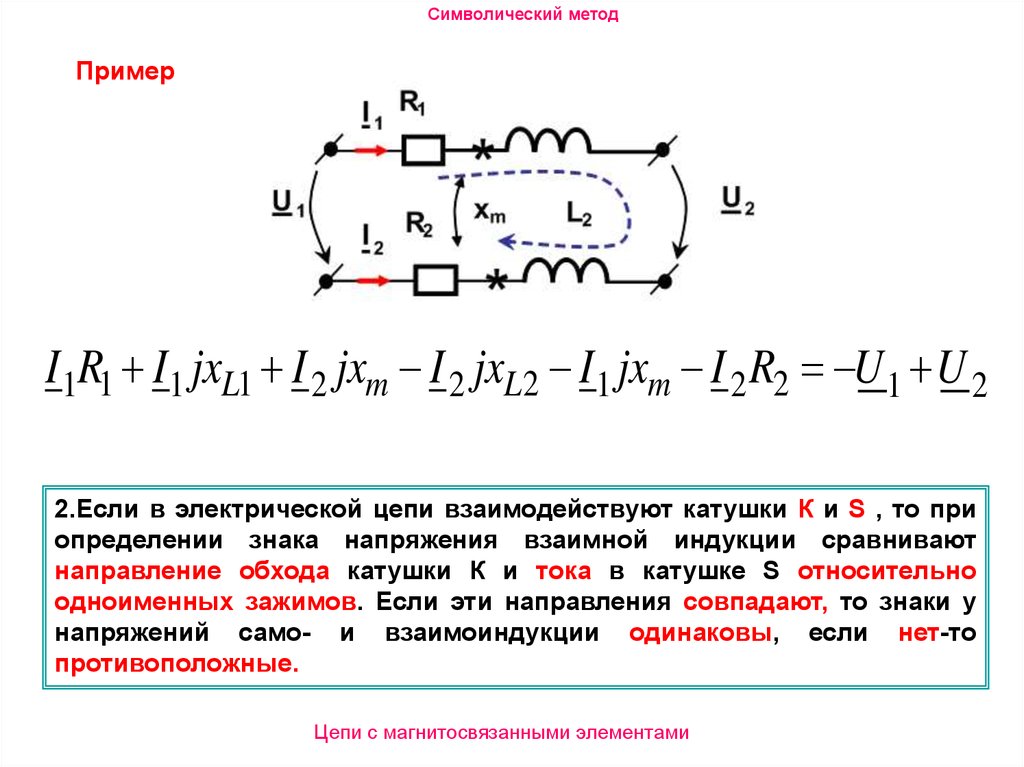
Символический метод
Пример
I 1R1 I 1 jxL1 I 2 jxm I 2 jxL2 I 1 jxm I 2 R2 U 1 U 2
2.Если в электрической цепи взаимодействуют катушки К и S , то при
определении знака напряжения взаимной индукции сравнивают
направление обхода катушки К и тока в катушке S относительно
одноименных зажимов. Если эти направления совпадают, то знаки у
напряжений само- и взаимоиндукции одинаковы, если нет-то
противоположные.
Цепи с магнитосвязанными элементами

9.

Символический метод
M
I1
U1
R1 R2
*L
1
L2
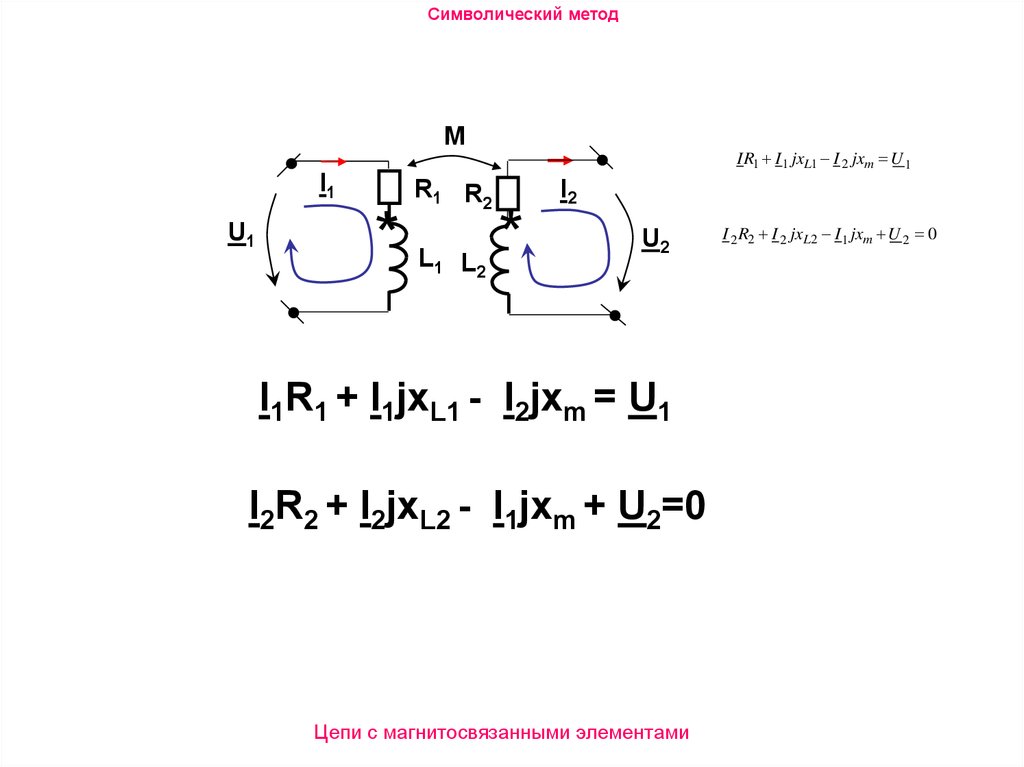
IR1 I 1 jxL1 I 2 jxm U 1
I2
*
U2
I1R1 + I1jxL1 - I2jxm = U1
I2R2 + I2jxL2 - I1jxm + U2=0
Цепи с магнитосвязанными элементами
I 2 R2 I 2 jxL 2 I 1 jxm U 2 0

10.

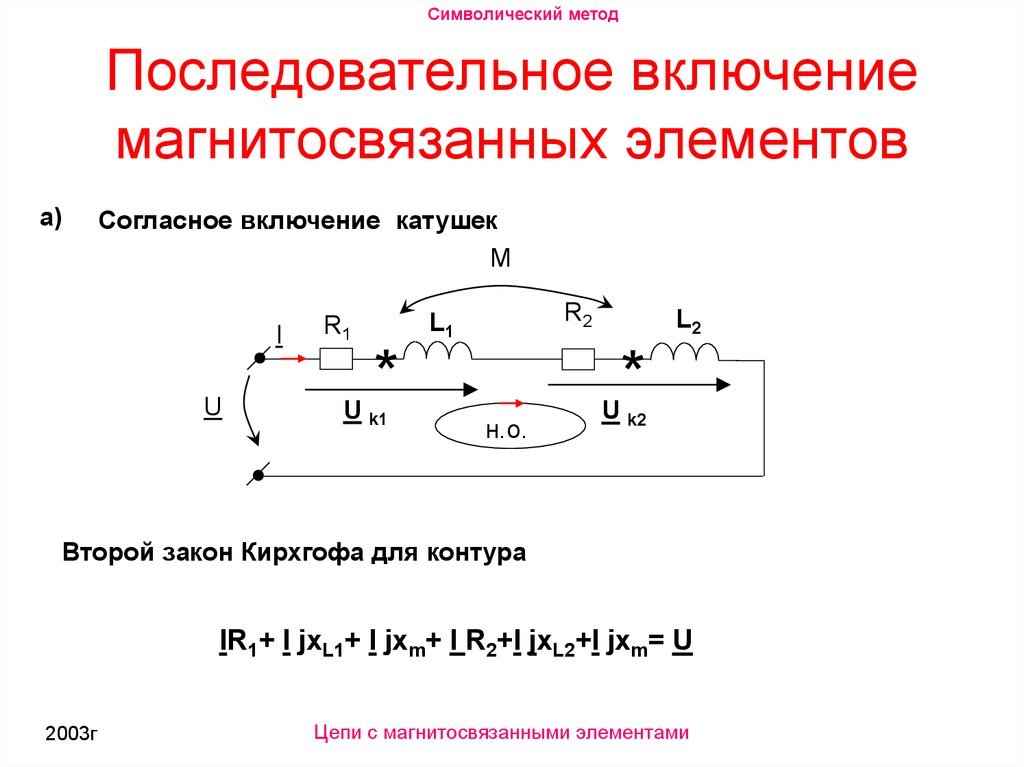
Символический метод
Последовательное включение
магнитосвязанных элементов
а)
Согласное включение катушек
M
I
U
R2
L1
R1
*
U
k1
н.о.
L2
*
U
k2
Второй закон Кирхгофа для контура
IR1+ I jxL1+ I jхm+ I R2+I jxL2+I jxm= U
2003г
Цепи с магнитосвязанными элементами

11. Последовательное включение магнитосвязанных элементов

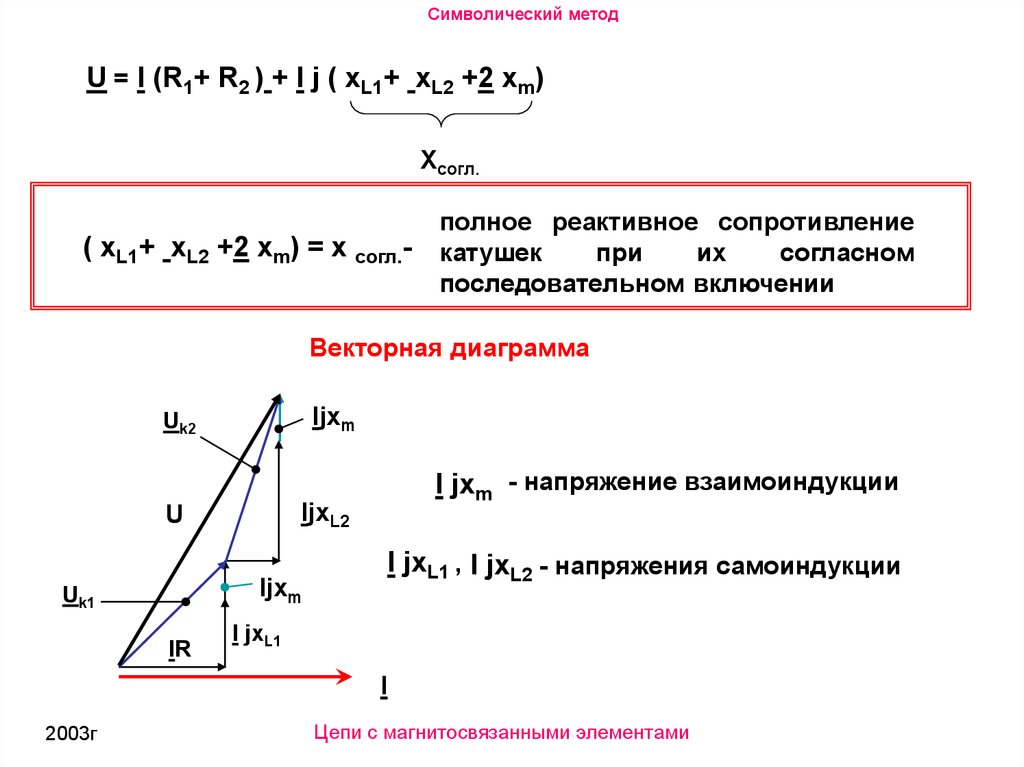
Символический метод
U = I (R1+ R2 ) + I j ( xL1+ xL2 +2 xm)
Xсогл.
( xL1+ xL2 +2 xm) = х согл.-
полное реактивное сопротивление
катушек
при
их
согласном
последовательном включении
Векторная диаграмма
Ijxm
Uk2
IjxL2
U
Ijxm
Uk1
IR
I jxm - напряжение взаимоиндукции
I jxL1 , I jxL2 - напряжения самоиндукции
I jxL1
I
2003г
Цепи с магнитосвязанными элементами

12.

в) Встречное включение катушек
M
I
U
R2
L1
R1
*
U
k1
н.о.
L2
U k2
*
Уравнение по второму закону Кирхгофа для контура
I R1+ I jxL1- I jхm+ I R2+I jxL2- I jxm=U
U = I (R1+ R2 ) + I j ( xL1+ xL2 - 2 xm)
Xвстречн.

13.

Символический метод
( xL1+ xL2 - 2 xm) = х встречн.-
Полное реактивное сопротивление
катушек при их последовательном
встречном включении
Векторная диаграмма
I jxL2
I jxL1
U
Uk1
2003г
- I jxm
- I jxm
Uk2
IR2
IR1
I
Цепи с магнитосвязанными элементами

14.

Символический метод
Общий принцип расчета цепей с
взаимной индукцией
Расчет цепей
со взаимной индукцией М, без
предварительных преобразований, можно осуществлять
только по законам Кирхгофа, методу контурных токов,
методу наложения. Все остальные методы ( узловых
потенциалов, эквивалентного генератора, преобразования
электрических цепей ) для расчета цепей со взаимной
индукцией не могут использоваться, так как токи в ветвях
зависят не только от разности потенциалов обусловленной
источником питания, но и от взаимодействия ветвей друг с
другом.
2003г
Цепи с магнитосвязанными элементами

15.

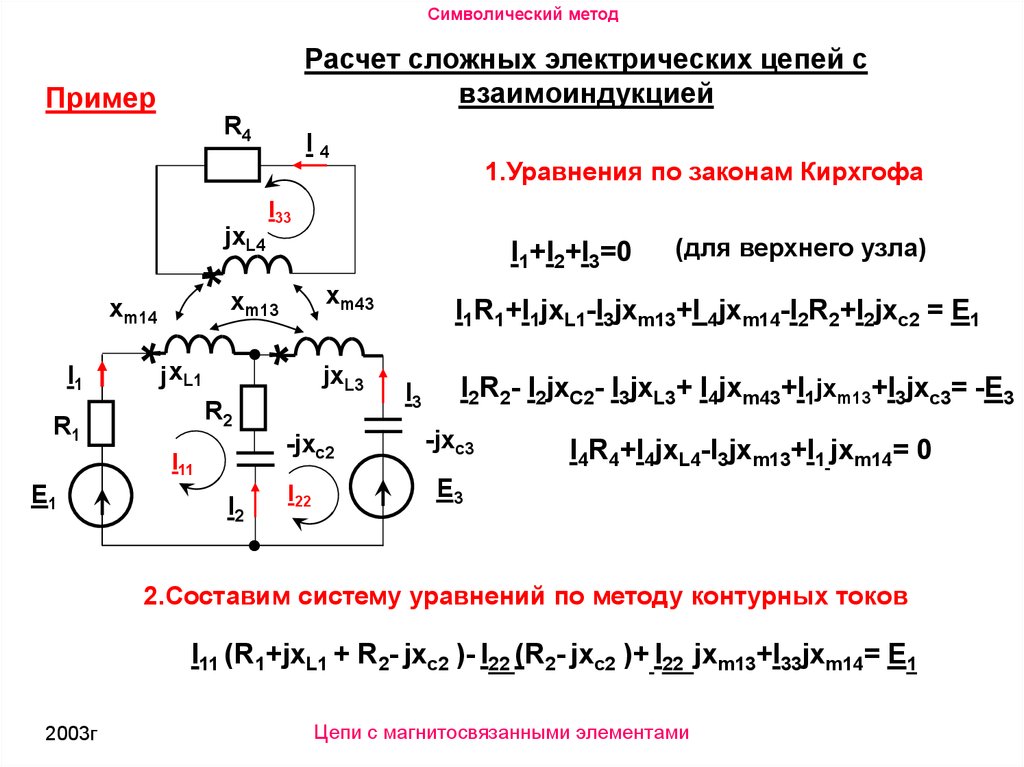
Символический метод
Расчет сложных электрических цепей с
взаимоиндукцией
Пример
R4
I4
1.Уравнения по законам Кирхгофа
I33
jxL4
*
I1+I2+I3=0
j xL1
jxL3
R2
R1
-jxc2
I11
E1
I1R1+I1jxL1-I3jxm13+I 4jxm14-I2R2+I2jxc2 = E1
*
*
I1
xm43
xm13
xm14
(для верхнего узла)
I2
I22
I3
I2R2- I2jxC2- I3jxL3+ I4jxm43+I1jxm13+I3jxc3= -E3
-jxc3
I4R4+I4jxL4-I3jxm13+I1 jxm14= 0
E3
2.Составим систему уравнений по методу контурных токов
I11 (R1+jxL1 + R2- jxc2 )- I22 (R2- jxc2 )+ I22 jxm13+I33jxm14= E1
2003г
Цепи с магнитосвязанными элементами

16.

Символический метод
I22( R2- jxC2+ jxL3- jxc3)- I11( R2- jxC2) +I11 jxm13+I33jxm43=- E3
I33 (R4+jxL4 )+I11jxm14+I22 jxm34= 0
Полученные системы уравнений достаточно сложны,
так
как
учитывают
наводимые
потоками
взаимоиндукции
напряжения
в
катушках
индуктивности. Для упрощения расчетов можно
произвести эквивалентную замену индуктивных
связей. Тогда получим обычную электрическую цепь,
при расчетах можно использовать любые известные
методы.
2003г
Цепи с магнитосвязанными элементами

17.

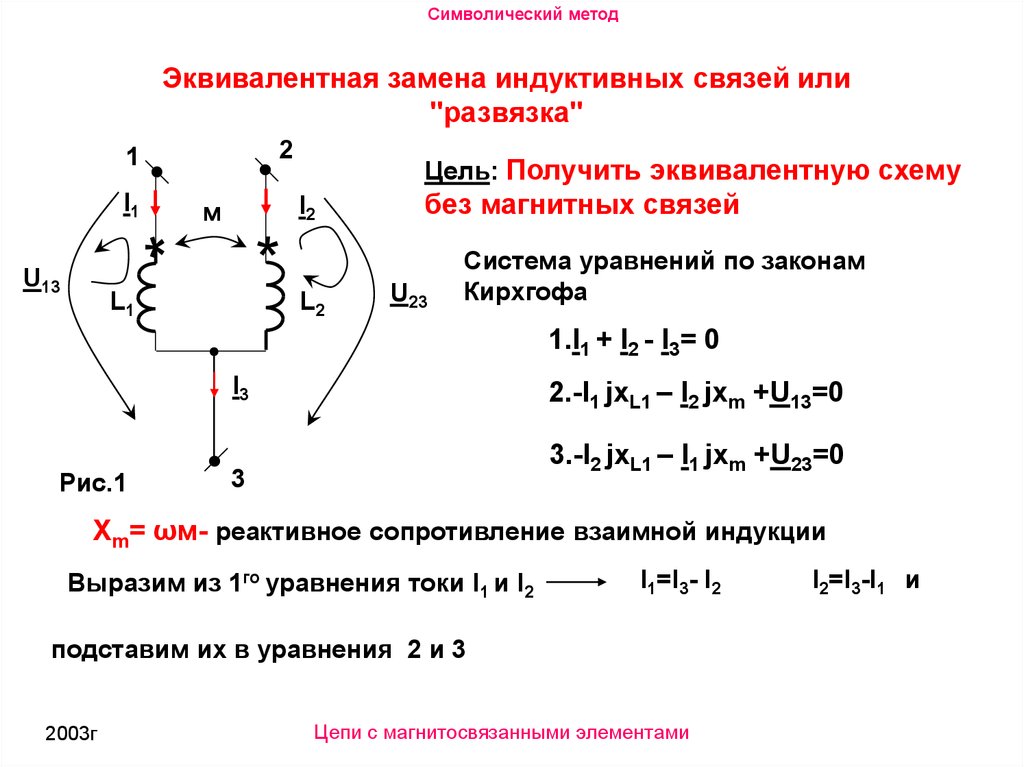
Символический метод
Эквивалентная замена индуктивных связей или
"развязка"
2
1
I2
м
*
I1
U13
Цель: Получить эквивалентную схему
*
L1
L2
без магнитных связей
U23
Система уравнений по законам
Кирхгофа
1.I1 + I2 - I3= 0
2.-I1 jxL1 – I2 jxm +U13=0
I3
Рис.1
3.-I2 jxL1 – I1 jxm +U23=0
3
Xm= ωм- реактивное сопротивление взаимной индукции
Выразим из 1го уравнения токи I1 и I2
I1=I3- I2
подставим их в уравнения 2 и 3
2003г
Цепи с магнитосвязанными элементами
I2=I3-I1 и

18.

Символический метод
I1(jxL1- jxm)+ I3jxm= U13
4. I1jxL1+I3jxm-I1jxm=U13
5. I2jxL2+I3jxm-I2jxm=U23
I2(jxL1- jxm)+ I3jxm= U23
6.
7.
По уравнениям (6) и (7) может составлена электрическая схема
1
2
I1
jxL1
U13
jxL2
-jxm
-jxm
+jxm
I3
Рис.2
2003г
I2
U23
В электрической цепи Рис.2 уже нет
магнитной связи, однако в ветвях 1 и
2, а также за узлом появились
дополнительные сопротивления хм.
Цепь
"развязана."
Полученная
электрическая цепь эквивалентна
заданной. В цепи рис.2 и заданной
одинаковы токи I1 , I2 ,I3 , а также
напряжения U13 и U23.
3
Цепи с магнитосвязанными элементами

19.

Символический метод
Правило знаков при эквивалентной
замене индуктивных связей
Если две индуктивно связанных катушки подключены к узлу
одинаковыми зажимами ,то при "развязке" в свои ветви (где
находятся катушки) добавляются сопротивления ( -jХm), а в
ветвь
за
узлом
сопротивление
(+jxm).Если
катушки
присоединены разноименными зажимами , то знаки у
сопротивлений xm противоположные.
2003г
Цепи с магнитосвязанными элементами

20.

Символический метод
I1R1+ I1 jxL1+I2 jxm-I2 jxL2-I1 jxm-I2R2= - U1+ U2
2003г
Цепи с магнитосвязанными элементами