Similar presentations:
Индуктивно связанные цепи. Лекция №13
1. Дисциплина: Теоретические основы электротехники
2.
23. Лекция №13
Тема: Индуктивносвязанные цепи
4. Учебные вопросы
1. Индуктивная связь катушек.Коэффициент связи.
2. Согласное и встречное включение
катушек.
3. Определение коэффициента связи и
взаимной индуктивности между
индуктивно связанными катушками
4. Расчет цепей синусоидального тока с
последовательно соединенными и
индуктивно связанными катушками.
5. Литература
1. Бессонов Л.А.Теоретические основы
электротехники.
Электрические цепи:
учебник для бакалавров. –
М. : Издательство Юрайт,
2012, с. 119-124
6.
1. Индуктивная связь катушек.Коэффициент связи
Явление взаимоиндукции основано на законе
электромагнитной индукции
В 1831 Майкл
Фарадей
открыл
явление
электромагни
тной
индукции.
Это закон устанавливает взаимосвязь между
магнитными и электрическими явлениями.
Формулировка: ЭДС электромагнитной
индукции, в контуре численно равна и
противоположна по знаку скорости изменения
магнитного потока сквозь поверхность,
ограниченную этим контуром.
d
di
e
L
dt
dt
7.
В том случае, когда изменение тока в одном изэлементов цепи приводит к появлению ЭДС в другом
элементе цепи, говорят, что эти два элемента
индуктивно связаны, а возникающую ЭДС
называют ЭДС взаимоиндукции.
Явление взаимоиндукции –
это явление наведения ЭДС
в одной электрической цепи
при изменении в ней
потокосцепления,
вызванного изменением
тока в другой электрической
цепи.
Связь магнитных потоков
катушек обусловливает их
индуктивную связь.
Взаимно индуктивная связь
проявляется в наведении
ЭДС (называемой ЭДС
взаимоиндукции) в одной
катушке при изменении
тока в другой близко
расположенной катушке.
Индуктивно связанными цепями называются цепи,
в которых наводятся ЭДС взаимоиндукции.
8.
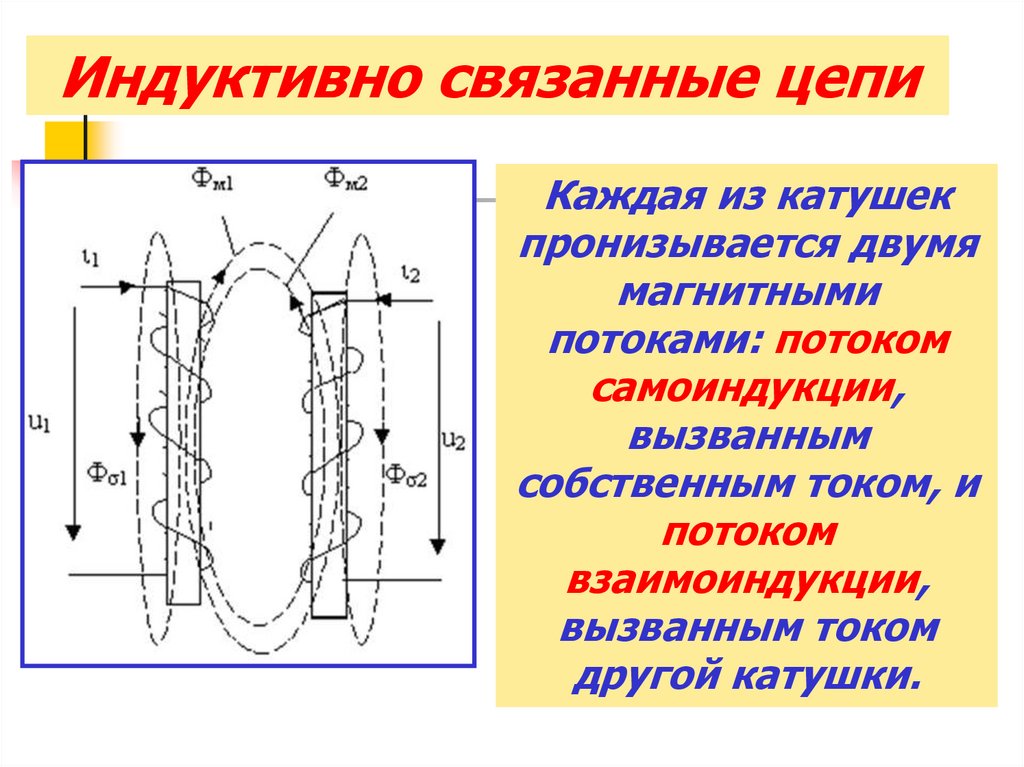
Индуктивно связанные цепиКаждая из катушек
пронизывается двумя
магнитными
потоками: потоком
самоиндукции,
вызванным
собственным током, и
потоком
взаимоиндукции,
вызванным током
другой катушки.
9.
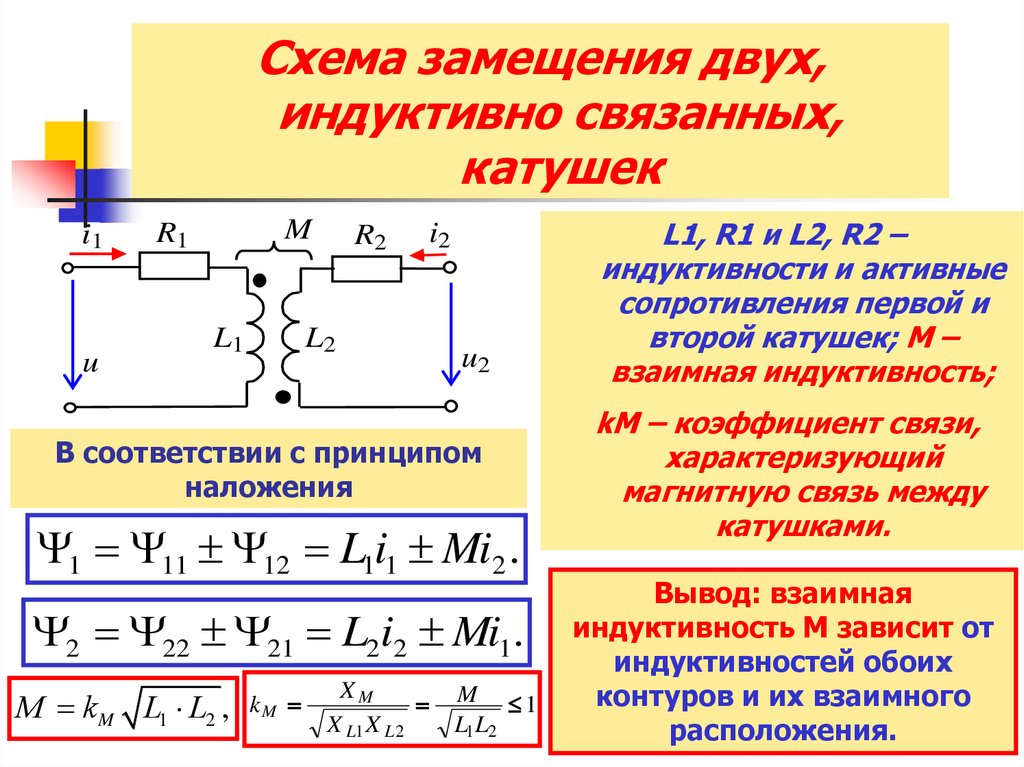
Схема замещения двух,индуктивно связанных,
катушек
i1
u
M
R1
L1
R2
i2
L2
u2
В соответствии с принципом
наложения
1 11 12 L1i1 Mi2 .
2 22 21 L2i2 Mi1.
М kM L1 L2 ,
kM
XM
X L1 X L 2
M 1
L1 L2
L1, R1 и L2, R2 –
индуктивности и активные
сопротивления первой и
второй катушек; М –
взаимная индуктивность;
kM – коэффициент связи,
характеризующий
магнитную связь между
катушками.
Вывод: взаимная
индуктивность M зависит от
индуктивностей обоих
контуров и их взаимного
расположения.
10.
Степень индуктивнойсвязи элементов
характеризуется
коэффициентом
магнитной связи
где :
М – взаимная индуктивность элементов
цепи (размерность – Гн);
L1 и L2 – собственные индуктивности этих
элементов
k ≤1 (в пределе, когда магнитный поток одной
катушки полностью пронизывает витки другой, k=1;
при отсутствии магнитной связи k=0.)
10
11.
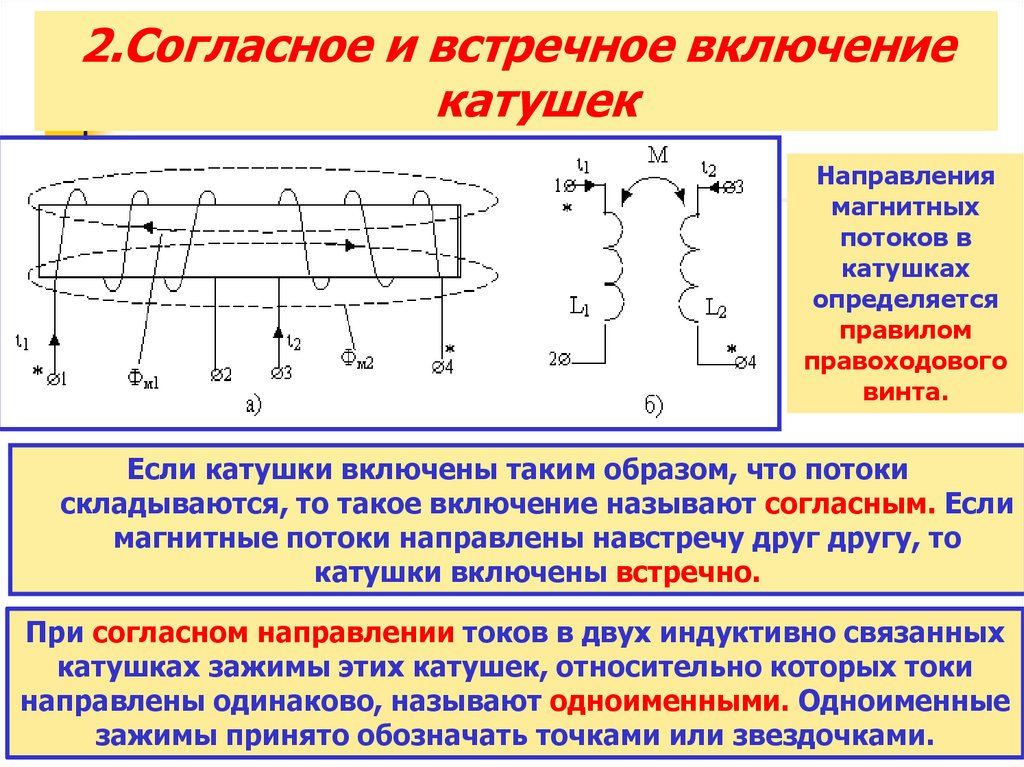
2.Согласное и встречное включениекатушек
Направления
магнитных
потоков в
катушках
определяется
правилом
правоходового
винта.
Если катушки включены таким образом, что потоки
складываются, то такое включение называют согласным. Если
магнитные потоки направлены навстречу друг другу, то
катушки включены встречно.
При согласном направлении токов в двух индуктивно связанных
катушках зажимы этих катушек, относительно которых токи
направлены одинаково, называют одноименными. Одноименные
зажимы принято обозначать точками или звездочками.
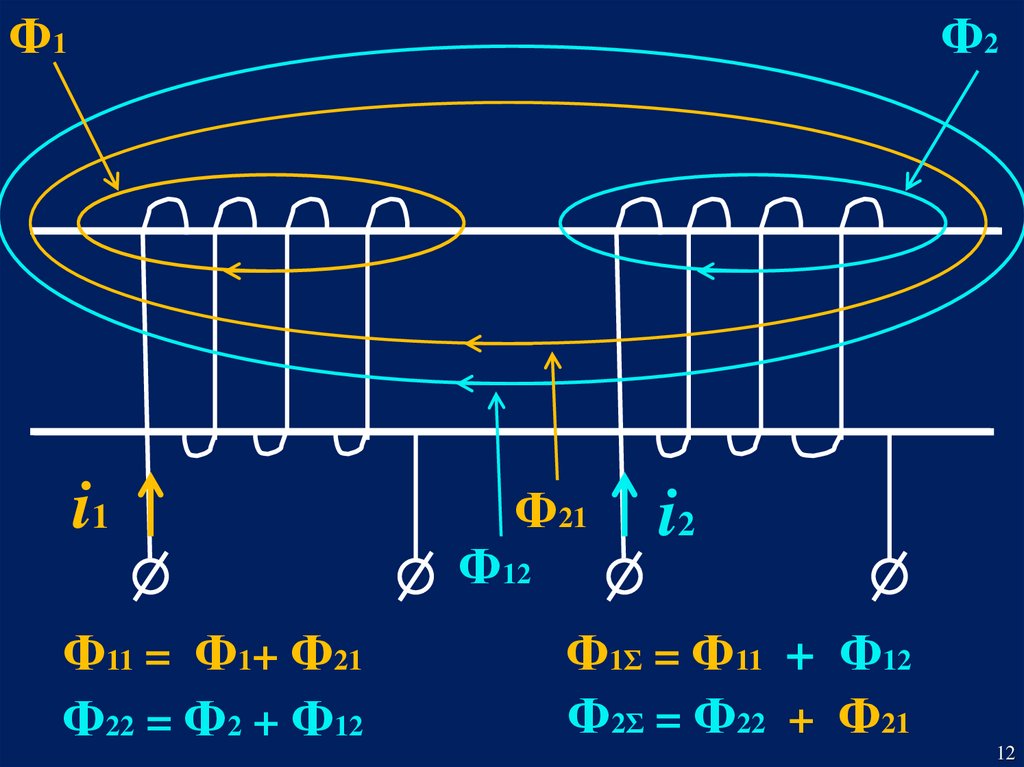
12.
Ф1Ф2
i1
Ф11 = Ф1+ Ф21
Ф22 = Ф2 + Ф12
Ф21
Ф12
i2
Ф1Σ = Ф11 + Ф12
Ф2Σ = Ф22 + Ф21
12
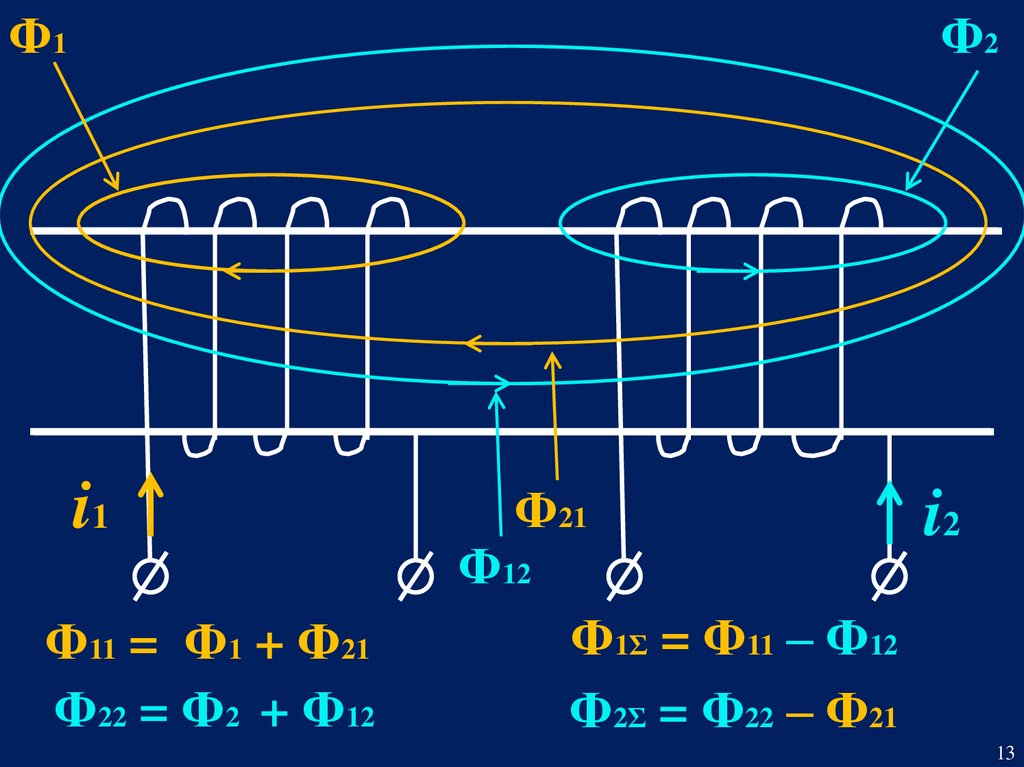
13.
Ф1Ф2
i1
Ф11 = Ф1 + Ф21
Ф22 = Ф2 + Ф12
Ф21
Ф12
i2
Ф1Σ = Ф11 – Ф12
Ф2Σ = Ф22 – Ф21
13
14.
В общем случае:Ф1Σ = Ф11
Ф2Σ = Ф22
Ф12
Ф21
С учётом того, что
14
15.
1516.
1617.
В соответствии с закономэлектромагнитной индукции Фарадея
получим:
17
18.
Катушки можно включить так, что ЭДСсамоиндукции будет суммироваться с ЭДС
взаимной индукции либо вычитаться.
Один из зажимов каждой катушки на схеме
помечают, например, точкой или звездочкой.
Этот знак означает начала обмоток катушек.
При одинаковой ориентации токов
относительно начала обмоток потоки будут
суммироваться, а при различной - вычитаться
18
19.
При согласном включениикатушек
19
20.
При встречном включении катушек20
21.
Напряжения на зажимахиндуктивно связанных катушек
M
R1
i1
L1
u
L2
R2
d 1
di1
di2
u1 R1i1
R1i1 L
M
;
dt
dt
dt
i2
u2
d 2
di2
di1
u 2 R2 i2
R2 i2 L
M
.
dt
dt
dt
U 1 ( R1 j L1 ) I 1 j M I 2 ( R1 jX L1 ) I 1 jX M I 2
U 2 ( R2 j L2 ) I 2 j M I 1 ( R2 jX L 2 ) I 2 jX M I1
где
jX M j M
комплекс сопротивления взаимоиндукции;
знак плюс (+М) ставят при согласном включении катушек;
знак минус ( М) при их встречном включении.
22.
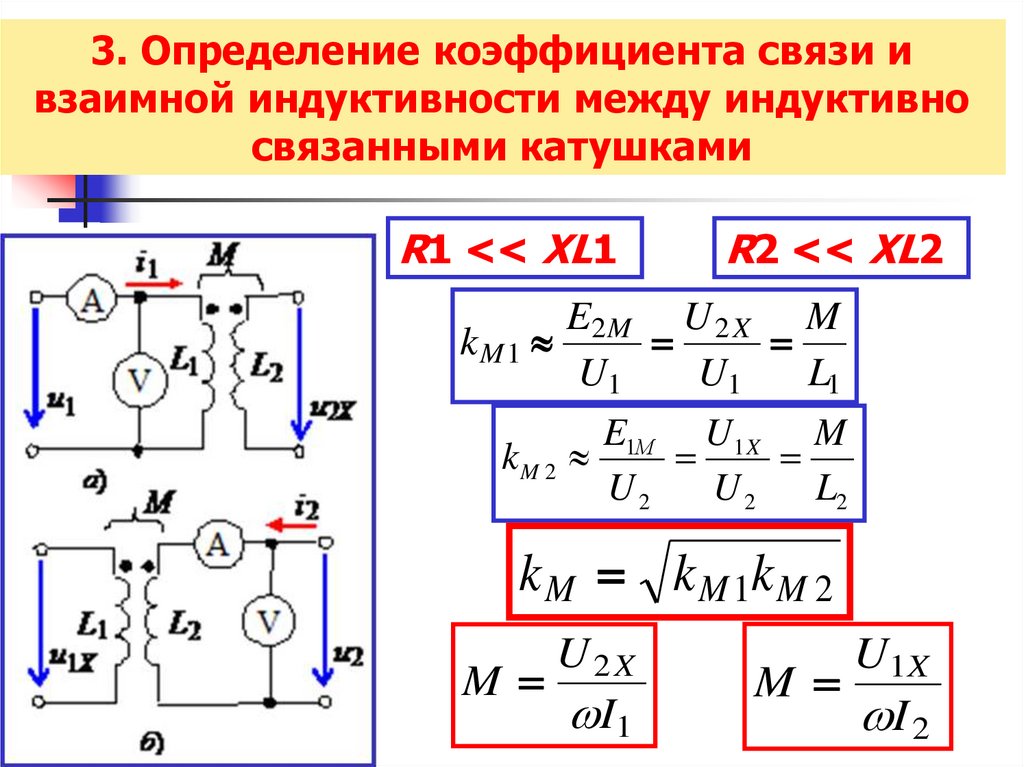
3. Определение коэффициента связи ивзаимной индуктивности между индуктивно
связанными катушками
R1 << XL1
R2 << XL2
E2 M U 2 X M
kM1
U1
U1
L1
E1М U1 X M
kM 2
U2
U2
L2
k M k M 1k M 2
U2X
M
I1
U1 X
M
I 2
23.
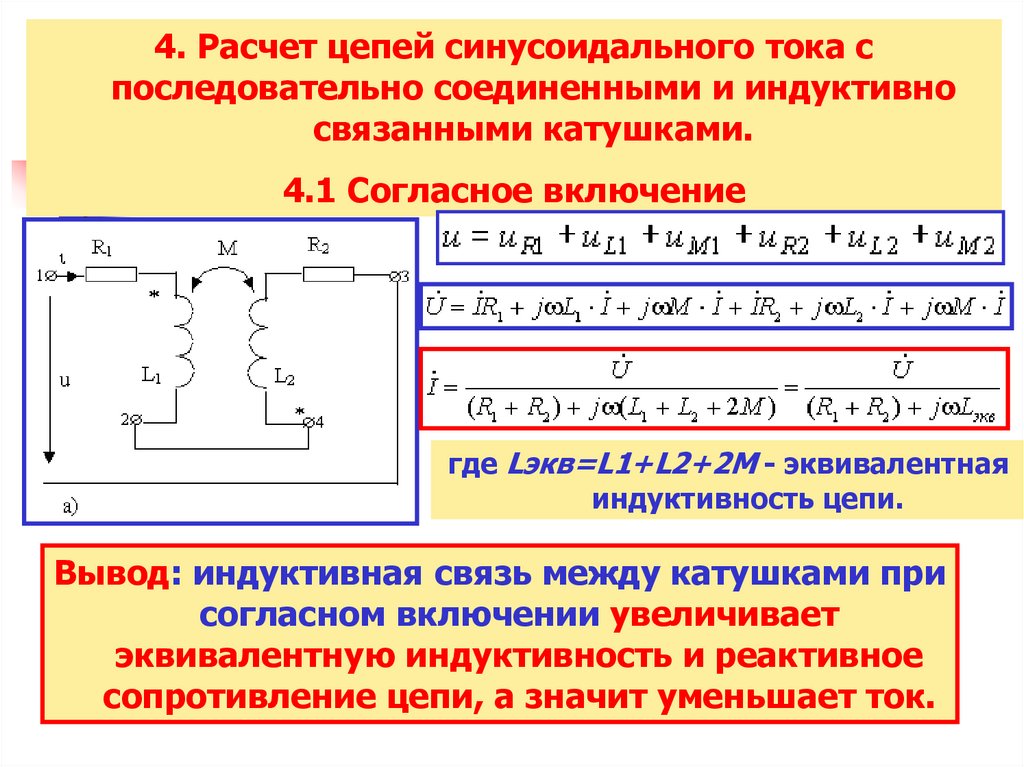
4. Расчет цепей синусоидального тока споследовательно соединенными и индуктивно
связанными катушками.
4.1 Согласное включение
где Lэкв=L1+L2+2M - эквивалентная
индуктивность цепи.
Вывод: индуктивная связь между катушками при
согласном включении увеличивает
эквивалентную индуктивность и реактивное
сопротивление цепи, а значит уменьшает ток.
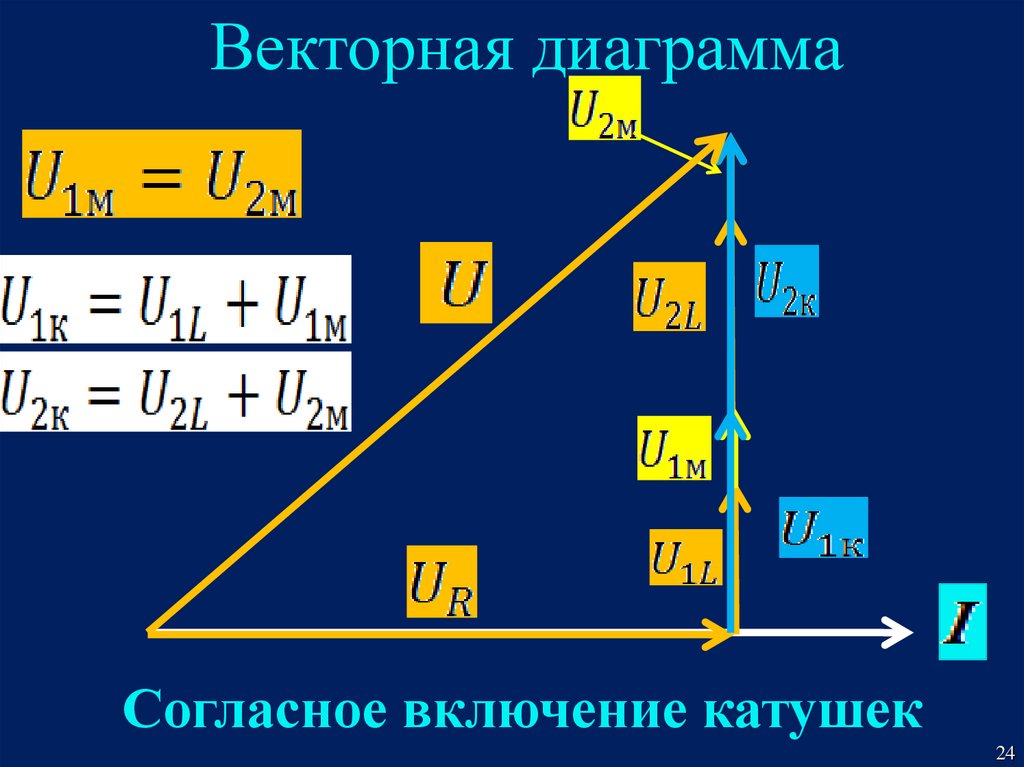
24.
Векторная диаграммаСогласное включение катушек
24
25.
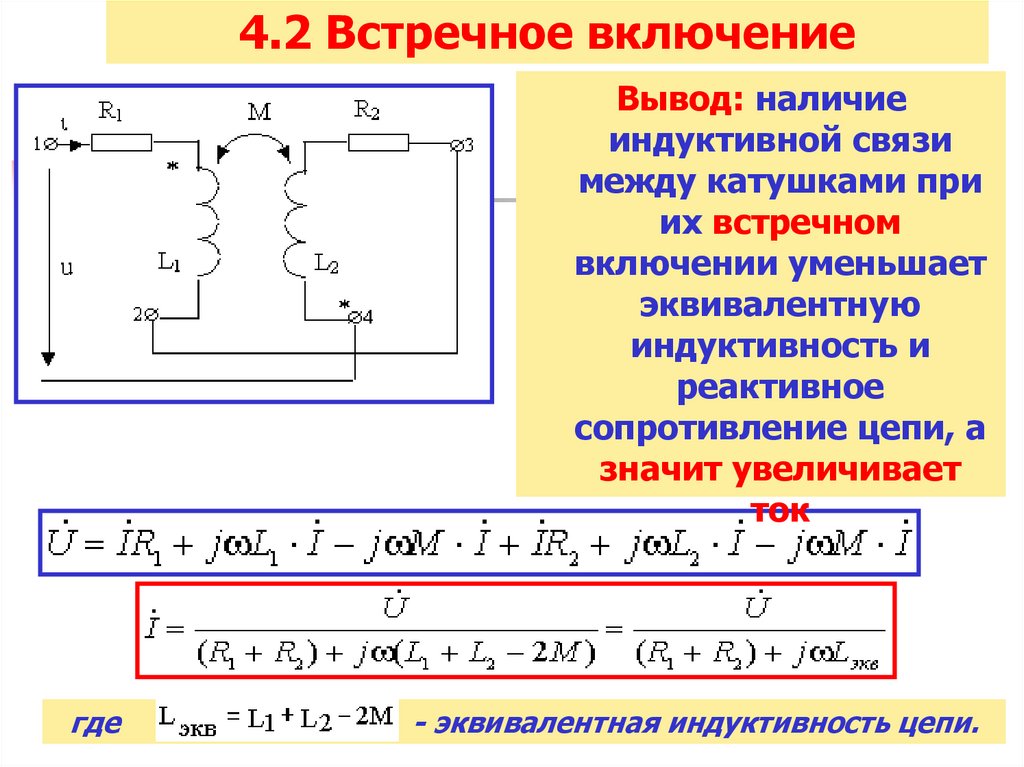
4.2 Встречное включениеВывод: наличие
индуктивной связи
между катушками при
их встречном
включении уменьшает
эквивалентную
индуктивность и
реактивное
сопротивление цепи, а
значит увеличивает
ток
где
- эквивалентная индуктивность цепи.
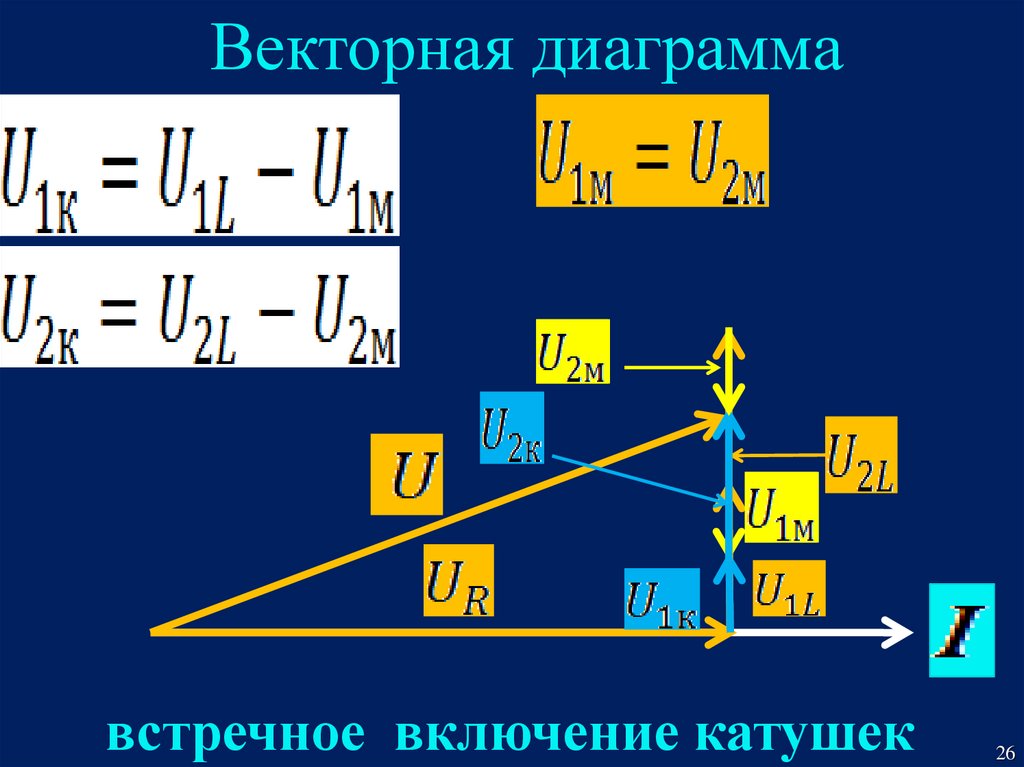
26.
Векторная диаграммавстречное включение катушек
26








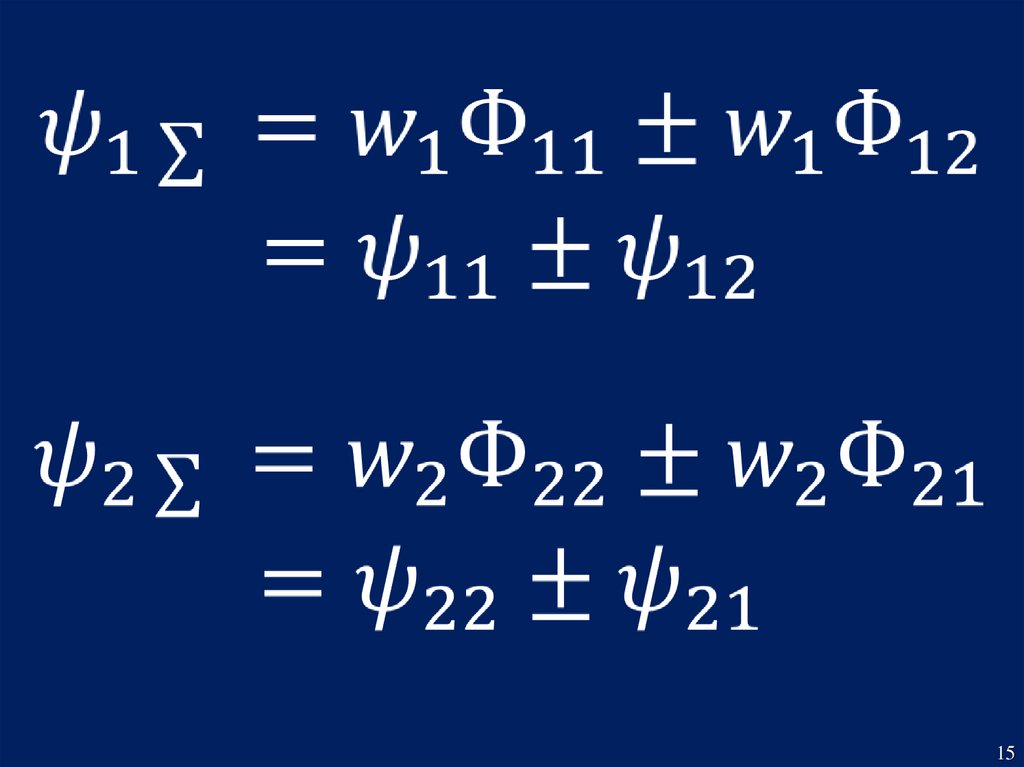
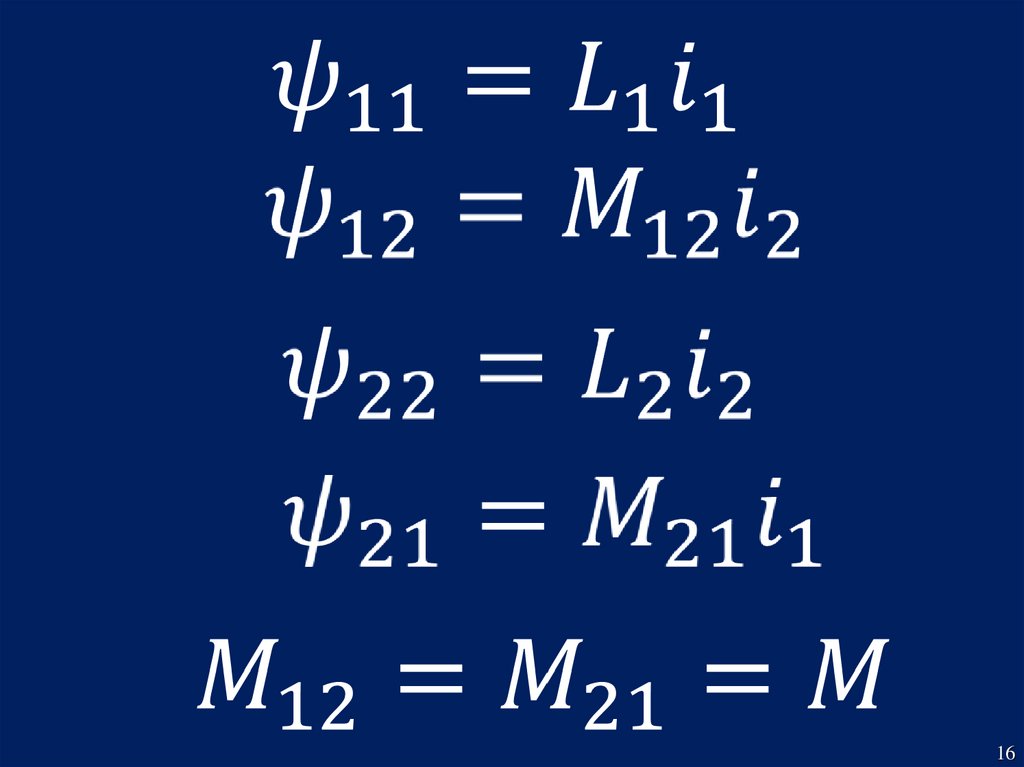





 physics
physics








