Свойства и методы расчета цепей постоянного тока (i=I=const). Лекция 2

1.

Лекция 2
Свойства и методы расчета цепей постоянного тока (i=I=const)
Отличие расчета цепей постоянного и переменного тока
i L
R
i
L
u
R
di
uL L
dt
i = I = const
L
L
uL=0
i
uL 0
Индуктивность не оказывает сопротивления постоянному
току.
В цепях постоянного тока (в стационарных режимах) вместо
индуктивности включают перемычку (идеальный проводник).

2.

iC
R
C
iC=0
LuС
duc
iC C
dt
R
т.к.
L
uС=uхх
uC=UC=const
i
iC 0
Конденсатор не пропускает постоянный ток.
В цепях постоянного тока (в стационарных режимах)
конденсатор эквивалентен разрыву .
РЕЗЮМЕ: на постоянном токе имеют место только
резистивные цепи (один пассивный элемент - резистор).

3.

Топологические понятия теории цепей. Законы Кирхгофа.
Типовая задача - на токораспределение. Известны параметры
и источники, - найти токи.
x (t)
y (t)
=I
воздействие
R
отклик
L
Для решения задач на токораспределение
в неразветвленных цепях применяют –i закон Ома,
L
в разветвленных- Rзаконы Кирхгофа
(1845 г.– Густав Роберт Кирхгоф
)
C
Законы Кирхгофа являются топологическими законами.
Топология – очертания, геометрия схемы.
Основные топологические понятия:
ветвь, узел, контур, граф

4.

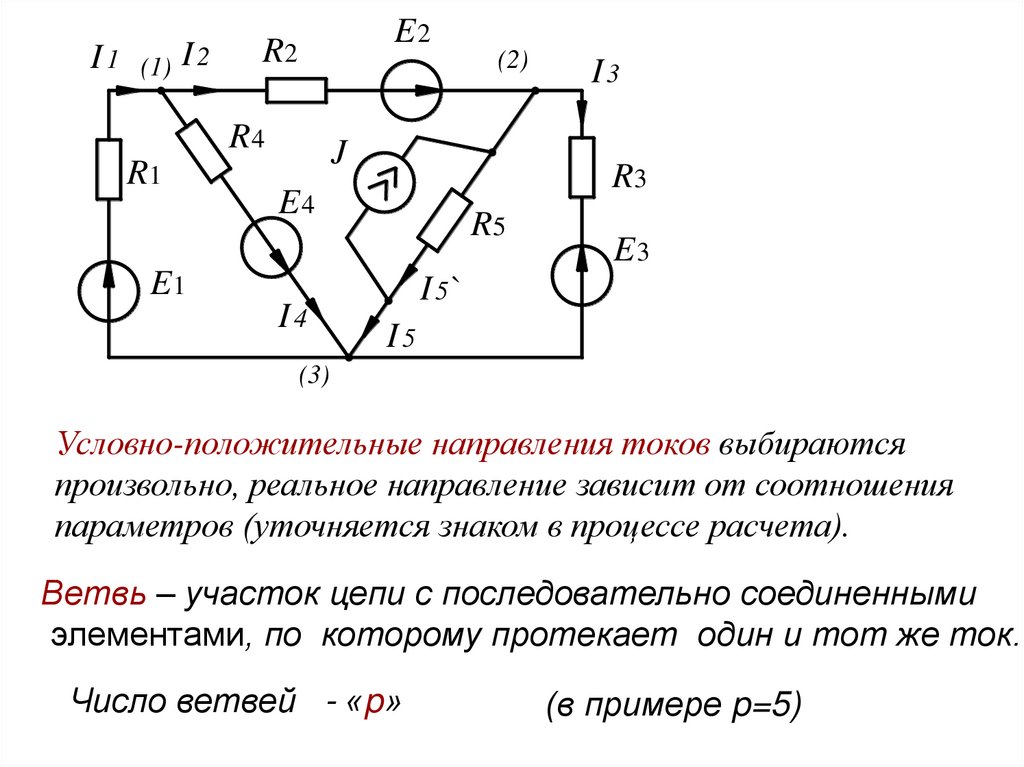
I 1 (1) I 2
E2
R2
(2)
R4
R1
J
R3
E4
R5
E1
I4
I3
E3
I 5`
I5
(3)
Условно-положительные направления токов выбираются
произвольно, реальное направление зависит от соотношения
параметров (уточняется знаком в процессе расчета).
Ветвь – участок цепи с последовательно соединенными
элементами, по которому протекает один и тот же ток.
Число ветвей - «p»
(в примере p=5)

5.

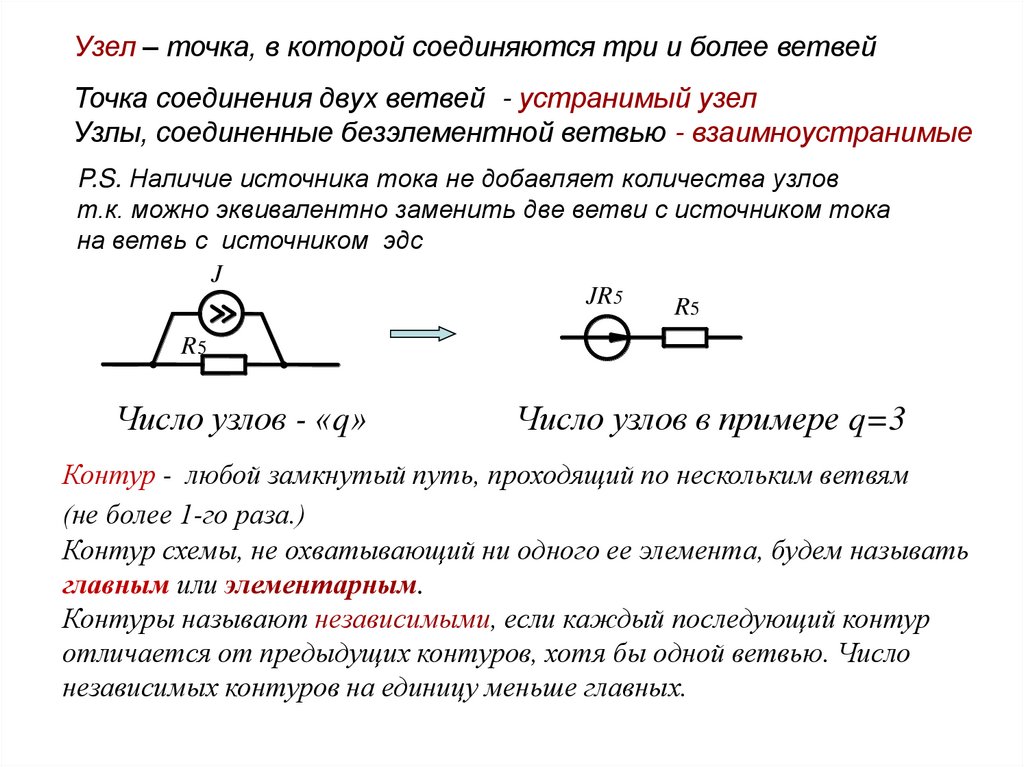
Узел – точка, в которой соединяются три и более ветвей
Точка соединения двух ветвей - устранимый узел
Узлы, соединенные безэлементной ветвью - взаимноустранимые
P.S. Наличие источника тока не добавляет количества узлов
т.к. можно эквивалентно заменить две ветви с источником тока
на ветвь с источником эдс
J
J
JR5
R5
R5 JR5
R5
R5
Число узлов - «q»
q=3
E 2 Число узлов в примере
a
I 1 (1)
(2)
E2 I 2
Ia
3
R
2
I
2
I
1
(2)
(1) - любой замкнутый путь,
Контур
ветвям
I 3 проходящий по нескольким
R
1
R3
R4
R
1
J
(не более 1-го
R3
E
R4 раза.)
R
1
R
3
J
Контур
R1 схемы, не охватывающий
R3ни одного ееEэлемента, будем называть
R2
главным или элементарным.
Контуры называют независимыми, если каждый последующий контур
отличается от предыдущих контуров, хотя бы одной ветвью. Число
независимых контуров на единицу меньше главных.

6.

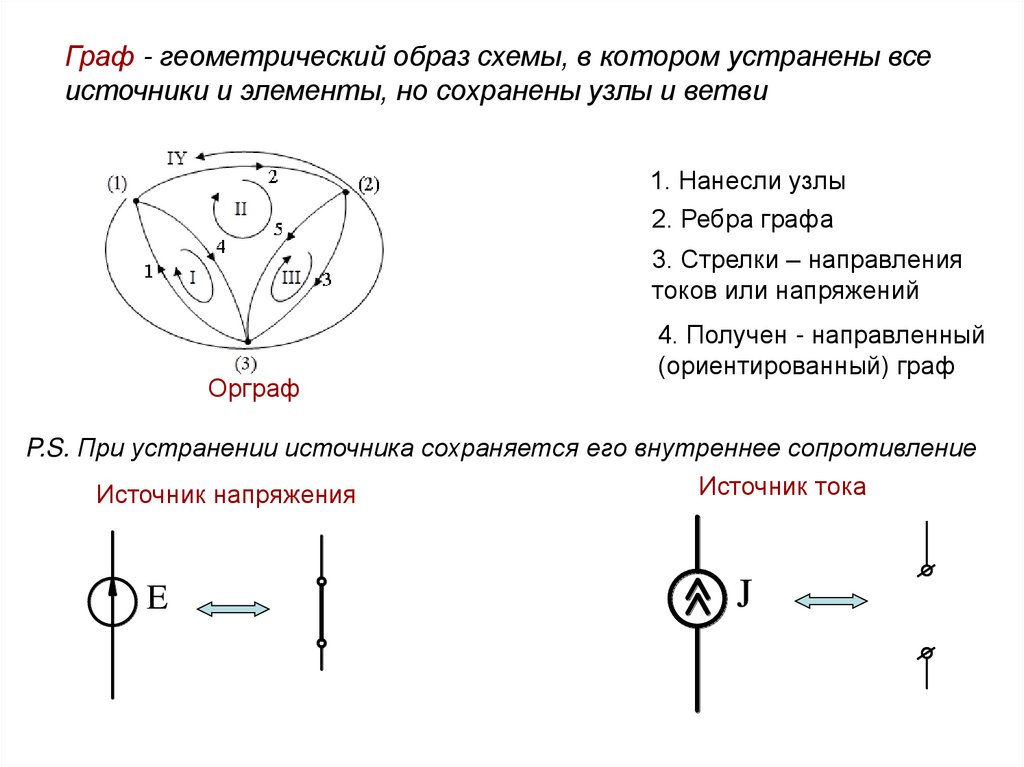
Граф - геометрический образ схемы, в котором устранены все
источники и элементы, но сохранены узлы и ветви
1. Нанесли узлы
2. Ребра графа
3. Стрелки – направления
токов или напряжений
Орграф
4. Получен - направленный
(ориентированный) граф
P.S. При устранении источника сохраняется его внутреннее сопротивление
Источник тока
Источник напряжения
E
J

7.

Два топологических закона Кирхгофа
Первый закон Кирхгофа
p
Алгебраическая сумма токов в любом узле в любой
момент времени равна нулю
(ни в каком узле не может быть накапливания зарядов)
I 0
k 1
k
Правило знаков: токи, направленные к узлу записывают со знаком
«– », от узла со знаком «+».
Второй закон Кирхгофа
Алгебраическая сумма напряжений в любом контуре цепи в любой
момент времени равна нулю.
Или алгебраическая сумма напряжений на пассивных элементах
контура равна алгебраической сумме ЭДС в этом контуре
U E
или
I k Rk E k
Так как
U Ek Ek
Правило знаков: со знаком «+» слагаемые записывают в случае, если
напряжение, ток и ЭДС совпадают с принятым направлением обхода контура

8.

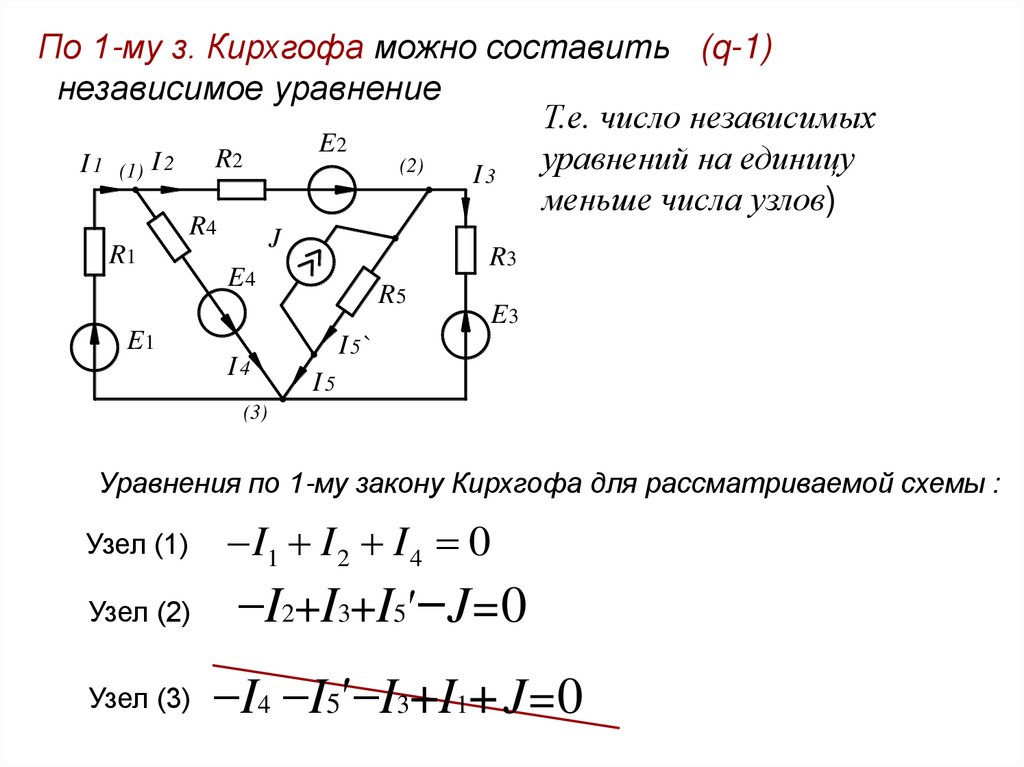
По 1-му з. Кирхгофа можно составить (q-1)
независимое уравнение
Т.е. число независимых
E2
R
2
уравнений на единицу
I 1 (1) I 2
(2)
I3
меньше числа узлов)
R4
R1
J
R3
E4
R5
E1
I4
E3
I 5`
I5
(3)
Уравнения по 1-му закону Кирхгофа для рассматриваемой схемы :
Узел (1)
I1 I 2 I 4 0
Узел (2)
−I2+I3+I5′−J=0
Узел (3)
−I4 −I5′−I3+I1+ J=0

9.

Для получения независимых уравнений по 2-му закону Кирхгофа
рассматриваются независимые контуры.
Независимым наз. контур, содержащий в себе хотя бы одну новую
ветвь, не включённую в другие контуры.
Число независимых контуров всегда совпадает с количеством
внутренних элементарных ячеек.
Пример:
в схеме 7 контуров, но независимых – 3 (по числу ячеек)

10.

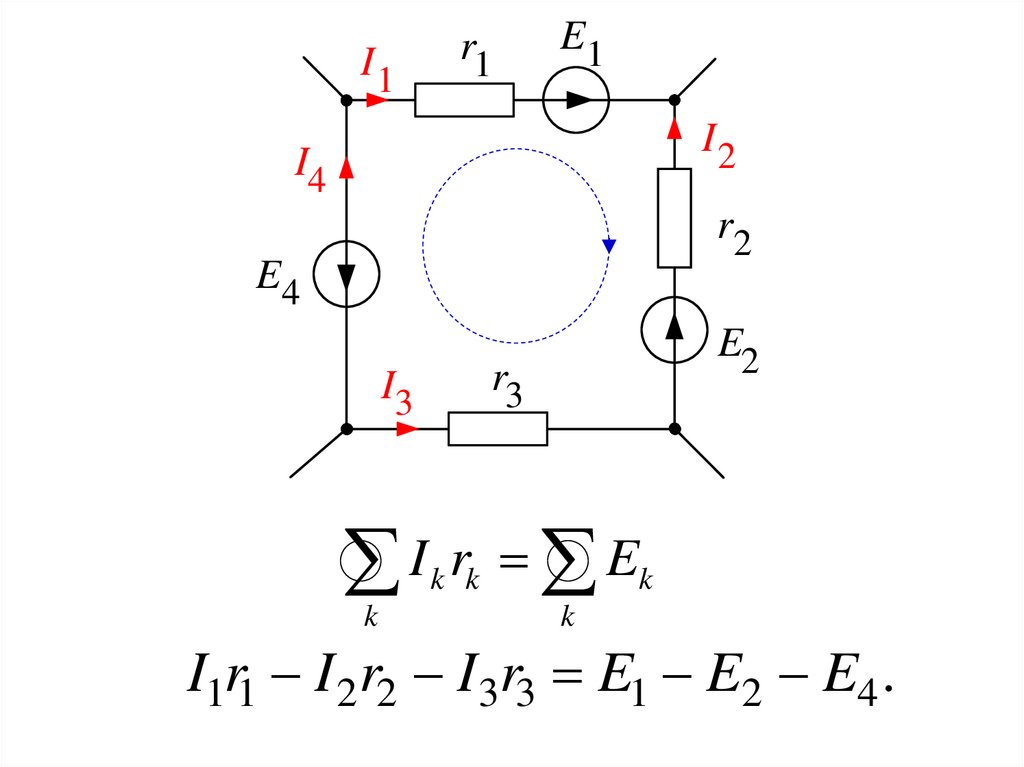
I1
r1
E1
I2
I4
r2
E4
E2
r3
I3
I r E
k k
k
k
k
I1r1 I 2r2 I 3r3 E1 E2 E4 .

11.

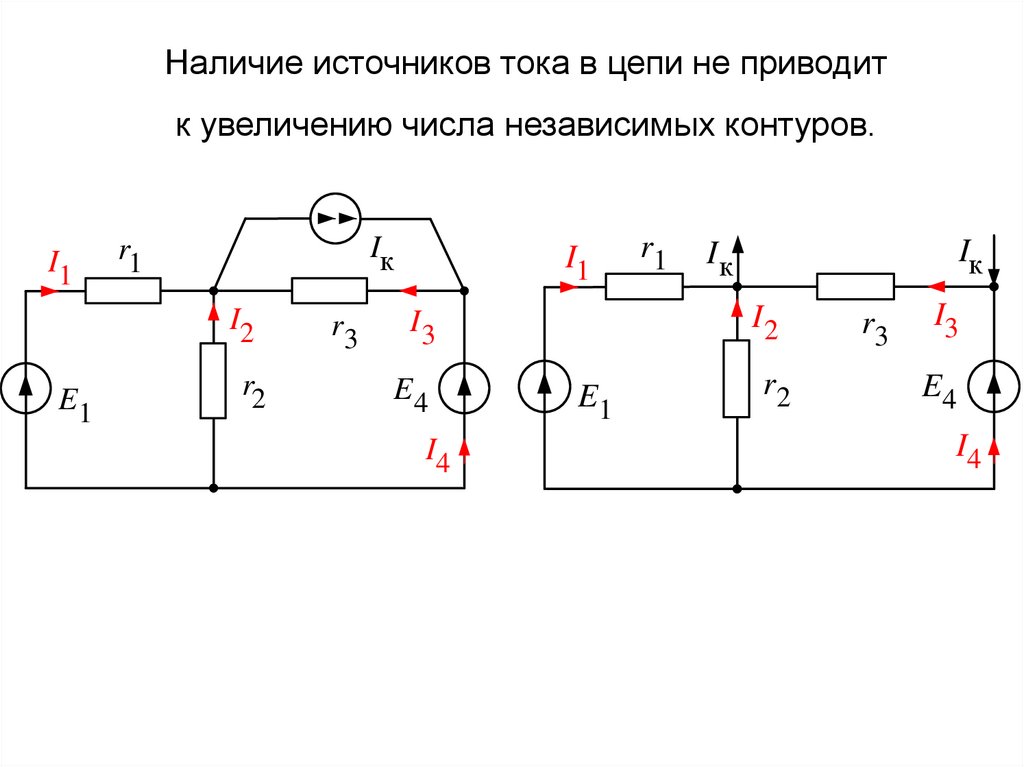
Наличие источников тока в цепи не приводит
к увеличению числа независимых контуров.
I1
Iк
r1
I2
E1
r2
r3
I1
I4
Iк
Iк
I2
I3
E4
r1
E1
r2
r3
I3
E4
I4

12.

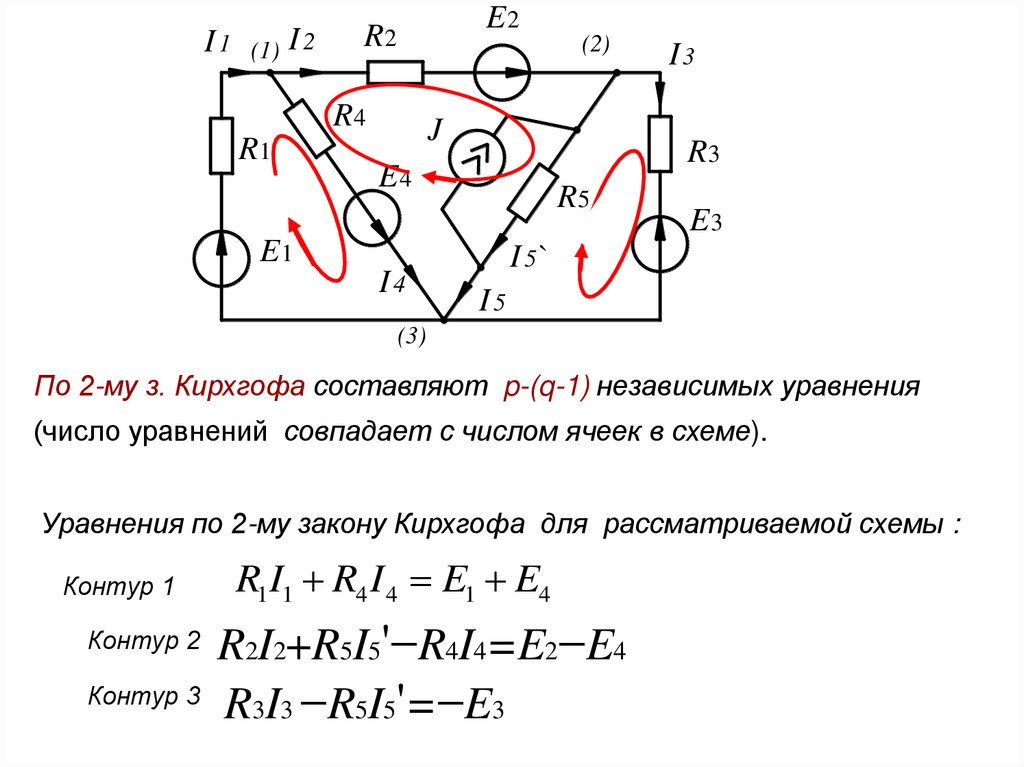
I 1 (1) I 2
E2
R2
(2)
R4
R1
J
R3
E4
R5
E1
I4
I3
E3
I 5`
I5
(3)
По 2-му з. Кирхгофа составляют p-(q-1) независимых уравнения
(число уравнений совпадает с числом ячеек в схеме).
Уравнения по 2-му закону Кирхгофа для рассматриваемой схемы :
Контур 1
R1I1 R4 I 4 E1 E4
R2I2+R5I5'−R4I4=E2−E4
Контур 3
R3I3 −R5I5'=−E3
Контур 2

13.

Порядок расчета с помощью законов Кирхгофа
1. Задаемся условно положительными направлениями токов в ветвях
(знак определяется расчетом)
2. Определяем число ветвей «p», узлов «q» и независимых контуров
(число ячеек)
3. Выбираем произвольно направление обхода контуров
4. Составляем (q-1) уравнение по 1-му закону Кирхгофа
(число узлов без одного)
5. Недостающее число уравнений p-(q-1) составляем по 2-му закону
Кирхгофа для независимых контуров (число независимых контуров
равно числу ячеек)
1-ый закон Кирхгофа
2-ой закон Кирхгофа
«p» уравнений
В совокупности 1-ый и 2-ой законы Кирхгофа дают «p» уравнений т.е. полностью
определяют состояние цепи (совместное решение уравнений позволяет определить токи
всех ветвей).
Законы Кирхгофа используют, как правило, для проверки правильности
расчета более совершенными способами

14.

Для рассматриваемой схемы:
Матрица коэффициентов
уравнений по з. Кирхгофа
1 1 0
0 1 1
K R1 0 0
0 R2 0
0 0 R3
1
0
R4
R4
0
0
1
0
R5
R5
−I2+I3+I5'−J=0
R1I1 R4 I 4 E1 E4
R2I2+R5I5'−R4I4=E2−E4
R3I3 −R5I5'=−E3
P.S. В уравнениях по 1-му з. Кирхгофа
коэффициенты «±1» или «0»,
по 2-му з. Кирхгофа – «сопротивление
ветви» или «0»
Матрица искомых
токов
I1
Решение
I
2
1
I I3
I K W
I4
I 5
Матрица активных
элементов (источников)
0
J0
W E1 E4
E
E
4
2
E3
I1 I 2 I 4 0

15.

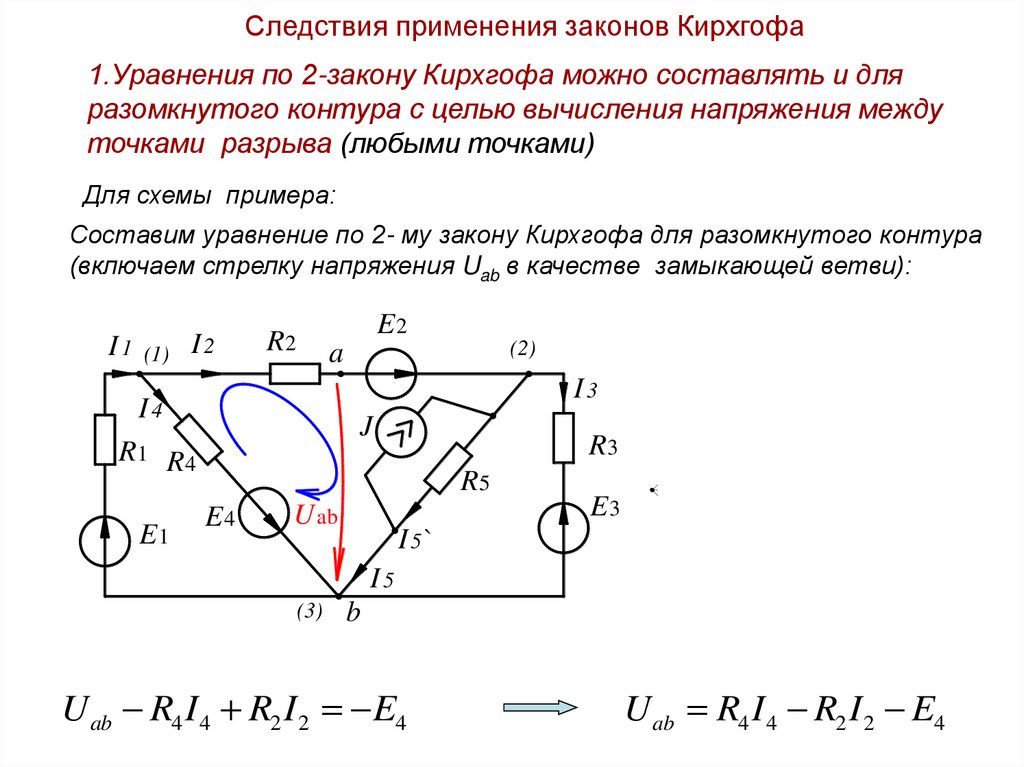
Следствия применения законов Кирхгофа
1.Уравнения по 2-закону Кирхгофа можно составлять и для
разомкнутого контура с целью вычисления напряжения между
точками разрыва (любыми точками)
Для схемы примера:
Составим уравнение по 2- му закону Кирхгофа для разомкнутого контура
(включаем стрелку напряжения Uab в качестве замыкающей ветви):
I 1 (1) I 2
E2
R2
I3
I4
J
R1 R4
E1
(2)
a
R3
R5
E4
U ab
E3
I 5`
I5
(3)
b
U ab R4 I 4 R2 I 2 E4
U ab R4 I 4 R2 I 2 E4

16.

a
I1
r1
r3
b
I2
Uad
g
c
r5
r2
E1
I3
r4
f
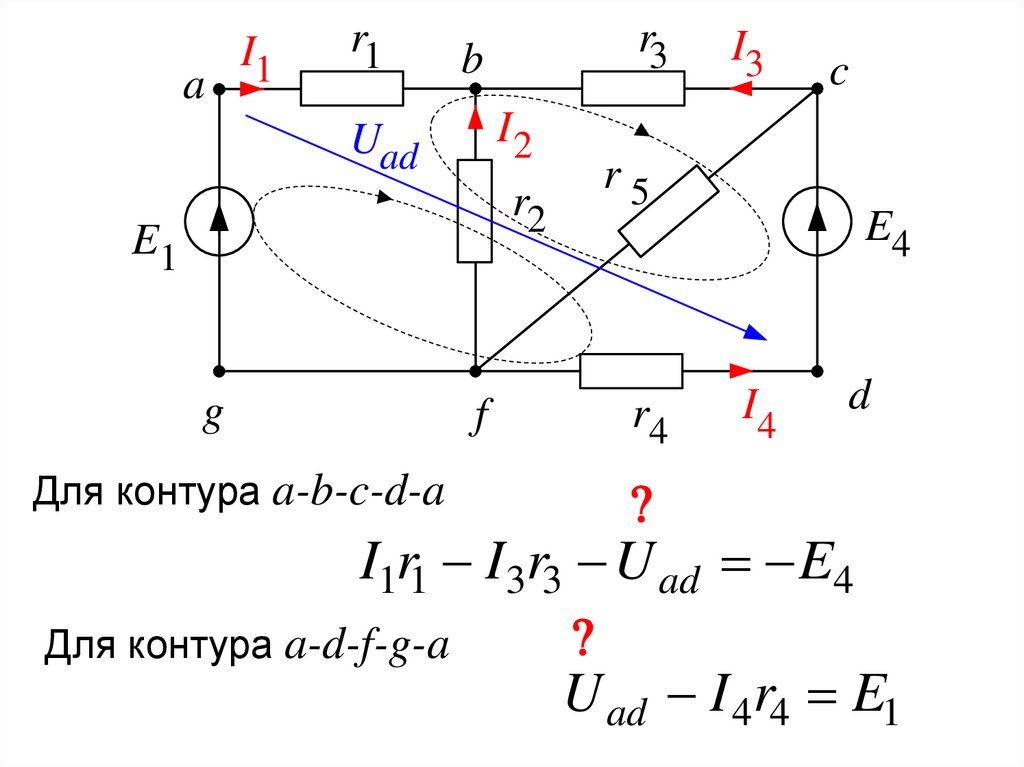
Для контура a-b-c-d-a
E4
I4
d
I1r1 I 3r3 U ad E4
Для контура a-d-f-g-a
U ad I 4 r4 E1

17.

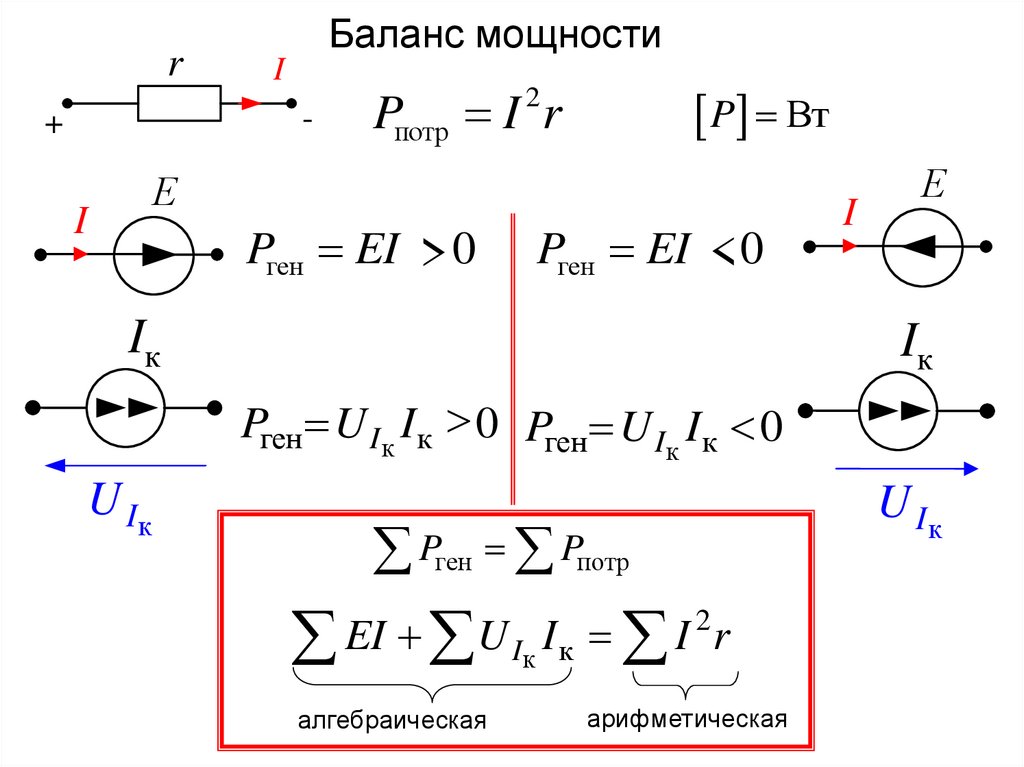
3. Баланс мощности (является следствием закона сохранения
энергии и служит для проверка правильности расчета)
генерируемой мощности = потребляемой мощности
Pпотр I 2 R
арифметическая сумма, всегда ˃0
Pген Pист.напр. Pист.тока
Pген EI J kU k
Источник напряжения
E
E I
I
E
E I
I
Pген.=Pпотр.
Правило знаков
E I
Pген EI 0
E I
алгебраическая сумма
Pген EI 0
Источник тока
Jk
Jk
Uk
J k Uk
Jk
Uk
Uk
J U k
Pген J kU k 0
J U k
Pген J kU k 0

18.

r
Баланс мощности
I
-
+
I
P Вт
Pпотр I 2 r
Е
Pген EI > 0
Pген EI < 0
Iк
I
Е
Iк
Pген U Iк Iк 0 Pген U I Iк
0
к
U Iк
Pген Pпотр
2
EI
U
I
I
Iк к r
алгебраическая
арифметическая
U Iк

19.

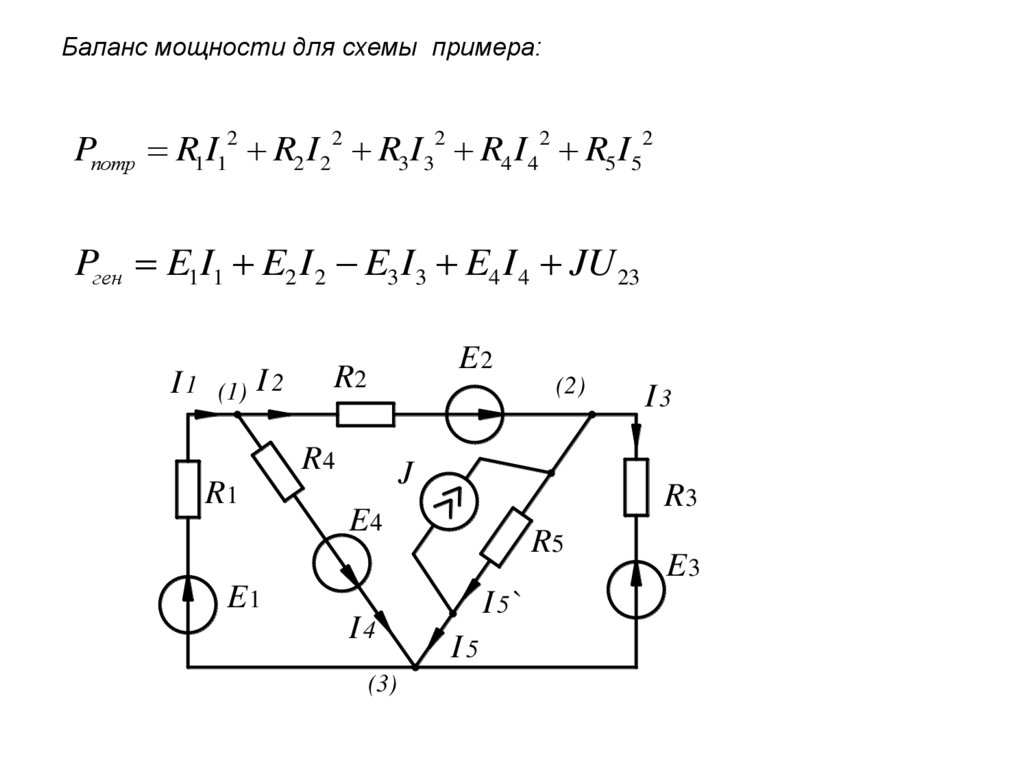
Баланс мощности для схемы примера:
Pпотр R1I12 R2 I 22 R3 I32 R4 I 42 R5 I52
Pген E1I1 E2 I 2 E3 I3 E4 I 4 JU 23
I 1 (1) I 2
E2
R2
(2)
R4
R1
J
R3
E4
R5
E1
I4
(3)
I3
I 5`
I5
E3

20.

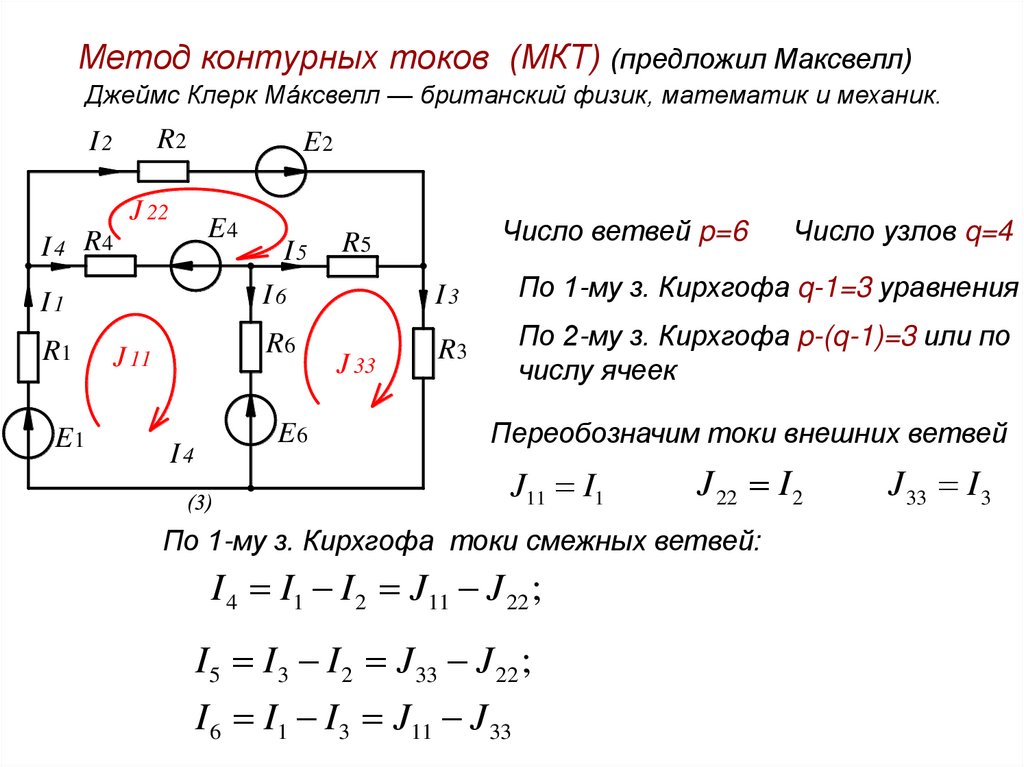
Метод контурных токов (МКТ) (предложил Максвелл)
Джеймс Клерк Ма́ксвелл — британский физик, математик и механик.
R2
I2
J 22
E2
E4
I 4 R4
I5
Число ветвей p=6
R5
Число узлов q=4
I1
I6
I3
По 1-му з. Кирхгофа q-1=3 уравнения
R1
R6
R3
По 2-му з. Кирхгофа p-(q-1)=3 или по
числу ячеек
E1
J 11
I4
E6
J 33
Переобозначим токи внешних ветвей
J11 I1
J 22 I 2
По 1-му з. Кирхгофа токи смежных ветвей:
I 4 I1 I 2 J11 J 22 ;
I5 I3 I 2 J 33 J 22 ;
I 6 I1 I 3 J11 J 33
J 33 I 3

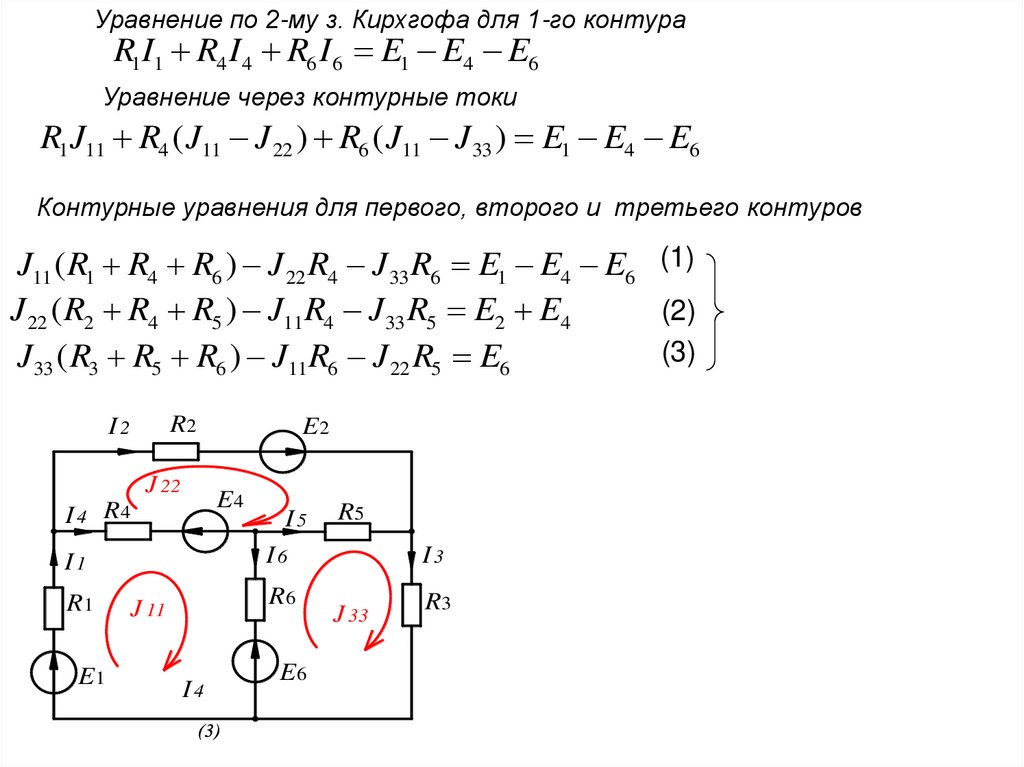
21.

Уравнение по 2-му з. Кирхгофа для 1-го контура
R1I1 R4 I 4 R6 I 6 E1 E4 E6
Уравнение через контурные токи
R1 J11 R4 ( J11 J 22 ) R6 ( J11 J 33 ) E1 E4 E6
Контурные уравнения для первого, второго и третьего контуров
J11 ( R1 R4 R6 ) J 22 R4 J 33 R6 E1 E4 E6 (1)
(2)
J 22 ( R2 R4 R5 ) J11R4 J 33 R5 E2 E4
(3)
J 33 ( R3 R5 R6 ) J11 R6 J 22 R5 E6
R2
I2
J 22
E4
I 4 R4
E1
I5
R5
I6
I1
R1
E2
R6
J 11
I4
E6
I3
J 33
R3

22.

R11 J11 R12 J 22 R13 J 33 ... E11
R21 J11 R22 J 22 R23 J 33 ... E22
R31 J11 R32 J 22 R33 J 33 ... E33
контурные уравнения
в канонической форме
........
Rii - собственное сопротивление i – того контура = арифметической сумме
сопротивлений контура (всегда >0)
Rij - сопротивления смежных ветвей с соответствующим знаком
( с «+» если в смежной ветви контурные токи сонаправлены,
-
знак « » если смежные контурные токи встречны
Ekk - контурная ЭДС= алгебраической сумме ЭДС в k – том контуре:
«+», если стрелка ЭДС совпадает с направлением обхода контура
-
« », если встречна

23.

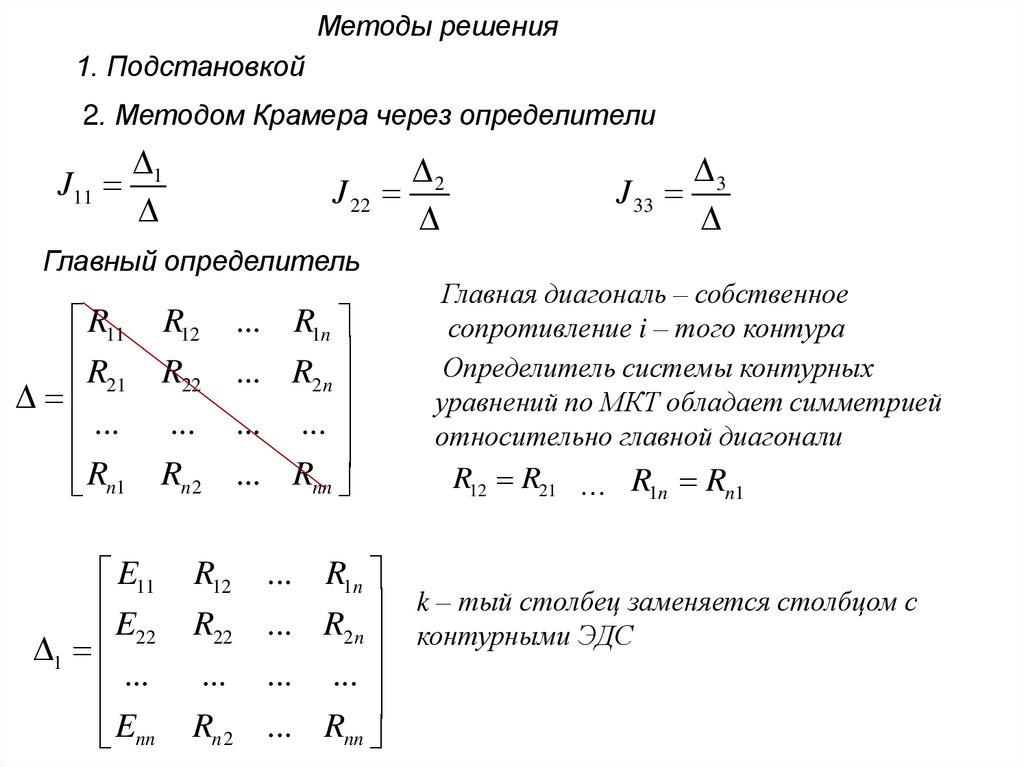
Методы решения
1. Подстановкой
2. Методом Крамера через определители
1
J11
J 22
2
J 33
3
Главный определитель
R11
R
21
...
Rn1
E11
E
1 22
...
Enn
R12
R22
...
Rn 2
R12
R22
...
Rn 2
... R1n
... R2 n
... ...
... Rnn
... R1n
... R2 n
... ...
... Rnn
Главная диагональ – собственное
сопротивление i – того контура
Определитель системы контурных
уравнений по МКТ обладает симметрией
относительно главной диагонали
R12 R21 … R1n Rn1
k – тый столбец заменяется столбцом с
контурными ЭДС

24.

Решение с помощью ПК
Система уравнений в матричной форме:
Rk J k Ek
J11
J
22
J
k ...
J nn
J k Rk Ek
1
R11
R
21
R
k ...
Rn1
R12
R22
...
Rn 2
... R1n
... R2 n
... ...
... Rnn
E11
E
22
E
k ...
Enn

25.

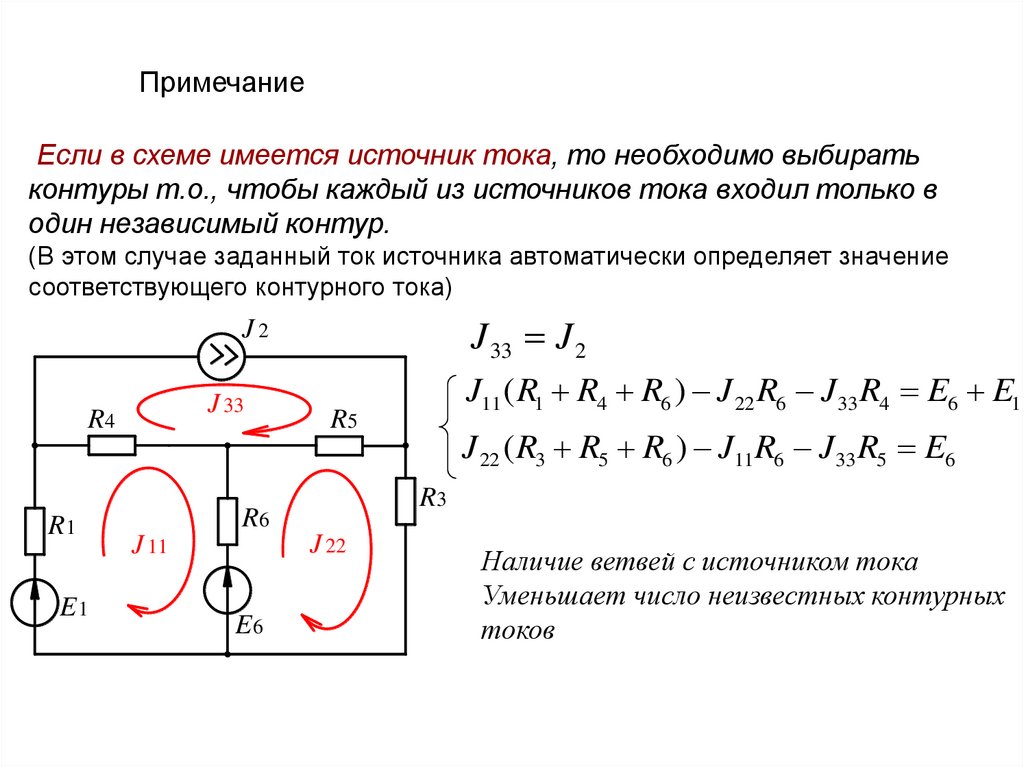
Примечание
Если в схеме имеется источник тока, то необходимо выбирать
контуры т.о., чтобы каждый из источников тока входил только в
один независимый контур.
(В этом случае заданный ток источника автоматически определяет значение
соответствующего контурного тока)
J 33 J 2
J2
J 33
R4
R1
E1
R5
J 22
E6
J 22 ( R3 R5 R6 ) J11 R6 J 33 R5 E6
R3
R6
J 11
J11 ( R1 R4 R6 ) J 22 R6 J 33 R4 E6 E1
Наличие ветвей с источником тока
Уменьшает число неизвестных контурных
токов

26.

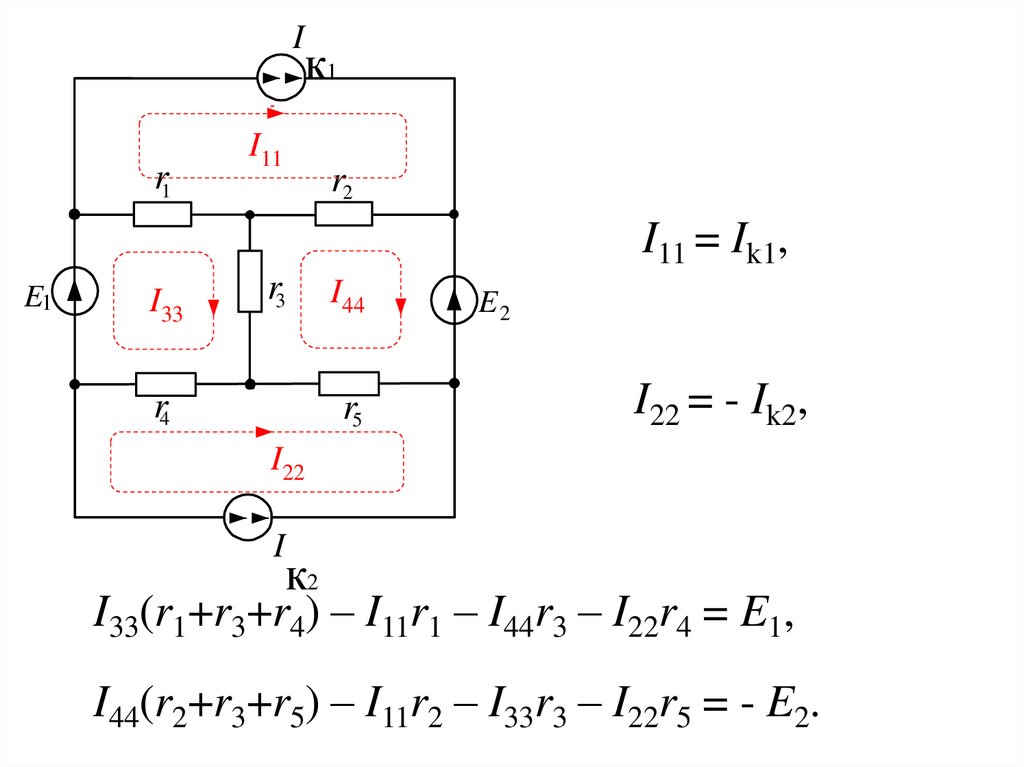
I
r1
к1
I11
r2
I11 = Ik1,
E1
I33
r3
r4
I44
r5
E2
I22 = - Ik2,
I22
I
к2
I33(r1+r3+r4) – I11r1 – I44r3 – I22r4 = E1,
I44(r2+r3+r5) – I11r2 – I33r3 – I22r5 = - E2.

27.

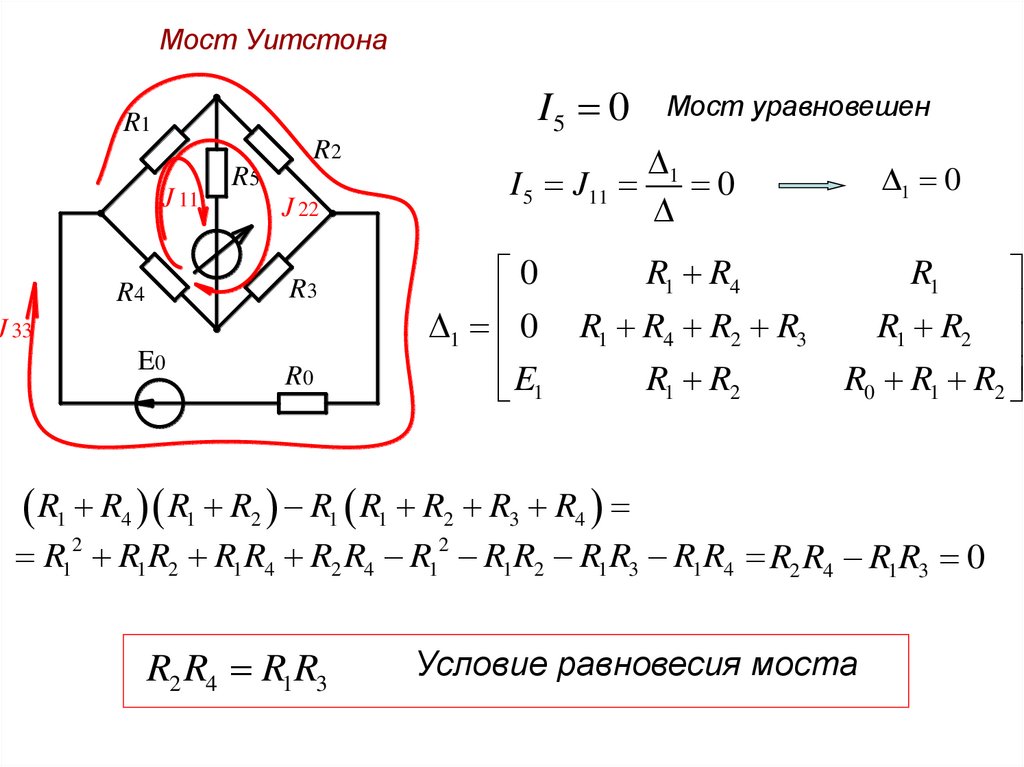
Мост Уитстона
I5 0
R1
R2
J 11
R5
J 22
R3
R4
J 33
E0
R0
Мост уравновешен
E3 1 E
I 5 J11
0
0
1 0
E1
R1 R4
R1 R4 R2 R3
R1 R2
1 0
R1
R1 R2
R0 R1 R2
R1 R4 R1 R2 R1 R1 R2 R3 R4
R12 R1 R2 R1 R4 R2 R4 R12 R1 R2 R1 R3 R1 R4 R2 R4 R1R3 0
R2 R4 R1R3
Условие равновесия моста

28.

Выводы
Контурным током называют условный расчетный ток, протекающий
последовательно по всем ветвям контура;
2. Для контурных токов справедлив 2-й закон Кирхгофа;
3. Число контурных токов, а, следовательно, и число расчетных уравнений по
методу контурных токов определяется числом независимых контуров;
4. Контурные токи рекомендуется выбирать по внутренним элементарным
контурам. В этом случае матрица контурных сопротивлений получается
симметричной относительно главной диагонали. Элементы главной
диагонали этой матрицы положительны, все остальные отрицательные;
5. При составлении уравнений схемы, содержащей независимые источники
тока, рекомендуется преобразовать их в источники напряжения (ЭДС).
Либо выбирать независимые контуры таким образом, что бы ветви с
источниками тока входили только в один контур. В этом случае
контурный ток таких контуров будет равен току источника тока с
соответствующим знаком. «+», если направление контурного тока
совпадает с направлением тока источника тока и «-» в противном
случае;
6. Токи ветвей схемы определяются алгебраической суммой контурных
токов, протекающих по ветви.
1.