Производная функции в точке

1.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Лекция 2
ПРОИЗВОДНАЯ ФУНКЦИИ
В ТОЧКЕ

2.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная обратной функции
Пусть для функции f (x) существует обратная функция f –1.
Имеем:
f 1 f ( x) f 1( y) x;
f f 1( y) f ( x) y.
По теореме о производной сложной функции:
f
1
f ( x) f
f ( x) f ( x) f ( y) f ( x)
1
1

3.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная обратной функции
Так как
Отсюда:
или
f 1 f ( x) x ,
то
f
1
1
f ( x) f
f
1
( y)
f ( x)
(f
( y) f ( x) ( x) 1
1
,
f ( x)
y f ( x)
1
y f ( x)
1
( y ))
,

4.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arcsin x, x [ 1;1]
Имеем:
f 1( y ) sin y x,
(arcsin x)
y ;
2 2
1
1
1
( f ( y )) (sin y )
1
1
1
cos y
1 sin 2 y
1 x2

5.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arccos x, x [ 1;1]
Имеем:
f 1( y) cos y x,
(arccos x)
y [0; ]
1
1
1
( f ( y )) (cos y )
1
1
1
sin y
1 cos2 y
1 x2

6.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arctg x, x R
Имеем:
f 1( y ) tg y x,
1
1
y ;
2 2
1
1
(arctg x) 1
( f ( y )) (tg y )
cos y
2
1 tg y
2
1 x2

7.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производные элементарных функций
Обратные тригонометрические функции
y arcctg x, x R
Имеем:
f 1( y) ctg y x,
y [0; ]
1
1
(arcctg x) 1
( f ( y )) (ctg y )
sin y
2
1
1 ctg y
2
1
1 x2

8.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Таблица производных
(a x ) a x ln a
(e x ) e x
( x ) x 1
1
(log a x) log a e
x
(ln x)
x 2
(c) 0
1
x
1
(arcsin x)
x
(sin x) cos x
1
1 x2
1
(arccos x)
1 x2
(cos x) sin x
(arctg x)
1
(tg x)
2
cos x
(ctg x)
1
2
sin x
1
1 x2
(arcctg x)
1
1 x2

9.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Таблица производных сложной функции
Пусть
u u(x)
(au ) au ln a u
(eu ) eu u
(u ) u 1 u
u
(log a u ) log a e
u
1
(ln u ) u
u
u 2
1
u
(arcsin u )
u
(sin u ) cos u u
u
1 u2
u
(arccosu )
1 u2
(cos u ) sin u u
1
(tg u )
u
2
cos u
(ctg u )
1
2
sin u
(arctg u )
u
1 u2
u (arcctg u )
u
1 u2

10.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Гиперболические функции
1) гиперболический косинус
e x e x
ch x
2
2) гиперболический синус
e x e x
sh x
2
3) гиперболический тангенс
sh x e x e x
th x
x x
ch x e e
4) гиперболический котангенс
ch x e x e x
cth x
x x
sh x e e

11.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
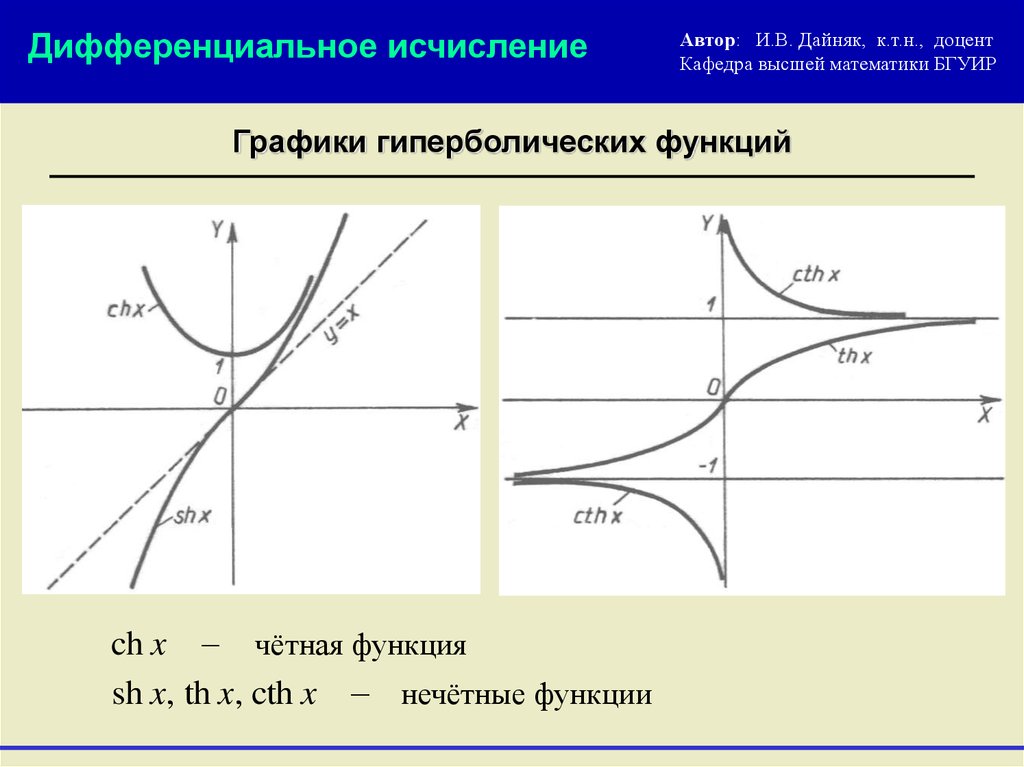
Графики гиперболических функций
ch x чётная функция
sh x, th x, cth x нечётные функции

12.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Гиперболические функции
Основные соотношения:
Производные:
ch2 x sh2 x 1
(ch x) sh x
ch 2 x ch2 x sh2 x
(sh x) ch x
sh 2 x 2 sh x ch x
(th x)
sh( x y) sh x ch y ch x sh y
ch( x y) ch x ch y sh x sh y
th x th y
th( x y)
1 th x th y
1
ch2 x
(cth x)
1
sh 2 x

13.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Основные правила дифференцирования (повторение)
1) константу можно выносить за знак производной
(c u ) c u
2) формула производной суммы
(u v) u v
3) формула производной произведения
(u v) u v u v
4) формула производной частного
u u v u v
v
v2
(v( x) 0)

14.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная сложной функции (повторение)
Пусть функция g(x) имеет производную в точке x0, а
функция f (y) имеет производную в точке y0 = g(x0). Тогда
сложная функция f (g(x)) имеет производную в точке x0,
вычисляемую по формуле
f ( x0 ) f ( y0 ) g ( x0 ),
y g ( x)

15.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Нахождение производной функции
Пример:
Найти производную функции
x2
3
x2
y ln
sin e 2 x
3x 1
Решение:
Воспользуемся основными правилами дифференцирования:

16.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Пусть функция f (x) > 0.
По теореме о производной сложной функции:
1
ln f ( x)
f ( x)
f ( x)
Выразим отсюда производную:
f ( x) f ( x) ln f ( x)

17.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Пример 1:
Найти производную функции
Решение:
y xn , n N.

18.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Логарифмическое дифференцирование применяется для
нахождения производной сложной функции вида
y f ( x) g (x) ,
представляющей собой «функцию в степени функция».

19.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Логарифмическое дифференцирование
Пример 2:
Найти производную функции
Решение:
y
x
cos x
.

20.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной параметрически
Пусть функция у переменной х задана параметрически:
x j (t ),
y y (t ), t T
где функции j(t), y(t) определены в некоторой окрестности
точки t0.
Предположим, что функция x = x (t) имеет обратную функцию
t = t (x), определённую в некоторой окрестности точки x0 = x (t0),
а также существуют производные x’(t0) и y’(t0).
Тогда:
1 yt
y x y x t ( x) yt t x yt
xt xt
yt (t0 )
y x ( x0 )
xt (t0 )

21.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной параметрически
Пример:
dy
Найти производную
функции, заданной уравнениями
dx
x 2 sin 2t ,
Решение:
y cos2 t.

22.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной неявно
Пусть функция у переменной х задана неявно уравнением
F ( x, y) 0
Для нахождения у’х :
1. Дифференцируем тождество по переменной х как
сложную функцию, предполагая, что у = f (х).
2. Из полученного уравнения пытаемся выразить у’х = f‘ (х).

23.

Дифференциальное исчисление
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
Производная функции, заданной неявно
Пример:
Найти производную неявной функции, заданной уравнением
e y x y e,
в точке х0 = 0.
Решение:

24.

Высшая математика
Автор: И.В. Дайняк, к.т.н., доцент
Кафедра высшей математики БГУИР
math.mmts-it.org