Производная функции

1. Производная функции

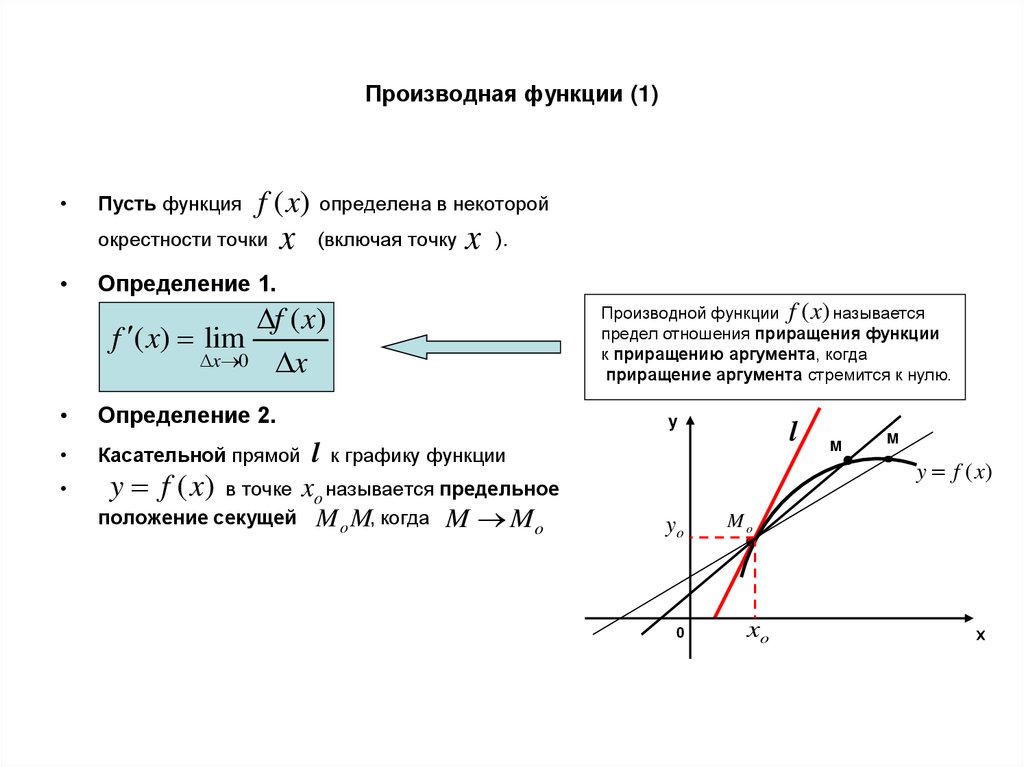
2. Производная функции (1)

Пусть функция
f (x)
окрестности точки
x
определена в некоторой
(включая точку
x
).
Определение 1.
f ( x)
f ( x) lim
x 0 x
Определение 2.
Касательной прямой
в точке
положение секущей
y f (x)
Производной функции f (x) называется
предел отношения приращения функции
к приращению аргумента, когда
приращение аргумента стремится к нулю.
y
l
l к графику функции
xo называется предельное
M o M, когда M M o
M
M
y f (x)
yo
0
Mo
xo
х

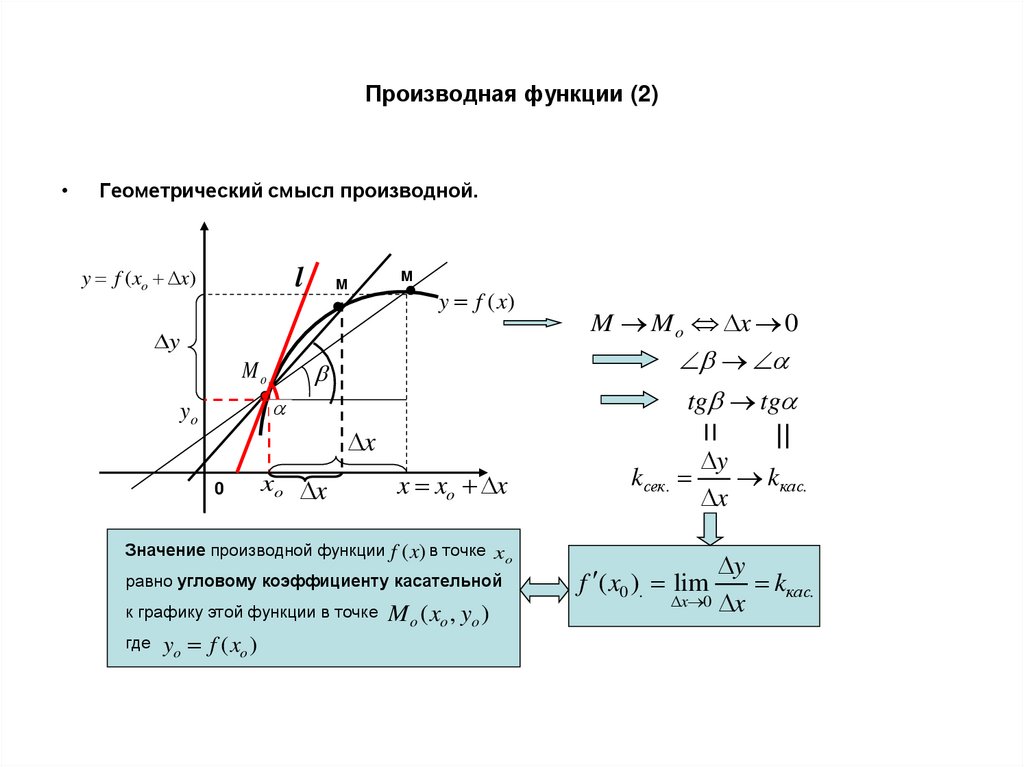
3. Производная функции (2)

Геометрический смысл производной.
y f ( xo x)
l
M
M
y f (x)
y
Mo
tg tg
yo
x
0
xo x
x xo x
Значение производной функции f (x) в точке xo
равно угловому коэффициенту касательной
к графику этой функции в точке
где
M M o x 0
yo f ( xo )
M o ( xo , yo )
kсек.
y
kкас.
x
y
kкас.
x 0 x
f ( x0 ). lim

4.

Производная – одно из фундаментальных понятий математики. Оно возникло
в XVII веке в связи с необходимостью решения ряда задач из физики,
механики и математики, но в первую очередь следующих двух: определение
скорости прямолинейного движения и построения касательной к прямой.
Независимо друг от друга И.Ньютон и Г.Лейбниц разработали аппарат,
которым мы и пользуемся в настоящее время.
И.Ньютон в основном опирался на физическое представление о мгновенной
скорости движения, считая его очевидным и сводя к нему другие случаи
производной, а Г.Лейбниц использовал понятие бесконечно малой.
Исчисление, созданное Ньютоном и Лейбницем, получило название
дифференциального исчисления. С его помощью был решен целый ряд задач
теоретической механики, физики и астрономии. В частности, используя
методы дифференциального исчисления, ученые предсказали возвращение
кометы Галлея, что было большим триумфом науки XVIII в. С помощью тех же
методов математики изучали в XVII и XVIII вв. различные кривые, нашли
кривую, по которой быстрее всего падает материальная точка, научились
находить кривизну линий. Большую роль в развитии дифференциального
исчисления сыграл Л.Эйлер, написавший учебник “Дифференциальное
исчисление”.
Основные понятия дифференциального исчисления долгое время не были
должным образом обоснованы. Однако в начале XIX в. французский
математик О.Коши дал строгое построение дифференциального исчисления
на основе понятия предела.
Применяемая сейчас система обозначения для производной восходит к
Лейбницу и Лагранжу.
В настоящее время понятия производной находит большое применение в
различных областях науки и техники.

5.

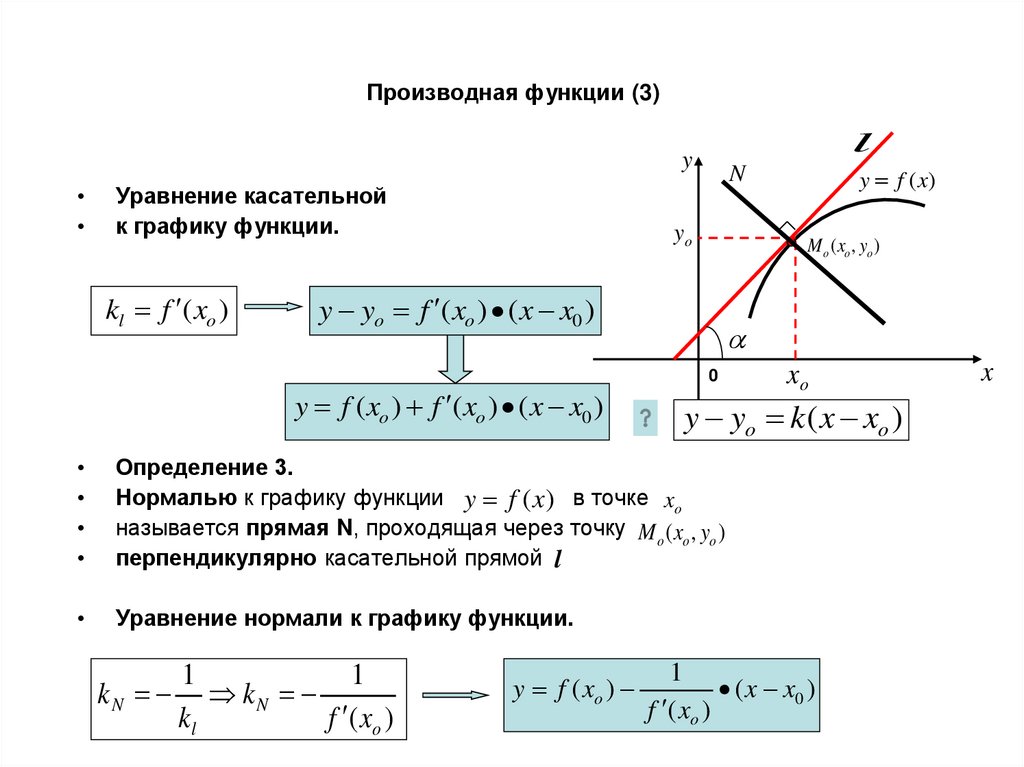
6. Производная функции (3)

l
y
Уравнение касательной
к графику функции.
kl f ( xo )
N
yo
M o ( xo , yo )
y yo f ( xo ) ( x x0 )
0
y f ( xo ) f ( xo ) ( x x0 )
Определение 3.
Нормалью к графику функции y f (x) в точке xo
называется прямая N, проходящая через точку M o ( xo , yo )
перпендикулярно касательной прямой l
Уравнение нормали к графику функции.
y f ( xo )
xo
y yo k ( x xo )
1
1
kN kN
kl
f ( xo )
y f (x)
1
( x x0 )
f ( xo )
x

7. Производная функции (4)

Связь между существованием производной
– и непрерывностью функции.
–
Теорема.
f ( x) f ( x) непрерывнав т. x
–
Доказательство.
f ( x)
x 0 x
f ( x) lim
f ( x )
f ( x) ( x)
x
где 0 при х 0
f ( x) f ( x) x ( x) x
f ( x) 0 при x 0
f ( x) непрерывна в т. х

8. Производная функции (5)

Правила дифференцирования.
Пусть
Тогда
1.
2.
3.
4.
f ( x) и g ( x)
( f ( x) g ( x)) f ( x) g ( x)
( f ( x) g ( x)) f ( x) g ( x) f ( x) g ( x)
(C f ( x)) C f ( x)
f ( x) f ( x) g ( x) f ( x) g ( x)
, если g ( x) 0
2
g ( x)
(
g
(
x
))
Доказательство 1 правила (для суммы).
1 шаг.
2 шаг.
3 шаг.
( f g ) f g
( f g ) f g
x
x x
( f g )
f
g
lim
lim
x 0
x 0 x
x 0 x
x
т о ест ь
( f ( x) g ( x)) f ( x) g ( x)
lim

9. Вывод формулы производной произведения

Пусть существуют производные u и v.
y u v ,y y (u u) (v v)
y (u u) (v v) - uv v u u v u v
y
u
v
v
v
u u
x
x
x
x
y
u
v
v
lim
v lim
u lim u
x 0 x
x 0 x
x 0 x
x 0
x
y lim
u
v
v
lim
v
u
lim
lim
u
lim
x
0
x 0 x
x 0
x 0 x
x
Т.к. u и v не зависят от x

10. Рассмотрим последнее слагаемое:

Так как функция u – имеет производную по условию, то она
непрерывна, следовательно, по 2-му определению
непрерывности:
lim u 0
x 0
v
v
x 0 x
Также по условию существует производная lim
Значит
v
0
x 0 x
lim u lim
x 0
В итоге имеем
y u v u v

11. Производная функции (6)

–
Таблица производных основных
элементарных функций.
–
1.
(C ) 0
–
2.
( x ) n x
–
3.
–
4.
–
5.
–
6.
–
7.
–
–
–
n
n 1
(a x ) a x ln a
(e x ) e x
( x) 1
( x 2 ) 2 x
x 2 1 x
1
(loga x)
1 x ln a
(ln x)
x
(sin x) cos x
8. (cosx) sin x
1
9. (tg x)
cos2 x
1
(
ctg
x
)
10.
sin 2 x
11.
12.
13.
14.
(arcsin x)
(arccosx)
1
1 x2
1
1 x2
1
1 x2
1
(arcctgx)
1 x2
(arctgx)

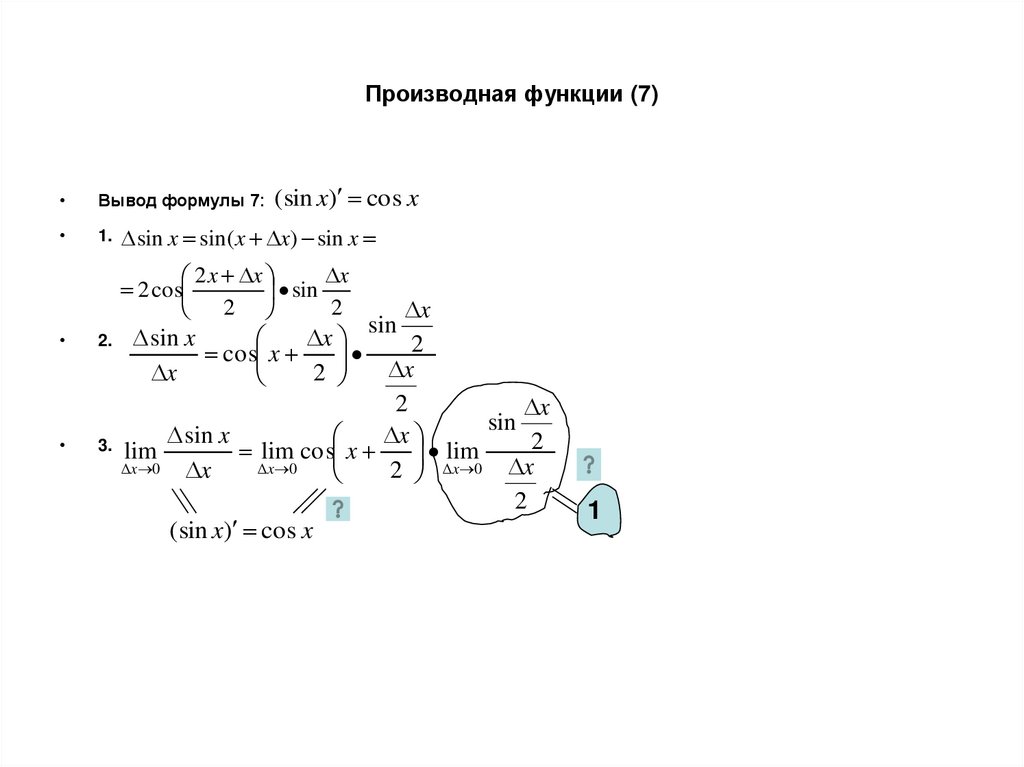
12. Производная функции (7)

Вывод формулы 7:
1.
(sin x) cos x
sin x sin(x x) sin x
x
2 x x
2 cos
sin
2
2
2.
3.
x
sin x
x
2
cos x
x
x
2
2
x
sin
sin x
x
2
lim
lim cos x
lim
x 0
x 0
x
2 x 0 x
2
(sin x) cos x
sin
1

13.

y ln x
y ln( x x ) ln x
y
ln( x x ) ln x
lim
x 0 x
x 0
x
x x
x x
ln
ln
x
x
x
lim
lim
x 0
x 0
x
x
x
x
ln 1
x
1
x
lim
lim x lim
x 0
x 0 x
x 0 x x
x
x
y ' lim
При вычислении предела использована формула таблицы эквивалентных
бесконечно малых:
x
x x
ln 1
при
0
~
x x
x
1
(ln x)'
x

14. Производная функции

y e x
y ex
y e x x e x
y
e x x e x
y ' lim
lim
x 0 x
x 0
x
e x e x e x
e x (e x 1)
lim
lim
x 0
x 0
x
x
e x x
lim
ex
x 0 x
При вычислении предела использована формула таблицы
эквивалентных бесконечно малых:
e x 1 ~ x
при
x 0
(e )' e
x
x

15. Производная функции (8)

Производная сложной функции.
Теорема.
1. y(x) – сложная функция, то есть
y f (u ) , u ( x)
y( x) f ( ((x))
y ( x) f (u ) ( x)
где u ( x)
2. ( x) в т. х
3. f (u ) в т. u , причем
y yu u x
значение u ( x)
Доказательство.
1..Возьмем x 0 u y
(предполагаем, что u 0 )
y u
2. y
u x
y
y
u
lim
lim
lim
x 0 x
x 0 u x 0 x
y
u
lim
lim
u 0 u x 0 x
x
3.
(ч.т.д.)

16. Таблица производных сложной функции

u = u(x) является функцией от x.
( u n ) nu n 1 u
( a u ) a u ln a u
( eu ) eu u
1
(log a u )
u
u ln a
1
(lnu ) u
u
(sinu ) cos u u
(cos u ) sinu u
1
u
2
cos u
1
( ctg u ) 2 u
sin u
1
( arc sinu )
u
2
1 u
1
(arccos u )
u
1 u2
1
( arctg u )
u
2
1 u
1
( arcctg u )
u
2
1 u
( tg u )

17. примеры

По формуле: ( u5 ) 5u 4 u
(( 1 2 x )5 ) 5( 1 2 x )4 ( 1 2x ) 5( 1 2x )4 2 10( 1 2x )4
По формуле: (sinu ) cos u u
(sin 7 x ) cos 7 x ( 7 x ) 7 cos 7 x
По формуле: ( u 2 ) 2u u
(sin2 x ) 2 sin x (sin x ) 2 sin x cos x sin 2x

18. примеры

1
По формуле: (lnu ) u
u
(lncos x )
1
1
(cos x )
sin x tg x
cos x
cos x
По формуле: ( arc sinu )
( arc sin 4 x )
1
1 ( 4 x )2
1
1 u
( 4 x )
2
u
4
1 ( 4 x )2

19. Производная функции (9)

Примеры.
1.
y ln sin x
y ln u , u sin x
y
2.
1
1
cos x
cos x ctgx
u
sin x
y ln 2 sin x
y u 2 , u ln t , t sin x
1
1
y 2u cos x 2 ln sin x
cos x
t
sin x
2ctgx ln sin x

20. Примеры производной сложной функции.

Производная произведения и частного.
(u v)' u' v u v'
y 2 x tg 4x ;
y' 2 x ln 2 ( 1) tg 4x 2 x
1
1
4;
2
2 tg 4x cos 4x
'
u u ' v v' u
v
v2
y
e 2 x sin 5x
(1 4x ) 2
;
(2e 2 x 5 cos 5x )(1 4x ) 2 (e 2 x sin 5x ) 2(1 4x ) 4
y
;
(1 4x ) 4
'

21. Примеры производной сложной функции.

Примеры производной сложной функции.
y x ln 5 (1 8x 2 );
1
80x ln 4 (1 8x 2 )
y' 1 5 ln (1 8x )
( 16x ) 1
;
2
2
1 8x
1 8x
4
2
2
2x 3
2x 3
y 3 cos arctg
cos 3 arctg
;
5
5
2
1
2
2x 3
2x 3
y' cos 3 arctg
sin arctg
3
5
5
1
2x 3
1
5
2
2
;
5

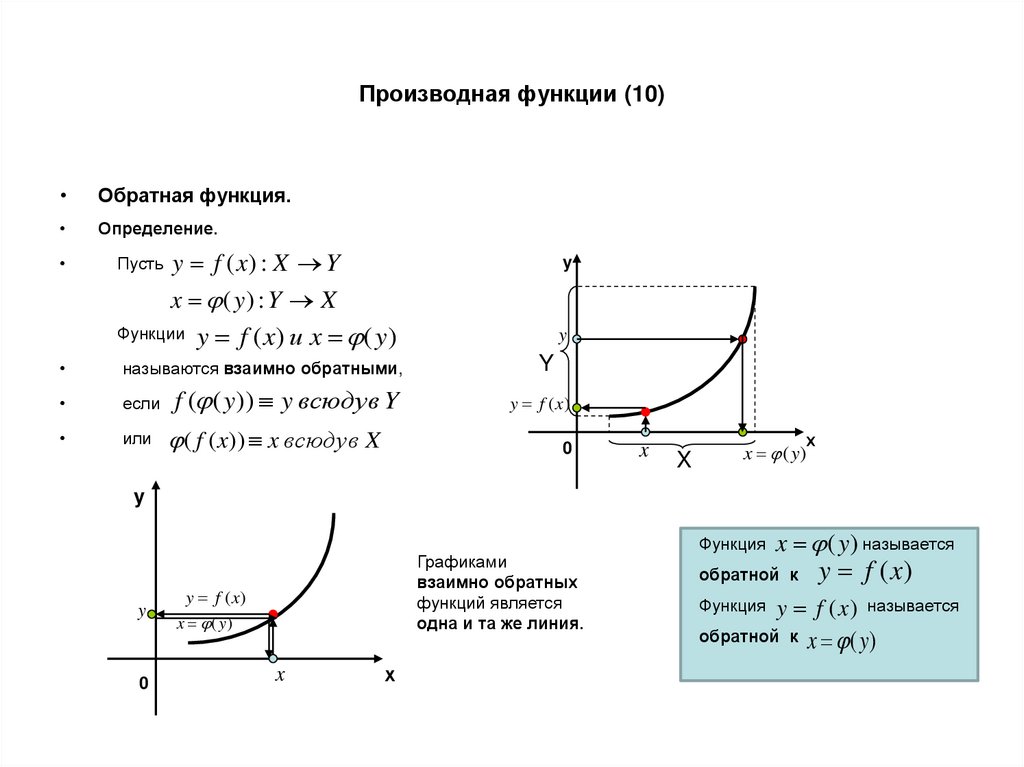
22. Производная функции (10)

Обратная функция.
Определение.
y f ( x) : X Y
y
x ( y) : Y X
Функции y f ( x) и x ( y)
y
Пусть
называются взаимно обратными,
если
или
f ( ( y)) y всюду в Y
( f ( x)) x всюду в X
Y
y f (x)
0
x
х
X
x ( y)
y
y
0
Графиками
взаимно обратных
функций является
одна и та же линия.
y f (x)
x ( y)
x
х
Функция
x ( y) называется
обратной к
Функция
y f (x)
y f (x)
обратной к
называется
x (y)

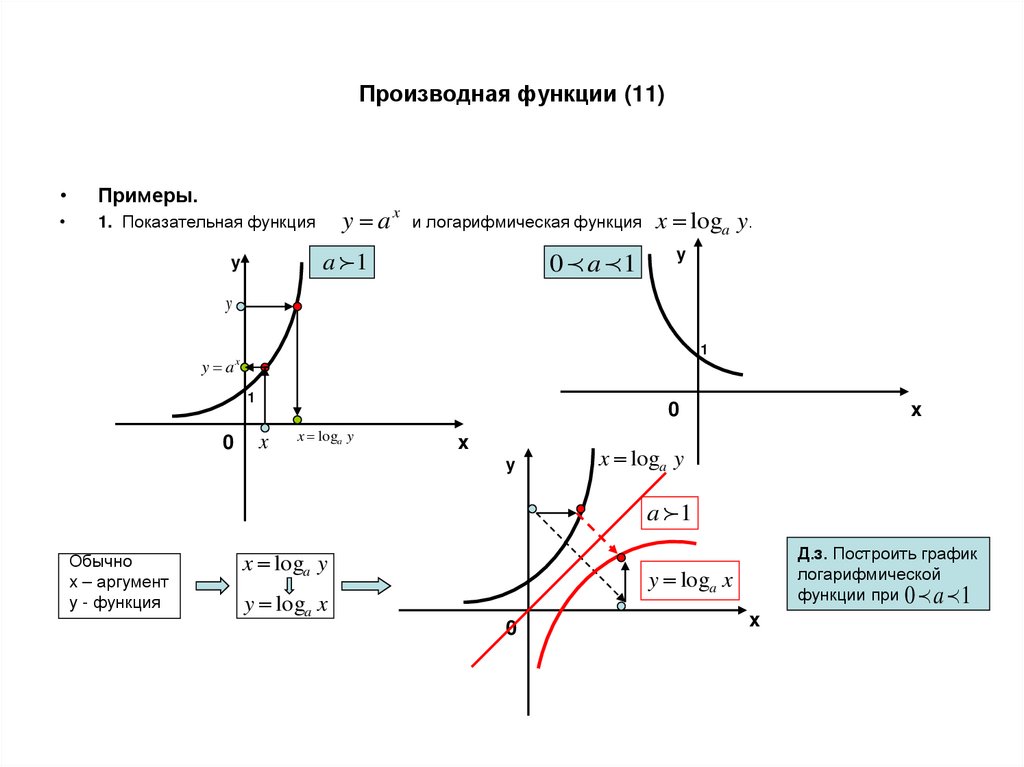
23. Производная функции (11)

Примеры.
1. Показательная функция
y ax
и логарифмическая функция
a 1
y
0 a 1
x loga y.
y
y
1
y ax
1
0
0
x
x loga y
x
y
x
x loga y
a 1
Обычно
x – аргумент
y - функция
x loga y
Д.з. Построить график
логарифмической
функции при 0 a 1
y loga x
y loga x
0
x

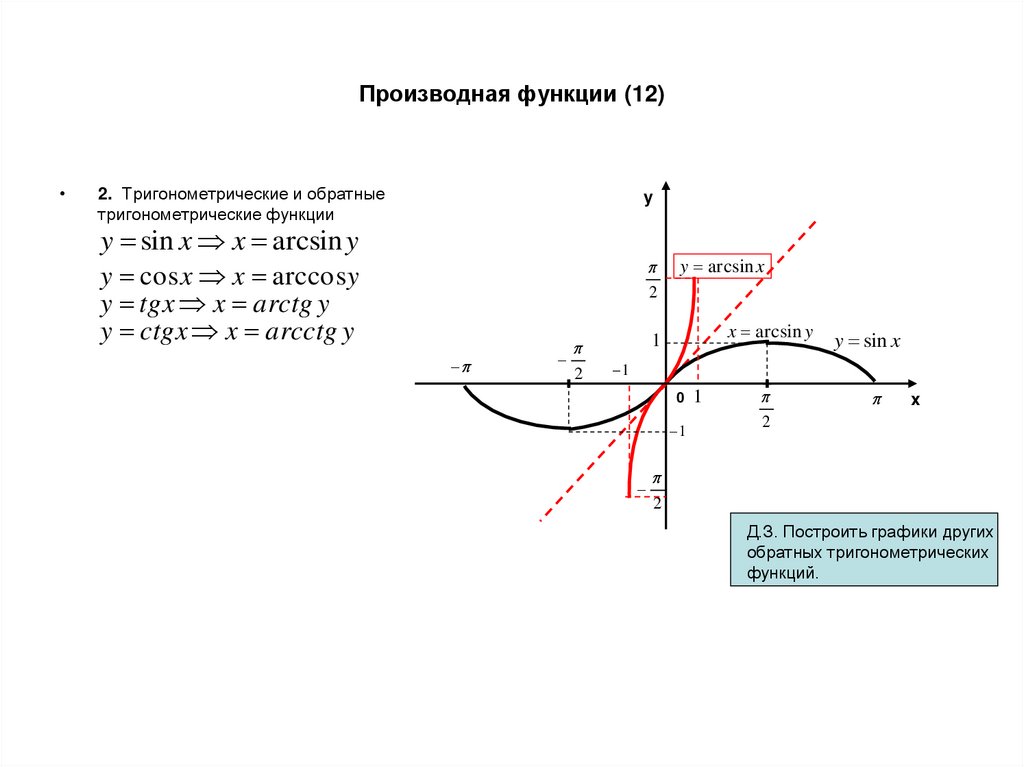
24. Производная функции (12)

2. Тригонометрические и обратные
тригонометрические функции
y
y sin x x arcsin y
y cos x x arccosy
y tgx x arctg y
y ctgx x arcctg y
2
x arcsin y
1
2
y arcsin x
y sin x
1
0
1
1
2
x
2
Д.З. Построить графики других
обратных тригонометрических
функций.

25. Производная обратной функции

• Пусть для функции y = f(x) существует обратная функция
x = φ(y), f(x) в точке x0 имеет конечную производную f ' ( x0 ) .
Тогда обратная функция x = φ(y) в соответствующей точке
1
.
y0 f ( x0 ) имеет производную, равную ' ( y0 )
f ' ( x0 )

26. Доказательство теоремы о производной обратной функции

• Придадим значению y y0 произвольное приращение y , тогда
соответствующее приращение x получит функция x = φ(y).
При y 0 ввиду однозначности функции y = f(x) и x 0 . Тогда
x
1
y
y
x
Если y 0 , то, в силу непрерывности функции x = φ(y) и x 0.
x
1
1
1
lim
.
y
y 0 y
y 0 y
f
'
(
x
)
0
lim
x y 0 x
' ( y0 ) lim

27. Следовательно, или

1
. или
Следовательно, ' ( y0 )
f ' ( x0 )
1
x' y
y'x

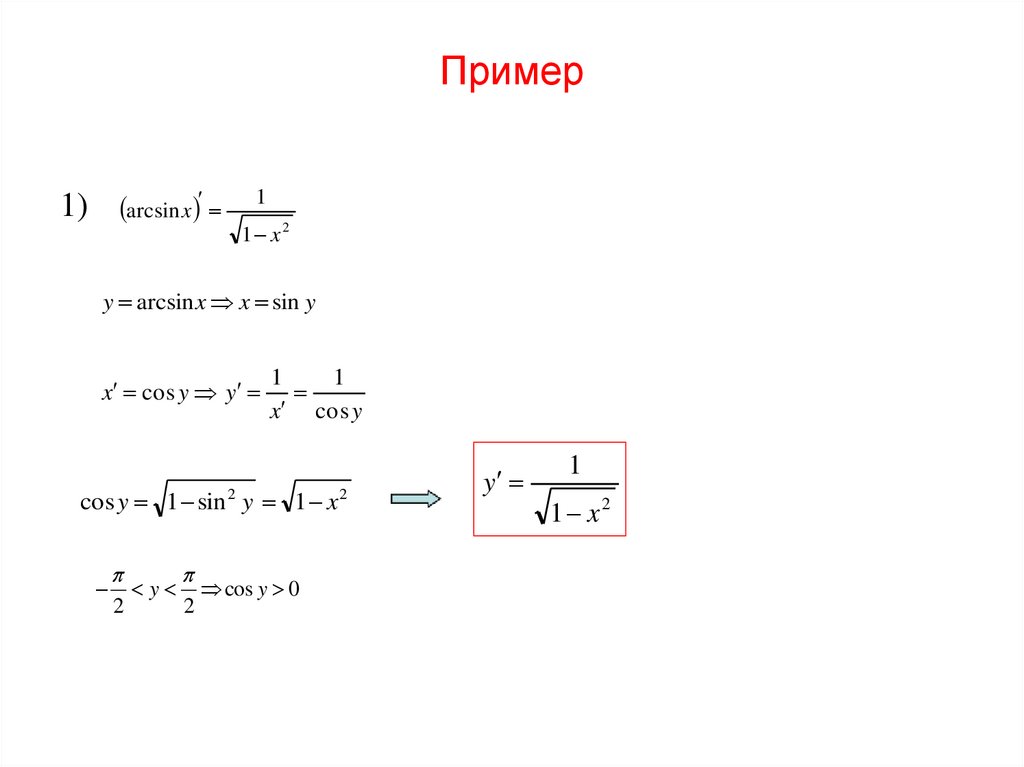
28. Пример

1) arcsin x
1
1 x2
y arcsin x x sin y
x cos y y
1
1
x cos y
cos y 1 sin 2 y 1 x 2
2
y
2
cos y 0
y
1
1 x2

29. Производная функции

y arctg x
• Пусть
y arctg x
x
Эта функция является обратной для
y'x
1
x' y
1
1
x tg .y
1
1 tg y
2
1
1 x
cos 2 y
1
2
1
tg
y.
так как
2
cos y
В результате
1
(arctg x)'
1 x2
2
,

30. Производная функции (15)

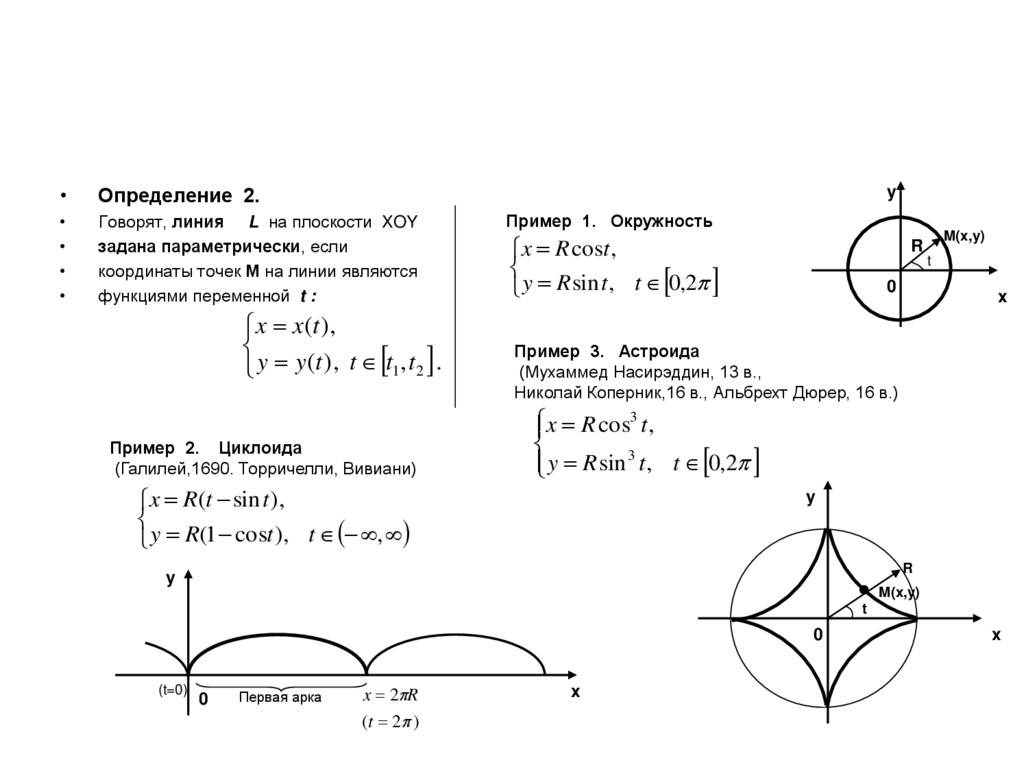
Определение 2.
Говорят, линия L на плоскости XOY
задана параметрически, если
координаты точек М на линии являются
функциями переменной t :
y
x x(t ),
y y (t ), t t1 , t 2 .
Пример 2. Циклоида
(Галилей,1690. Торричелли, Вивиани)
Пример 1. Окружность
x R cost ,
y R sin t , t 0,2
R
0
M(x,y)
t
x
Пример 3. Астроида
(Мухаммед Насирэддин, 13 в.,
Николай Коперник,16 в., Альбрехт Дюрер, 16 в.)
3
x R cos t ,
3
y R sin t , t 0,2
x R(t sin t ),
y R(1 cost ), t ,
y
R
y
M(x,y)
t
0
(t=0)
0
Первая арка
x 2 R
(t 2 )
x
x

31. Производная функции, заданной параметрически

Пусть функция y от x задана параметрически:
x x(t )
,
y y (t )
t1 t t2
t – параметр (вспомогательная переменная) .
Пусть x(t) и y(t) имеют производные для всех t из интервала
[t1 , t2 ] и пусть x(t) имеет обратную функцию t = Ф(x),
также имеющую производную.

32.

• Тогда функцию y можно рассматривать как сложную
функцию y = y(t), а t = Ф(x), т.е. Y=y(Ф(x)).
( t – промежуточный аргумент).
По правилу нахождения производной сложной функции:
y ' x y 't t ' x .
По теореме об обратной функции
y 't
y'x
x't
t 'x
1
x't
, тогда

33. Циклоида

34. Астроида

35. Производные высших порядков.

Определение 1.
Производная y f (x)
называется производной
первого порядка функции
Определение 2.
Производная от производной первого порядка
называется производной второго порядка
функции
y f (x)
y f ( x) : y ( f ( x))
Пример.
y ax
y a x ln a ;
y a x (ln a) 2 ;
Определение 3.
Производная от производной (n-1) -порядка
называется производной
y ( n ) a x (ln a) n
функции
n – порядка
y f ( x) : y(n) ( f (n 1) ( x))

36. Правило Лопиталя.

–
Теорема 1.
–
Теорема 2.
–
Пусть выполнены условия:
–
Пусть выполнены условия:
–
1) функции f ( x) и g ( x)
являются бесконечно малыми
–
1) функции f ( x) и g ( x)
–
–
при x x ( или при
o
–
2)
–
3) lim
–
x ) ;
f ( x) и g ( x)
f ( x)
или lim
A
x xo
x g ( x)
Тогда lim f ( x ) lim f ( x ) A
x xo g ( x )
x xo g ( x )
( или при x )
f ( x)
A
g ( x)
( правило раскрытия неопределенности 0 )
0
–
являются бесконечно большими
–
при x xo
( или при
x );
f ( x) и g ( x)
–
2)
–
3) lim
–
Тогда
x xo
lim
x xo
f ( x)
A
g ( x)
f ( x)
или lim
A
x g ( x)
f ( x)
f ( x)
lim
A
x xo g ( x )
g ( x)
( или при x )
( правило раскрытия неопределенности
)

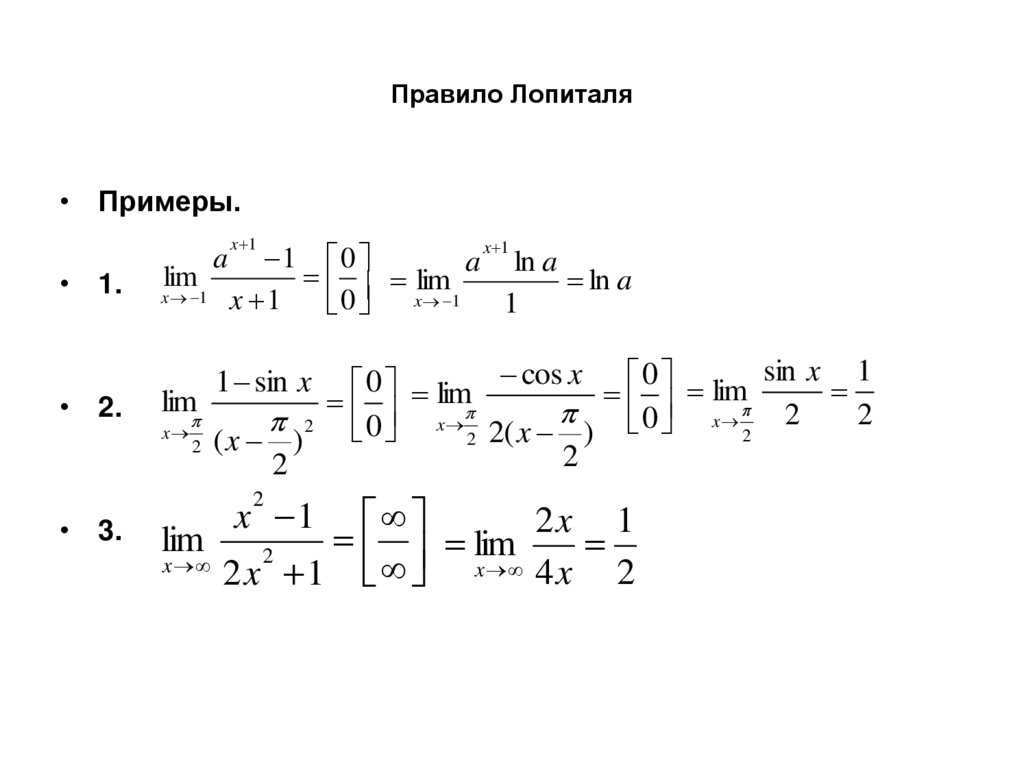
37. Правило Лопиталя

• Примеры.
• 1.
• 2.
lim
x 1
a
x 1
0 lim cos x 0 lim sin x 1
lim
0 x 2
2
x
2
0
x
2
2
(
x
)
2
)
2 (x
2
2
1 sin x
x 1
2x 1
lim
2
lim
x
2 x 1 x 4 x 2
2
• 3.
x 1
1 0
a ln a
lim
ln a
x 1
x 1
0
1