Similar presentations:
Производная функции. Определение производной
1. Производная функции
Определение производнойГеометрический смысл производной
Связь между непрерывностью и
дифференцируемостью
Производные основных элементарных функций
Правила дифференцирования
Производная сложной функции
Производная неявно заданной функции
Логарифмическое дифференцирование
2. Определение производной
Пусть функция y = f(x) определена в некотором интервале (a; b).Аргументу x придадим некоторое приращение x :
x x (a; b )
Найдем соответствующее приращение функции:
y f ( x x ) f ( x )
y
Если существует предел lim
x 0
x
y
f(x+ Δx )
y
f(x )
0
x
х
x+Δx
х
то его называют производной
функции y = f(x) и обозначают
одним из символов:
y ;
f ( x );
dy
dx
3. Определение производной
Итак, по определению:f ( x x ) f ( x )
y lim
x 0
x
Функция y = f(x) , имеющая производную в каждой точке интервала
(a; b), называется дифференцируемой в этом интервале;
операция нахождения производной функции называется
дифференцированием.
Значение производной функции y = f(x) в точке x0 обозначается
одним из символов:
y ( x0 );
f ( x0 );
y x
0
Если функция y = f(x) описывает какой – либо физический процесс,
то f ’(x) есть скорость протекания этого процесса – физический
смысл производной.
4. Геометрический смысл производной
Возьмем на непрерывной кривой L две точки М и М1:y
f(x+ Δx )
f(x )
М1
y
М
М
x
α φ
0
Через точки М и М1 проведем
секущую и обозначим через φ
угол наклона секущей.
х
x+Δx
х
y
tg
x
f ( x x ) f ( x )
x
При x 0 в силу непрерывности функции y также
стремится к нулю, поэтому точка М1 неограниченно приближается
по кривой к точке М, а секущая ММ1 переходит в касательную.
lim lim tg tg
x 0
x 0
5. Геометрический смысл производной
f ( x x ) f ( x )y
lim
tg
k
x 0
x
Производная f ’(x) равна угловому коэффициенту касательной к
графику функции y = f(x) в точке,yабсцисса
которой равна x.
Если точка касания М имеет координаты (x0; y0 ), угловой
коэффициент касательной есть k = f ’(x0 ).
Уравнение прямой с угловым коэффициентом:
y y 0 кf '((xx-0 )(
x 0x)- x 0 )
Уравнение
Уравнение
касательной
нормали
Прямая, перпендикулярная касательной в точке касания,
называется нормалью к кривой. f ' ( x 0 )
1
1
1
k норм
y y0
( x x0 )
k кас
f ' ( x0 )
f ' ( x0 )
6. Связь между непрерывностью и дифференцируемостью функции
ТеоремаЕсли функция f(x) дифференцируема в некоторой точке , то
она непрерывна в ней.
Доказательство:
Пусть функция y = f(x) дифференцируема в некоторой
точке х, следовательно существует предел:
y
y
( x )
lim
f
f ( x ) ( x )
x 0
x
x
где ( x ) 0 при x 0
По теореме о связи
функции, ее предела и
y
0
y f ( x ) x ( x ) x lim
бесконечно
малой
x 0
Функция y = f(x) – непрерывна.
функции
Обратное утверждение не верно: непрерывная функция может не
иметь производной.
7. Производные основных элементарных функций
n1 Степенная функция: y x
n Z
Придадим аргументу x приращение x, тогда функция получит
приращение:
y x x x
n
n
Формула бинома Ньютона:
n( n 1) n 2 2
a b a na b
a b
2!
n( n 1) ( n k 1) n k k
a b bn
k!
n
n
n 1
K – факториал
k! 1 2 3 k
8. Производные основных элементарных функций
По формуле бинома Ньютона имеем:y x x x n
n(n 1) n 2 2
n
n 1
n
n
( x nx x
x x x ) x
2!
y
n(n 1) n 2
n 1
Тогда:
nx
x x x n 1
x
2!
y
n 1 n(n 1) n 2
n 1
lim
lim
nx
x
x
x
x 0
x x 0
2!
n
nx n 1
x ' nx
n
n 1
9. Производные основных элементарных функций
2Логарифмическая функция:
y ln x
x
x x
y ln x x ln x ln
ln 1
x
x
x
x
ln 1
1
1
y
x
x lim
lim
lim
lim
x 0
x 0
x 0
x 0
x x
x
x
x
1
ln x '
x
x x
ln 1
~
x
x
Аналогично выводятся правила дифференцирования
при xдругих
0
основных элементарных функций.
10. Правила дифференцирования
Пусть u(x) , v(x) и w(x) – дифференцируемые в некотороминтервале (a; b) функции, С – постоянная.
(C ) 0
(u v ) u v
(u v ) u v u v (C u ) C u
(u v w ) u v w u v w u v w
u u v u v
C
C
v
2
2
v
v
v
v
11. Производная сложной функции
Пусть y = f(u) и u = φ(x) , тогда y = f(φ(x)) – сложная функция спромежуточным аргументом u и независимым аргументом x.
Теорема
Если функция u = φ(x) имеет производную u x в точке x а
функция y = f(u) имеет производную y u в соответствующей точке
u , то сложная функция имеет производную y x , которая
находится по формуле:
y x y u u x
Это правило остается в силе, если промежуточных аргументов
несколько:
y f (u );
u (v );
v g( x )
y x y u uv v x
y f ( (g ( x )))
12. Пример
Вычислить производную функции1 sin x
y 3
x ln x
1 sin x
y 3
x ln x
(1 sin x ) ( x 3 ln x ) (1 sin x ) ( x 3 ln x )
2
3
x ln x
(1 (sin x ) ) ( x 3 ln x ) (1 sin x ) (( x 3 ) ln x x 3 (ln x ) )
x ln x
2
3
1
cos x x ln x (1 sin x ) (3 x ln x x )
x
2
3
x ln x
3
2
32
13. Пример
Вычислить производную функцииy cos(ln12 x )
Данную функцию можно представить следующим образом:
y cos u; u v 12 ; v ln x
y x y u uv v x
y u sin u sinv 12 sin ln12 x
u 12v 11 12 ln11 x
1
v
x
y sin ln12 x 12 ln11 x
Коротко:
y (cos(ln 12 x )) sin(ln 12 x ) (ln12 x )
sin(ln 12 x ) 12 ln11 x (ln x )
1
x
14. Производная неявно заданной функции
Если функция задана уравнением y = f(х) , разрешеннымотносительно y, то говорят, что функция задана в явном виде.
Под неявным заданием функции понимают задание функции в
виде уравнения не разрешенного относительно y:
F ( x; y ) 0
Для нахождения производной неявно заданной функции
необходимо продифференцировать уравнение по х, рассматривая
при этом y как функцию от х, и полученное выражение разрешить
относительно производной.
( x ) ( y ) 3( xy ) 0
3 x 3y y 3( x y xy ) 0
x 3 y 3 3 xy 0
2
3
3
2
x 2 y 2 y y xy 0
y x2
y 2
y x
15. Логарифмическое дифференцирование
В ряде случаев для нахождения производной целесообразнозаданную функцию сначала прологарифмировать, а затем
результат продифференцировать.
Такую операцию называют логарифмическим
дифференцированием.
x 2 4 ( x 1)3 e x
x 2 4 ( x 1)3 e x
y
ln y ln
5
5
2x 5
2x 5
3
ln y 2 ln x ln( x 1) x 5 ln( 2 x 5)
4
y 2 3 ( x 1)
(2x 5)
1 5
y
x 4 x 1
2x 5
2 4
3
x
y 2
3
10
x
(
x
1
)
e
y
y
1
y
x 4x 4
2x 5
2x 5 5
16. Логарифмическое дифференцирование
Пусть u = u(x) и v = v(x) – дифференцируемые функции.Функция y u( x )
v(x)
называется степенно – показательной.
Производная такой функции находится только с помощью
логарифмического дифференцирования.
y sin x
x 2 1
ln y ln sin x
x 2 1
ln y ( x 2 1) ln sin x
y
( x 2 1) ln sin x ( x 2 1) (ln sin x )
y
y
cos x
x 2 1
2
y 2 x ln(sin x ) ( x 1)
y sin x
y
sin x









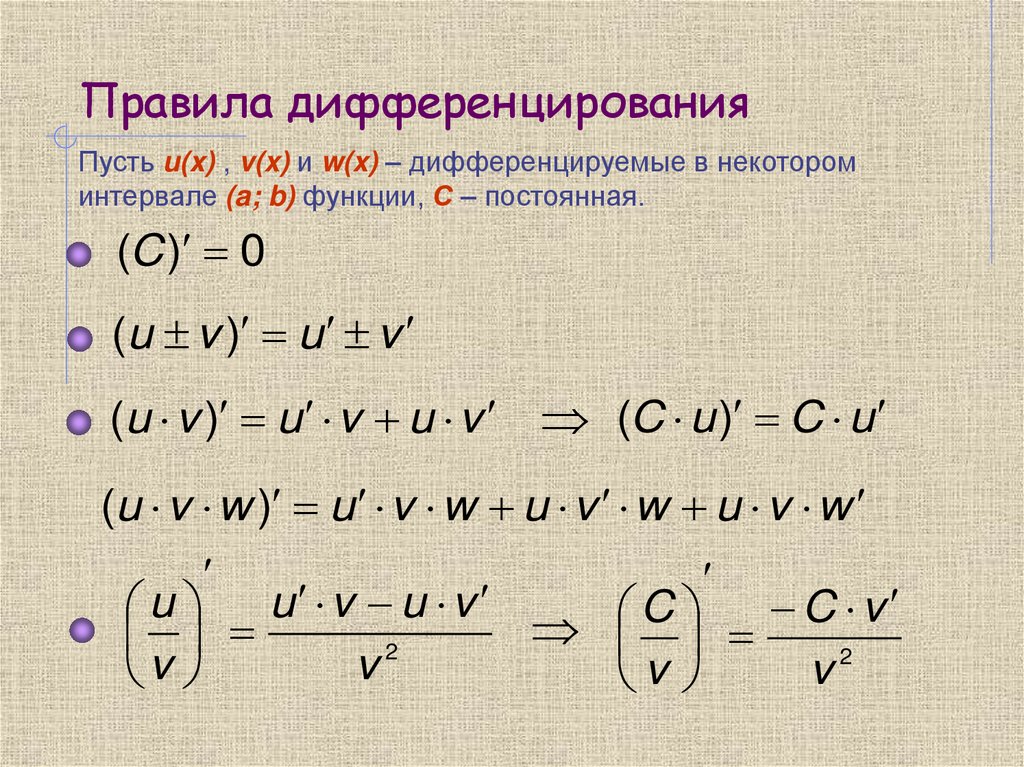






 mathematics
mathematics








