Сечения тетраэдра

1. Сечения тетраэдра

2. Сечение тетраэдра.

Многоугольник,
составленный
из отрезков,
Сечение
тетраэдра.
по которым секущая плоскость пересекает
D
грани многогранника,
называется
сечением
α
многогранника.
N
Отрезки, из которых
состоит сечение,
M
называются следами секущей плоскости на
C
гранях.
Плоскость
Пусть плоскость
Треугольник
пересекаетA
пересекает
рёбра
МNP называется
тетраэдра
тетраэдр, тогда
точках
сечением
∆вона
MNP
– М,N,P,
сечение.
называется
тетраэдра
а грани - этой
по
секущей
отрезкам
плоскостью…
MN,
плоскостью
MP, NP…
P
B
Запишите в
тетрадь.

3. Сечение тетраэдра может быть так же четырёхугольником.

D
α
M
N
A
C
Q
P
MNPQ – сечение.

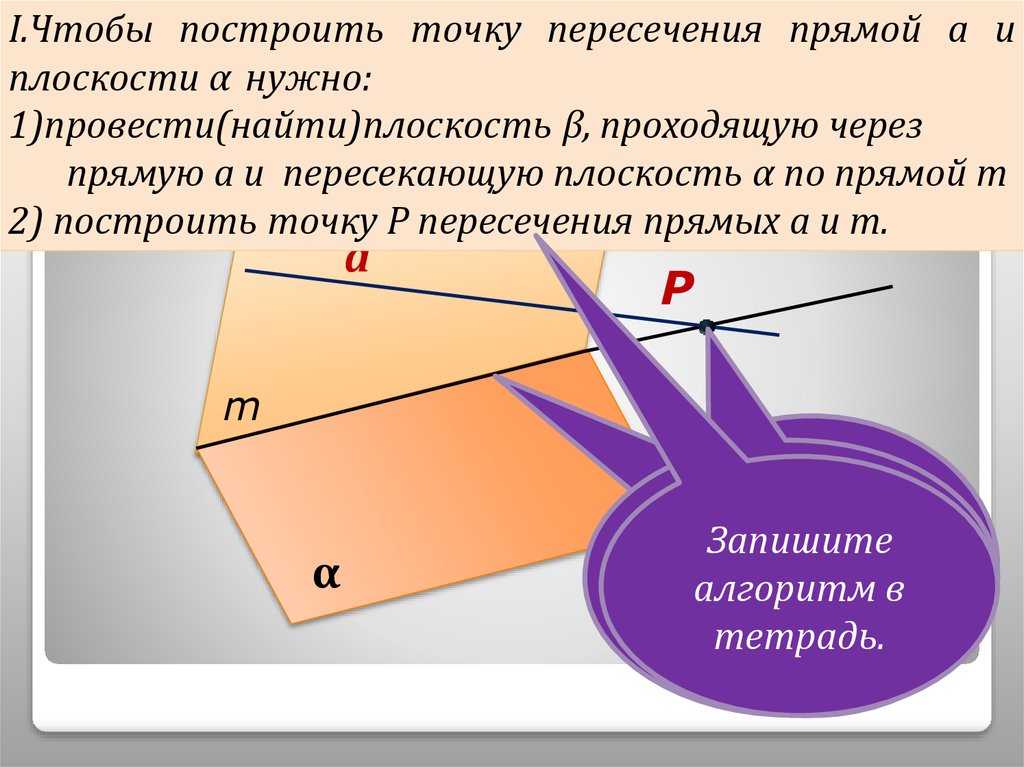
4. I.Прямая а пересекает плоскость α. Построить точку пересечения.

I.Чтобы построить точку пересечения прямой а и
I.Прямая
а пересекает плоскость
плоскости
α нужно:
1)провести(найти)плоскость
β, проходящую
через
α. Построить точку
пересечения.
прямую а и пересекающую плоскость α по прямой т
β прямых а и m.
2) построить точку Р пересечения
а
P
m
α
Через
Пересечём
прямую
Точка
Р общая
апрямую
проведём
ас
точка
прямой β,
аи
Запишите
плоскость
линией
Ответ:
плоскости
α, т.к.
пересекающую
пересечения
алгоритм
в
прямая
т лежит
плоскость
ααпо
плоскостей
и
тетрадь.
в плоскости
α.
β:прямой
прямойтт.
а Р

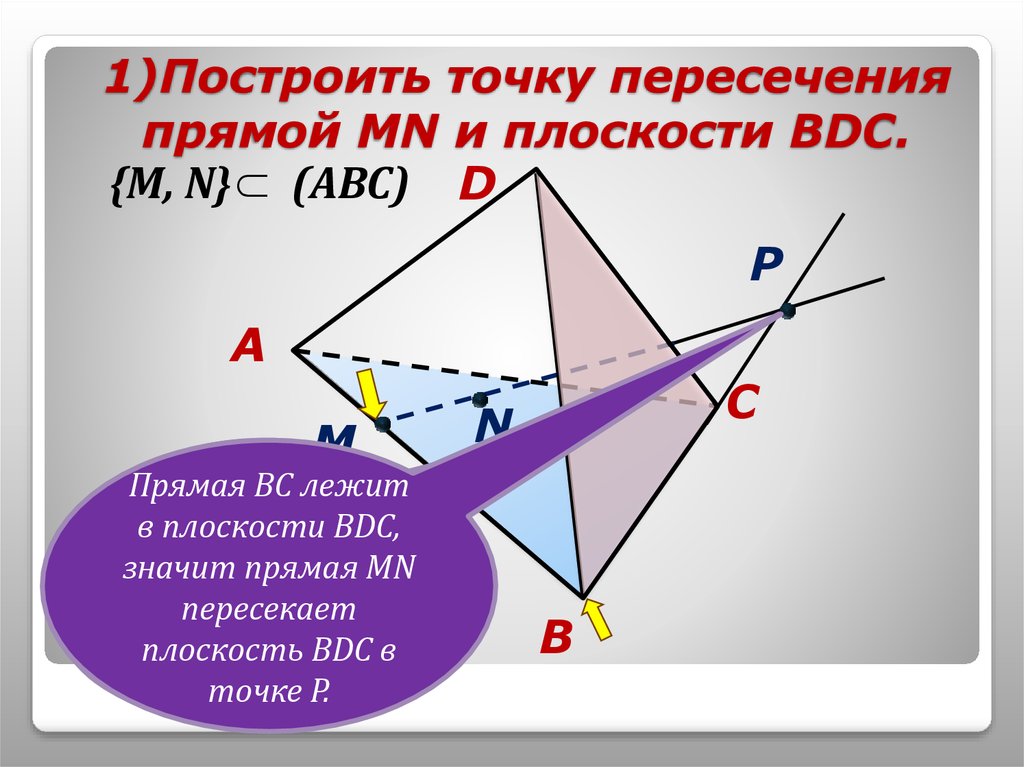
5. 1)Построить точку пересечения прямой МN и плоскости BDC.

{М, N} (АВС) D
P
A
M
Через прямую
МN
Прямая
ВС лежит
проходитBDC,
в плоскости
Прямая
МN
Ответ:
плоскость
АВС,
значит
прямая
МN
с
пересекающая
пересекает
MNпересекается
(
BDC
)
P
прямой ВСBDC
в в
плоскость
BDC
плоскость
поточке
прямой
точкеР.Р.ВС.
C
N
B

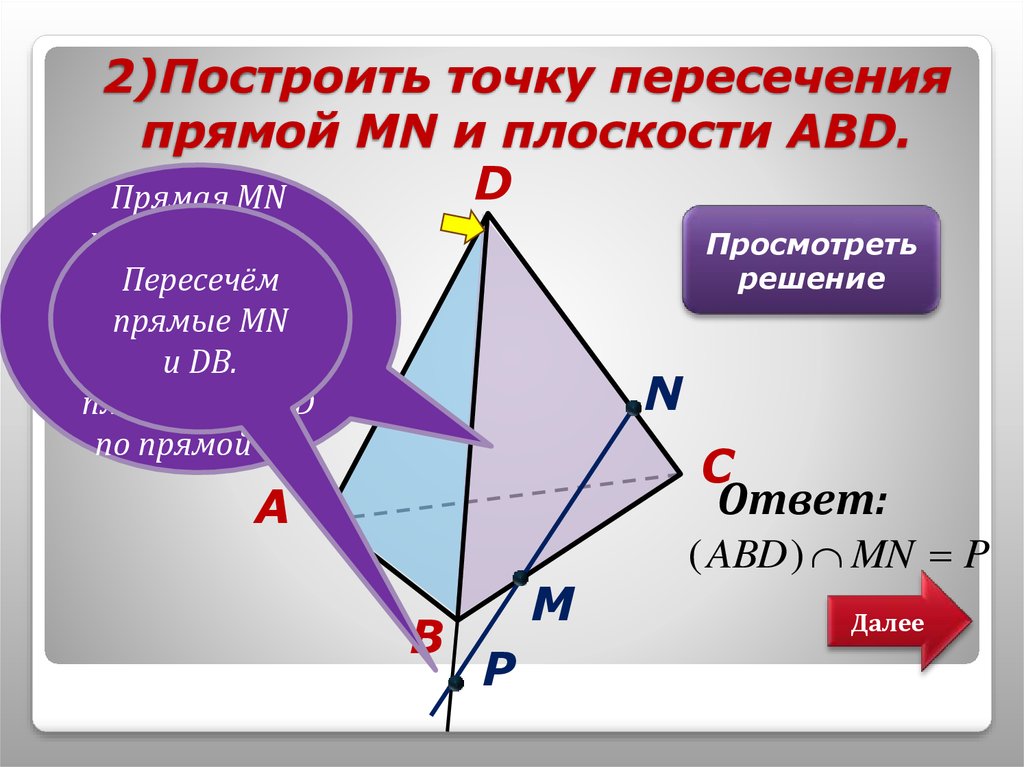
6. 2)Построить точку пересечения прямой МN и плоскости АBD.

D
Прямая MN
принадлежит
плоскости
Пересечём
ВDC,
прямые
которая
MN
пересекает
и DB.
плоскость AВD
по прямой DB
Просмотреть
решение
N
C
Ответ:
A
B
M
P
( ABD ) MN P
Далее

7. II. Пусть прямая АВ не параллельна плоскости α . Построить линию пересечения плоскостей α и АВС, если точка С принадлежит

II.Чтобы
построить
линию
пересечения
II. Пусть прямая АВ не параллельна
плоскостиαα. Построить
и плоскости
АВС пересечения
плоскости
линию
α, {А, В}α иα,АВС,
(С
АВ ||если
α), нужно:
плоскостей
точка С
1)
построитьплоскости
точку пересечения
прямой
АВ
принадлежит
α
С
,
АВ
β
и плоскостиAα - точку
BР ;
P
2) точка Р и С общие точки плоскостей
(АВС)
и α, значит (АВС) α = СР
m
C
Значит
По условию
прямаяи
построению
искомая
Построим
α СР
точки
прямая
СиР
точку
Запишите
пересечения
пересечения
общие для
алгоритм в
прямой
АВ
с
( АВСплоскостей
)
СР
плоскостей
тетрадь.
плоскостью
АВС
АВСииα.α. α.

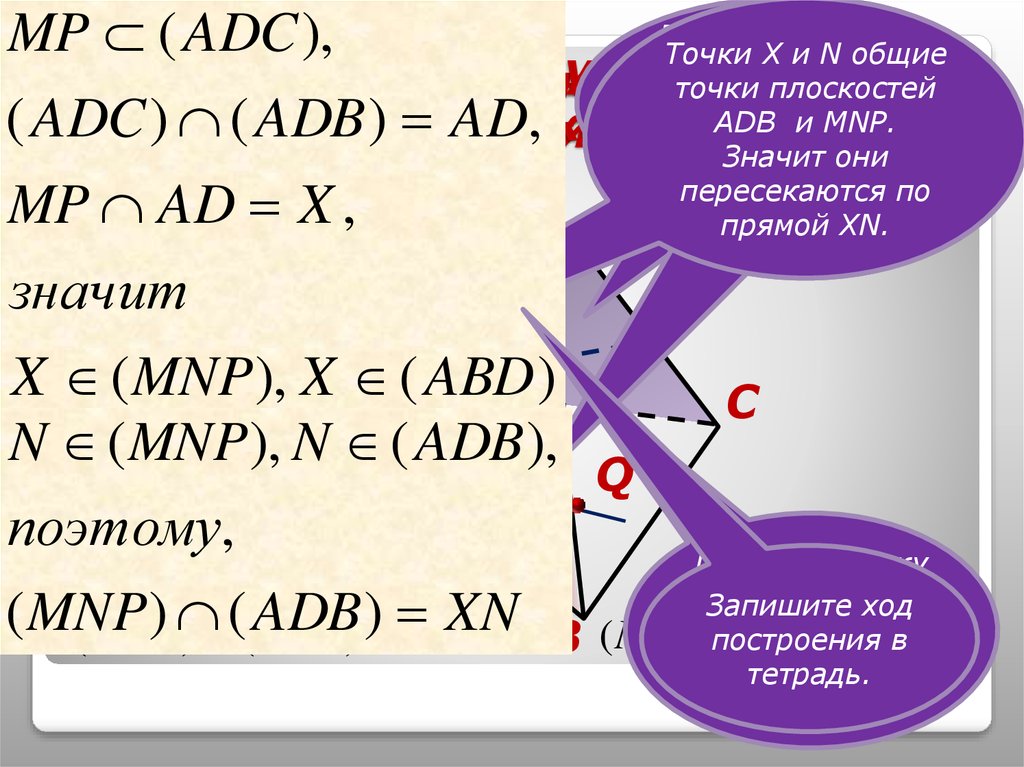
8. 3).Построить прямую пересечения плоскостей МNP и АDB.

MP ( ADC ),
Прямая
МР лежит
Прямая
МР
Точки Х и N общие
в плоскости
ADС,
лежит
в
Построить отрезок пересечения
точки
плоскостей
пересекающей
плоскости
ADС,
ADВ
и MNP.
пересечения
плоскостей
МNP
плоскости МNP
и грани
АDB.
плоскость
ADВи
по
Значит
они
пересекающей
прямой AD.
АDB.
пересекаются
по
плоскость ADВ
прямой ХN.
3).Построить прямую
( ADC ) ( ADB ) AD,
D
N
(
ADB
)
MP AD X ,
значит
A
M
по прямой AD.
P
X ), X ( ABD )
X ( MNP
C
R ),
N ( MNP), N ( ADB
Q
поэтому,
N
Построим точку
Ответ:
пересечения
Запишите
ход
( MNP
)
(
ADB
)
XN
прямой
МР
св QR
ABD
( MNP ) ( ADB ) XN
B ( MNP)построения
плоскостью
тетрадь.ADB
(точку Х).

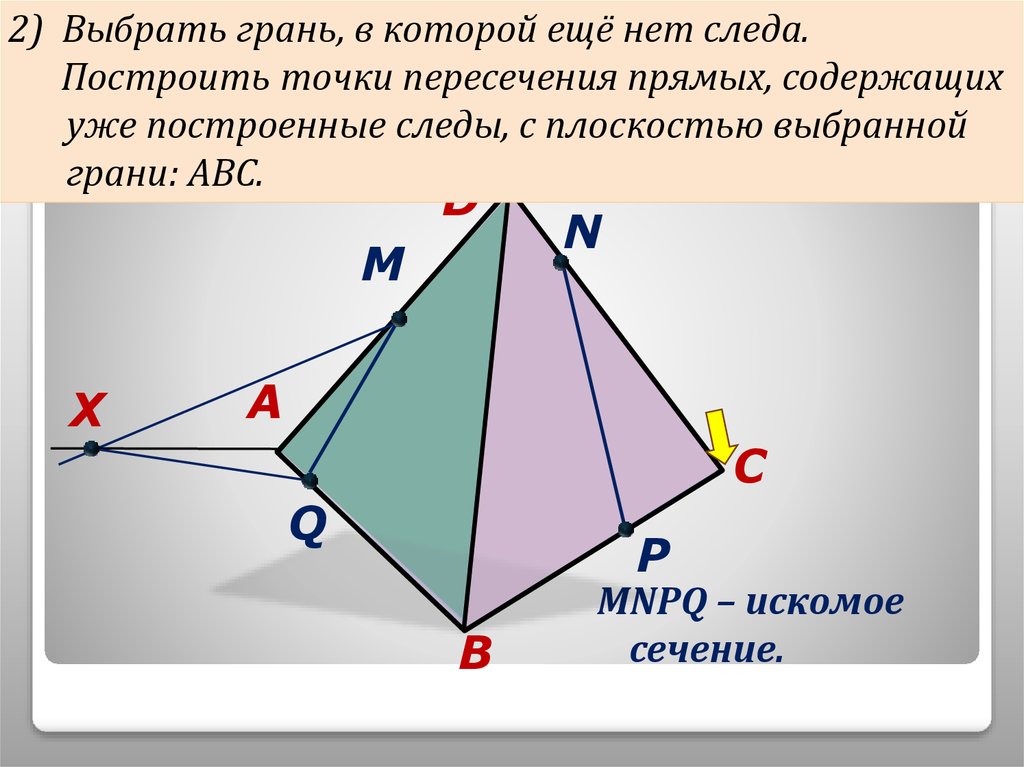
9. Алгоритм построения сечения тетраэдра плоскостью, проходящей через три данные точки M,N,P.

2) Выбрать грань, в которой ещё нет следа.
4)
1)Отметить
Построить
и обозначить
следыпостроения
секущей
точки,
плоскости
в которых
впрямую,
тех
3)Через
построенные
точки
провести
по
Алгоритм
сечения
Построить точки пересечения прямых, содержащих
гранях,
эта
прямая
в которых
пересекает
есть
2рёбра
общие
грани
точки
АВС
с ней.
и достроить
которой
секущая
плоскость
пересекает
тетраэдра
плоскостью,
проходящей
уже построенные следы, с плоскостью выбранной
остальные
следы.
плоскость
выбранной
грани АВС.
через
точки M,N,P.
грани: АВС. три данные
D
M
X
N
A
C
Q
P
B
MNPQ – искомое
сечение.

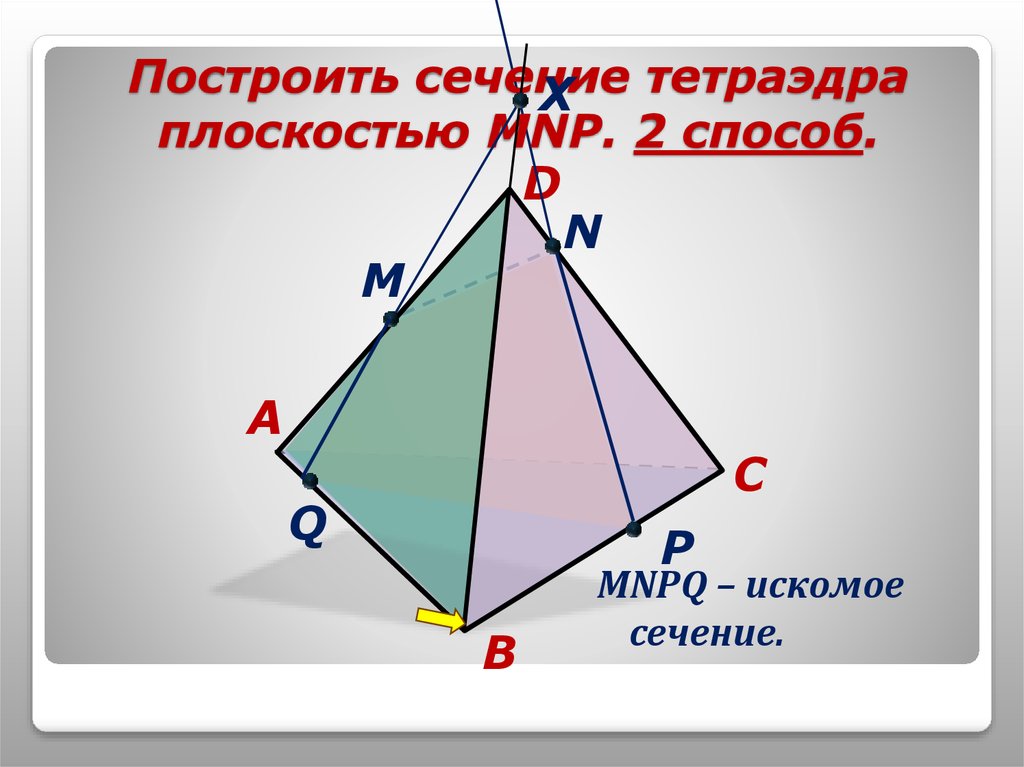
10. Построить сечение тетраэдра плоскостью MNP. 2 способ.

Построить сечение
тетраэдра
X
плоскостью MNP. 2 способ.
D
N
M
A
C
Q
P
B
MNPQ – искомое
сечение.

11. №1. (Решите самостоятельно задачу). Построить сечение тетраэдра плоскостью MNP.

Второй
способ:
A
D
Просмотреть
решение
M
N
Q
P
B
X
C
X
Далее

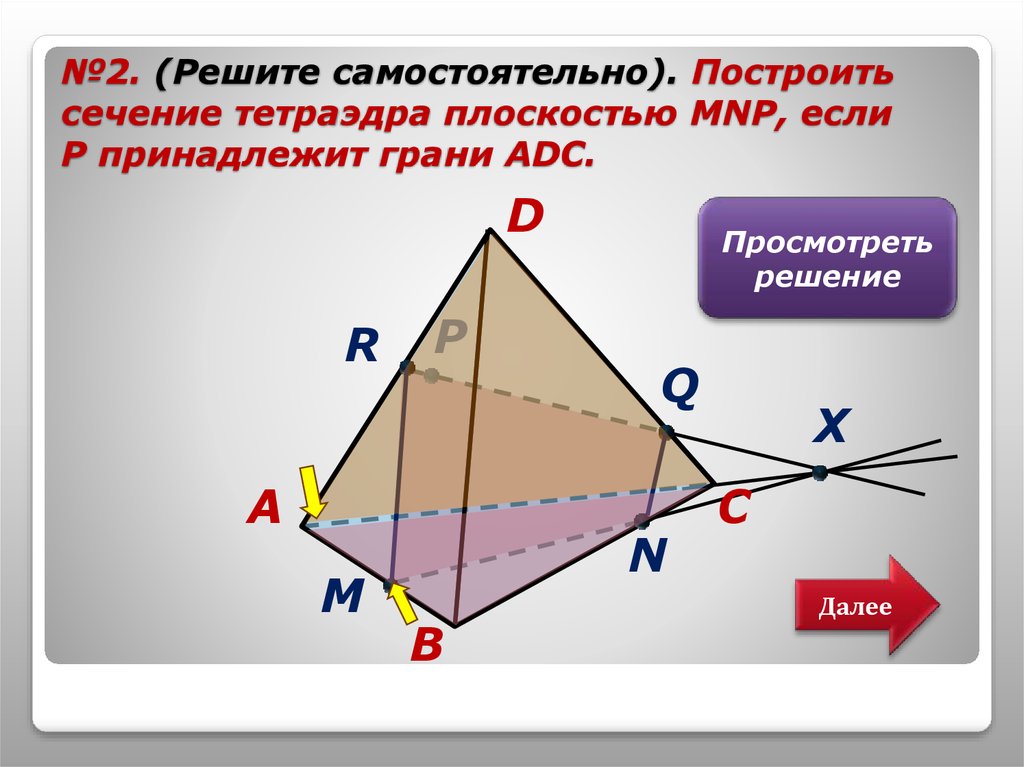
12. №2. (Решите самостоятельно). Построить сечение тетраэдра плоскостью MNP, если Р принадлежит грани АDC.

D
R
P
A
M
Просмотреть
решение
Q
N
B
X
C
Далее

13. №3. Построить сечение тетраэдра плоскостью α, параллельной ребру CD и проходящей через т. F, лежащую на плоскости DBC, и точку

№3. Построить сечение тетраэдра
Продолжите
фразу:
AD. CD и
α, F (BDC), M
Дано:
α||DC,
{M;F}
плоскостью α, параллельной
ребру
Если
даннаясечение
прямая
а F,
параллельна
проходящей
через
т.
лежащую
Построить
тетраэдра
DABC на
некоторой
плоскости
то любая
плоскости
DBC, иα,точку
М.
1) Т.к. α||DC, то (DBC) α=FP
D
плоскость,
проходящая
эту
BD=N.
и FP||DC, FP через
BC=P, FP
прямую а и непараллельная
2)
Т.
к.
α||DC,
то
(DAC)
α=MQ
плоскости
α,
пересекает
плоскость
α
M
N
и
MQ||DC,
MQ
AC=Q.
параллельной
прямой
по прямой b,………………………………………а.
F
3)α α||DC,
(ADB)=
MN,
значит
C α плоскость
A
α||DC,
значит
ADC
(ABC)=QP.
Q
по
DC || NP пересекает
иплоскость
NP α,αBDC
значит
P
пересекает
прямой, α по
B
DC||α, следовательно
Продолжите…
прямой, DC и
параллельной
параллельной
DC и
MNPQ – проходящей
искомое через
сечение.
проходящей
точку Mчерез
точку F

14.

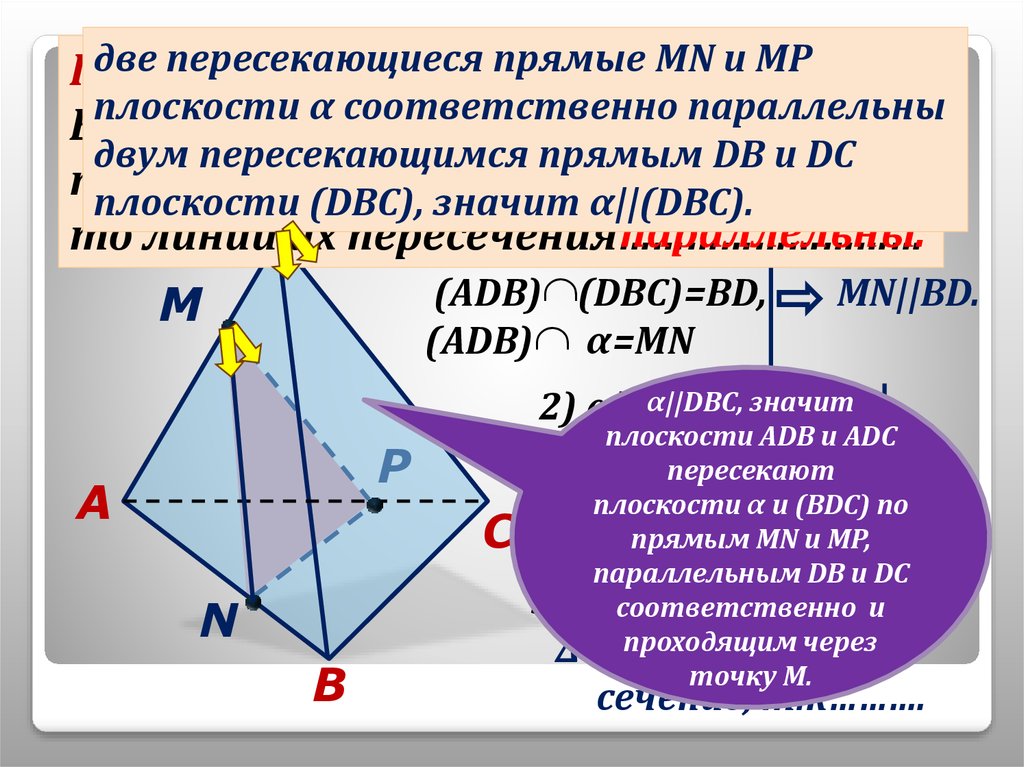
две
пересекающиеся
прямые
MN
и
MP
Продолжите
фразу:
№4. Построить
сечение
тетраэдра
Дано:
α||DBC,
M
α,
M
AD.
плоскости α соответственно параллельны
Если
две параллельные
плоскости
плоскостью
α, параллельной
грани BDC
двум
пересекающимся
прямым DB
и DC
Построить
сечение тетраэдра
DABC
и проходящей
через
точку М.
пересечены
третьей
плоскостью,
плоскости
(DBC),
плоскостью
α значит α||(DBC).
то линии
D их пересечения………………………
1) α||DВC,параллельны.
(ADB) (DBC)=BD,
MN||BD.
M
(ADB) α=MN
P
A
N
B
α||DВC, значит
2) α||DВC,
плоскости ADВ и ADC
(ADC)
(DBC)=CD,
пересекают
α=MN
плоскости
α и (ВDС) по
(ADC)
C
прямым MN и МР,
MP||CD.
параллельным DB и DС
(ABC)=NP. и
3) α соответственно
проходящим
через
∆ MNP
– искомое
точку M.
сечение, т.к……….

15.

№5.Решите самостоятельно и запишите ход
решения.
Просмотреть
Построить сечение
тетраэдра плоскостью α,
проходящей через точку
М и отрезок PN, если
решение
PN||AB и М принадлежит плоскости (АВС).
D
N
Р
A
R
М
Q
B
1) NP||АВ
NP||(ABC)
NP α,
α (ABC) =MQ
MQ||NP.
AC=R.
NP||(AВC),
значит
2)MQ
MNP
C
пересекает
α плоскость
(ADC)=NR,
(BDC)=PQ.
αплоскость
AВС по
прямой MQ,
RNPQ-искомое
параллельной NP и
сечение.
Далее
проходящей через
точку M.