Построение сечений многогранников

1.

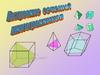
2. Многогранником называют

тело, поверхность которого состоит из конечного
числа плоских многоугольников.
Элементы многогранника: вершины, ребра, грани.

3. Сечением поверхности геометрических тел называется

плоская фигура, полученная в
результате пересечения тела
плоскостью и содержащая точки,
принадлежащие как поверхности
тела, так и секущей плоскости

4.

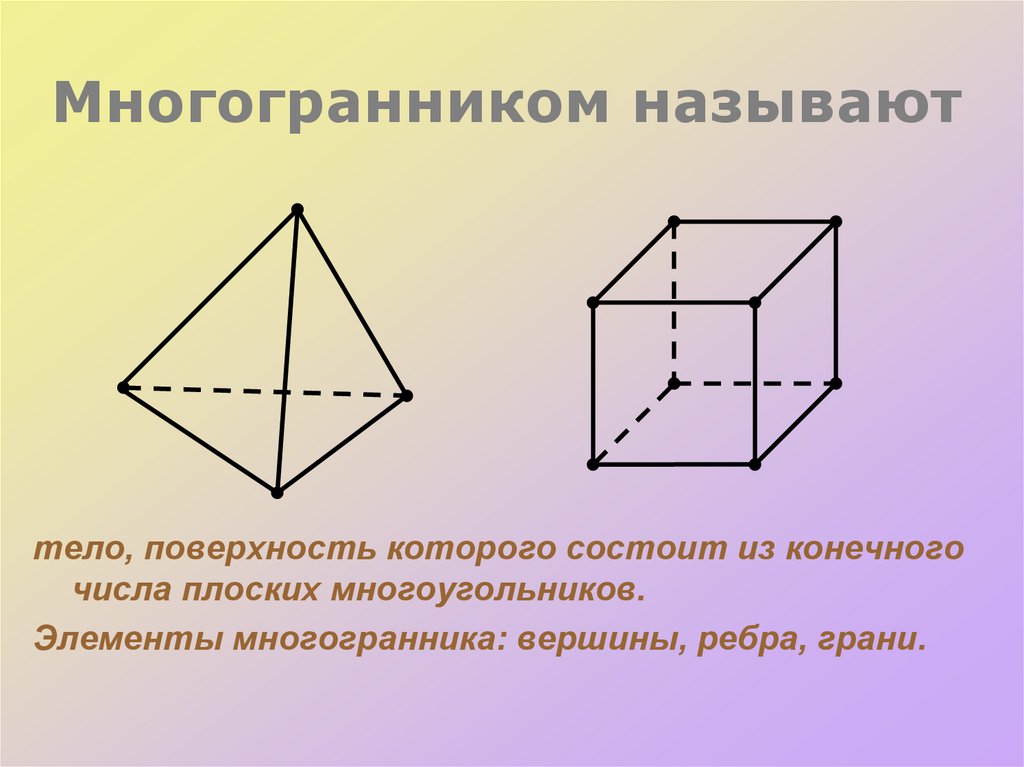
5. Плоскость (в том числе и секущую) можно задать следующим образом

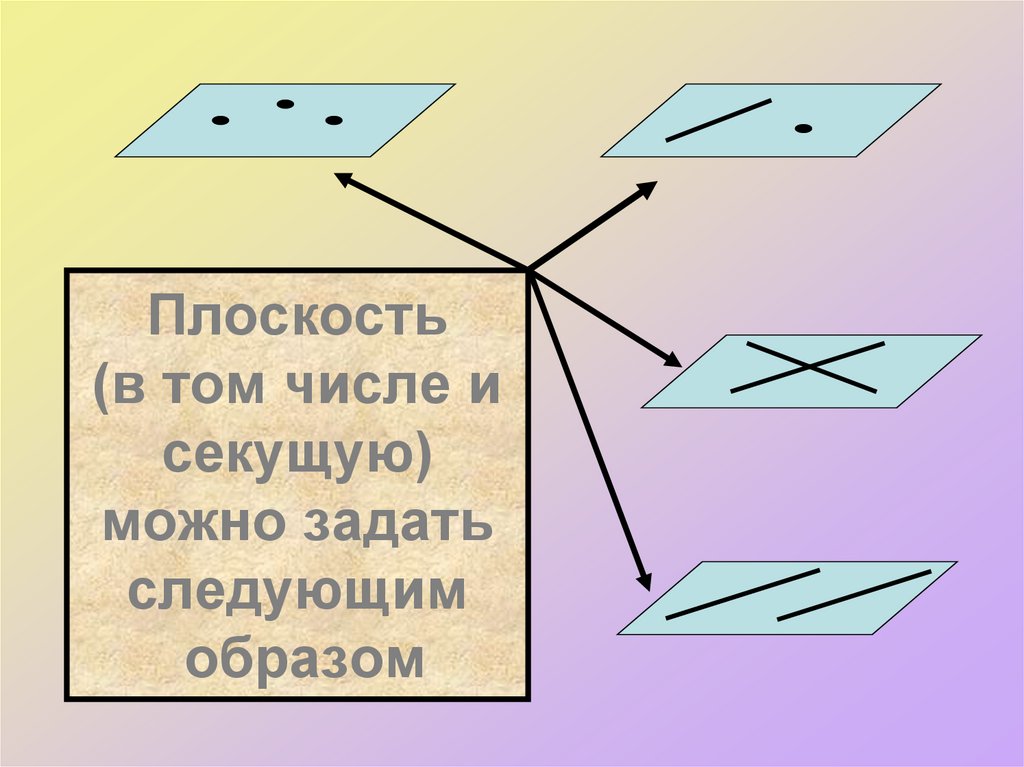
6. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

7. Чтобы решить задачу построения сечения многогранника надо знать:

• что значит построить сечение многогранника
плоскостью;
• как могут располагаться относительно друг друга
многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника
плоскостью считается решенной.
Существует три основных метода построения
сечений многогранников:
• Метод следов.
• Метод вспомогательных сечений.
• Комбинированный метод.

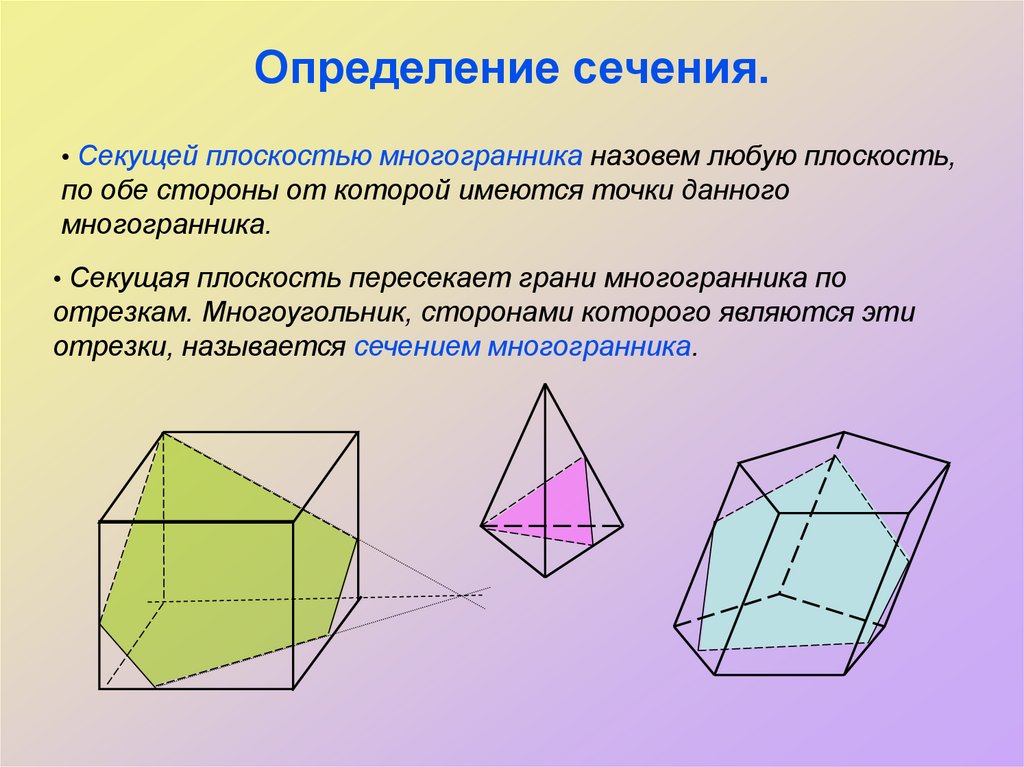
8. Определение сечения.

• Секущей плоскостью многогранника назовем любую плоскость,
по обе стороны от которой имеются точки данного
многогранника.
• Секущая плоскость пересекает грани многогранника по
отрезкам. Многоугольник, сторонами которого являются эти
отрезки, называется сечением многогранника.

9.

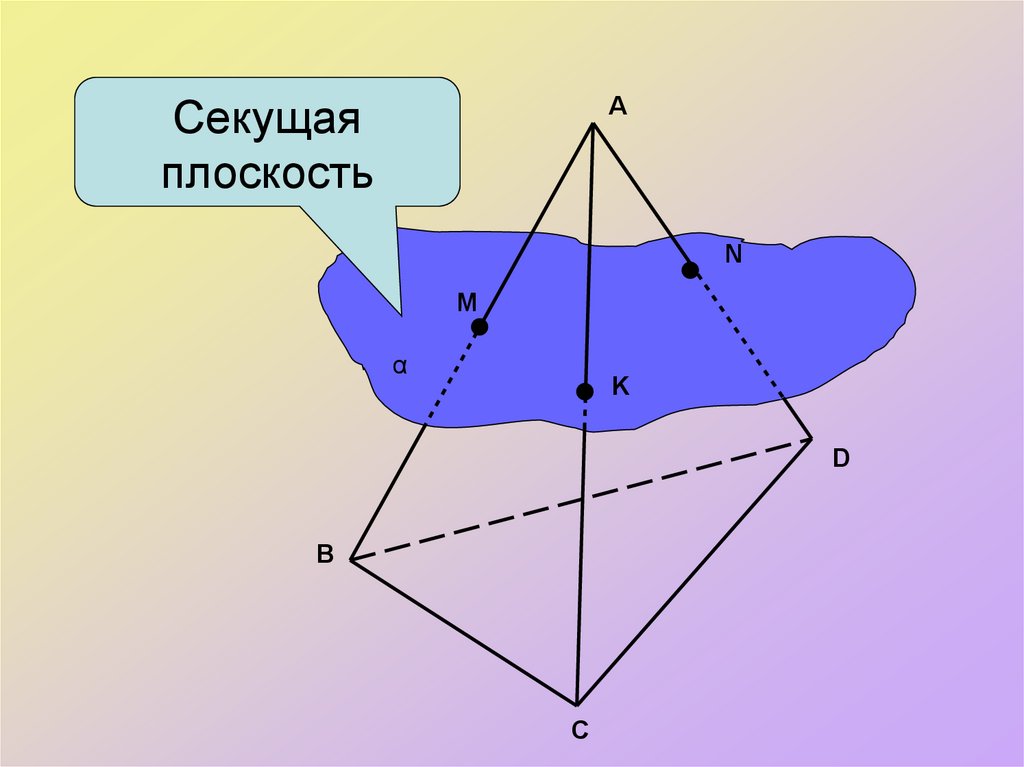
А
Секущая
плоскость
N
M
α
K
D
В
С

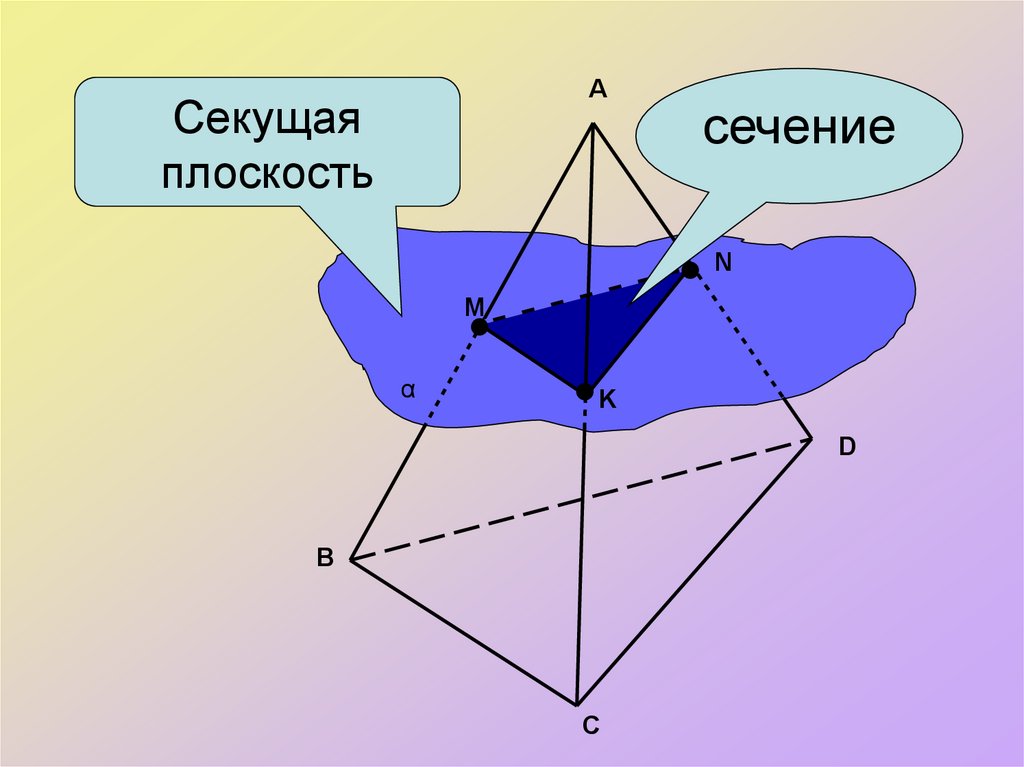
10.

A
Секущая
плоскость
сечение
N
M
α
K
D
B
C

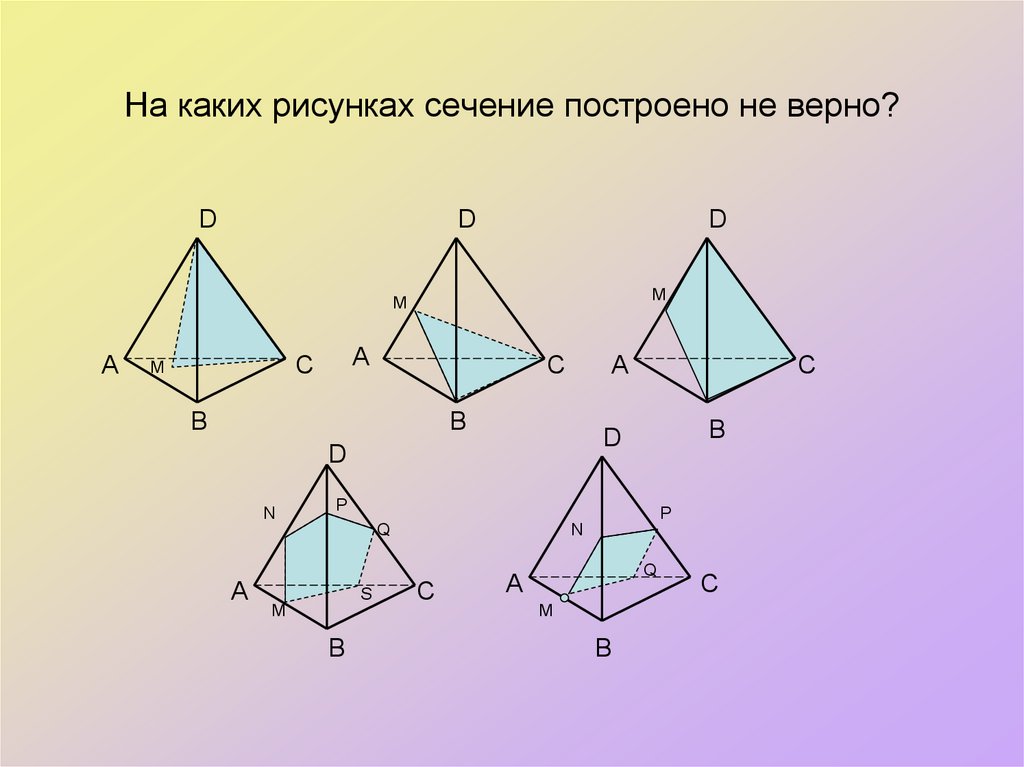
11. На каких рисунках сечение построено не верно?

D
D
D
M
M
А
А
C
M
А
C
B
B
P
P
Q
А
B
D
D
N
C
S
M
B
N
C
Q
А
M
B
C

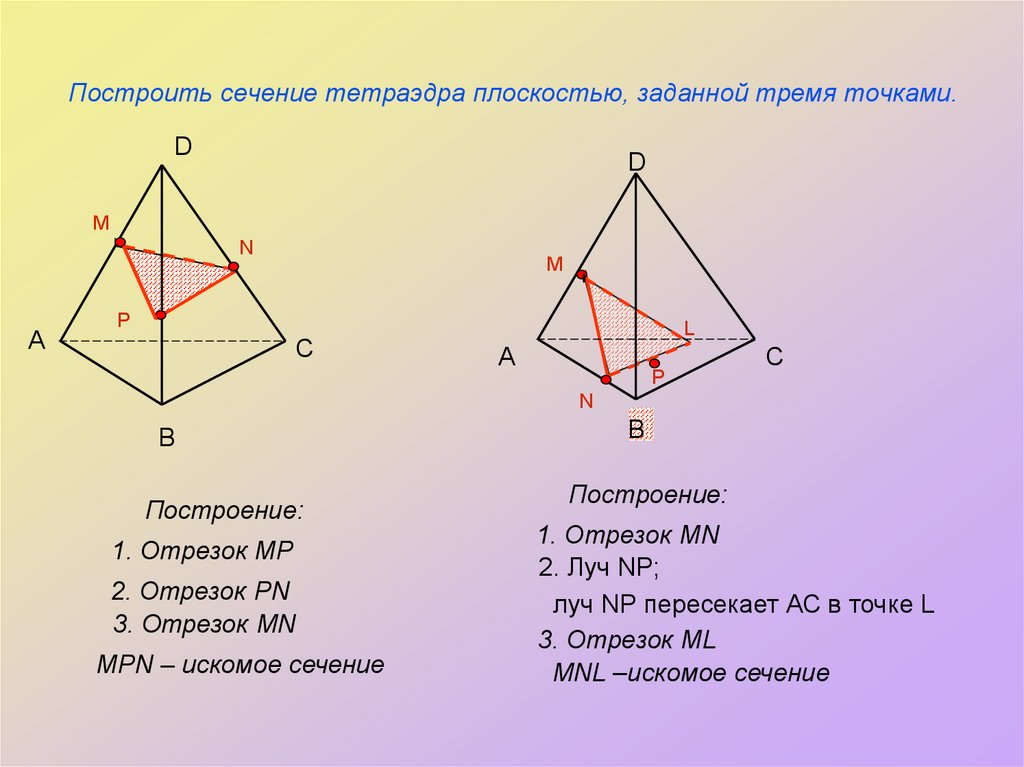
12. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
D
M
N
А
M
P
С
L
А
P
С
N
В
Построение:
1. Отрезок MP
2. Отрезок PN
3. Отрезок MN
MPN – искомое сечение
В
Построение:
1. Отрезок MN
2. Луч NP;
луч NP пересекает АС в точке L
3. Отрезок ML
MNL –искомое сечение

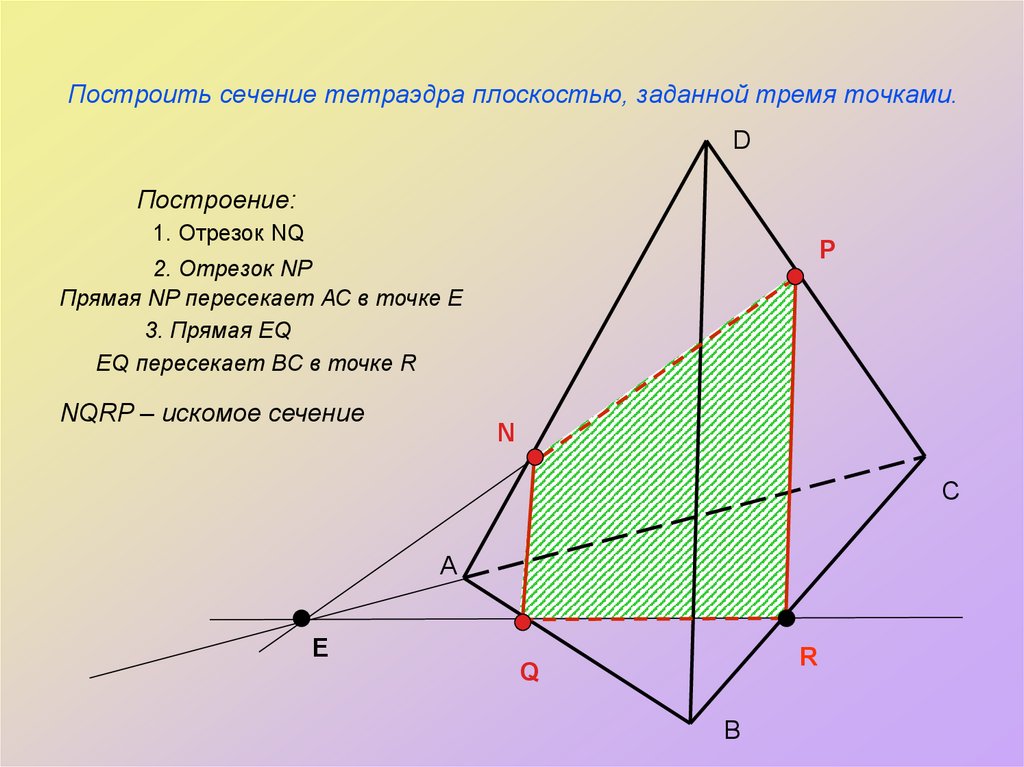
13. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
Построение:
1. Отрезок NQ
P
2. Отрезок NP
Прямая NP пересекает АС в точке Е
3. Прямая EQ
EQ пересекает BC в точке R
NQRP – искомое сечение
N
С
А
E
R
Q
В

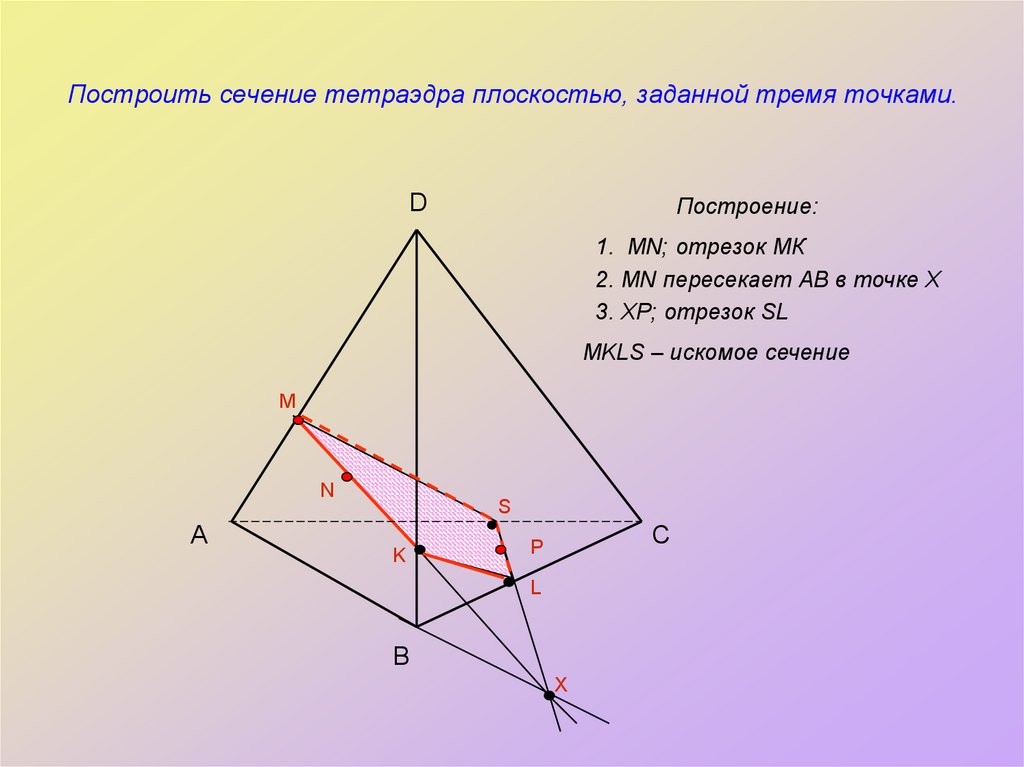
14. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
Построение:
1. MN; отрезок МК
2. MN пересекает АВ в точке Х
3. ХР; отрезок SL
MKLS – искомое сечение
M
N
А
S
K
C
P
L
B
X

15.

Аксиоматический метод
Метод следов
Суть
метода
заключается
в
построении
вспомогательной прямой, являющейся изображением
линии пересечения секущей плоскости с плоскостью
какой-либо грани фигуры . Удобнее всего строить
изображение линии пересечения секущей плоскости с
плоскостью нижнего основания. Эту линию называют
следом секущей плоскости. Используя след, легко
построить изображения точек секущей плоскости,
находящихся на боковых ребрах или гранях фигуры .

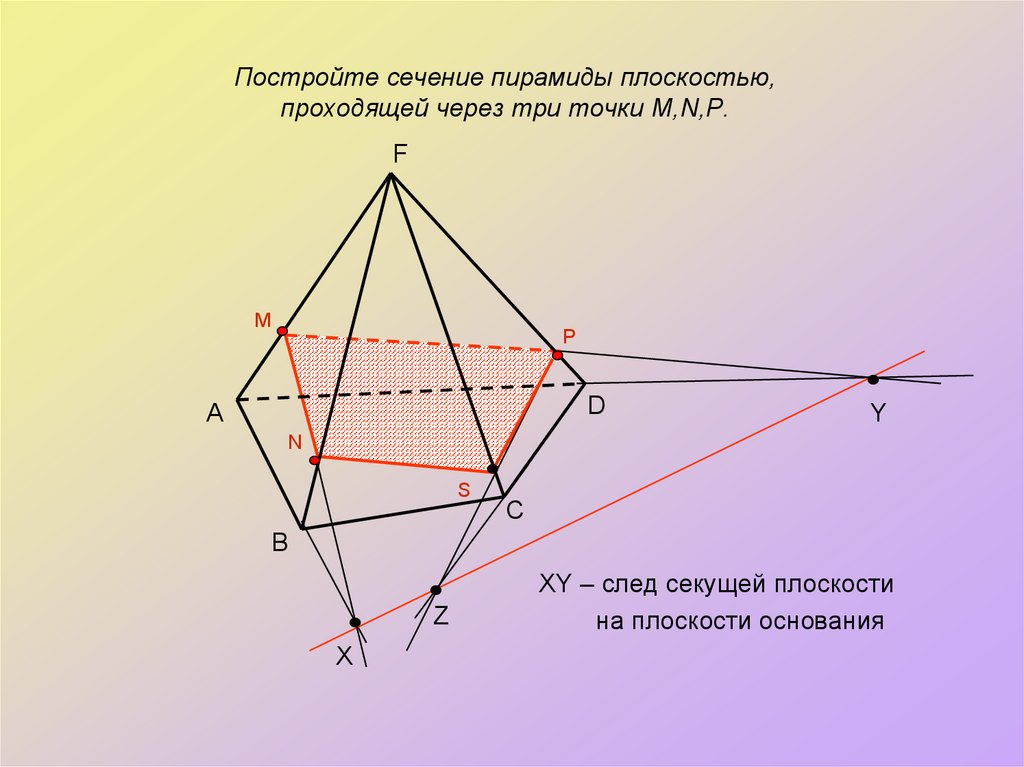
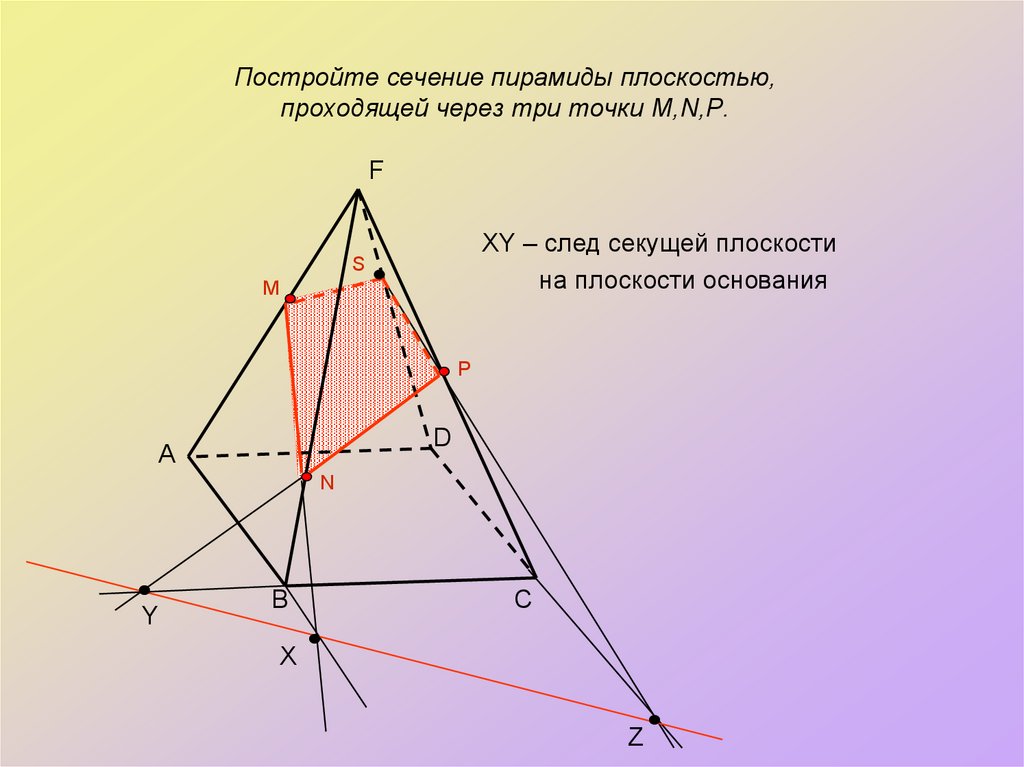
16. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
M
P
D
А
Y
N
S
C
B
Z
X
XY – след секущей плоскости
на плоскости основания

17. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
XY – след секущей плоскости
на плоскости основания
S
M
P
D
А
N
Y
B
C
X
Z

18.

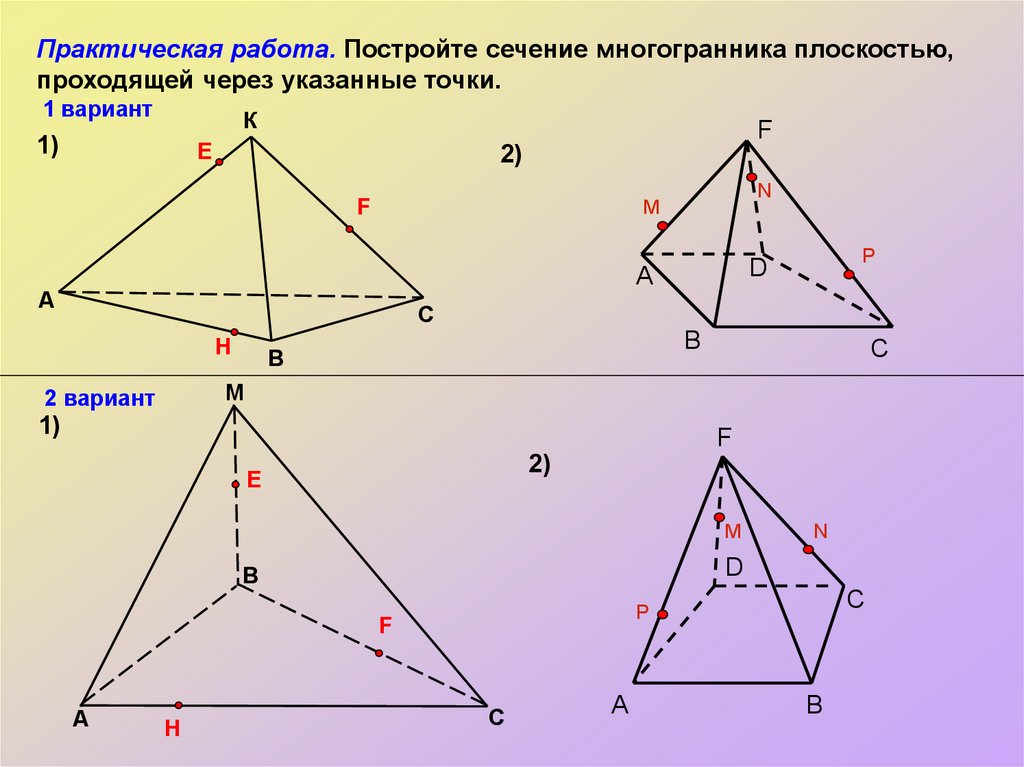
Практическая работа. Постройте сечение многогранника плоскостью,
проходящей через указанные точки.
1 вариант
К
1)
F
E
2)
F
N
M
А
A
P
D
С
H
B
В
C
M
2 вариант
1)
F
2)
E
M
D
В
H
C
P
F
A
N
С
А
B

19.

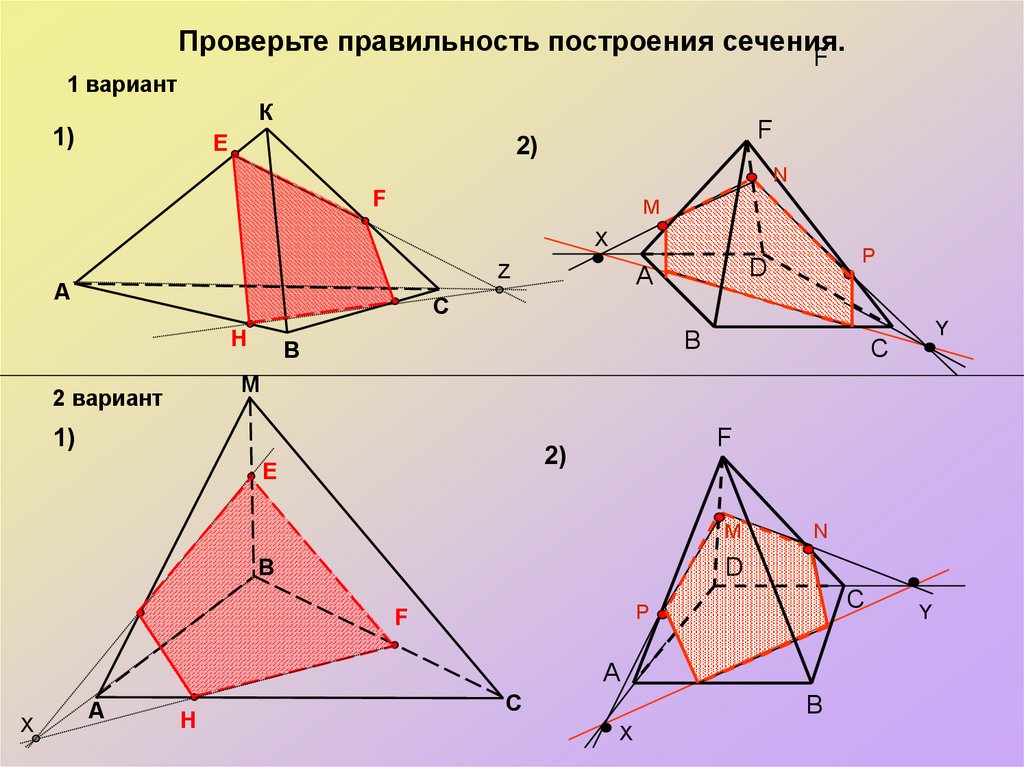
Проверьте правильность построения сечения.
F
1 вариант
К
1)
E
F
2)
N
F
M
X
A
P
D
А
Z
С
H
B
В
M
2 вариант
1)
F
2)
E
M
В
N
D
C
P
F
А
X
A
Y
C
H
С
B
X
Y

20.

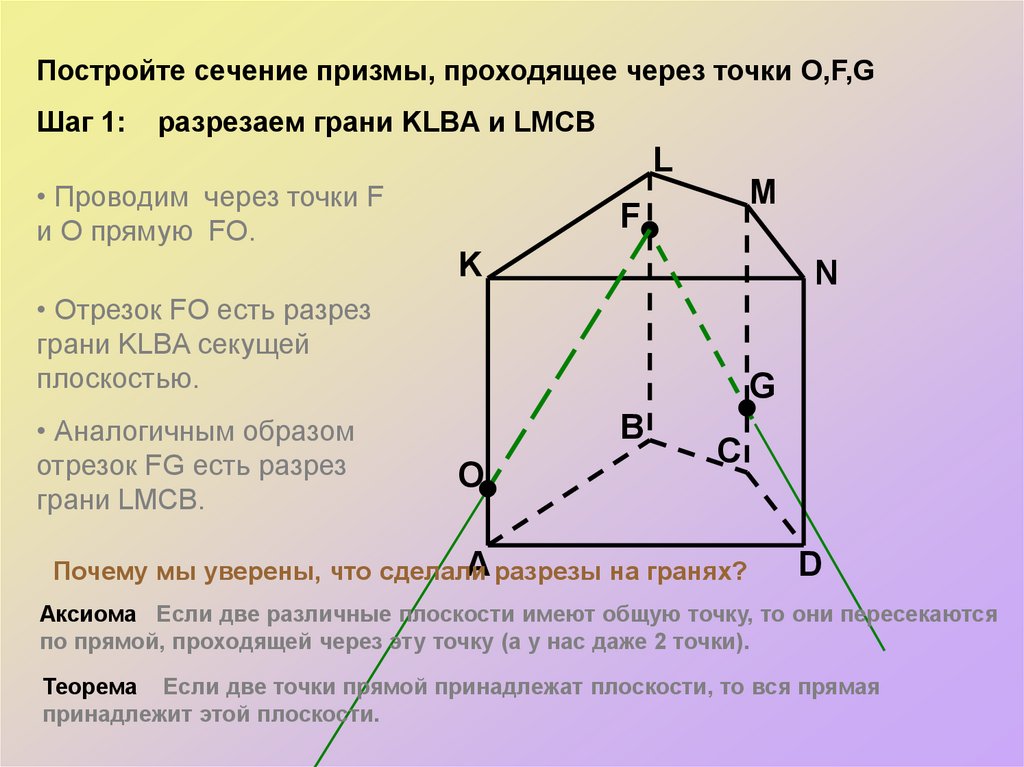
Постройте сечение призмы, проходящее через точки O,F,G
Шаг 1:
разрезаем грани KLBA и LMCB
L
• Проводим через точки F
и O прямую FO.
M
F
K
N
• Отрезок FO есть разрез
грани KLBA секущей
плоскостью.
• Аналогичным образом
отрезок FG есть разрез
грани LMCB.
G
B
O
C
A разрезы на гранях?
Почему мы уверены, что сделали
D
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

21.

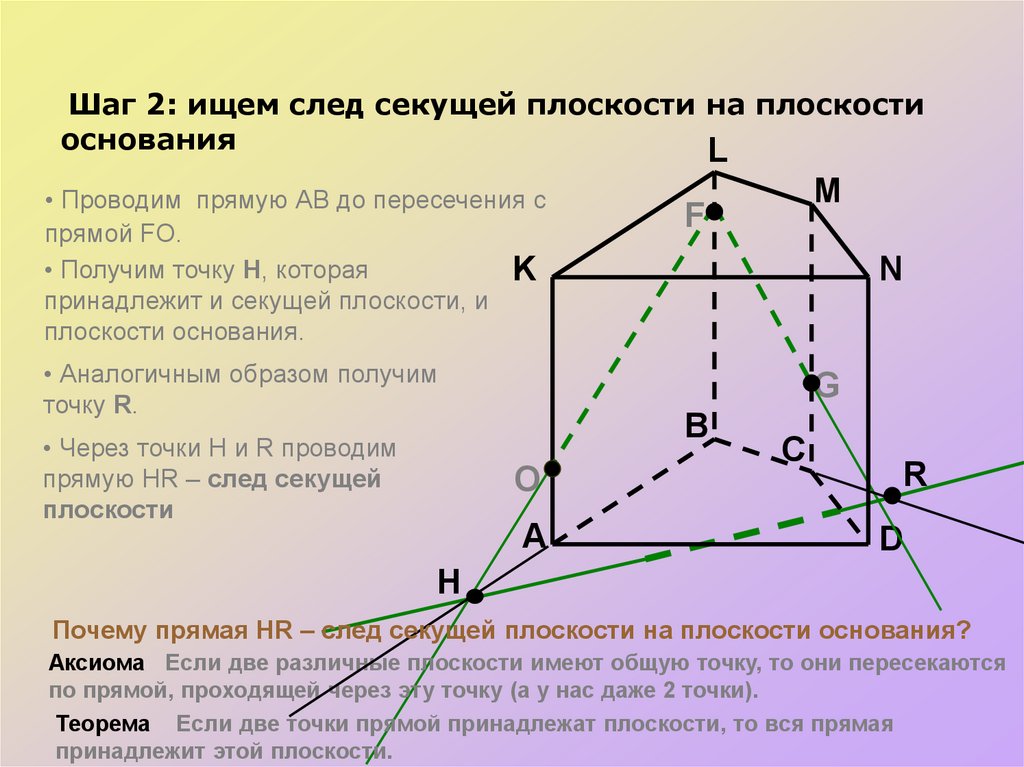
Шаг 2: ищем след секущей плоскости на плоскости
основания
L
• Проводим прямую АВ до пересечения с
прямой FO.
• Получим точку H, которая
K
принадлежит и секущей плоскости, и
плоскости основания.
• Аналогичным образом получим
точку R.
• Через точки H и R проводим
прямую HR – след секущей
плоскости
M
F
N
G
B
O
A
C
R
D
H
Почему прямая HR – след секущей плоскости на плоскости основания?
Аксиома Если две различные плоскости имеют общую точку, то они пересекаются
по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

22.

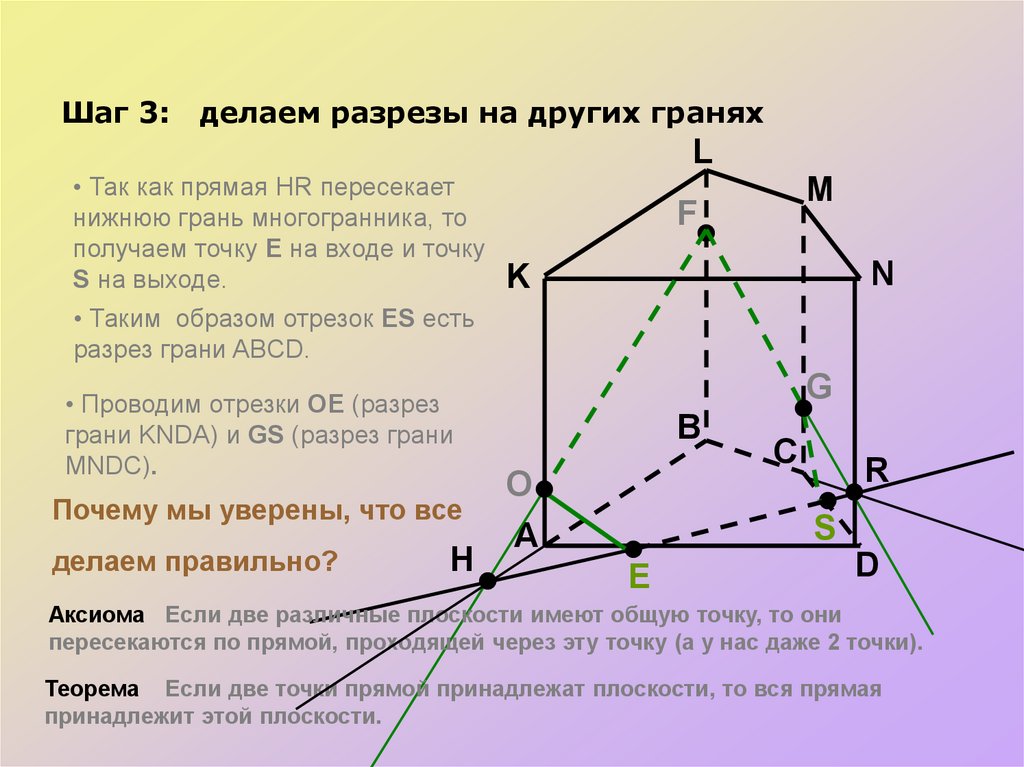
Шаг 3:
делаем разрезы на других гранях
L
• Так как прямая HR пересекает
нижнюю грань многогранника, то
получаем точку E на входе и точку
S на выходе.
M
F
N
K
• Таким образом отрезок ES есть
разрез грани ABCD.
• Проводим отрезки ОЕ (разрез
грани KNDA) и GS (разрез грани
MNDC).
Почему мы уверены, что все
делаем правильно?
H
G
B
O
A
C
R
S
E
D
Аксиома Если две различные плоскости имеют общую точку, то они
пересекаются по прямой, проходящей через эту точку (а у нас даже 2 точки).
Теорема Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.

23.

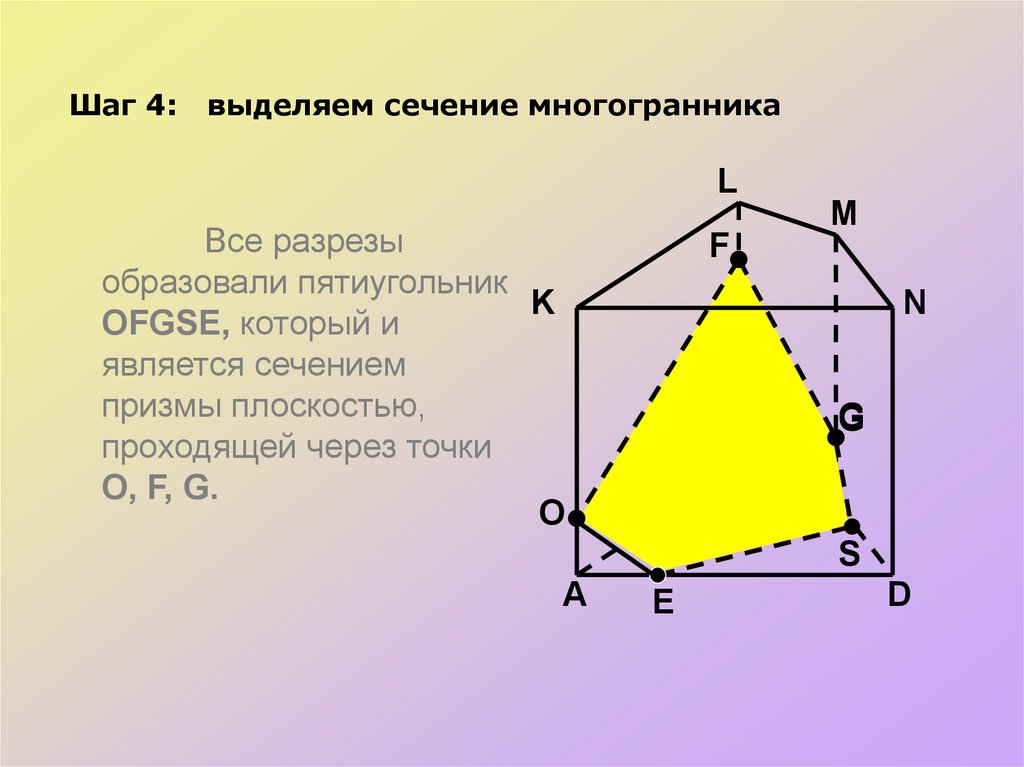
Шаг 4:
выделяем сечение многогранника
L
M
Все разрезы
образовали пятиугольник
K
OFGSE, который и
является сечением
призмы плоскостью,
проходящей через точки
O, F, G.
O
F
N
G
B
C
S
A
E
D

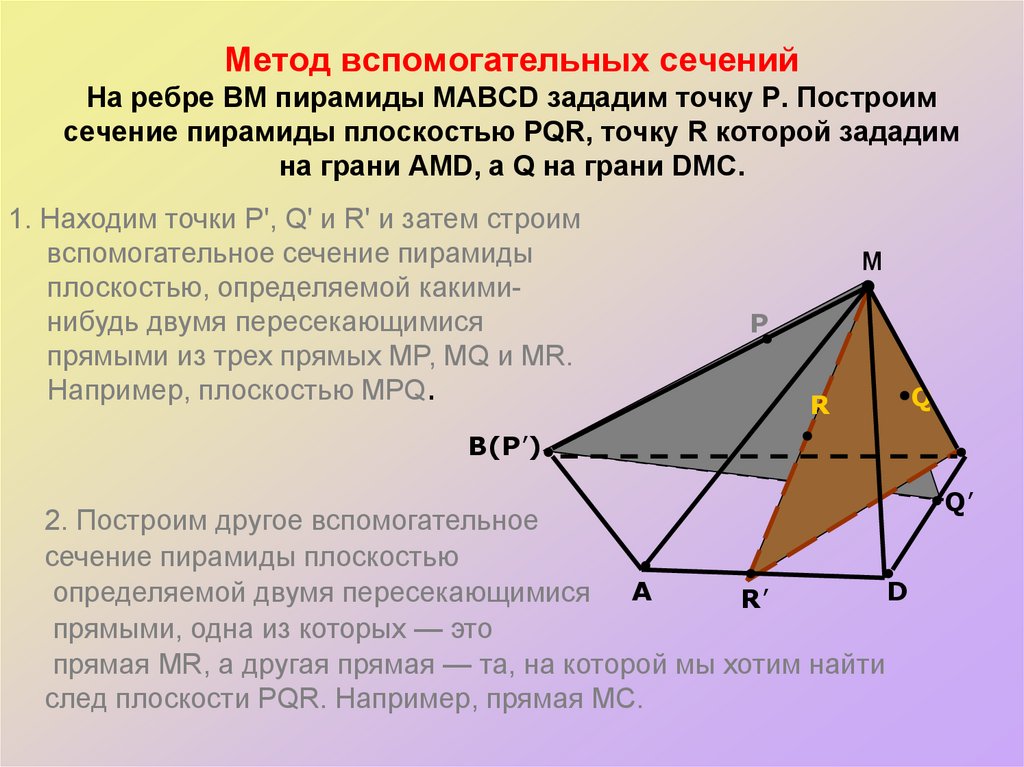
24. Метод вспомогательных сечений На ребре BM пирамиды MABCD зададим точку Р. Построим сечение пирамиды плоскостью PQR, точку R

которой зададим
на грани АMD, а Q на грани DMC.
1. Находим точки Р', Q' и R' и затем строим
вспомогательное сечение пирамиды
плоскостью, определяемой какиминибудь двумя пересекающимися
прямыми из трех прямых MP, MQ и МR.
Например, плоскостью МРQ.
М
P
R
Q
B(P’)
2. Построим другое вспомогательное
сечение пирамиды плоскостью
D
определяемой двумя пересекающимися A
R’
прямыми, одна из которых — это
прямая MR, а другая прямая — та, на которой мы хотим найти
след плоскости PQR. Например, прямая МС.
Q’

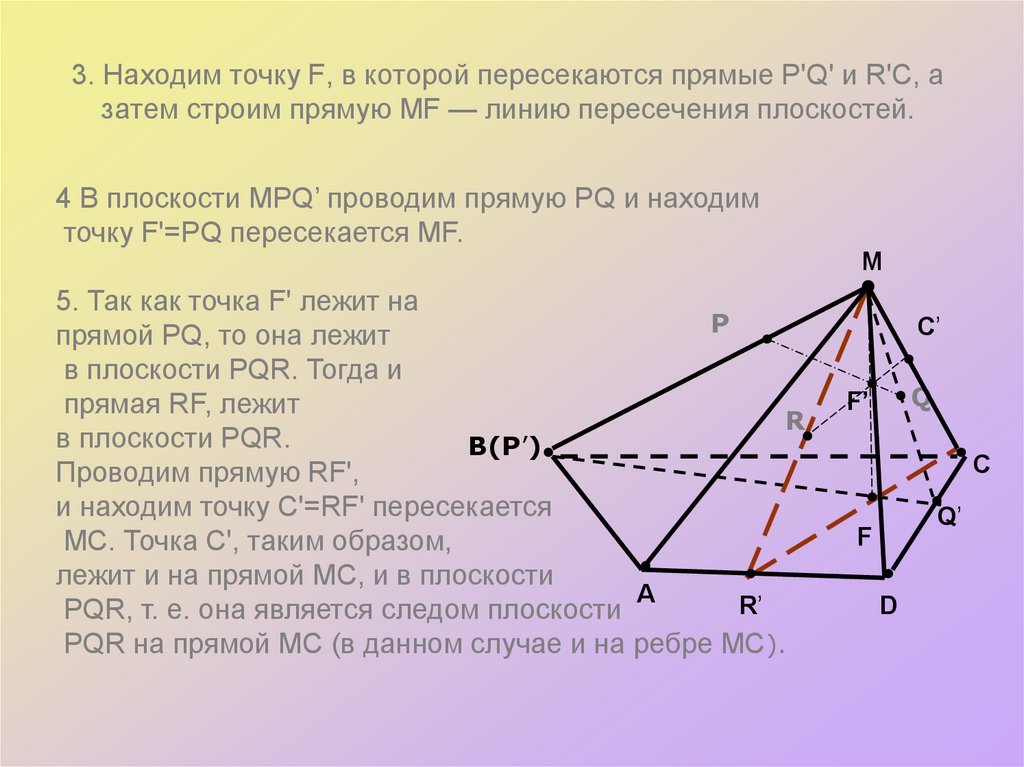
25. 3. Находим точку F, в которой пересекаются прямые Р'Q' и R'С, а затем строим прямую MF — линию пересечения плоскостей.

4 В плоскости MPQ’ проводим прямую PQ и находим
точку F'=PQ пересекается MF.
5. Так как точка F' лежит на
P
прямой PQ, то она лежит
в плоскости PQR. Тогда и
прямая RF, лежит
R
в плоскости PQR.
B(P’)
Проводим прямую RF',
и находим точку С'=RF' пересекается
МС. Точка С', таким образом,
лежит и на прямой МС, и в плоскости
А
R’
PQR, т. е. она является следом плоскости
PQR на прямой МС (в данном случае и на ребре МС).
М
C’
Q
F’
C
Q’
F
D

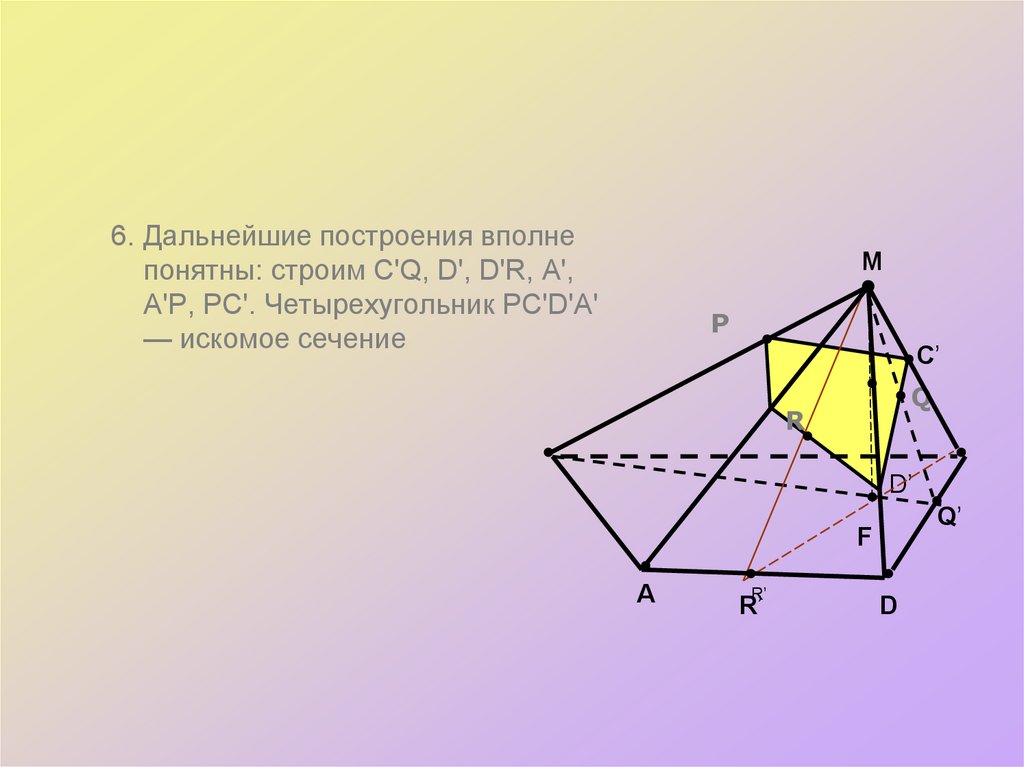
26.

6. Дальнейшие построения вполне
понятны: строим C'Q, D', D'R, А',
А'Р, РС'. Четырехугольник РС'D'А'
— искомое сечение
М
P
C’
Q
R
D’
Q’
F
А
R’
R’
D

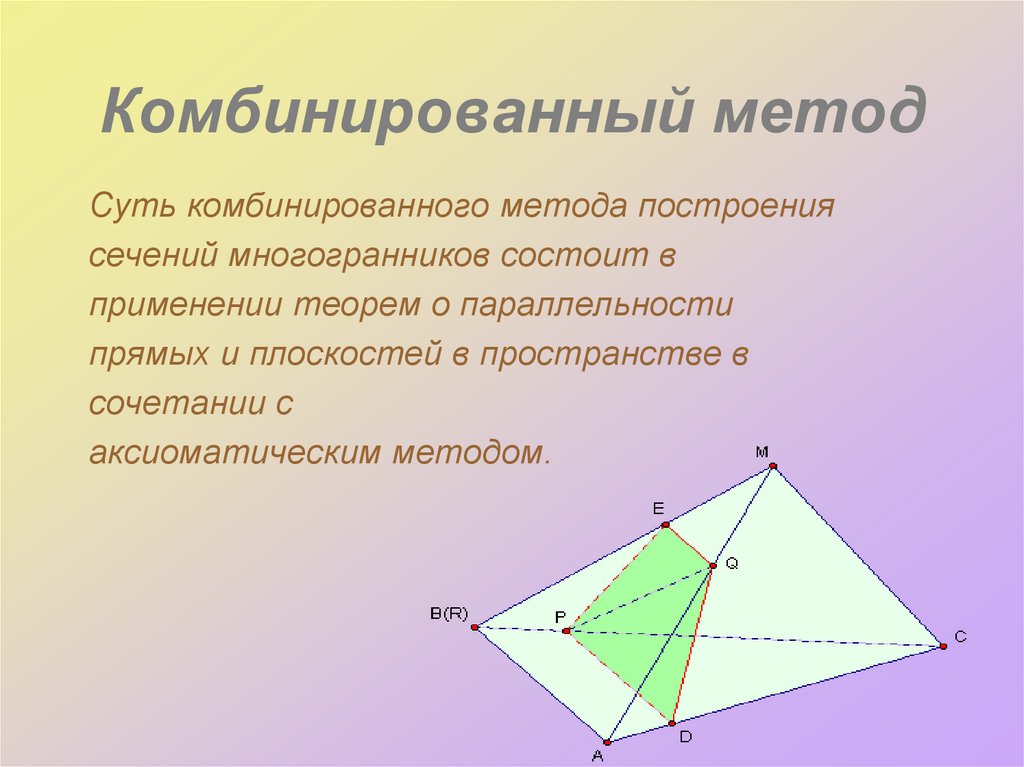
27. Комбинированный метод

Суть комбинированного метода построения
сечений многогранников состоит в
применении теорем о параллельности
прямых и плоскостей в пространстве в
сочетании с
аксиоматическим методом.

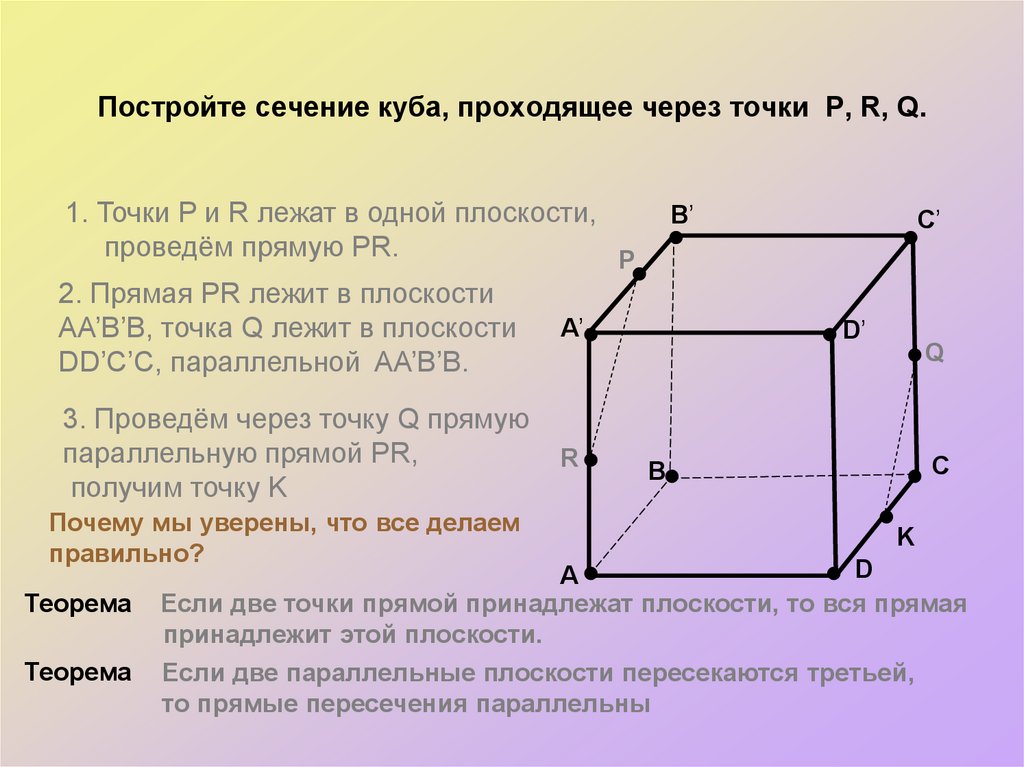
28. Постройте сечение куба, проходящее через точки P, R, Q.

1. Точки P и R лежат в одной плоскости,
проведём прямую PR.
P
2. Прямая PR лежит в плоскости
A’
AA’B’B, точка Q лежит в плоскости
DD’C’C, параллельной AA’B’B.
3. Проведём через точку Q прямую
параллельную прямой PR,
получим точку K
Почему мы уверены, что все делаем
правильно?
Теорема
Теорема
R
B’
C’
D’
Q
C
B
K
D
A
Если две точки прямой принадлежат плоскости, то вся прямая
принадлежит этой плоскости.
Если две параллельные плоскости пересекаются третьей,
то прямые пересечения параллельны

29.

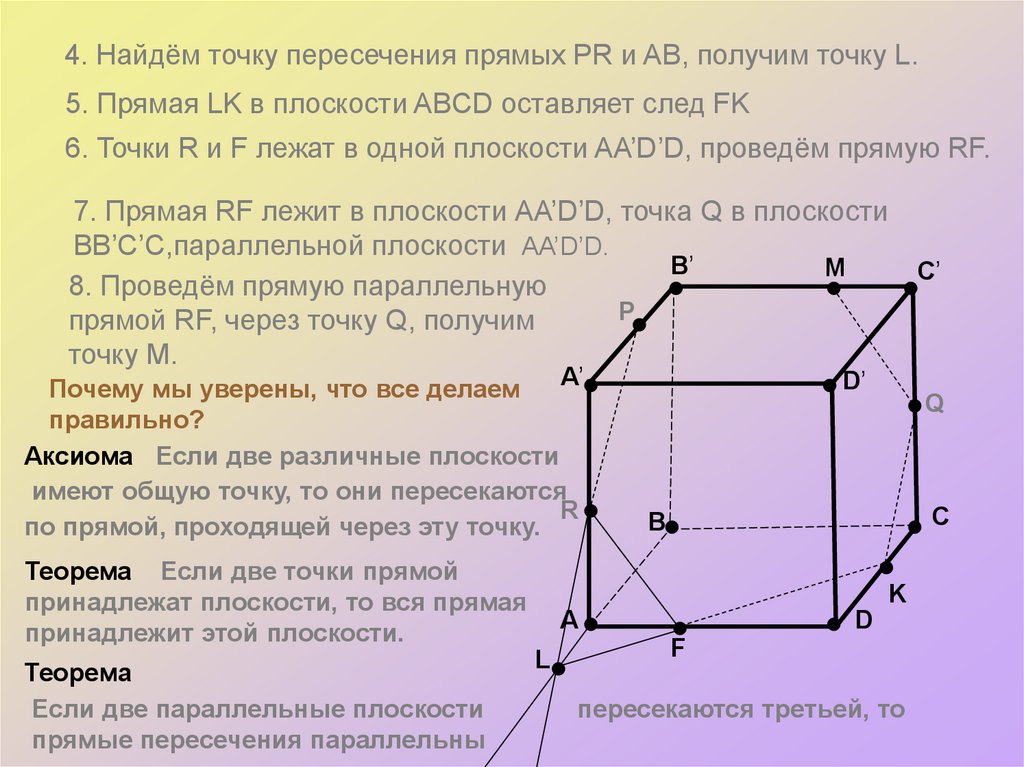
4. Найдём точку пересечения прямых PR и AB, получим точку L.
5. Прямая LK в плоскости ABCD оставляет след FK
6. Точки R и F лежат в одной плоскости AA’D’D, проведём прямую RF.
7. Прямая RF лежит в плоскости АA’D’D, точка Q в плоскости
BB’C’C,параллельной плоскости AA’D’D.
B’
M
C’
8. Проведём прямую параллельную
P
прямой RF, через точку Q, получим
точку M.
A’
Почему мы уверены, что все делаем
правильно?
Аксиома Если две различные плоскости
имеют общую точку, то они пересекаются
R
по прямой, проходящей через эту точку.
Теорема Если две точки прямой
принадлежат плоскости, то вся прямая
принадлежит этой плоскости.
Теорема
Если две параллельные плоскости
прямые пересечения параллельны
D’
Q
C
B
K
A
L
D
F
пересекаются третьей, то

30.

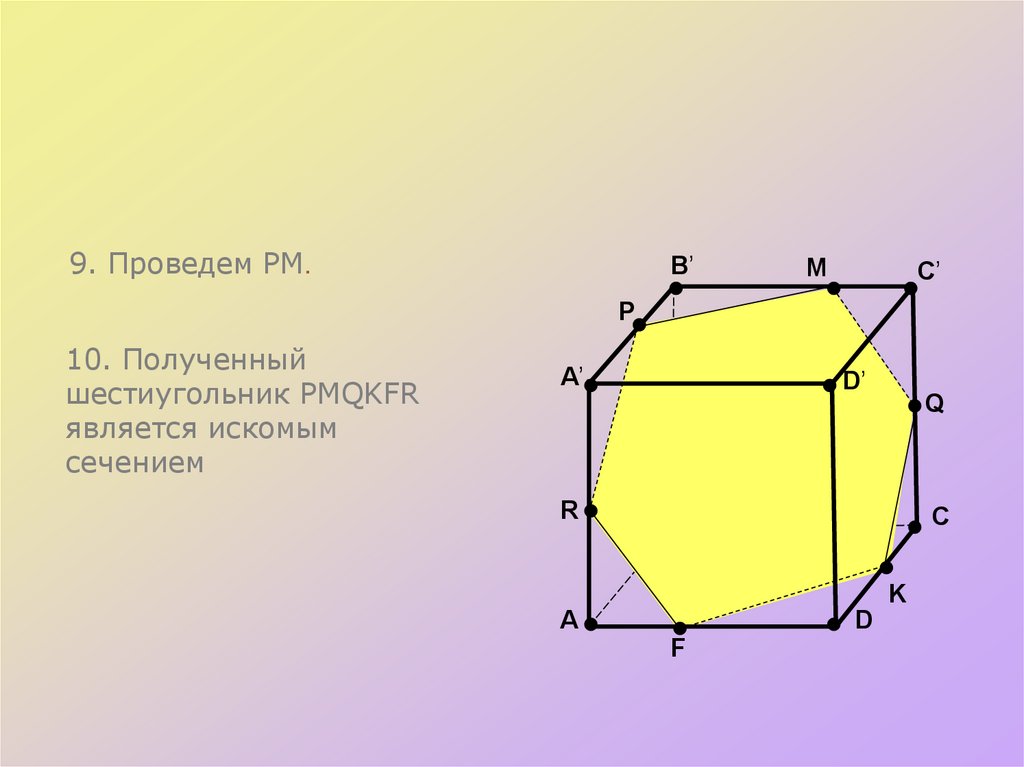
9. Проведем PM.
B’
M
C’
P
10. Полученный
шестиугольник РMQKFR
является искомым
сечением
A’
R
D’
Q
C
B
K
A
D
F

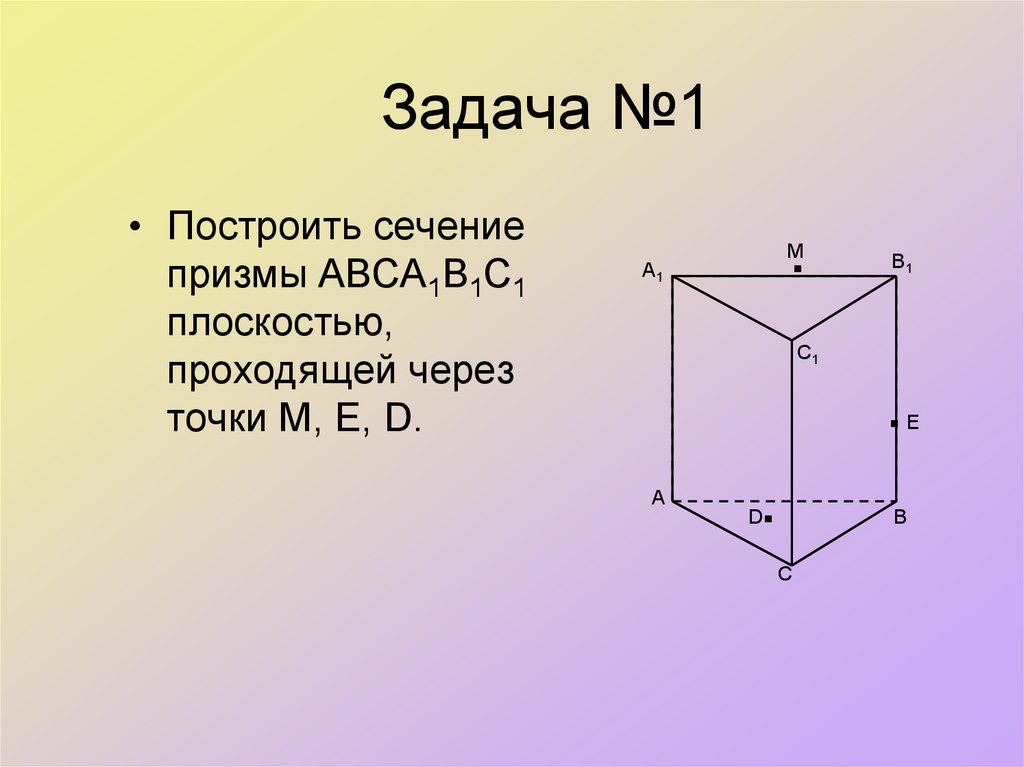
31. Задача №1

• Построить сечение
призмы АВСА1В1С1
плоскостью,
проходящей через
точки М, Е, D.
.
М
А1
В1
С1
.
А
.
D
С
Е
В

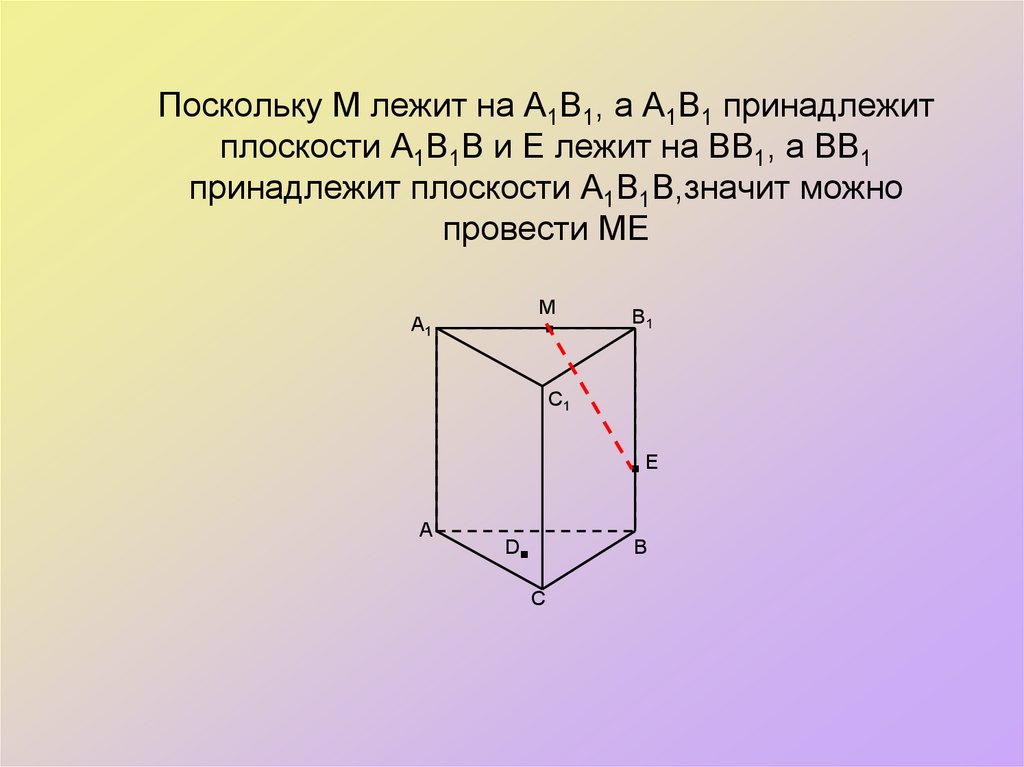
32. Поскольку М лежит на А1В1, а А1В1 принадлежит плоскости А1В1В и Е лежит на ВВ1, а ВВ1 принадлежит плоскости А1В1В,значит можно

провести МЕ
.
М
А1
В1
С1
.
Е
А
.
D
С
В

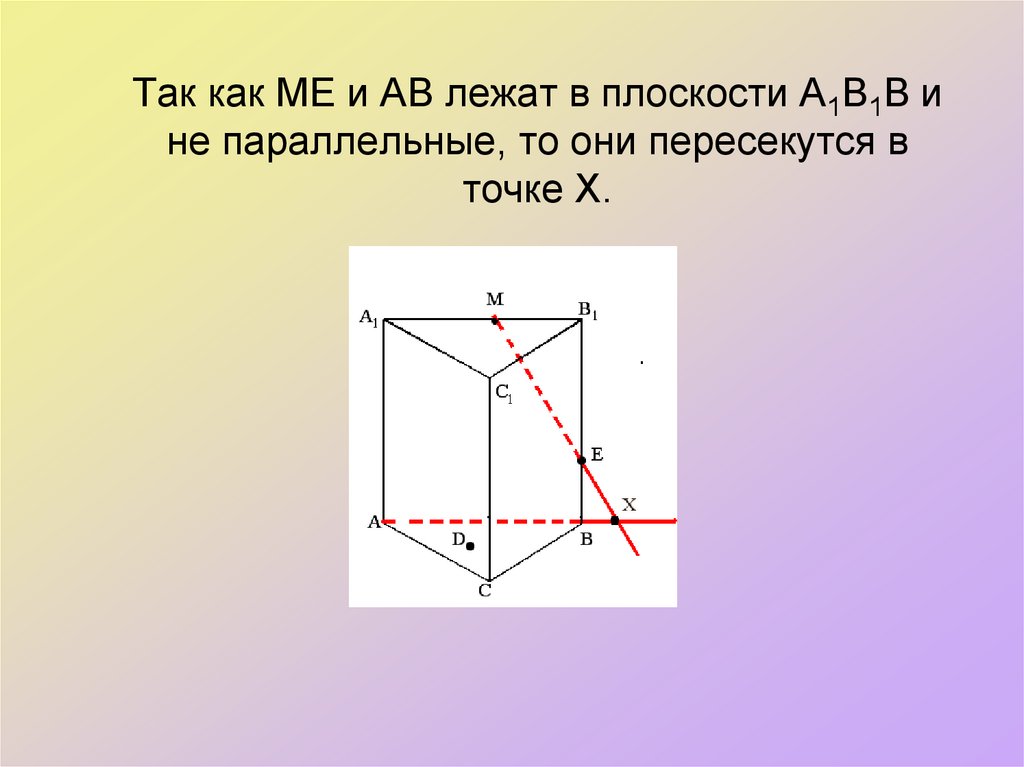
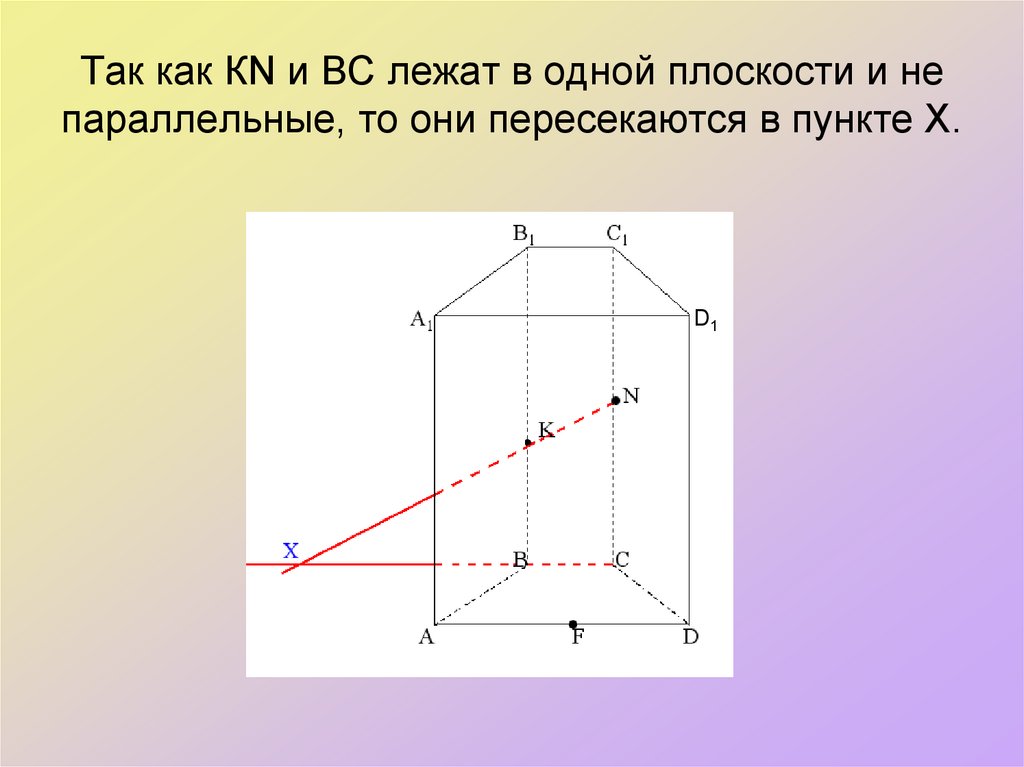
33. Так как МЕ и АВ лежат в плоскости А1В1В и не параллельные, то они пересекутся в точке Х.

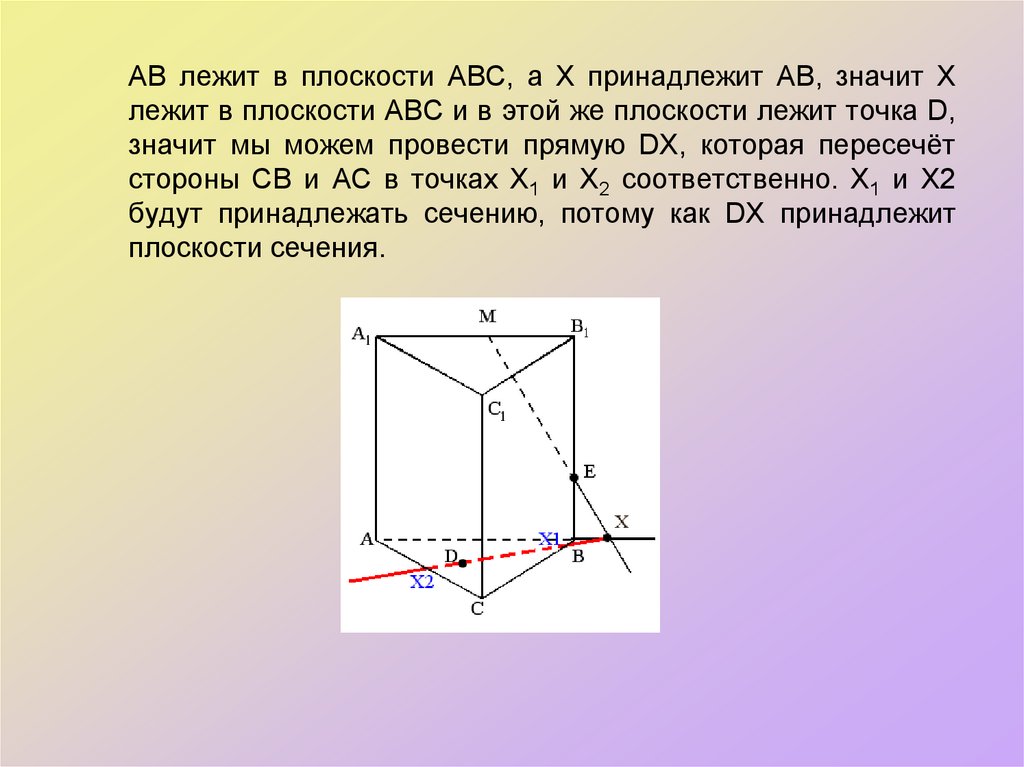
34. АВ лежит в плоскости АВС, а Х принадлежит АВ, значит Х лежит в плоскости АВС и в этой же плоскости лежит точка D, значит мы

можем провести прямую DX, которая пересечёт
стороны СВ и АС в точках Х1 и Х2 соответственно. Х1 и Х2
будут принадлежать сечению, потому как DX принадлежит
плоскости сечения.

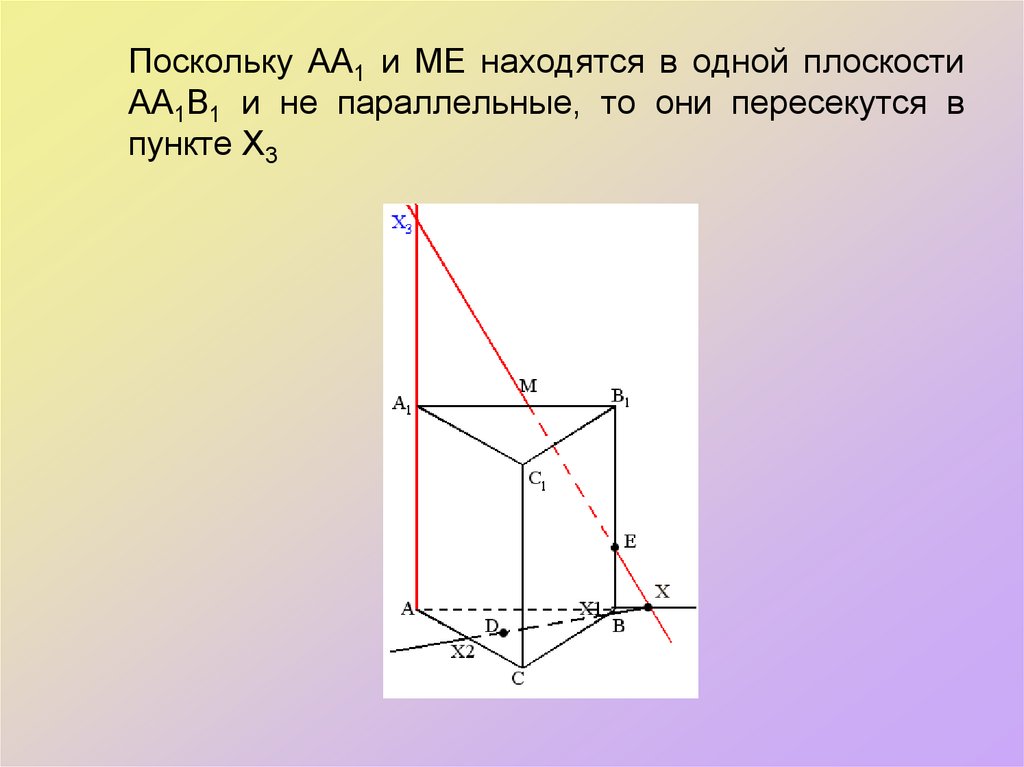
35. Поскольку АА1 и МЕ находятся в одной плоскости АА1В1 и не параллельные, то они пересекутся в пункте Х3

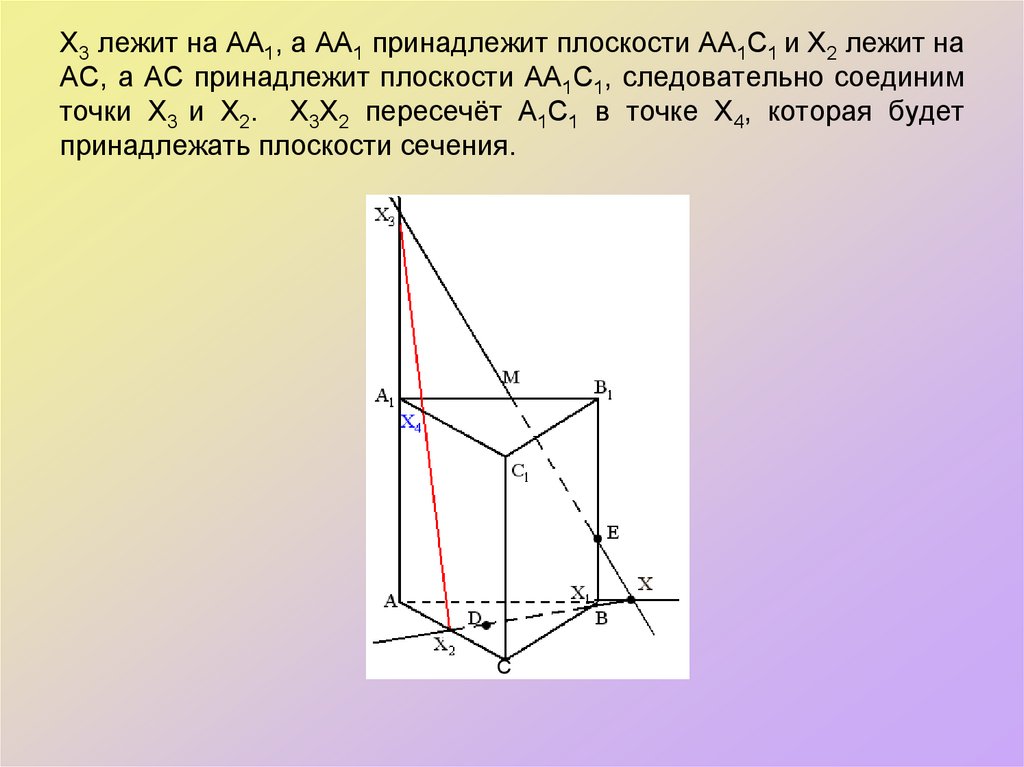
36. Х3 лежит на АА1, а АА1 принадлежит плоскости АА1С1 и Х2 лежит на АС, а АС принадлежит плоскости АА1С1, следовательно соединим

точки Х3 и Х2. Х3Х2 пересечёт А1С1 в точке Х4, которая будет
принадлежать плоскости сечения.
С

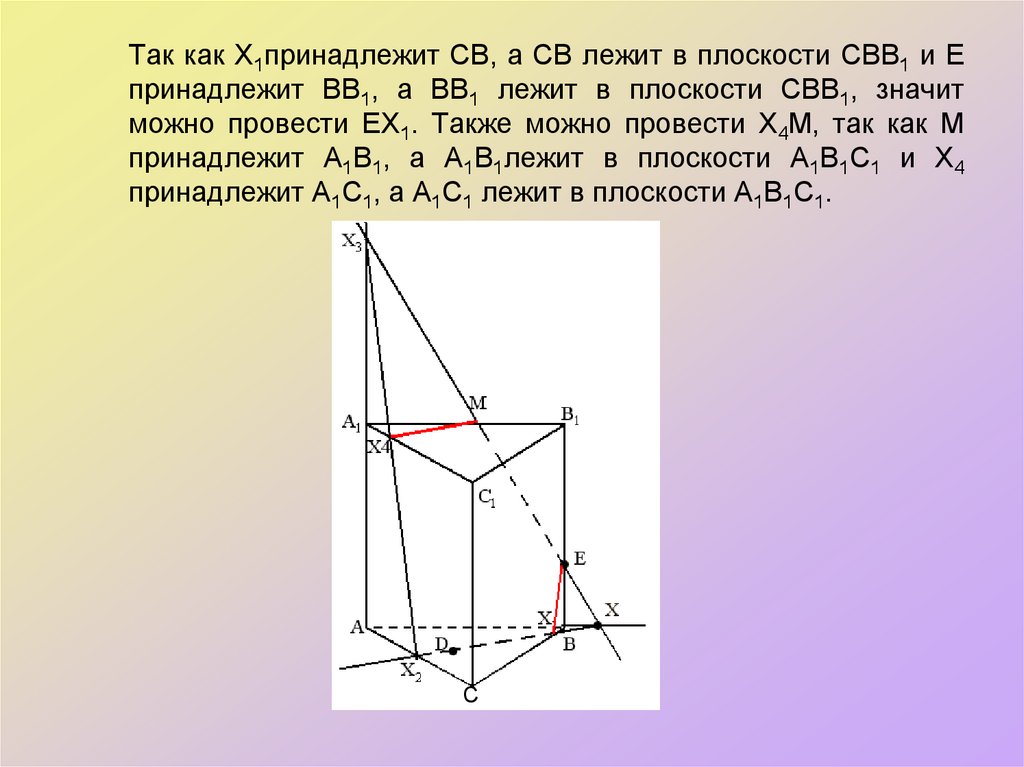
37. Так как Х1принадлежит СВ, а СВ лежит в плоскости СВВ1 и Е принадлежит ВВ1, а ВВ1 лежит в плоскости СВВ1, значит можно провести

ЕХ1. Также можно провести Х4М, так как М
принадлежит А1В1, а А1В1лежит в плоскости А1В1С1 и Х4
принадлежит А1С1, а А1С1 лежит в плоскости А1В1С1.
С

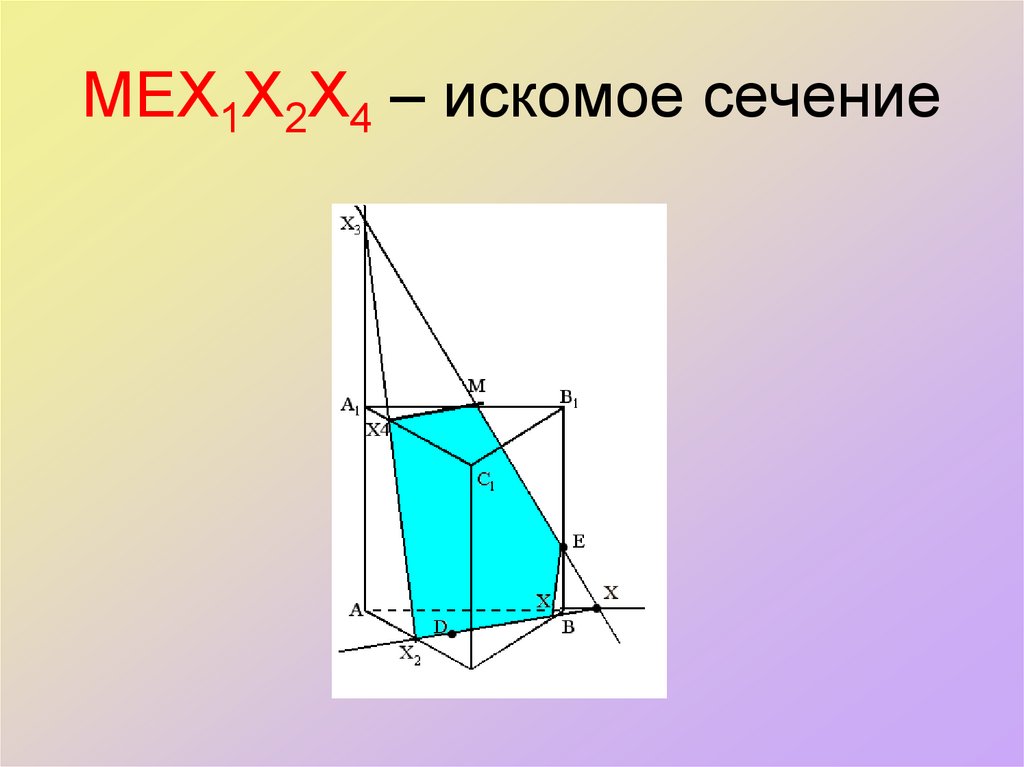
38. МЕХ1Х2Х4 – искомое сечение

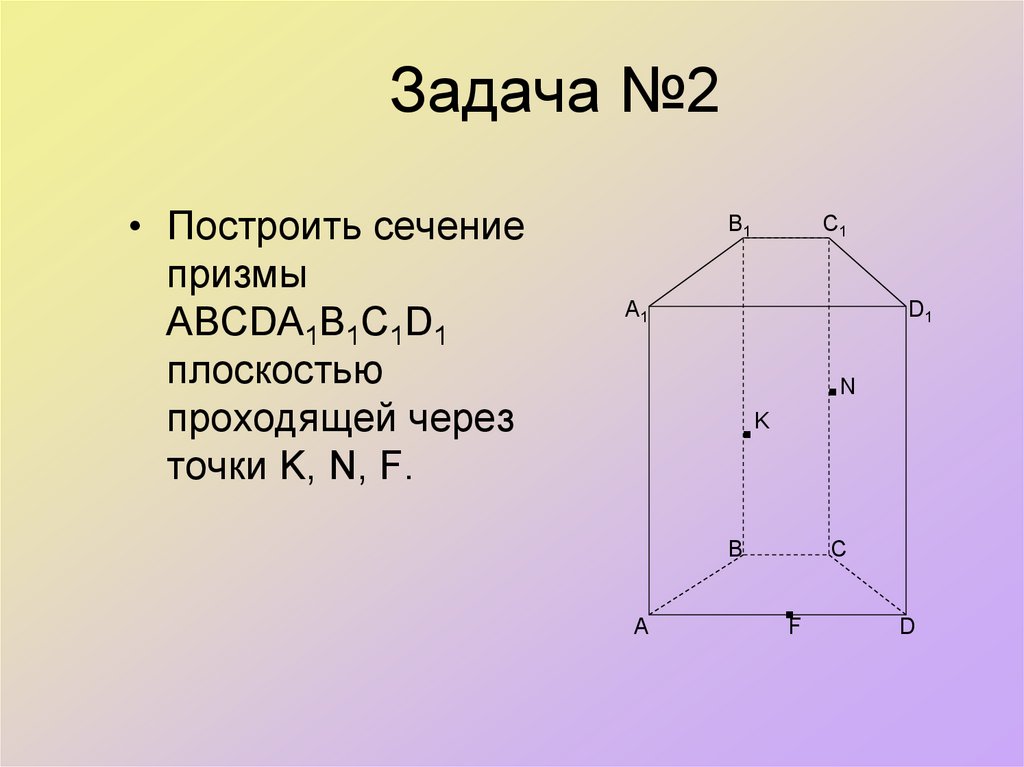
39. Задача №2

• Построить сечение
призмы
АВСDА1В1С1D1
плоскостью
проходящей через
точки K, N, F.
В1
С1
А1
D1
.
N
.
K
В
А
С
.
F
D

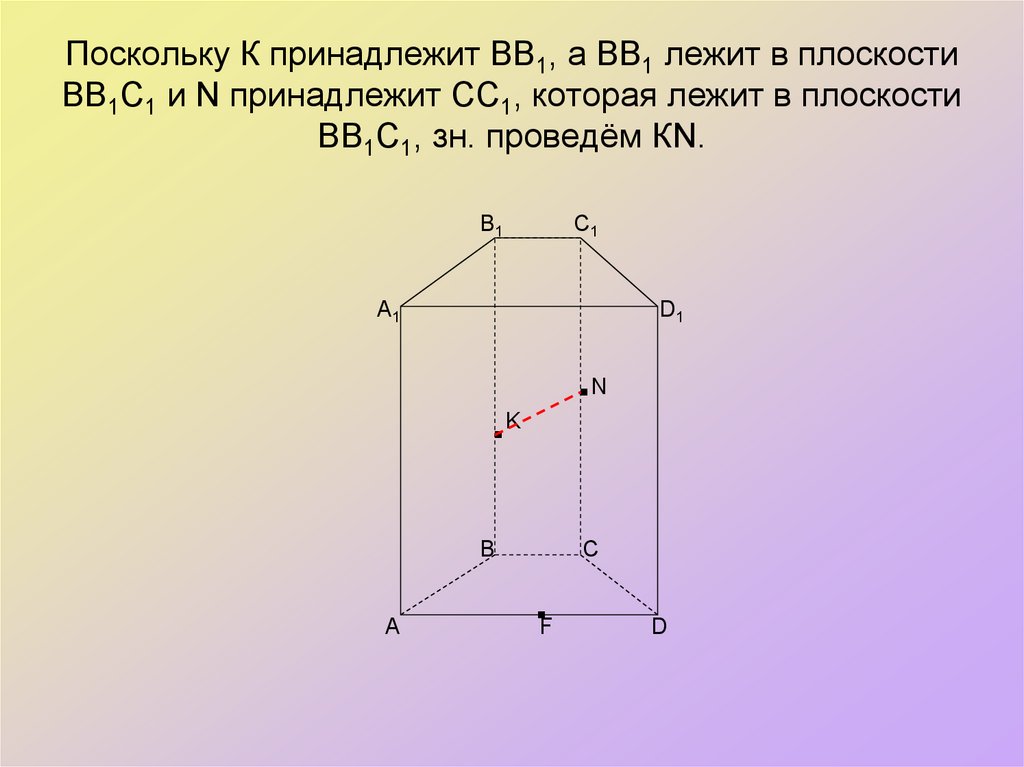
40. Поскольку К принадлежит ВВ1, а ВВ1 лежит в плоскости ВВ1С1 и N принадлежит СС1, которая лежит в плоскости ВВ1С1, зн. проведём

КN.
В1
С1
А1
D1
.
N
.
K
В
А
С
.
F
D

41. Так как КN и ВС лежат в одной плоскости и не параллельные, то они пересекаются в пункте Х.

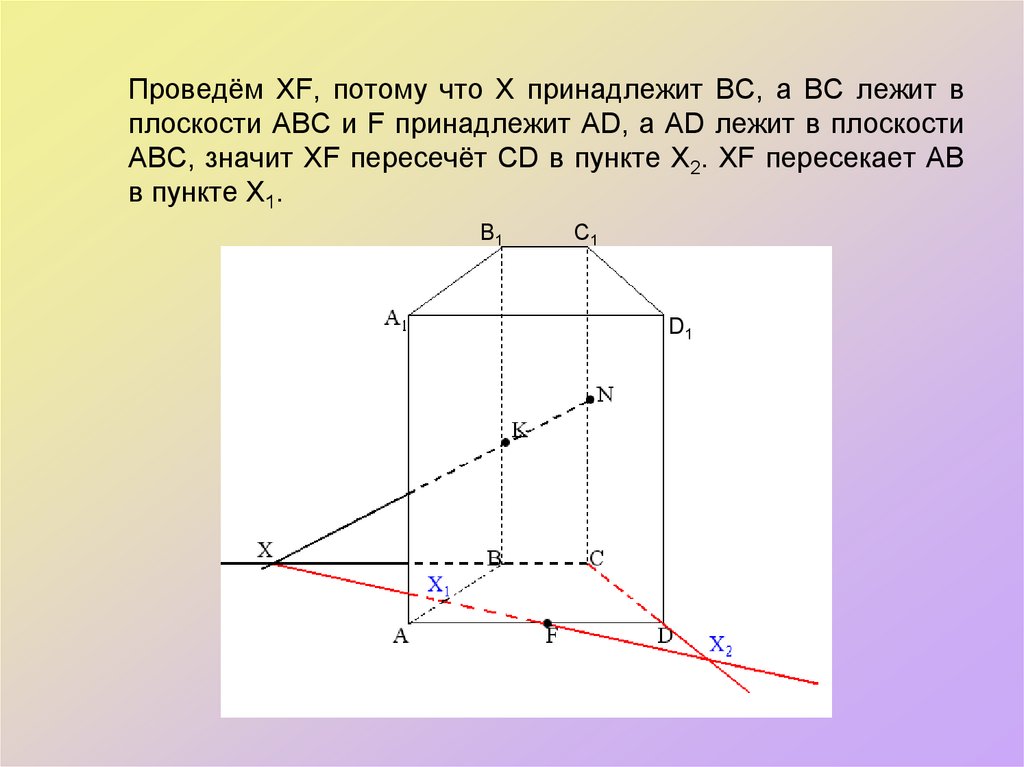
D1

42. Проведём ХF, потому что Х принадлежит ВС, а ВС лежит в плоскости АВС и F принадлежит АD, а АD лежит в плоскости АВС, значит ХF

пересечёт CD в пункте Х2. ХF пересекает АВ
в пункте Х1.
В1
С1
D1

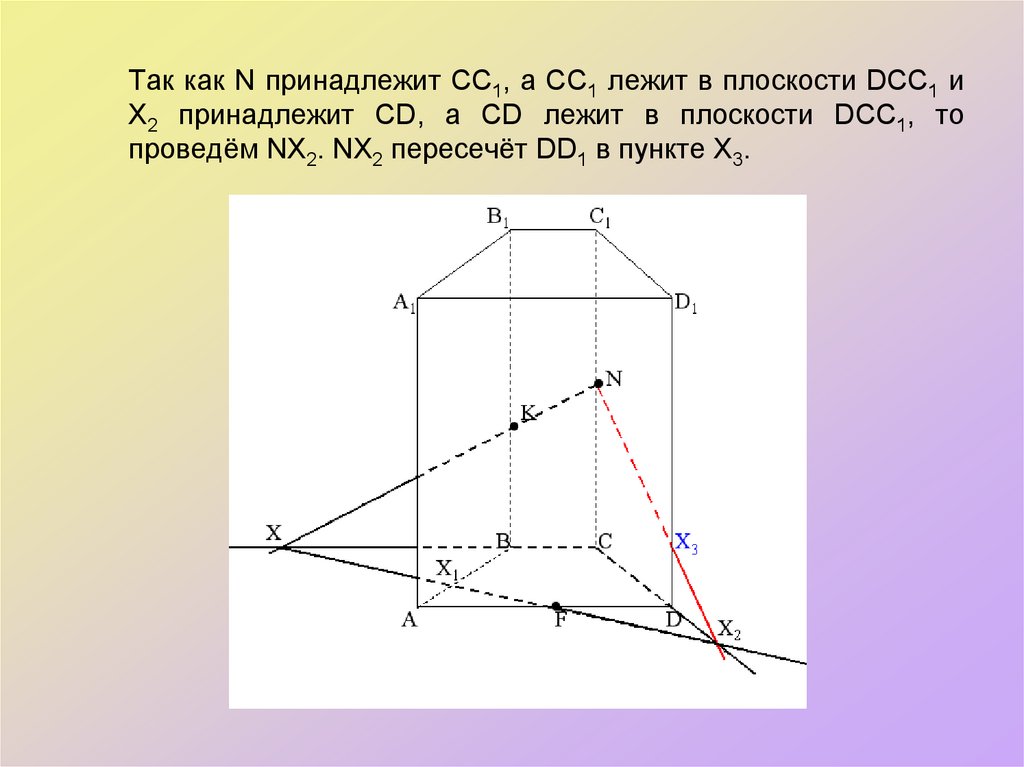
43. Так как N принадлежит СС1, а СС1 лежит в плоскости DСС1 и Х2 принадлежит СD, а СD лежит в плоскости DСС1, то проведём NХ2. NХ2

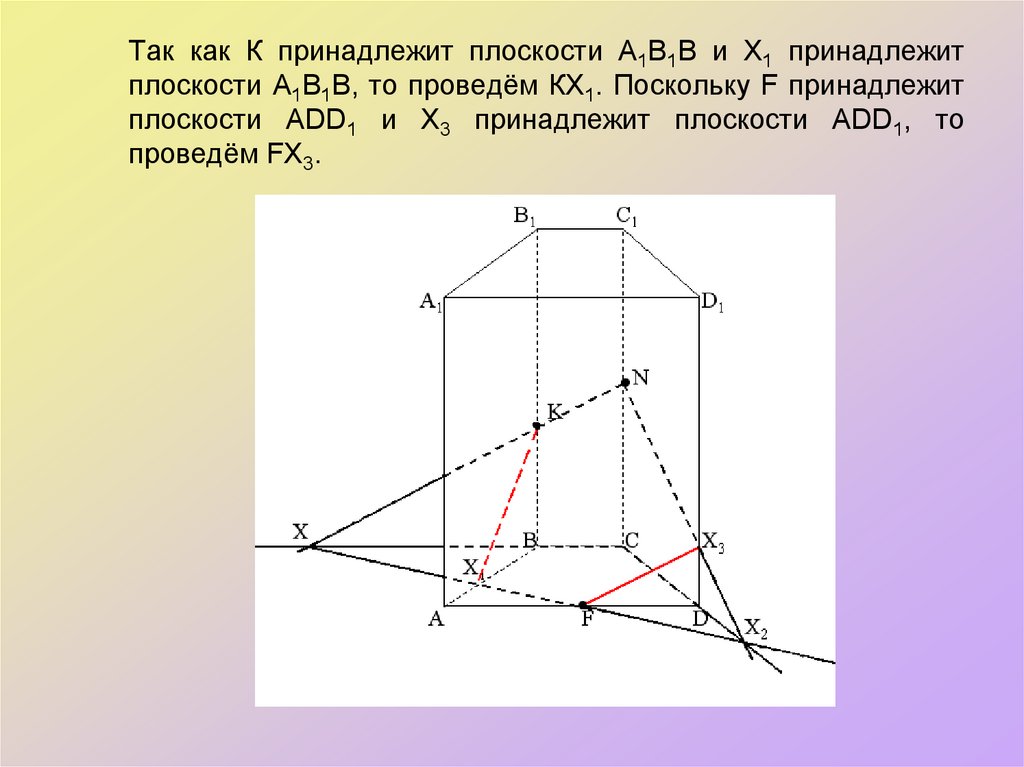
пересечёт DD1 в пункте Х3.

44. Так как К принадлежит плоскости А1В1В и Х1 принадлежит плоскости А1В1В, то проведём КХ1. Поскольку F принадлежит плоскости АDD1

и Х3 принадлежит плоскости АDD1, то
проведём FХ3.

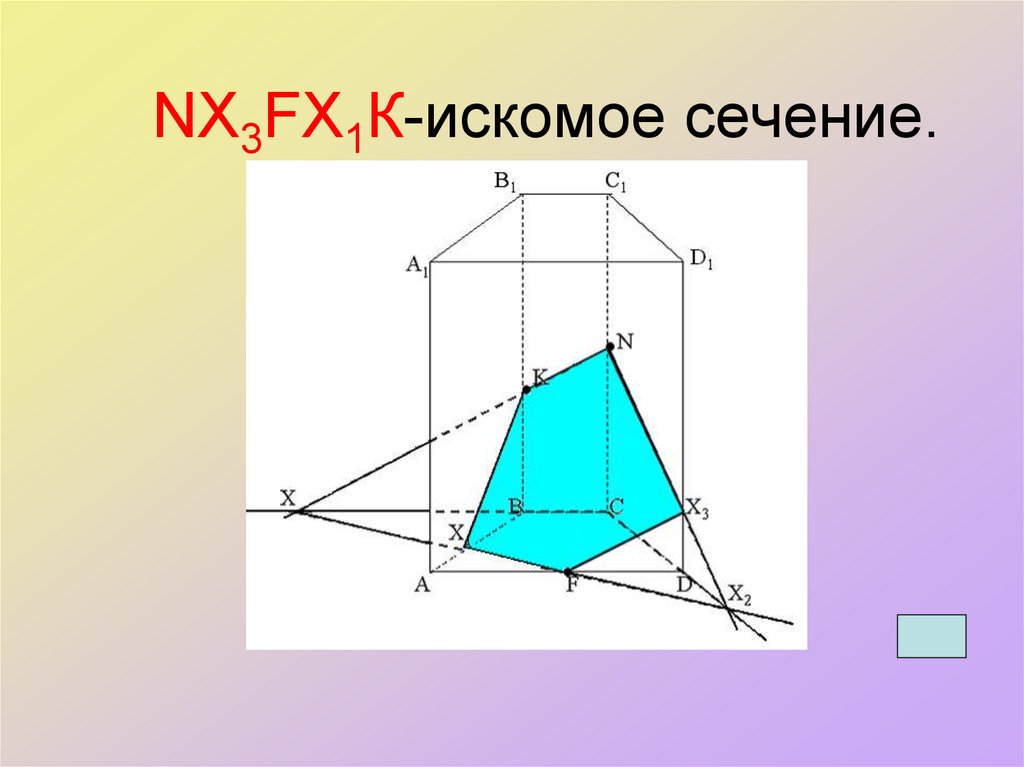
45. NХ3FХ1К-искомое сечение.

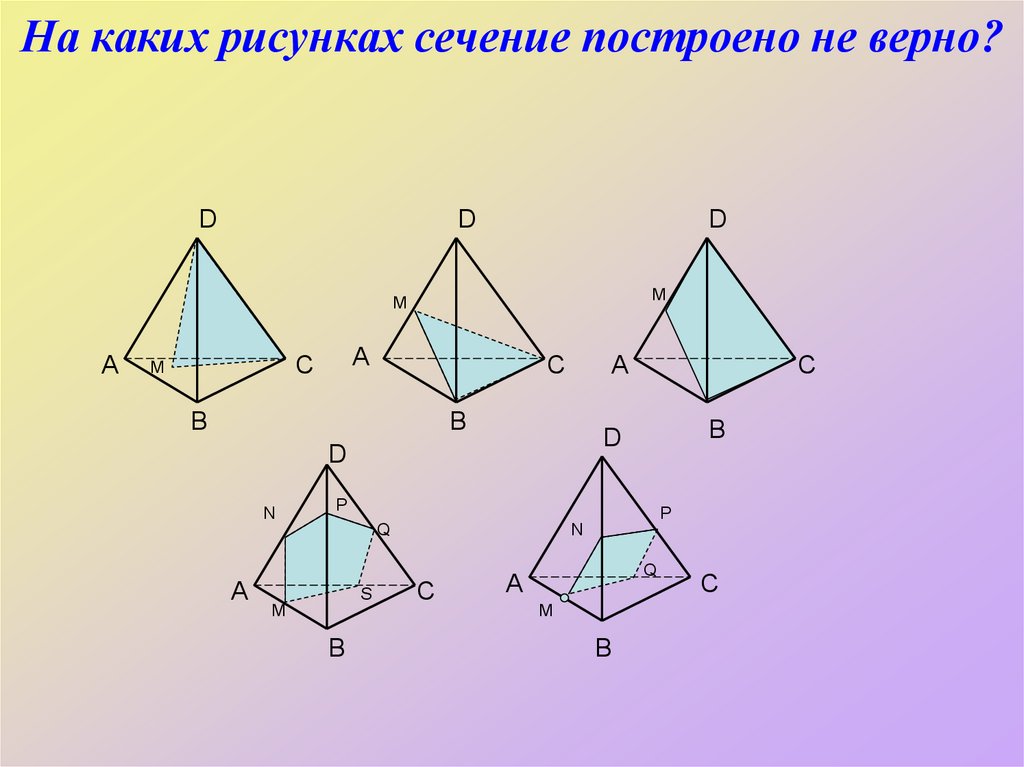
46. На каких рисунках сечение построено не верно?

D
D
D
M
M
А
А
C
M
А
C
B
B
P
P
Q
А
B
D
D
N
C
S
M
B
N
C
Q
А
M
B
C

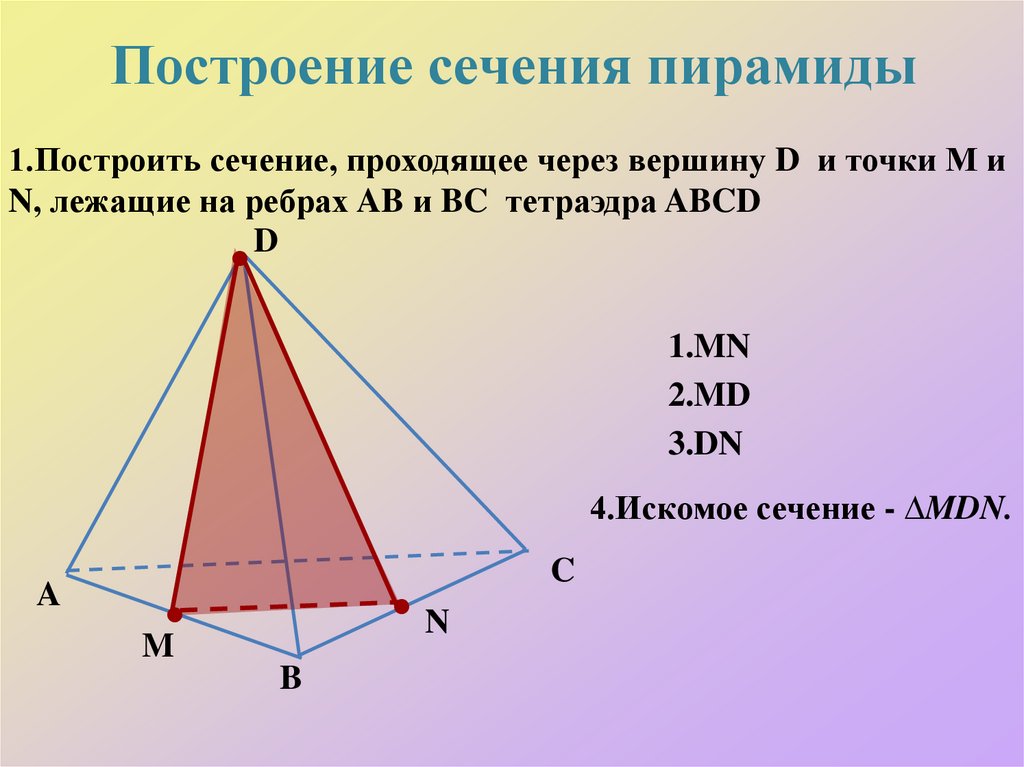
47. Построение сечения пирамиды

1.Построить сечение, проходящее через вершину D и точки М и
N, лежащие на ребрах AB и BC тетраэдра ABCD
D
1.MN
2.MD
3.DN
4.Искомое сечение - ∆MDN.
A
•N
M
B
C

48.

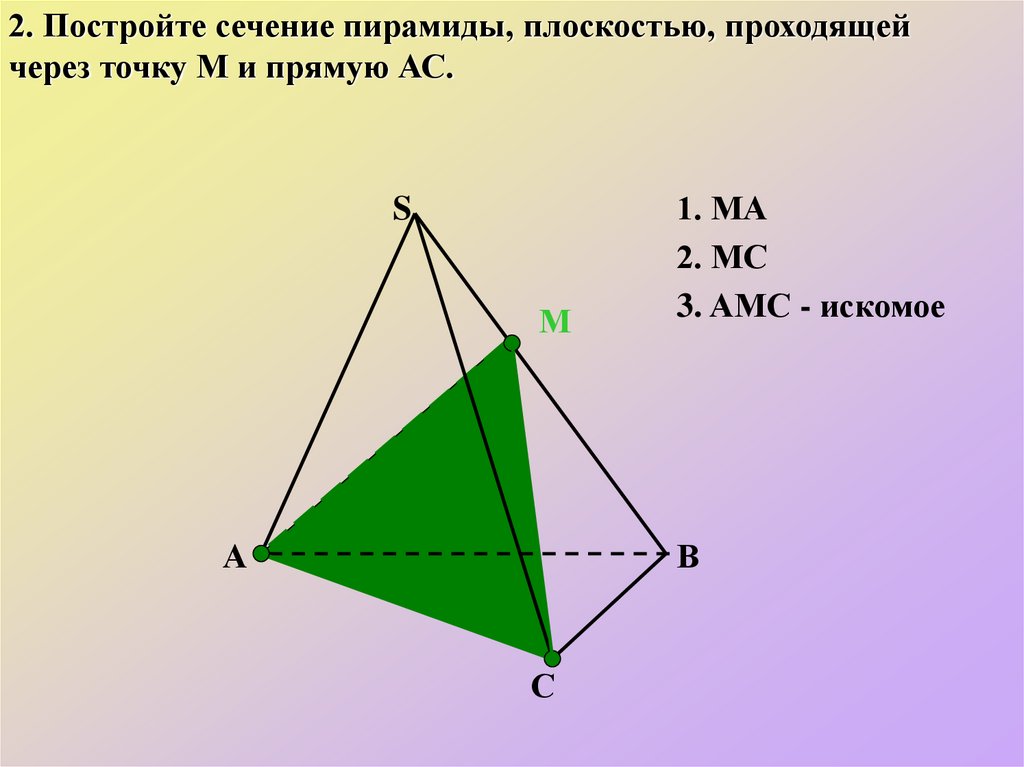
2. Постройте сечение пирамиды, плоскостью, проходящей
через точку М и прямую АС.
S
М
А
1. МА
2. МС
3. АМС - искомое
В
С

49.

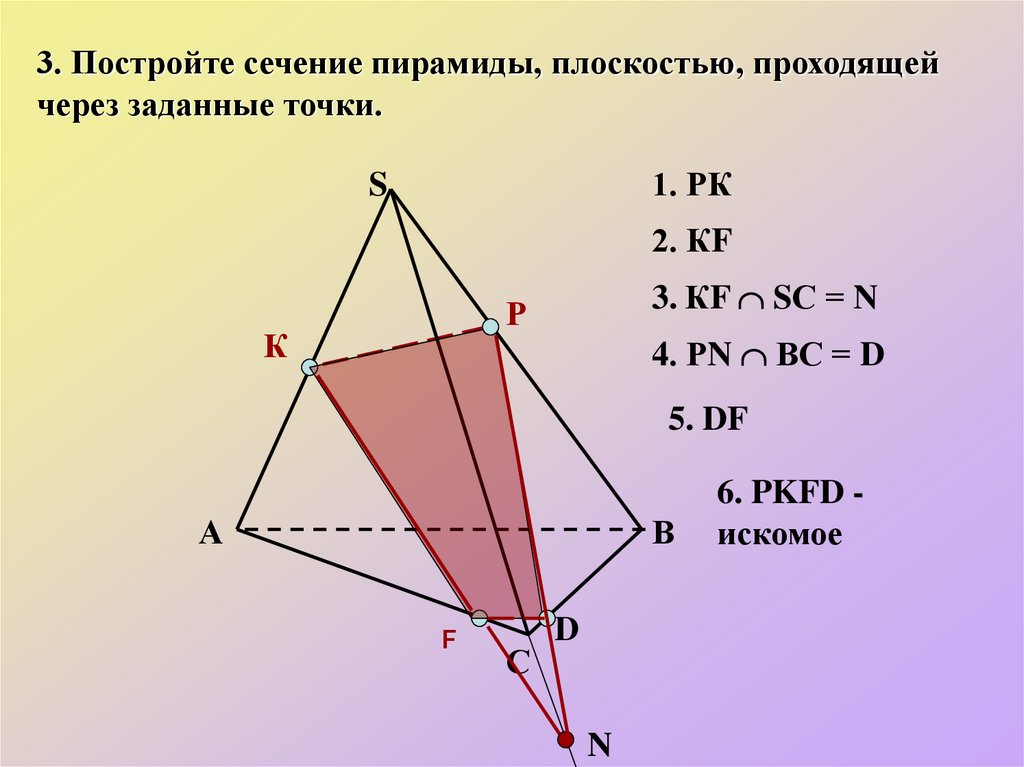
3. Постройте сечение пирамиды, плоскостью, проходящей
через заданные точки.
1. РК
S
2. КF
3. КF SС = N
Р
К
4. РN ВС = D
5. DF
А
В
F
С
D
N
6. PKFD искомое

50.

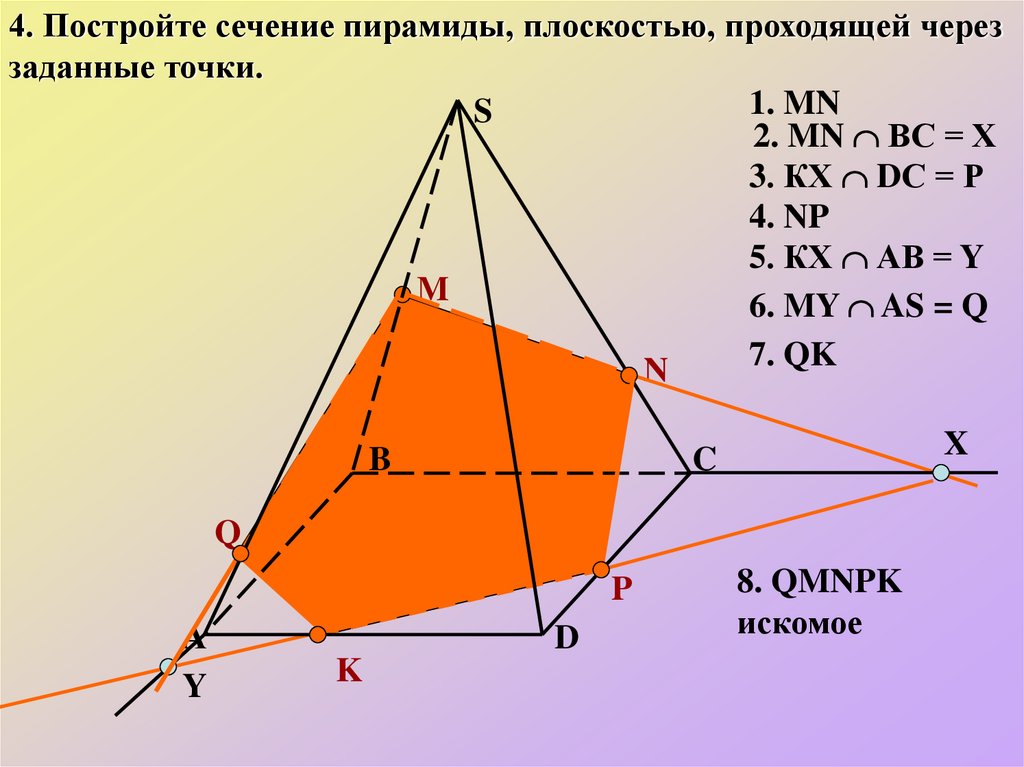
4. Постройте сечение пирамиды, плоскостью, проходящей через
заданные точки.
1. MN
S
2. MN ВС = Х
3. КХ DС = Р
4. NP
5. КХ АВ = Y
M
6. MY AS = Q
7. QK
N
B
X
C
Q
P
А
Y
D
K
8. QMNPK
искомое

51.

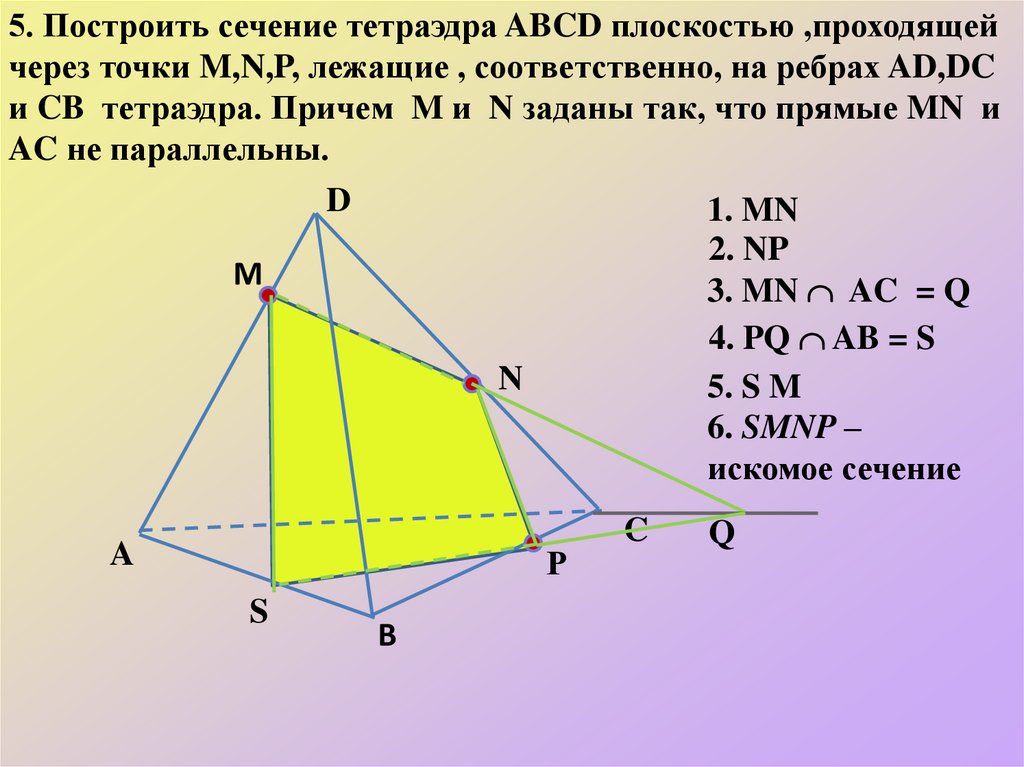
5. Построить сечение тетраэдра ABCD плоскостью ,проходящей
через точки M,N,P, лежащие , соответственно, на ребрах AD,DC
и CB тетраэдра. Причем M и N заданы так, что прямые MN и
AC не параллельны.
D
1. MN
2. NP
3. MN AC = Q
4. PQ AB = S
5. S M
6. SMNP –
искомое сечение
М
N
A
Р
S
В
C
Q

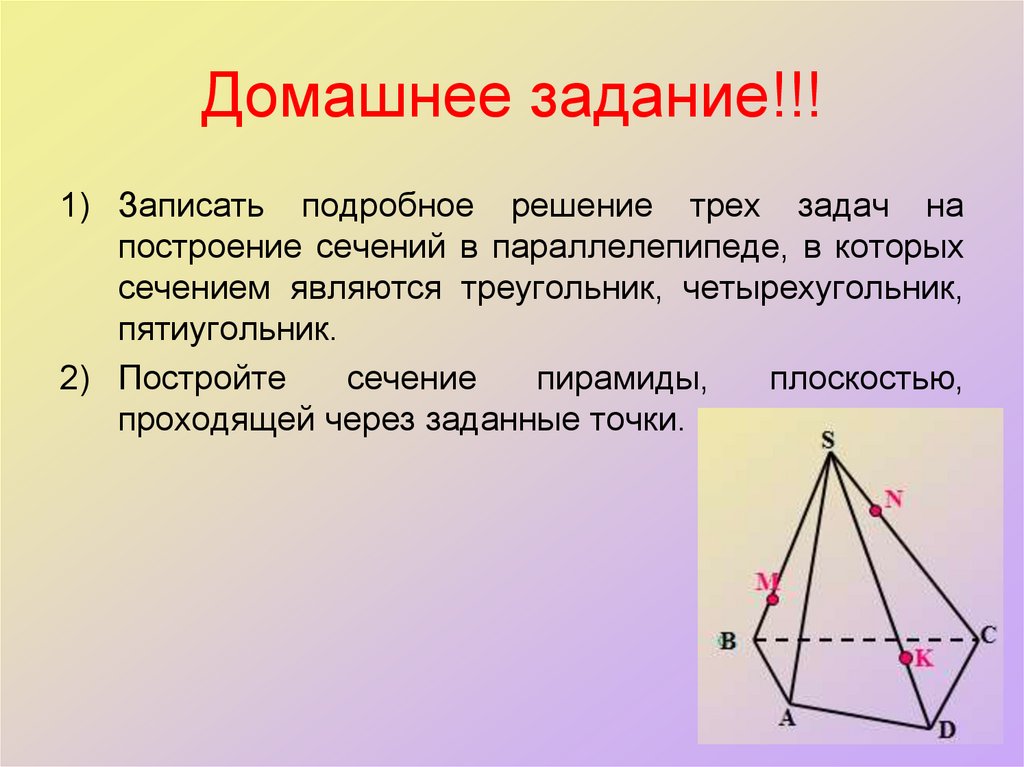
52. Домашнее задание!!!

1) Записать подробное решение трех задач на
построение сечений в параллелепипеде, в которых
сечением являются треугольник, четырехугольник,
пятиугольник.
2) Постройте
сечение
пирамиды,
плоскостью,
проходящей через заданные точки.