Построение сечений многогранников

1. Презентация выполнена учителем математики МОУ лицея № 28 имени Н.А.Рябова г.Тамбова Беляевой О.П.

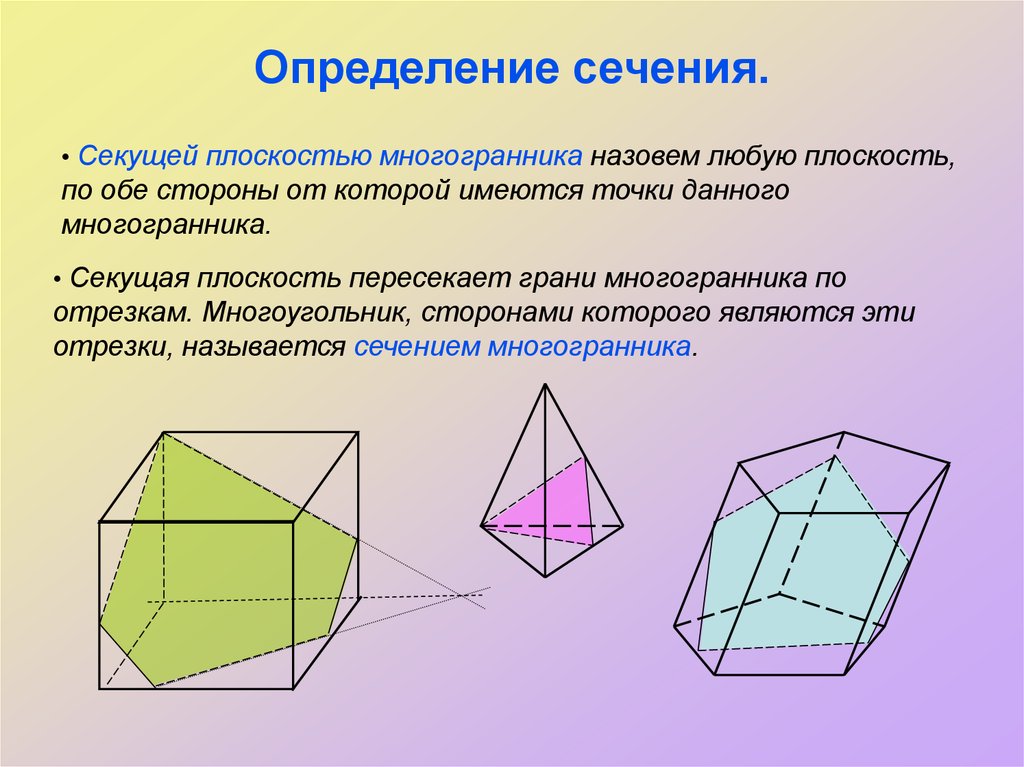
2. Определение сечения.

• Секущей плоскостью многогранника назовем любую плоскость,
по обе стороны от которой имеются точки данного
многогранника.
• Секущая плоскость пересекает грани многогранника по
отрезкам. Многоугольник, сторонами которого являются эти
отрезки, называется сечением многогранника.

3.

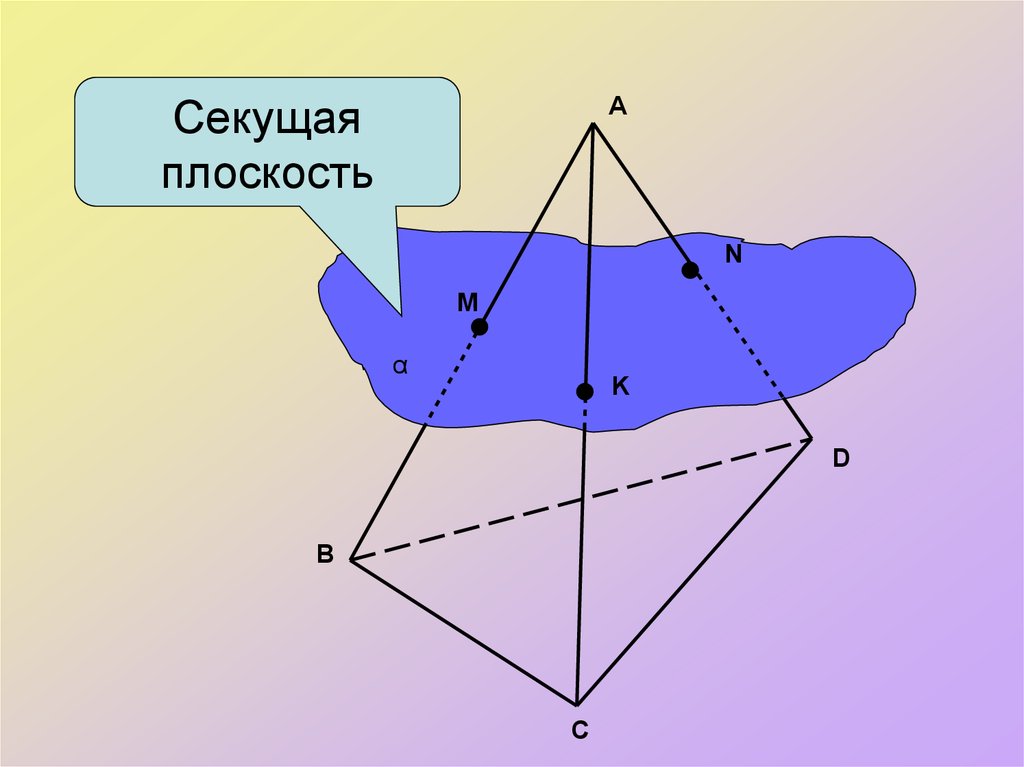
А
Секущая
плоскость
N
M
α
K
D
В
С

4.

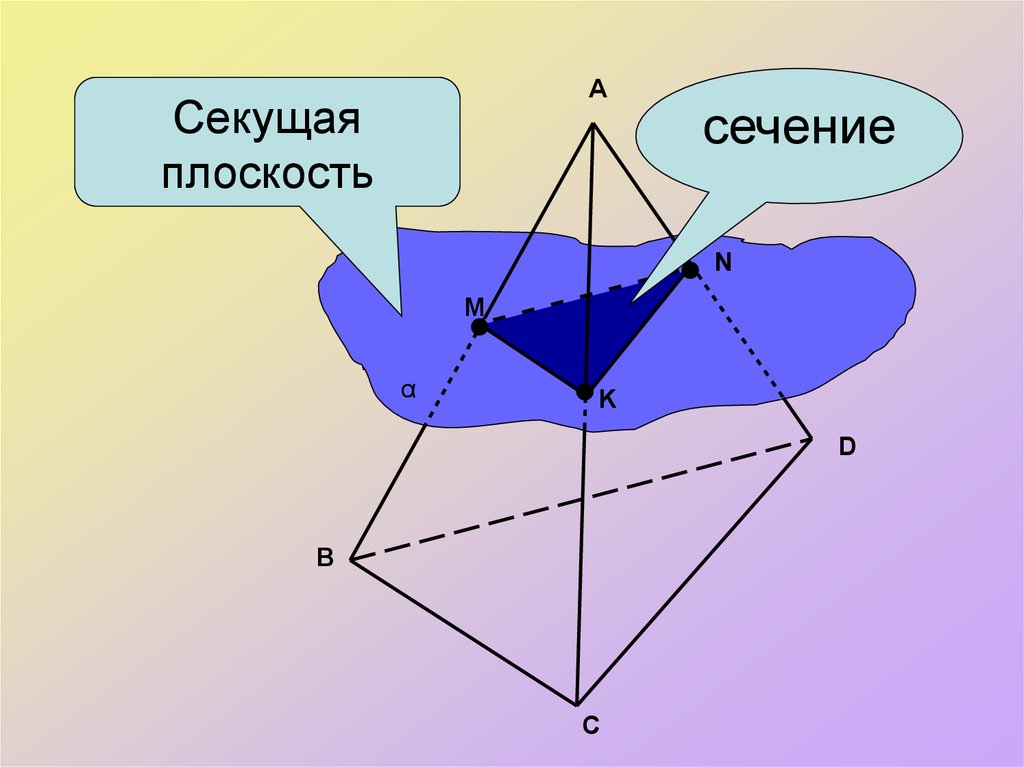
A
Секущая
плоскость
сечение
N
M
α
K
D
B
C

5. На каких рисунках сечение построено не верно?

D
D
D
M
M
А
А
C
M
А
C
B
B
P
P
Q
А
B
D
D
N
C
S
M
B
N
C
Q
А
M
B
C

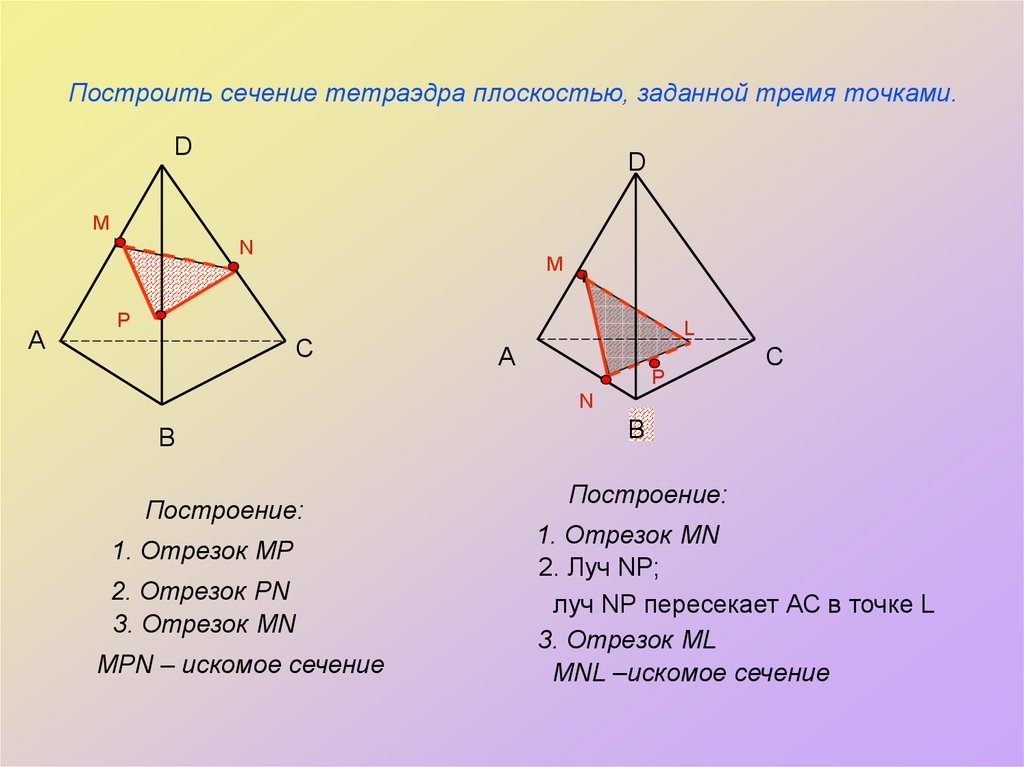
6. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
D
M
N
А
M
P
С
L
А
P
С
N
В
Построение:
1. Отрезок MP
2. Отрезок PN
3. Отрезок MN
MPN – искомое сечение
В
Построение:
1. Отрезок MN
2. Луч NP;
луч NP пересекает АС в точке L
3. Отрезок ML
MNL –искомое сечение

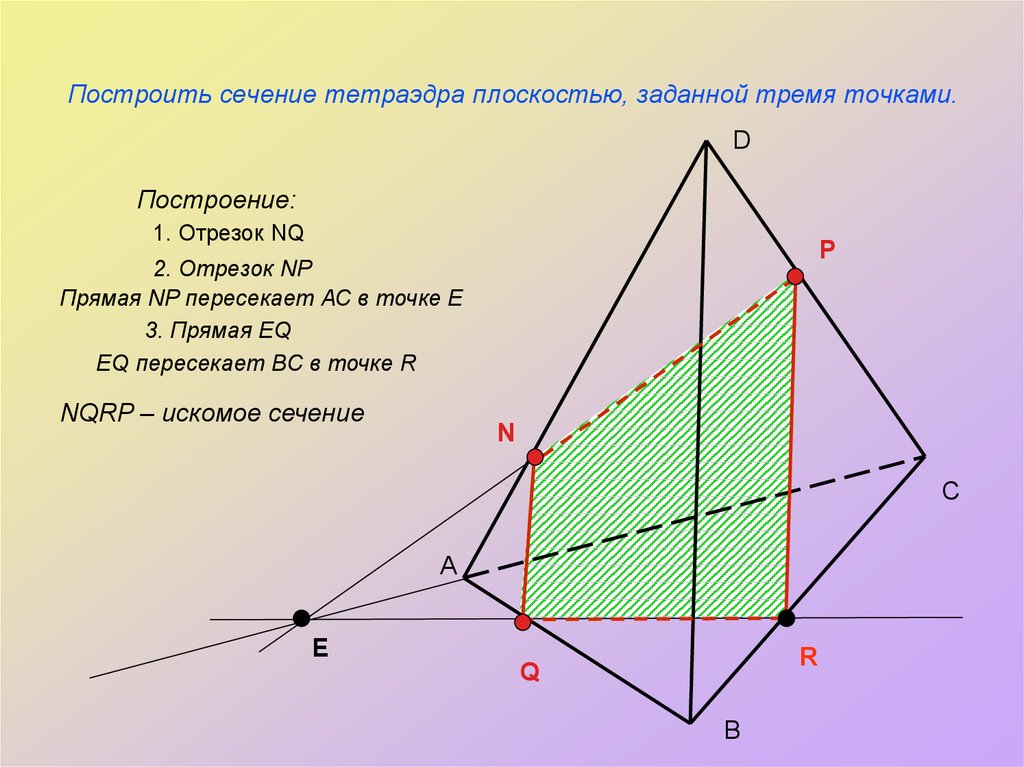
7. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
Построение:
1. Отрезок NQ
P
2. Отрезок NP
Прямая NP пересекает АС в точке Е
3. Прямая EQ
EQ пересекает BC в точке R
NQRP – искомое сечение
N
С
А
E
R
Q
В

8. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
Построение:
1. MN; отрезок МК
2. MN пересекает АВ в точке Х
3. ХР; отрезок SL
MKLS – искомое сечение
M
N
А
S
K
C
P
L
B
X

9.

Аксиоматический метод
Метод следов
Суть метода заключается в построении
вспомогательной прямой, являющейся изображением
линии пересечения секущей плоскости с плоскостью
какой-либо грани фигуры . Удобнее всего строить
изображение линии пересечения секущей плоскости с
плоскостью нижнего основания. Эту линию называют
следом секущей плоскости. Используя след, легко
построить изображения точек секущей плоскости,
находящихся на боковых ребрах или гранях фигуры .

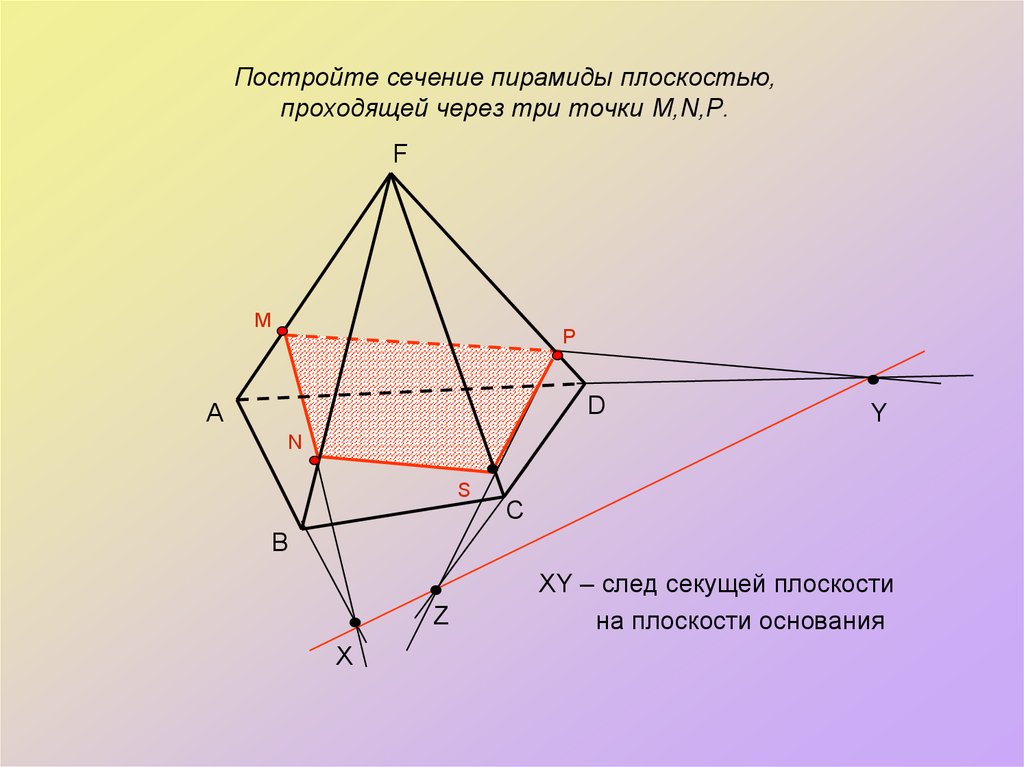
10. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
M
P
D
А
Y
N
S
C
B
Z
X
XY – след секущей плоскости
на плоскости основания

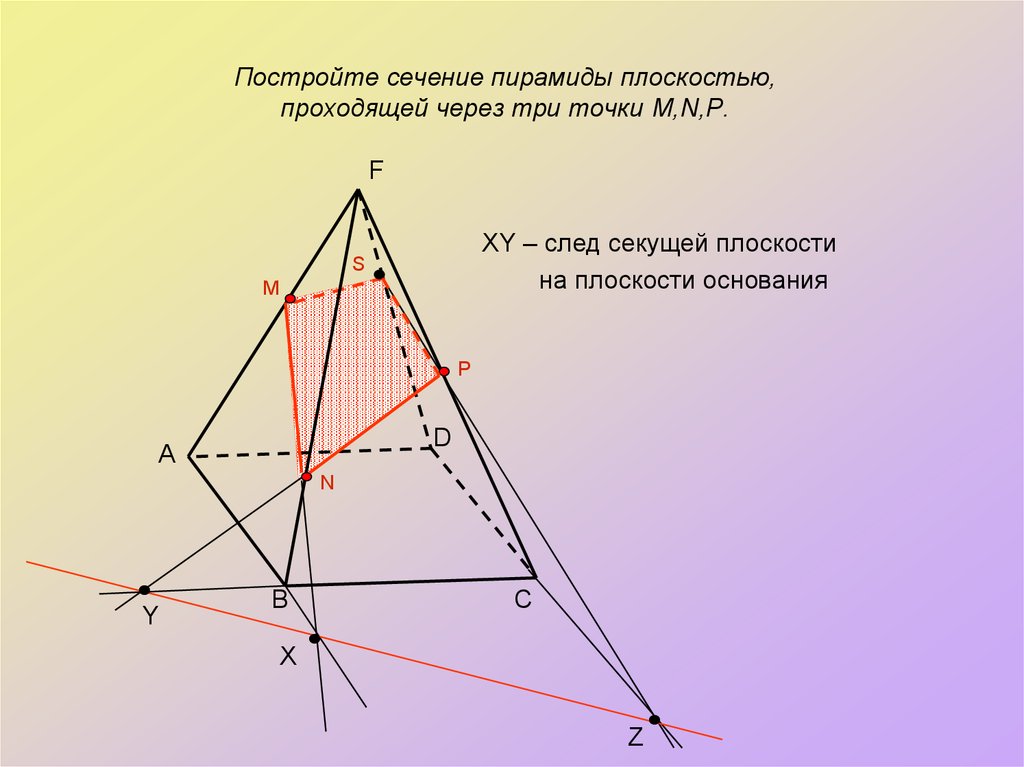
11. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
XY – след секущей плоскости
на плоскости основания
S
M
P
D
А
N
Y
B
C
X
Z

12.

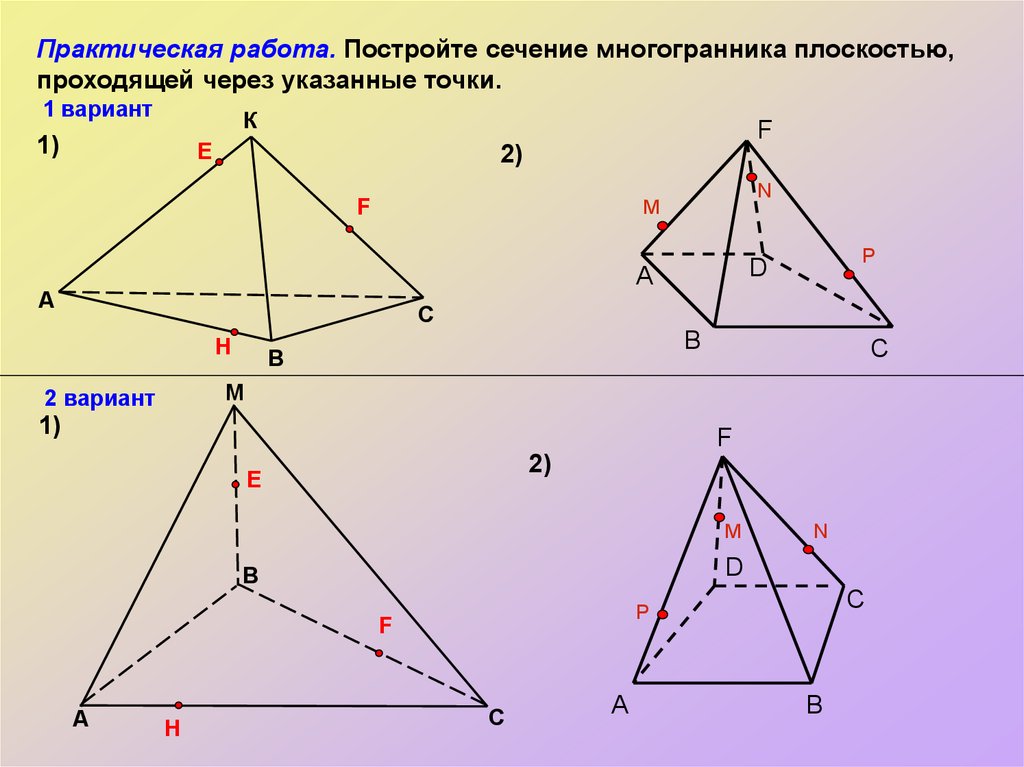
Практическая работа. Постройте сечение многогранника плоскостью,
проходящей через указанные точки.
1 вариант
К
1)
F
E
2)
F
N
M
А
A
P
D
С
H
B
В
C
M
2 вариант
1)
F
2)
E
M
D
В
H
C
P
F
A
N
С
А
B

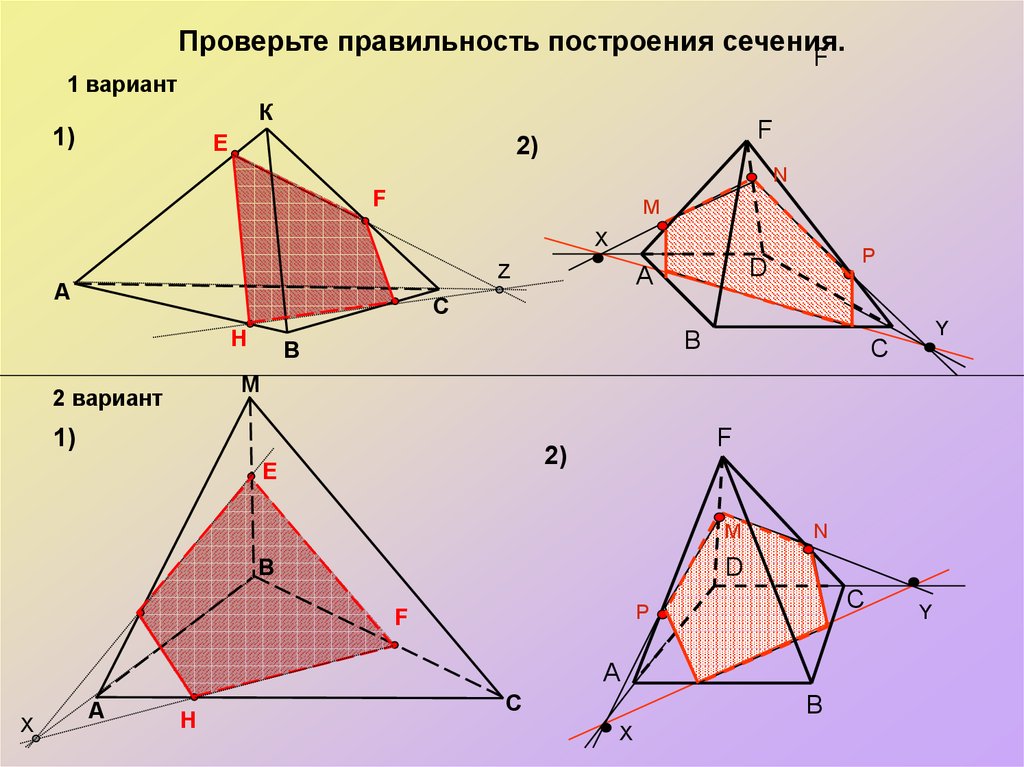
13.

Проверьте правильность построения сечения.
F
1 вариант
К
1)
E
F
2)
N
F
M
X
A
P
D
А
Z
С
H
B
В
M
2 вариант
1)
F
2)
E
M
В
N
D
C
P
F
А
X
A
Y
C
H
С
B
X
Y

14.

Домашнее задание:
1. § 4. п.14. учебника
2. № 72, №73, № 74, №75.