Сечения призмы и пирамиды

1.

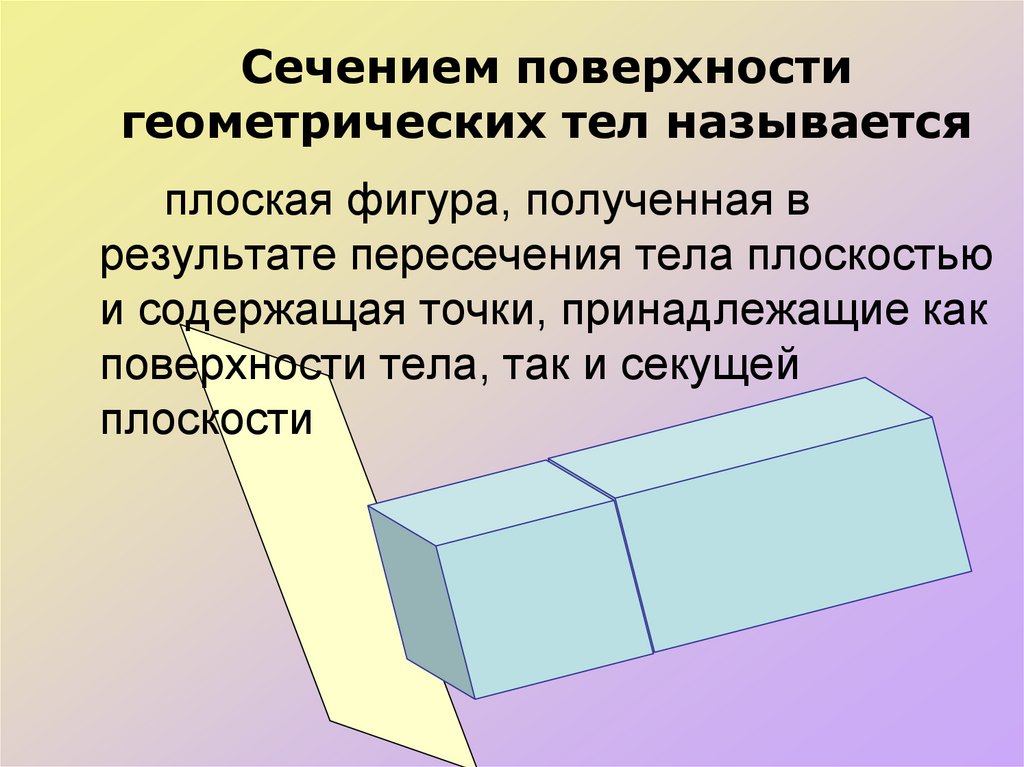
2. Сечением поверхности геометрических тел называется

плоская фигура, полученная в
результате пересечения тела плоскостью
и содержащая точки, принадлежащие как
поверхности тела, так и секущей
плоскости

3.

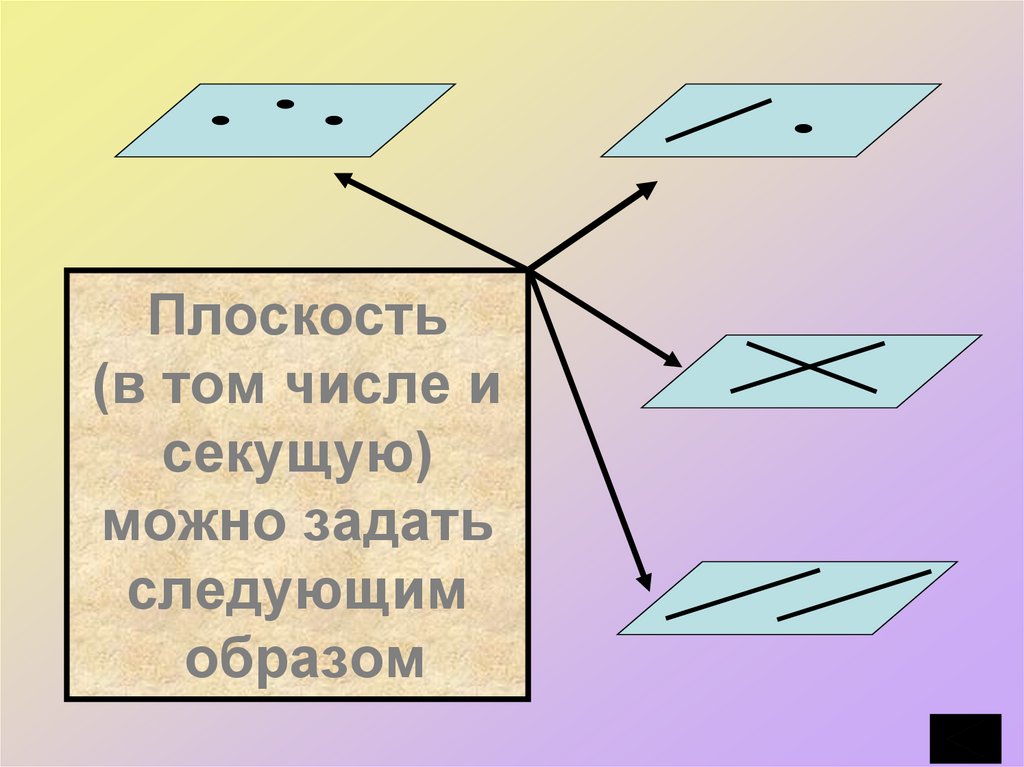
4. Плоскость (в том числе и секущую) можно задать следующим образом

5.

А
Секущая
плоскость
N
M
α
K
D
В
С

6.

A
Секущая
плоскость
сечение
N
M
α
K
D
B
C

7.

Секущая плоскость пересекает грани
многогранника по прямым, а точнее
по отрезкам - разрезам.
Так как секущая плоскость идет
непрерывно, то разрезы образуют
замкнутую фигуру-многоугольник.
Полученный таким образом
многоугольник и будет сечением
тела.

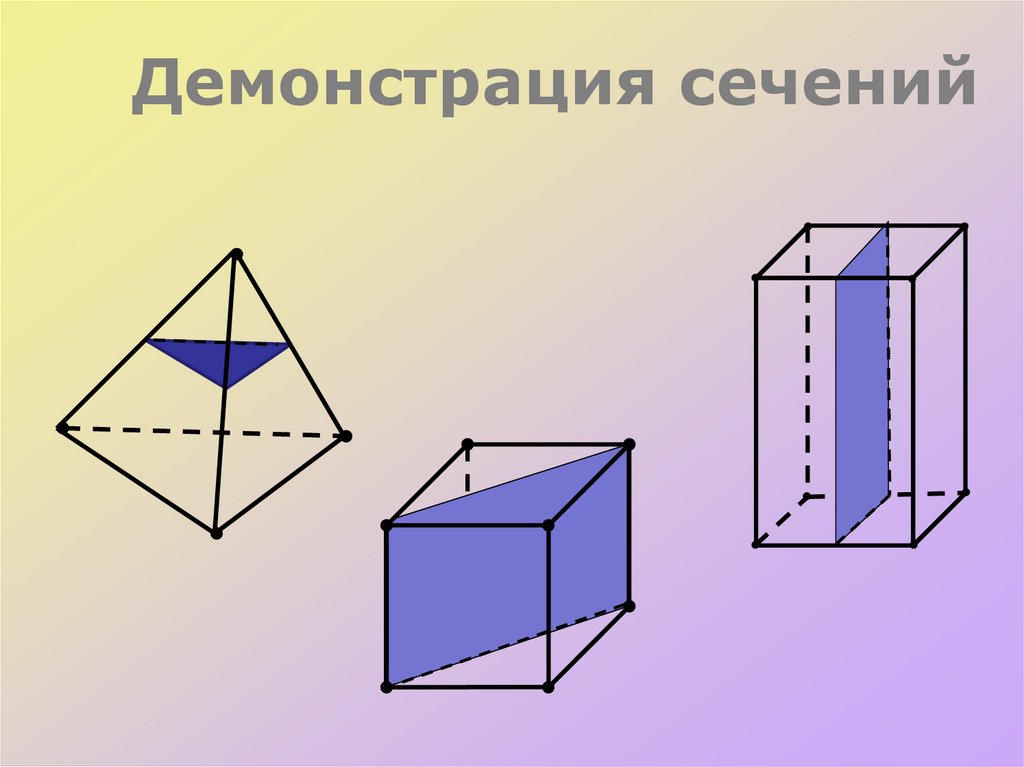
8. Демонстрация сечений

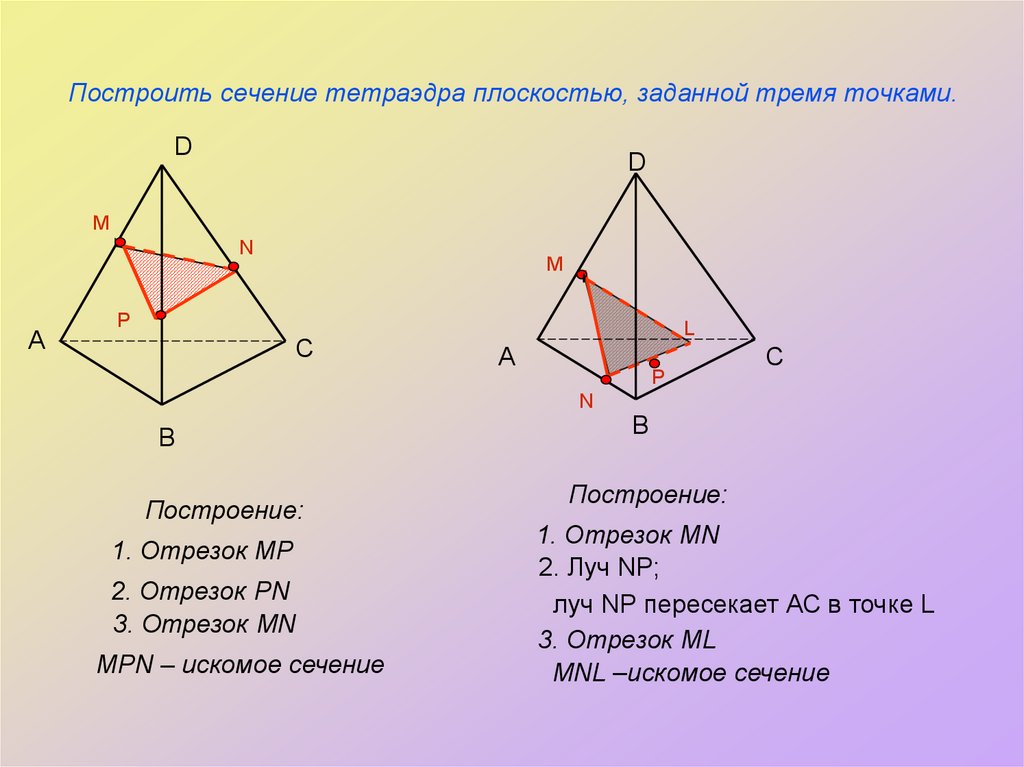
9. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
D
M
N
А
M
P
С
L
А
P
N
В
Построение:
1. Отрезок MP
2. Отрезок PN
3. Отрезок MN
MPN – искомое сечение
С
В
Построение:
1. Отрезок MN
2. Луч NP;
луч NP пересекает АС в точке L
3. Отрезок ML
MNL –искомое сечение

10. Метод следов Следом называется прямая пересечения плоскости сечения и плоскости какой-либо грани. Чтобы построить след, нужно

знать две
его точки, лежащие одновременно в
секущей плоскости и плоскости
рассматриваемой грани.
Если след построен, то отрезок, по
которому он пересекается с плоскостью,
дает сторону сечения, лежащую в этой
плоскости.

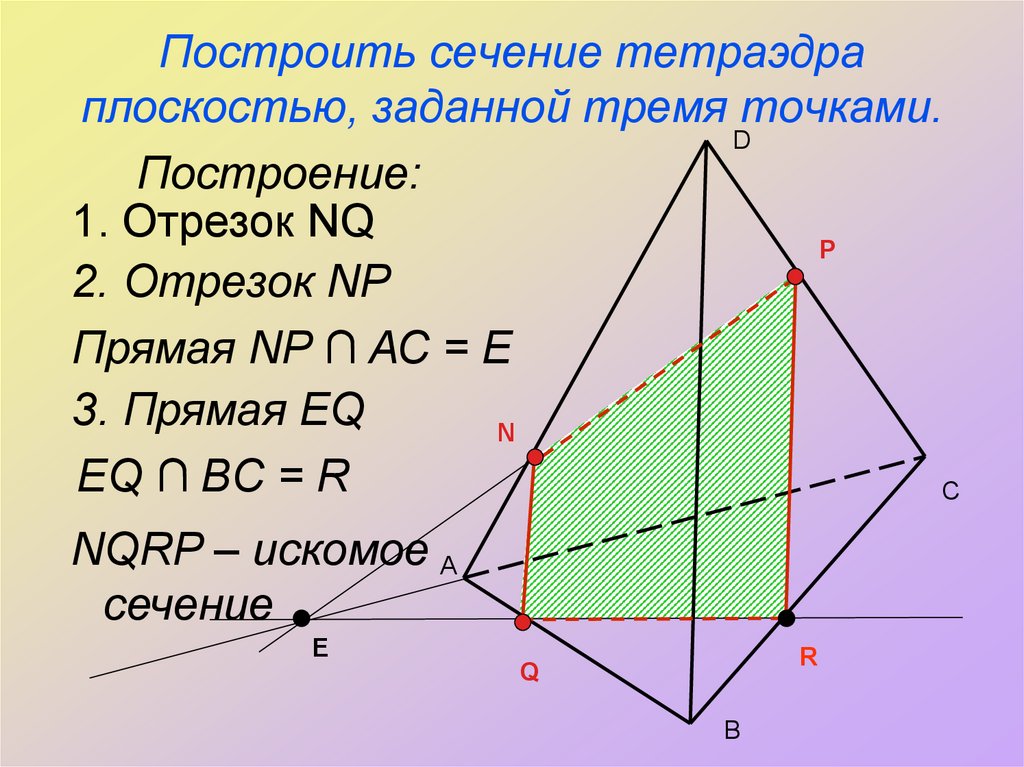
11. Построить сечение тетраэдра плоскостью, заданной тремя точками.

D
Построение:
1. Отрезок NQ
P
2. Отрезок NP
Прямая NP ∩ АС = Е
3. Прямая EQ
N
EQ ∩ BC = R
С
NQRP – искомое А
сечение
E
R
Q
В

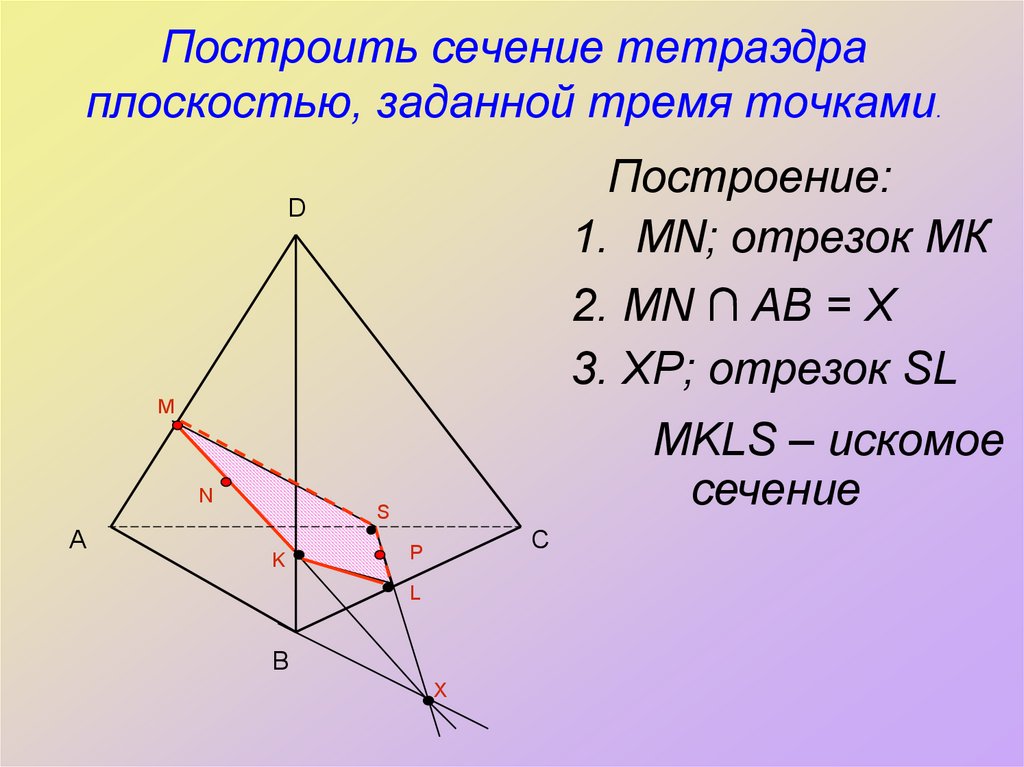
12. Построить сечение тетраэдра плоскостью, заданной тремя точками.

Построение:
1. MN; отрезок МК
2. MN ∩ АВ = Х
3. ХР; отрезок SL
D
M
N
А
MKLS – искомое
сечение
S
K
C
P
L
B
X

13. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.

F
XY – след секущей
плоскости
на плоскости
основания
S
M
P
D
А
N
Y
B
C
X
Z

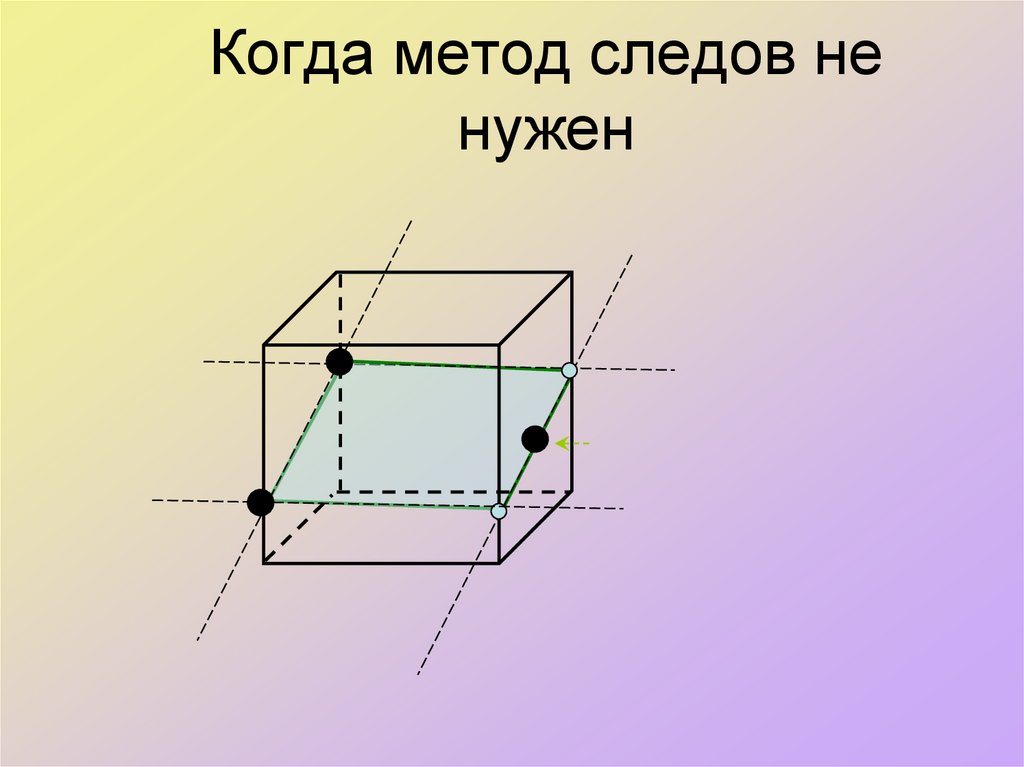
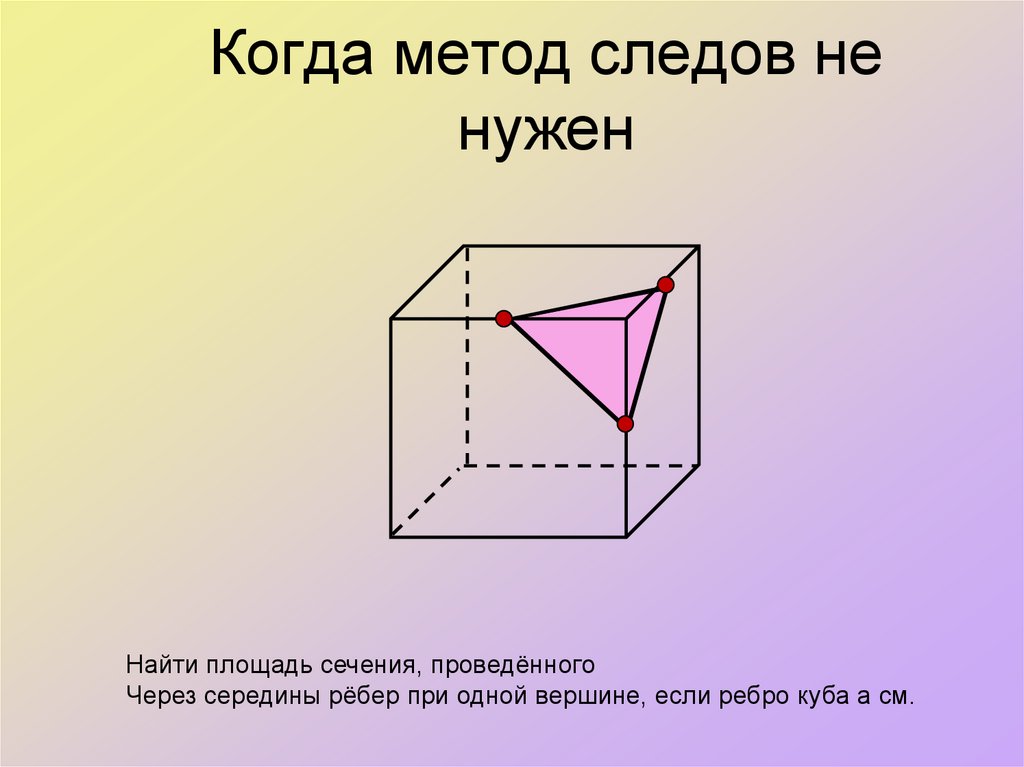
14. Когда метод следов не нужен

15. Когда метод следов не нужен

Найти площадь сечения, проведённого
Через середины рёбер при одной вершине, если ребро куба а см.

16.

Задача 3. Построить сечение плоскостью,
проходящей через точки К, L, М.
Построение:
1. ML 2. ML ∩ D1А1 = E
3. EK 4. EK ∩ А1B1 = F
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
М
D
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое
сечение

17.

Задача 2. Построить сечение плоскостью,
проходящей через данные точки Е, F, K.
Построение:
К
1. KF
В1
C1
2. FE
F
3. FE ∩ АB = L
А1
D1
4. LN ║ FK
5. LN ∩ AD = M
E
6. EM
N
В
7. KN
С
EFKNM – искомое
А
сечение
М
D
L
Пояснения
Пояснения
кк построению:
кк построению:
Пояснения
построению:
Пояснения
построению:
3.
Прямые
1.
FEпрямую
и АВ,точки
лежащие
K
и E,
F,
в принадлежащие
одной
плоскости
5.
Прямая
LN
пересекает
AD в точке
M.
2. Соединяем
Соединяем
точки
Fребро
и
принадлежащие
4.
Проводим
LN параллельно
FK (если
Пояснения
к
построению:
Пояснения
к
построению:
АА1В1одной
В, пересекаются
плоскости
вА
В1ВСВ.
DL .
1точке
одной
плоскости
АА
секущая
плоскость
пересекает
1 11 1
6.
Соединяем
точки
Е
и
М,
принадлежащие
7. Соединяем точки К и N, принадлежащие
противоположные
грани,
то она пересекает их
однойплоскости
плоскости ВСС
АА
D.
1D
1
одной
В
.
1 1
по параллельным отрезкам).

18.

Практическая работа. Постройте сечение многогранника плоскостью,
проходящей через указанные точки.
1 вариант
К
1)
F
E
2)
F
N
M
А
A
P
D
С
H
B
В
C
M
2 вариант
1)
F
2)
E
M
D
В
H
C
P
F
A
N
С
А
B