Similar presentations:
Динамика. Нүкте динамикасы. Механикалық система динамикасы
1.
ДинамикаДинамика – денеге түсірілген күштер мен олардың әсерінен болатын
қозғалыстарды зерттейтін теориялық механика бөлімі.
Динамика
Нүкте динамикасы
Механикалық система
динамикасы
Нүкте динамикасы – материялық нүктені оған әсер ететін күштерін ескеріп
зерттейді.
Негізгі объект – материялық нүкте – мөлшерін елемеуге болатын массасы
бар ұсақ бөлшектер.
Механикалық система динамикасы – әрбір нүктенің орны мен
қозғалысы басқа нүктелердің орны мен қозғалысына тәуелді болып келетін
бір-бірімен байланысты материялық нүктелер жиынтығы.
2.
Динамиканың заңдары – динамиканың негізіне Галилей мен Ньютонашқан заңдар жатады.
■
Инерция заңы (Галилея-Ньютона заңы) – тыныштық күйде немесе
бірқалыпты түзу сызықты қозғалыста болатын материялық нүкте
ешқандай себепсіз өзіндік күйін өзгерте алмайды. Материялық денелердің
күш әсерінен өзіндік жылдамдығын шапшаңырақ немесе баяуырақ өзгертетін
қасиетін Галилей инерттілік деп атады. Инерция заңы орындалатын координат
системасын инерция санақ системасы дейміз.
■
■ Күш пен үдеудің пропорциональдық заңы (Динамиканың негізгі
теңдеуі – Ньютонның II заңы) – Материялық нүкте үдеуі әсер етуші күшке
пропорционал және күш бағытымен бағыттас:
немесе
1
ma F .
a
m
G
m .
g
Мұндағы m – нүкте массасы (инерттілік шамасы), кг өлшенеді және
Салмақты еркін түсу үдеуіне бөлгенге тең.
F – берілген күш, өлшем Н (1 Н күш массасы 1 кг нүктеге 1 м/c2 үдеу
береді, яғни 1 Н = 1/9.81 кг-с).
F
3.
Әсер және кері әсер заңы (Ньютонның III заңы) – Екіматериялық нүктенің өзара әсерлесу күштерінің шамалары
бір-бірне тең бір түзудің бойымен қарама-қарсы
бағытталған:
■
F1,2
F1, 2 F2,1
F2,1
m1
m2
Күш әсерінің тәуелсіздігі туралы заң – Егер материялық
нүктеге бір мезгілде бірнеше күш әсер етсе, онда нүкте үдеуі
әсер ететін күштердің әрқайсысының нүктеге беретін
үдеулерінің геометриялық қосындысына тең:
■
a ( F1 , F2 ,...) a1 ( F1 ) a2 ( F2 ) ....
немесе
a ( R ) a1 ( F1 ) a2 ( F2 ) ....
4.
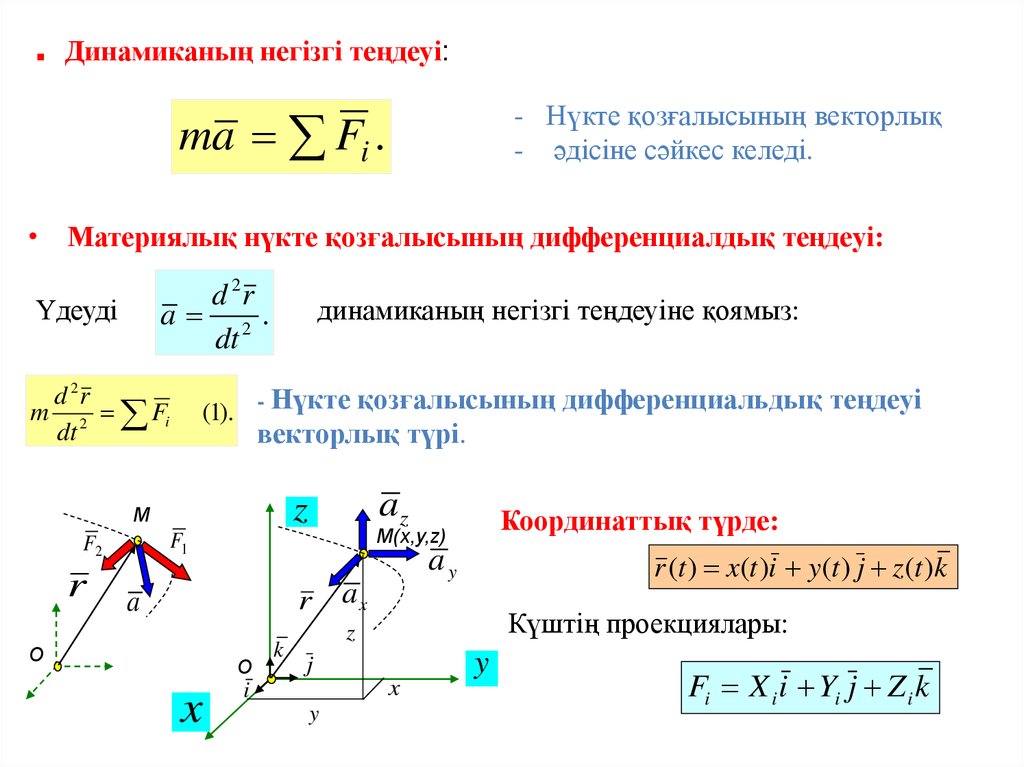
■Динамиканың негізгі теңдеуі:
- Нүкте қозғалысының векторлық
- әдісіне сәйкес келеді.
ma Fi .
• Материялық нүкте қозғалысының дифференциалдық теңдеуі:
d 2r
a 2.
dt
Үдеуді
d 2r
m 2 Fi
dt
динамиканың негізгі теңдеуіне қоямыз:
(1). - Нүкте қозғалысының дифференциальдық теңдеуі
векторлық түрі.
ay
r
a
O
O
x
Координаттық түрде:
M(x,y,z)
F1
F2
r
az
z
M
k
r (t ) x(t )i y(t ) j z (t )k
ax
Күштің проекциялары:
z
y
j
x
i
y
Fi X i i Yi j Z i k
5.
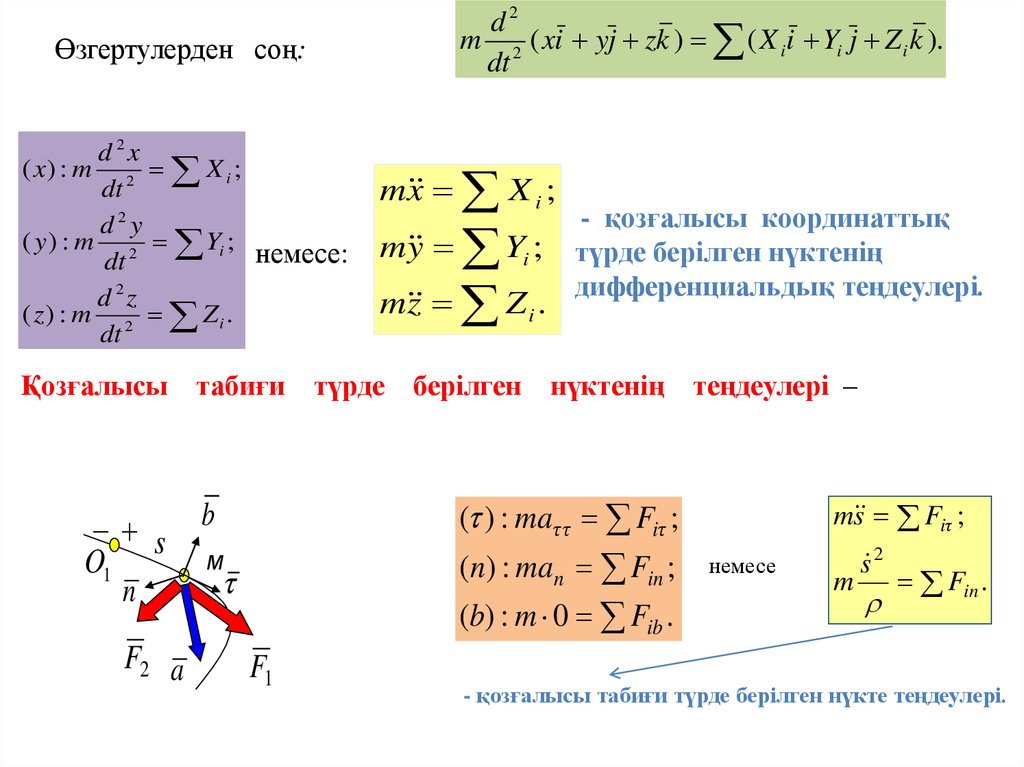
d2m 2 ( xi yj zk ) ( X i i Yi j Z i k ).
dt
Өзгертулерден соң:
d 2x
( x) : m 2 X i ;
dt
d2y
( y ) : m 2 Yi ;
немесе:
dt
d 2z
( z) : m 2 Zi .
dt
Қозғалысы табиғи
s
O1
n
F2 a
m x X i ;
m y Yi ;
m z Z i .
түрде
- қозғалысы координаттық
түрде берілген нүктенің
дифференциальдық теңдеулері.
берілген нүктенің теңдеулері –
( ) : maτ τ Fiτ ;
(n) : man Fin ;
b
M
(b) : m 0 Fib .
F1
m s Fiτ ;
немесе
m
s 2
Fin .
- қозғалысы табиғи түрде берілген нүкте теңдеулері.
6.
Нүкте динамикасының екі негізгі есебі:Бірінші есеп (тура есеп): Нүктенің берілген қозғалысы(
қозғалыс теңдеуі, траектория) арқылы әсер ететін күштерді
анықтау.
Екінші есеп( кері есеп): Нүктеге әсер ететін күштер арқылы
нүкте қозғалысын анықтау. Қозғалыстың параметрлерін табу
( қозғалыс теңдеуі, қозғалыс траекториясы).
7.
Динамиканың тура есебін шешу – бірнеше мысалдар келтірейік:1 мысал. Салмағы G тең лифтің кабинасы тростың бойымен a үдеумен жоғары көтеріледі.
Тростың тартылу күшін табу:
1. Объекті таңдаймыз (лифтің кабинасы ілгерлемелі қозғалады, оны
материялық нүкте деп қарастырамыз).
2. Байланысты алып тастаймыз(трос) да оны R реакциясымен алмастырамыз.
y
R
3. Динамиканың негізгі заңының теңдеулерін құрастырамыз:
4. у өсіне проекциялаймыз:
( y ) : ma y R G. ma Fi G R .
a
G
Тростың реакциясын анықтаймыз:
Тростың тартылу күшін табамыз:
T R ; T R G(1
ay
g
).
ay
G
R G ma y G a y G(1 ).
g
g
Бір қалыпты қозғалыста кабинаның ay = 0 ,онда тростың
тартылуы салмаққа тең: T = G.
Трос үзілгенде T = 0, онда кабинаның үдеуі еркін түсу
үдеуіне тең: ay = -g.
8.
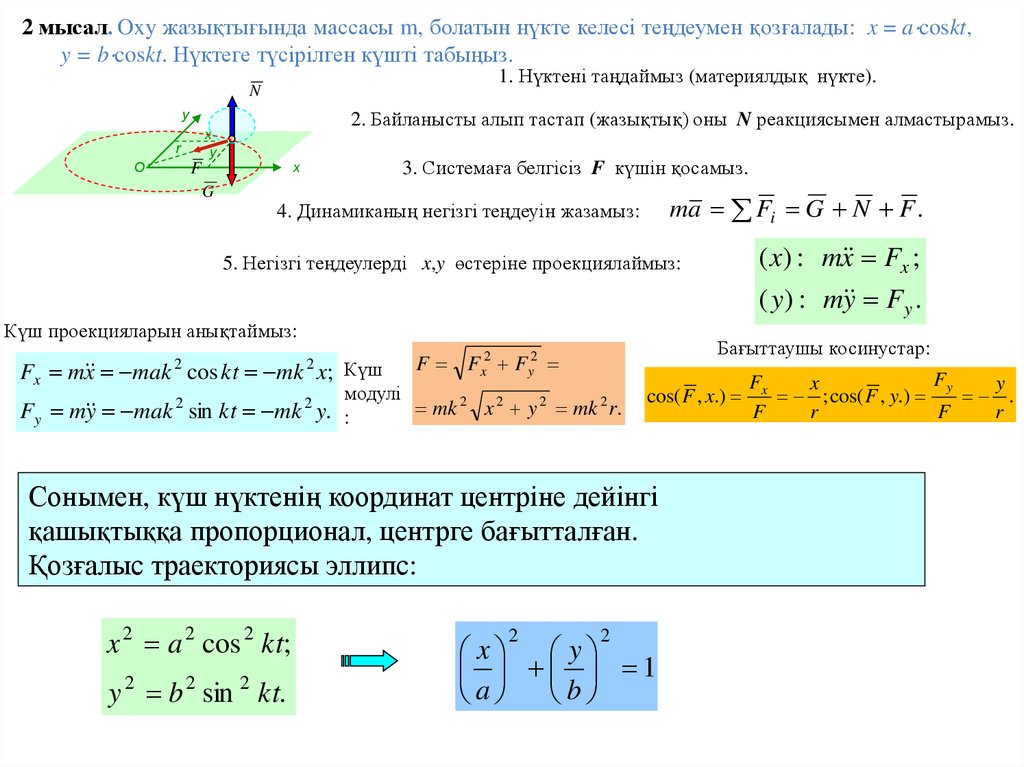
2 мысал. Oxy жазықтығында массасы m, болатын нүкте келесі теңдеумен қозғалады: x = a coskt,y = b coskt. Нүктеге түсірілген күшті табыңыз.
1. Нүктені таңдаймыз (материялдық нүкте).
N
2. Байланысты алып тастап (жазықтық) оны N реакциясымен алмастырамыз.
y
x
y
r
O
3. Системаға белгісіз F күшін қосамыз.
x
F
G
ma Fi G N F .
4. Динамиканың негізгі теңдеуін жазамыз:
( x) : m x Fx ;
( y) : m y Fy .
5. Негізгі теңдеулерді x,y өстеріне проекциялаймыз:
Күш проекцияларын анықтаймыз:
Fx m x mak cos kt mk x; Күш
2
2
Бағыттаушы косинустар:
F Fx2 Fy2
модулі
mk 2 x 2 y 2 mk 2 r.
Fy m y mak 2 sin kt mk 2 y. :
cos( F , x.)
Сонымен, күш нүктенің координат центріне дейінгі
қашықтыққа пропорционал, центрге бағытталған.
Қозғалыс траекториясы эллипс:
x 2 a 2 cos 2 kt;
y 2 b 2 sin 2 kt.
2
2
x y
1
a b
Fy
Fx
x
y
; cos( F , y.)
.
F
r
F
r
9.
3 мысал: Салмағы G –ға тең жүк ұзындығы l ға тең жіпке ілініп, жазықтықта шеңбер жасапқандай да бір жылдамдықпен қозғалады. Жіп вертикаль өстен бұрышына ауытқиды. Жіптің
тартылыс күшін және жүктің жылдамдығын табыңыз.
1. Объектті таңдаймыз (жүк).
l
Rb
n
an
G
2. Байланысты алып (трос) реакция R алмастырамыз.
3. Динамиканың теңдеуі:
ma Fi G R .
( ) : maτ 0;
4. Динамиканың теңдеуін ,n, b өстеріне жіктейміз:
Жіптің тартылыс күшін
анықтаймыз:
G
T R ; T R
.
cos
( n) : man R sin ;
(b) : 0 R cos G.
Жіптің реакциясын екінші теңдеуге
қоямыз, содан жүктің жылдамдығын
табамыз:
G v2
G
sin .
g l sin cos
v
gl sin 2
.
cos
10.
4 мысал: Салмағы G тең автомобиль доңес көпірмен V жылдамдықпен кележатыр (қисықтық радиусы R). Автомобилдің көпірге түсіретін қысымын тап.
N
v
1. Объекті таңдаймыз (автомашинаның
өлшемдерін ескермей, нүкте деп
қарастырамыз).
Fтр
R
G
n
2. Байланысты алып тастаймыз (бұдыр бет)
оны N реакциясымен және үйкеліс күші Fүйк
алмастырамыз.
3. Динамиканың теңдеуі: ma Fi G N Fтр .
4. Динамиканың теңдеуін n өсіне проекциялаймыз: (n) : man G N .
Осыдан нормаль реакцияны табамыз:
v2
v2
N G man G m
G (1
).
R
gR
Автомобилдің көпірге қысымын анықтаймыз:
v2
Q N ; Q G(1
).
gR
Осыдан жылдамдықтың көпірге түсірілген қысымының нөл (Q = 0)
кезіндегі жылдамдығын табамыз:
v gR .
11.
Динамиканың кері есебінің шешуі – жалпы жағдайда нүктетеңдеулері уақытқа, координатқа, жылдамдыққа тәуелді.
Нүкте қозғалысының теңдеулері 2-ші дәрежелі дифференциалдық
теңдеулермен өрнектеледі:
X ;
m y Y ;
m z Z .
m x
i
i
i
12.
Интегралдағаннан кейін әрқайсысындада алты тұрақты шығады C1, C2,…., C6:x f1 (t , C1 , C 2 , C3 );
y f 2 (t , C1 , C 2 , C3 );
z f 3 (t , C1 , C 2 , C3 ).
x f 4 (t , C1 , C 2 ,..., C 6 );
y f 5 (t , C1 , C 2 ,..., C 6 );
z f 6 (t , C1 , C 2 ,..., C 6 ).
Тұрақтыла C1, C2,…., C6
t = 0 болғандағы алты шарттың көмегімен анықталады:
x x0 ;
x x 0 ;
y y0 ;
y y 0 ;
z z0 ;
z z 0 .
x f1 (t , x 0 , y 0 , z 0 );
y f 2 (t , x 0 , y 0 , z 0 );
z f 3 (t , x 0 , y 0 , z 0 ).
Табылған мәндерді орнына қойғаннан кейін:
x f 4 (t , x 0 , y 0 , z 0 , x0 , y 0 , z 0 );
y f 5 (t , x 0 , y 0 , z 0 , x0 , y 0 , z 0 );
z f 6 (t , x 0 , y 0 , z 0 , x0 , y 0 , z 0 ).
Сонымен, материялық нүкте әсер еткен
күштер системасының нәтижесінде
бастапқы шарттарға байланысты күрделі
қозғалыста болады.
13.
Механикалық системаның динамикасы.Механикалық система немесе материялық нүктелер системасы – деп кез
келген нүктенің(дененің) орны мен қозғалысы басқа нүктелер(денелер) орны
мен қозғалыстарына тәуелді болып келетін нүктелер(денелер) жиынтығын
атайды.
Еркін нүктелер системасы – қозғалысы әсер ететін күштермен ғана
анықталатын, кеңістікте кез келген бағыттағы қозғалысы ешқандай
байланыстармен шектелмейтін материялық нүктелер системасы(күн
системасының барлық денелері бір-бірімен тартылыс күшетрі арқылы
байланысқан. Планеталар осы күштердің әсерінен өз орбиталарының бойымен
еркін қозғалады).
Еркін емес(еріксіз) материялық система– материялық нүктелердің
қозғалысы немесе денелерді шектейтін байланыстар (мысалы, механизм,
машина және т.б.).
14.
Системағаәсер етуші күштер. Алдында келтірген(активті және реактивті)
күштерден басқа қосымша күштердің түрлеріне тоқталайық:
1. Сыртқы күштер(e) – системаның нүктелеріне не денелеріне системаға
жатпайтын нүктелер мен денелердің әсері.
2. Ішкі күштер (i) – системадағы нүктелер мен денелердің өзара әсерлесуі.
Мұнда бір күш сыртқы да ішкі де күш болуы мүмкін, ол механикалық
системаны қарастыруымызға байланысты.
Мысалы: Күн системасында, Жер мен Ай және олардың арасындағы
тартылыс күші ішкі күш болады. Ал Жер мен Айға келсек, күннің тартылыс
күші – сыртқы күш деп есептелінеді:
Осыдан ішкі күштердің екі қасиетін алуға
болады:
R i Fki 0.
1. Ішкі күштердің басты векторы нолге тең:
Күн
Л
Ай
Жер
2. Ішкі күштердің кез келген нүктеге қатысты
басты моменті нолге тең:
i
M Oi M kO
0.
Координат осьтеріне проекциялары:
X ki 0; Yki 0; Z ki 0.
M kxi 0; M kyi 0; M kzi 0.
15.
Күштің импульсі – күштің, осы күштің әсер етуінің элементаруақытына көбейтіндісін көрсететін, күш әсерінің векторлық
шамасы:
t2
S F dt
t1
t2
Координат остеріне проекциялары: ( x) : S x Xdt;
( y ) : S y Ydt ;
t1
Күш тұрақты болса:
t2
( z ) : S z Zdt.
t1
S F (t 2 t1 ).
Координат остеріне проекциялары:
S x X (t 2 t1 );
S y Y (t 2 t1 );
t2
S z Z (t 2 t1 );
t1
16.
Күштің қозғалыс мөлшері – материялық нүктенің массасы менжылдамдығының көбейтіндісіне тең векторлық шама:
Q mv .
Материялық нүкте системасының қозғалыс мөлшері – материялық
нүктелердің қозғалыс мөлшерлерінің геометриялық қосындысы:
Q Q1 Q2 ... Qn Qk .
Q Qk mk vk mk
drk
d
( mk rk ).
dt
dt
Массалар центрінің анықтамасы бойынша:
m
MrC mk rk .
Q
v
Онда: Q d ( Mrc ) M drC MvC .
dt
dt
Қозғалыс мөлшерінің векторы системаның массасы мен
Q MvC . массалар центрінің жылдамдығының көбейтіндісіне тең.
17.
Қозғалыс мөлшерінің өзгеруі туралы теорема –dQ
e
R .
dt
Қозғалыс мөлшері векторынан уақыт бойынша алынған
туынды системаның сыртқы күштерінің басты
векторына тең.
Нүктенің қозғалыс мөлшері моменті немесе кез келген нүктеге
қатысты қозғалыстың кинетикалық моменті – материялық нүктенің
радиус векторы мен қозғалыс мөлшерінің векторының векторлық
көбейтіндісіне тең:
K O r Q r mv .
Қозғалыс мөлшері моментінің өзгеруі туралы теорема –
dK O
M Oe .
dt
Қозғалыс мөлшері моментінен уақыт бойынша алынған
туынды системаның сыртқы күштерінің сол центрге
қатысты моменттерінің басты моментіне тең.














 physics
physics








