Similar presentations:
Механикалық гармониялық тербелістер. Өшетін тербелістер. Еріксіз тербелістер. Толқындар
1. Дәріс тақырыбы: Механикалық гармониялық тербелістер. Өшетін тербелістер. Еріксіз тербелістер. Толқындар.
2. Гармониялық тербелістердің кинематикасы
3. Гармониялық тербелістің сипаттамалары:
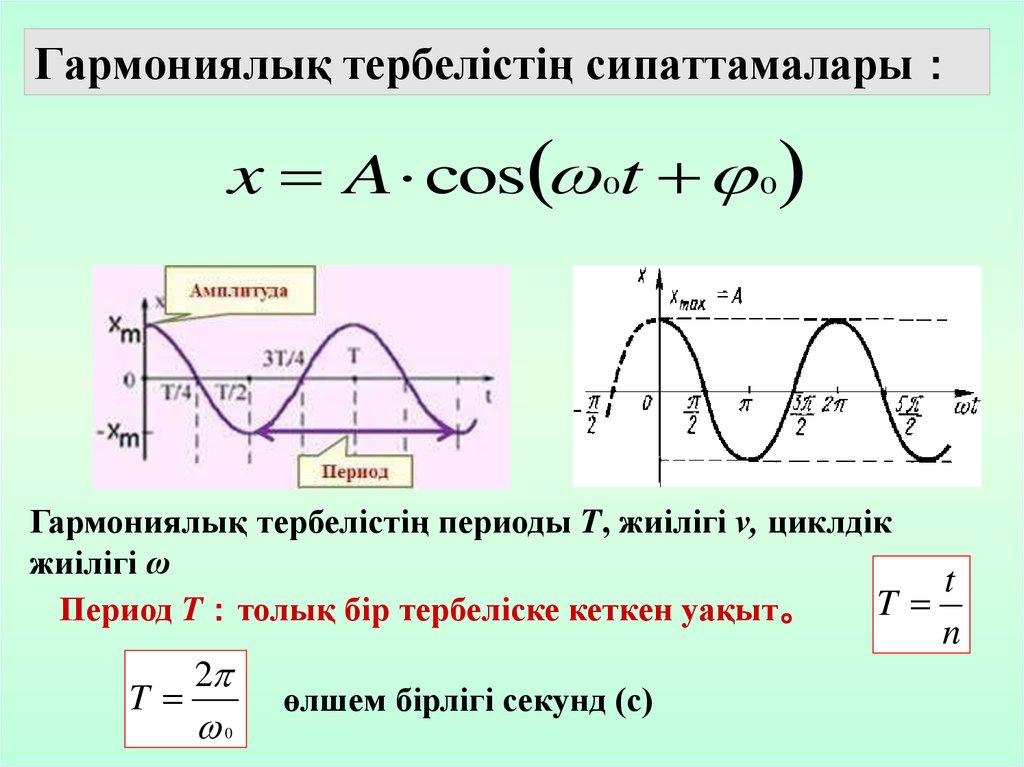
Гармониялық тербелістің сипаттамаларыx A cos 0t 0
Гармониялық тербелістің периоды T, жиілігі ν, циклдік
жиілігі ω
t
T
Период T толық бір тербеліске кеткен уақыт。
T
2
0
n
өлшем бірлігі секунд (с)
4.
Жиілік ν уақыт бірлігіндегі тербелістер саны.2
0
2
0 2
T
өлшем бірлігі Герц=1/c
ω ─ циклдік жиілік
Гармониялық тербелістің қозғалыс теңдеуін келесі
түрде де жазуға болады
x A cos( 2 t 0)
2
немесе x A cos( t 0)
T
5.
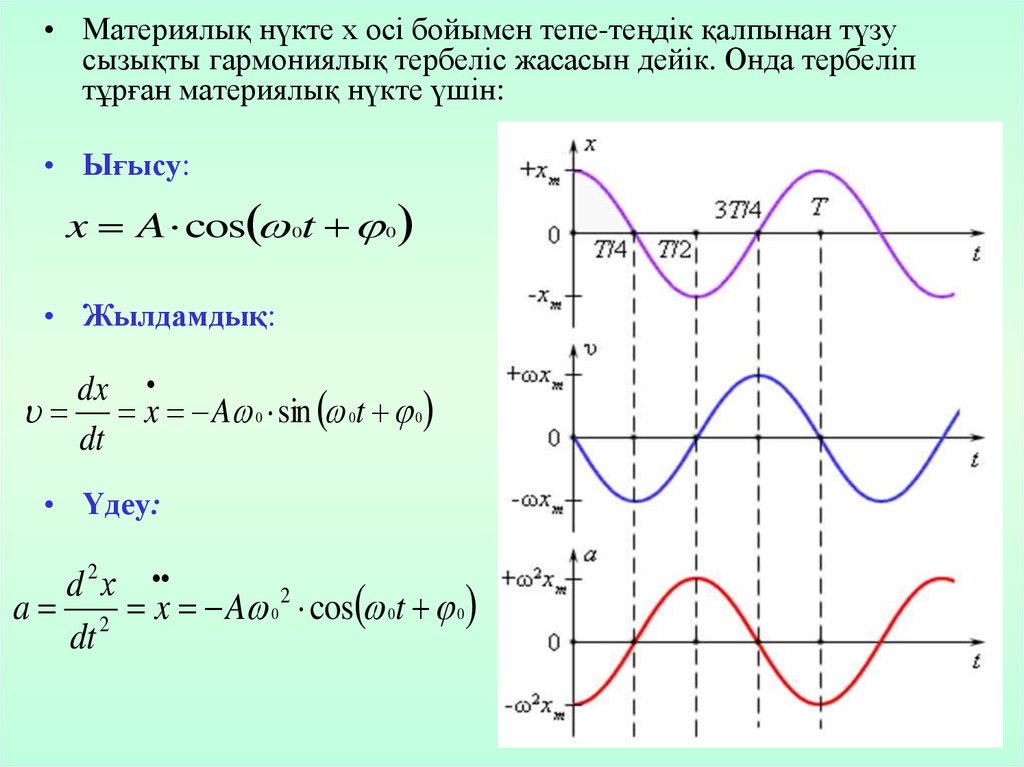
• Материялық нүкте х осі бойымен тепе-теңдік қалпынан түзусызықты гармониялық тербеліс жасасын дейік. Онда тербеліп
тұрған материялық нүкте үшін:
• Ығысу:
x A cos 0t 0
• Жылдамдық:
dx
x A 0 sin 0t 0
dt
• Үдеу:
d 2 х
a 2 x A 0 2 cos 0t 0
dt
6.
Еркін гармониялық тербелістердің дифференциалдық теңдеуіх х 0
2
0
гармониялық тербелістердің екінші ретті
дифференциалдық теңдеуі, оның шешімі:
x A cos 0t 0 .
Гармониялық тербелістердің пайда болу шарттары:
серпімді қайтарушы күштің әсері; үйкелістің өте аз болуы.
2
mх m 0 х;
F kх;
k m 02 ;
Массасы m тербеліп тұрған материялық нүктеге әсер етуші
күш:
F m х mA cos( 0t 0 )
2
0
2
0
Сонымен, материялық нүктеге әсер етуші күш ығысуға
пропорционал және ығысуға қарама-қарсы бағытталған (тепетеңдік күйге қарай).
7.
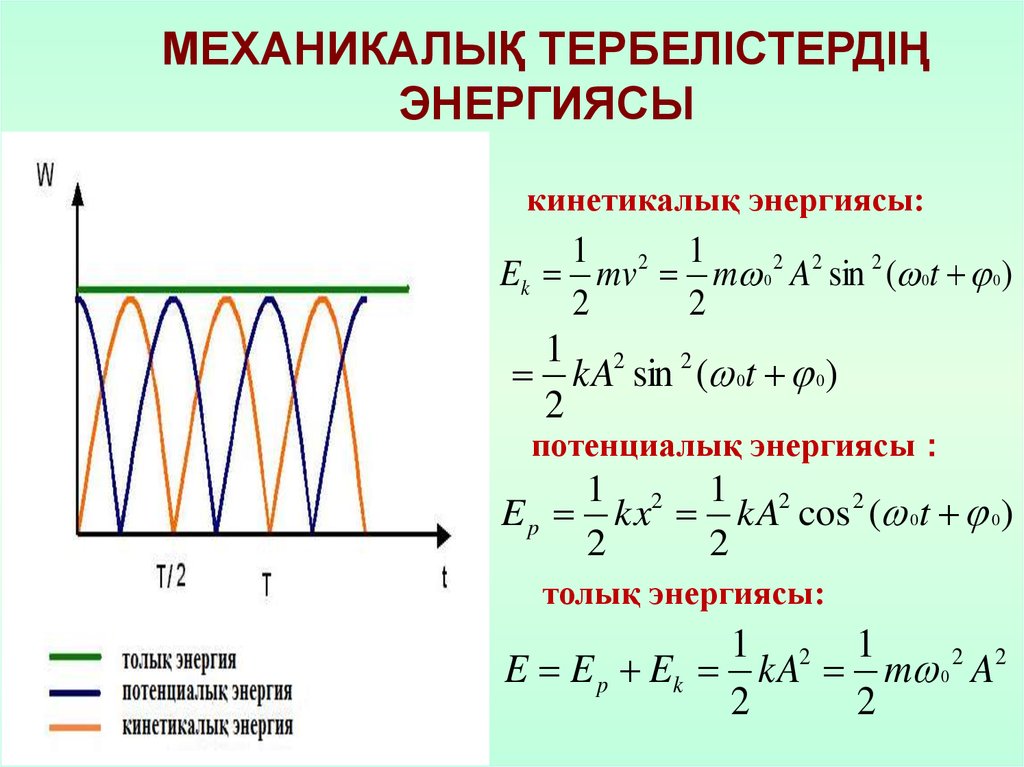
МЕХАНИКАЛЫҚ ТЕРБЕЛІСТЕРДІҢЭНЕРГИЯСЫ
кинетикалық энергиясы:
1 2 1
Ek mv m 0 2 A2 sin 2 ( 0t 0)
2
2
1 2 2
kA sin ( 0t 0)
2
потенциалық энергиясы
1 2 1 2
E p kx kA cos 2 ( 0t 0)
2
2
толық энергиясы:
1 2 1
E E p Ek kA m 0 2 A2
2
2
8.
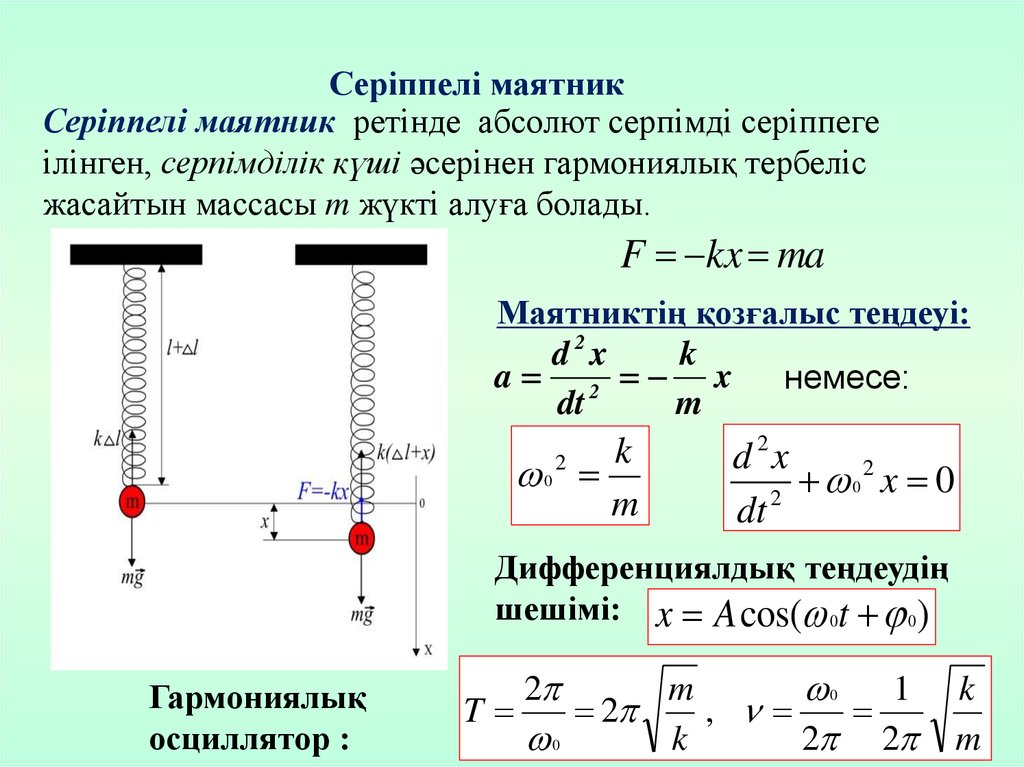
Серіппелі маятникСеріппелі маятник ретінде абсолют серпімді серіппеге
ілінген, серпімділік күші әсерінен гармониялық тербеліс
жасайтын массасы m жүкті алуға болады.
F kx ma
Маятниктің қозғалыс теңдеуі:
d2x
k
a 2 x немесе:
dt
m
k
0
m
2
d 2x
2
0 x 0
dt 2
Дифференциялдық теңдеудің
шешімі: x A cos( 0t 0)
Гармониялық
осциллятор :
2
m
0 1
T
2
,
0
k
2 2
k
m
9.
Математикалық маятникМатематикалық
маятник
созылмайтын салмақсыз, үзындығы l
жіпке ілінген, ауырлық күші әсерінен
үйкелісіз тербеліс жасайтын материялық
нүктеден тұратын идеалданған жүйені
айтады.
Ауытқу бұрышы -ның кіші мәндерінде:
Кері қайтарушы күш:
F1 mg sin mg mg
d 2x
x
Қозғалыс теңдеуі: m 2 F1 mg
l
dt
немесе
d 2x g
x 0;
2
dt
l
x
~
l
2
0
g
l
Тербеліс периоды:
2
T
2
0
x
l
d 2x
2
0 x 0;
2
dt
l
g
x A cos 0t 0 ;
10.
Физикалық маятникФизикалық маятник деп дененің массалар центрі арқылы
өтпейтін оське бекітілген, ауырлық күші әсерінен іліну осі
айналасында тербеліс жасап тұрған қатты денені айтады.
Егер маятник тепе-теңдік қалпынан қандай-да
бір бұрышқа ауытқыса, онда кері қайтарушы
күш моменті
M F l mgl sin mgl
Басқа жағынан, кіші бұрыштар үшін
F mg sin
Бұдан шығатыны:
немесе
d 2
J 2 mgl 0
dt
d 2 mgl
0;
2
dt
J
mgl
;
J
- кері қайтарушы күш
d 2
M J J 2
dt
d 2
2
0 0
dt 2
11.
T 2J
2
mgl
L
;
g
A cos t ;
0
0
Физикалық маятниктің келтірілген ұзындығы деп – периоды
физикалық маятниктің периодына тең математикалық маятниктің
ұзындығын айтады.
J
L
ml
12. Өшетін тербелістер
13.
Өшетін тербеліс деп үйкеліс салдарынан тербелмелі жүйеэнергиясының уақыт өте кемуіне байланысты,
тербелістің біртіндеп әлсіреуін айтады.
Тербеліп тұрған дененің жылдамдығы аз болған кезде
үйкеліс күші жылдамдыққа кері пропорционал болады.
γ үйкеліс коэффициенті
dx
F
dt
Дифференциалдық теңдеуі
k
ω0: циклдік жиілік
m
2
0
d2x
dx
m 2
kx
dt
dt
2
m
өшу коэффициенті
ω0 , β мәндерін жоғарғы теңдеуге қойсақ, онда
14.
Өшетін тербеліс теңдеуі келіп шығадыd 2x
dx
2
2
0x 0
2
dt
dt
x A(t ) cos( t 0 )
мұндағы A(t) – кейбір уақыт функциясы.
Орта кедергісі аз болған кезде β < ω0
x A0 e t cos( t )
A A0 e
t
Өшетін тербеліс амплитудасы
15.
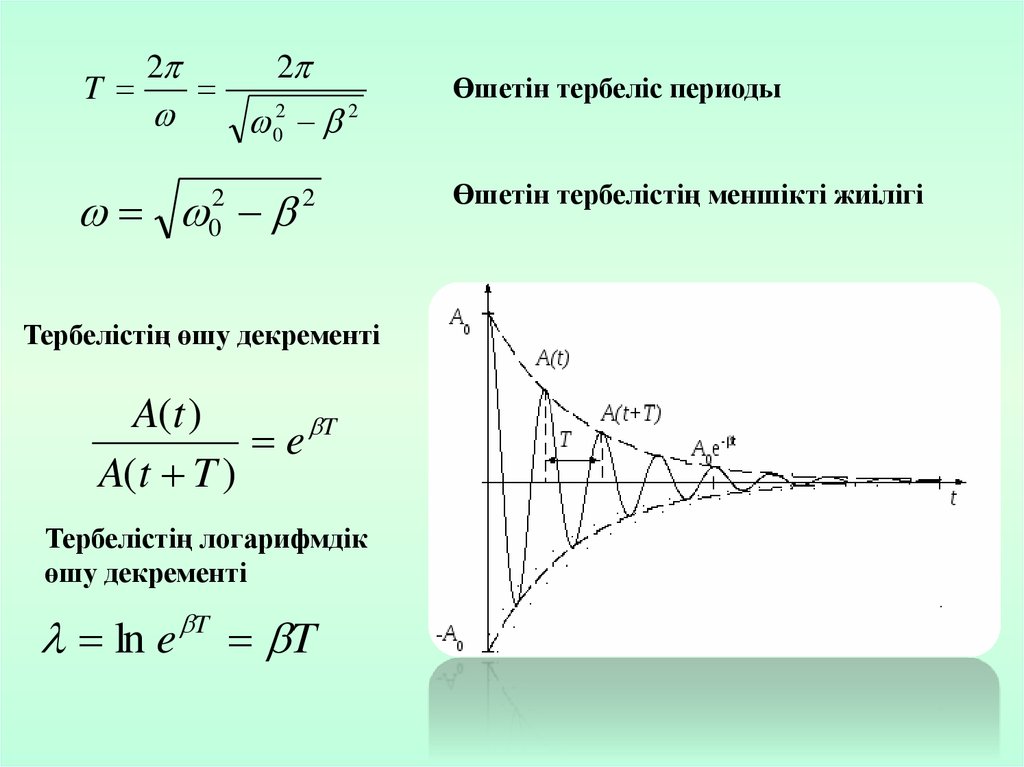
T2
2
2
0
Өшетін тербеліс периоды
2
02 2
Өшетін тербелістің меншікті жиілігі
Тербелістің өшу декременті
A(t )
e T
A(t T )
Тербелістің логарифмдік
өшу декременті
ln e T T
15
16.
17. Еріксіз тербелістер, резонанс
18.
Сыртқы периодты күштер әсерінен болатын тербелісеріксіз тербеліс деп аталады (нақты тербелістер).
Сыртқы периодты күш F ( t ) F0 cos t
d2x
dx
онда m 2 kx F0 cos t
dt
dt
F0
k
2
егер 0 , 2 , f 0
m
m
m
d2x
dx
2
онда
2
0 x f 0 cos t
2
dt
dt
шешімі x A0 e t cos( 02 2 t ' ) A cos( t )
Еріксіз тербеліс = өшетін тербеліс + гармониялық тербеліс
19.
(1) Көп уақыттан кейін, еріксіз тербеліс тұрақтытербеліске айналады, оның периоды сыртқы күштің
периодына тең болады.
x A cos( 0t 0)
(2) Тұрақты еріксіз тербеліс пен периодты сыртқы күш
арасында белгілі бір фаза φ айырымы болады.
(3)
2
A
, tg 2
2
2
2
2 2
( 0 ) 4
0
f0
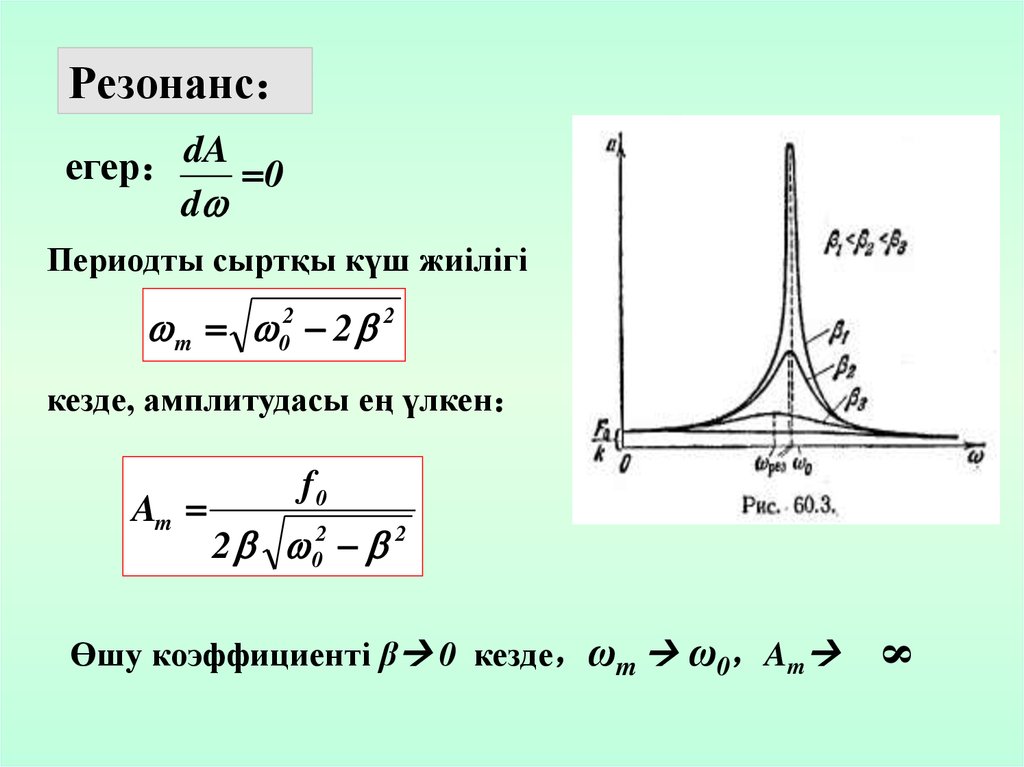
20. Резонанс:
Резонансегер dA 0
d
Периодты сыртқы күш жиілігі
m 02 2 2
кезде, амплитудасы ең үлкен
Am
f0
2 02 2
8
Өшу коэффициенті β 0 кезде ωm ω0 Am
21. Бір бағыттағы, жиіліктері бірдей гармониялық тербелісті қосу
x1 A1 cos( 0t 1 )x2 A2 cos( 0t 2 )
x x1 x2 A1 cos( 0t 1 ) A2 cos( 0t 2 )
Қорытқы тербеліс те
гармониялық тербеліс
болып саналады.
x A cos( 0t 0)
22.
At = 0 уақыттағы векторлық сұлбасы
A A12 A22 2 A1 A2 cos( 2 1 )
A2
φ2
A1 sin 1 A2 sin 2
tg
A1 cos 1 A2 cos 2
β
φ
x2
φ1
x1
A1
x
Қорытқы амплитуданы фаза айырымы арқылы анықтайды:
(1) Δφ= φ2–φ1= ± 2kπ
A1
A2
A
x
(2) Δφ= φ2–φ1= ± (2k+1)π
π
A1
Amax=A1+A2
бағыттас
A
A2
x
қарама-қарсы
Amin=A1 - A2
x
23. Бір бағыттағы, әртүрлі жиіліктегі гармониялық тербелістерді қосу
Егер тербелістердің жиілігі бірдей болмаса Δφ үнеміөзгеріп отырады. Сондықтан қорытқы тербеліс
амплитудасы да өзгеріп отырады. Бұл кезде қорытқы
тербеліс гармониялық болмай қалады.
егер
x1 A cos( 1 t )
x 2 A cos( 2 t )
онда x x1 x 2 A(cos 1 t cos 2 t )
2 1
2 1
2 A cos(
t ) cos(
t)
2
2
2 1
2 A cos(
t ) қорытқы тербеліс амплитудасы
2
0 ~ A аралығында өзгеріп отырады.
24.
Екі тербелістің жиілігі бірдей болмаса, қорытқы тербелісамплитудасы бірде күшейіп, бірде әлсіреп отырады.
2 1
25.
2526. Механикалық гармониялық толқындар
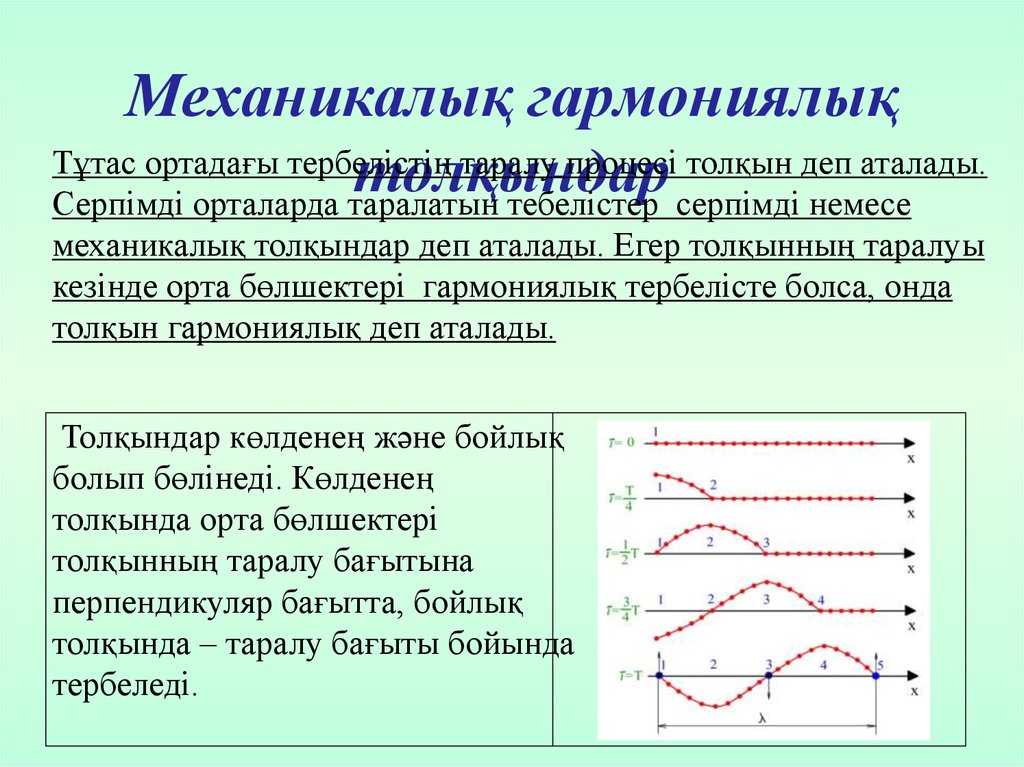
Механикалық гармониялықТұтас ортадағы тербелістің таралу процесі толқын деп аталады.
толқындар
Серпімді орталарда таралатын тебелістер серпімді немесе
механикалық толқындар деп аталады. Егер толқынның таралуы
кезінде орта бөлшектері гармониялық тербелісте болса, онда
толқын гармониялық деп аталады.
Толқындар көлденең және бойлық
болып бөлінеді. Көлденең
толқында орта бөлшектері
толқынның таралу бағытына
перпендикуляр бағытта, бойлық
толқында – таралу бағыты бойында
тербеледі.
27.
Толқынның негізгіқасиеті – зат
тасымалынсыз
энергия
тасымалдануы
T
28.
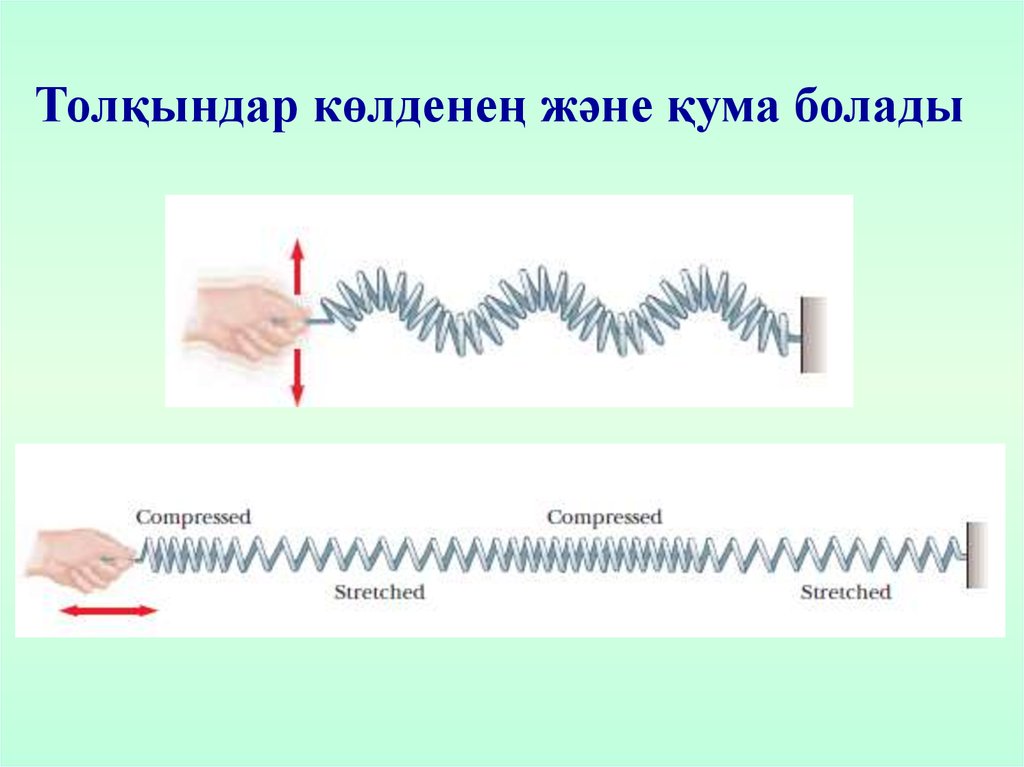
Толқындар көлденең және қума болады29.
Қума толқындар деп, тербеліс бағытытолқынның таралу бағытымен сәйкес
келетін толқындарды атайды.
30.
Көлденең толқындар деп, тербелісбағыты толқын бағытына
перпендикуляр болатын толқындарды
атайды.
31.
Бірдей фазада тербелетін ең жақын нүктеніңара қашықтығы толқын ұзындығы деп
аталады. Бұл шама толқынның тербеліс Т
периоды мен жылдамдығының көбейтіндісіне
тең:
T
v
мұндағы: – толқынның таралу жылдамдығы;
1
v
– тербеліс жиілігі.
T
32.
ТОЛҚЫН ТЕҢДЕУІТолқын теңдеуі – тербелетін нүктенің оның
координаталары мен уақытының
функциясы ретінде анықтайтын қатынас.
A cos t
( x, t ) A cos (t t )
t
x
x
( x, t ) A cos t
33.
ТОЛҚЫНДЫҚ ТЕҢДЕУ1
2
2
2
2
2
x
y
z t
2
2
2
2
1
2 2
t
2

























 physics
physics








