Similar presentations:
Электромагниттік толқындар
1.
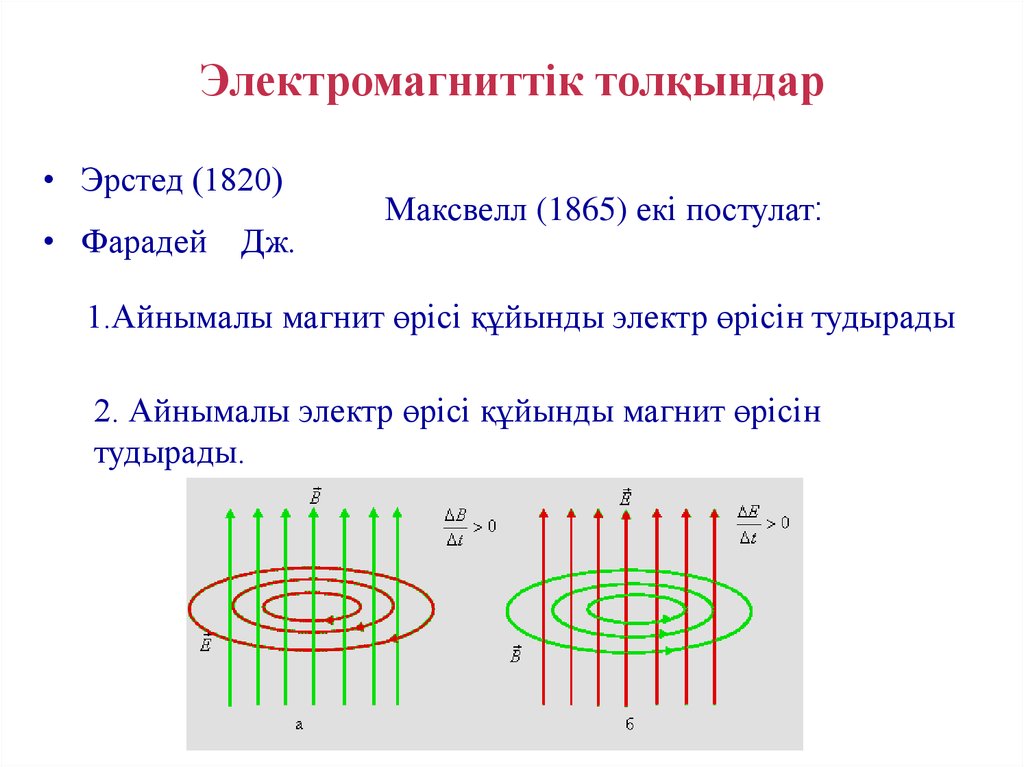
Электромагниттік толқындар• Эрстед (1820)
• Фарадей Дж.
Максвелл (1865) екі постулат:
1.Айнымалы магнит өрісі құйынды электр өрісін тудырады
2. Айнымалы электр өрісі құйынды магнит өрісін
тудырады.
2.
Егер катушканың орам сандарын да азайта бастасақ,онда индуктивтілік кемиді.
Ашық тербелмелі контурдың сыйымдылығы мен индуктивтілігі
өте аз.
Сондықтан
дірілдеткіштегі
электромагниттік
өріс
тербелістерінің меншікті жиілігі аса жоғары болады.
3.
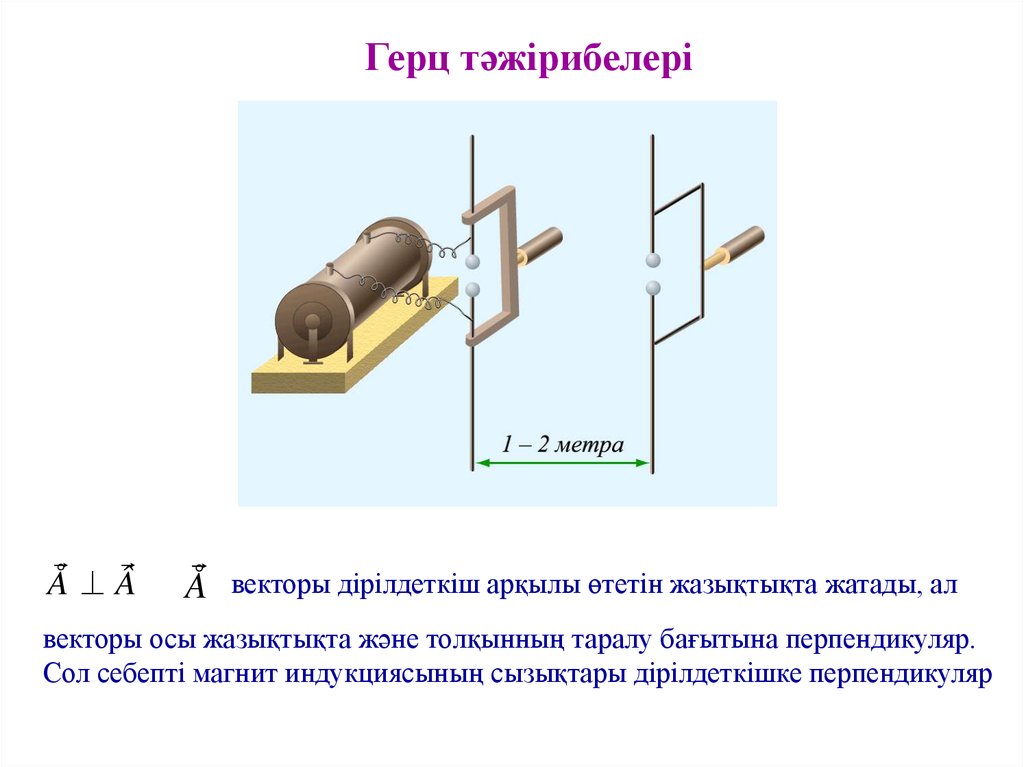
Герц тәжірибелеріÅ Â
Å
векторы дірілдеткіш арқылы өтетін жазықтықта жатады, ал
векторы осы жазықтықта және толқынның таралу бағытына перпендикуляр.
Сол себепті магнит индукциясының сызықтары дірілдеткішке перпендикуляр
4.
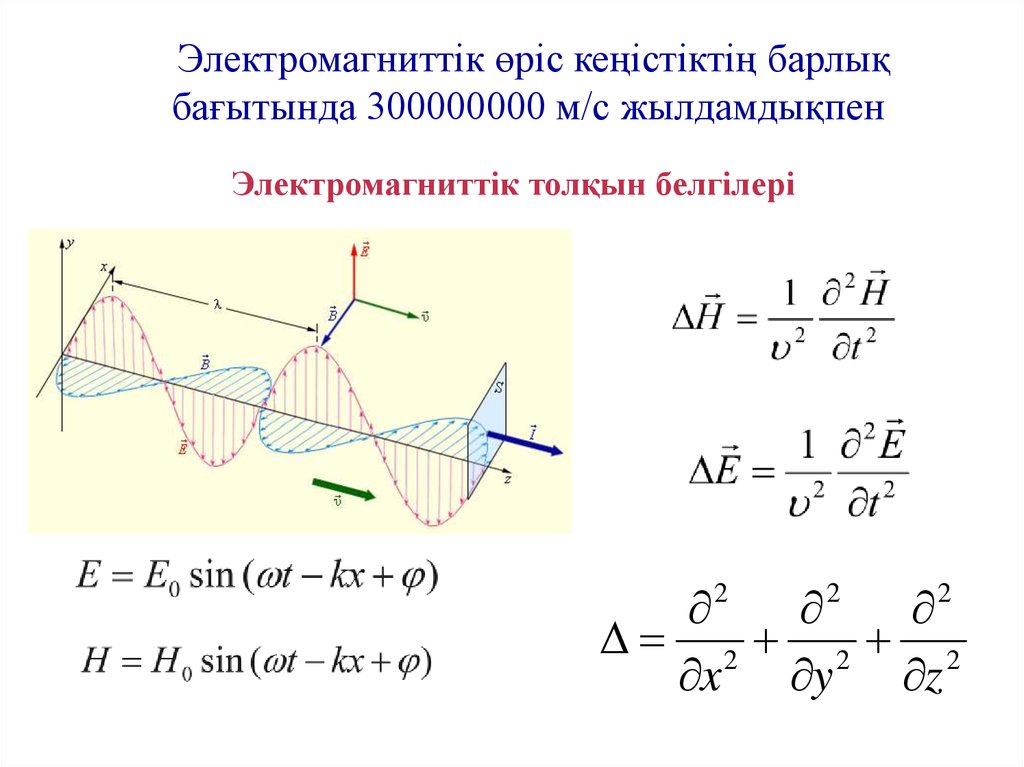
Электромагниттік өріс кеңістіктің барлықбағытында 300000000 м/с жылдамдықпен
Электромагниттік толқын белгілері
2 2 2
x y z
2
2
2
5.
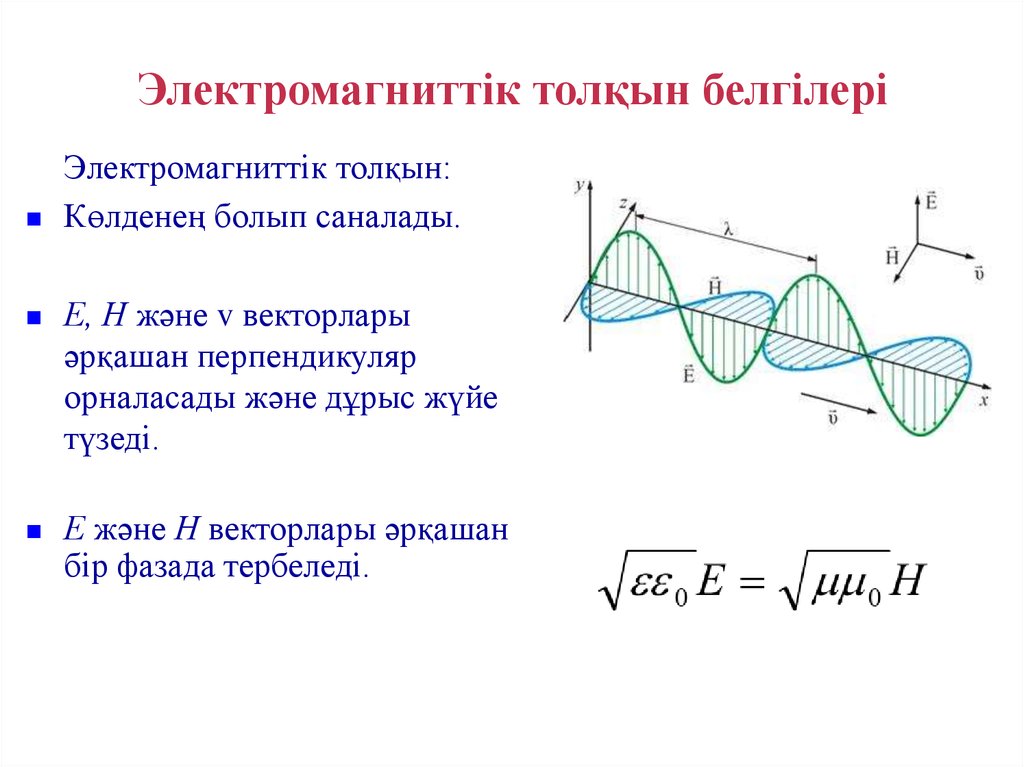
Электромагниттік толқын белгілеріЭлектромагниттік толқын :
Вакуумде жарық жылдамдығымен тарайды:
Жарық - электромагниттік толқын.
Бірдей фазада тербелетін ең жақын екі нүктенің
арақашықтығы электромагниттік толқын ұзындығын береді.
ñÒ
ñ
6.
Электромагниттік толқын белгілеріЭлектромагниттік толқын:
Көлденең болып саналады.
Е, Н және v векторлары
әрқашан перпендикуляр
орналасады және дұрыс жүйе
түзеді.
Е және Н векторлары әрқашан
бір фазада тербеледі.
7.
Электромагниттік толқындарды анықтау мүмкіндігі,олардың энергияны тасымалдайтының көрсетеді.
wэ
wм
0 E 2
2
- электр энергиясының көлемдік тығыздығы
B2
2 0
-магнит өрісінің энергиясының көлмдік тығыздығы.
Электромагниттік өріс энергиясының тығыздығы
wэл wм
w wэ wм 2wэ
8.
Энергия тығыздығын толқын таралу жылдамдығынакөбейтсек, онда энергия ағынының тығыздығын табамыз.
S w 0 0 EH
1
0 0
EH
S EH
E H
- Умов-Пойнтинг
векторы
9.
Физика кафедрасыМультимедиялық презентация
Баспа: “Оптика”
Пән атауы: “Физика 2”
Тақырып: Интерференция
Авторы:
ф-м.ғ.к.Салькеева А.К.,
10.
Дәріс жоспары1.
Жарық толқындардың қасиеттері
2. Жарық толқындардың
интерференциясы
3. Уақытша және қеңістік
когеренттілік
4. Интерферометрлар
11.
XVII ғасырда жарықтың табиғатын түсіндіру үшінекі теория пайда болды:
1. Ньютонның корпускулалық теориясы. Осы теория
бойынша : жарық – ол бөлшектердің ағыны
(корпускула).
2. Гюйгенс толқын теориясы: жарық ерекше ортада эфирде таралатын серпімді толқынды білдіреді.
Осы құбылысты жарық дуализм дейді.
Максвелл
теориясы бойынша: жарық
электромагниттіқ толқын.
– ол
12.
• Толқын теориясыГюйгенс принципине
негізделеді. Толқын жететін әрбір нүкте екінші
реттік толқындар центрі болып табылады.Осыдан
пайда болған екінші жаңа толқындар, толқын шебі
болып есептеледі.
13.
Жарық толқындардың диапазоны0,40мкм ≤ λ ≤ 0,75 мкм
λ = с·T = с ∕ ν
с = 3·108 м/c
v = (0,75 – 0,40) ∙ 1015 Гц.
14.
Интерференция пайда болу үшін толқындаркогерентті болу қажет.
Жиілігі
бірдей және фазалардың айырымы
тұрақты толқындар когерентті болып саналады.
Монохроматтіқ толқындар – жиіліктері бірдей
толқындар
Екі
(немесе бірнеше) когерентті жарық
толқындарының қабатасуы кезінде жарық ағыны
кеністіктік
қайта
бөліп
тарату
жүреді,
нәтижесінде бір жерде қарқындылық максимумы,
бір жерде қарқындылық минимумы пайда болады.
Бұл құбылыс жарық интерференциясы деп
аталады.
15.
ИНТЕРФЕРЕНЦИЯ ортаныңәр
түрлі
нүктесінде екі немесе
бірнеше
когерентті
толқындардың
бірігуі
кезіндегі
тербелістің
уақыт өте келе тұрақты
ұлғайуы немеме азайуы
(жарықтың
ортада
таралуы).
16.
17.
ЕКІ КОГЕРЕНТТІ КӨЗДЕН ТЕРБЕЛІСТЕРДІҚОСУ
M
S1
x1 A1 cos t 1
x2 A2 cos t 2
x x1 x2 Acos( t )
S2
18.
Өрістердің кернеулігі Е1 және Е2 бақылау нүктедесызық бойында тербелістер жасайды:
Е1=Е01 cos ( t+ 1)
E2=E02 cos ( t+ 2)
Қорытынды тербелістерінің амплитудасы:
E2=E012+E022+2 E01E02cos (φ2-φ1)
Нәтижелі тербеліс амплитудасы
19.
Когерентті емес толқындар үшін (φ2- φ1) үзіліссізөзгереді
cos 2 1 0
I ~ А2
I1 I 2
I I1 I 2
I 2I1
20.
ЕКІ КОГЕРЕНТТІ КӨЗДЕН ТЕРБЕЛІСТЕРДІҚОСУ
2 1 const
-толқындар когеренты
I I1 I 2 2 I1I 2 cos 2 1
cos 2 1 0
I I1 I 2
cos 2 1 0
I I1 I 2
21.
I1 I 2cos 2 1 1
I 4I1 max
cos 2 1 1
I 0 min
22.
ИНТЕРФЕРЕНЦИЯИнтерференция
нәтижесі
тербелістердің фазаларының әр
байланысты болады.
біріккен
түрлілігіне
I I1 I 2 2 I1I 2 cos 2 1
23.
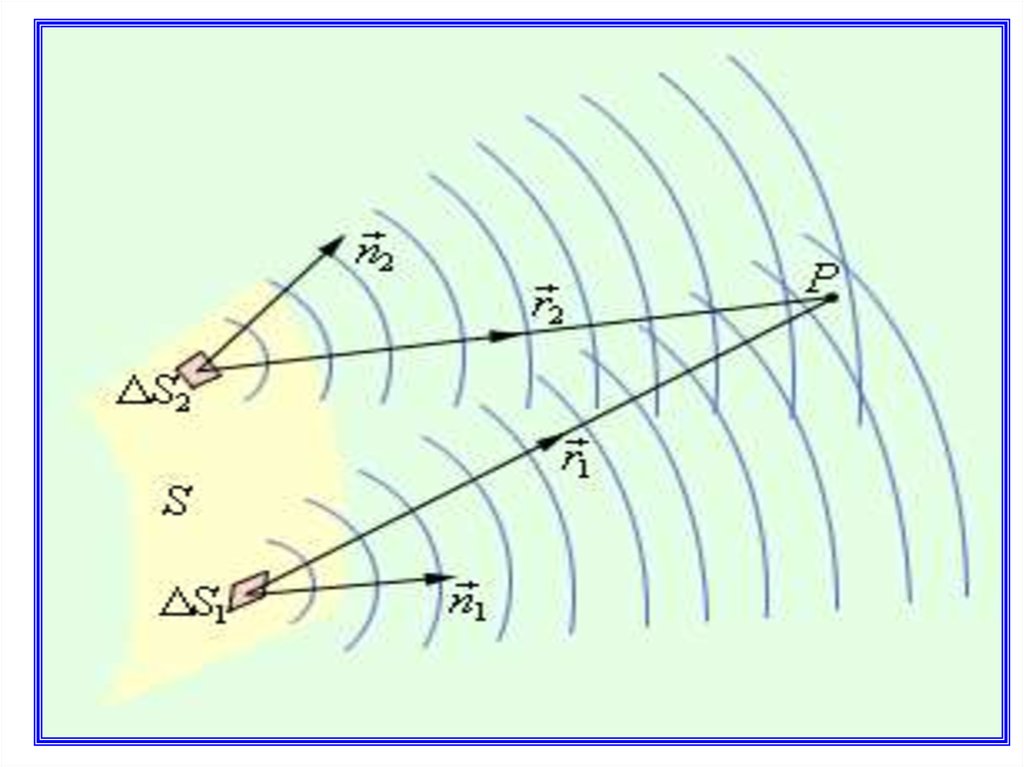
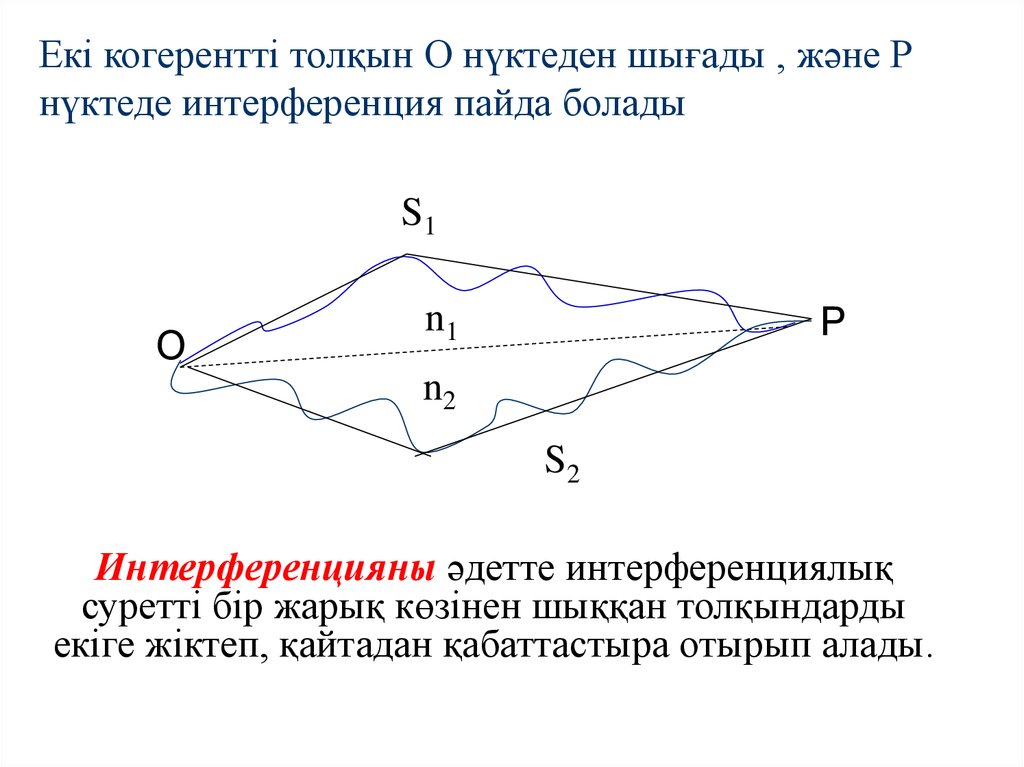
Екі когерентті толқын О нүктеден шығады , және Рнүктеде интерференция пайда болады
S1
O
n1
P
n2
S2
Интерференцияны әдетте интерференциялық
суреттi бiр жарық көзiнен шыққан толқындарды
екiге жiктеп, қайтадан қабаттастыра отырып алады.
24.
МАКСИМУМ ЖӘНЕ МИНИМУМДАРШАРТЫ
S2
S1
2 A2 cos t
1 A1 cos t
2
1
S2 S1
S2 n2 S1n1
c
c
2 1
2 c / n2
1 c / n1
c
S n
2
2
S1n1
2
2
c
Tc
25.
L nS- Оптикалық жол үзындығы
L2 L1
2
2
c
Tc
Оптикалық жүрістің
айрымы
2
26.
k2k , k 0, 1, 2...
интерференциялдық
максимум шарты
2k 1
2
2
k , k 0, 1, 2...
интерференциялдық
минимум шарты
27.
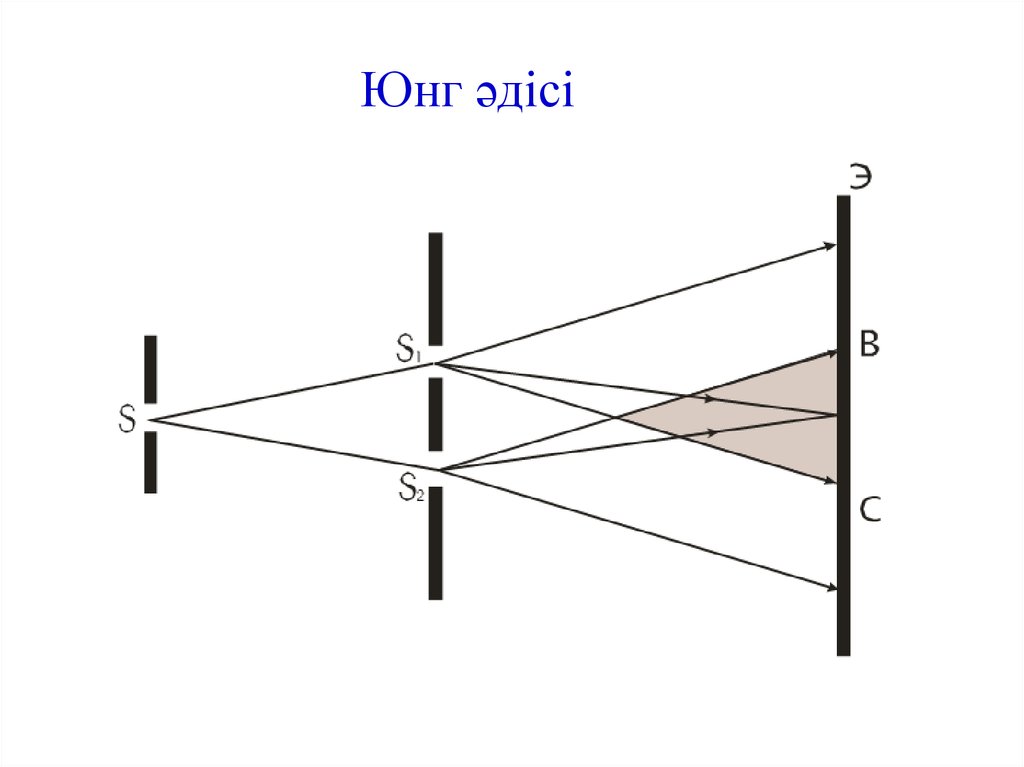
Юнг әдісі28. Юнг әдісі
Томас ЮнгЕкі саңылау арқылы өту
кезінде
толқындардың
бөлінуінің
нәтижесінде
когеренттік толқындар
алынады.
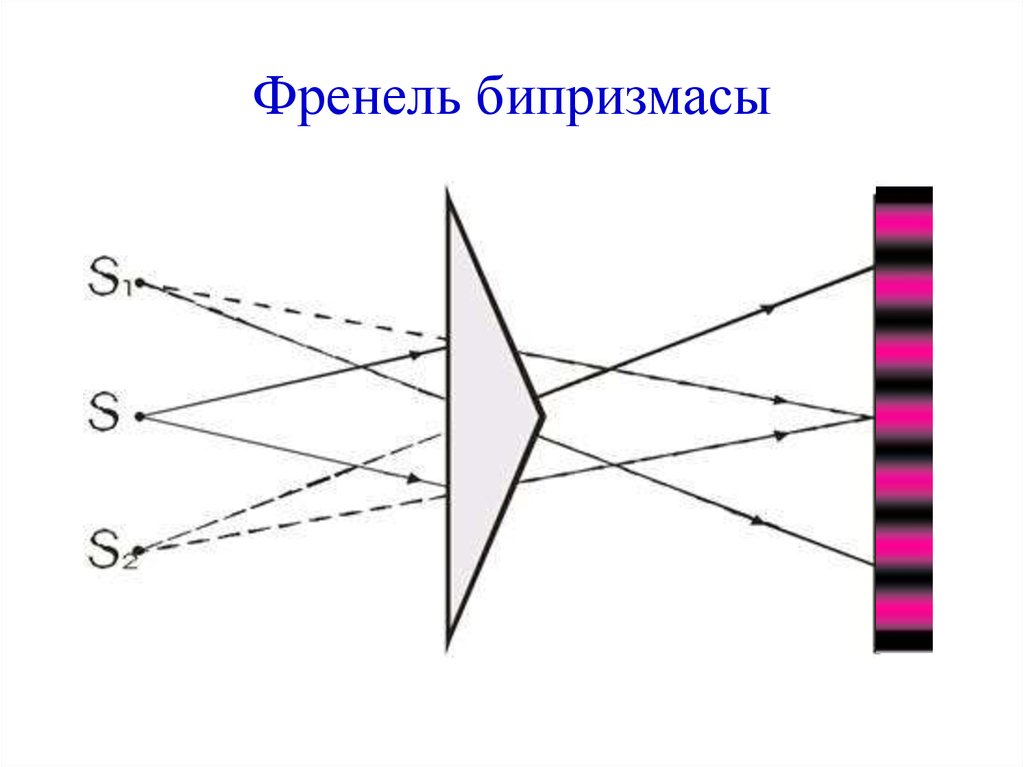
29. Френель бипризмасы
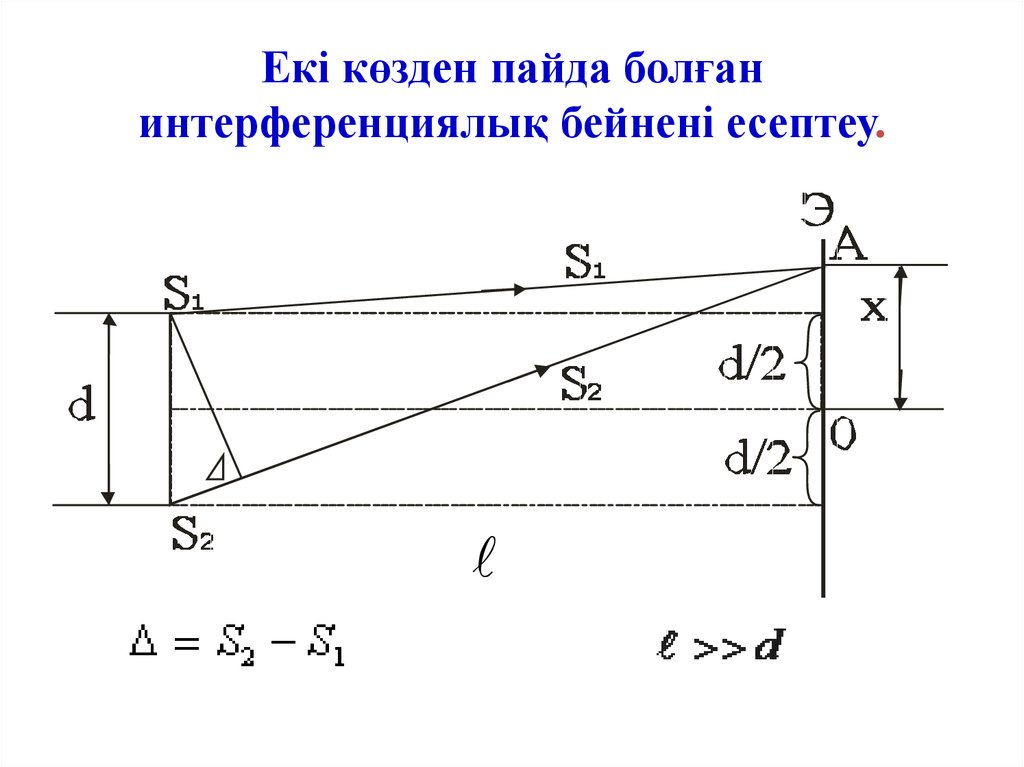
30. Екі көзден пайда болған интерференциялық бейнені есептеу.
31.
S S 2 xd2
2
2
1
xd
Қарқындылық
m
(интенсивтіліктің) максимумы:
32.
минимумы байқалады:X min
1
m
2 d
2m 1
2
(m = 0,1,2,…)
Интерференция жолағының ені — көршілес екі
максимумдар (немесе минимумдар) арасындағы
қашықтық
33.
интерференциялықтүзу қалыңдығы
интерференциялық түзу
қалыңдығы – екі корші минимум
мен макасимум ара қашықтығы.
y
L
d
34.
Жұқа пленкадағы интерференция.n ОС СВ (ОА 0 / 2)
35.
n n00 / 2
n n0
0 / 2
OC CB d / cos r
n OC CB 2nd / cos r
OA OB sin i 2d tgr sin i
sin i n sin r
Сыну заңына сәйкесті,
2dn cos r 2dn 1 sin r 2d n sin i
2
2
2
36.
n n0(m = 0,1,2,…)
37.
d — пленка қалыңдығы; п — оның сыну көрсеткіші; i–түсу бұрышы; r- сыну бұрышы; т = 1 , 2, 3, ....
38.
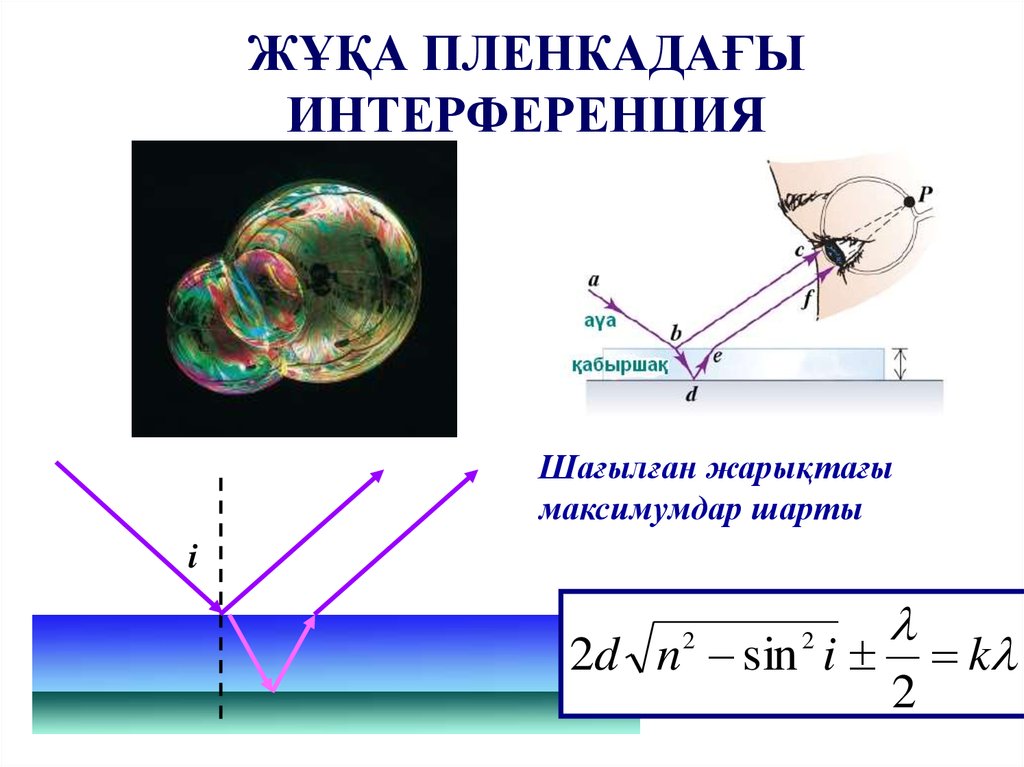
ЖҰҚА ПЛЕНКАДАҒЫИНТЕРФЕРЕНЦИЯ
Шағылған жарықтағы
максимумдар шарты
i
2d n sin i
2
2
2
k
39.
ЖҰҚА ПЛЕНКАДАҒЫИНТЕРФЕРЕНЦИЯ
n1 n, n2 n
2
1
n1
n
n2
2nd
2nd
2
2
k
оптикалық өте тығыз ортадан шағылу кезіндегі тербеліс
фазасы қарама-қарсы жарты толқынды жоғалтуға
эквивалентті өзгереді.
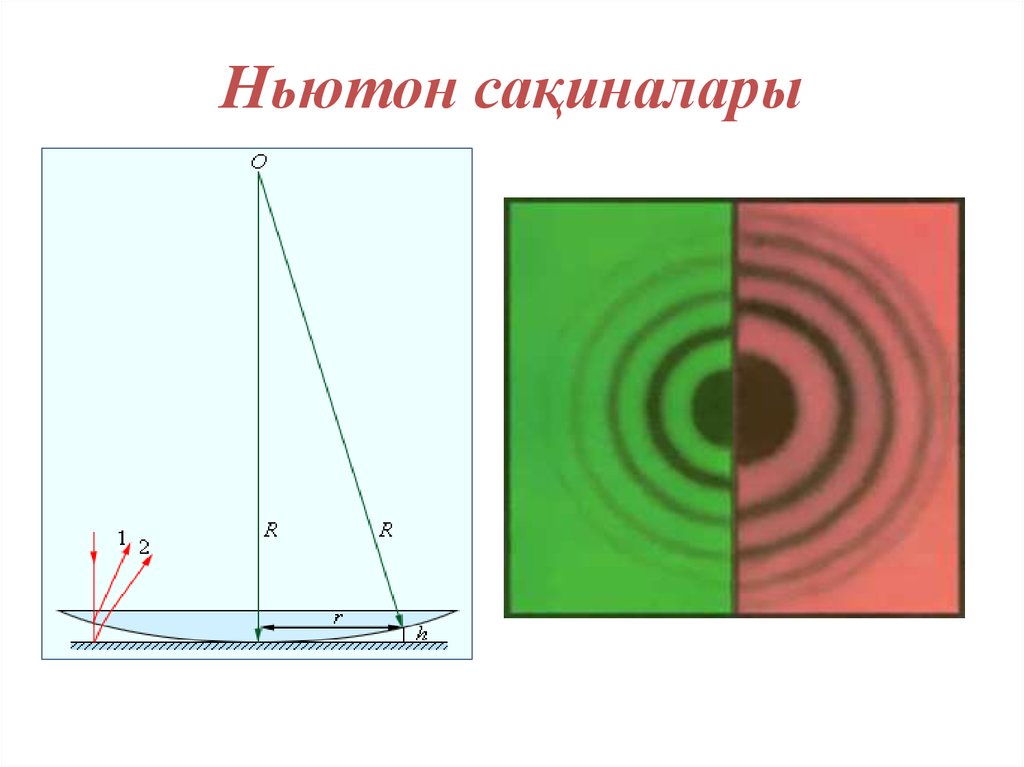
40. Ньютон сақиналары
41.
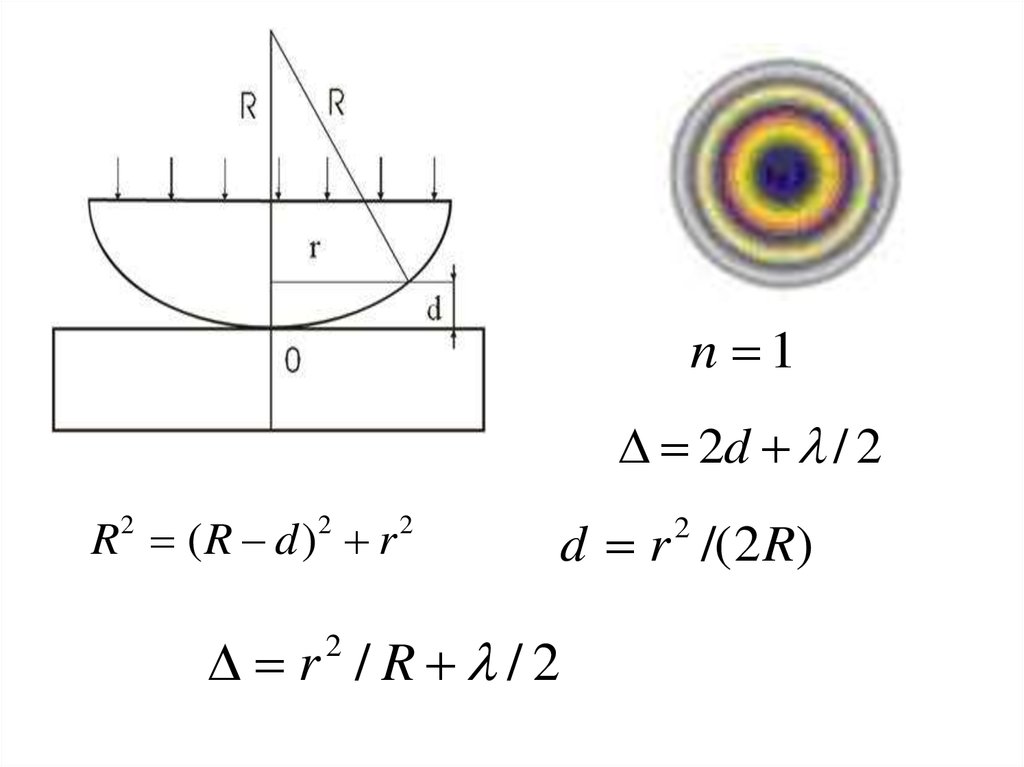
n 12d / 2
R (R d ) r
2
2
2
r /R /2
2
d r /( 2 R)
2
42.
шағылғанжарықта
сақиналар радиусы
(m=1, 2, 3 ,…).
шағылған
жарықта
сақиналар радиусы
(m=1, 2, 3 ,…).
ашық
күңгірт
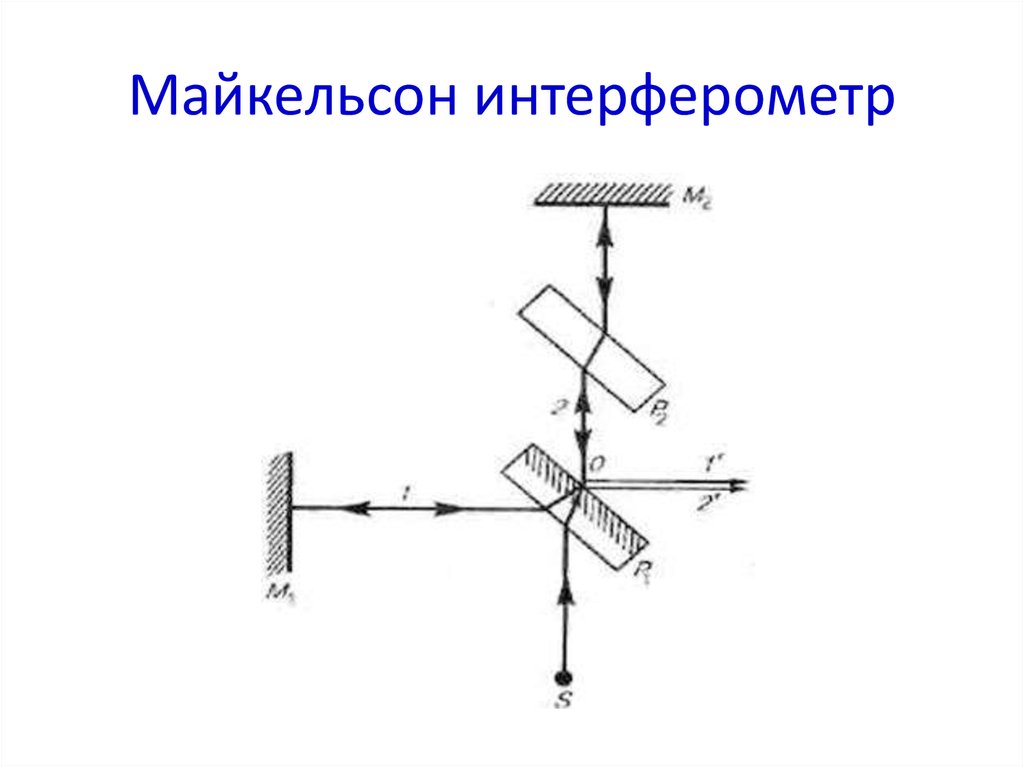
43. Майкельсон интерферометр
44.
Назараударғандарыңызға
рахмет!

























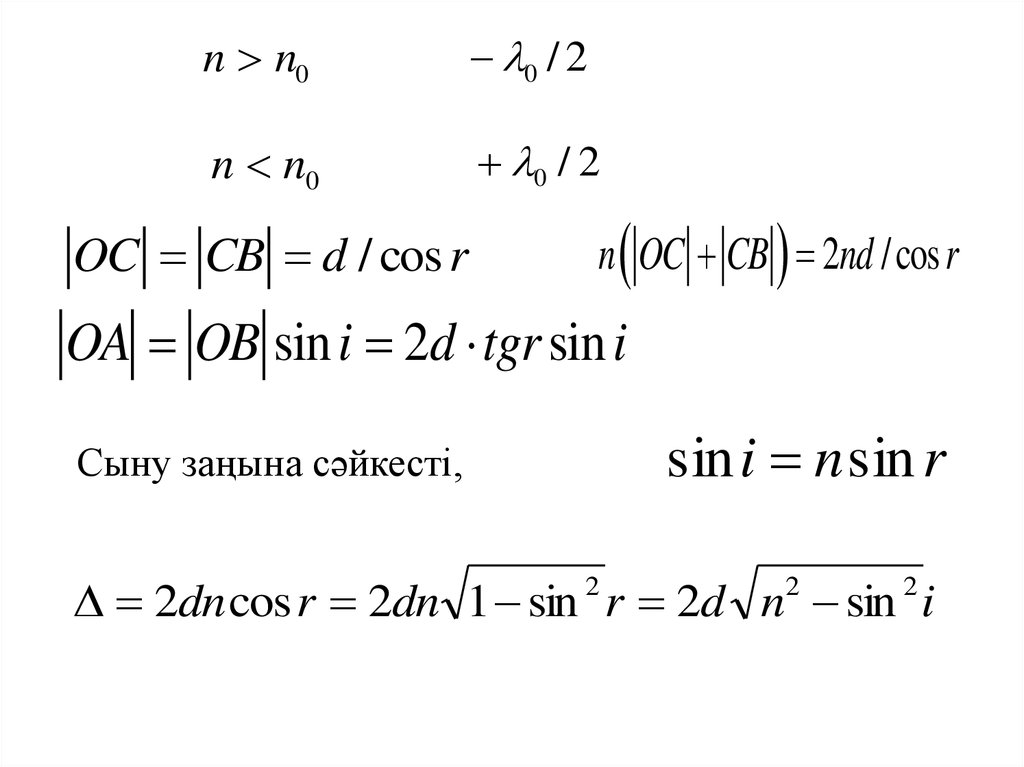
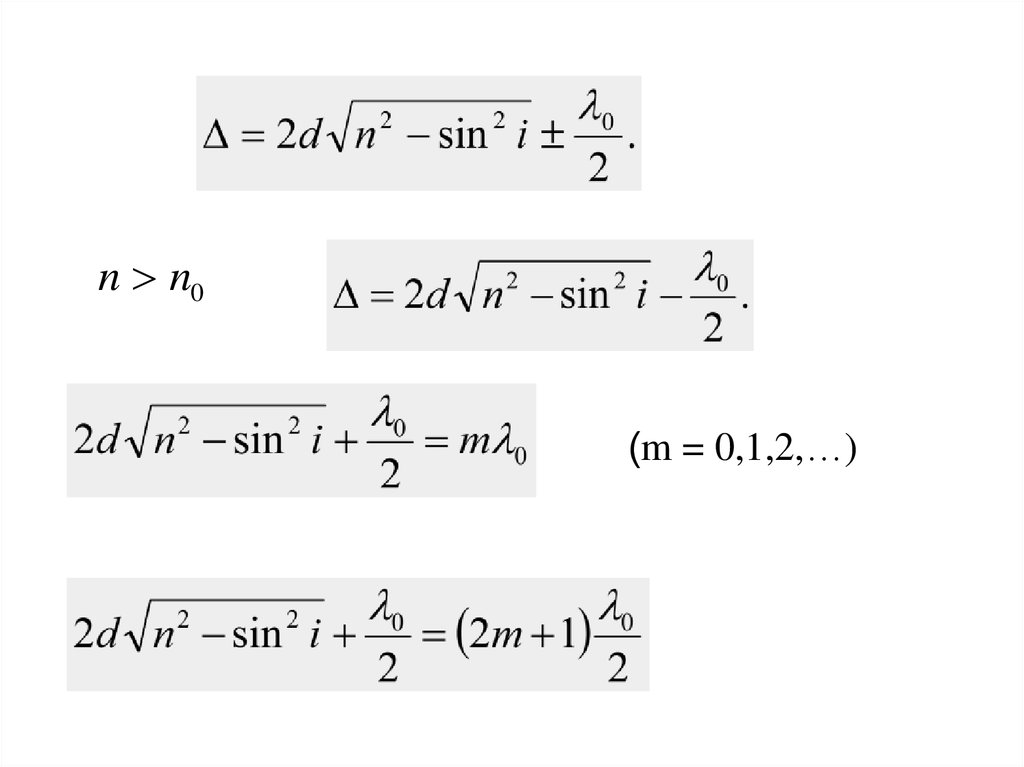




 physics
physics








