Кинематика. Нүкте кинематикасы. Қатты дене кинематикасы

1.

Кинематика
Нүкте кинематикасы
Қатты дене кинематикасы
• Кинематика – теориялық механика пәнінің кинематика
бөлімінде, дене қозғалысы оны қозғалысқа келтіретін күштерді
ескермей қарастырылады да және дене қозғалысының
геометриялық параметрлері (траектория, жылдамдық, үдеу)
анықталады.
• Нүкте кинематикасы – екі мәселе қарастырады:

2.

• 1. Нүктенің қозғалыс теңдеуі – қозғалыстағы
нүктенің берілген санақ жүйесіне қарағандағы
орны уақытқа тәуелді теңдеулер арқылы беріледі.
• Осы теңдеулер арқылы қозғалыстағы нүктенің
барлық
кинематикалық
сипаттамаларын
(траекториясын, жылдамдығын, үдеуін) табу;
• 2. Қозғалыс траекториясы – қозғалып бара жатқан
нүктенің кеңістіктегі геометриялық орындарын
қосатын үздіксіз сызық.

3.

1. Кинематикада нүкте қозғалысы үш түрде: векторлық,
координаттық, және табиғи тәсілдермен беріледі.
M
r r (t )
Векторлық тәсіл:
Радиус-вектордың бағыты, мәні беріледі.
r
z
x x(t );
O
M
y y (t );
z z (t ).
Координаттық тәсіл:
z
Нүктенің координаттары беріледі.
O
x
x
y
y

4.

Табиғи тәсіл:
Нүктенің қозғалыс теңдеуі мен траекториясы беріледі.
z
s
O1
s s (t );
M
z
f ( x , y , z ) 0.
O
x
y
x
y

5.

2. Қозғалыстың траекториясын анықтау үшін координаттық
тәсілдің теңдеулерінен уақытты жою керек:
r (t ) x(t )i y(t ) j z (t )k
Барлық үш тәсіл де бір-біріне эквивалентті және бір-бірімен
байланысты.
Векторлық пен координаттық:
Соңғы екі теңдеу қозғалыстың траекториясын сипаттайды.
x x(t ) t t ( x);
y y (t ) y[t ( x)] y ( x);
z z (t ) z[t ( x)] z ( x).

6.

Мысал:
x t
x t t x
y R2 t 2 ;
y R 2 t 2 R 2 x 2 или x 2 y 2 R 2 ;
z c.
z c.
z
Соңғы екі теңдеу радиусы R болатын
цилиндр, биіктігі с-ға тең, z өсіне
параллель болады. Сонда нүктенің
траекториясы радиусы R-ға тең
шеңбер
x
O
y

7.

• Нүкте жылдамдығы – нүктенің бірлік уақытта орын
ауыстыру тездігін (шапшаңдығын) анықтайтын физикалық
шама.
Нүктенің жылдамдығын анықтаудың үш түрі:
Векторлық тәсіл: Нүктенің екі түрлі уақыттағы t және t1= t + t
жағдайын салыстырамыз:
r
Δr
r;
t
M
M1
vср
Δr
vорт
Δt
r1
O
MM1
t1 t Δt r1 r Δr ;
-
t уақыттағы орта жылдамдық,
хорда бойымен бағытталған
t 0 дағы шек:
Δr
v
Δt lim 0
Δt

8.

dr
v
dt
- t уақытындағы жылдамдық векторы, ол
траекторияға жанама бағытталған.
Радиуса-вектор мен координаттардың байланысы:
r (t ) x(t )i y(t ) j z (t )k
Координаттық тәсіл:
Векторлық тәсілді жылдамдықты анықтау үшін қолданамыз:
dr (t )
d
v
x(t )i y (t ) j z (t ) k
dt
dt
dx
dy
dz
i
j
k vxi v y j vz k
dt
dt
dt

9.

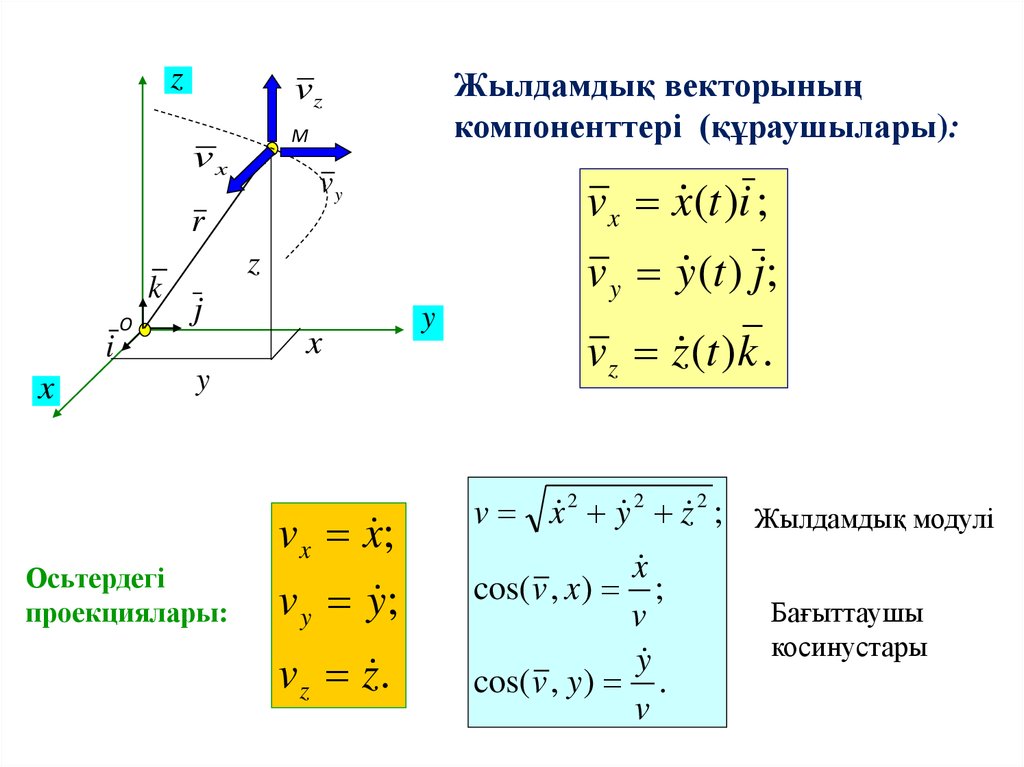
z
Жылдамдық векторының
компоненттері (құраушылары):
vz
M
vx
v x x (t )i ;
vy
r
k
i
x
O
v y y (t ) j;
z
j
x
y
Осьтердегі
проекциялары:
v x x ;
v y y ;
v z z .
y
v z z (t )k .
v x 2 y 2 z 2 ; Жылдамдық модулі
x
cos( v , x) ;
Бағыттаушы
v
косинустары
y
cos( v , y ) .
v

10.

Табиғи тәсіл:
Жылдамдық векторы:
v s .
Жанамаға проекциясы:
v s .

11.

Нүкте үдеуі – Үдеу нүкте жылдамдығының бірлік уақытта сан мәні
мен бағытының өзгеруін сипаттайтын векторлық шама.
Нүкте үдеуін анықтаудың үш тәсілі :
Векторлық тәсіл:
Δv
aорт
Δt
v
M
r
O
Δr
M1
v1
v
r1
Шекке көшсек:
Δt lim 0
dv d 2 r
a
2
dt dt
- орта үдеу векторы траекторияның
ойық жағына бағытталады.
Δt
lim 0
Δv
a
Δt
Δv dv
Δt
dt
үдеу векторы жанама жазықтықта жатады
- және траекторияның ойық жағына бағытталады.
-

12.

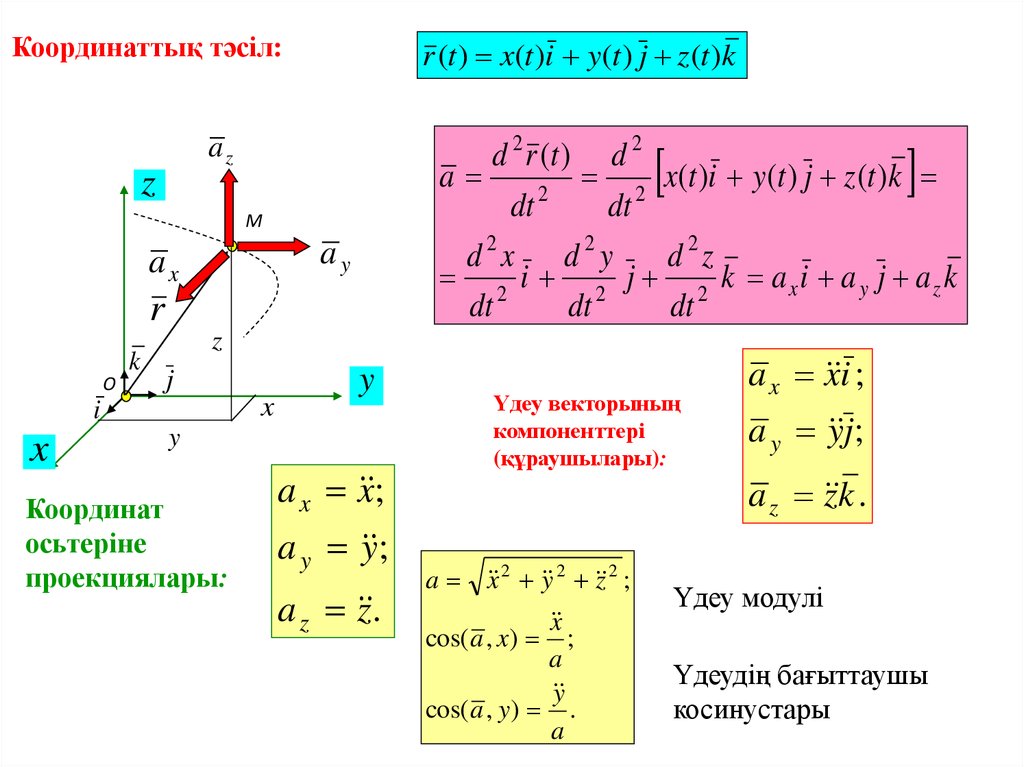
Координаттық тәсіл:
r (t ) x(t )i y(t ) j z (t )k
z
M
ay
ax
r
O
k
z
j
x
i
x
d 2 r (t ) d 2
a
2 x(t )i y (t ) j z (t )k
2
dt
dt
d 2x d 2 y
d 2z
2 i 2 j 2 k axi a y j az k
dt
dt
dt
az
y
y
Координат
осьтеріне
проекциялары:
a x x ;
a y y ;
a z z .
Үдеу векторының
компоненттері
(құраушылары):
a x 2 y 2 z 2 ;
x
;
a
y
cos( a , y ) .
a
a x x i ;
a y y j;
a z z k .
Үдеу модулі
cos( a , x)
Үдеудің бағыттаушы
косинустары

13.

Табиғи тәсіл:
dv d
d
a
( s ) s s
.
dt dt
dt
Жанамаға перпендикуляр n бірлік векторын енгіземіз,
ол қисықтықтың центріне бағытталған.
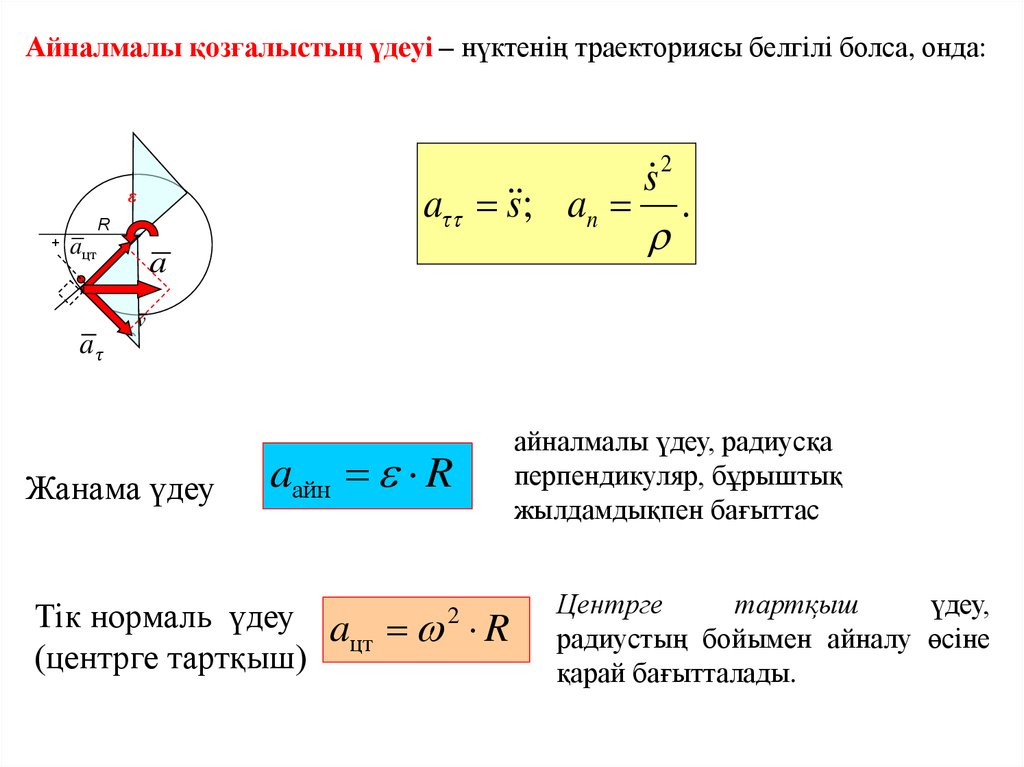
a s
Удеу модулі
s 2
a a τ an .
n.
a a τ an ;
2
2
aτ s ;
Үдеудің және n өстеріне проекциялары:
an
s 2
.

14.

Бірқалыпты айнымалы қозғалыс –
егер барлық уақытта да,
aτ s const.
Яғни жанама үдеу өзгермейді.
vτ v τ 0 a τ t
t2
s s0 vτ 0t aτ
2
- бірқалыпты айнымалы қозғалыстың жылдамдығы
-
бірқалыпты айнымалы қозғалыстың теңдеуі

15.

Қатты дене кинематикасы – қозғалыстың бес түрі:
1. Ілгерілемелі (ползун, насостың поршені, паравоздың
дөңгелектері(спарник), түзу жолмен жүру, лифтің кабинасы, купенің есігі).
2. Айналмалы (маховик, кривошип, кәдімгі есік).
3. Жазықпараллеь немесе жазық (шатун, локомотивтің дөңгелегі).
4. Сфералық (гироскоп).
5. Қозғалыстың жалпы жағдайы немесе еркін ұшу (оқ, тас, аспан денесі)
Ілгерілемелі қозғалыс – Қатты дененің онымен
өзгерместей болып бекітілген түзуі өзінің бастапқы
қалпына параллель қалып отыратын қозғалысы.

16.

Ілгерілемелі қозғалыстағы дене нүктелерінің траекториялары,
жылдамдықтары және үдеулері туралы теорема –
Ілгерілемелі қозғалыста дене нүктелерінің траекториялары, жылдамдықтары
мен үдеулерінің әрбір уақыт кезінде мәндері мен бағыттары бірдей, яғни дене
нүктелері конгурентті қозғалыста болады.
rA (t ) rB (t ) const ,
A нүктесінің жылдамдығы
B нүктесінің(геометриялық,
яғни векторы)
жылдамдығына тең.
vA (t ) vB (t ).
A нүктесінің үдеуі B
нүктесінің(геометриялық,
яғни векторы) үдеуіне тең.
aA (t ) aB (t ).

17.

Сонымен,
ілгерілемелі
қозғалыстың
барлық
кинематикалық
сипаттамаларын(
траектория,
жылдамдық және үдеу) оның жалғыз ғана нүктесінің
қозғалысы арқылы анықтауға болады.
Қатты дененің айналмалы қозғалысы – Егер
қозғалыстағы дененің кем дегенде екі нүктесі
қозғалмайтын болса, онда мұндай дене тұрақты өстен
айналмалы қозғалыста болады.

18.

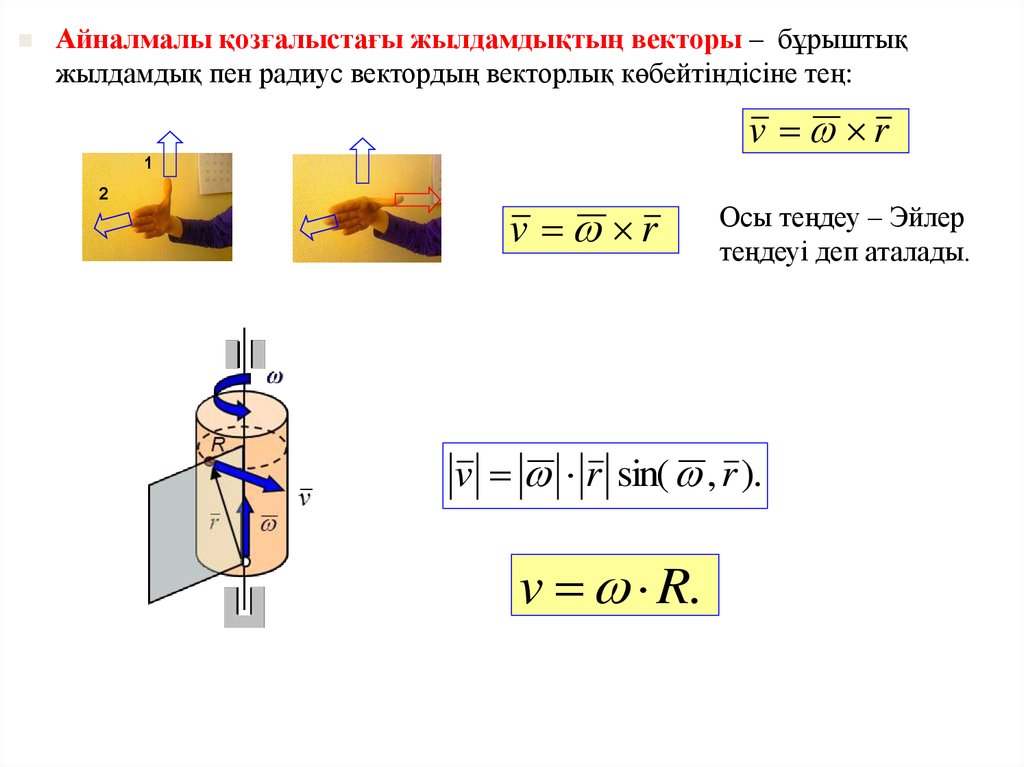
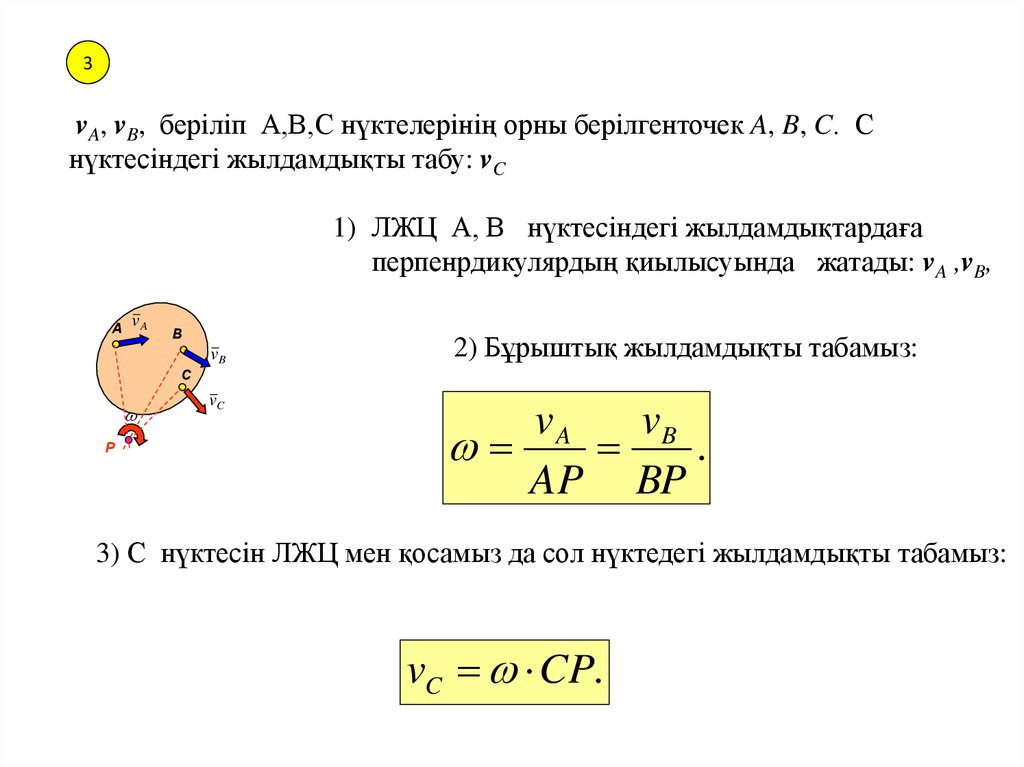
(t )
ω
P
- Айналмалы
ω
қозғалыстың теңдеуі
Бұрыштық жылдамдық – бұрылу
бұрышының
уақытқа
тәуелді
бірінші туындысы.
Q
d
dt
бұрыштық жылдамдық
Бұрыштық жылдамдықты доғалық бағытпен көрсетеді.

19.

Бұрыштық үдеу – бұрылу бұрышының уақытқа тәуелді екінші
туындысы.
ε
ω
d
dt
-бұрыштық үдеу
P
Q
Бұрыштық үдеу доғалық бағытпен көрсетіледі
Бірқалыпты айналу – бұрыштық
const.
0
.
жылдамдық тұрақты.
0 t.
Бірқалыпты айнымалы айналу – бұрыштық үдеу тұрақты.
0 t.
t2
0 0t .
2
const.

20.

Енді φ айналу бұрышы мен N айналым саны және бұрыштық жылдамдық пен техникада жиі
кездесетін айналу жиілігінің (n,
байланыстарды қарастырамыз.
айн
мин
) араларындағы механика есептерін шығаруда пайдаланатын
Шеңбер бойымен дене өз өсінен бір рет айналғанда, φ=2π радианға (3600 ) бұрылады, ал N
айналым санына сәйкес айналу бұрышы:
φ=2π N.
айн
Егер дененің бір минуттағы айналу жиілігін n,
деп алсақ, онда дененің
мин
бұрыштық жылдамдығы
ω=
2