Системы логических уравнений

1. Системы логических уравнений (B15)

2. №1. Сколько различных решений имеет логическое уравнение:

(a ¬ b) (b ¬ c) (c ¬ d) (d ¬ e) = 1
Решение:
Ответ: 6
(a → b) (b → c) (c → d) (d → e) (e → f)=1
Ответ:
7
(X1 → X2) (X2 → X3) … (X99 → X100) = 1
Ответ: 101
Ответ:
11

3.

(x1 → x2) (x2 → x3) (x3 → x4) (x4 → x5) = 1
(z1 → z2) (z2 → z3) (z3 → z4) = 1
Решение:
Ответ: 30
(x1 → x3) (x3 → x5) … (x9 → x11) = 1
(x2 → x4) (x4 → x6) … (x8 → x10) = 1
Ответ: 42

4. №2. Сколько существует различных наборов значений логических переменных, которые удовлетворяют всем условиям?

(x1 → x2) (x2 → x3) (x3 → x4) (x4 → x5) = 1
(x5 → x1) = 1
Решение:
Ответ: 2

5.

(x1 → x2) (x2 → x3) (x3 → x4) (x4 → x5) = 1
(z1 → z2) (z2 → z3) (z3 → z4) = 1
x1 z1 = 1
Решение:
Ответ: 10
(X1 X2) (X2 X3) (X3 X4) (X4 X5)=1
(Y1 Y2) (Y2 Y3) (Y3 Y4) (Y4 Y5)=1
X5 Y5 = 0
Решение:
Ответ: 11

6. №4. Сколько существует различных наборов значений логических переменных, которые удовлетворяют перечисленным условиям?

(X1 X2) (X2 X3) (X3 X4) (X4 X5) 1
(Y1 Y2) (Y2 Y3) (Y3 Y4) (Y4 Y5) 1
X1 Y1 1
Решение:
Ответ:
64
(X1 X2) (X2 X3) (X3 X4) (X4 X5)=1
( Y1 Y2) ( Y2 Y3) ( Y3 Y4) ( Y4 Y5)=1
X1 Y1 = 0
Решение:
Ответ: 25

7.

(x1 → x2) (x2 → x3) (x3 → x4) (x4 → x5) = 1
(y1 → y2) (y2 → y3) (y3 → y4) (y4 → y5) = 1
x1 → y1 = 1
Решение:
Ответ:
31
(x1 x2) (x2 x3) (x3 x4) (x4 x5) = 1
(у1 у2) (у2 у3) (у3 у4) (у4 у5) = 1
y5 x5 = 1
Ответ:
31

8. № 5. Сколько различных решений имеет система уравнений:

(x1 ≡ x2) (x2 ≡ x3)=1
(x2 ≡ x3) (x3 ≡ x4)=1
(x3 ≡ x4) (x4 ≡ x5)=1
……
(x8 ≡ x9) (x9 ≡ x10)=1
Ответ: 20
Решение:
Ответ: 178
Решение:

9.

(x2 ≡ x1) (x2 ≡ x3)=1 (A → B) + (C → D) =1
(x3 ≡ x1) (x3 ≡ x4)=1
...
Решение:
(x9 ≡ x1) (x9 ≡ x10)=1
Ответ: 15
(x10 ≡ x1) = 0
Решение:
Ответ:
18

10.

¬(X1 X2) (X3 X4) = 1
¬(X3 X4) (X5 X6) = 1
¬(X5 X6) (X7 X8) = 1
¬(X7 X8) (X9 X10) =1
Решение:
Ответ:
192

11. № 7. Сколько различных решений имеет система логических уравнений:

(X1 X2) ↔ (X3 X4) = 1
(X3 X4) ↔ (X5 X6) = 1
(X5 X6) ↔ (X7 X8) = 1
(X7 X8) ↔ (X9 X10) = 1
Решение:
Ответ: 364
Решение:
Ответ:
X1 ¬X2 ¬X3 X4 = 1
X3 ¬X4 ¬X5 X6 = 1
X5 ¬X6 ¬X7 X8 = 1
X7 ¬X8 ¬X9 X10 = 1
64

12.

((X1 X2) + (X3 X4))*(¬(X1 X2) + ¬(X3 X4)) = 1
((X3 X4) + (X5 X6))*(¬(X3 X4) + ¬(X5 X6)) = 1
.......
((X7 X8) + (X9 X10))*(¬(X7 X8) + ¬(X9 X10)) = 1
Решение:
Ответ:
64

13.

X1 X 2 X1 X 2 X 3 X 4 X 3 X 4 1
X 3 X 4 X 3 X 4 X 5 X 6 X 5 X 6 1
X 5 X 6 X 5 X 6 X 7 X 8 X 7 X8 1
X 7 X 8 X 7 X 8 X 9 X10 X 9 X10 1
Решение:
Ответ:
192

14.

X1 X 2 X1 X 2 X 3 X 4 X 3 X 4 1
X 3 X 4 X 3 X 4 X 5 X 6 X 5 X 6 1
X5 X 6 X5 X 6 X 7 X8 X 7 X8 1
X 7 X 8 X 7 X 8 X 9 X 10 X 9 X 10 1
X 9 X 10 X 9 X 10 X 11 X 12 X 11 X 12 1
Решение:
Ответ:
224

15.

A ¬B ¬C D = 1
C ¬D ¬E F = 1
E ¬F ¬G H = 1
G ¬H ¬I J = 1
I ¬J ¬A B = 1
Ответ: 244
Решение:
A B C ¬D = 1
C D E ¬F = 1
E F G ¬H = 1
G H I ¬J = 1
I J A ¬B = 0
Ответ: 120
Решение:

16. №11. Сколько различных решений имеет система уравнений:

Решение:
Ответ:
3

17.

X1 X2 X1 X2 X2 X3 X2 X3 1
X2 X3 X2 X3 X3 X4 X3 X4 1
X7 X8 X7 X8 X8 X9 X8 X9 1
Решение:
Ответ:
110

18.

x 1 x2 x3 x4 x5 = 1
y 1 y2 y3 y4 y5 = 0
Решение:
Ответ:
231

19. Сколько различных решений имеет система уравнений:

x1 x2 x3 x4 x5 x6 = 1
y1 y2 y3 y4 y5 y6 = 1
x1 y1 = 1
Решение:
Ответ:
1387

20.

(x1 x2) (x2 x3) (x3 x4) = 1
( у1 у2) ( у2 у3) ( у3 у4) =1
(x1 y1) (x2 y2) (x3 y3) (x4 y4) = 1
Решение:
Ответ:
15

21.

(x1 x2) (x2 x3) (x3 x4) = 1
( у1 у2) ( у2 у3) ( у3 у4)=1
(x1 y1) (x2 y2) (x3 y3) (x4 y4)=1
Рассмотрим систему из
первых двух уравнений.
Х1
1
0
Х2
1
1
0
Х3
1 1
1
0
Х4
1 1
1
1
0
Получили 5 решений.
Y1
1
0
Y2
1
1
0
Y3
1 1
1
0
Y4
1 1
1
1
0
Получили 5 решений.
Т.к. переменные независимы, то всего решений: 5*5=25
Выясним, какие из этих решений не подходят для третьего уравнения.
X1 Y1 = 0
4 решения
X2 Y2 = 0
1
3 решения
0 0 0 0
0 0 0
1
0 0 0
1
0 0 0
1
0 0 0 0
1
1 0 0
1
1 0 0
1
1 0 0 0
1
1 1 0
1
1 1 0
1
1 1 0 0
1
1 1 1 0
Всего 6 решений. Однако, решения
из первой таблицы уже учтены в
первом уравнении и их повторно
считать не надо. Ответ: 3 решения.

22. №11_d. Сколько различных решений имеет система уравнений:

(x1 x2) (x2 x3) (x3 x4) = 1
( у1 у2) ( у2 у3) ( у3 у4)=1
(x1 y1) (x2 y2) (x3 y3) (x4 y4)=1
Рассмотрим систему из
первых двух уравнений.
Х1
1
0
Х2
1
1
0
Х3
1 1
1
0
Х4
1 1
1
1
0
Получили 5 решений.
Y1
1
0
Y2
1
1
0
Y3
1 1
1
0
Y4
1 1
1
1
0
Получили 5 решений.
Т.к. переменные независимы, то всего решений: 5*5=25
Выясним, какие из этих решений не подходят для третьего уравнения.
X1 Y1 = 0
X2 Y2 = 0
4 решения
3 решения
1
0 0 0 0
0
0 0 0
1
1 0 0 0
1
0 0 0
1
1 1 0 0
1
1 0 0
1
1 1 1 0
1
1 1 0
X3 Y3 = 0
1
2 0решения
0 0
0 0
0
0 0
1
0 0
1
0 0
0
0 0
1
0 0
1
0 0
1
0 0
1
1 0
1
1 0
1
1 0
Всего 6 решений. Однако, решения
из первой и второй таблиц уже
учтены в первом и втором
уравнениях и их повторно считать
не надо. Ответ: 2 решения.

23.

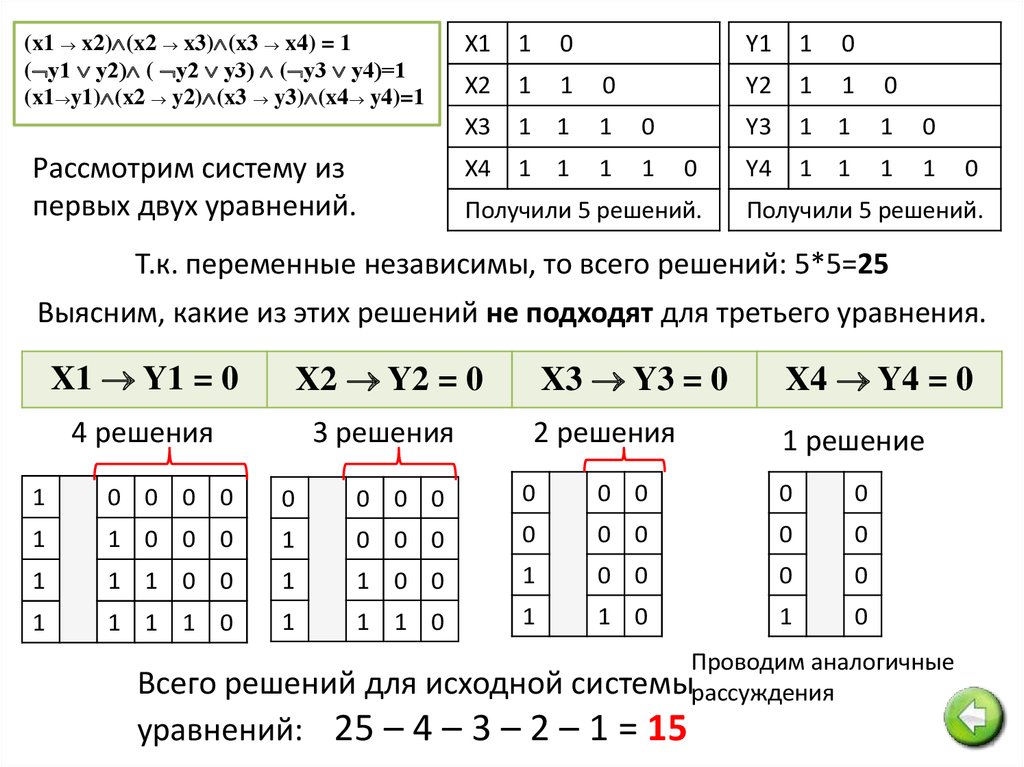
(x1 x2) (x2 x3) (x3 x4) = 1
( у1 у2) ( у2 у3) ( у3 у4)=1
(x1 y1) (x2 y2) (x3 y3) (x4 y4)=1
Рассмотрим систему из
первых двух уравнений.
Х1
1
0
Х2
1
1
0
Х3
1 1
1
0
Х4
1 1
1
1
0
Получили 5 решений.
Y1
1
0
Y2
1
1
0
Y3
1 1
1
0
Y4
1 1
1
1
0
Получили 5 решений.
Т.к. переменные независимы, то всего решений: 5*5=25
Выясним, какие из этих решений не подходят для третьего уравнения.
X1 Y1 = 0
X2 Y2 = 0
4 решения
3 решения
X3 Y3 = 0
X4 Y4 = 0
2 решения
1 решение
1
0 0 0 0
0
0 0 0
0
0 0
0
0
1
1 0 0 0
1
0 0 0
0
0 0
0
0
1
1 1 0 0
1
1 0 0
1
0 0
0
0
1
1 1 1 0
1
1 1 0
1
1 0
1
0
Проводим аналогичные
для исходной системырассуждения
Всего решений
уравнений: 25 – 4 – 3 – 2 – 1 = 15

24.

1. Поляков К.Ю., Системы логических
уравнений, Информатика, №14-2011
2. Путилов В.В, Системы логических уравнений,
http://www.it-n.ru
3. Демидова М.В., Решение задачи типа B10
КИМов ЕГЭ по информатике 2011 года
посредством построения дерева. ,
http://www.it-n.ru
4. Ройтберг М., Подготовка к ЕГЭ 2012.,
http://EGE-GO.RU