Логические операции компьютеров

1.

Что вы знаете
о логических основах компьютеров?

2. Логические операции

инверсия
конъюнкция
дизъюнкция
импликация
эквивалентность
исключающее или

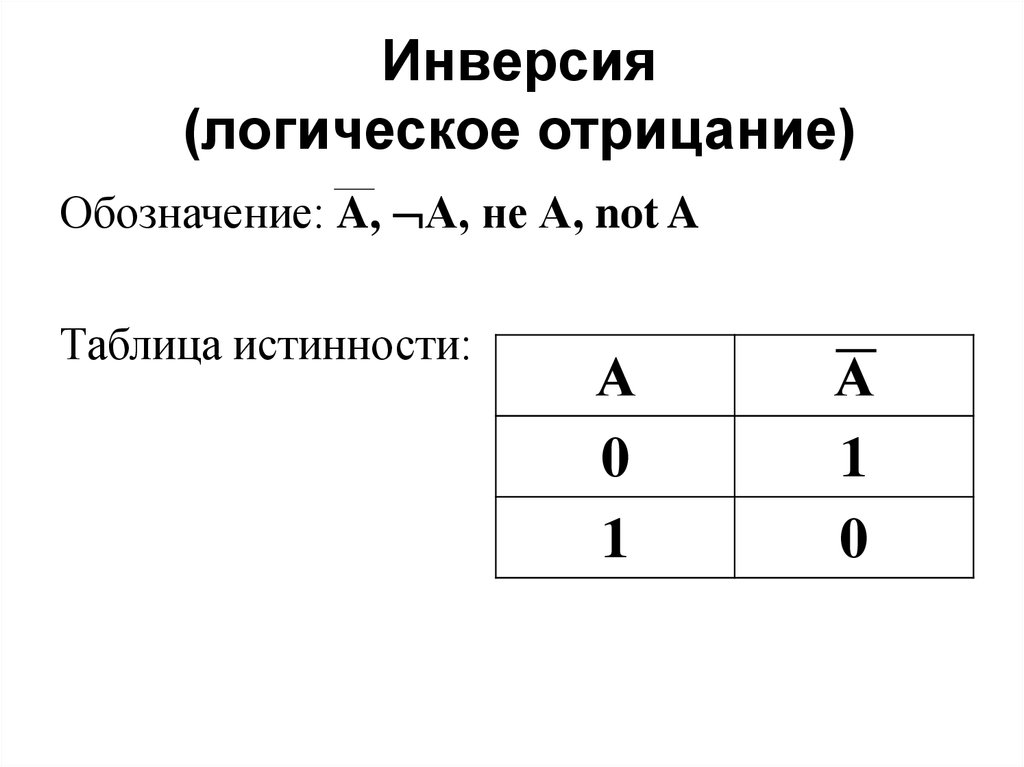
3. Инверсия (логическое отрицание)

Обозначение: A, А, не А, not A
Таблица истинности:
А
0
1
А
1
0

4. Конъюнкция (логическое умножение)

Обозначение: A&B, A B, А В, А и В, А and В
Таблица истинности:
А
0
0
1
1
B
0
1
0
1
A&B
0
0
0
1

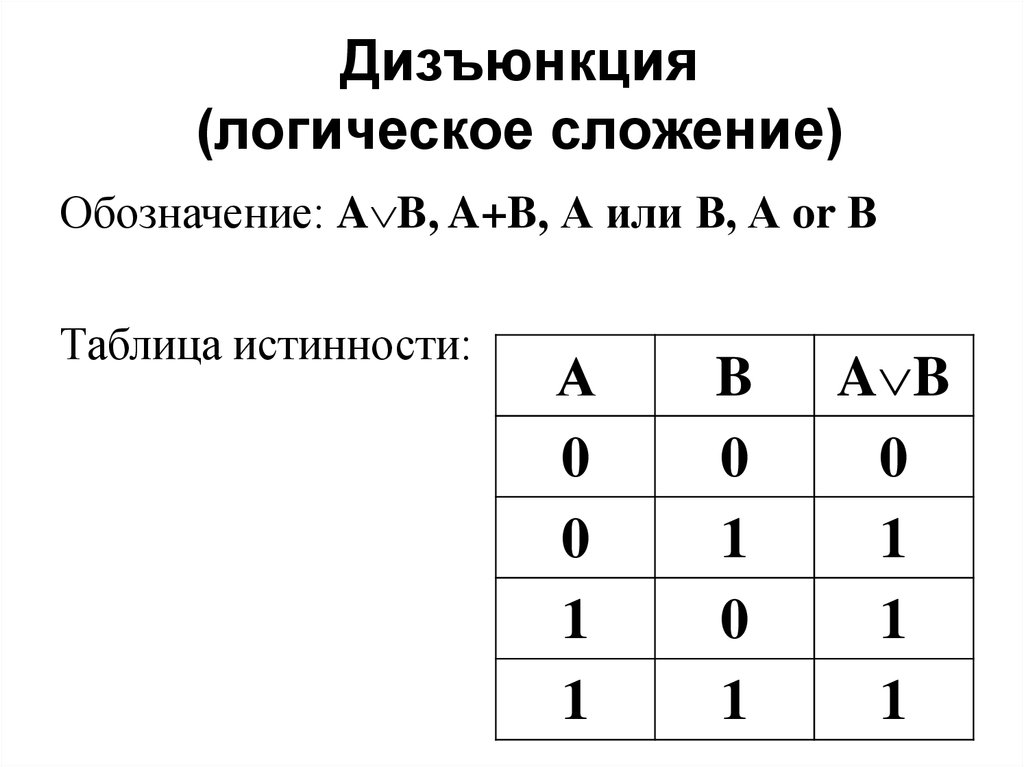
5. Дизъюнкция (логическое сложение)

Обозначение: A B, A+B, А или В, А or В
Таблица истинности:
А
0
0
1
1
B
0
1
0
1
A B
0
1
1
1

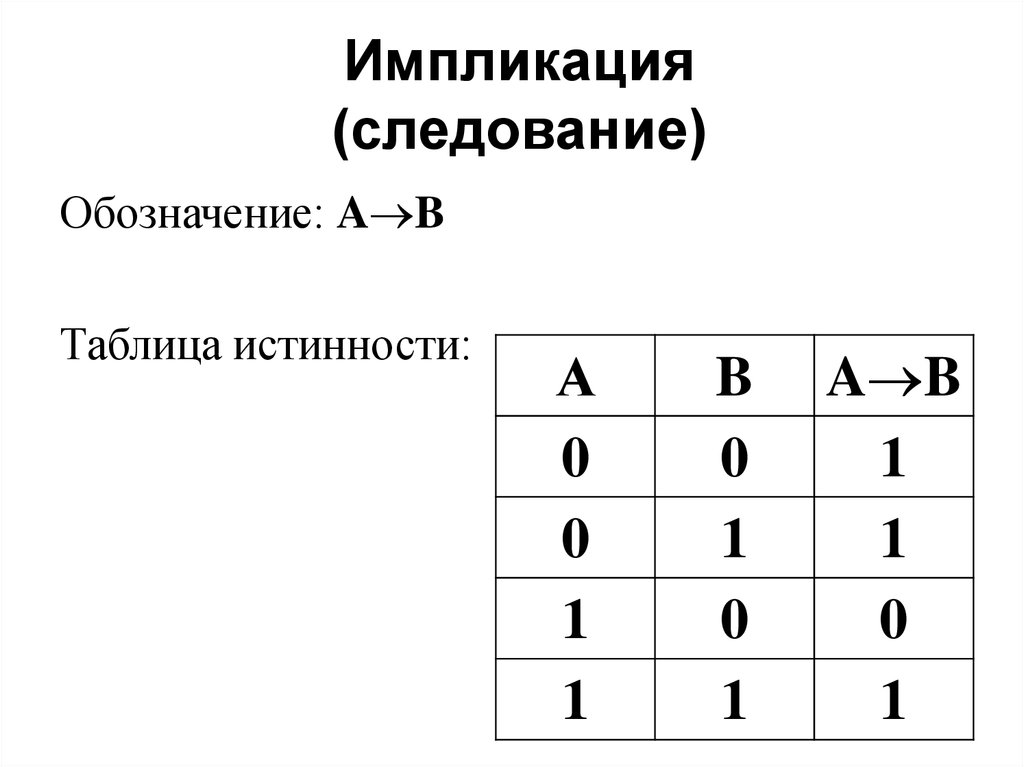
6. Импликация (следование)

Обозначение: A B
Таблица истинности:
А
0
0
1
1
B
0
1
0
1
A B
1
1
0
1

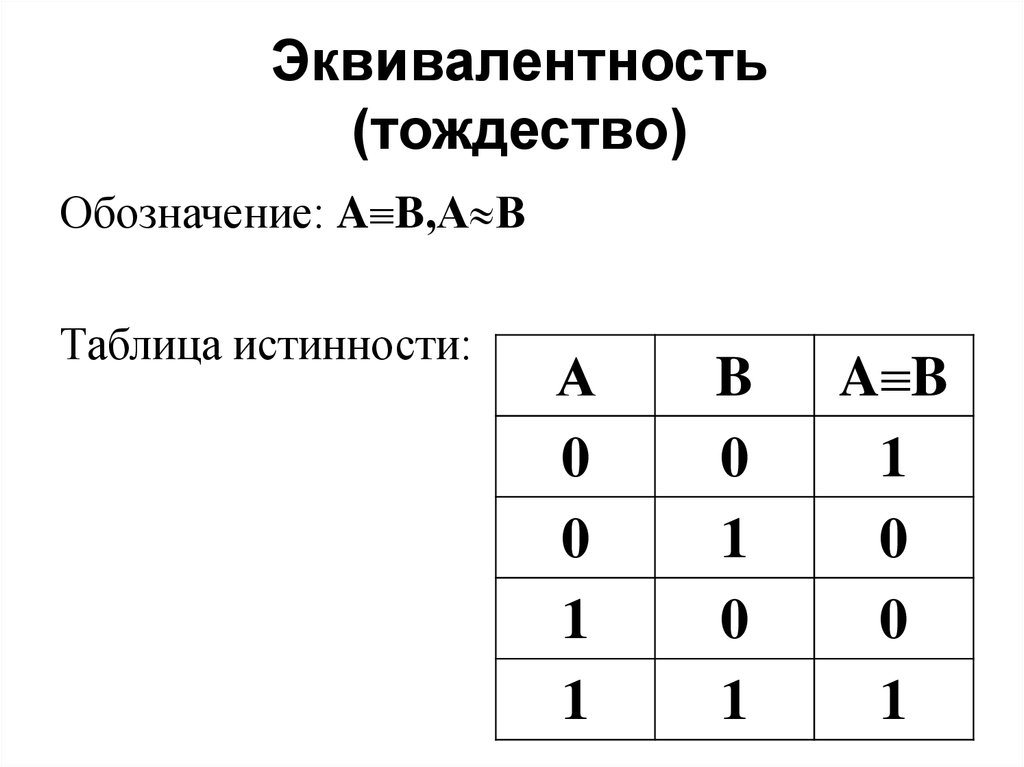
7. Эквивалентность (тождество)

Обозначение: A B,А В
Таблица истинности:
А
0
0
1
1
B
0
1
0
1
A B
1
0
0
1

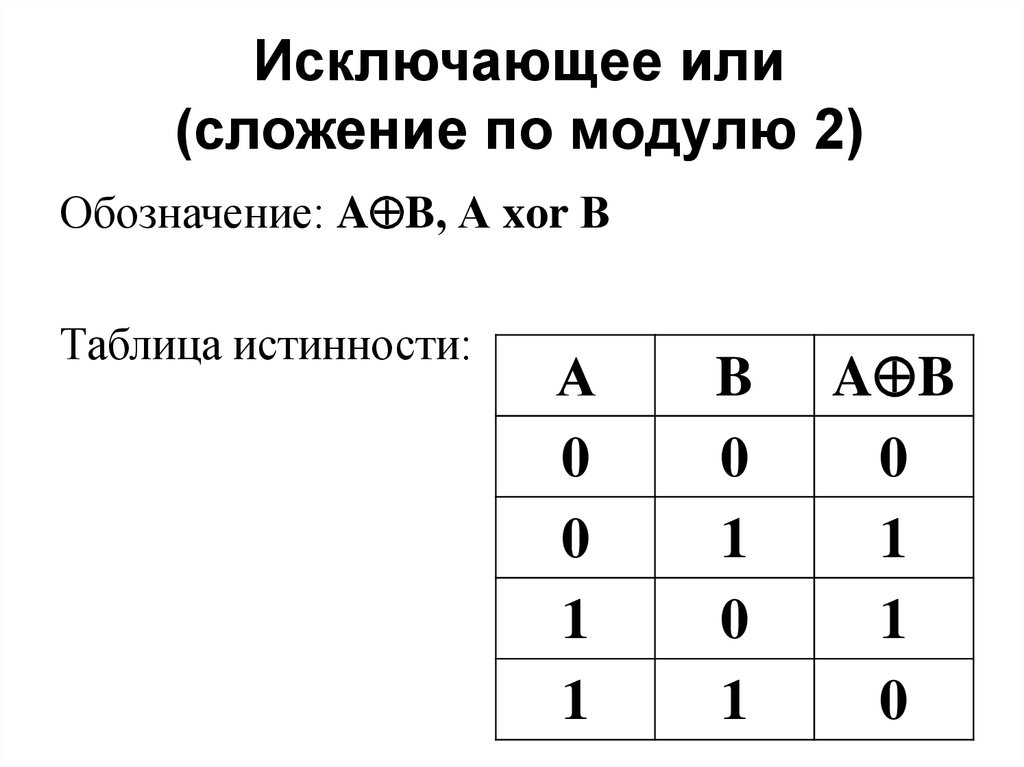
8. Исключающее или (сложение по модулю 2)

Обозначение: A B, А xor В
Таблица истинности:
А
0
0
1
1
B
0
1
0
1
A B
0
1
1
0

9. Приоритет логических операций

1)
2)
3)
4)
5)
6)
инверсия
конъюнкция
дизъюнкция
импликация
эквивалентность
исключающее или

10. Алгоритм составления таблиц истинности

1. Посчитать количество переменных (n) в логическом выражении.
2. Определить число строк в таблице, которое равно m=2n .
3. Посчитать количество логических операций и определить
количество столбцов в таблице, которое равно: количество
переменных + количество операций.
4. Ввести название столбцов в таблицу в соответствие
с последовательностью выполнения логических операций с учетом
скобок и приоритетов.
5. Заполнить столбцы входных переменных наборами значений.
6. Провести заполнение таблицы истинности по столбцам, выполняя
логические операции.

11. Выполните задание

Сколько различных решений имеет система уравнений
(X1 X2) (X2 X3) = 1
(X2 X3) (X3 X4) = 1
...
(X5 X6) (X6 X7) = 1
где x1, x2, …, x7 – логические переменные?
В ответе не нужно перечислять все различные наборы значений
переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.

12.

13. Решение системы логических уравнений

Метод отображений
Е.В.Хламов, Е.А.Мирончик

14. Выполните задание

Сколько различных решений имеет система уравнений
(X1 X2) (X2 X3) = 1
(X2 X3) (X3 X4) = 1
...
(X5 X6) (X6 X7) = 1
где x1, x2, …, x7 – логические переменные?
В ответе не нужно перечислять все различные наборы значений
переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.

15. Алгоритм решения

1. Составить таблицу истинности к первому уравнению системы в
строгом порядке следования переменных
(X1 X2) (X2 X3) = 1
X1
X2
X3
1
2
3
0
0
0
1
1
1
0
0
1
1
0
0
0
1
0
0
0
1
0
1
1
0
1
1
1
0
0
0
1
1
1
0
1
0
0
1
1
1
0
1
0
0
1
1
1
1
1
1

16. Алгоритм решения

2. Выписать такие наборы переменных, которые приводят в
результате к получению «1».
(X1 X2) (X2 X3) = 1
X1
X2
X3
1
2
3
0
0
0
1
1
1
0
0
1
1
0
0
0
1
0
0
0
1
0
1
1
0
1
1
1
0
0
0
1
1
1
0
1
0
0
1
1
1
0
1
0
0
1
1
1
1
1
1

17. Алгоритм решения

2. Выписать такие наборы переменных, которые приводят в
результате к получению «1».
(X1 X2) (X2 X3) = 1
X1
X2
X3
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1

18. Алгоритм решения

2. Дописать вверху таблицы переменные второго уравнения,
стоящие на соответствующих местах
(X1 X2) (X2 X3) = 1
(X2 X3) (X3 X4) = 1
X2
X3
X4
X1
X2
X3
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1

19. Алгоритм решения

2. Выделить в таблице значения переменных, которые встречаются
в обоих уравнениях
(X1 X2) (X2 X3) = 1
(X2 X3) (X3 X4) = 1
X2
X3
X4
X1
X2
X3
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1

20. Алгоритм решения

3. Определить количество одинаковых переменных,
встречающихся в обоих уравнениях. В данных уравнениях
их 2 (X2, X3).
(X1 X2) (X2 X3) = 1
(X2 X3) (X3 X4) = 1
X2
X3
X4
X1
X2
X3
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1

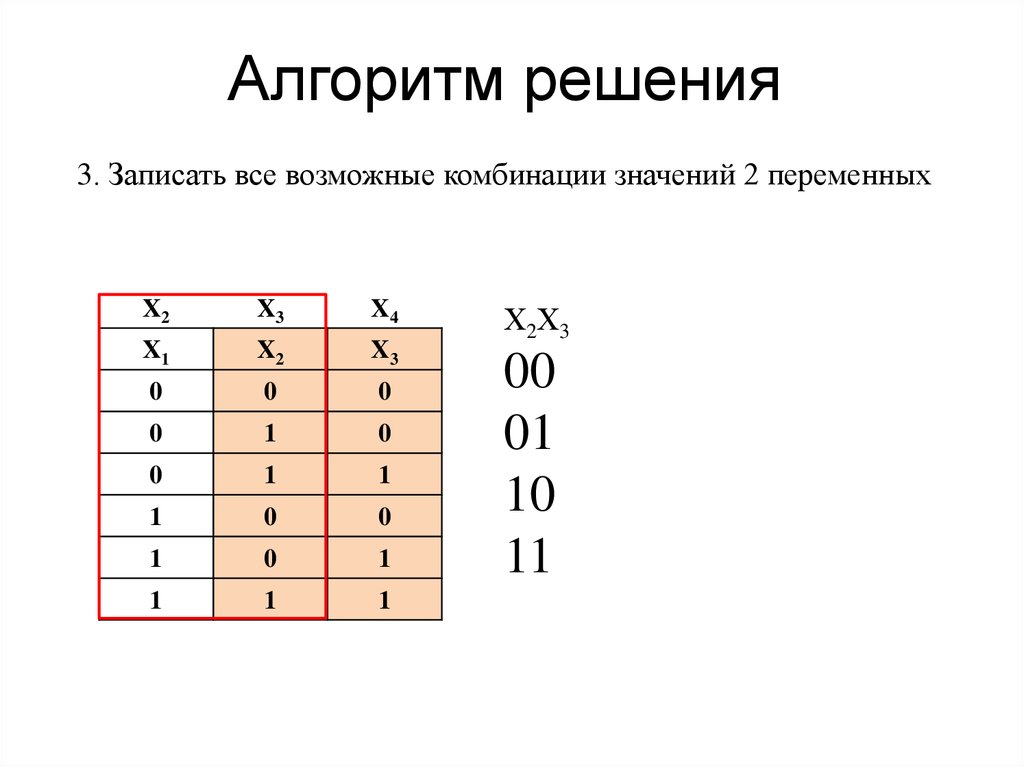
21. Алгоритм решения

3. Записать все возможные комбинации значений 2 переменных
X2
X3
X4
X1
X2
X3
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
Х2Х3
00
01
10
11

22. Алгоритм решения

3. Выписать из таблицы все комбинации второго уравнения (в
красной рамке), соответствующие строкам таблицы первого
уравнения (оранжевое). Количество выписанных комбинаций
должно совпадать с количеством строк таблицы (6 строк).
X2
X3
X4
X1
X2
X3
Х2Х3 Х2Х3
0
0
0
0
1
0
0
1
1
1
0
0
1
0
1
1
1
1
00=00+10
01=10
10=01
11=01+11

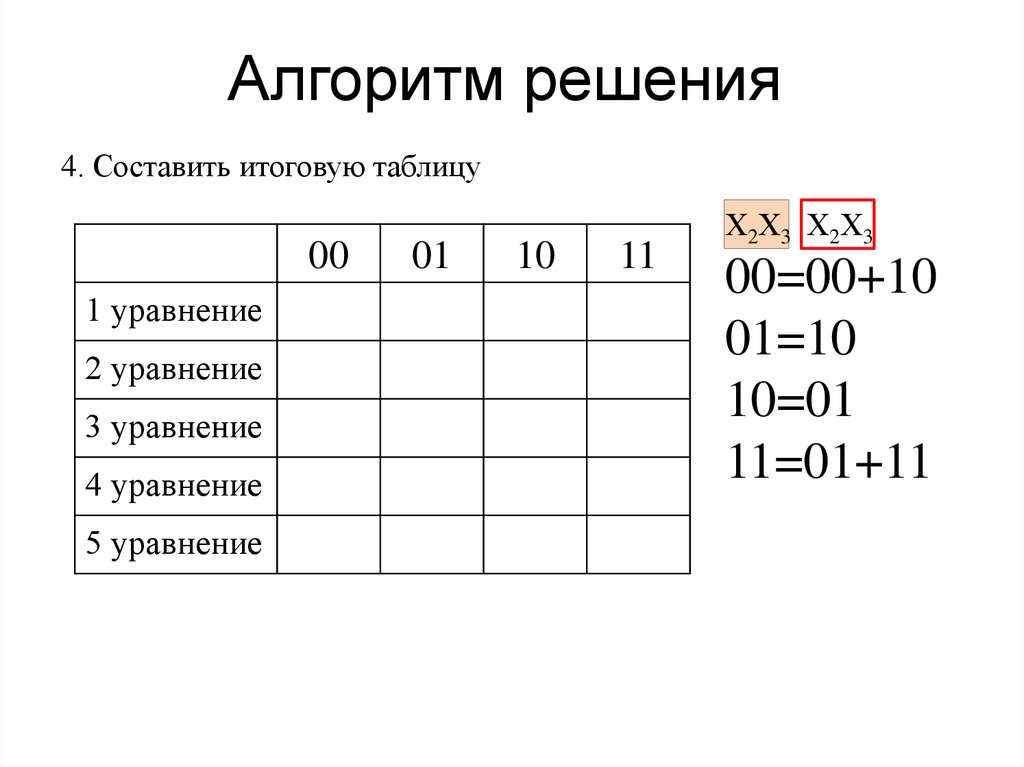
23. Алгоритм решения

4. Составить итоговую таблицу
00
1 уравнение
2 уравнение
3 уравнение
4 уравнение
5 уравнение
01
10
11
Х2Х3 Х2Х3
00=00+10
01=10
10=01
11=01+11

24. Алгоритм решения

4. Заполнить первую строку итоговой таблицы соответственно
количеству полученных комбинаций в первом уравнении
1 уравнение
2 уравнение
3 уравнение
4 уравнение
5 уравнение
00
2
01
1
10
1
11
2
Х2Х3 Х2Х3
00=00+10 (2)
01=10
(1)
10=01
(1)
11=01+11 (2)

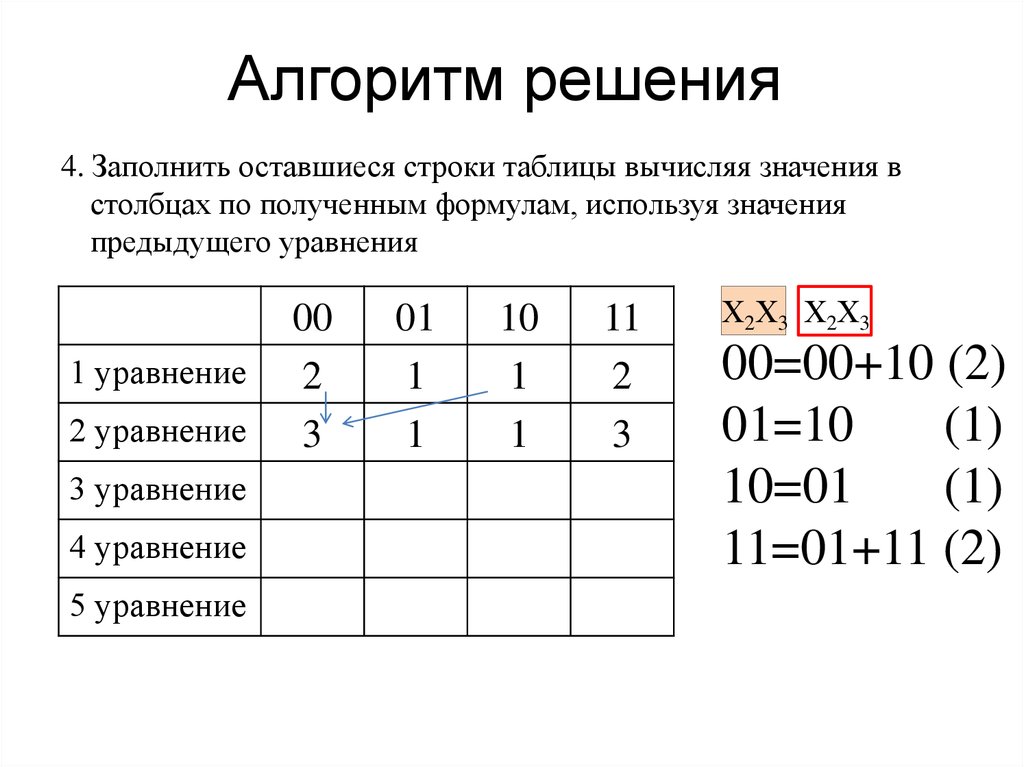
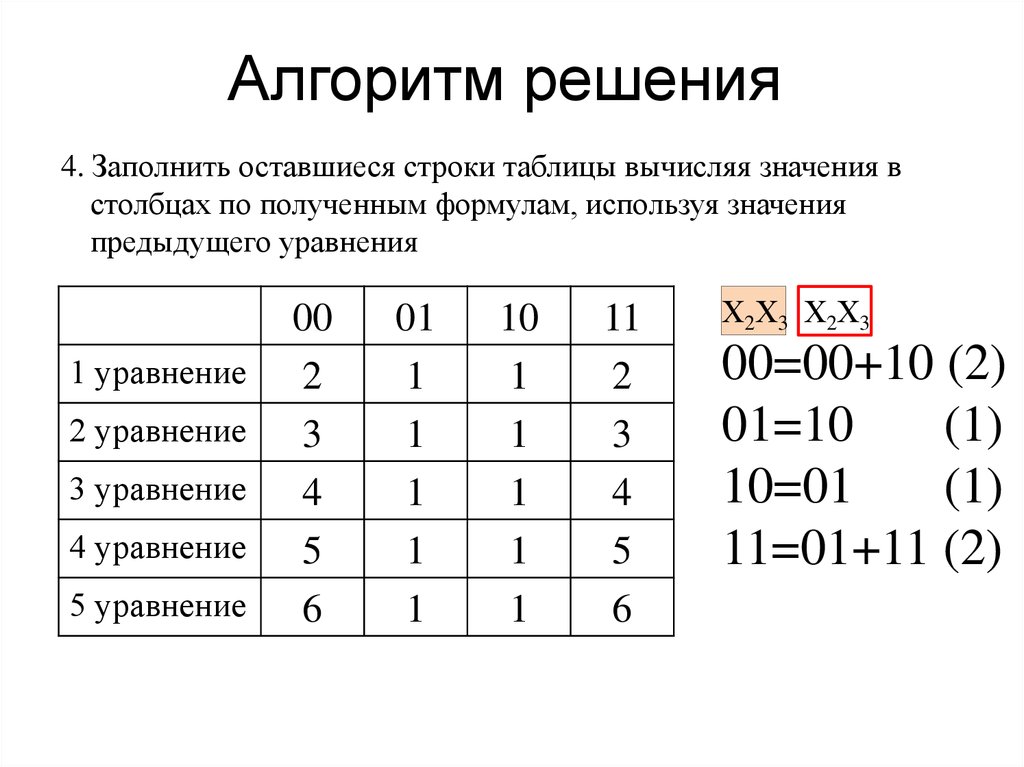
25. Алгоритм решения

4. Заполнить оставшиеся строки таблицы вычисляя значения в
столбцах по полученным формулам, используя значения
предыдущего уравнения
1 уравнение
2 уравнение
3 уравнение
4 уравнение
5 уравнение
00
2
3
01
1
1
10
1
1
11
2
3
Х2Х3 Х2Х3
00=00+10 (2)
01=10
(1)
10=01
(1)
11=01+11 (2)

26. Алгоритм решения

4. Заполнить оставшиеся строки таблицы вычисляя значения в
столбцах по полученным формулам, используя значения
предыдущего уравнения
1 уравнение
2 уравнение
3 уравнение
4 уравнение
5 уравнение
00
2
3
4
5
6
01
1
1
1
1
1
10
1
1
1
1
1
11
2
3
4
5
6
Х2Х3 Х2Х3
00=00+10 (2)
01=10
(1)
10=01
(1)
11=01+11 (2)

27. Алгоритм решения

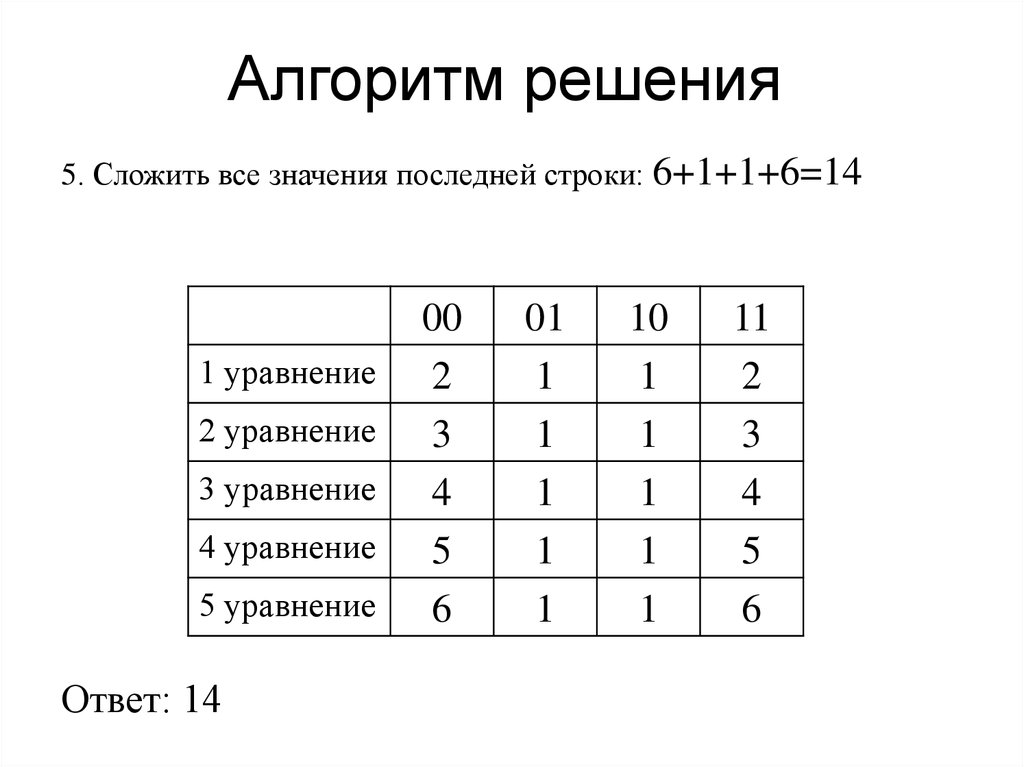
5. Сложить все значения последней строки: 6+1+1+6=14
1 уравнение
2 уравнение
3 уравнение
4 уравнение
5 уравнение
Ответ: 14
00
2
3
4
5
6
01
1
1
1
1
1
10
1
1
1
1
1
11
2
3
4
5
6

28. Задание для самостоятельного решения

Сколько различных решений имеет система уравнений
(x1 x2) ( x1 x3) = 0
(x2 x3) ( x2 x4) = 0
...
(x7 x8) ( x7 x9) = 0
где x1, x2, …, x9 – логические переменные?
В ответе не нужно перечислять все различные наборы значений
переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.

29. Эталон решения

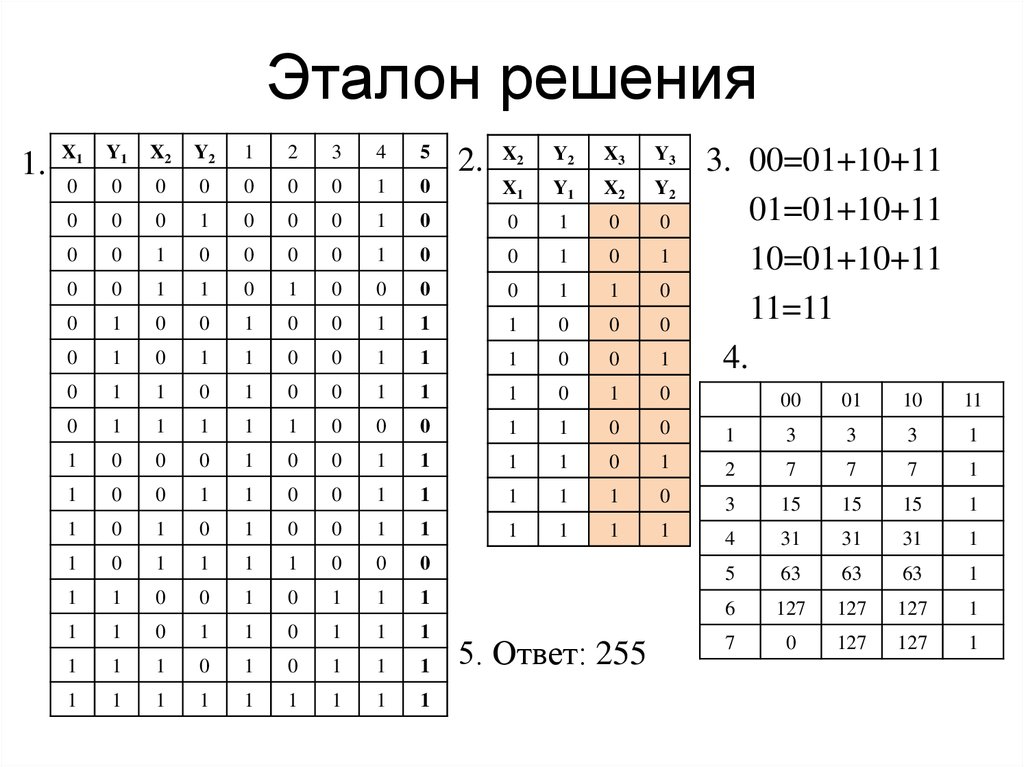
1.
X1
X2
X3
1
2
3
4
5
X2
X3
X4
0
0
0
1
0
1
0
0
X1
X2
X3
0
0
1
1
0
1
1
0
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
1
1
0
1
1
1
1
0
1
0
1
0
0
1
1
0
1
1
1
0
1
1
0
1
1
1
0
0
0
1
1
0
1
1
0
0
0
0
1
0
1
1
1
1
1
1
0
0
0
0
0
3. 00=00
01=00+10
10=01+11
11=11
4.
2.
00
01
10
11
1
1
2
2
1
2
1
3
3
1
3
1
4
4
1
4
1
5
5
1
5
1
6
6
1
6
1
7
7
1
7
1
8
8
1
5. Ответ: 18

30. Задание для работы в парах

Сколько различных решений имеет система уравнений
(x1 x2 x3) (x1 y1)
(x2 x3 x4) (x2 y2)
(x3 x4 x5) (x3 y3)
(x4 x5 x6) (x4 y4)
(x5 x6 x7) (x5 y5)
x6 y6 = 1
=1
=1
=1
=1
=1
где x1, x2, …, x6, y1, y2, …, y6, – логические переменные?
В ответе не нужно перечислять все различные наборы значений
переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.

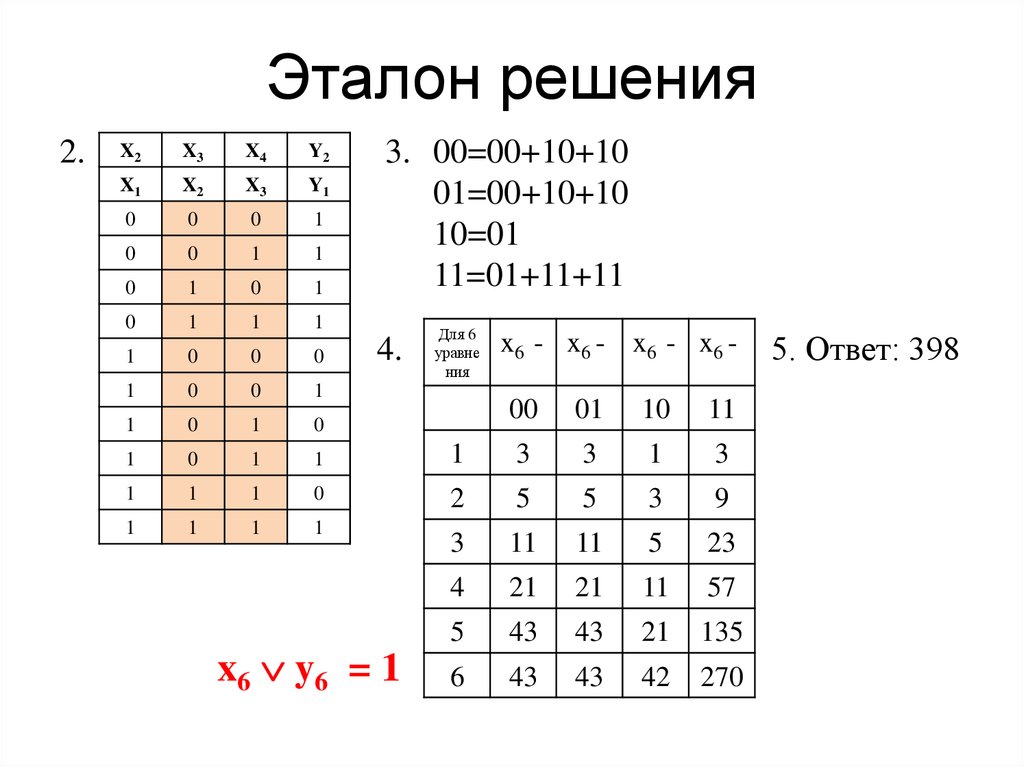
31. Эталон решения

2.
X2
X3
X4
Y2
X1
X2
X3
Y1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
1
1
0
1
1
1
1
3. 00=00+10+10
01=00+10+10
10=01
11=01+11+11
4.
x6 y6 = 1
Для 6
уравне
ния
x6 - x6 - x6 - x 6 00
01
10
11
1
3
3
1
3
2
5
5
3
9
3
11
11
5
23
4
21
21
11
57
5
43
43
21
135
6
43
43
42
270
5. Ответ: 398

32. Задание для индивидуальной работы

Сколько различных решений имеет система уравнений
(x1 y1) ((x2 y2) (x1 y1)) = 1
(x2 y2) ((x3 y3) (x2 y2)) = 1
...
(x6 y6) ((x7 y7) (x6 y6)) = 1
x7 y7 = 1
где x1, x2, …, x6, y1, y2, …, y6, – логические переменные?
В ответе не нужно перечислять все различные наборы значений
переменных, при которых выполнено данное равенство.
В качестве ответа нужно указать количество таких наборов.

33. Эталон решения

1.
X1
Y1
X2
Y2
1
2
3
4
5
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
1
0
0
1
0
0
0
1
0
0
1
0
X2
Y2
X3
Y3
0
X1
Y1
X2
Y2
1
0
0
1
0
0
0
1
0
0
1
0
1
1
0
0
0
0
1
1
0
1
0
0
1
1
1
0
0
0
1
1
0
0
1
1
1
0
0
1
1
0
1
0
0
1
1
1
0
1
0
1
1
1
1
1
0
0
0
1
1
0
0
1
0
0
0
1
0
0
1
1
1
1
0
1
0
0
1
1
0
0
1
1
1
1
1
0
1
0
1
0
0
1
1
1
1
1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
1
1
1
1
0
1
1
0
1
1
1
1
1
1
0
1
0
1
1
1
1
1
1
1
1
1
1
1
1
2.
3. 00=01+10+11
01=01+10+11
10=01+10+11
11=11
4.
00
01
10
11
1
3
3
3
1
1
2
7
7
7
1
1
0
3
15
15
15
1
1
1
4
31
31
31
1
5
63
63
63
1
6
127
127
127
1
7
0
127
127
1
5. Ответ: 255

34.

сегодня я узнал …
было трудно…
я понял, что…
я научился…
я смог…
меня удивило…