Логические основы компьютерной техники

1. Логические основы компьютерной техники

ЛОГИЧЕСКИЕ ОСНОВЫ
КОМПЬЮТЕРНОЙ ТЕХНИКИ
2016
Парамонов А.И.

2.

2

3. Основные понятия алгебры логики

3
АЛГЕБРА ЛОГИКИ – математический
аппарат, с помощью которого
записывают (кодируют), упрощают,
вычисляют и преобразовывают
логические высказывания.
Логическое высказывание – любое
утверждение, в отношении которого
можно сказать истинно оно или ложно.

4. Логическая (двоичная, булева) переменная

4
— это такая переменная, которая может
принимать одно из двух значений:
истина или ложь ( 1 (единица) или 0 (ноль),
да или нет).
Логические переменные выступают
аргументами логических функций.

5. Логическая константа

5
—
это
такая
постоянная
величина,
значением которой может быть истинно
или ложно (да или нет, единица или ноль).

6. Логическая функция

6
— это такая функция, которая может
принимать одно из двух значений:
истинно или ложно (да или нет, единица
или ноль) в зависимости от текущих
значений ее аргументов, в качестве
которых
используются
логические
переменные.

7.

7
Логическая (булева, переключательная)
функция f,
зависящая от n переменных x1,x2, … xn,
принимает значения только 0 или 1.
Булева функция – это функция,
аргументы и значение которой принадлежат
множеству {0, 1}.
f(x1,x2, …, xn)

8.

8
Логическая функция может быть одного (n = 1)
или нескольких (n > 1) аргументов.
Значение логической функции определяется
комбинацией
конкретных
значений
переменных, от которых она зависит.
Комбинация конкретных значений переменных
(аргументов функции) называется набором.
Количество различных наборов (N) для «n»
переменных вычисляется по формуле N = 2n.

9.

9
Булеву функцию от n переменных можно
рассматривать как n-местную алгебраическую
операцию на множестве B={0,1}.
При этом алгебра <B;Ω> , где Ω –
множество
всевозможных
булевых
функций, называется алгеброй логики (или,
булевой алгеброй).

10. Способы задания булевых функций

10
словесным описанием;
таблицей истинности;
логическим выражением.
Используется в случае
сравнительно несложной
логической функции

11. Таблица истинности

11
является универсальным средством задания
логической функции.
Включает все наборы для заданного количества
переменных,
определяющих
значение
логической функции, с указанием значений,
которые примет функция для каждого набора.
В одной таблице истинности может задаваться
несколько логических функций, зависящих от
одних и тех же переменных.

12.

12
Табличный способ предполагает, что в
левой части будут записаны все возможные
двоичные наборы длины n (комбинации
значений переменных x1,x2, … xn),
а в правой части будут представлены
значения функций на этих наборах.

13. Пример таблицы истинности трех переменных

13
№
х1
х2
х3
y1
0
0
0
0
1 Логические
0
0
1
2
0
1
0
функции,
3 Значения
0
1
1
заданные
на
4 функций
1
0
0
одинаковых
5
1
0
1
для каждого
переменных
6 набора
1
1
0
x11, x2,1 x3 1
7
0
1
1
0
1
0
0
1
Двоичные наборы
y2
y3
yn
…
удобно
1 представлять
1
0
набора»
1«номером
0
1
Логические
1(целое
1 десятичное0
переменные
1 Двоичные
0число)
–
0 наборы
1
0
0 логических
0
1
0 переменных
1
–
1
0
1

14.

14
Логическая функция называется «полностью
определенной», если для нее заданы значения
по всем возможным наборам.
Функция называется «частично определенной»,
если для некоторых наборов значения функции
не заданы.
Максимальное
количество
полностью
определенных функций от «n» переменных
определяется как M =(22)n

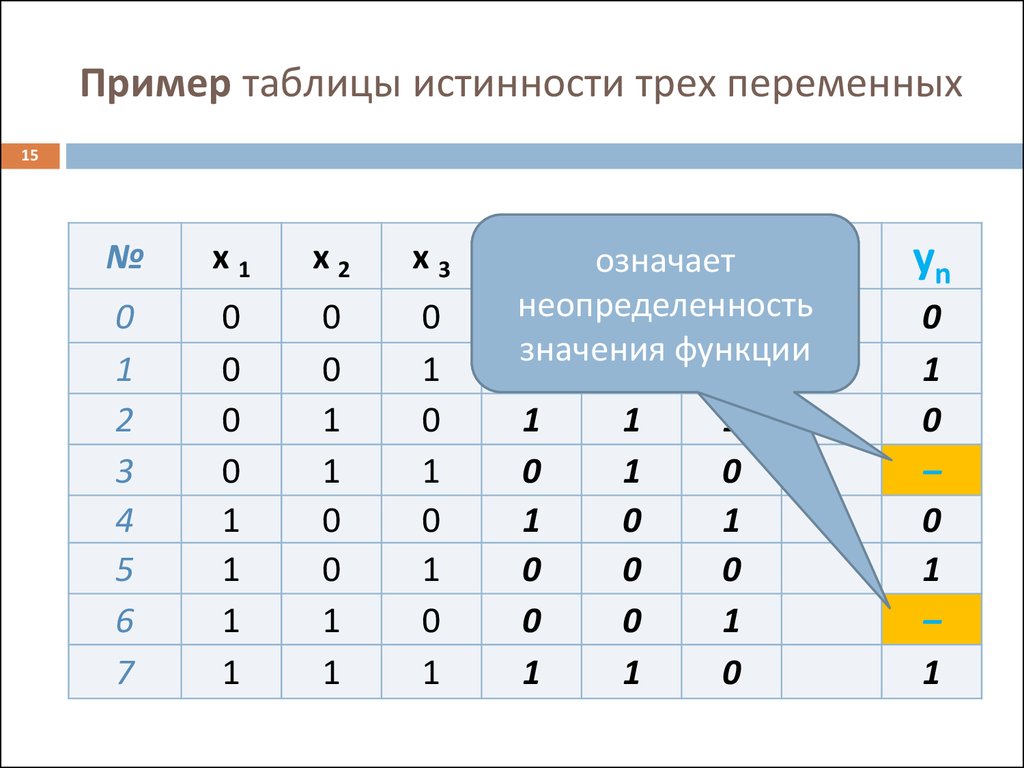
15. Пример таблицы истинности трех переменных

15
№
х1
х2
х3
0
1
2
3
4
5
6
7
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
y1
означает
y2 y3 …
неопределенность
0
1
1
значения функции
1
1
0
1
1
1
0
1
0
1
0
1
0
0
0
0
0
1
1
1
0
yn
0
1
0
–
0
1
–
1

16.

16
Булевы функции от большого числа
переменных таблицей истинности задавать
сложно (громоздко).
Например,
Для функции от 8 логических переменных
необходимо 28 = 256 двоичных наборов.
Для представления функций многих
переменных
удобно
использовать
модификацию таблицы истинности.

17.

17
x j, x j+1, … , x n
x1,x2, …, xj-1
00...0
00...1
...
11...1
00...0
0
1
...
1
00...1
1
0
...
0
...
...
...
...
11...1
1
0
1

18.

18
При аналитическом способе задания
булевой функции используется формула, т.е.
аналитическое выражение, построенное из
операций булевой алгебры.

19. Логическое выражение

19
– комбинация логических переменных и
констант,
связанных
элементарными
базовыми логическими функциями (или
логическими операциями), которые могут
разделяться скобками.

20.

20
Набор
элементарных
логических
операций, с помощью которых можно
задать любую, сколь угодно сложную
логическую
функцию,
называется
функционально
полной
системой
логических функций (ФПСЛФ).
Иногда такую систему называют
базисом.

21.

21
В качестве элементарных логических
функций функционально полных систем
этих функций используются функции
одной или двух логических переменных.

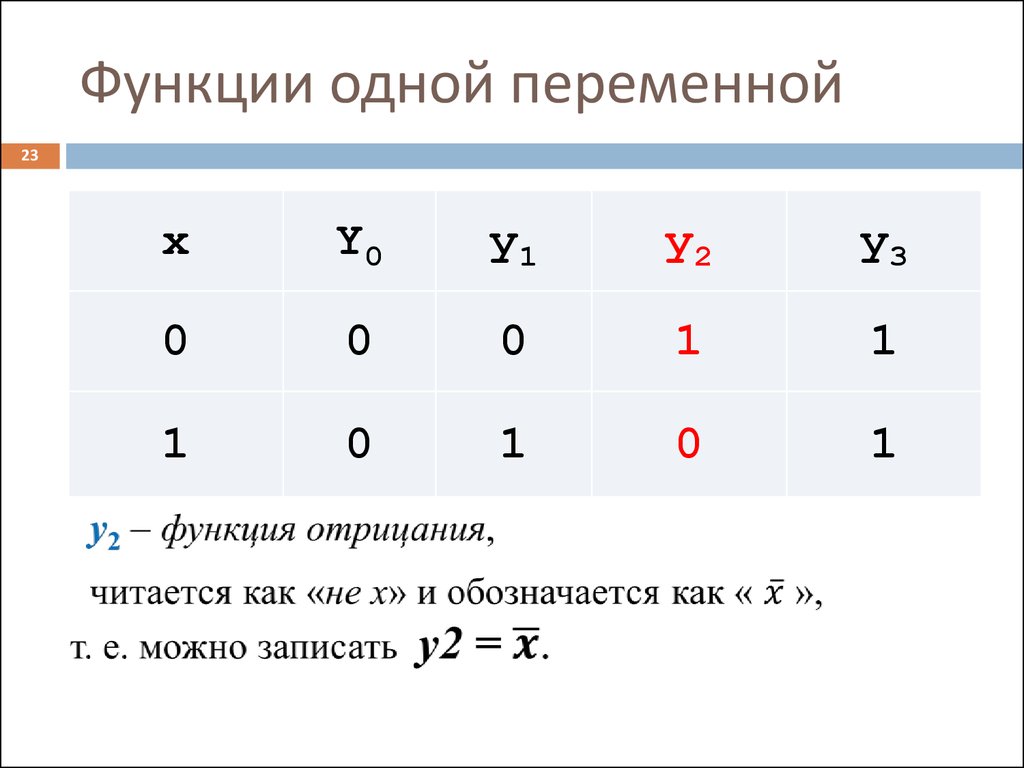
22. Функции одной переменной

22
x
Y0
y1
y2
y3
0
0
0
1
1
1
0
1
0
1
y0 = 0 – константа;
y1 равна значению переменной x;
y2 равна значению, обратному значению переменной х;
y3 = 1 – константа.

23. Функции одной переменной

23
x
Y0
y1
y2
y3
0
0
0
1
1
1
0
1
0
1

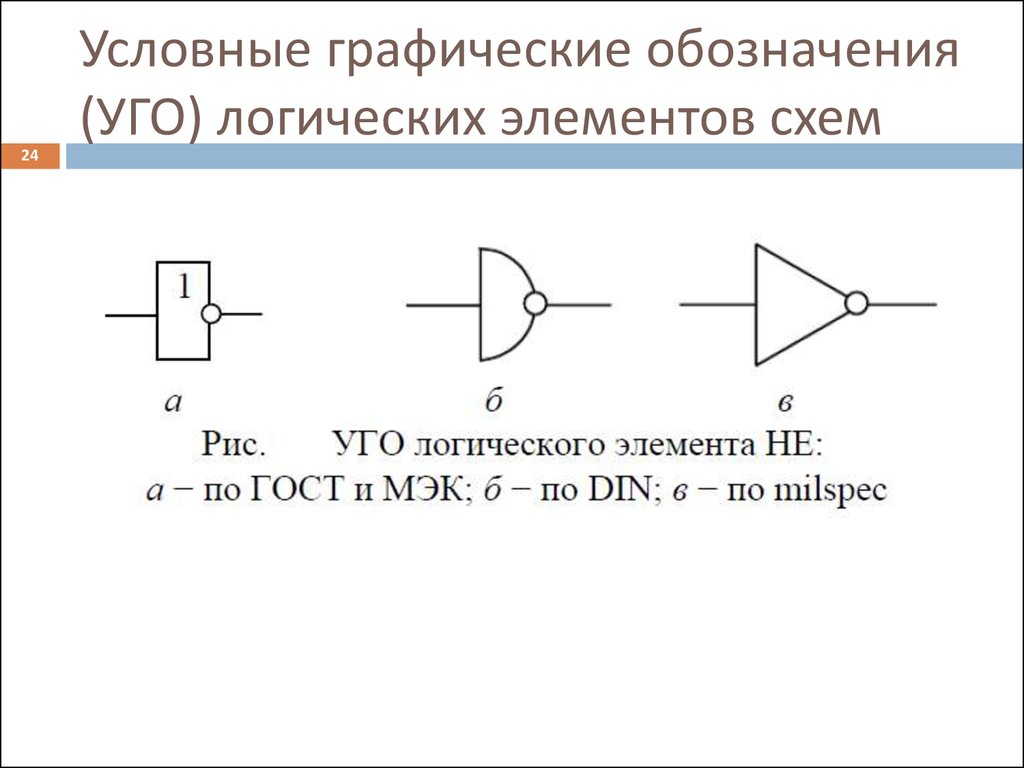
24. Условные графические обозначения (УГО) логических элементов схем

24
Условные графические обозначения
(УГО) логических элементов схем

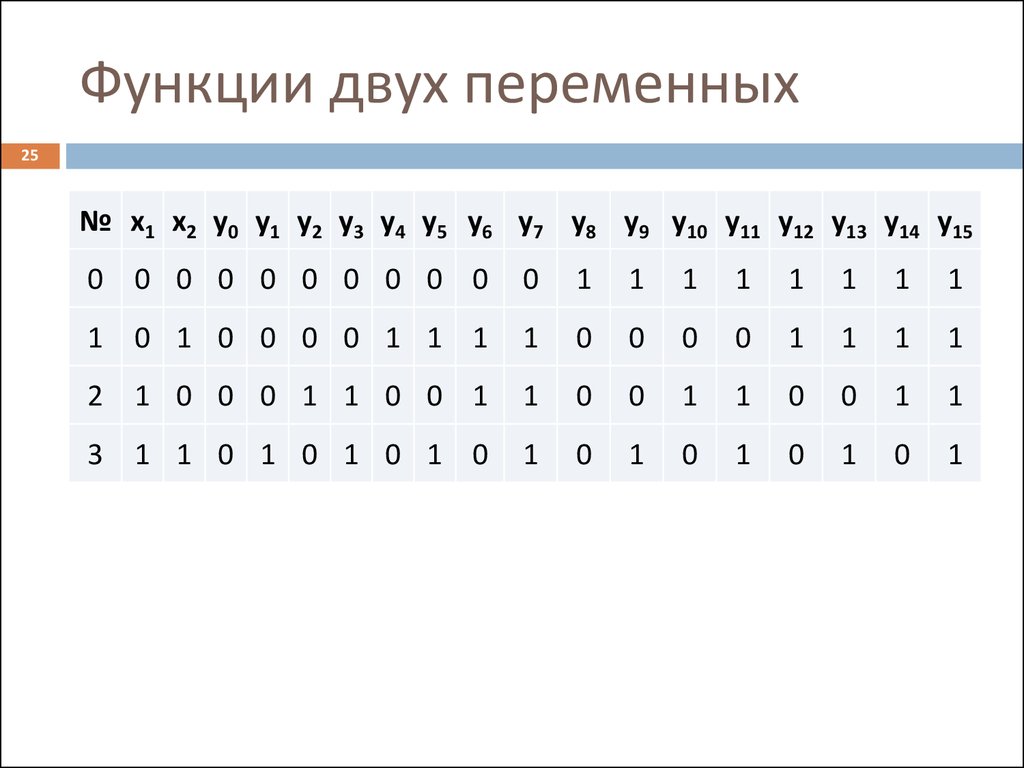
25. Функции двух переменных

25
№ х1 х2 y0 y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 y14 y15
0
0 0 0 0 0 0 0 0 0
0
1
1
1
1
1
1
1
1
1
0 1 0 0 0 0 1 1 1
1
0
0
0
0
1
1
1
1
2
1 0 0 0 1 1 0 0 1
1
0
0
1
1
0
0
1
1
3
1 1 0 1 0 1 0 1 0
1
0
1
0
1
0
1
0
1

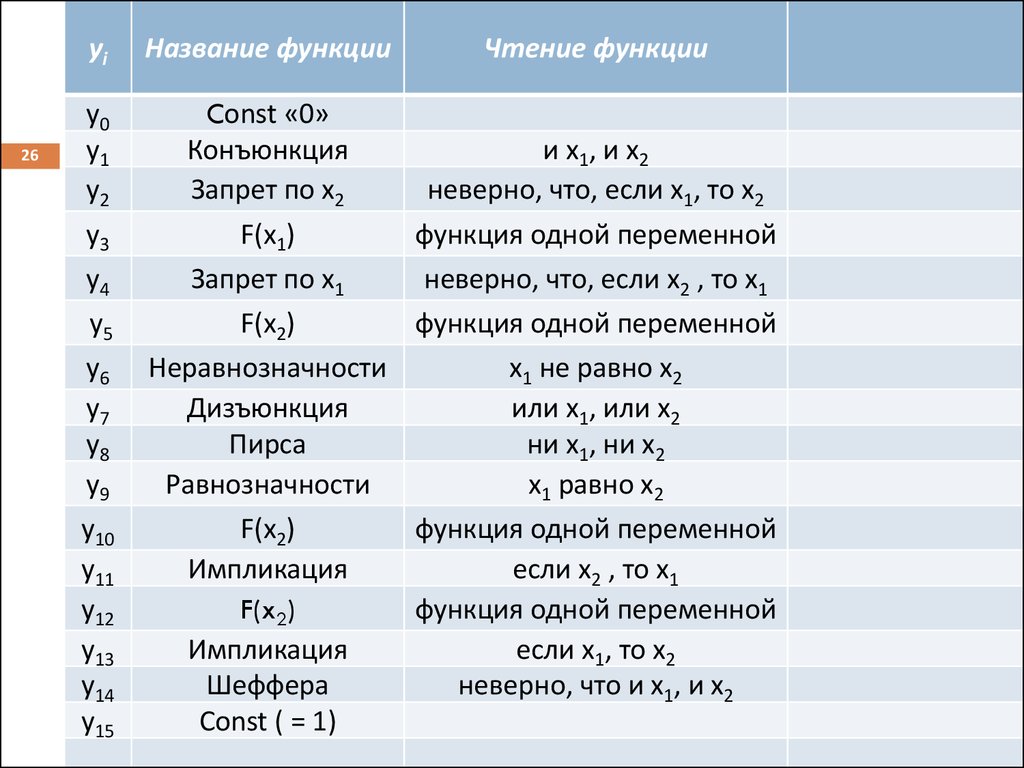
26.

26
yi
Название функции
Чтение функции
y0
y1
y2
y3
y4
y5
y6
y7
y8
y9
y10
y11
y12
y13
y14
y15
Const «0»
Конъюнкция
Запрет по х2
F(х1)
Запрет по х1
F(х2)
Неравнозначности
Дизъюнкция
Пирса
Равнозначности
F(х2)
Импликация
F(x2)
Импликация
Шеффера
Const ( = 1)
и х1, и х2
неверно, что, если х1, то х2
функция одной переменной
неверно, что, если х2 , то х1
функция одной переменной
х1 не равно х2
или х1, или х2
ни х1, ни х2
х1 равно х2
функция одной переменной
если х2 , то х1
функция одной переменной
если х1, то х2
неверно, что и х1, и х2

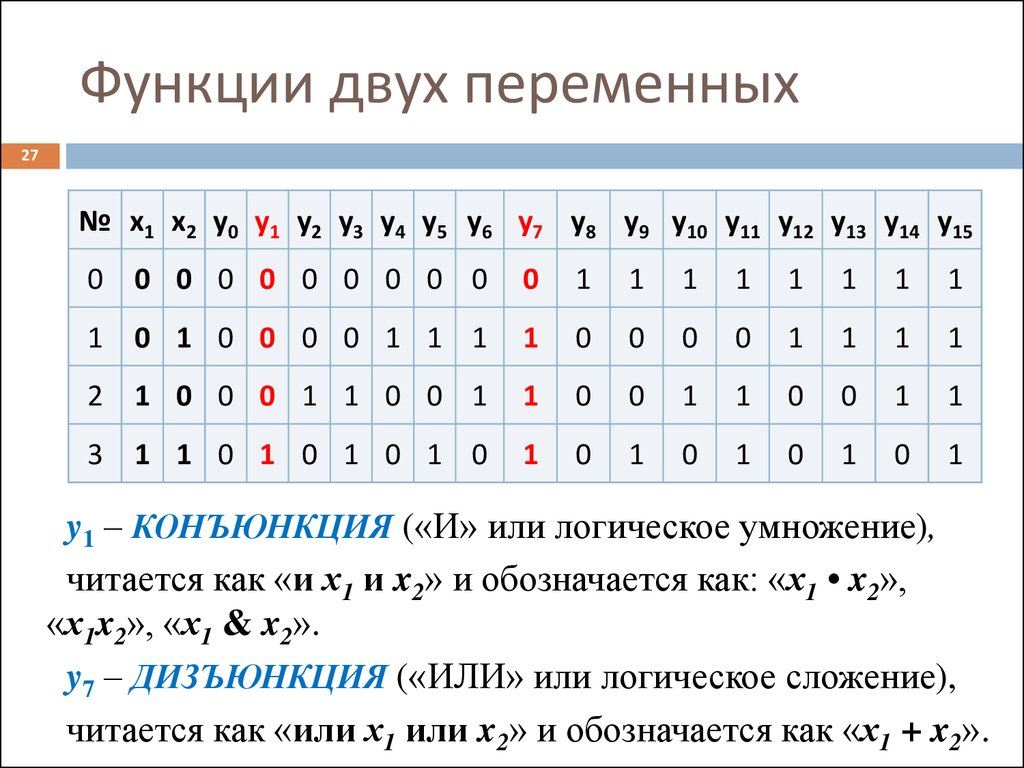
27. Функции двух переменных

27
№ х1 х2 y0 y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 y14 y15
0
0 0 0 0 0 0 0 0 0
0
1
1
1
1
1
1
1
1
1
0 1 0 0 0 0 1 1 1
1
0
0
0
0
1
1
1
1
2
1 0 0 0 1 1 0 0 1
1
0
0
1
1
0
0
1
1
3
1 1 0 1 0 1 0 1 0
1
0
1
0
1
0
1
0
1
y1 – КОНЪЮНКЦИЯ («И» или логическое умножение),
читается как «и х1 и x2» и обозначается как: «х1 • x2»,
«х1x2», «х1 & x2».
y7 – ДИЗЪЮНКЦИЯ («ИЛИ» или логическое сложение),
читается как «или х1 или x2» и обозначается как «х1 + x2».

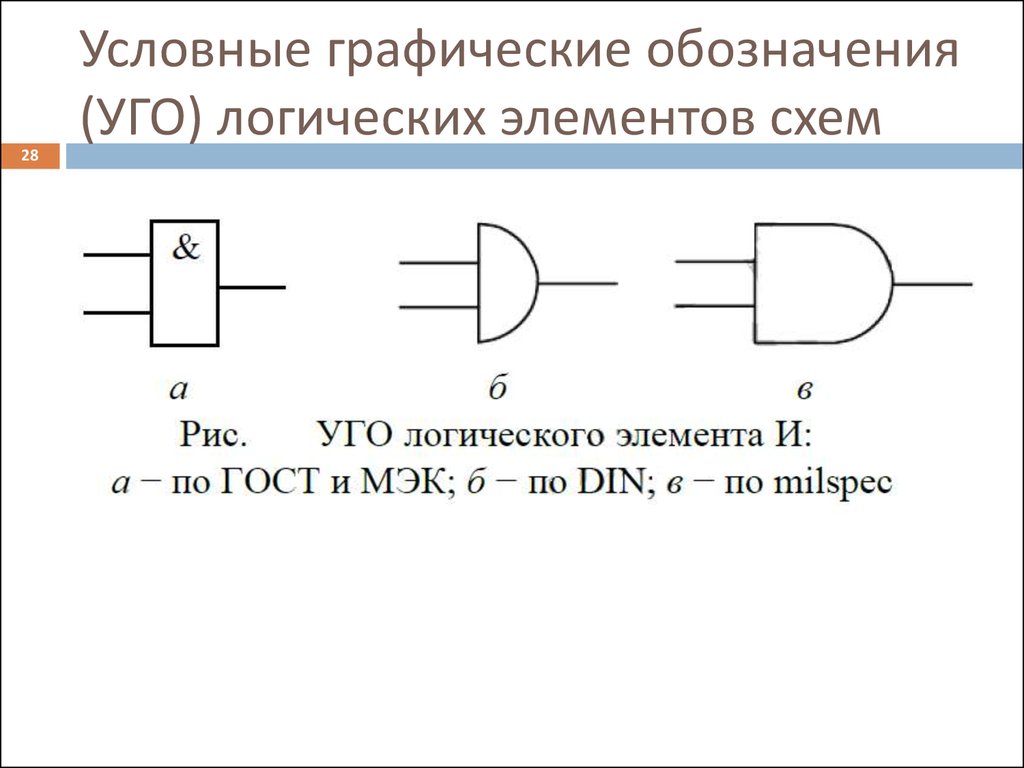
28. Условные графические обозначения (УГО) логических элементов схем

28
Условные графические обозначения
(УГО) логических элементов схем

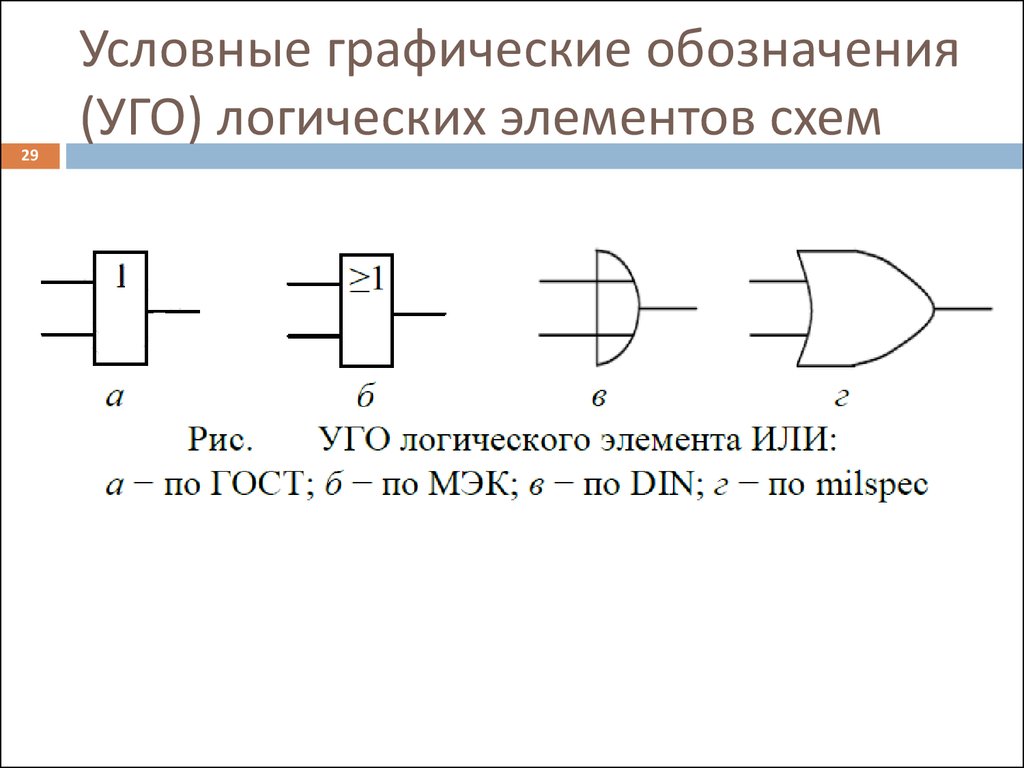
29. Условные графические обозначения (УГО) логических элементов схем

29
Условные графические обозначения
(УГО) логических элементов схем

30.

30
Наиболее распространенной в алгебре
логики является ФПСЛФ, которая в качестве
базовых логических функций использует
функцию одной переменной «НЕ» (функция
отрицания)
и
две
функции
двух
переменных: «И» (конъюнкция) и «ИЛИ»
(дизъюнкция).
Эта система получила название система
булевых функций, или булевый базис.

31.

31
Из всех функций от двух переменных
можно выделить еще так называемые
«Стрелка Пирса» и «Штрих Шеффера».
Они выступают как функционально полные
системы и могут записываться в следующем
виде:
у x x x x ,
8
1
2
1
2
y x x x x2
14
1 2
1
.

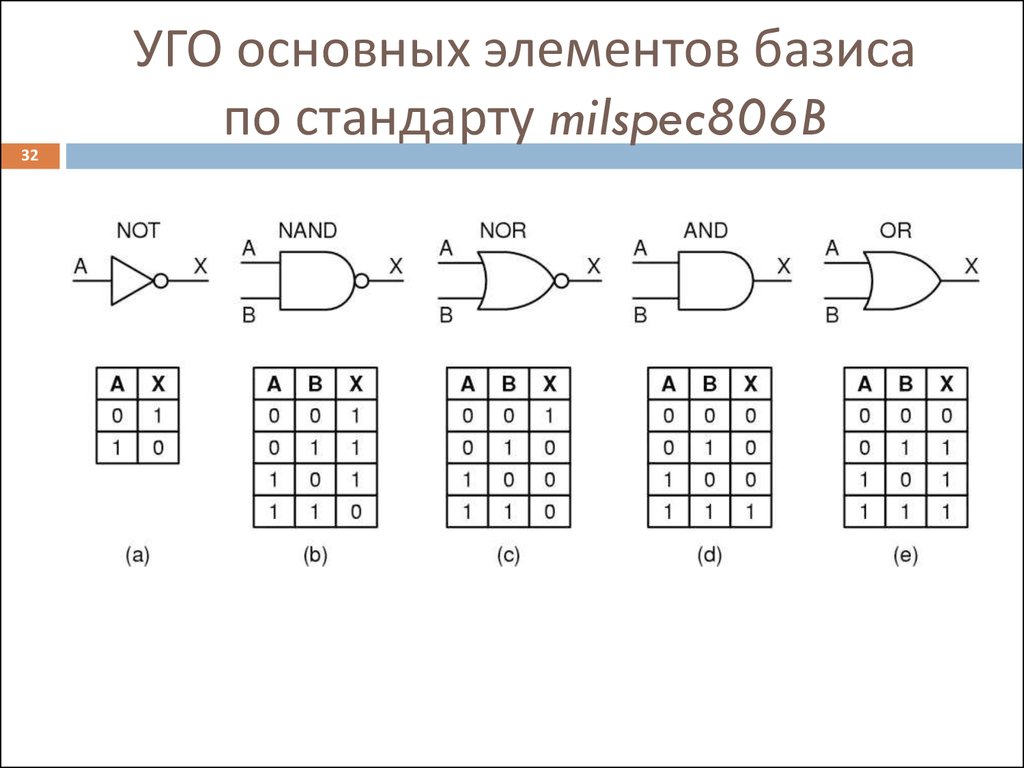
32. УГО основных элементов базиса по стандарту milspec806B

32
УГО основных элементов базиса
по стандарту milspec806B

33. Булева алгебра

33
В алгебре логики выделяют целый
раздел «алгебра Буля», посвященный
булевому базису.
В алгебре Буля логические выражения
включают логические операции И, ИЛИ, НЕ,
которые могут быть использованы в самых
различных сочетаниях.

34. Джордж Буль – создатель алгебры логики

34

35. Булева алгебра

35
При
оценке
значения
логического
выражения необходимо решить его для
конкретного набора переменных.
В алгебре Буля применяется следующая
приоритетность выполнения операций:
сначала рассчитываются значения
имеющих место отрицаний и скобок,
затем выполняется операция И;
самый низший приоритет у операции ИЛИ.

36. Законы булевой алгебры:

36
Переместительный (коммутативный)
Закон справедлив(ассоциативный)
и для конъюнкции и для
Сочетательный
дизъюнкции.
Распределительный (дистрибутивный)
х1 + х2 + х3 + х4 = х4 + х3 + х2 + х1
от перемены
мест
логических
слагаемыхде
сумма
не меняется.
Закон
инверсии
(Правило
Моргана)
х1 х2 х3 х4 = х4 х3 х2 х1
рефлексивности
отЗакон
перемены
мест логических сомножителей их
произведение не меняется.
Закон поглощения
Закон справедлив для любого количества
логических операндов.

37. Законы булевой алгебры:

37
Сочетательный (ассоциативный)
Закон справедлив и для конъюнкции и для
дизъюнкции.
х1 + х2 + х3 + х4 = (х2 + х3) + х1 + х4.= (х1 + х4 ) + (х2 + х3)
при логическом сложении отдельные слагаемые можно
заменить их суммой.
х 1 х 2 х 3 х 4 = ( х 2 х 3) х 1х 4 = ( х 1 х 4) ( х 2 х 3)
при логическом умножении отдельные логические
сомножители можно заменить их произведением.

38. Законы булевой алгебры:

38
Распределительный (дистрибутивный)
х 1 + х 2 х 3 = ( х 1 + х 2) ( х 1 + х 3)
дизъюнкция переменной и конъюнкции эквивалентна
конъюнкции дизъюнкций этой переменной с
сомножителями.
( х 1 + х 2) х 3 = х 1 х 3 + х 2 х 3
конъюнкция переменной и дизъюнкции равносильна
дизъюнкции конъюнкций этой переменной со
слагаемыми.

39. Законы булевой алгебры:

39
Закон инверсии (Правило де Моргана)
x x x x
1
2
1
2
отрицание суммы равно произведению отрицаний;
x x x x
1
2
1
2
отрицание произведения равно сумме отрицаний.
Правило де Моргана справедливо для любого числа
переменных:

40. Законы булевой алгебры:

40
Закон рефлексивности
Сочетательный (ассоциативный)
Распределительный (дистрибутивный)
Операции с одинаковыми операндами.
Закон инверсии (Правило де Моргана)
Правило повторения (идемпотентности):
х1 + х1 + х1 + х1 +
...
+ х1 = х1
х 1 х 1 х 1(коммутативный)
... х 1 = х 1
Переместительный
Закон поглощения
при любом числе повторений.

41. Законы булевой алгебры:

41
Закон поглощения
Доказательство:
х1 + (х1•х2) = (х1 •1) + (х1•х2) = х1 •(1 + х2) = х1•1 = х1
х1•(х1+х2) = (х1•х1) + (х1•х2) = х1 +(х1•х2) = х1

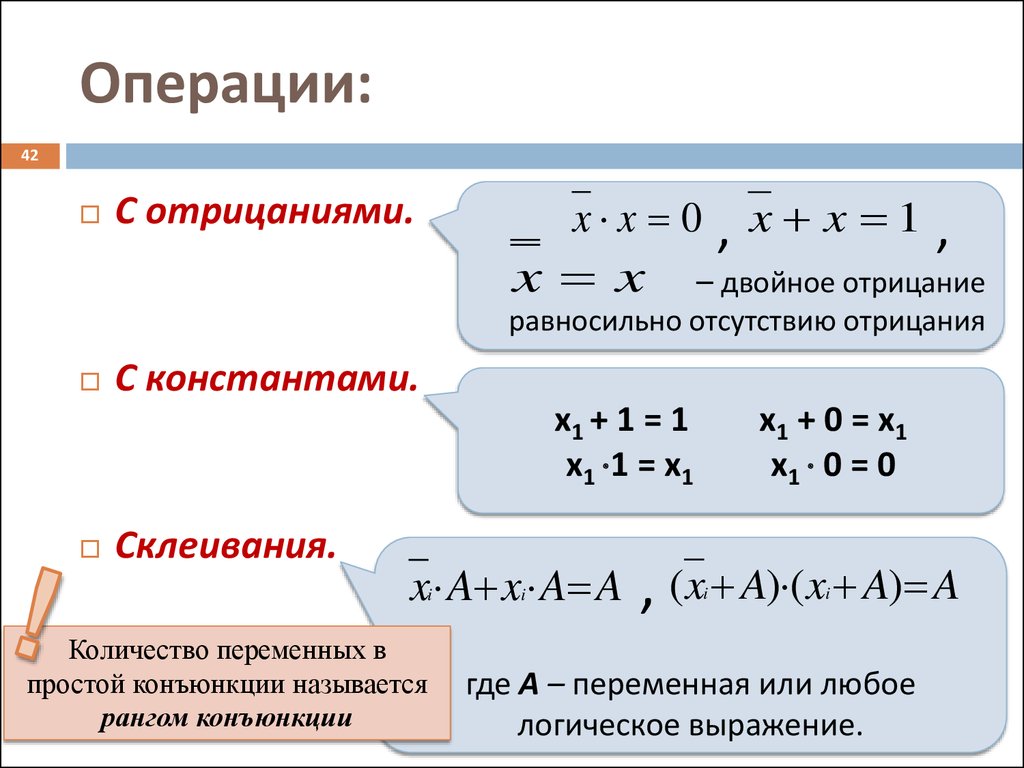
42. Операции:

42
x x 0
С отрицаниями.
x x
,
x x 1
,
– двойное отрицание
равносильно отсутствию отрицания
С константами.
х1 + 1 = 1
х1 1 = х1
Склеивания.
x A x A A
i
Количество переменных в
простой конъюнкции называется
рангом конъюнкции
i
х1 + 0 = х1
х1 0 = 0
, ( x A) (x A) A
i
i
где А – переменная или любое
логическое выражение.

43. Литература по теме:

43
Лысиков Б. Г. Арифметические и логические основы
цифровых автоматов // Минск: Высшая школа, 1980. –
268 с.
Савельев А. Я. Прикладная теория цифровых
автоматов: учебник для вузов по специальности ЭВМ //
М.: Высшая школа, 1987. – 462 с.
Шевелев Ю. П. Дискретная математика. Ч. 1: Теория
множеств. Булева алгебра Автоматизированная
технология обучения «Символ»): Учебное пособие //
Томск. гос. ун-т систем управления и
радиоэлектроники, 2003. — 118 с.