Компьютерная дискретная математика. Нормальные формы

1. Нормальные формы

Компьютерная дискретная математика
Нормальные формы
Лекция 6
Н.В. Белоус
Факультет компьютерных наук
Кафедра ПО ЭВМ, ХНУРЭ
ХНУРЭ, кафедра ПО ЭВМ, Тел. 7021-446, e-mail: [email protected]

2. Совершенная нормальная форма

Среди
множества
эквивалентных
формул, представляющих выбранную
булеву функцию f, выделяется одна
формула,
которая
называется
совершенной
нормальной
формой
функции f, имеет регламентированную
логическую структуру и однозначно
определяется по функции f .
2

3. Обозначения

x,σ B={0,1}
x , если 0
x
x , если 1
1, x
x
0 , x
x x x
3

4. Теорема о дизъюнктивном разложении функции f(x1,…,xn) по k переменным

Любую булеву функцию f(x1,x2,…,xn) можно
представить в следующей форме:
f(x1,…,xk,xk+1,…,xn)=
x1 x2 … xk f( 1, 2,…, k,xk+1,…,xn)
1
2
k
( 1, 2,…, k)
4

5. Теорема о дизъюнктивном разложении функции

Запись ( 1, 2,…, k )
означает
многократную
дизъюнкцию, которая берется по всем возможным
наборам значений ( 1, 2,…, k) при любом k (1≤k≤n).
f( 1, 2,…, k,xk+1,…,xn) представляет значение
функции на интерпретации x1,x2,…,xn, когда вместо
значений переменных x1,x2,…,xk, по которым
ведется
разложение,
подставлены
значения
1, 2,…, k.
5

6. Пример

Получить дизъюнктивное разложение функции
f ( x, y, z, t ) ( x y z) t по переменным x, z.
f ( x, y, z, t ) x 1 z 2 f ( 1 , y, 2 , t ) x z f (0, y,0, t )
x z f (0, y,1, t ) x z f (1, y,0, t ) x z f (1, y,1, t )
f ( 0 , y ,0 , t ) (0 y 0) t 0 ,
f ( 0 , y ,1 , t ) ( 0 y 1 ) t t ,
f ( 1 , y ,0 , t ) ( 1 y 0 ) t 0 ,
f ( 1 , y ,1 , t ) ( 1 y 1 ) t y t .
Подставим f(0,y,0,t), f(0,y,1,t), f(1,y,0,t), f(1,y,1,t) в
формулу дизъюнктивного разложения
f ( x , y, z ,t ) x z 0 x z t x z 0 x z ( y t )
x z t x z y t
6

7. Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по одной переменной

Любую булеву функцию f(x1,x2,…,xn) можно
представить в следующей форме:
f(x1, x2, …, xn)=
x
σi
i
f(x1, x2, …, xi-1, i, xi+1, …, xn)
i
7

8. Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по всем n переменным

Любую булеву функцию f(x1,x2,…,xn) 0 можно
представить в следующей форме:
f(x1,x2,…,xn) =
x1 x2 … xn
1
2
n
( 1, 2,…, n)
f( 1, 2,…, n) = 1
8

9. Пример

Получить дизъюнктивное разложение функции
f ( x , y , z ) xy z по всем переменным.
Определим значение функции на каждой из
интерпретаций:
f ( 0 ,0 ,0 ) 0 0 0 0 1 1
f ( 1 ,0 ,0 ) 1 0 0 0 1 1
f ( 0 ,0 ,1 ) 0 0 1 0 0 0
f ( 1 ,0 ,1 ) 1 0 1 0 0 0
f ( 0 ,1 ,0 ) 0 1 0 0 1 1
f ( 1 ,1 ,0 ) 1 1 0 1 1 1
f ( 0 ,1 ,1 ) 0 1 1 0 0 0
f ( 1 ,1 ,1 ) 1 1 1 1 0 1
f ( x , y , z ) x0 y0 z0 x0 y1z0 x 1 y0 z0 x 1 y1 z0
x 1 y 1 z 1 x y z x y z x y z xy z xyz
9

10. Определения и понятия

Элементарной
конъюнкцией
называется
конъюнкция любого числа булевых переменных,
взятых с отрицанием или без него, в которой каждая
переменная встречается не более одного раза.
Примеры
Элементарными конъюнкциями для функции от
одной переменной могут быть y, z,
двух переменных x y, x z
трех переменных x y z , x y z , x y z .
10

11. Определения и понятия

Дизъюнктивной нормальной формой (ДНФ)
называется формула, представленная в виде
дизъюнкции элементарных конъюнкций.
Примеры:
f(x, y,z)= x y x z x y z x ДНФ
f(x, y,z)= x y x y z
f(x, y,z)= x y z
ДНФ
–
11

12. Определения и понятия

Элементарная конъюнкция
x1 x2 … xn
называется конституентой единицы (минтермом)
функции f(x1,x2,…,xn), если f( 1, 2,…, n)=1, то есть
интерпретация, обращающая в единицу данную
элементарную конъюнкцию, обращает в единицу и
функцию f.
1
2
n
12

13. Свойства конституенты единицы

Конституента единицы функции n переменных
имеет вид x1 x2 … xn и соответствует
интерпретации ( 1, 2,…, n).
Конституента единицы обладает следующими
свойствами:
Конституента единицы равна единице только на
соответствующей ей интерпретации.
Конституента единицы однозначно определяется
номером соответствующей ей интерпретации.
Конъюнкция
любого
числа
различных
конституент единицы функции равна нулю.
1
2
n
13

14. Определение и понятия

Совершенной дизъюнктивной нормальной
формой (СДНФ) булевой функции называется
формула, представленная в виде дизъюнкции
конституент единицы данной функции.
Примеры:
f(x, y,z)= x y z x y z
f(x, y,z)= x y z
f(x, y,z)= x yz
СДНФ
ДНФ
СДНФ
14

15. Определения и понятия

Совершенной конъюнктивной нормальной
формой (СКНФ) функции называется формула,
представленная в виде конъюнкции конституент
нуля данной функции.
Примеры
f(x, y,z)= x y z
f(x, y,z)= ( x y ) ( y z ) z
f(x, y,z)= ( x y z ) ( x y z )
СКНФ
КНФ
СКНФ
15

16. Следствия из определений СДНФ и СКНФ булевых функций

Для каждой булевой функции f(x1,x2,…,xn), не
являющейся
константой
нуля,
существует
представление в виде СДНФ.
Для каждой булевой функции f(x1,x2,…,xn), не
являющейся константой единицы, существует
представление в виде СКНФ.
Две различные булевы функции не могут иметь
одинаковые СДНФ или СКНФ.
Для каждой булевой функции f(x1,x2,…,xn)
существует представление в виде формулы булевой
алгебры, содержащей только операции дизъюнкции,
конъюнкции и отрицания.
16

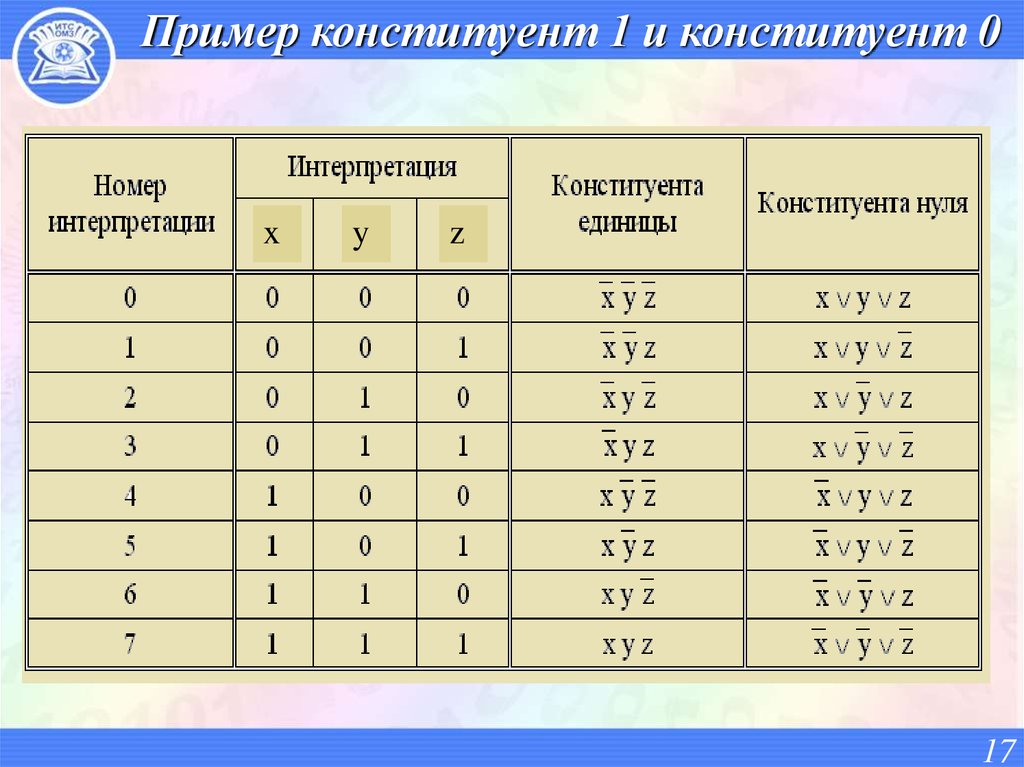
17. Пример конституент 1 и конституент 0

x
y
z
17

18. Алгоритм перехода от таблицы истинности булевой функции к СДНФ

• Выделить все интерпретации ( 1, 2,…, n), на
которых значение функции равно единице.
• Записать
конституенты
единицы
вида
x1 x2 … xn , соответствующие отмеченным
интерпретациям.
• Получить
СДНФ
функции
посредством
соединения операцией дизъюнкции записанных
конституент единицы.
1
2
n
18

19. Алгоритм перехода от таблицы истинности булевой функции к СДНФ. Пример

Получить СДНФ для функций f13(x,y).
Функция f13(x,y)
x
0
y
f13(x,y)
f8(x,y)
0
1
1
0
1
0
1
1
0
1
0
1
1
0
0
f 13 ( x , y ) x y x y x y x y xy xy
0 0
0 1
1 1
f8 ( x , y ) x y x y
0
0
19

20. Алгоритм перехода от таблицы истинности булевой функции к СКНФ

1. Выделить все интерпретации ( 1, 2,…, n), на
которых значение функции равно нулю
2. Записать конституенты нуля вида х х ... х ,
соответствующие выделенным интерпретациям.
3. Записав конъюнкцию конституент нуля, получить
СКНФ функции.
1
2
n
1
2
n
20

21. Алгоритм перехода от таблицы истинности булевой функции к СКНФ

Пример
Получить СКНФ для функций f7(x,y) и f9(x,y).
x
0
y
f7(x,y)
f9(x,y)
0
1
1
0
1
0
1
1
0
1
1
f7 ( x, y )
0
1
x1 y 1 x0 y 0 х y
0
1
f 9 ( x , y ) ( x0 y 1 ) ( x 1 y 0 )
( x1 y0 ) ( x0 y1 ) ( x y ) ( x y )
21

22. Алгоритм построения таблицы истинности функции, заданной СДНФ

1. Построить таблицу истинности, содержащую 2n
интерпретаций вида ( 1, 2,…, n).
2. Отметить в таблице истинности все интерпретации
( 1, 2,…, n),
соответствующие
конституентам
единицы вида х х ... х из заданной СДНФ.
3. Напротив выделенных интерпретаций в столбец
значения функции записать единицы.
4. Напротив оставшихся интерпретаций в столбец
значения функции записать нули.
1
2
n
1
2
n
22

23. Алгоритм перехода от произвольной формулы алгебры логики к СДНФ

1. Исключить константы, используя законы действий с
константами.
2. Опустить знаки отрицания непосредственно на
переменные, используя законы де Моргана.
3. Используя дистрибутивный закон, раскрыть скобки.
К полученным элементарным конъюнкциям
применить
законы
идемпотентности
и
противоречия, упростить их и привести подобные.
Результатом выполнения указанных действий
является получение ДНФ булевой функции.
23

24. Алгоритм перехода от произвольной формулы алгебры логики к СДНФ. Продолжение

4. Построить конституенты единицы функции,
введением в каждую элементарную конъюнкцию
недостающих переменных, используя закон
исключенного третьего.
5. С помощью дистрибутивного закона раскрыть
скобки и привести подобные, используя закон
идемпотентности
6. Полученная
формула
соответствует
СДНФ
функции.
24

25. Примеры

Пример 1. Переход от СДНФ к таблице истинности
Пример 2. Переход от СКНФ к таблице истинности
25