Математическая логика и теория алгоритмов

1. Математическая логика и теория алгоритмов

каф. ПМиК
доцент , к. ф.-м. н.
Мачикина Елена Павловна

2. Электронные ресурсы Режим доступа: http://www.iprbookshop.ru/

Балюкевич Э.Л. Математическая логика и теория
алгоритмов [Электронный ресурс]: учебное пособие/
Балюкевич Э.Л., Ковалева Л.Ф.— Электрон. текстовые
данные.— М.: Евразийский открытый институт, 2009.— 188
c.—
Маньшин М.Е. Математическая логика и теория
алгоритмов [Электронный ресурс]: учебное пособие/
Маньшин М.Е.— Электрон. текстовые данные.—
Волгоград: Волгоградский институт бизнеса, Вузовское
образование, 2009.— 106 c.
Жоль К.К. Логика [Электронный ресурс]: учебное пособие
для вузов/ Жоль К.К.— Электрон. текстовые данные.— М.:
ЮНИТИ-ДАНА, 2012.— 400 c.
Новиков Ф. А. Дискретная математика для программистов:
учеб. пособие /. - 3- изд. - СПб.: ПИТЕР, 2009. - 383с.

3. Электронные ресурсы Режим доступа: http://www.iprbookshop.ru/ ЭБС «IPRbooks», по паролю

Электронные ресурсы
www.intuit.ru
Бесплатный доступ после регистрации

4. Электронные ресурсы

1.
Теория булевых функций
2.
Логические исчисления
3.
Алгоритмические системы

5.

1. Булевы
функции

6. 1. Булевы функции

1.1 Определения

7. 1.1 Определения

Функция f:{0,1}n {0,1}
от n переменных
x1, x2, …, xn
называется булевой

8.

Утверждение
Для
булевой функции от n
аргументов существует 2n
различных наборов аргументов.

9. Утверждение

Поскольку каждая булева функция
имеет конечное количество наборов
аргументов, то булеву функцию
можно задать в виде таблицы

10.

Базовые логические связки –
отрицание, конъюнкция,
дизъюнкция, импликация,
эквиваленция

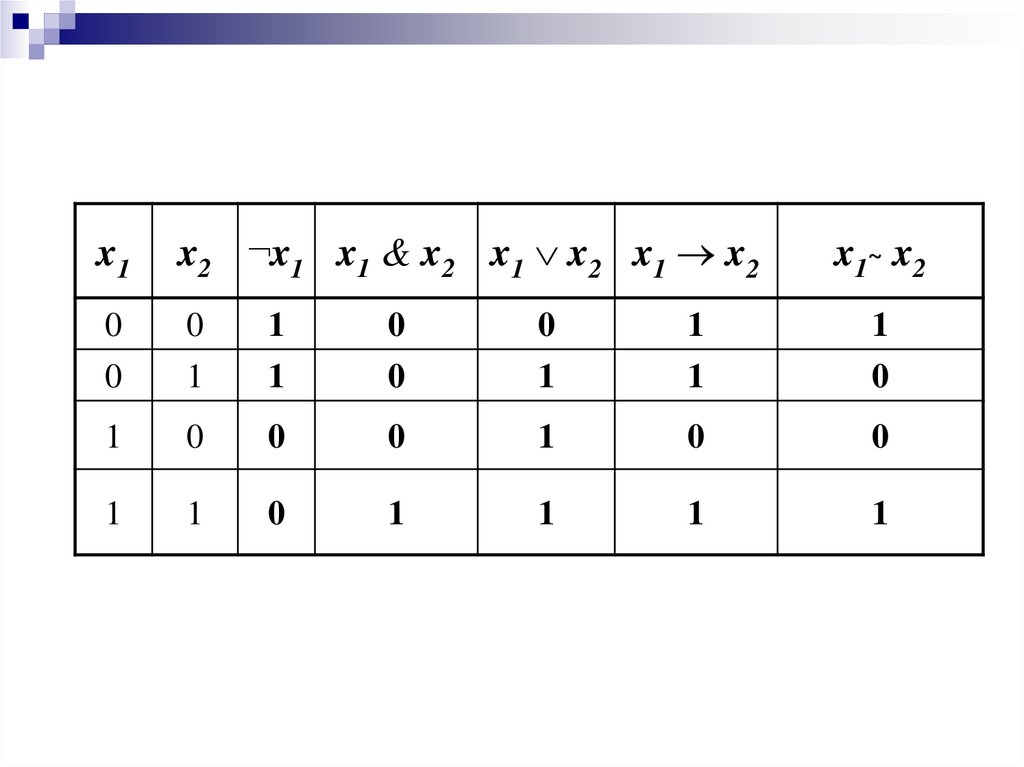
11.

x1
x2 ¬x1 x1 & x2 x1 x2 x1 x2
0
0
1
0
0
1
1
0
1
1
0
1
1
0
1
0
0
0
1
0
0
1
1
0
1
1
1
1
x1~ x2

12.

Из логических переменных с помощью логических
связок можно составлять конструкции, которые
образуют формулы алгебры логики
Пусть {xi | i I} – некоторое множество логических
переменных.
Определим рекурсивно понятие формулы алгебры
логики:
любая логическая переменная является
формулой (атомарной);
если и – формулы, то выражения , x , где
x – логическая операция, являются формулами;
никаких других формул нет.

13. Из логических переменных с помощью логических связок можно составлять конструкции, которые образуют формулы алгебры логики

Пусть даны формулы булевых функций
F(y1, y2, …, ym ),
f1(x1, x2, …, xn ), …, fm(x1, x2, …, xn ).
Тогда подстановкой формул fi в формулу
F называется следующая конструкция:
(F| yi fi )(x1, x2, …, xn)
F(f1(x1, x2, …, xn ), …, fm(x1, x2, …, xn )).

14.

Пример
F(y1, y2 )= y1~ y2
f1(x1, x2 )= x1
f2(x1, x2 )= x1& x2
(F| yi fi )(x1, x2) = x1 ~ (x1& x2)

15.

Теорема (О подстановке формул)
Если F(y1, y2, …, ym ) и fi (x1, x2, …, xn
) – формулы алгебры логики, то
(F| yi fi )(x1, x2, …, xn ) также
является формулой.

16.

Формулы, реализующие одну и ту же
функцию, называются равносильными
(т.е. на всех наборах переменных их
значение истинности совпадает).
Отношение равносильности формул
является отношением эквивалентности.

17.

Правило подстановки
Если в равносильных формулах:
F(y1, y2, …, ym ) G(y1, …, ym ) – вместо всех
вхождений некоторой переменной yi
подставить одну и ту же формулу, то
получатся равносильные формулы.
Правило замены
Если в формуле F заменить некоторую
подформулу yi на равносильную gi, то
получатся равносильные формулы.

18.

ФАЛ, при образовании которых
используются только операции
отрицания, конъюнкции и дизъюнкции,
называются булевыми формулами.
Теорема Для любой формулы алгебры
логики существует равносильная
ей булева формула.

19.

Для булевых функций выполняется ряд
равносильностей
Операции с константами:
1) A 1 1;A & 1 A; 2)A 0 A;
A & 0 0.
Противоречие:
A & A 0.
Исключение третьего:
A A 1.
Идемпотентность:
A & A A;
A A A.
Двойное отрицание: A A.
Коммутативность:A & B B & A; A B B A.
Ассоциативность:
(A B) C A (B C); (A&B)&C A&(B&C).
Дистрибутивность:
A & (B C) (A & B) (A & C);
A (B & C) (A
B) & (A C).
Законы де Моргана: (A&B) A B; (A B)
A & B.

20.

при выполнении преобразований часто
используются законы поглощения:
1) A & (A B) A; A A & B A;
2) A & (A B) A & B; A A & B A B.
А также А→В ¬АvВ; А~В (А→В )&(В →А)

21. Для булевых функций выполняется ряд равносильностей

1.2 Принцип
двойственности

22.

Пусть f(x1, x2, …, xn ) – булева функция.
Двойственной к ней называется функция
f*(x1, x2, …, xn ) ¬f (¬ x1, ¬ x2, …, ¬ xn ).
Из определения видно, что f**=f.
Если двойственная функция f* совпадает с
исходной функцией f, то такая функция f
называется самодвойственной.

23. 1.2 Принцип двойственности

Пример
f1(x1
)= x1
f1 *(x1
f2(x1, x2 )= x1& x2
)= ¬f1(¬ x1 )= x1
x2 )= ¬ f2(¬ x1, ¬ x2 )=
= ¬ (¬ x1& ¬ x2)= x1V x2
f2* (x1,

24.

Теорема (Общий принцип двойственности)
Если G(x1, …, xn ) получена
подстановкой формул fi
из F(y1, …, ym )
G(x1, …, xn ) (F| yi fi )(x1, …, xn ),
то G*(x1, …, xn ) (F*| yi f*i )(x1, …, xn ).

25. Пример

Теорема
(Принцип двойственности для булевых
функций)
Двойственная к булевой функции
может быть получена заменой
констант 0 на 1, 1 на 0,
дизъюнкции на конъюнкцию,
конъюнкции на дизъюнкцию и
сохранением структуры формулы
(т.е. соответствующего
исходному порядка действий).

26.

1.3 Нормальные
формы

27. Теорема (Принцип двойственности для булевых функций)

Табличный способ определения истинности
сложного выражения имеет ограниченное
применение. Тогда может быть использован
способ приведения формул к нормальной
форме.
Аналитическое выражение функции (или
формула) находится в нормальной форме,
если в ней отсутствуют знаки
эквивалентности, импликации, двойного
отрицания, а знаки отрицания находятся
только при переменных.

28.

Элементарной дизъюнкцией
(конъюнкцией) называется
дизъюнкция переменных и/или их
отрицаний
ДНФ – это дизъюнкция
элементарных конъюнкций.
КНФ – это конъюнкция элементарных
дизъюнкций.

29. 1.3 Нормальные формы

ДНФ (КНФ) называется совершенной,
если каждая переменная формулы
входит в каждую элементарную
конъюнкцию (дизъюнкцию) ровно
один раз.

30.

Примеры
Элементарные дизъюнкции: x y, z.
Элементарные конъюнкции: x&¬y&z,
x.
f(x,y,z) = x&y&z ¬x&y – ДНФ
f(x,y,z) = (x y)&z – КНФ.

31.

Введем обозначения
x, 1
x
x, 0

32.

Теорема
О разложении булевой функции по k
переменным
f ( x1 ,...,xn ) V
1 ,..., k
x1 1 x2 2 ...xk k f ( 1 , 2 ,..., k , xk 1 ,...,xn )

33. Примеры

Доказательство
Выберем какой-либо набор значений
для переменных x1, …, xn.
Пусть это будет 1, …, n.
i
Заметим, что i
1,
0 ,
i i
i i

34.

Подставим в правую часть формулировки
теоремы вместо x1, …, xn набор 1, …, n.
Получим.
V 1 1 2 2 ... k k f ( 1 , 2 ,..., k , k 1 ,..., n )
( 1 ,..., k )
Поскольку коэффициент перед функцией равен 1
только при равных значениях i и i, в
разложении останется только один член
1 1 ... k k f ( 1 ,..., k , k 1 ,..., n )
и i= i, т.е.
f ( 1 ,..., k , k 1 ,..., n )

35.

Получена левая часть формулы
теоремы. Поскольку набор был
выбран произвольно, получаем, что
утверждение верно любого набора
x1, …, xn

36. Теорема

Следствие 1 Разложение Шеннона
f ( x1 , x2 ,..., xn ) x1 f (0, x2 ,..., xn ) x1 f (1, x2 ,..., xn )

37. n=3, k=2

Следствие 2
При k=n
1 2
n
f ( x1 ,..., xn ) V x1 x2 ...xn
f 1

38. Доказательство

Построение СДНФ
1. Найти строки в таблице истинности , где
значение функции f истинное.
2. Каждому найденному набору 1, …, n.
поставить в соответствие конъюнкцию
~
x1 & ~
x2 & ... & ~
xn
xi , åñëè i 1
~
xi
xi , åñëè i 0
где
3. Составить дизъюнкцию из полученных
конъюнкций

39.

Построение СКНФ
1. Найти строки в таблице истинности , где
значение функции f ложное.
2. Каждому найденному набору 1, …, n.
поставить в соответствие дизъюнкцию
~
x1 ~
x 2 ... ~
xn
xi , åñëè i 0
~
xi
xi , åñëè i 1
где
3. Составить конъюнкцию из полученных
дизъюнкций

40.

Получение из ДНФ.
Если некоторое произведение ДНФ
не содержит какой-либо переменной,
то необходимо домножить это
произведение на дизъюнкцию этой
переменной и ее отрицания и
применить дистрибутивный закон.

41.

Получение из КНФ.
Если некоторая элементарная
дизъюнкция КНФ не содержит какойлибо переменной, то необходимо
дизъюнктивно добавить в нее
произведение этой переменной и ее
отрицания и применить
дистрибутивный закон.

42.

x y z f
0 0 0 1
0 0 1 1
Получим СДНФ и СКНФ по
таблице истинности
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 1
f ( x, y, z ) x y z x yz xyz x yz xyz ÑÄÍÔ ,
f ( x, y, z ) ( x y z )( x y z )( x y z ) ÑÊÍÔ