Similar presentations:
Математическая логика
1.
1Нажать здесь для запуска
презентации
2.
2КУРС ЛЕКЦИЙ
ВЫХОД
НАЧАТЬ
3.
МАТЕМАТИЧЕСКАЯЛОГИКА
ВВЕДЕНИЕ
ЛОГИКА
ВЫСКАЗЫВАНИЙ
ЛОГИКА
ПРЕДИКАТОВ
ИСЧИСЛЕНИЕ
ПРЕДИКАТОВ
ТЕСТ
НАЗАД
3
4. ГЛАВА I ЛОГИКА ВЫСКАЗЫВАНИЙ
§ 1. Логические операции над высказываниями§ 2. Формулы и булевы функции
§ 3. Равносильность формул
§ 4. Преобразование формул
§ 5. Применение логики высказываний
НАЗАД
4
5. ГЛАВА II ЛОГИКА ПРЕДИКАТОВ
Введение§ 6. Предикаты и функции. Логические операции над
предикатами
§ 7. Термы и формулы
§ 8. Значение термов и формул
§ 9. Равносильность. Преобразование формул
§ 10. Модели. Логическое следование
НАЗАД
5
6. ГЛАВА III ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
Введение§ 11. Основные понятия
§ 12. Свойства отношения выводимости
§ 13. Непротиворечивость, полнота, множества Хенкина
§ 14. Основные теоремы об исчислении предикатов
§ 15. Другая формулировка исчисления предикатов
НАЗАД
6
7.
ВведениеНАЧАЛО
ДАЛЕЕ
7
8. Введение.
Логика изучает способы рассуждения, то естьправила, позволяющие из данных утверждений (посылок)
выводить
новые
утверждения
(заключения).
Логика
развивается с древнейших времен, с тех пор, когда люди
почувствовали необходимость убедительного обоснования
утверждений.
Уже
самостоятельную
Математическая
Аристотель
выделял
область
логика
изучает
ее
как
знаний.
доказательные
рассуждения, применяемые в математике. С античных
времен математики доказывали свои результаты (развитая
НАЗАД
ДАЛЕЕ
8
9. Введение.
системадоказательств
содержится
в
знаменитых
«Началах» Евклида), не испытывая нужды в специальном
обосновании самих методов доказательства. Однако в
конце
XIX
века
обоснования.
возникла
Исследование
необходимость
такого
некоторых
проблем
математического анализа привело немецкого математика
Г. Кантора
к
созданию
теории
оказалась
очень
полезной, так как
на языке теории
множеств можно
сформулировать
практически
математические понятия. Можно
множеств, которая
все
было, следовательно,
надеяться, что появилась теория, образующая единый
НАЗАД
ДАЛЕЕ
9
10. Введение.
фундамент сильно «разветвившихся» к тому времениразделов математики. Однако оказалось, что в теории
множеств есть противоречия (парадоксы). Для устранения
парадоксов теории множеств и сохранения ее в качестве
основы математики немецкий математик Д. Гильберт
предложил примерно следующую программу:
НАЗАД
ДАЛЕЕ
10
11. Введение.
Программа Д. ГильбертаI.
проанализировать
и
описать
используемую
в
математике часть языка;
II.
точно
сформулировать
аксиомы,
то
есть
принимаемые без доказательства утверждения о
множествах;
III. проанализировать
и
описать
используемые
в
математике рассуждения (правила вывода);
IV. доказать, что из аксиом по этим правилам нельзя
вывести противоречие, то есть заведомо ложное
утверждение.
НАЗАД
ДАЛЕЕ
11
12. Введение.
Важнейшимв
описанной
программе
является,
конечно, последний пункт, именно он обеспечивает
надежную
(свободную
от
противоречий)
основу
математики, однако для его реализации необходимо
выполнить сначала предшествующие пункты программы,
так как строго доказывать можно только точно описанные
свойства полностью определенных объектов.
Интересно, что задолго до Гильберта, в XVII веке,
похожие идеи развивал немецкий математик и философ
Г.Лейбниц.
НАЗАД
ДАЛЕЕ
12
13. Введение.
Он писал о возможности и желательности созданиястрогого
языка
и
четких
правил
преобразования
выражений этого языка, используя которые можно было
бы решать математические и не только математические
проблемы посредством «вычислений». Идеи Лейбница не
были поняты современниками, истинная их глубина
обнаружилась только в XX веке.
В процессе работы над программой Гильберта
математическая
логика
сформировалась
как
самостоятельный раздел математики. Выяснилось, однако,
что полностью эту программу реализовать нельзя:
НАЗАД
ДАЛЕЕ
13
14. Введение.
австрийский математик К. Гедель показал, что многиеважные математические объекты не допускают полного
аксиоматического описания. Но первые три пункта
программы Гильберта были реализованы полностью. В
настоящее
время
математическая
логика
является
развитой областью науки, имеет глубокие связи с другими
разделами математики и многочисленные практические
приложения,
а
значение
некоторых
ее
результатов
выходит далеко за пределы собственно математики. В
последнее
время
интерес
к
математической
логике
стимулирует ее тесная связь с информатикой.
НАЗАД
ДАЛЕЕ
14
15.
НАЗАДДАЛЕЕ
15
16.
§ 1. Логические операциинад высказываниями
НАЗАД
ДАЛЕЕ
16
17. Глава I. Логика высказываний. § 1. Логические операции над высказываниями.
Высказыванием в классической логике называютутверждение, истинное или ложное, но не истинное и
ложное одновременно.
Примеры высказываний:
2·2=4;
2·2=5;
Москва – столица России.
Понятие высказывания не такое простое, каким кажется
на первый взгляд. Рассмотрим, например, предложение
«Утверждение
в
кавычках
ложно»,
выражающее
собственную ложность.
НАЗАД
ДАЛЕЕ
17
18. Глава I. Логика высказываний. § 1. Логические операции над высказываниями.
Легко понять, что оно не истинно и не ложно и,следовательно, не является высказыванием.
Математическая логика рассматривает не смысл
каждого
конкретного
истинностное
значение
высказывания,
(истинно
оно
а
только
или
его
ложно).
Абстрагироваться от смысла высказываний позволяет
понятие высказывательной переменной, принимающей в
качестве значений только И (истина) и Л (ложь). Такие
переменные будем обозначать буквами p, q, r, …,
используя при необходимости индексы.
НАЗАД
ДАЛЕЕ
18
19. Глава I. Логика высказываний. § 1. Логические операции над высказываниями.
Мы будем изучать операции над высказывательнымипеременными, то есть способы построения из данных
высказываний новых, более сложных. Например, из
высказываний p и q можно построить следующие
высказывания: p и q; p или q; если p, то q; не p. Эти
высказывания называют соответственно конъюнкцией,
дизъюнкцией, импликацией высказываний p и q и
отрицанием высказывания p.
Введем
для них обозначения
p q, p q, p q,
p соответственно.
НАЗАД
ДАЛЕЕ
19
20. Глава I. Логика высказываний. § 1. Логические операции над высказываниями.
определениеКонъюнкция ( p q ) истина в точности тогда, когда
оба конъюктивных члена истинны.
Дизъюнкция ( p q ) ложна в точности тогда, когда
оба дизъюктивных члена ложны.
Импликация
( p q ) ложна в точности тогда, когда
ее посылка p истинна, а заключение q - ложно.
Отрицание ( p ) истинно в точности тогда, когда
высказывание p ложно.
НАЗАД
ДАЛЕЕ
20
21. Глава I. Логика высказываний. § 1. Логические операции над высказываниями.
Определения основных логических операций можнотакже записать в виде таблицы 1 (таблицы истинности).
p q p q p q p q
p
И И
И
И
И
Л
И Л
Л
И
Л
Л
Л И
Л
И
И
И
Л Л
Л
Л
И
И
Таблица 1
Введенные операции над высказываниями – это основные
операции математической логики. В
следующем
параграфе мы докажем, что в определенном смысле
через них можно выразить все операции над
НАЗАД
ДАЛЕЕ
21
22.
§ 2. Формулы и булевыфункции
НАЗАД
ДАЛЕЕ
22
23. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Введемважное
понятие
высказываний.
Формула
которое
построить
можно
формулы
обозначает
с
логики
высказывание,
помощью
введенных
логических операций из высказываний, обозначаемых
переменными.
НАЗАД
ДАЛЕЕ
23
24. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
определениеЛюбая высказывательная переменная есть формула.
Если и
– формулы, то выражения ( ) ,
( p q) (q p)
( ) , ( ) , – также
формулы;
других
формул нет.
НАЗАД
ДАЛЕЕ
24
25. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Определения такого типа называют индуктивными.Они задают простейшие объекты (в нашем случае –
высказывательные переменные) и указывают способ
построения более сложных объектов из уже построенных.
Многие важные понятия нашего курса будут определены
индуктивно.
Покажем, как с помощью данного определения
можно
убедиться
в
том,
что
выражение
(( p q ) ( p )) есть формула. Для этого выпишем
в порядке возрастания сложности
все
подформулы
данного выражения:
НАЗАД
ДАЛЕЕ
25
26. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
p, q, q, p, ( p ), ( p q ), . Применяя по очереди кэтим выражениям данное определение, убеждаемся, что
это формулы. Заметим, что если бы данное выражение не
было формулой, мы не смогли бы его таким образом
«вывести».
Следовательно,
существует
алгоритм,
позволяющий по любому выражению узнать, является ли
оно формулой.
Приведем еще пример индуктивного определения, а
именно, дадим строгое определение понятия подформулы
формулы .
НАЗАД
ДАЛЕЕ
26
27. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
определениеЕсли
– высказывательная
переменная,
единственная ее подформула – она сама;
то
если
имеет один из видов: ( ) , ( ) , ( ) ,то ее
подформулы – она сама и все подформулы формул
и ; если , то подформулы – она сама и
все подформулы формулы .
НАЗАД
ДАЛЕЕ
27
28. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Формулы будем обозначать буквами ,используя
при
необходимости
индексы.
и ,
Запись
( p1 ,..., pn ) означает, что формула не содержит
высказывательных
переменных, отличных от p1 ,…, pn .
Например,
рассмотренной
для
выше
формулы
( p, q ) ( p, q, r ) .
Для упрощения записей в дальнейшем внешние
скобки в формулах мы будем, как правило, опускать.
Скобки, охватывающие подформулы, будем опускать
лишь в тех случаях,
НАЗАД
ДАЛЕЕ
28
29. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
когдапорядок
выполнения
логических
операций
в
формуле однозначно определен следующим соглашением:
сначала отрицание, затем конъюнкция
и дизъюнкция,
затем импликация.
Пусть дана формула ( p1 ,..., pn ) . Каждому набору
элементов 1 ,..., n множества {И, Л} сопоставим элемент
этого же множества
( 1 ,..., n ) , называемый значением
формулы
(на наборе значений переменных 1 ,..., n )
в соответствии со следующим определением.
НАЗАД
ДАЛЕЕ
29
30. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
определениеЕсли ( p ,..., p ) p , то ( ,..., ) ;
1
n
i
1
n
i
если , то ( ,..., ) ( ,..., ) ;
1
n
1
n
если * , то
( ,..., ) ( ,..., ) * ( ,..., )
1
n
1
n
1
n
(здесь * - один из символов , , ).
НАЗАД
ДАЛЕЕ
30
31. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Такимобразом,
значение
формулы
при
значениях переменных p можно найти, подставляя
i
i
i вместо pi в и производя вычисления по
таблице истинности для логических операций (см. табл. 1).
Например, для рассмотренной выше формулы ( p, q )
имеем: ( И, Л ) (И ( Л)) ( И) (И И) И
И И И.
НАЗАД
ДАЛЕЕ
31
32. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
определениеn-местная булева функция – это функция f ( p1 ,..., pn )
от
n
аргументов,
принимающая определенное
значение f ( 1 ,..., n ) {И, Л} при
любом наборе
1 ,..., n значений аргументов, где i {И, Л} .
Другими словами, f отображает n- ю декартову
степень множества {И, Л} в {И, Л}.
НАЗАД
ДАЛЕЕ
32
33. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Любую булеву функцию можно задать таблицей, вкоторой перечислены все возможные наборы значений
аргументов и соответствующие им значения функции. Из
таблицы 1 видно, что основные логические опереции
можно рассматривать как булевы функции. Таблицей 2
задана двухместная булева функция, не совпадающая ни с
одной из логических операций, определенных таблицей 1.
НАЗАД
p
q
f(p,q)
И
И
И
И
Л
Л
Л
И
Л
Л
Л
И
Таблица 2
ДАЛЕЕ
33
34. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
pq
¬q
¬p
¬¬p
p ¬q
И
И
И
Л
И
И
И
И
Л
Л
Л
И
И
И
Л
И
Л
И
Л
Л
И
Л
Л
И
И
Л
И
Л
Таблица 3
Определение значения формулы показывает, что
любая формула
логики
высказываний
( p1 ,..., pn )
задает n - местную булеву функцию. Соответствующую
таблицу называют таблицей истинности формулы . Для
удобства вычислений в таблице истинности указывают
также значения всех подформул формулы .
НАЗАД
ДАЛЕЕ
34
35. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Табл. 3 есть таблица истинности формулы (( p q )( p )) .
Любая ли булева функция может быть задана
подходящей формулой логики
высказываний? Ответ
положителен: любую булеву функцию можно выразить
через функции
, , .
Следующий фундаментальный результат является
основой многих приложений логики высказываний (в
частности – в электронике).
НАЗАД
ДАЛЕЕ
35
36. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Теорема о функциональной полноте. Длялюбой булевой функции
f ( p1 ,..., pn ) найдется формула
логики высказываний ( p1 ,..., pn ) такая, что f ( 1 ,..., n )
( 1 ,..., n ) при всех i {И, Л}.
Доказательство. Рассмотрим сначала случай,
когда
f ( 1 ,..., n ) Л при
случае надо подобрать
ложна.
всех
i {И, Л} . В этом
формулу , которая
Из определений конъюнкции и
следует,
что
этим
свойством
всегда
отрицания
обладает формула
p1 p1 p2 ... pn .
НАЗАД
ДАЛЕЕ
36
37. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
(Для упрощения записи мы опустили скобки; можно дляопределенности считать, что они группируются влево.
Аналогичные сокращения будем применять и далее.)
Теперь рассмотрим случай, когда функция f истинна
хотя бы на одном наборе значений своих переменных.
Пусть
( 1 ,..., n ),..., ( 1 ,..., n )
1
1
m
m
(1)
– это все наборы значений переменных, на которых f
истинна; в рассматриваемом случае m ≥ 1.
НАЗАД
ДАЛЕЕ
37
38. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Сопоставим набору ( 1j ,..., nj ) формулу j 1j ... nj ,где i j pi при i j И и i j pi при i j Л . Из
определения конъюнкции и вида формулы j следует,
что она истинна на наборе ( 1j ,..., nj ) и
ложна на всех
других наборах значений переменных. Отсюда и из
определения
дизъюнкции
следует,
что
формула
1 ... m истинна на всех наборах (1) и ложна на
всех других наборах. Поэтому значения формулы
совпадают со значениями функции
значений переменных.
НАЗАД
f на всех наборах
■
ДАЛЕЕ
38
39. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Например, для функции из таблицы 2 получим:q ( p1 p2 ) ( p2 p2 ) .
Сделаем
некоторые
дополнительные
замечания.
Булевы функции {g1,…, gk} образуют полную систему, если
любая булева функция может быть получена подходящей
суперпозицией (подстановкой) функции g1,…, gk . Формула
из доказательства теоремы о функциональной полноте
содержит только конъюнкции, дизъюнкции и отрицания.
Поэтому теорему можно переформулировать так: система,
булевых функций { , , } полна. Существуют и другие
полные системы, например, { , } .
НАЗАД
ДАЛЕЕ
39
40. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Для доказательства полноты этой системы достаточновыразить дизъюнкцию в виде суперпозиции функций ,
. Это нетрудно: p q ( p q ) . Существуют даже
полные системы из одной функции. Примером является
функция
равенствами
p|q
(штрих Шеффера),
И | И=Л,
определяемая
И | Л=Л | И=Л | Л=И.
Для
доказательства полноты системы { | } достаточно выразить
функции из полной системы { , } через | . Следующие
легко проверяемые равенства дают искомые выражения:
p p | p, p q ( p q ) ( p | q ) ( p | q ) | ( p | q ) .
НАЗАД
ДАЛЕЕ
40
41. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
определениеФормулу логики высказываний называют:
общезначимой, или тождественно истинной, или
тавтологией, если она истинна при всех наборах
значений входящих в нее переменных.
выполнимой, если она истинна хотя бы на одном
наборе значений переменных.
тождественно ложной, если она ложна при всех
значениях переменных.
НАЗАД
ДАЛЕЕ
41
42. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Дляпроверки
общезначимости
(выполнимости,
тождественной ложности) формулы достаточно построить
таблицу истинности и убедиться, что значения формулы,
соответственно, все истинны, не все ложны, все ложны.
Например, формула из таблицы 3 не общезначима, но
выполнима.
Основные тавтологии.
Для любых формул
, и следующие формулы
являются тавтологиями:
НАЗАД
ДАЛЕЕ
42
43. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
1. ( ) ;2. ( ) (( ( )) ( )) ;
3. ( ( )) ;
4. ( ) ;
5. ( ) ;
6. ( ) ;
7. ( ) ;
8. ( ) (( ) (( ) )) ;
9. ( ) (( ) ) ;
10. .
НАЗАД
ДАЛЕЕ
43
44. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Предоставляемчитателю
доказать
тавтологичность
формул 1 – 10 с помощью таблиц истинности. Существует
еще
один
способ
доказательства
общезначимости,
который проиллюстрируем на примере формулы 9.
Допустим, что она не общезначима, то есть ложна на
некотором наборе
значений своих переменных. По
определению импликации, на этом наборе ( ) И , а
(( ) ) Л . Из последнего равенства получаем:
( ) И и Л , откуда И . Из ( ) И ,
по определению импликации, следует, что И .
НАЗАД
ДАЛЕЕ
44
45. Глава I. Логика высказываний. § 2. Формулы и булевы функции.
Из( ) И так
же
выводим:
И , то есть
Л . Итак, формула
истинна и ложна на одном и
том
переменных.
же
наборе
значений
Полученное
противоречие доказывает общезначимость формулы 9.
НАЗАД
ДАЛЕЕ
45
46.
§ 3. Равносильностьформул
НАЗАД
ДАЛЕЕ
46
47. Глава I. Логика высказываний. § 3. Равносильность формул.
определениеДве формулы логики высказываний равносильны
( ) , если они принимают одинаковые значения
( p q) (q p)
при всех значениях входящих в них переменных.
Равносильность
формулы
истинны
или
ложны
одновременно, они описывают одну и ту же булеву
функцию.
НАЗАД
ДАЛЕЕ
47
48. Глава I. Логика высказываний. § 3. Равносильность формул.
Это позволяет преобразовывать формулы в более удобную(для какой-либо цели) форму.
Свойства отношения равносильности
1. Отношение
рефлексивно,
симметрично
и
транзитивно.
2. Если и , то , 1
1
1 ,
1
1
1
1
1
и .
3. Формулы и равносильны тогда и только
тогда, когда формула ( ) ( ) общезначима.
НАЗАД
ДАЛЕЕ
48
49. Глава I. Логика высказываний. § 3. Равносильность формул.
Доказательства.1. Рефлексивность означает, что для любой
формулы ; симметричность означает, что из
следует ;
транзитивность означает, что и
следует . Теперь ясно,
что
свойство 1
легко следует из определения равносильности.
2. Проверим
свойство 2
для
конъюнкции (для
остальных
операций
доказательство
проводится
аналогично).
Пусть
p1,…, pn – все
переменные,
входящие в формулы , , 1 , 1 .
НАЗАД
ДАЛЕЕ
49
50. Глава I. Логика высказываний. § 3. Равносильность формул.
По определению равносильности надо доказать, что( 1 )( 1 ,..., n ) совпадает с ( 1 )( 1 ,..., n ) при всех
i {И, Л} . Из определения значения формулы и данных
равносильностей получаем:
( 1 )( 1 ,..., n ) ( 1 ,..., n ) 1 ( 1 ,..., n ) ( 1 ,..., n ) 1 ( 1 ,
..., n ) ( 1 )( 1 ,..., n ) , что и требовалось доказать.
3. Пусть
и
p1,…, pn – все
переменные,
входящие в и . Для доказательства общезначимости
формулы достаточно доказать общезначимость формул
и . Рассмотрим для примера первую из них.
НАЗАД
ДАЛЕЕ
50
51. Глава I. Логика высказываний. § 3. Равносильность формул.
При любых значениях переменных p1,…, pn значенияформул
и одинаковы. Тогда, по определению
импликации, формула истинна при всех значениях
переменных, то есть она общезначима. Аналогичным
образом из общезначимости формулы выводим, что
.
■
Заметим, что свойства 1 и 2 аналогичны свойствам
равенства алгебраических выражений, а свойство 3
связывает понятия равносильности и общезначимости.
НАЗАД
ДАЛЕЕ
51
52. Глава I. Логика высказываний. § 3. Равносильность формул.
Докажемеще
одно
свойство
равносильности,
позволяющее выполнять равносильные преобразования
подформул данной формулы.
Теорема о замене.
Пусть – подформула
/ – результат замены некоторого
формулы ,
а
вхождения
в на формулу / . Тогда из /
следует / .
Доказательство.
Заметим
сначала,
что
формулировка говорит о фиксированном вхождении
потому, что может входить
в несколько
раз.
Разберем сначала частный случай, когда совпадает с .
НАЗАД
ДАЛЕЕ
52
53. Глава I. Логика высказываний. § 3. Равносильность формул.
В этом случае / совпадает с / и утверждение очевидно.В общем случае утверждение докажем индукцией по
числу вхождений логических операций в формулу .
Пусть число вхождений равно 0 (базис индукции). Тогда
– высказывательная переменная, и единственная ее
подформула – она сама. Поэтому утверждение вытекает из
разобранного частного случая.
Предположим, что теорема доказана для всех формул
с
числом
вхождений
не
более
n (индукционное
предположение), а имеет n + 1 вхождений логических
операций.
НАЗАД
ДАЛЕЕ
53
54. Глава I. Логика высказываний. § 3. Равносильность формул.
По определению формулы, имеет один из следующихвидов: ( 1 2 ), ( 1 2 ), ( 1 2 ), 1 . Рассуждения для
всех вариантов однотипны, поэтому доказательство
проведем
только
для
случая
1 2 .
В
силу
разобранного частного случая можно считать, что не
совпадает с
. Поэтому рассматриваемое вхождение
находится в одной из формул 1 , 2 . Предположим для
определенности, что оно находится в 1 . Поскольку 1
имеет не более n вхождений логических операций, для нее
/
выполнено индукционное предложение, то есть
1
1 .
НАЗАД
ДАЛЕЕ
54
55. Глава I. Логика высказываний. § 3. Равносильность формул.
Из определения / следует, что она совпадает с формулой( 1 2 ) .
/
получаем
Отсюда и из свойства 2 равносильности
/.
■
При преобразовании алгебраических выражений
используют известные из школы алгебраические правила.
Для преобразования формул также нужны некоторые
исходные равносильности.
Свойства отношения равносильности
Для любых формул
,
и справедливы
следующие равносильности:
НАЗАД
ДАЛЕЕ
55
56. Глава I. Логика высказываний. § 3. Равносильность формул.
1. ( ) ( ) ;3. ( ) ( ) ;
( ) ( )
5.
;
( ) ( )
7.
;
( ) ( ) ( ) ;
9.
10. ( ) ( ) ( ) .
2. ;
4. ( ) ( ) ;
6. ( ) ( ) ;
( ) ( )
8.
;
Доказательство. Докажем для примера первую
равносильность,
представляя
проверку
остальных
читателю. Установим сначала равносильность формул
p q и p q .
НАЗАД
ДАЛЕЕ
56
57. Глава I. Логика высказываний. § 3. Равносильность формул.
Дляэтого
достаточно
построить
общую
таблицу
истинности (табл. 4) для этих формул иубедиться в
совпадении соответствующих столбцов.
p
q
¬p
p→q
¬p q
И
И
Л
И
И
И
Л
Л
Л
Л
Л
И
И
И
И
Л
Л
И
И
И
Таблица 4
Пусть теперь и – произвольные формулы.
НАЗАД
ДАЛЕЕ
57
58. Глава I. Логика высказываний. § 3. Равносильность формул.
При любых значениях входящих в них переменныхони принимают значения И или Л. Значения формул
( ) и ( ) можно получить из этих значений так
же, как в таблице 4, следовательно, они совпадают.
Заметим,
что
мы
привели
необходимые
для
дальнейшего
лишь
наиболее
равносильности.
Существуют и другие важные равносильности, некоторые
из них будут рассмотрены в §5. Для удобства ссылок
укажем названия равносильностей 1 – 10:
• 1 – закон исключения импликации;
• 2 – закон двойного отрицания;
НАЗАД
ДАЛЕЕ
58
59. Глава I. Логика высказываний. § 3. Равносильность формул.
• 3 и 4 – законы Де Моргана;• 5 и 6 – законы коммутативности;
• 7 и 8 – законы ассоциативности;
• 9 и 10 – законы дистрибутивности;
Равносильности с номерами 2n + 1 и 2n + 2 (при
n {1,2,3,4}) называют двойственными, поскольку они
переходят одна в другую при замене конъюнкции на
дизъюнкцию и наоборот.
Заметим
еще,
что
равносильности
5-8
и
10
аналогичны известным алгебраическим законам, если
отождествить конъюнкцию со сложением,
НАЗАД
ДАЛЕЕ
59
60. Глава I. Логика высказываний. § 3. Равносильность формул.
а дизъюнкцию – с умножением. Как и в алгебре, иззаконов
коммутативности
и
ассоциативности
легко
вывести, что в дизъюнкции (конъюнкции) нескольких
формул скобки можно не ставить, поскольку при всех
расстановках скобок и перестановках членов получаем
равносильные формулы.
Например, ( 1 2 ) ( 3 4 )
( 4 3 ) ( 2 1 ),поэтому эти формулы можно записать
проще: 1 2 3 4 . Легко также вывести обобщения
законов дистрибутивности. Например, ( 1 ... m ) ( 1
... n ) ( i j ) , где i {1,..., m}, j {1,..., n}.
i, j
НАЗАД
ДАЛЕЕ
60
61.
§ 4. Преобразованиеформул
НАЗАД
ДАЛЕЕ
61
62. Глава I. Логика высказываний. § 4. Преобразование формул.
Применимполученные
результаты
к
преобразованию формул.
определение
Формулой специального вида назовем формулу без
импликаций, у которой отрицания относятся только
к переменным.
НАЗАД
( p q) (q p)
ДАЛЕЕ
62
63. Глава I. Логика высказываний. § 4. Преобразование формул.
Примеры формул специального вида: p p; p;(( r q ) q ) r . Выражения p; p q; ( p q ) не
являются формулами специального вида.
Формулы специального вида можно описать и иначе,
например, как формулы, не имеющие подформул вида:
( ); ( ); ( ); .
Еще одно равносильное описание: это формулы,
построенные из переменных и отрицаний переменных: с
помощью конъюнкции и дизъюнкции. Иными словами,
формулы
специального
вида
можно
определить
индуктивно следующими правилами:
НАЗАД
ДАЛЕЕ
63
64. Глава I. Логика высказываний. § 4. Преобразование формул.
переменные и отрицания переменных являютсяформулами специального вида; если и – формулы
специального вида, то и ( ), ( ) – также формулы
специального вида. Несложную проверку равносильности
этих
описаний
первоначальному
определению
предоставляем читателю. Покажем, что любую формулу
можно «привести к специальному виду».
Предложение. Для любой формулы найдется
равносильная ей формула специального вида.
НАЗАД
ДАЛЕЕ
64
65. Глава I. Логика высказываний. § 4. Преобразование формул.
Доказательство.Опишем
позволяющий
привести
к
произвольную
формулу
.
алгоритм,
специальному
С
виду
помощью закона
исключения импликации находим сначала формулу без
1
импликаций,
равносильную
последовательно
применяем
к
формуле
. Далее
полученной
формуле
законы Де Моргана, то есть заменяем подформулы вида
( ) и ( ) соответственно на ( ) и
( ) , убирая на каждом шаге получившиеся при
этом двойные отрицания.
НАЗАД
ДАЛЕЕ
65
66. Глава I. Логика высказываний. § 4. Преобразование формул.
Через к онечное числоравносильную
шагов получим формулу
2
1 и не содержащую подформул вида
( ); ( ); ( ); . Она и будет искомой
формулой специального вида.
■
Рассмотрим еще более простой класс формул.
НАЗАД
ДАЛЕЕ
66
67. Глава I. Логика высказываний. § 4. Преобразование формул.
определения1. Элементарной дизъюнкцией называется формула,
являющаяся либо переменной, либо
отрицанием
переменной,
нескольких
либо
( p q) (q p)
дизъюнкцией
переменных и отрицаний переменных.
2. Конъюнктивной
нормальной
формой
(КНФ)
называется формула, являющаяся либо элементарной
дизъюнкцией, либо конъюнкцией
элементарных
дизъюнкций.
НАЗАД
ДАЛЕЕ
67
68. Глава I. Логика высказываний. § 4. Преобразование формул.
Примеры элементарных дизъюнкций: p; q; p p;p q p r .
В
общем случае
дизъюнкцию можно записать в виде:
элементарную
1 ... m , где
m 1 и каждая i есть либо переменная, либо отрицание
Формулы i называют членами этой
дизъюнкции. Согласно §3, скобки между членами
переменной.
дизъюнкции можно не ставить. КНФ можно записать в
виде:
1 ... n ,
где n 1 и
каждая
j
есть
элементарная дизъюнкция. Если заменить дизъюнкцию
умножением, а
превратится
НАЗАД
конъюнкцию – сложением, то
в сумму произведений, то есть
в
КНФ
очень
ДАЛЕЕ
68
69. Глава I. Логика высказываний. § 4. Преобразование формул.
простое алгебраическое выражение.Поскольку
любая
КНФ
является
формулой
специального вида, следующая теорема есть усиление
доказанного выше предложения.
Теорема о приведении к КНФ. Для любой
формулы найдется равносильная ей КНФ.
Доказательство.
В
силу
доказанного
предложения достаточно проверить, что любую формулу
специального
вида
можно
привести
к
КНФ.
Доказательство проведем индукцией по числу вхождений
символов
НАЗАД
и в формулу .
ДАЛЕЕ
69
70. Глава I. Логика высказываний. § 4. Преобразование формул.
Если число вхождений равно0, то
есть
либо
переменная, либо отрицание переменной; в любом из этих
случаев
есть КНФ. Предположим, что утверждение
доказано для формул с числом вхождений не более n, и
пусть имеет n + 1 вхождений
и . Тогда имеет
вид 1 2 или 1 2. По индукционному предположению
найдутся КНФ 1 и 2 равносильные соответственно
формулам 1 и 2 . Если 1 2 , то 1 2 , и
формула 1 2 есть КНФ. Остается рассмотреть случай
1 2 1 2 , где 1 и 2 – КНФ.
НАЗАД
ДАЛЕЕ
70
71. Глава I. Логика высказываний. § 4. Преобразование формул.
Пусть 1 1 ... m и 2 1/ ... n, где иi
j –
элементарные дизъюнкции. Согласно §3, ( / ) .
i
j
i
,
j
/
Поскольку
каждая
из формул ( i j ) является
элементарной дизъюнкцией, формула ( i j / ) есть
/
i, j
КНФ.
Если в последнем определении поменять ролями
конъюнкцию и дизъюнкцию, то получится двойственные
понятия элементарной конъюнкции и дизъюнктивной
нормальной
формы
(ДНФ).
Двойственное
к
доказательству теоремы рассуждение показывает, что
любую формулу можно привести к ДНФ.
НАЗАД
ДАЛЕЕ
71
72. Глава I. Логика высказываний. § 4. Преобразование формул.
Другоедоказательство
доказательства
теоремы
этого
легко
извлечь
о функциональной
из
полноте.
Построенная в нем формула есть ДНФ.
Следующая теорема дает еще один способ проверки
общезначимости формулы.
Теорема об общезначимости КНФ. КНФ
общезначима тогда и только тогда, когда каждая ее
элементарная дизъюнкция содержит по крайней мере два
члена, один из которых является переменой, а другой –
отрицанием этой переменной.
НАЗАД
ДАЛЕЕ
72
73. Глава I. Логика высказываний. § 4. Преобразование формул.
Доказательство. Пусть КНФ имеет вид ...1
n , где i – элементарные дизъюнкции. Допустим, что
каждая содержит члены qi и qi , где qi – некоторая
i
переменная. При любых значениях переменных одна из
формул
qi , qi
истинна, а значит, и формула i
истинна. Следовательно, все формулы
По
i общезначимы.
определению конъюнкции данная КНФ
также
общезначима.
Обратно, пусть данная КНФ общезначима и p1,…, pm
– все входящие в нее переменные.
НАЗАД
ДАЛЕЕ
73
74. Глава I. Логика высказываний. § 4. Преобразование формул.
По определению конъюнкции, все конъюнктивные членыi общезначимы. Надо проверить, что формула i (для
i = 1,…, n) содержит члены p j и p j для некоторого j.
Допустим противное: для любого j хотя бы одна из формул
p j , p j не является членом дизъюнкции . Определим
значение j так: если p j является членом i , то j И
в противном случае j Л . Тогда при значениях p j
j все члены дизъюнкции ложны. По определению
дизъюнкции i ( 1 ,..., m ) Л , что
противоречит
общезначимости формулы
НАЗАД
.
■
ДАЛЕЕ
74
75. Глава I. Логика высказываний. § 4. Преобразование формул.
Предлагаем читателю сформулировать и доказатьтеорему о тождественной ложности ДНФ, двойственную
теореме об общезначимости КНФ.
Поясним полученные результаты примером. Пусть
требуется привести к КНФ формулу ( p q )
( p r ) и узнать, общезначима ли она. Сначала
приводим ее к специальному виду: ( p q ) ( p
r ) ( p q ) ( p r ) ( p q ) ( p
r ) ( p q ) ( p r ) . Далее приводим полученную
формулу к КНФ: ( p p ) ( p r ) ( q p ) ( q r ).
НАЗАД
ДАЛЕЕ
75
76. Глава I. Логика высказываний. § 4. Преобразование формул.
Изпоследней
общезначима
теоремы
следует,
что
не
(рассмотрите
вторую
элементарную
дизъюнкцию).
НАЗАД
ДАЛЕЕ
76
77.
§ 5. Применение логикивысказываний
НАЗАД
ДАЛЕЕ
77
78. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Рассмотренныепонятия
и
результаты
математической логики постоянно используют в разных
областях
деятельности.
Приведем
примеры
такого
использования.
Для правильного формулирования необходимых и
достаточных условий очень важно понимать связь этих
понятий
с импликацией.
Истинность импликации
p q
означает, что p есть достаточное условие для q, а q есть
необходимое условие для p. Например, если p означает
«все
стороны
четырехугольника
равны»,
а
–
q
«четырехугольник является квадратом»,
НАЗАД
ДАЛЕЕ
78
79. Глава I. Логика высказываний. § 5. Применение логики высказываний.
то q – достаточное условие для p, p – необходимое условиедля q, p не является достаточным для q и q не является
необходимым для p. Выражение «p есть необходимое и
достаточное условие для q» означает, что p достаточно для
q и q достаточно для p или что утверждения p и q
равносильны.
Равносильности логики высказываний могут быть
полезны
при
выполнении
алгебраических
преобразований. Пусть, например, надо преобразовать
выражение (( x 2 y ) (( x y ) ( x 3))) в
2
НАЗАД
ДАЛЕЕ
79
80. Глава I. Логика высказываний. § 5. Применение логики высказываний.
равносильнуюсовокупность
неравенств.
Уравнения
фиксированных
значениях
систем
и
уравнений
неравенства
числовых
и
при
переменных
истинны или ложны, поэтому их можно заменить
высказывательными переменными, тогда превратиться в
формулу логики высказываний. Применяя основные
( ( x 2 y ) (( x 2
y ) ( x 3))) ( x 2 y ) ( ( x 2 y ) ( x 3)) .
По теореме трихотомии
( x 3) x 3 , поэтому
2
( x 2 y ) (( x y ) ( x 3)) . По дистрибутивности
получим: (( x 2 y ) ( x 2 y )) (( x 2 y ) ( x 3)) .
равносильности из §3, получим:
НАЗАД
ДАЛЕЕ
80
81. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Система (совокупность) некоторых условий – уравнений инеравенств – есть, в сущности, конъюнкция (дизъюнкция)
этих условий. Поэтому
систем
x 2 y,
2
x y
равносильно совокупности
и
x 2 y,
x 3.
Аналогичные преобразования можно применять при
решении уравнений, неравенств и их систем. Пусть,
например, требуется решить неравенство x 1 x 4 9,
которое обозначим через . Дизъюнкция (x 1)
( 1 x 4) ( x 4) истинна при любом x.
НАЗАД
ДАЛЕЕ
81
82. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Тогда . По закону дистрибутивности, (( x 1)) ( ( 1 x 4)) ( ( x 4)) . По определению
модуля, (( x 1 x 4 9) ( x 1)) (( x 1 x 4 9)
( 1 x 4)) (( x 1 x 4 9) ( x 4)) .Решая полученную
совокупность систем линейных неравенств, получим, что
равносильно условию ( x 3) ( x 6).
Приведем
примеры
применения
логики
высказываний к проверке правильности рассуждений.
Обычно рассуждение состоит в том, что из некоторых
данных
утверждений
(посылок)
выводят
другое
утверждение (заключение).
НАЗАД
ДАЛЕЕ
82
83. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Схематически такое рассуждение можно записать в виде1 ,..., n
, где 1 ,..., n – посылки, а – заключение.
Рассуждение считают правильным, если заключение
истинно всякий раз, когда истинны посылки. В этом
случае говорят, что логически следует из
1 ,..., n
и
записывают это в виде 1 ,..., n | . Если утверждения
1 ,..., n , записаны формулами логики высказываний,
то с помощью таблиц истинности можно без
определить,
верно
ли
правильных рассуждений
рассуждение.
являются
труда
Примерами
известные
еще
Аристотелю правило «модус толленс»:
НАЗАД
ДАЛЕЕ
83
84. Глава I. Логика высказываний. § 5. Применение логики высказываний.
p q, q | p и правило простой конструктивнойдилеммы: p r , q r , p q | r . Проверим способом «от
противного» справедливость первого правила. Если бы
оно было неверным, то при некоторых значениях p и q
посылки p q и q были бы истинными, а заключение
p – ложным. Но тогда p = И, а поскольку p q И ,
то
и q = И.
Полученное противоречие доказывает
утверждение.
Из определений конъюнкции и импликации следует,
что способ рассуждения 1 ,..., n | правилен в точности
тогда, когда формула
НАЗАД
1 ... n общезначима.
ДАЛЕЕ
84
85. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Следовательно, правильным рассуждениям соответствуетнекоторые
тавтологии,
которые
поэтому
называют
законами логики. Например, основная тавтология 8 из §2
является, по существу, другой формой записи правила
простой конструктивной дилеммы.
Рассмотрим рассуждение, далекое от математики
(логика присутствует в любом рассуждении!): «Если бы
«Спартак» играл хорошо, то он был бы чемпионом или
серебряным
призером.
«Спартак»
не
чемпион,
следовательно, он играет плохо». Покажем, что это
рассуждение неправильно.
НАЗАД
ДАЛЕЕ
85
86. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Введем следующие высказывания: p – «Спартак» играетхорошо, q – «Спартак» является чемпионом, r – «Спартак»
является
серебряным
призером.
С
помощью
этих
высказываний приведенное рассуждение можно записать
в виде p ( q r ) или формулой (( p ( q r )) q )
p . По таблице истинности убеждаемся, что эта
формула не общезначима. Поэтому рассуждение неверно.
Если бы любое рассуждение можно было записать
формулой логики высказываний, то мы получили бы
полное решение проблемы правильности рассуждений,
НАЗАД
ДАЛЕЕ
86
87. Глава I. Логика высказываний. § 5. Применение логики высказываний.
то есть упомянутая во введении идея Лейбница была быреализована. Это, однако, не так. Например, анализ
следующего, очевидно, правильного рассуждения нельзя
провести с помощью логики высказываний: «Все люди
смертны. Цезарь – человек. Следовательно, Цезарь
смертен». В следующей главе мы изучим более богатый
язык, на котором можно выразить больше утверждений. В
частности,
упомянутое
рассуждение
будет
проанализировано в §8.
Опишем коротко основные идеи применения логики
высказываний в электронике.
НАЗАД
ДАЛЕЕ
87
88. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Функциональным элементом (ФЭ) называют устройство снесколькими входами и одним выходом. Внутреннюю
структуру ФЭ мы рассматривать не будем, нас интересует
только как ФЭ «работает»: на каждый вход может быть
подано одно из двух значений напряжения – высокое или
низкое; ФЭ перерабатывает любой набор значений
напряжений
на
входах
в
определенное
значение
напряжения на выходе, также высокое или низкое. На
рис. 1 в виде прямоугольника изображен функциональный
элемент с входами p1, …, pn и выходом q.
НАЗАД
ДАЛЕЕ
88
89. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Обозначив высокое напряжение И, а низкое – Л, мывидим, что каждый ФЭ «вычисляет» или «реализует»
некоторую булеву функцию q = f (p1, …,pn). В электронике
используют много различных типов ФЭ. Есть среди них и
такие, которые реализуют функции (§ § 1, 2).
p1
p2
p1
q
pn
p2
рис. 1
НАЗАД
1
3
рис. 2
2
4
p1
q
p2
q
рис. 3
ДАЛЕЕ
89
90. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Допустим, что у нас есть ФЭ, реализующий булевыфункции g1, …,gk . Присоединяя выходы одних ФЭ к
входам
других,
можно
строить
сложные
схемы,
называемые схемами из ФЭ в базисе g1, …,gk . На рисунках
2 и 3 приведены примеры схем в базисе { , , } . При
изображении схем принимают следующее соглашение:
сигнал идет слева направо и сверху вниз. Легко понять,
что схема из ФЭ в базисе g1, …,gk реализует некоторую
суперпозицию функции g1, …,gk .
НАЗАД
ДАЛЕЕ
90
91. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Например, в схеме на рис. 2 мы можем пронумероватьвыходы всех ФЭ и, двигаясь слева направо, связать с
каждым выходом реализуемую на нем функцию: 1) p1 ,
2) p2 , 3) p1 p2 , 4) ( p1 p2 ) p2 . Понятно, что схема
на рис. 2 реализует последнюю из этих функций. И
наоборот, любая суперпозиция булевых функций g1, …,gk
может быть реализована подходящей схемой из ФЭ в
базисе {g1, …,gk } . Если система {g1, …,gk } полная, то
любую булеву функцию можно реализовать схемой в
базисе {g1, …,gk } .
НАЗАД
ДАЛЕЕ
91
92. Глава I. Логика высказываний. § 5. Применение логики высказываний.
В частности, из теоремы о функциональной полнотеследует, что любую булеву функцию можно реализовать
схемой в базисе { , , } . Более того, из доказательства
теоремы о функциональной полноте видно, как такую
схему построить.
Например, булеву функцию таблицы 1 описывает
формула q ( p1 p2 ) ( p1 p2 ) . Поэтому ее реализует
схема S, изображенная на рис. 4.
Займемся теперь построением схемы, вычисляющей
сумму p1+ p2 двоичных цифр p1 и p2 .
НАЗАД
ДАЛЕЕ
92
93. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Аналогичные,используют
но,
в
конечно,
более
вычислительных
сложные
машинах.
схемы
Двоичное
сложение определяют равенства: 0 + 0 = 0; 0 + 1 = 1 + 0 = 1
и 1 + 1 = 10. Обозначая 0 и 1 соответственно через И и Л,
получим следующую таблицу 5, в которой q и r обозначают
соответственно младший и старший разряды суммы p1+ p2.
p1 p2 r q
И И И И
Л И И Л
Таблица 5
Л И И Л
Л Л Л И
НАЗАД
ДАЛЕЕ
93
94. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Следовательно, булеву функцию для q реализует схема S нарис. 4, а булева функция для r есть p p
1
схема, изображенная на рис. 5.
2
и её реализует
Объединяя эти схемы
(рис. 6), получим схему из ФЭ с двумя входами p1, p2 и
двумя выходами q и r, вычисляющую сумму двоичных
цифр p1 и p2 .
p1
p2
рис. 4
НАЗАД
p1
q
p2
S
рис. 5
p1
S
q
p2
r
r
рис. 6
ДАЛЕЕ
94
95. Глава I. Логика высказываний. § 5. Применение логики высказываний.
В заключение покажем, как можно применятьлогику высказываний для упрощения схем из ФЭ. Две
схемы эквивалентны, если они реализуют одну и ту же
булеву функцию. Более простой будем считать схему с
меньшим числом ФЭ. Для упрощения некоторой схемы из
ФЭ строим соответствующую ей формулу, упрощаем эту
формулу
с
помощью
равносильностей
логики
высказываний и по упрощенной формуле строим новую
схему, которая, конечно эквивалентна исходной.
НАЗАД
ДАЛЕЕ
95
96. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Заметим, что наряду с основными равносильностями из §3для «сокращения» формул
в
базисе
{ , , } часто
применяют следующие равносильности: ; ;
( ) ; ( ) ; Л; И;
И ; Л ; Л Л; И И . Здесь через И (Л)
обозначена
произвольная
тождественно
истинная
(тождественно ложная) формула.
Упростим, например, схему изображенную на рис. 2.
Ей соответствует формула q ( p1 p2 ) p2 . По закону
дистрибутивности, q ( p1 p2 ) ( p2 p2 ) .
НАЗАД
ДАЛЕЕ
96
97. Глава I. Логика высказываний. § 5. Применение логики высказываний.
Применяя сформулированные вышеравносильности,
получим: q ( p1 p2 ) И ( p1 p2 ) . Наконец, по
закону
Де Моргана
q ( p1 p2 ) . Соответствующая
упрощенная схема изображена на рис. 3. Эту схему можно
было бы
еще упростить, если бы у нас был
ФЭ,
реализующий функцию | из §2. Тогда ( p1 p2 ) p1 | p2 ,
и соответствующая схема в базисе { | } состоит всего из
одного ФЭ.
НАЗАД
ДАЛЕЕ
97
98.
НАЗАДДАЛЕЕ
98
99. Глава II. Логика предикатов. Введение.
Вэтой
предикатов,
главе
мы
достаточный
математических
рассмотрим
язык
для
большинства
утверждений.
записи
Важную
логики
роль
в
формировании этого языка сыграли немецкий математик
Г. Фреге и американский философ Ч. Пирс, которые
ввели в рассмотрение предикаты и кванторы. Развитию
языка
логики
итальянского
предикатов
математика
Д.
способствовали
Пеано
и
работы
английского
философа Б. Рассела. Окончательно этот язык описан Д.
Гильбертом.
НАЗАД
ДАЛЕЕ
99
100. Глава II. Логика предикатов. Введение.
Польский математик А. Тарский дал точное определениеистинности формулы в алгебраической системе, описав
тем самым смысл формул логики предикатов.
НАЗАД
ДАЛЕЕ
100
101.
§ 6. Предикаты и функции.Логические операции над
предикатами
НАЗАД
ДАЛЕЕ
101
102. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
определениеn-местным предикатом на множестве A называют
отображение,
сопоставляющее
любой
( p q) (q p)
последовательности из n элементов множества A
однозначно определенный элемент из множества
{И, Л}.
НАЗАД
ДАЛЕЕ
102
103. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Предикаты обычно задают выражениями, которыесодержат переменные и при любых принадлежащих
множеству A значениях этих переменных принимают
значения
из
множества
высказывательных
{И,
Л}.
переменных,
В
отличии
от
переменные,
принимающие значения из данного множества A, будем
называть предметными. Для обозначения предикатов
будем применять предикатные переменные P, Q, R. Вместе
с предикатной переменной можно указывать также
предметные
переменные,
от
которых
зависит
соответствующий предикат.
НАЗАД
ДАЛЕЕ
103
104. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Примеры предикатов на множестве N = {0, 1, 2, …}:«x – простое число»,
«x<2y»,
«x сравнимо с y по модулю z».
Эти предикаты можно обозначать соответственно через
P(x), Q(x, y), R(x, y, z). Предикатные переменные называют
также предикатными символами. В нашем примере P, Q и
R являются соответственно одноместным, двухместным и
трехместным предикатными символами. В математике часто
используют,
например,
предикатные символы:
НАЗАД
следующие
двухместные
, , ||, , , .
ДАЛЕЕ
104
105. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Как уже говорилось, при подстановке элементов А вместопредметных переменных предикат принимает значение из
{И, Л}
множества
определенных
(например,
для
предикатов,
выше, P(13)=И, Q(3, 1)=Л, R(5, 7, 2)=И).
Поэтому над предикатами можно выполнять операции
логики
высказываний. При
этом
получим
новые
предикаты на том же множестве, например:
P( x ) Q( x, x ), Q( x, y ) Q( y , z ) Q( x, z ) .
Значения
таких
предикатов
можно
вычислить
в
соответствии с определениями логических операций (§ 1),
НАЗАД
ДАЛЕЕ
105
106. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
поэтому для предикатов справедливы многие утверждениялогики высказываний. Например, можно естественным
образом
определить
равносильность
и
производить
равносильные преобразования предикатов. По существу,
мы этим уже занимались при решении примеров из § 5.
Основное отличие логики предикатов от логики
высказываний в
том, что
над предикатами
можно
выполнять две новые логические операции:
«навешивание» квантора общности
и
квантора существования .
НАЗАД
ДАЛЕЕ
106
107. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Пусть P( x1 ,..., xn ) – предикат на множестве А. Навешиваяквантор общности (существования) по переменной
xi ,
получим предикат xi P( x1 ,..., xn ) (соответственно xi P( x1 ,
..., xn ) ), который означает, что для любого значения xi
верно P( x1 ,..., xn ) (существует xi , для которого верно
P( x1 ,..., xn ) ). Важно отметить, что эти новые предикаты не
зависят от xi , то есть являются (n-1)-местными. Для
одноместного предиката P(x) выражения x P(x ) и x P(x )
определяют высказывания. Например, для предиката на
множестве N «x – простое число»
простое число)
НАЗАД
и
выражения
x (x –
x ( x – простое число) задают
ДАЛЕЕ
107
108. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
соответственно ложное иистинное высказывания. С
похожей ситуацией читатель встречался в других разделах
математики. Например, значения выражений
b
a
и
i
i
cos xdx не зависят соответственно от переменных i и x.
a
НАЗАД
ДАЛЕЕ
108
109. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
определениеПусть P(x) – одноместный предикат на множестве А.
Высказывание x P(x ) истинно в точности тогда,
( p q) (q p)
когда P(x)=И для всех х из А. Высказывание x P(x )
истинно в точности тогда, когда P(x)=И хотя бы при
одном значении x A .
НАЗАД
ДАЛЕЕ
109
110. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Из определения следует, что высказывание x P(x )ложно в точности тогда, когда P(x)=Л хотя бы при одном
из A, а высказывание x P(x ) ложно в
точности тогда, когда P(x)=Л для всех х из А. Определение
значении x
можно применять для нахождения значений предикатов
xi P( x1 ,..., xn ) и xi P( x1 ,..., xn ) при n > 1.
Для этого
надо сначала зафиксировать значения всех переменных,
отличных от
xi (именно от них зависят эти предикаты).
После такой фиксации предикат Р будет зависеть только
от xi , что
позволит
использовать
данное
выше
определение.
НАЗАД
ДАЛЕЕ
110
111. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Итак,мы
ввели следующие
операции
над
предикатами: , , , , , . Определим еще некоторые
понятия, которые
операции,
позволят, используя
описанные
построить весьма богатый язык
логики
предикатов.
НАЗАД
ДАЛЕЕ
111
112. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
определениеn-местной функцией на множестве А называют
отображение,
сопоставляющее
любой
( p q) (q p)
последовательности из n элементов множества А
однозначно определенный элемент из А.
НАЗАД
ДАЛЕЕ
112
113. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Функцииобычно
задают
выражениями
с
предметными переменными, принимающими значения в
А
при
любых
обозначения
значениях
функции
переменных
используют
из
А.
Для
функциональные
символы f, g, h, за которыми указывают предметные
переменные. Например, в выражениях f(x), g(x, y), h(x, y, z)
через f, g и h обозначены соответственно одноместный,
двухместный и трехместный функциональные символы.
Часто
применяют
символы,
и
устоявшиеся
функциональные
например,
двухместные
функциональные
символы «+», «·», «–» и одноместные символы √ , sin, cos .
НАЗАД
ДАЛЕЕ
113
114. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Будемиспользовать
также
так
называемые
константные символы, то есть имена для фиксированных
элементов изучаемых множеств. Примеры константных
символов: 0, 1, i, e, .
Имея некоторые предикатные, функциональные и
константные символы, можно построить много новых
выражений, описывающих предикаты. Например, из
введенных выше символов можно построить выражения:
P(f(x)), f(x) = g(y, x), sin y < sin x.
НАЗАД
ДАЛЕЕ
114
115. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
определениеСигнатурой
предикатных,
символов.
НАЗАД
называют
произвольное
функциональных
и
множество
константных
( p q) (q p)
ДАЛЕЕ
115
116. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Для описания некоторой теории, например, какоголибо раздела математики, в сигнатуру вводят необходимыесимволы. Так, для некоторых разделов алгебры удобно
1 { , , ,0,1} , а для
тригонометрии – сигнатуру 2 { , , , sin, cos,0,1} .
использовать
сигнатуру
Заметим, что символ равенства «=» в сигнатуру обычно не
включают. Тем не менее, его всегда можно использовать
при
построении
выражений,
поскольку
предикат
равенства определен на любом множестве. В следующем
параграфе с каждой сигнатурой
формулы сигнатуры
НАЗАД
мы свяжем понятие
.
ДАЛЕЕ
116
117. Глава II. Логика предикатов. § 6. Предикаты и функции. Логические операции над предикатами.
Формулы и образуют язык логики предикатов, на которомможно записать многие математические утверждения.
НАЗАД
ДАЛЕЕ
117
118.
§7. Термы и формулыНАЗАД
ДАЛЕЕ
118
119. Глава II. Логика предикатов. § 7. Термы и формулы.
Здесьи
далее
обозначает
произвольную
фиксированную сигнатуру. Для краткости упоминание о
ней будем иногда опускать. Опишем один из видов
осмысленных
сигнатуры
НАЗАД
выражений
языка
логики
предикатов
.
ДАЛЕЕ
119
120. Глава II. Логика предикатов. § 7. Термы и формулы.
определениеТермами
сигнатуры
называют
выражения,
построенные индуктивно по следующим правилам:
( p q) (q p)
любая предметная переменная есть терм;
любой константный символ из
есть терм;
если ƒ – n-местный функциональный символ из
и t1,….., tn – термы, то выражение ƒ(t1,….., tn) тоже
терм.
НАЗАД
ДАЛЕЕ
120
121. Глава II. Логика предикатов. § 7. Термы и формулы.
Предметные переменные будем обозначать буквамиa, b, x, y, а термы
буквами u, s, t, применяя при
необходимости индексы.
Примеры
термов
сигнатуры
{+,·,0,1}
дают
выражения: 0, 1, x+y, x·x+y·y. Легко понять, что в данном
случае
термы,
натуральными
по
существу
коэффициентами.
суть
многочлены
Термами
с
сигнатуры
{+,·,sin,cos} являются, например, sin(x+y), sin x · sin y, y · cos
x, то есть тригонометрические выражения. В курсе
информатики
рассматривают
термы,
называя
их
арифметическими выражениями.
НАЗАД
ДАЛЕЕ
121
122. Глава II. Логика предикатов. § 7. Термы и формулы.
Введем теперь важное понятие формулы сигнатуры. Формулы описывают предикаты, которые можно
построить с помощью логических операций из равенства
и
предикатов,
символами из
НАЗАД
функций
и
констант,
обозначенных
.
ДАЛЕЕ
122
123. Глава II. Логика предикатов. § 7. Термы и формулы.
определениеФормулами сигнатуры
называют выражения,
построенные индуктивно по следующим правилам:
( p q) (q p)
выражения s = t и P(t1 ,..., t n ) ,где s, t, t1,….., tn – термы,
а
P – n-местный
предикатный
символ
из
,
являются формулами; если и – формулы, а х
– предметная переменная, то выражения ( ),
( ), ( ), , x , x являются формулами.
НАЗАД
ДАЛЕЕ
123
124. Глава II. Логика предикатов. § 7. Термы и формулы.
Как и в логике высказываний, существует алгоритм,позволяющий по данному выражению узнать, является ли
оно формулой данной конечной сигнатуры. Он состоит,
грубо говоря, в выписывании всех подформул данного
выражения до тех пор, пока не будет «выведено» само
выражение. Если это удалось, то выражение является
формулой, в противном случае – нет. Например, для
выражения
a b( (a 0) x (a x b))
последовательность
подформул
выглядит
следующим
a 0, (a 0), x( a x b)), (a 0) x(a x b),
b( ( a 0) x ( a x b)), . Поэтому есть формула.
образом:
НАЗАД
ДАЛЕЕ
124
125. Глава II. Логика предикатов. § 7. Термы и формулы.
определения1. Формулы, не содержащие логических операций,
назовем простейшими; из определения формулы
p q ) в (точности
q p)
следует, что простейшими (являются
формулы вида s = t и P(t1 ,..., t n ) .
2. В выражениях x (x ) и x (x ) подформулу
называют областью действия квантора по x.
3. Вхождение переменной x в некоторую формулу
называют свободным, если оно не находится в
области действия квантора x.
НАЗАД
ДАЛЕЕ
125
126. Глава II. Логика предикатов. § 7. Термы и формулы.
определения4. Переменная входит в формулу свободно, если
существует хотя бы одно ее свободное вхождение в
эту формулу.
( p q) (q p)
5. Предложением называют формулу без свободных
переменных.
НАЗАД
ДАЛЕЕ
126
127. Глава II. Логика предикатов. § 7. Термы и формулы.
Основное свойство свободных переменных состоит втом,
что
значение
формулы
зависит
от
значений
свободных переменных и не зависит от остальных
переменных. Это легко усмотреть из определений § 6 (см.
точное определение значения формулы в § 8). Поэтому
каждое предложение имеет фиксированное значение из
множества {И, Л}, и с помощью предложений можно
записывать утверждения. Например, рассмотренное выше
предложение
a b( ( a 0) x (a x b))
утверждает,
что любое уравнение первой степени имеет решение.
НАЗАД
ДАЛЕЕ
127
128. Глава II. Логика предикатов. § 7. Термы и формулы.
Предложение x y (sin( x y ) sin x cos y cos x sin y )выражает
формулу
синуса
суммы, а
предложение
t (0 t x(sin( x t ) sin x)) – периодичность синуса.
В заключении параграфа условимся о некоторых
обозначениях. Формулы будем обозначать буквами , ,
. В логике предикатов важную роль играет операция
подстановки
термов
t1 ,..., t n
в
формулу вместо
свободных вхождений переменных x1 ,..., xn . Для описания
такой подстановки формулу будем записывать в виде
( x1 ,..., xn ) при этом переменные xi попарно различны.
НАЗАД
ДАЛЕЕ
128
129. Глава II. Логика предикатов. § 7. Термы и формулы.
Результат одновременной подстановки термов ti вместовсех
свободных вхождений переменных x в
i
обозначают (t1 ,..., t n ) . Аналогично можно определить
операцию подстановки термов ti вместо переменных xi
в данный терм s s ( x ,..., x ) . Индукцией по построению
1
n
формулы (терма s) можно убедиться, что (t1 ,..., t n )
( s (t1 ,..., t n )) является формулой (термом). Подстановка
термов
в
формулу
требует одной предосторожности,
которую опишем в следующем соглашении: обозначение
(t1 ,..., t n ) применяют
только
если
в
результате
подстановки никакая переменная,
НАЗАД
ДАЛЕЕ
129
130. Глава II. Логика предикатов. § 7. Термы и формулы.
входящая в термы t1 ,..., t n , не попадает в область действияквантора по этой переменной. Необходимость этого
ограничения поясним на примере формулы ( x ) y ( x
y ) , означающей «существует элемент, больший x».
Примером допустимой подстановки является (z 1)
y ( z 1 y ) ; эта формула означает «существует элемент,
больший z + 1», что соответствует интуитивному смыслу
подстановки. Недопустима подстановка ( y ) y ( y y ) ,
приводящая
к
утверждению
«существует
элемент,
меньший самого себя» вместо ожидаемого утверждения
«существует элемент, больший y».
НАЗАД
ДАЛЕЕ
130
131. Глава II. Логика предикатов. § 7. Термы и формулы.
Во избежание аналогичных недоразумений и принятоописанное соглашение.
НАЗАД
ДАЛЕЕ
131
132.
§ 8. Значение термов иформул
НАЗАД
ДАЛЕЕ
132
133. Глава II. Логика предикатов. § 8. Значение термов и формул.
Определим значения термов и формул сигнатуры. Поскольку в формулы могут входить свободные
переменные
и
сигнатурные
символы,
сначала
надо
зафиксировать множество А (в котором принимают
значения
предметные
переменные),
значения
сигнатурных символов и свободных переменных в А.
Предикатные, функциональные и константные символы
были введены для обозначения предикатов и функций на
А и элементов из А.
НАЗАД
ДАЛЕЕ
133
134. Глава II. Логика предикатов. § 8. Значение термов и формул.
Поэтому фиксирование значений сигнатурных символовможно понимать как выбор интерпретации I, то есть
отображения,
сопоставляющего
предикатному
символу
P
каждому
n-местному
некоторый n-местный
предикат PI на А, каждому n-местному функциональному
символу f из
– некоторую n-местную функцию fI на А и
каждому константному символу с из – элемент сI из А.
НАЗАД
ДАЛЕЕ
134
135. Глава II. Логика предикатов. § 8. Значение термов и формул.
определениеАлгебраической системой сигнатуры
называют
пару (А; I), состоящую из непустого множества А и
( p q) (q p)
интерпретации I всех сигнатурных символов А.
НАЗАД
ДАЛЕЕ
135
136. Глава II. Логика предикатов. § 8. Значение термов и формул.
Алгебраическиесистемы
или,
короче,
просто
системы можно встретить во всех разделах математики.
Примеры систем сигнатуры {+,·,0,1}: (R,+,·,0,1), где R –
множество всех действительных чисел, а интерпретация
сигнатурных символов стандартна; (M, +I ,·I, 0I, 1I), где M –
множество все 2 × 2 – матриц с действительными
коэффициентами, +I
и
·I – сложение и умножение
матриц, 0I и 1I – нулевая и единичная матрицы из M.
Часто алгебраическую систему удобно обозначать
одной буквой А=(А; I), при этом интерпретации символов
P, f, c из обозначают соответственно PA , f A, cA.
НАЗАД
ДАЛЕЕ
136
137. Глава II. Логика предикатов. § 8. Значение термов и формул.
Пусть теперь t t ( x1 ,..., xk ) – терм сигнатуры ,не содержащий переменных, отличных от указанных. В
любой системе А=(А; I) сигнатуры
этот терм задает
k-местную функцию
заданных
t A ( x1 ,..., xk ) , значение которой при
значениях
найти
xi ai A можно
последовательным вычислением
значений
функций,
символы которых входят в t. Например, для терма t ( x, y )
(( x x y ) 1) 1
при
стандартной
интерпретации
сигнатуры {+,·,1} на множестве натуральных чисел N
имеем: t ( 2,3) (( 2 2 3) 1) 1 (( 4 3) 1) 1 (7 1) 1
8 1 9 .
НАЗАД
ДАЛЕЕ
137
138. Глава II. Логика предикатов. § 8. Значение термов и формул.
Точноеопределение
дадим
индукцией
по
построению t.
определение
Если t xi , то t A ( a1 ,..., ak ) ai ; если t c , то
t A (a1 ,..., ak ) с A ; если t f (t1 ,..., t n ) и значения b j
( p q) (q p)
A
t j (a1 ,..., ak ) уже определены по предложению
индукции, то t A ( a1 ,..., ak ) f A (b1 ,..., bn ) .
НАЗАД
ДАЛЕЕ
138
139. Глава II. Логика предикатов. § 8. Значение термов и формул.
Значениятермов
согласованы
с
операцией
подстановки.
Теорема. Если терм
u ( y1 ,..., ym ) есть результат
подстановки термов si ( y1 ,..., ym ) вместо переменных xi в
t ( x1 ,..., xk ) , то есть u t ( s1 ,..., sk ) , то при всех
a1 ,..., am A справедливо равенство u A (a1 ,..., am )
A
A
,
где
bi si (a1 ,..., am ) .
t (b1 ,..., bk )
терм
Доказательство.
Проведем
индукцию
по
построению t, то есть по количеству l(t) вхождений в t
функциональных символов. При l(t) = 0 либо t xi , либо
t=c.
НАЗАД
ДАЛЕЕ
139
140. Глава II. Логика предикатов. § 8. Значение термов и формул.
Если t = xi, то u = si, откудаu A (a1 ,..., am ) siA (a1 ,..., am )
bi t A (b1 ,..., bk ) . Если t = c, то u = c, откуда u A (a1 ,..., am )
c A t A (b1 ,..., bk ) . Пусть l(t) > 0 и для термов s с l(s) < l(t)
t f (t1 ,..., t n ) ,
u f (u1 ,..., un ) , где u j ( y1 ,..., ym ) t j ( s1 ,..., sk ) ;
A
1 j n , по
u j (a1 ,..., am ) t Aj (b1 ,..., bk )
при
утверждение теоремы справедливо. Тогда
предположению индукции, откуда u A (a1 ,..., am ) f A (u1A (a1 ,
..., am ),..., unA (a1 ,..., am )) f A (t1A (b1 ,..., bk ),..., t nA (b1 ,..., bk ))
t A (b1 ,..., bk ) .
■
Перейдем теперь к формулам.
НАЗАД
ДАЛЕЕ
140
141. Глава II. Логика предикатов. § 8. Значение термов и формул.
Пусть( x1 ,..., xk ) – формула сигнатуры , все
свободные
переменные
которой
находятся
среди
указанных, и А=(А; I) – алгебраическая система сигнатуры
. Формула
построена с помощью операций , , ,
, , из простейших формул вида s = t, P(t1 ,..., t n ) , где s,
t, t1 ,..., t n – термы сигнатуры , P – предикатный символ
из
.
Ясно, что термы задают функции на A, а
простейшие формулы описывают некоторые предикаты
на A. Применяя к этим предикатам логические операции в
соответствии с их определением в §6, получим, что
задает на A предикат, зависящий от
НАЗАД
x1 ,..., xk ;
ДАЛЕЕ
141
142. Глава II. Логика предикатов. § 8. Значение термов и формул.
этот предикат обозначим через A ( x1 ,..., xk ) . Точноеопределение значения A ( a1 ,..., ak ) этот предикат при
xi ai A дадим индукцией по построению .
НАЗАД
ДАЛЕЕ
142
143. Глава II. Логика предикатов. § 8. Значение термов и формул.
определениеЕсли есть s = t, то A ( a1 ,..., ak ) И
в точности
тогда, когда совпадают s A ( a1 ,..., ak ) и t A ( a1 ,..., ak ) ;
( p q ) A( q A p )
если есть P(t1 ,..., t n ) , то (a1 ,..., ak ) P (t1 (a1 ,...,
A
A
;
если
есть
,
то
(a1 ,...,
(
)
ak ),..., t n (a1 ,..., ak ))
A
ak ) A (a1 ,..., ak ) A (a1 ,..., ak ) , и аналогично для
операций , и ; если есть x ( x, x1 ,..., xk ),
то A ( a1 ,..., ak ) И в точности тогда, когда A (b, a1 ,
..., ak ) И при любом b A ;
НАЗАД
ДАЛЕЕ
143
144. Глава II. Логика предикатов. § 8. Значение термов и формул.
продолжение определенияесли есть x ( x, x1 ,..., xk ) , то A ( a1 ,..., ak ) И в
точности тогда, когда A (b, a1 ,..., ak ) И хотя бы при
одном b A .
НАЗАД
( p q) (q p)
ДАЛЕЕ
144
145. Глава II. Логика предикатов. § 8. Значение термов и формул.
Заметим, что в любой системе A предложениезадает высказывание, то есть A {И, Л} .
Как и для термов, значения формул согласованы с
операцией
подстановки
термов
в
формулу
вместо
свободных вхождений переменных. А именно, пусть
( y1 ,..., ym ) – результат подстановки в формулу
свободных
( x1 ,..., xn ) термов ti ( y1 ,..., ym ) вместо
вхождений переменных xi. Тогда для любых a ,..., a из А
1
справедливо
m
равенство A (a1 ,..., am ) A (b1 ,..., bn ) , где
bi ti (a1 ,..., ak ) . Доказательство этого факта аналогично
A
доказательству предшествующей теоремы.
НАЗАД
ДАЛЕЕ
145
146. Глава II. Логика предикатов. § 8. Значение термов и формул.
Проиллюстрируем примером процедуру нахождениязначения формулы. Рассмотрим предложение x y ( f ( x )
f ( y ) x y ) сигнатуры { f }. Это предложение в системе
(R; x2) ложно (поскольку предикат x 2 y 2 x y ложен
при x = –1, y = 1), а в системе (R; x) – истинно (поскольку
предикат x y x y истинен при всех x, y R ).
НАЗАД
ДАЛЕЕ
146
147. Глава II. Логика предикатов. § 8. Значение термов и формул.
определения1. Формула общезначима в системе А, если она
истинна в А при любых значениях свободных
( p q) (q p)
переменных.
2. Формула общезначима, если она истинна в любой
системе
при
любых
значениях
свободных
переменных.
НАЗАД
ДАЛЕЕ
147
148. Глава II. Логика предикатов. § 8. Значение термов и формул.
Примеробщезначимой
( x(P( x) Q( x )) P(c )) Q(c)
формулы – предложение
сигнатуры
{P, Q, c}.
Проверим, что в произвольной системе А оно истинно.
Если посылка импликации ложна в А, то вся импликация
истинна. Пусть посылка истинна
в
А. Тогда, по
определению конъюнкции, формулы
x (P( x) Q( x )) и
P(c) истинны в А. По определению значения формулы,
импликация
[P( c)]A [Q(c)]A истинна.
Поскольку
[P( c)]A И , то и [Q(c)]A И . Итак, посылка и заключение
данного предложения истинны в А, поэтому и само оно
истинно в А.
НАЗАД
ДАЛЕЕ
148
149. Глава II. Логика предикатов. § 8. Значение термов и формул.
Этотпример
интересен
тем,
что
дает
строгое
доказательство правильности рассуждения из §5, которое
невозможно
проанализировать
с
помощью
логики
высказываний. Наше предложение является записью
этого рассуждения, если Q(x) означает «x смертен», P(x) –
«x - человек», а c обозначает Цезаря.
Предложение x y ( x y y x ) ,
напротив, не
общезначимо, поскольку оно ложно в системе 2×2-матриц
с действительными коэффициентами, если символ «· »
интерпретировать как умножение матриц.
НАЗАД
ДАЛЕЕ
149
150. Глава II. Логика предикатов. § 8. Значение термов и формул.
Общезначимыеформулы
являются
важным
объектом дальнейшего изучения. В логике предикатов
задача описания общезначимых формул гораздо сложнее,
чем в логике высказываний. Выделим сначала простой
подкласс общезначимых формул.
НАЗАД
ДАЛЕЕ
150
151. Глава II. Логика предикатов. § 8. Значение термов и формул.
определениеТавтологией сигнатуры
которая может
логики
называют формулу,
быть получена
высказываний
из тавтологии
( p q) (q p)
подстановкой
форму
сигнатуры вместо высказываний переменных.
НАЗАД
ДАЛЕЕ
151
152. Глава II. Логика предикатов. § 8. Значение термов и формул.
Ясно, чтолюбая
тавтология
сигнатуры
общезначима. Примеры тавтологий – формулы
x P(x )
( x P( x)) и x P( x) (Q( y ) x P( x)) . Они получены
подстановкой из тавтологий p p и p ( q p )
соответственно. Формулы
x (P( x ) P( x )) и x P(x)
x P(x ) общезначимы, но не тавтологии.
Простота понятия тавтологии проявляется в том, что
легко сформулировать алгоритм, выясняющий по любой
формуле
конечной
сигнатуры,
является
ли
она
ДАЛЕЕ
152
тавтологией.
НАЗАД
153. Глава II. Логика предикатов. § 8. Значение термов и формул.
Подчеркнем,что
в
логике
высказываний
понятия
тавтологии и общезначимой формулы совпадают, а в
логике предикатов класс общезначимых формул шире
класса тавтологий.
НАЗАД
ДАЛЕЕ
153
154.
§9. Равносильность.Преобразование формул
НАЗАД
ДАЛЕЕ
154
155. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Влогике
предикатов,
в
отличие
от
логики
высказываний, существуют два естественных понятия
равносильности.
определение 1
Формулы называют равносильными в системе А,
если они принимают одинаковые значения в А при
( p q) (q p)
всех значениях в них свободных переменных.
НАЗАД
ДАЛЕЕ
155
156. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
определение 2Формулы
называют
равносильными, если
они
принимают одинаковые значения в любой системе
( p q) (q p)
при всех значениях свободных переменных.
НАЗАД
ДАЛЕЕ
156
157. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Ясно, что формулы равносильны в точности тогда,когда равносильны в любой системе. Равносильность
(равносильность в системе А) формул
и будем
обозначать так: ( ) . Результаты этого параграфа
A
справедливы для обоих отношений равносильности. Для
кратности будем их формулировать только д ля отношения
.
Свойства отношения равносильности.
1. Отношение
рефлексивно,
симметрично и
транзитивно.
НАЗАД
ДАЛЕЕ
157
158. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
2. Если и 1 1 ,то 1 1 , 1
1 , 1 1 , и x x , x x
для любой предметной переменной x.
3. Формулы
и
равносильны тогда и только
тогда, когда формула ( ) ( ) общезначима.
Доказательства. Свойства 1, 3 и относящиеся к
конъюнкции, дизъюнкции, импликации и отрицанию
равносильности свойства 2 читатель легко докажет
самостоятельно, следуя доказательствам соответствующих
утверждений из §3.
НАЗАД
ДАЛЕЕ
158
159. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Докажем свойство 2 для квантора общности. Пустьи
все свободные
переменные
этих формул
содержатся среди
x1 ,..., xk , x . Надо понимать, что
A
A
равенство [ x ] ( a1 ,..., ak ) [ x ] ( a1 ,..., ak ) верно в
любой системе A=(A; I) при любых a ,..., a из А. Пусть
1
k
[ x ]A (a1 ,..., ak ) И . Тогда A ( a1 ,..., ak , b) И при любом
b A . Поскольку , то и A (a1 ,..., ak , b) И при
любом b A , откуда [ x ]A ( a1 ,..., ak ) И . Если же
[ x ]A (a1 ,..., ak ) Л, то A ( a1 ,..., ak , b) Л при некотором
b A , и A (a1 ,..., ak , b) Л при этом же b. Тогда
[ x ]A (a1 ,..., ak ) Л . Равносильность доказана.
НАЗАД
ДАЛЕЕ
159
160. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Аналогичным образом легко доказать свойство 2 дляквантора существования.
В логике предикатов справедлива теорема о замене.
Она имеет такую же формулировку, как в §3, и может
быть доказана по той же схеме. Поэтому здесь ее
доказательство не приводим.
Основные равносильности логики
предикатов.
Равносильности логики высказываний из §3 справедливы
и для формул логики предикатов.
НАЗАД
ДАЛЕЕ
160
161. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Кроме того, для любых формул и справедливыследующие основные равносильности, в которых x –
предметная переменная, не входящая свободно в , а y –
предметная переменная, не входящая в .
1. ( x ) x ( ) ;
2. ( x ) x ( ) ;
3. x x ( ) ;
4. x x ( ) ;
5. x x ( ) ;
6. x x ( ) ;
7. x ( x ) y ( y ) ;
8. x ( x ) y ( y ) ;
Доказательства. Равносильность 2n+2 двойственна
равносильности 2n+1 ( n {0,1,2,3}) , если и считать
взаимно двойственными.
НАЗАД
ДАЛЕЕ
161
162. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Каждая равносильность следует из двойственной кней. Покажем для примера, как равносильность 2 можно
вывести
из
равносильности
1.
Допустим,
что
равносильность 1 справедлива для любой формулы. Тогда
x( ) x( ). Используя основную равносильность
2 (§3) и свойства равносильности, получим: x( )
( x( )) x( ) x
. Равносильность 2
доказана.
Приведенное
достаточно
доказать
рассуждение
показывает,
равносильности
с
что
нечетными
номерами.
НАЗАД
ДАЛЕЕ
162
163. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Докажем равносильности 1 и 5, оставляя доказательстваравносильностей 3 и 7 читателю для самостоятельной
работы.
Зафиксируем систему A=(A; I) и значения в А всех
свободных переменных равносильности 1 и проверим, что
при этих значениях [ ( x )]A [ x( )]A . Пусть сначала
[ ( x )]A И . Тогда [ x ]A Л , поэтому при A (a)
Л некотором a A . Следовательно, [ ] (a) И и
[ x( )]A И . Если же [ ( x )]A Л , то [ x ]A И ,
A (a) И при всех a A и [ x( )]A Л .
A
Равносильность 1 доказана.
НАЗАД
ДАЛЕЕ
163
164. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Для доказательства равносильности 5 снова зафиксируемсистему A=(A; I) и значения всех входящих в эту
равносильность свободных переменных. Заметим, что по
условию x не входит в число этих переменных, т.е.
значение x пока не зафиксировано. Надо проверить, что
[ x ]A [ x( )]A . Пусть сначала [ x ]A И ,
тогда хотя бы одно из значений A , [ x ]A истинно. Если
A И , то [ ]A (a) И при любом a A , откуда
[ x( )]A И . Если же [ x ]A И , то A (a ) И
A
[
]
(a) И для всех a A и опять
при любом a A,
[ x( )]A И .
НАЗАД
ДАЛЕЕ
164
165. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Наконец, рассмотрим случай, когда [ x ]A Л .при
A (a) Л
некотором значении a из А. Следовательно, [ ]A ( a ) Л
и [ x( )]A Л .
Тогда A [ x ]A Л ,
поэтому
Это завершает проверку равносильности 5.
■
Равносильности 1 и 2 называют законами Де
Моргана для кванторов, равносильности 3 - 6 – правилами
вынесения кванторов, равносильности 7 и 8 – правилами
замены связанной переменной.
Выведем необходимое для главы 4 следствие.
НАЗАД
ДАЛЕЕ
165
166. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Онокасается
«ограниченных»
часто
используемых
кванторов.
в
математике
Например, определение
непрерывности функции f(x) в точке x0 выглядит так:
0 0 x( x x0 ) f ( x) f ( x0 ) . Здесь 0 и
0 – ограниченные кванторы, в которых переменные
и
пробегают не все множество
R, а лишь
его
подмножества, указанные в ограничениях 0 и 0 .
Поскольку ограничения являются формулами, в общем
случае выражения с ограниченными кванторами можно
записать в виде x ( x )
и
формулы, причем формула
НАЗАД
x ( x ) ,
где
и –
является ограничением.
ДАЛЕЕ
166
167. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Читать эти выражения следует так:истинно для любого x, удовлетворяющего условию ;
существует x, удовлетворяющее условию , для которого
истинно.
Ясно, что смысл этих выражений описывают следующие
формулы с обычными кванторами: x ( ) и x ( ).
Таким образом, ограниченные кванторы
определены
через обычные, их используют лишь для кратности и
удобства
записи.
Например,
в
определении
непрерывности можно использовать обычные кванторы:
(0 (0 x( x x0 ) f ( x) f ( x0 ) ))) .
НАЗАД
ДАЛЕЕ
167
168. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Докажем, что законы Де Моргана справедливы дляограниченных кванторов.
Следствие. ( x ) x ( ) и
( x ) x ( ) .
Докажем для примера первую равносильность:
( x ) ( x( )) x ( ) x ( )
x( ) x ( ) .
■
Перейдем к преобразованиям формул.
НАЗАД
ДАЛЕЕ
168
169. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
По аналогии с соответствующим определением влогике высказываний (см. §4) формулой специального
вида назовем формулу без импликаций, в которой
отрицания относятся только к простейшим подформулам.
Как и в §4, но с использованием законов Де Моргана для
кванторов, легко проверить, что любую формулу логики
предикатов можно привести к специальному виду. С
помощью этого результата покажем, что бескванторные,
т.е. не содержащие кванторов формулы
сигнатуры
{<,+,· ,0,1}, по существу, совпадают с выражениями,
знакомыми читателю из алгебры.
НАЗАД
ДАЛЕЕ
169
170. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Предложение. Любая бескванторная формуласигнатуры {<,+,· ,0,1} равносильна в системе R=(R; I), где
I – стандартная интерпретация сигнатурных символов,
подходящей
совокупности
уравнений
и
систем
неравенств
алгебраических
с
натуральными
дана
бескванторная
коэффициентами.
Доказательство.
формула
Пусть
. Найдем равносильную ей бескванторную
формулу 1 специального вида. Согласно §7, 1 построена
из простейших формул s = t, s < t и их отрицаний с
помощью и .
НАЗАД
ДАЛЕЕ
170
171. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Заменим входящие в 1 отрицания простейших формулпо следующим правилам: ( s t ) ( s t t s ) и ( s t )
R
R
( s t t s ) . В результате получим равносильную в
1
R
R формулу 2 , которая построена из простейших формул
с помощью и . Приведя 2
к ДНФ ( см. §4), в
которой роль высказывательных переменных играют
простейшие формулы, найдем равносильную ей в R
формулу
3 . Эта формула есть либо элементарная
конъюнкция, либо дизъюнкция нескольких элементарных
конъюнкций простейших формул.
НАЗАД
ДАЛЕЕ
171
172. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Из определения терма следует, что значения в R любоготерма сигнатуры {<,+,· ,0,1} совпадают со значениями
некоторого многочлена с натуральными коэффициентами.
В §5 отмечено, что дизъюнкция и конъюнкция условий
описывают соответственно совокупность и систему этих
условий. Поэтому формула
систем
алгебраических
описывает совокупность
уравнений
натуральными коэффициентами.
и
неравенств с
■
В заключении параграфа докажем возможность
приведения любой формулы к некоторому виду.
НАЗАД
ДАЛЕЕ
172
173. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
определениеФормулу
специального
вида
называют
предваренной, если она либо бескванторная, либо
( p q) (q p)
имеет вид Q1 x1... Q k xk , где Qi – кванторы, xi –
попарно различные переменные и формула
не
содержит кванторов.
НАЗАД
ДАЛЕЕ
173
174. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Теорема о приведении кпредварительному виду.
Любая формула логических предикатов равносильна
некоторой предваренной формуле.
Доказательство.
формула
Пусть
дана произвольная
. Она равносильна подходящей формуле
специального
вида
1 .
Доказательство
проведем
индукцией по числу n( 1 ) вхождений символов
в 1 . Если n( 1 ) 0 , то формула 1
имеет предваренный вид.
НАЗАД
, , ,
бескванторная и
ДАЛЕЕ
174
175. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Допустим, что n( 1 ) n 1 и для формул с меньшимчислом вхождений утверждение верно. Формула 1 имеет
видов: x , x , ( ), ( ) – и, по
индукционному предположению, формулы и можно
один
из
привести к предваренному виду: 1 Q1 x1... Q n xn 2 ( x1 ,
..., xn ), 1 R 1 y1... R m ym 2 ( y1 ,..., ym )
кванторы,
,
где
Qi, Rj –
n≥0
и
формулы
2 и 2 –
1 x ( x) ,
то
1 u 1 (u )
, где
u–
переменная, u {x1 ,..., xn } ,
и
m ≥ 0,
бескванторные.
Если
подходящая
новая
равносильна предваренной формуле.
НАЗАД
ДАЛЕЕ
175
176. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
1 x рассуждения аналогичны. Рассмотримслучай 1 (для 1 рассуждение аналогично).
Для
Выберем различные
переменные a1 ,..., an , b1 ,..., bm ,
входящие в формулы
и
не
. Применяя свойства
равносильности и равносильности 3 - 8 из §7, получим:
1 1 1 Q1 a1... Q n an 2 (a1 ,..., an ) R 1 b1... R m bm 2 (b1 ,..., bm )
Q1 a1... Q n an R 1 b1... R m bm ( 2 (a1 ,..., an ) 2 (b1 ,..., bm )).
Последняя формула – предваренная.
НАЗАД
■
ДАЛЕЕ
176
177. Глава II. Логика предикатов. § 9. Равносильность. Преобразование формул.
Пример приведения к предваренной форме:x y P( x, y ) x y Q( x, y ) x y P( x, y ) x y Q( x, y )
x y P( x, y ) x y Q( x, y ) a b P(a, b) c d Q(c, d )
a b c d ( P(a, b) Q(c, d )).
НАЗАД
ДАЛЕЕ
177
178.
§10. Модели. Логическоеследование
НАЗАД
ДАЛЕЕ
178
179. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Напомним, что мы рассматриваем произвольнуюфиксированную сигнатуру
и что предложения – это
формулы без свободных переменных.
определение
Модельно для множества предложений Т называют
алгебраическую систему, в которой все предложения
из Т истинны.
НАЗАД
( p q) (q p)
ДАЛЕЕ
179
180. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Если Т состоит из одного предложения, то модель дляТ называют моделью для этого предложения.
определение
Система А=(А; I) конечна (бесконечна), если А –
конечное (бесконечное) множество.
( p q) (q p)
Следующее
утверждение
демонстрирует
содержательность понятия истинности формулы логики
предикатов: с его помощью можно различить конечные и
бесконечные множества.
НАЗАД
ДАЛЕЕ
180
181. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Предложение. Существует формула без свободныхпеременных,
имеющая
бесконечную
модель,
но
не
имеющая конечной модели.
Доказательство. Докажем, что такой формулой
является предложение
a x ( a f ( x)) x y ( f ( x) f ( y ) x y )
сигнатуры { f }. Обозначим через и члены
конъюнкции в формуле . Бесконечной моделью для
является, например, система N=(N; x+1).
Действительно, N И , поскольку предикат x ( a x 1)
на N истинен при a 0 N , и N И,
НАЗАД
ДАЛЕЕ
181
182. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
так как предикат x 1 y 1 x yистинен при всех
N
x, y N . Следовательно, И .
Докажем, что не имеет конечных моделей.
Предположим
модель для .
противное:
пусть А=(А; f) – конечная
Тогда N N И . Для получения
противоречия достаточно найти последовательность an
( n N) парно различных элементов из А. Пусть a0 –
элемент из А, для которого [ x ( a0 f ( x ))] A И , и
an 1 f (an ) при любом n N . Остается проверить, что
все элементы
an попарно
различны,
а
для
этого
достаточно доказать, что an k 1 ak при всех n, k N .
НАЗАД
ДАЛЕЕ
182
183. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Последнее утверждение проверим индукцией по k. Приk = 0 (базис индукции)
an 1 a0
следует из того, что
an 1 f (an ) и a0 f (an ) по выбору a. Допустим, что
n N истинно
an k 1 ak
(предположение индукции), и докажем, что an k 2 ak 1
при
всех
соотношение
для всех n N(шаг индукции). Если бы было an k 2 ak 1,
т.е. f (an k 1 ) f (ak ) , то из N И получили бы an k 1
ak , что противоречит предположению индукции.
■
Рассмотрим важное понятие логического следования.
НАЗАД
ДАЛЕЕ
183
184. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
определениеПредложение
логически следует из множества
предложений Т (
является логическим следствием
( p q) (q p)
Т), если истинно в любой модели для Т.
Понятия модели и логического следования можно
применять не только для предложений, но и для
произвольных формул.
НАЗАД
ДАЛЕЕ
184
185. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
определения1. Моделью для множества формул Т называется
алгебраическая система, в которой все формулы из Т
( p q) (q p)
общезначимы.
2. Формула
формул Т, если
логически
следует из множества
общезначима в любой модели
для Т.
НАЗАД
ДАЛЕЕ
185
186. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
ЗаписьT |
означает, что логически следует
из Т. Если T { 0 ,..., n } – конечное множество, то вместо
T | иногда удобнее писать 0 ,..., n | . В случае
пустого множества Т вместо T | будем писать | .
Свойства логического следования.
Для любого множества предложений Т и любых
предложений
и
справедливы
следующие
утверждения.
1. T | в точности тогда, когда множество T { }
не имеет модели.
2. | в точности тогда, когда
НАЗАД
общезначимо.
ДАЛЕЕ
186
187. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
3. T | ( ) равносильно тому, что T { } | .4. Для непустого конечного множества T { 0 ,..., n }
условие T | равносильно общезначимости предложения
0 ( 1 ... ( n )...) .
Доказательства.
1. Достаточно
проверить, что
следует из Т, тогда и только тогда, когда
модель. Действительно, если
логически не
T { } имеет
логически не следует из
Т, то, по определению, найдется модель А для Т, в которой
ложно. Тогда А – модель для T { } .
НАЗАД
ДАЛЕЕ
187
188. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Если же А – модель дляT { } , то А – модель для Т и
A Л , поэтому логически не следует из Т. Свойство
1 доказано.
2. Полагая в свойстве 1 Т=Ø получим, что условие
| равносильно тому, что не имеет модели, то есть
ложно, а истинно в любой системе А. Отсюда
следует свойство 2.
3. Из
равносильности ( ) следует,
что А есть модель для ( ) в точности тогда, когда А
есть модель для множества { , } .
НАЗАД
ДАЛЕЕ
188
189. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
По свойству 1, условие Т | ( ) равносильно тому,что Т { ( )} не имеет модели. Тогда и Т { , }
(Т { }) { } не имеет модели, а это, опять по
свойству 1, равносильно условию T { } | .
4. Свойство 4 следует из свойств 2 и 3. Например, при
n = 2 из свойства 3 выводим равносильность следующих
утверждений:
0 , 1 , 2 | ; 0 , 1 | ( 2 ); 0 | 1 ( 2 ); | 0 ( 1
( 2 )) . По свойству 2 последнее условие
равносильно общезначимости формулы
0 ( 1 ( 2 )) .
НАЗАД
ДАЛЕЕ
189
190. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Свойство 1 описывает связь между логическимследованием и существованием модели, свойства 2 и 4 –
связь между общезначимостью и логическим следованием,
а свойство 3 – связь между логическим следованием и
импликацией.
Поясним введенные понятия примерами.
множество G
сигнатуры
состоит из
следующих
Пусть
предложений
g { , 1 , e}:
1) x y z ( x ( y z ) ( x y ) z ) ;
2) x( x e x) ;
3) x( x x 1 e) ;
НАЗАД
ДАЛЕЕ
190
191. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Это известные аксиомы группы. Модели для G –алгебраические системы сигнатуры
g в которых эти
аксиомы истинны. В алгебре такие системы называют
группами. Логические следствия множества G – это
предложения сигнатуры
g истинные во всех группах,
т.е. формулируемые на языке логики предикатов теоремы
теории групп. Мы приведем пример такой теоремы в §14, а
сейчас покажем, как свойства логического следования
можно применить для доказательства того, что некоторое
утверждение не является теоремой теории групп.
НАЗАД
ДАЛЕЕ
191
192. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Рассмотрим предложение x y ( x y y x ) . Посвойству 1 логического следования для доказательства
того, что логически не следует из G, достаточно найти
модель для множества G { } . Пусть М – множество
всех невырожденных 2 × 2-матриц с действительными
коэффициентами,
а
символы
g
сигнатуры
интерпретированы как произведение матриц, операция
обращения матрицы
и
единичная матрица
из
М
соответственно. Ясно, что при такой интерпретации I
система (М; I) является
моделью для
G { } , что
завершает доказательство.
НАЗАД
ДАЛЕЕ
192
193. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Второй пример связан с геометрией. Пусть Т –множество
всех
аксиом
планиметрии
Евклида,
записанных формулами подходящей сигнатуры (проще
всего «переводу» на язык логики предикатов поддаются
аксиомы Гильберта). Тогда логические следствия Т – это
утверждения, истинные всякий раз, когда истинны
аксиомы
планиметрии.
Иными
словами,
логические
следствия Т – это теоремы планиметрии, формулируемые
на языке логики предикатов. Обозначим через
пятый
постулат Евклида о параллельных:
НАЗАД
ДАЛЕЕ
193
194. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
через точку А, не лежащую не прямой l, в плоскости,определяемой точкой А и прямой l, проходит ровно одна
прямая, не пересекающаяся с l. Как известно, – одна
из аксиом планиметрии, т.е. Т . Пусть Т 0 Т\ { } –
множество всех аксиом планиметрии, отличных от пятого
постулата. Важнейшая геометрическая проблема, которую
математики не могли решить в течение многих веков –
следует ли пятый постулат из Т0?
российский
математик
Только в XIX веке
Н. И. Лобачевский
вплотную
подошел к доказательству того, что не следует из Т0.
НАЗАД
ДАЛЕЕ
194
195. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Итальянскийматематик
математик
А.
Клейн
Е.
Бельтрами
обосновали
Лобачевского, построив модель для
и
немецкий
рассуждения
T0 { } . Одной из
основных причин того, что проблема пятого постулата так
долго не поддавалась решению, было отсутствие точного
определения интуитивно ясного понятия логического
следования. Лишь после того, как такое определение было
сформулировано, удалось относительно просто решить
указанную
проблему.
Последний
пример
связан
с
арифметикой. Обозначим через СА следующее множество
предложений сигнатуры {<,+,· ,0,1} .
НАЗАД
ДАЛЕЕ
195
196. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
1. 0 1 1 ;2. x ( x 1 0) ;
3. x y ( x 1 y 1 x y ) ;
4. x ( x 0 x ) ;
5. x y ( x ( y 1) ( x y ) 1) ;
6. x ( x 0 0) ;
7. x y ( x ( y 1) ( x y ) x ) ;
8. x ( x 0) ;
9. x y ( x y x y y x ) ;
10. x y ( x y 1 x y x y ) ;
Здесь есть сокращение для ( ) ( ) .
Предложения
1 - 10
называют
аксиомами
слабой
арифметики (СА). Они выражают некоторые свойства
натуральных чисел.
НАЗАД
ДАЛЕЕ
196
197. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Читателю легко проверить, что система N=(N; <, +, , 0, 1)при стандартной интерпретации сигнатурных символов
является моделью для СА. Ее называют стандартной
моделью, в отличие от других, «экзотических» моделей,
одну из которых рассмотрим ниже. Из определения
логического следования вытекает, что любое следствие
аксиом слабой арифметики истинно в N. Интересен
вопрос, верно ли обратное, т.е. всякое ли истинное в N
предложение следует из СА?
Покажем, что это не так. Определим систему М=(М;
<, +, , 0, 1) следующим образом.
НАЗАД
ДАЛЕЕ
197
198. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Пусть М получено из N добавлением единственногоэлемента , т.е. М N { }. Предикат < на М зададим
так: при x, y N значение x < y определено обычным
x истинно при всех
x M ; выражение y ложно при y N . Функцию
«+» на М зададим так: при x, y N значение x + y
образом;
выражение
определено стандартно, в остальных случаях
x y .
Функцию «·» на М определим следующим образом: при
x, y N значение x · y обычное; 0 0 ; y при
y M и y 0; x
при x M . Наконец, пусть
символы 0 и 1 имеют обычные значения.
НАЗАД
ДАЛЕЕ
198
199. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Несложным разбором случаев можно проверить, что всеаксиомы слабой арифметики истинны в М, то есть М –
модель для СА.
Для примера проверим аксиому 7. Пусть x, y M;
надо показать, что x ( y 1) ( x y ) x . При x, y N это
очевидно. При x N и y имеем
x ( y 1) x
x ( x y ) x . При x и y M имеем
x ( y 1) ( y 1) ( x y ) ( x y ) x .
Примеры
предложений, истинных в
N
и не
следующих из СА: x ( x x ) и x ( x 1 x ) .
НАЗАД
ДАЛЕЕ
199
200. Глава II. Логика предикатов. § 10. Модели. Логическое следование.
Длядоказательства
достаточно
проверить
(согласно
свойству 1 логического следования), что М – модель для
СА { , } , т.е. что M M Л . Для это следует
из того, что , а для – из того, что 1 .
НАЗАД
ДАЛЕЕ
200
201.
НАЗАДДАЛЕЕ
201
202. Глава III. Исчисление предикатов. Введение.
Во второй главе понятие логического следования былоопределено
с
использованием
абстрактных
понятий
предиката, модели и т. д. Между тем, со времен Евклида
математики
доказывали
теоремы,
не
используя
эти
понятия в явном виде. Точное определение доказательства
(вывода)
сформулировал
Д.
Гильберт.
В
1930
г.
К. Гедель доказал теорему о полноте, связавшую понятия
выводимости и логического следования (доказуемость и
истинность).
НАЗАД
ДАЛЕЕ
202
203. Глава III. Исчисление предикатов. Введение.
Онже
дал
первое
доказательство
существовании
модели,
которая,
демонстрирует
наличие
у
исследования.
Важное
теоремы
в
сущности,
математики
дополнение
к
о
предмета
теореме
о
существовании модели – теорему компактности – доказал
в 1936 г. А. И. Мальцев. В данной главе мы изучим эти
замечательные
результаты,
составляющие
основу
аксиоматического метода в математике.
НАЗАД
ДАЛЕЕ
203
204.
§ 11. Основные понятияНАЗАД
ДАЛЕЕ
204
205. Глава III. Исчисление предикатов. § 11. Основные понятия.
С каждойсигнатурой
свяжем
некоторый
математический аппарат, позволяющий «выводить» одни
формулы
из
других. Его
предикатов сигнатуры
называют
исчислением
и обозначают ИП( ). Сначала
перечислим аксиомы. Пусть , t , f и Р – соответственно
любая формула, любой терм, n-местный функциональный
символ и n-местный предикатный символ сигнатуры .
НАЗАД
ДАЛЕЕ
205
206. Глава III. Исчисление предикатов. § 11. Основные понятия.
определениеАксиомами
ИП ( )
являются:
все
тавтологии
сигнатуры
(§ 8); кванторные аксиомы x (x)
(t ) и (t ) x ( x); аксиомы равенства x ( x x),
x y ( x y y x), x y z ( x y y z x z ),
x1 y1... xn yn ( x1 y1 ... xn yn f ( x1 ,..., xn )
f ( y1 ,..., yn )),
x1 y1... xn yn ( x1 y1 ... xn yn P( x1 ,..., xn )
P( y1 ,..., yn )).
НАЗАД
ДАЛЕЕ
206
207. Глава III. Исчисление предикатов. § 11. Основные понятия.
Теперьопределим
формулирующие
правила
некоторые
вывода,
типичные
точно
способы
математических рассуждений
НАЗАД
ДАЛЕЕ
207
208. Глава III. Исчисление предикатов. § 11. Основные понятия.
определениеПравилами вывода ИП( ) называют выражения
( y)
, ( y)
,
,
, в которых и
x ( x) x ( x)
– любые формулы сигнатуры , а у – предметная
переменная, не входящая свободно в нижнюю
формулу соответствующего правила.
Будем
называть
-правилом,
эти
правила
-правилом
и
соответственно
-правилом
и
говорить, что нижняя формула выведена по
соответствующему правилу из верхних.
НАЗАД
ДАЛЕЕ
208
209. Глава III. Исчисление предикатов. § 11. Основные понятия.
Свойства аксиом и правил вывода.1. Все аксиомы общезначимы.
2. Если формула выведена по некоторому правилу из
формул, общезначимых в системе А, то она
общезначима в А.
3. Если в любой аксиоме (любом правиле вывода)
заменить все вхождения константного символа с
на переменную z, не входящую в эту аксиому (это
правило вывода), то получим аксиому (правило
вывода).
НАЗАД
ДАЛЕЕ
209
210. Глава III. Исчисление предикатов. § 11. Основные понятия.
Доказательства.1. Свойство 1 для тавтологий и аксиом равенства
очевидно.
Проверим
общезначимость
(t ) x ( x ) , предоставляя
формулы
рассмотрение
второй
кванторной аксиомы читателю. Фиксируем произвольную
алгебраическую систему А = (А; I) и значения в А всех
свободных переменных данной формулы. Терм t примет
значение t A A . При [ (t )]A Л формула истина по
определению импликации. Если же, [ (t )]A A (t A ) И
A
A
[
x
(
x
)]
И
[
(
t
)
x
(
x
)]
И.
то
, откуда
НАЗАД
ДАЛЕЕ
210
211. Глава III. Исчисление предикатов. § 11. Основные понятия.
2. Свойство 2 для -правила следует из определенияимпликации. Проверим его для -правила, предоставляя
рассмотрение -правила читателю. Пусть
формула
( y ) общезначима в А. Рассуждая «от противного»,
допустим, что формула
x (x) не общезначима в А.
Тогда она ложна в А при некоторых значениях ее
свободных переменных. Зафиксируем эти значения (при
этом значение переменной у не будет зафиксировано). По
определению
импликации, [ x ( x)]A И и A Л .
По определению квантора существования, A (a ) И при
некотором a A .
НАЗАД
ДАЛЕЕ
211
212. Глава III. Исчисление предикатов. § 11. Основные понятия.
Присвоим переменной у значение а, после чего значениявсех свободных переменных формулы
( y)
будут
зафиксированы, а ее значение, следовательно, определено.
Из A (a ) И и
A Л следует, что [ ( y ) ]A Л
при этих значениях переменных,
что противоречит
предположению.
3. Доказательства свойства 3 для всех аксиом и
правил
вывода
практически
одинаковы,
поэтому
рассмотрим только -правило. Пусть имеем конкретный
вариант этого правила, содержащий некоторые формулы
(c ) и (c ) .
НАЗАД
ДАЛЕЕ
212
213. Глава III. Исчисление предикатов. § 11. Основные понятия.
После подстановки z вместо с получим выражение( z ), ( z ) ( z ) , которое является вариантом
-правила.
( z)
■
Теперь введем основные понятия этой главы.
НАЗАД
ДАЛЕЕ
213
214. Глава III. Исчисление предикатов. § 11. Основные понятия.
определение 1Выводом формулы из множества формул Т
называют последовательность формул 1 ,..., k , в
которой k и каждый элемент либо аксиома,
либо
принадлежит
Т, либо
предшествующих формул
выведен
из
последовательности по
одному из правил вывода.
НАЗАД
ДАЛЕЕ
214
215. Глава III. Исчисление предикатов. § 11. Основные понятия.
определение 2Формулу называют выводимой из множества
| ), если существует вывод формулы
формул Т( Т
из Т.
Если Т – конечное множество, T { 0 ,..., n },то удобно
писать 0 ,..., n | ; если Т пусто, пишут просто | .
Докажем первый результат о связи выводимости и
логического следования.
НАЗАД
ДАЛЕЕ
215
216. Глава III. Исчисление предикатов. § 11. Основные понятия.
Предложение.Если выводима из Т, то
логически следует из Т.
Доказательство. Пусть 1 ,..., k – вывод из Т.
Применяя к формулам
расположения в
и правил
(в
порядке
их
i
последовательности) свойства аксиом
вывода 1
и
2, получим, что все они
общезначимы в любой модели для Т. В том числе и
k общезначима в любой модели для Т. ■
В заключение параграфа рассмотрим пример вывода, на
котором поясним используемую далее терминологию.
НАЗАД
ДАЛЕЕ
216
217. Глава III. Исчисление предикатов. § 11. Основные понятия.
Следующая последовательность формул является выводомформулы x ( x ) x ( x ) в исчислении предикатов,
т. е. выводом из пустого множества Т:
1) ( x ) x ( x ) – кванторная аксиома;
2) ( ( x ) x ( x )) ( x ( x ) ( x )) – тавтология;
3) x ( x ) ( x ) – выведена из 1 и 2 по -правилу;
4) x ( x ) x ( x ) – выведена из 3 по -правилу;
5) ( x ( x ) x ( x )) ( x ( x ) x ( x ))
– тавтология;
6) x ( x ) x ( x ) – выведена из 4 и 5 по -правилу;
НАЗАД
ДАЛЕЕ
217
218. Глава III. Исчисление предикатов. § 11. Основные понятия.
Трудно понять, как «придуман» этот вывод, еслипросматривать его сверху вниз. При поиске вывода
обычно не двигаются от аксиом к выводимой формуле, а
последовательно пытаются получить ее из какого-нибудь
правила
вывода,
чтобы
прийти
к
более
простым
формулам. В нашем примере формула не может быть
получена применением кванторных правил. Поэтому надо
применить
правила
-правило,
выбрать
как
причем
можно
формулу из этого
более простой. Мы
воспользовались часто применяемым в доказательствах
законом контрапозиции
НАЗАД
p q q p и
законом
ДАЛЕЕ
218
219. Глава III. Исчисление предикатов. § 11. Основные понятия.
двойного отрицания. В результате вывод формулы 6сведен к тавтологии и формуле 4, которая удобней
-правилу.
формулы 6 тем, что может быть получена по
Аналогичные рассуждения применяем к формуле 4 и
продолжаем процесс, пока не дойдем до аксиом.
Иногда удобно записать вывод следующим образом:
x , ( x ) ( x )
x
x x , ( x x ) ( x x )
x x
Рис. 7
НАЗАД
ДАЛЕЕ
219
220. Глава III. Исчисление предикатов. § 11. Основные понятия.
Такую запись называют выводом формулы в видедерева. Название связано с тем, что изображенная на
рис. 8 фигура напоминает дерево, в «корне» которого
находится выводимая формула, «листьями» являются ак-
сиомы, а «рост» дерева происходит по правилам вывода.
Любой вывод
Т тоже можно записать в виде
из
1 ,..., k
дерева, в котором «листьями» могут быть не только
аксиомы, но и формулы из Т. Обратно, любое дерево
вывода легко представить в виде последовательности. Для
этого
достаточно
занумеровать
входящие
в
дерево
формулы слева направо и сверху вниз и выписать их в
НАЗАД
ДАЛЕЕ
220
221. Глава III. Исчисление предикатов. § 11. Основные понятия.
порядке возрастания номеров.Математики
описанные
два
постоянно
используют
способа
представления
вывода. Когда математик ищет доказательство, 1
2
он сводит доказываемое утверждение к более
3
простым, пока не придет к аксиомам. Таким
4
5
образом он строит дерево вывода. Излагая же
6
найденное доказательство, он описывает его
Рис. 8
в виде последовательности, двигаясь от аксиом
к теоремам.
НАЗАД
ДАЛЕЕ
221
222.
§ 12. Свойства отношениявыводимости
ДАЛЕЕ
222
223. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Одноиз
важнейших
свойств
отношения
выводимости описывает теорема дедукции.
Теорема дедукции. Соотношения Т | ( )
и
Т { } |
равносильны
для
всех предложений
, формул и множеств формул Т.
Доказательство. Пусть Т | ( ) и 1 ,..., k –
вывод
формулы
( ) k
из
Т.
Тогда
последовательность 1 ,..., k , , является выводом из
это
справедливо для любой
Т { } . Заметим, что
формулы , а не только для предложений.
НАЗАД
ДАЛЕЕ
223
224. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Обратно,пусть
Т { } | .
Соотношение
Т | ( ) будем доказывать индукцией по длине вывода
1 ,..., k формулы k из Т { } . При k = 1 (базис
аксиома,
либо
1 либо
принадлежит множеству Т { } . В первом случае
индукции)
формула
искомым
выводом
последовательность
из Т является
, ( ),
. Это
формулы
рассуждение проходит и в случае
Т . Наконец, если
, то искомый вывод состоит из единственной
тавтологии .
НАЗАД
ДАЛЕЕ
224
225. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Пусть k > 1, и предположим, что для выводов, длинакоторых меньше k, утверждение Т | ( ) справедливо
(предположение индукции). При 1 ≤ i < k
последовательность 1 ,..., i , есть вывод i , из
Т { } ,
и, по предположению индукции, имеем Т | ( i ) . По
определению вывода, k либо аксиома, либо принадлежит
Т { } , либо выведена из предыдущих формул i (i < k)
по одному из правил вывода. В первых двух случаях
доказательство соотношения
Т | ( k ) такое же, как
в базисе индукции.
НАЗАД
ДАЛЕЕ
225
226. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Разберем третий случай. Пусть k выведена из i иj по -правилу. Тогда j i k . Рассмотрим дерево
вывода, изображенное на рис. 9, в котором Е и D – деревья
вывода формул
i и j
из Т (эти выводы
существуют по предположению индукции), А – формула
( i ) (( ( i k )) ( k )) . Поскольку А –
основная тавтология 2 из § 2, это действительно есть
дерево вывода k из Т, следовательно, Т | ( k ) .
Предположим теперь, что k выведена из i (i < k) по
-правилу (аналогичное
рассуждение для
-правила
читатель может провести самостоятельно).
НАЗАД
ДАЛЕЕ
226
227. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Тогда k ( x 1 ( x)) и i ( 1 ( y )) для некоторыхформул , 1 и предметной переменной у, не входящей
свободно в k .
Рассмотрим дерево вывода на рис. 10, в котором Е –
формулы i из
(( ) x 1 ( x)) ( ( x 1 ( x)))
дерево
вывода
Т, А – формула
и
B – формула
( ( 1 ( y ))) (( ) 1 ( y )) . Это дерево вывода
формулы 1 ,..., k из Т, т. к. А и В – тавтологии. Таким
образом, Т |– ( 1 ,..., k ) .
НАЗАД
■
ДАЛЕЕ
227
228. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
EE
i , A
j , ( j ) ( k )
D
i , B
( ) 1 ( y )
k
( ) x 1 ( x), A
Рис. 9
k
Рис. 10
Докажем
еще
некоторые
свойства
отношения
выводимости.
НАЗАД
ДАЛЕЕ
228
229. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Свойства отношения выводимости.Пусть S и Т – любые множества формул , и ,
если не оговорено противное, – произвольные формулы.
Т , то Т | .
2. Если Т | , то Т 0 | для
1. Если
подходящего
конечного множества Т 0 Т .
3. Если
S |
и все
формулы
множества S
выводимы из Т, то Т | .
4. Если Т { } | и Т { } | , то Т { } |
( и – предложения).
НАЗАД
ДАЛЕЕ
229
230. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
5. Если Т { } |и Т { } | , то Т | ( –
предложение).
6. Т | тогда и только тогда, когда Т | и
Т | .
Доказательство.
1. Свойство 1 очевидно.
2. Пусть 1 ,..., k – вывод формулы k из Т. Ясно, что
эта
последовательность
есть
одновременно
вывод
формулы из конечного множества Т 0 { i | 1 i k ,
i Т} .
НАЗАД
ДАЛЕЕ
230
231. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
3. Рассмотрим дерево выводаформулы из S (см.,
например, рис. 11). В «листьях» этого дерева находятся
либо аксиомы, либо формулы из S. Отберем из них все
формулы i из S ( 1 и 2 на рис. 11). По условию, для
каждой из этих формул существует дерево Di, ее вывода из
Т (D1 и D2 для формул 1 и 2 на рис. 11). «Нарастим»
теперь дерево вывода формулы из S, присоединяя для
каждого i «корень» дерева Di , к «листу» i (результат
этой операции для дерева, изображенного на рис. 11,
показан на рис. 12). Легко понять, что полученное дерево
является деревом вывода формулы
НАЗАД
из Т.
ДАЛЕЕ
231
232. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
D22
D1
E
D
, A
, B
1
, ( )
Рис. 11
4. Пусть Т { } |
Рис. 12
и
дедукции Т | ( ) и
НАЗАД
Рис. 13
Т { } | . Тогда по теореме
Т | ( ) .
ДАЛЕЕ
232
233. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Рассмотрим дерево вывода, изображенное на рис. 13, вкотором D и Е – деревья вывода формул и
Т, B ( ) (( ) ) и A ( ) B ,
A – основная тавтология 8 из § 2, поэтому рассматриваемое
из
дерево есть дерево вывода формулы из Т { } .
5. Аналогичное рассуждение с использованием основной
тавтологии 9 вместо тавтологии 8 доказывает свойство 5.
6. Подобным же образом, используя основные тавтологии
3 – 5, нетрудно доказать свойство 6. ■
Свойства 4
и
5 можно наглядно представить
следующим образом:
НАЗАД
ДАЛЕЕ
233
234. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
T { } | ; T { } | T { } | ; T { } |,
.
T { } |
T |
Эти выражения, в сущности, описывают способы
рассуждений,
позволяющие
сводить
доказательство
нижних соотношений к доказательству верхних. Таким
образом,
свойства выводимости позволяют получать
T1 | 1 ;...; Tn | n
выражения вида
, которые можно
T |
интерпретировать и применять как правила вывода. Такие
«дополнительные» правила вывода обосновывают способы
рассуждения, широко используемые в математике.
НАЗАД
ДАЛЕЕ
234
235. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Приведем некоторые из них, справедливые для любогомножества формул Т и любых формул ,
T | ( ); T | ( )
1)
,
T | ( )
3)
T |
,
T |
и :
T | ; T | ( )
2)
,
T |
4)
T | ; T |
,
T | ( )
T | ( )
5)
,
T |
T | ( )
6)
,
T |
T |
7)
,
T | ( )
T |
8)
.
T | ( )
НАЗАД
ДАЛЕЕ
235
236. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
определение 1Выражение вида Т | будем называть посылкой,
если оно стоит
в верхней части правила вывода,
заключением, если оно
находится
в
нижней
части правила вывода.
НАЗАД
ДАЛЕЕ
236
237. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
определение 2Последовательность
P1 ,…, Pn
правил вывода
называют квазивыводом
из Т, если каждая посылка
любого из этих правил либо является заключением
одного из предшествующих правил, либо имеет вид
| , где – аксиома исчисления предикатов, либо
имеет вид Т | , где Т .
НАЗАД
ДАЛЕЕ
237
238. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
определение 3Квазивывод P1 ,…, Pn , где заключение правила Pn
имеет вид
, будем называть квазивыводом
Т |
формулы из множества формул Т.
НАЗАД
ДАЛЕЕ
238
239. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Пример. Докажем, чтодля
любой
формулы
( x1 ,..., xn ) и любых термов t1,…,tn в исчислении
предикатов выводимы формулы x1... xn (t1 ,..., t n ) и
(t1 ,..., t n ) x1... xn . Квазивыводы этих двух формул
похожи, поэтому рассмотрим только первую из них. Для
сокращения записей будем считать, что n = 2. Выберем
переменные у1 и у2, не входящие в термы ti и формулу ,
и введем обозначения:
1 x1 x2 , 2 y1 y2 ( y1 , y2 ), (t1 , t2 ) .
Применяя
правило
силлогизма
и
-правило,
получим следующее «дерево квазивывода»:
НАЗАД
ДАЛЕЕ
239
240. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
| ( 1 x2 ( y1 , x2 )); | ( x2 ( y1 , x2 ) ( y1 , x2 ))| ( 1 ( y1 , y2 ))
| ( 1 y2 ( y1 , y2 )) | ( 2 y2 (t1 , t 2 )); | ( y2 (t1 , t 2 ) (t1 , t 2 ))
| ( 1 2 );
| ( 2 )
| ( 1 )
Посылки, стоящие в «листьях» этого дерева, имеют
вид | , где – кванторная
аксиома. Заметим, что
введение переменных у1, у2 обеспечивает применимость
-правила и законность подстановки t1 и t2 в формулу
(см. § 7).
НАЗАД
ДАЛЕЕ
240
241. Глава III. Исчисление предикатов. § 12. Свойства отношения выводимости.
Подчеркнем,является
выводом,
что
он
построенный
лишь
квазивывод
устанавливает
не
факт
выводимости формулы 1 . Впрочем, из квазивывода
нетрудно получить и вывод этой формулы в исчислении
предикатов.
НАЗАД
ДАЛЕЕ
241
242.
§ 13. Непротиворечивость,полнота, множества
Хенкина
НАЗАД
ДАЛЕЕ
242
243. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Понятия непротиворечивости и полноты относятся кчислу важнейших понятий математической логики и
математики в целом, а множества Хенкина (названные по
имени американского математика Л. Хенкина) играют
вспомогательную роль и нужны для доказательства
теоремы
огромное
о
существовании
не
только
модели,:
которая
математическое,
имеет
но
и
общеметодологическое значение.
Напомним,
что
мы
рассматриваем
формулы
некоторой произвольной, но фиксированной сигнатуры
(если не оговорено противное).
НАЗАД
ДАЛЕЕ
243
244. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
определениеЕсли
из множества формул выводима
формула,
то
его
противоречивым,
а
в
противном
любая
называв
случае
непротиворечивым
НАЗАД
ДАЛЕЕ
244
245. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Свойствапротиворечивых
и
непротиворечивых
множеств сформулируем в виде леммы.
Лемма. Справедливы следующие утверждения.
1. Множество формул Т противоречиво тогда и только
тогда, когда из него выводима хотя бы одна формула вида
.
2. Если множества формул Тn( n N ) непротиворечивы и
T0 T1 ..., то множество Tn непротиворечиво.
n
3. Если – предложение, Т – множество формул
и
T { } противоречиво, то T | .
НАЗАД
ДАЛЕЕ
245
246. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
4. Если множество формул Т непротиворечиво, то длялюбого предложения непротиворечиво хотя бы одно из
множеств T { } и T { } .
5. Если
множество
непротиворечиво,
то
предложений
и
S T { x ( x )}
множество
S { (с)}
непротиворечиво для любого не входящего в формулы из
S сигнатурного константного символа с.
Доказательства.
1. Если Т противоречиво, то
из него выводимы все
формулы, в частности формула .
НАЗАД
ДАЛЕЕ
246
247. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Обратно, пусть T | ( ) . Проверим, что тогда из Твыводима
формула .
произвольная
Рассмотрим
последовательность , , . Это вывод
, т. к. – тавтология. Из
| , по свойству 3 выводимости, следует T | .
из
2. Предположим, что свойство 2 неверно, т. е. множества
Тn
непротиворечивы,
а
их
объединение
противоречиво, T | ( ) . Тогда,
по
Т–
свойству 2
выводимости, S | ( ) для подходящего конечного
множества S T . Из конечности S следует, что S Tn для
некоторого n N .
НАЗАД
ДАЛЕЕ
247
248. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Тогда, посвойствам
выводимости 1
и
3, имеем:
Tn | ( ) , – т. е. Тn противоречиво. Полученное
противоречие доказывает утверждение 2.
3. Если T { } противоречиво, то T { } | ( ) .
Тогда, по
свойству
6
выводимости,
T { } |
,
T { } | . Следовательно (по свойству 5 выводимости),
T | , что и требовалось доказать.
4. Для
доказательства
утверждения
4
предположим
противное: Т непротиворечиво, а оба множества T { } ,
T { } противоречивы. Тогда, по
утверждению
3,
имеем: T | и T | , откуда по дополнительному
НАЗАД
ДАЛЕЕ
248
249. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
правилу вывода 4 получаем: T | ( ) , а это несогласуется с предположением о непротиворечивости Т.
5. Предположим, что
утверждение
5
неверно:
S
непротиворечиво, а S { (с )} противоречиво. Тогда S
{ (с)} | , где 1 1 по теореме дедукции. Пусть
1 ,..., k – вывод формулы (c ) из S, k ( (c) ) .
Заменим в этом выводе все вхождения константы с на
переменную z, не входящую в формулы
вывода. По
свойству 3 аксиом и правил вывода (§ 11), полученная
последовательность формул есть вывод (z ) из S
НАЗАД
ДАЛЕЕ
249
250. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
(участвующие в выводе формулы из S при замене с на z неменяются, т. к. по условию с в них не входит).
Следовательно, S | ( ( z ) ) . По -правилу,
S | ( x ( x ) ) , откуда
по
теореме
дедукции
S { x ( x )} | . Но S S { x ( x )} , поэтому S | .
Свойство 5 теперь следует из непротиворечивости S. ■
НАЗАД
ДАЛЕЕ
250
251. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
определение 1Непротиворечивое множество Т предложений
называют полным, если для любого
сигнатуры
предложения этой сигнатуры верно одно из
соотношений: T | , T | .
НАЗАД
ДАЛЕЕ
251
252. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
определение 22. Полное множество Т предложений сигнатуры
называют множеством
Хенкина, если для любого
выводимого
из
Т предложения вида
x (x)
существует константный символ c такой, что
T | (c ) .
НАЗАД
ДАЛЕЕ
252
253. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Приведемпример
полного
множества.
Для
произвольной алгебраической системы А сигнатуры
обозначим
через Th(А) множество всех предложений
сигнатуры
, истинных в А. Это полное множество, т. к.
для любого предложения одно из предложений ,
истинно в
А. Можно доказать в некотором
смысле
обратное утверждение: для любого полного множества
предложений найдется система А такая, что Th(А) =
= { | T | } .
НАЗАД
ДАЛЕЕ
253
254. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Свойства полных множеств.Для
всякого полного множества
предложений
и
справедливы
Т
и любых
следующие
утверждения (здесь и далее символ обозначает
равносильность утверждений, стоящих справа и слева от
него).
1. T | T | .
2. T | ( ) T | или T | .
3. T | ( ) T |
НАЗАД
или T | .
ДАЛЕЕ
254
255. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Доказательство.1. Если T | , то T | означало бы, по свойству 6
выводимости, противоречивость Т. В обратную сторону
утверждение легко следует из полноты Т.
2. Утверждение
2
в
одну
сторону
следует
из
дополнительных правил вывода 7 и 8 (§ 12). Обратно,
предположим, что T | ( ) , и допустим, что из Т не
выводимо и из Т не выводимо . Тогда по свойству
1
имеем: T | и T | , откуда, по
свойству 6
выводимости, T | ( ) .
НАЗАД
ДАЛЕЕ
255
256. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Используя тавтологию ( ) , получаем:| ( ) , откуда T | ( ) , а это, учитывая
предположение T | ( ),означало бы противоречивость
множества Т.
3. Последовательно
применяя
закон
исключения
импликации, свойство 2 и свойство 1, получим следующую
цепочку эквивалентностей:
T | ( ) T | ( ) T |
из Т не выводимо или
НАЗАД
или
T |
T | . ■
ДАЛЕЕ
256
257. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
определениеТерм называют константным, если он не содержит
символов переменных.
Множество
всех константных термов сигнатуры
обозначим через М( ).
НАЗАД
ДАЛЕЕ
257
258. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Свойства множеств Хенкина.Для любого множества Хенкина Т и любой формулы
(x) справедливы следующие утверждения.
1. T | x ( x ) T | (t ) для некоторого t M( ) .
2. T | x ( x ) T | (t ) для всех t M( ) .
Доказательство.
1. Если T | x ( x ) , то, по
определению
множества
Хенкина, T | (c ) для подходящего константного символа
c , причем c M( ) , что доказывает утверждение в
одну сторону. Обратно, пусть T | (t ) для некоторого
t M( ) .
НАЗАД
ДАЛЕЕ
258
259. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Используя кванторную аксиому (t ) x ( x ) и теоремудедукции, получим
(t ) | x ( x) . Тогда, по свойству 3
выводимости, T | x ( x ) .
2. Если T | x ( x ) , то, применяя
кванторную аксиому
x ( x ) (t ) , получаем T | (t ) для любого терма t, в том
числе и для t M( ) . Обратно, допустим, что T | (t )
для всех t M( )
(в
частности, T | (c ) для
любого
c ), и докажем, что T | x ( x) . Если это не так, то, по
свойству 1 полных множеств, T | x ( x ) . В § 11 мы
доказали, что | x ( x ) x ( x ) . Отсюда по теореме
дедукции x ( x ) | x ( x ) , и следовательно,
НАЗАД
ДАЛЕЕ
259
260. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
T | x ( x) . Тогда, по определению множества Хенкина,T | (c) для
некоторого
c . Это, с
соотношения T | (c ) , означает
вопреки условию. ■
Из
свойства
6
учетом
противоречивость Т
выводимости, свойств
полных
множеств и множеств Хенкина можно заключить, что
выводимость из множества Хенкина имеет глубокие
аналогии с истинностью формул в алгебраической системе
(см. § 8). Эта связь в следующем параграфе сыграет
важную
роль
при
доказательстве
теоремы
о
существовании модели.
НАЗАД
ДАЛЕЕ
260
261. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Следующая же теорема– основной результат данного
параграфа.
Теорема
о
расширении.
Для
любого
непротиворечивого множества предложений S сигнатуры
найдутся совокупность константных символов С и
множество Хенкина Т сигнатуры C такие, что S T .
Доказательство. Мы рассмотрим только случай
не более
чем
счетного множества
предполагать, что все символы из
, т. е. будем
можно занумеровать
натуральными числами.
НАЗАД
ДАЛЕЕ
261
262. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Читатель, знающий, что любое множество можно вполнеупорядочить,
легко
обобщит
приведенное
ниже
рассуждение на случай произвольной сигнатуры .
Пусть
C {cn | n N} – счетное
множество
. Множество
C счетно (это с
константных символов, не входящих в
всех
предложений
сигнатуры
очевидностью следует из кодирования формул (см. § 18),
но может быть доказано читателем и непосредственно),
поэтому все эти предложения можно расположить в
последовательность n (n Ν) .
НАЗАД
ДАЛЕЕ
262
263. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Определим по индукции последовательность множествTn (n Ν) следующим
образом, T0 S . Пусть T
n
построено. Если множество Tn { n } противоречиво, то
Tn { n }
непротиворечиво и не имеет вид x (x ) ,то полагаем
n
Tn 1 Tn { n }. Наконец, если Tn { n } непротиворечиво
и n имеет вид x (x ) ,то полагаем Tn 1 Tn { n , (ck )},
полагаем
Tn 1 Tn { n } . Если
где k – наименьшее число такое, что сk не входит в
формулы из Tn (в формулы из Tn входит лишь конечное
число элементов С, поэтому такое k существует).
НАЗАД
ДАЛЕЕ
263
264. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
Из определения ясно, что T0 T1 ... Проверим, чтомножество T Tn обладает свойствами, указанными в
n 0
формулировке
По
индукции
теоремы.
Во-первых,
убеждаемся,
что
S T0 T .
множества
Tn
непротиворечивы ( T0 S непротиворечиво по условию, и
если Tn непротиворечиво, то и
Tn 1
непротиворечиво
по построению и утверждениям 4, 5 леммы из этого
параграфа). Тогда, по утверждению 2 упомянутой леммы,
Т непротиворечиво. Докажем полноту Т. Действительно,
пусть – любое предложение сигнатуры C , тогда
n для некоторого n N .
НАЗАД
ДАЛЕЕ
264
265. Глава III. Исчисление предикатов. § 13. Непротиворечивость, полнота, множества Хенкина.
По построению либо n Tn 1 T , либо n Tn 1 T ,откуда T | или T | . Проверим, наконец, что Т –
множество Хенкина. Пусть из Т выводимо предложение
x (x)
C , тогда x ( x) n для
некоторого n N . Множество Tn { n }непротиворечиво
сигнатуры
(иначе, по утверждению 3 леммы, было бы T | и
T | , что влекло бы противоречивость множества Т).
Тогда, по построению, Tn 1 Tn { n , (ck )} .
Следовательно, T | (ck ) .
НАЗАД
■
ДАЛЕЕ
265
266.
§ 14. Основные теоремы обисчислении предикатов
НАЗАД
ДАЛЕЕ
266
267. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Перейдемтеперь
к
изложению
основных
результатов данной главы.
Теорема о существовании модели первоначально
была получена как следствие приводимых ниже теорем о
полноте и компактности. Мы изложим более позднее
прямое доказательство, принадлежащее Л. Хенкину.
Теорема о существовании модели. Любое
непротиворечивое множество предложений имеет модель.
Доказательство. Пусть S – непротиворечивое
множество предложений сигнатуры
НАЗАД
.
ДАЛЕЕ
267
268. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Мы хотимпостроить модель для
расширении, найдется
множество
S. По
теореме
Хенкина
о
T S
сигнатуры C . Нам достаточно найти модель А = (А; I)
для Т (где I – интерпретация на А сигнатуры C ),
поскольку
тогда алгебраическая система (А; I) будет
моделью для S. Идея доказательства заключается в том,
чтобы
для
построения множества
А использовать
множество М всех константных термов сигнатуры C .
Определим предикат на М следующим образом:
s t , если T | ( s t ) .
НАЗАД
ДАЛЕЕ
268
269. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Установим некоторые свойства этого предиката:(а) предикат рефлексивен, симметричен и транзитивен;
(б) для любого n-местного предикатного символа P из
s1 t1 ,..., sn t n и T | P( s1 ,..., sn ) следует T | P(t1 ,..., t n );
(в) для любого n-местного функционального символа f
из s1 t1 ,..., sn t n , следует f ( s1 ,..., sn ) f (t1 ,..., t n ) .
Доказательства
перечисленных
свойств
с
использованием аксиом равенства однотипны, поэтому для
примера докажем лишь симметричность.
Пусть s t , т. е. T | ( s t ) . Обозначим
через
( x, y ) формулу x y y x .
НАЗАД
ДАЛЕЕ
269
270. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Впримере
квазивывода
из
§ 12
доказано, что
x y | ( s, t ) . Формула x y – аксиома, поэтому
| x y , откуда (свойство 3 отношения выводимости,
§ 12) | ( s, t ) , т. е. | ( s t t s ) и по теореме дедукции
s t | (t s ) . Из последнего соотношения и T | ( s t )
получаем T | (t s ) , т. е. t s .
Теперь определим алгебраическую систему А, Пусть
А
–
множество
всех
классов
эквивалентности
по
отношению , т. е. элементами А являются множества
вида t {s | s M, s t} для t M . Из (а) следует, что
s t (s t ) .
НАЗАД
ДАЛЕЕ
270
271. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Интерпретацию сигнатурных символов на множестве Азададим следующим образом:
• для каждого n-местного предикатного символа
P и
любых t1, ..., tn из М полагаем
P A (t1 ,..., t n ) И T | P(t1 ,..., t n ) ;
f
и любых t1, ..., tn из М полагаем f A (t1 ,..., t n ) f (t1 ,..., t n ) ;
• для каждого константного символа c C полагаем
cA c.
• для каждого n-местного функционального символа
Из (б) и (в) следует, что эти определения корректны:
если ti и si из
НАЗАД
М таковы, что
s i ti (1 i n) , то
ДАЛЕЕ
271
272. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
P A (t1 ,..., t n ) P A ( s1 ,..., sn ) иf A (t1 ,..., tn ) f A ( s1 ,..., sn ) .
Следующее утверждение описывает значения терма,
полученного подстановкой (см, § 8) термов из М в терм
t(xi, . . ., хk) , все переменные которого находятся среди
указанных:
(г) t A ( s1 ,..., sk ) t ( s1 ,..., sk ) при любых s1, ..., sk из М.
Проверим (г) индукцией по построению t. Если t =
= xi, то t ( s1 ,..., sk ) si t ( s1 ,..., sk ) . Если
A
то t A ( s1 ,..., sk ) c t ( s1 ,..., sk ) .
t c C ,
Если t = f (t1,…,tn), то,
используя для термов s1, ..., sn предположение индукции,
НАЗАД
ДАЛЕЕ
272
273. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
получим:t A ( s1 ,..., sk ) f A (t1 ( s1 ,..., sk ),..., t n ( s1 ,..., sk )
A
A
f A t1 ( s1 ,..., sk ),..., t n ( s1 ,..., sk ) f (t1 ( s1 ,..., sk ),..., t n ( s1 ,..., sk ))
t ( s1 ,..., sk ) .
Значения формулы, полученной подстановкой (см.
§ 8) термов из М в формулу ( x1 ,..., xk ) , все свободные
переменные которой находятся среди указанных, и связь
этих значений с выводимостью из Т описывает следующее
утверждение:
НАЗАД
ДАЛЕЕ
273
274. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
(д) для любых s1, ..., sk из М имеемA ( s1 ,..., sk ) И T | ( s1 ,..., sk ) .
Утверждение (д) нетрудно проверить индукцией по
вид
s = t,
то
. Если имеет
A ( s1 ,..., sk ) И s A ( s1 ,..., sk ) t A ( s1 ,..., sk ) s( s1 ,..., sk )
построению
t ( s1 ,..., sk ) T | ( s1 ,..., sk ) . Так же легко рассмотреть
случай, когда P( x1 ,..., xk ) . Шаг индукции для всех
возможных
видов
( , , , , x , x )
требует схожих рассуждений, поэтому мы проведем его
только для x ( x, x1 ,..., xk ) . При этом будем считать,
что для
НАЗАД
утверждение (д) верно.
ДАЛЕЕ
274
275. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
дляA ( s1 ,..., sk ) И ( A ( s, s1 ,..., sk ) И
некоторого s M) (T | ( s, s1 ,..., sk ) для некоторого
s M) T | ( s1 ,..., sk ) .
Тогда
Последний шаг
этого рассуждения использует свойство
1 множеств Хенкина.
Теперь вернемся к доказательству теоремы. Осталось
проверить, что А – модель для Т. Действительно, если
T , то T | , а тогда по утверждению (д) A И . ■
Заметим, что противоречивое множество Т не имеет
модели, т. к. из Т выводимо предложение , ложное
в любой алгебраической системе.
НАЗАД
ДАЛЕЕ
275
276. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Это утверждение является обратнымк
теореме
о
существовании модели.
Следующая теорема
Геделя устанавливает связь
между логическим следованием и выводимостью.
Теорема
о
полноте
исчисления
предикатов.
логически следует из множества
предложений Т тогда и только тогда, когда выводимо
1. Предложение
из Т.
2. Предложение общезначимо тогда и только тогда,
когда оно выводимо в исчислении предикатов.
НАЗАД
ДАЛЕЕ
276
277. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Доказательство.Второе
утверждение
теоремы есть частный случай первого при Т = Ø . Первое
утверждение в одну сторону доказано в § 11. Осталось,
только, что
из
T |
таким
образом, доказать
следует
T | . Пусть T | . Тогда по свойству 1
логического следования (§ 10) множество T { } не
имеет
модели.
противоречиво
по
Следовательно, это
множество
теореме о существовании модели.
Тогда, по утверждению 3 леммы из § 10, T | , и по
третьему дополнительному правилу вывода (§12) T | . ■
НАЗАД
ДАЛЕЕ
277
278. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Весьмаполезный
признак
непротиворечивости
множества дает следующая теорема А. И. Мальцева.
Теорема
компактности.
Множество
предложений имеет модель тогда и только тогда, когда
каждое его конечное подмножество имеет модель.
Доказательство.
модель,
то
она
является
Если
Т
множество
моделью
и
для
имеет
любого
подмножества множества Т. Обратно, пусть каждое
конечное подмножество множества Т имеет модель.
Предположим, что Т не имеет модели.
НАЗАД
ДАЛЕЕ
278
279. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Тогдапо
теореме
о
существовании
Т
модели
противоречиво, т. е. из Т выводимо предложение вида
свойству
2
выводимости (§ 12),
. По
выводимо из некоторого конечного подмножества
S
множества
Т.
Но
тогда,
вопреки
условию,
противоречиво. Следовательно, Т имеет модель.
S
■
Доказанные в этом параграфе теоремы можно
трактовать
как
аксиоматического
теоретические
метода
–
основания
основного
метода
исследования в математике.
НАЗАД
ДАЛЕЕ
279
280. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
С позиций математической логики схема примененияэтого метода выглядит, в кратком изложении, следующим
образом.
Для
построения
некоторой
теории
сначала
выбирают основные понятия, не определяемые в этой
теории. Имена (обозначения) этих понятий обычно и
составляют сигнатуру
, в которой в дальнейшем
формулируют все изучаемые теорией факты, гипотезы,
теоремы и т. д. В планиметрии, например, точка, прямая и
принадлежность точки прямой – неопределяемые понятия,
поэтому в «планиметрическую» сигнатуру входят
НАЗАД
ДАЛЕЕ
280
281. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
предикаты Т(х) = « х – точка », L(x) = « х – прямая » и Р(x,у) = « x принадлежит у ». Затем выбирают аксиомы, т. е.
свойства основных понятий, признаваемые истинными
без доказательства. Аксиомы, как правило, записывают
формулами сигнатуры
. В нашем «планиметрическом»
примере в список аксиом надо включить, в частности,
следующую, утверждающую, что в
отношении Р(х, у)
могут находится только точка х и прямая у:
x y (P( x, y ) T( x) L( y )) .
Теорема о существовании модели гарантирует наличие
модели для любой непротиворечивой системы аксиом, т. е.
НАЗАД
ДАЛЕЕ
281
282. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
существование предмета исследования у соответствующейтеории. Аксиоматическая теория изучает общие свойства
всех моделей соответствующей системы аксиом. Свойства
моделей, выразимые на языке логики предикатов (будем
называть
их
формульными),
предложениям сигнатуры
соответствуют
тем
, которые логически следуют
из аксиом (см. § 10). Поэтому так велико значение теоремы
о полноте: она показывает, что все истинные формульные
утверждения теории могут быть доказаны с помощью
простых правил вывода исчисления предикатов.
НАЗАД
ДАЛЕЕ
282
283. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Можносказать,
что
эта
теорема
демонстрирует
достаточность (полноту) набора из трех основных правил
вывода
для
доказательства
всех
теорем:
какие
бы
изощренные рассуждения мы ни применяли, их всегда
можно заменить цепочкой (возможно, очень длинной)
применений основных правил вывода.
Докажем, например, что из множества G аксиом
группы
(см. § 10)
следует
утверждение
x 1 x e .
Доказательство использует аксиомы равенства и аксиомы
из G (номера применяемых аксиом группы мы укажем под
знаками равенства):
НАЗАД
ДАЛЕЕ
283
284. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
x 1 x ( x 1 x)e ( x 1 x) ( x 1 ( x 1 ) 1 ) (( x 1 x) x 1 ) ( x 1 ) 12
3
1
1 1
( x 1 ( x 1 x)) ( x 1 ) 1 x ( x 1 e)) ( x ) x 1 ( x 1 ) 1 e .
1
Рассмотрим
3
более
2
подробно
1
3
проблему
аксиоматического описания арифметики.
В § 10 мы ввели « арифметическую » сигнатуру
A { , , ,0,1} .
Каждому
числу
n N
сопоставим
константный терм этой сигнатуры n (будем называть его
«именем» числа n) следующим образом: 0 0,1 1, n 1
n 1 при n > 0. Например, именем числа 4 является
терм 4 ((1 1) 1) 1 . Перечисленные ниже свойства
имен чисел показывают, что аксиом слабой арифметики
НАЗАД
ДАЛЕЕ
284
285. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
(СА, см. § 10) достаточно, чтобы доказать изоморфизммножества термов
n натуральному ряду относительно
функций и предикатов сигнатуры .
A
Свойства имен натуральных чисел
Для любых m и n из N справедливы следующие
соотношения:
1) СА | m n m n ;
2) СА | m n m n ;
3) Если m ≠ n , то СА | m n ;
4) Если m ≥ n , то СА | m n ;
НАЗАД
ДАЛЕЕ
285
286. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
5) Если m < n , то СА | m n .Доказательство. (цифры под знаками равенства –
номера используемых аксиом СА, см. § 10),
1. Пусть сначала m = 0. Докажем по индукции, что
СА | (0 n n) . При n {0,1} имеем:
0 0 0 0 0 0 и 0 1 0 1 1 1 . Предположим,
4
4
что СА | (0 n n) для некоторого n > 0. Тогда
0 n 1 0 (n 1) (0 n) 1 n 1 n 1 .
5
Для случая m > 0 доказательство аналогично.
НАЗАД
ДАЛЕЕ
286
287. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
2. Свойство 2 легко проверить подобно свойству 1,используя дополнительно аксиомы слабой арифметики 6 и
7.
3. Пусть m ≠ n , предположим для определенности,
что m < n . Тогда m + k = n для некоторого k = i + 1.
Докажем индукцией по m, что СА | (m m k ) . При
m = 0 надо доказать, что СА | (0 i 1) или, учитывая
определение, СА | (0 i 1) . Последнее утверждение
следует из аксиомы 2 СА. Допустим, что СА | (m
m k ) для некоторого m.
НАЗАД
ДАЛЕЕ
287
288. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Из m 1 (m 1) k и аксиомы 5 СА выводим m 1(m k ) 1 m k 1, откуда, по аксиоме 3 СА, следует
m m k .
Последняя
формула
совместно
с
предположением индукции показывает, что множество
СА {m 1 m 1 k}
противоречиво,
а
это,
по
утверждению 3 леммы из § 13, означает, что СА | (m
1 m 1 k ) . Шаг индукции завершен, и утверждение 3
доказано.
4. Свойство 4 докажем для частного случая m = 4 и
n = 3 (в общем случае рассуждения аналогичны).
НАЗАД
ДАЛЕЕ
288
289. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Так же, как при доказательстве предыдущего свойства,достаточно
показать, что
множество
СА {4 3}
по
4 3 2 1
аксиоме 10 СА последовательно выводим: 4 2 4 2,
противоречиво. Действительно, из
4 1 4 1 4 2, 4 0 4 0 4 1 4 2 . Последняя
формула противоречит аксиоме 8 СА и свойству 3.
5. Пусть m < n .
Тогда, по свойствам 3
и
4,
СА | (m n) и СА | (n m) . Отсюда и из аксиомы
9 СА получаем СА | ( m n) .
НАЗАД
ДАЛЕЕ
289
290. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Таким образом, в СА выводимы все верныечисловые равенства и неравенства, если входящие в них
числа заменить соответствующими именами. Однако, как
показано в § 10, из СА логически не следуют и, по теореме
о полноте, не выводимы некоторые свойства натуральных
чисел, например,
свойство, выраженное
формулой
x ( x 1 x) . Расширяя систему аксиом, можно добиться
выводимости этой формулы.
НАЗАД
ДАЛЕЕ
290
291. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
определениеАрифметикой Пеано (ПА) будем называть слабую
с дополнительной аксиомой индукции:
арифметику
(0) x( ( x) ( x 1))) x ( x)
любая формула сигнатуры
НАЗАД
, где (x )
A .
ДАЛЕЕ
291
–
292. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
В ПА выводимы многие результаты теории чисел.Благодаря аксиоме индукции, для доказательства того, что
ПА | x ( x ) , достаточно показать, что ПА | (0)(базис
индукции) и ПА | x ( ( x ) ( x 1)) (шаг индукции). В
частности, упомянутая выше формула
x ( x 1 x )
выводима в ПА, т. к. ПА | (0 1 0) по аксиоме 2 СА и
ПА | x( ( x 1 x ) (( x 1) 1 x 1)) по аксиоме 3
СА.
Обозначим
через
СА и ПА множества
предложений, логически следующих из
соответственно, а
НАЗАД
через
СА
и
Th(N) – множество
ДАЛЕЕ
всех
ПА
всех
292
293. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
предложений,истинных
в
стандартной
модели
арифметики N (см. § 10). N – модель для СА и ПА, поэтому
С А П А Th(N) . Выше мы доказали, что СА ПА .
Если бы
ПАсовпадало с Th(N), то аксиом Пеано было бы
достаточно для вывода всех истинных утверждений
сигнатуры
A о натуральных числах. Это, однако, не так
(см. следствие из теоремы о неполноте в § 20), Если же
расширить систему аксиом максимально (до множества
Th(N)), то из нее, конечно, будут выводимы все истинные
в Т утверждения описываемые предложениями сигнатуры
A (формульные).
НАЗАД
ДАЛЕЕ
293
294. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Однако, как показывает теорема о нестандартной модели(см. ниже), существуют важные неформульные свойства
натуральных
чисел,
не
следующие
из
формульных
свойств. Их существование означает, что на языке логики
предикатов систему N нельзя описать с точностью до
изоморфизма.
НАЗАД
ДАЛЕЕ
294
295. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
определениеАлгебраическую систему А = (А; I ) сигнатуры A
назовем нестандартной,
если в А существует элемент,
больший всех элементов n для n N .
НАЗАД
ДАЛЕЕ
295
296. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Заметим,что
свойство,
описанное
в
определении
нестандартной системы, неформульное, т. к. требует
введения квантора общности по множеству A(N) значений
в А термов
n . В системе N множество A(N) есть
множество-носитель, но в произвольной системе А = (А; I)
сигнатуры
A множества А и A(N) могут, конечно, не
совпадать. В § 10 мы построили нестандартную модель для
СА. Следующая теорема показывает, что любая система
аксиом арифметики имеет такую модель.
Теорема
о
нестандартной
модели.
Существует нестандартная модель для множества Th(N).
НАЗАД
ДАЛЕЕ
296
297. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Доказательство.S Th(N) {n c | n N}
Рассмотрим
множество
предложений
сигнатуры
A {c} , где с – константный символ. Система N при
подходящей интерпретации константы с является моделью
любого конечного подмножества S, т. к. в записи
конечного подмножества предложений из S участвует
конечное число термов вида n и существует натуральное
число, превосходящее значения всех этих термов. По
теореме компактности (§ 14) найдется модель А = (А;I)
сигнатуры A {c} для всего множества S.
НАЗАД
ДАЛЕЕ
297
298. Глава III. Исчисление предикатов. § 14. Основные теоремы об исчислении предикатов.
Тогда элемент cA больше всех элементов [n]A для n N ,и следовательно, система А есть нестандартная модель для
Th(N). ■
Следствие. Если
алгебраическая
система
N
является моделью множества предложений Т сигнатуры
A , то Т
имеет
и
нестандартную
модель.
Доказательство. Если N – модель
для Т, то
T Th(N) . Поэтому построенная при доказательстве
предыдущей
теоремы
модель
нестандартной моделью и для Т.
НАЗАД
для
Th(N)
является
■
ДАЛЕЕ
298
299.
§ 15. Другая формулировкаисчисления предикатов
НАЗАД
ДАЛЕЕ
299
300. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Формулировкиисчисления
предикатов,
включающие различные наборы аксиом и правил вывода,
могут порождать одно и то же множество выводимых
формул. Нам будет нужна одна из таких формулировок,
обозначаемая ИП 1 ( ) . От ИП( ) она отличается тем,
что в качестве аксиом использует не все, а только
основные тавтологии сигнатуры
1 – 10 из § 2, в которых
формулы сигнатуры
(то есть тавтологии
, и – произвольные
), Преимущество ИП 1 ( ) в том,
что все аксиомы можно выписать в явном виде: десять
основных тавтологий, две кванторные аксиомы и пять
НАЗАД
ДАЛЕЕ
300
301. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
аксиом равенства. Все основные понятия из § 11ИП 1 ( ) без изменений.
Равносильность ИП 1 ( ) и ИП( ) доказывает
переносятся на
следующая теорема.
Теорема
о
равносильности
двух
определений исчисления предикатов. Формула
выводима из множества формул Т в ИП 1 ( ) тогда и
только тогда, когда она выводима из Т в ИП( ) .
Доказательство.
В
одну
сторону
теорему
доказать легко.
НАЗАД
ДАЛЕЕ
301
302. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
А именно, пусть выводима из Т вИП 1 ( ) , и 1 ,..., k
– ее вывод из Т в ИП 1 ( ). Все аксиомы и правила вывода
ИП 1 ( ) суть аксиомы и правила вывода
ИП( ) ,
поэтому 1 ,..., k есть вывод формулы из Т в ИП( ) .
Для доказательства обратного утверждения нужны
некоторые
результаты,
связанные
с
логикой
высказываний. Далее до следствия 1 включительно мы
будем
рассматривать
только
формулы
логики
высказываний. Определим для них понятие выводимости в
исчислении высказываний (ИВ).
НАЗАД
ДАЛЕЕ
302
303. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
определения1. Вывод формулы из множества формул Т в ИВ
есть последовательность
формул 1 ,..., k , в которой
k и любая из формул i – либо одна из
основных
тавтологий, либо
выведена
из
предшествующих формул по -правилу.
2. Формула выводима в ИВ, если она выводима в
ИВ из пустого множества формул.
НАЗАД
ДАЛЕЕ
303
304. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Выводимостьиз Т в ИВ будем обозначать
через T , а выводимость
в ИВ – через .
Например, следующая последовательность является
выводом в ИВ формулы :
1. ( )
– основная тавтология 1;
2. ( ( )) (( (( ) )) ( ))
– основная тавтология 2;
3. ( (( ) )) ( )
– из 1 и 2 по -правилу;
4. (( ) )
– основная тавтология 1;
5.
– из 4 и 3 по -правилу.
НАЗАД
ДАЛЕЕ
304
305. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Отношение обладает свойствами, аналогичнымисвойствам отношения | (см. § 12). Для него справедливы
теорема
дедукции
и
другие
утверждения
из § 12
(естественно, в формулировках этих результатов для ИВ
речь
идет
о
формулах
логики
высказываний).
Доказательства свойств выводимости в ИВ почти не
отличаются от приведенных в § 12 для ИП, только в
доказательстве теоремы дедукции кванторные правила
следует исключить, а
при рассмотрении
-правила
использовать доказанное выше соотношение .
НАЗАД
ДАЛЕЕ
305
306. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Как и в ИП, для доказательства выводимости в ИВдостаточно
построить
квазивывод.
В
«листьях»
квазивывода могут находиться соотношения вида T ,
где – основная тавтология или формула из Т. В качестве
примера
приведен квазивывод
в
ИВ соотношения
( ) для любой формулы :
НАЗАД
ДАЛЕЕ
306
307. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
( ),( ), ( ); ( ), ( )
( )
( ) ( ); ( ) ( )
( )
( )
Напомним, что запись ( p1 ,..., pn ) означает, что
все
высказывательные
переменные
формулы
содержатся среди указанных, а ( 1 ,..., n ) есть значение
формулы
при
pi i {И, Л} . Будем
также
использовать следующие обозначения: И и Л .
НАЗАД
ДАЛЕЕ
307
308. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Предложение. Для любой формулы ( p1 ,..., pn )и любых 1 ,..., n из {И, Л} справедливо соотношение
p1 1 ,..., pn n , где ( 1 ,..., n ) .
Доказательство. Проведем
индукцию
по
формулы . Если pi , то i и
предложение
для верно, т. к.
доказываемое
построению
соотношение имеет вид p1 1 ,..., pn n pi i . Предположим,
что для формул и предложение верно, а имеет
один из видов: , , , . Во всех этих
случаях рассуждения схожи, поэтому рассмотрим лишь
случай ( ) .
НАЗАД
ДАЛЕЕ
308
309. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Попредположению
индукции,
p1 1 ,..., pn n
и
p1 1 ,..., pn n , где ( 1 ,..., n ) и ( 1 ,..., n ) . Если
теперь мы установим, что
, , то отсюда по
свойству 3 из § 12 получим требуемое соотношение.
Итак, будем
доказывать, что , при
( ) . Перебирая возможные значения и из
{И, Л}, легко
понять, что
достаточно
установить
следующие соотношения: , ( ); , ( );
, ( ); , ( ) . Первые два из них
следуют из теоремы дедукции. Для двух других приведем
соответствующие квазивыводы:
НАЗАД
ДАЛЕЕ
309
310. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
, , , ; , , ,, ,
, ,
, ( )
, , ; , ,
, ( )
Во втором квазивыводе , , потому, что
, по -правилу. ■
Следствие 1.
Любая
тавтология
логики
высказываний выводима в ИВ.
НАЗАД
ДАЛЕЕ
310
311. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Доказательство.Пусть
( p1 , p2 ) – тавтология
(для упрощения записи будем считать, что зависит от
двух
переменных; в
общем
случае
доказательство
любых 1 , 2 из {И, Л},
аналогично). ( 1 , 2 ) И при
поэтому из доказанного выше предложения следует, что:
p1 , p2 ; p1 , p2 ; p1 , p2 ; p1 , p2 . Применяя
свойство 4 из § 12 к первым двум соотношениям, получим:
p1 , p2 p2 ; применяя
его к
последним двум
соотношениям, получим: p1 , p2 p2 . Применяя то
же свойство к только что выведенным соотношениям,
получим: p1 p1 , p2 p2 .
НАЗАД
ДАЛЕЕ
311
312. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Но, как доказано выше (см. пример квазивывода в ИВ),( p1 p1 ) и ( p2 p2 ) . Отсюда по свойству 3 из §
12 получаем . ■
Теперь вернемся к логике предикатов.
Следствие 2.
Любая тавтология сигнатуры
выводима в ИП 1 ( ).
Доказательство.
Пусть – тавтология сигнатуры
. Тогда
( 1 ,..., n ) для подходящей тавтологии ( p1 ,..., pn )
логики высказываний и формул 1 ,..., n сигнатуры
.
По следствию 1 имеем .
НАЗАД
ДАЛЕЕ
312
313. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Пусть 1 ,..., k – выводформулы
в
ИВ.
Из
доказательства следствия 1 видно, что формулы i (1 i k )
можно считать не зависящими ни от каких переменных,
кроме p1 ,..., pn . Положим i/ i ( 1 ,..., n ). Тогда 1/ ,..., n /
– вывод формулы в ИП 1 ( ) (т. к. если i – основная
высказываний, то i/ – основная
тавтология логики
тавтология сигнатуры
, а если i , выведена из j и
m по -правилу, то / тоже может быть выведена из j
i
и m / по -правилу).
Теперь
мы
■
можем
теоремы о равносильности
НАЗАД
завершить
доказательство
ИП( ) и ИП 1 ( ) .
ДАЛЕЕ
313
/
314. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Нам осталось проверить, что любая формула, выводимаяиз Т в ИП( ), выводима из Т и в ИП 1 ( ) . Допустим, что
T | в ИП( ) и рассмотрим соответствующее дерево
вывода D (например, изображенное на рис. 11 в § 12).
«Листьями» этого дерева являются аксиомы ИП( ) и
формулы из Т. Отберем из них все тавтологии 1 ,..., k
. По следствию 2 для каждой формулы
i (1 i k ) существует дерево Di ее вывода в ИП 1 ( ) .
сигнатуры
«Нарастим» дерево D, присоединив к каждому «листу»,
содержащему i , «корень» дерева Di.
НАЗАД
ДАЛЕЕ
314
315. Глава III. Исчисление предикатов. § 15. Другая формулировка исчисления предикатов.
Полученное дерево вывода D/ – для дерева на рис. 11 онопоказано на рис. 12 (см. § 12) – является деревом вывода в
в ИП 1 ( ) . ■
НАЗАД
ВЫХОД 315
























































































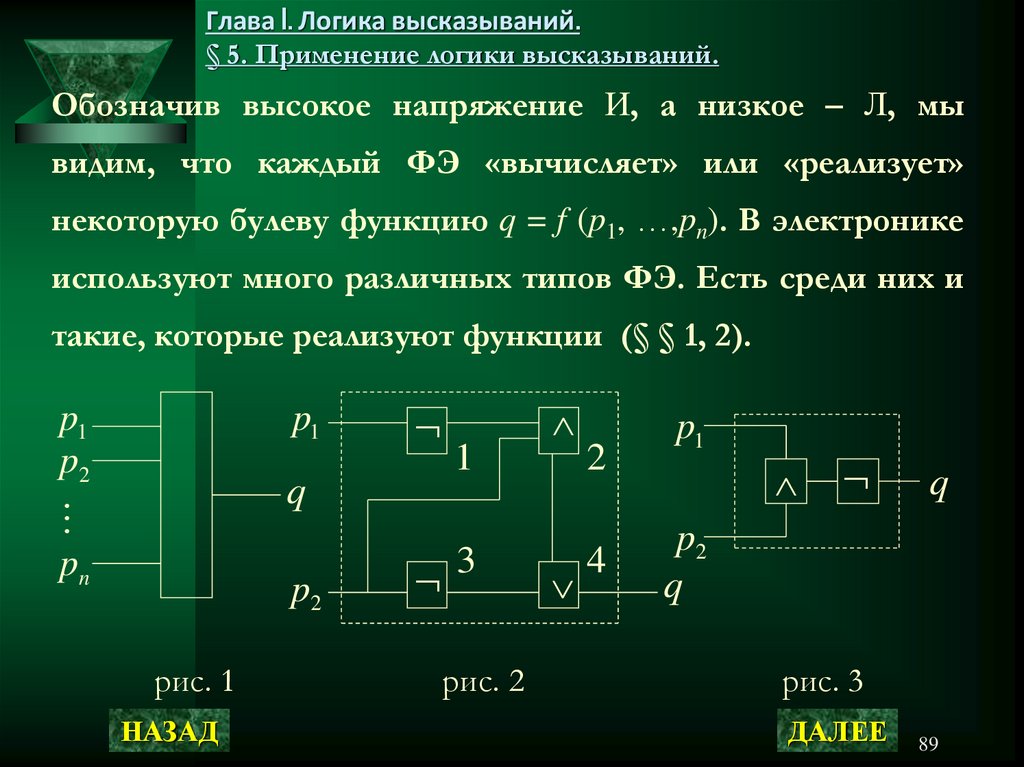

























































































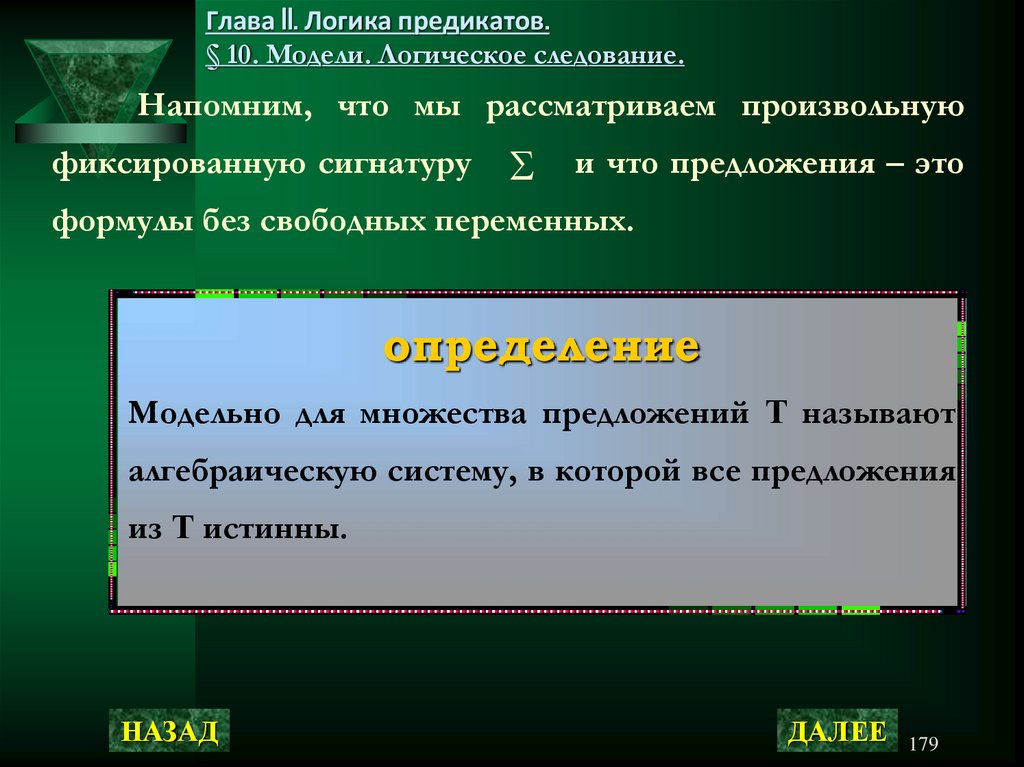








































































































































 mathematics
mathematics








