Similar presentations:
Дискретная математика. Курс лекций
1. Министерство науки и высшего образования Федеральное государственное бюджетное образовательное учреждение высшего образования
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯФедеральное государственное бюджетное образовательное учреждение высшего
образования
«КЕМЕРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
С. Г. Гутова, Е. С. Каган, М. А. Новосельцева
ДИСКРЕТНАЯ МАТЕМАТИКА
Курс лекций
Часть 2
Кемерово
2021
© Гутова С. Г. , Каган Е. С.,
Новосельцева М. А., 2022
© Кемеровский государственный
университет, 2022
ISBN 978-5-8353-
Об издании – 1, 2, 3
2.
ББК В19я73-5УДК 519.6(075.8)
Г 89
Издается по решению Научно-методического совета
Кемеровского государственного университета
Авторы:
Гутова Светлана Геннадьевна – кандидат технических наук, доцент кафедры прикладной математики, Каган Елена Сергеевна – кандидат
технических наук, заведующий кафедрой прикладной математики, Новосельцева М. А. – кандидат технических наук, доцент кафедры
прикладной математики
Г 89
Гутова, С. Г. Дискретная математика: курс лекций. Часть 2 [Электронный ресурс] / С. Г. Гутова, Е. С. Каган, М. А.
Новосельцева; КемГУ. – Электрон. дан. (1 Мб). – Кемерово: КемГУ, 2022 – 1 электрон. опт. диск (СD-ROM). – Систем. требования: Intel
Pentium (или аналогичный процессор других производителей), 12 ГГц; 512 Мб оперативной памяти; видеокарта SVGA, 1280x1024 High
Color (32 bit); 2 Мб свободного дискового пространства; операц. система Windows ХР/7/8; Power Point. – Загл. с экрана.
ISBN 978-5-8353Курс лекций разработан по дисциплине «Дискретная математика» для направления подготовки 01.03.02 Прикладная
математика и информатика и включает теоретический материал, примеры, снабженные анимацией. Может быть использован для
обеспечения лекционных занятий по дисциплине «Дискретная математика» студентами направлений подготовки 02.03.02
Фундаментальная информатика и информационные технологии и 02.03.03 Математическое обеспечение и администрирование
информационных систем, 09.03.03. Прикладная информатика и по дисциплине «Дискретная математика и математическая логика»
студентами направления 01.03.01. Математика, 02.03.01 Математика и компьютерные науки.
Все права защищены. Никакая часть данной книги не может быть воспроизведена в
какой бы то ни было форме без письменного разрешения владельцев авторских прав.
ББК В19я73-5
УДК 519.6(075.8)
ISBN
© Гутова С. Г., Каган Е. С., Новогсельцева М.
А., 2022
© Кемеровский государственный университет,
2022
3.
Текстовое электронное изданиеМинимальные системные требования:
Компьютер: Pentium 3 и выше, 12 ГГц; ОЗУ 512 Мб; 2 Мб на жестком
диске; видеокарта SVGA, 1280x1024 High Color (32 bit); привод
CD-ROM
Операционная система: Windows ХР/7/8
Программное обеспечение: Adobe Reader
© Гутова С. Г. , Каган Е. С.,
Новосельцева М. А., 2022
© Кемеровский государственный
университет, 2022
3
4. Введение
Курслекций
математика»
разработан
для
по
дисциплине
направления
«Дискретная
подготовки
01.03.02
Прикладная математика и информатика в соответствии с
требованиями ФГОС ВО и включает теоретический материал
и многочисленные примеры решения задач, снабженные
анимацией.
В результате усвоения
издания
примеров
и
материала настоящего учебного
выполнения предлагаемых к рассмотрению
у обучающихся
способности:
формируются
следующие
4
5. Введение
уметь доказывать основные теоремы дискретной математики,возможные сферы их связи и приложения в других областях
математического знания и дисциплинах профессионального
цикла;
выбирать методы решения научных и практических задач;
использовать аппарат теории множеств, теории графов,
теории кодирования в решении профессиональных задач.
5
6.
Конспект лекций может быть использован для обеспечениялекционных
занятий
по
дисциплине
«Дискретная
математика» студентами направлений подготовки 02.03.02
Фундаментальная информатика
и информационные
технологии и 02.03.03 Математическое обеспечение и
администрирование информационных систем, 09.03.03
Прикладная информатика и по дисциплине «Дискретная
математика
и
математическая
логика»
студентами
направления подготовки 01.03.01. Математика, 02.03.01
Математика и компьютерные науки.
6
7. Оглавление
ВведениеЛекция 1
Лекция 2
Лекция 3
Лекция 4
Лекция 5
Лекция 6
Лекция 7
Лекция 8
Лекция 9
Лекция 10
Лекция 11
Лекция 12
Лекция 13
7
8. Лекция 1
Основные определения. Таблицалогической функции
9. Основные определения
Логическое множество В={0, 1} [1-3],где 0 – ложь, нет, false; 1 – истина, да, truth.
Логическая функция (или функция
алгебры логики) это операция типа:
f : B B.
n
9
10. Иначе говоря, логическая функция от n переменных
y f x1 , x2 , ..., xnфункция, для которой выполняется:
y B, xi B, i 1, n.
10
11. Задание логической функции таблицей
xy
z
f (x,y,z)
0
0
0
0
0
0
1
1
0
1
0
0
….
….
….
….
В левой части перечислены все наборы
значений переменных в лексикографическом порядке.
В правой части – значение функции на
каждом наборе.
11
12. Множество логических функций от n переменных –
Р2 (n).Множество
всех
функций – Р2 [1-3].
логических
Замечание: количество наборов
значений переменных логической
функции от n переменных равно:
Bn B 2 .
n
n
12
13. Утверждение:
P2 n 2 .2
n
Доказательство:
Каждая логическая n переменных
функция задается вектор-столбцом.
Его длина k – равна числу наборов
значений аргументов [5]:
k 2 .
n
Всего различных столбцов 2
k
n
2 .
2
13
14.
Единичным набором значенийаргументов называется набор, на
котором функция равна 1 [1-3].
Единичным множеством
называется множество единичных
наборов функции f – M f .
14
15.
Нулевым набором значенийаргументов называется набор, на
котором функция равна 0.
Нулевым множеством называется
множество нулевых наборов
функции f – M f .
15
16.
Переменная xi называетсяфиктивной (несущественной),
если от ее значения не зависит
значение функции [1-3]:
f x1 , x2 , ..., xi 1 , 0, xi 1 , ..., xn
f x1 , x2 , ..., xi 1 ,1, xi 1 , ..., xn .
16
17. Таблица функций одной переменной
При n = 1 число логических функций равно:P2 1 2 4.
21
x
0
1
2
3
0
0
0
1
1
1
0
1
0
1
17
18. Названия функций одной переменной
0 ( х ) 0функция-константа 0;
3 ( х ) 1
функция-константа 1;
1( х ) х
тождество переменной х ;
2 ( х ) x
отрицание переменной х .
Функции-константы имеют 1 фиктивную
переменную х.
Функции тождество и отрицание – не имеют
фиктивных переменных.
18
19. Таблица функций двух переменных
При n = 2 число логических функций равно:P2 2 2 16.
22
x
у №0 №1 №2 №3 №4 №5 №6 №7
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
19
20. Продолжение таблицы логических функций 2 переменных
xу
№8
№9
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
№ 10 № 11 № 12 № 13 № 14 № 15
20
21. Названия и свойства функций двух переменных
xу
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
№0 №1 №2 №3 №4 №5 №6 №7
Функция № 0 – константа 0 .
Она принимает одно и то же значение 0 при
любых наборах значений аргументов.
21
22. Названия и свойства функций двух переменных
xу
№8
№9
№ 10
№ 11
№ 12
№ 13
№ 14
№ 15
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция № 15 – константа 1.
Она принимает одно и то же значение 1 при
любых наборах значений аргументов.
22
23. Названия и свойства функций двух переменных
xу №0 №1 №2 №3 №4 №5 №6 №7
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция № 1 – конъюнкция x и y.
Обозначение x y x & y x y xy
Конъюнкция принимает значение 1 только в
случае, когда х и у равны 1.
23
24. Названия и свойства функций двух переменных
xу №0 №1 №2 №3 №4 №5 №6 №7
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция № 7 – дизъюнкция x и y.
Обозначение x y.
Дизъюнкция принимает значение 1 тогда, когда
х или у равны 1 (т. е. хотя бы один аргумент).
24
25. Названия и свойства функций двух переменных
x у №8№ 9 № 10 № 11
0
0
1
1
1
0
1
0
0
1
0
0
1
1
0
№ 12
№ 13
№ 14 № 15
1
1
1
1
1
0
0
1
1
1
1
0
1
1
0
0
1
1
1
0
1
0
1
0
1
Функция № 9 – эквивалентность x и y.
Обозначение
x ~ y.
Эквивалентность принимает значение 1 только в
случае, когда х и у равны.
25
26. Названия и свойства функций двух переменных
xу №0 №1 №2 №3 №4 №5 №6 №7
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция № 6 – сложение по модулю 2 x и y.
x y.
Обозначение
Сложение по модулю 2 принимает значение 1
только в случае, когда сумма х и у нечетна.
26
27. Названия и свойства функций двух переменных
xу
№8
№9
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
№ 10 № 11 № 12 № 13 № 14 № 15
Функция № 13 – импликация x и y.
Обозначение
x y.
Импликация принимает значение 0 только в случае,
когда из «истины» следует «ложь».
27
28. Названия и свойства функций двух переменных
xу
№8
№9
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
№ 10 № 11 № 12 № 13 № 14 № 15
Функция № 11 – импликация у и х.
Обозначение
y х.
28
29. Названия и свойства функций двух переменных
xу
№8
№9
№ 10
№ 11
№ 12
№ 13
№ 14
№ 15
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
Функция № 14 – штрих Шеффера x и y.
Обозначение
x у.
Штрих Шеффера является отрицанием
конъюнкции:
x у ху.
29
30. Названия и свойства функций двух переменных
xу
№8
№9
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
№ 10 № 11 № 12 № 13 № 14 № 15
Функция № 8 – стрелка Пирса x и y.
Обозначение x y.
Стрелка Пирса является отрицанием дизъюнкции:
х у х у.
30
31. Функции с одной фиктивной переменной
Функции № 0 и № 15 – константы 0 и 1 имеютдве фиктивные переменные.
Фиктивную y имеют
№ 3 – тождество x и x у № 0
№3
№5
№ 10
№ 12
№ 15
№ 12 – отрицание x. 0 0
0
0
0
1
1
1
0 1
0
0
1
0
1
1
1 0
0
1
0
1
0
1
0
1
1
0
0
1
Фиктивную x имеют
№ 5 – тождество y и 1 1
№ 10 – отрицание y.
Общее количество функций с фиктивными
переменными равно 6.
31
32. Лекция 2
ДНФ и КНФ. Разложениефункции по переменным
33.
ДНФ и КНФ.Разложение функции по переменным
Формула алгебры логики – запись
суперпозиции логических функций с
использованием знаков переменных,
скобок и знаков логических функций
(логических связок):
33
34.
ДНФ и КНФ.Разложение функции по переменным
1 , 2 , 3 , , ~ , , I , .
Порядок записи логических связок
определяет иерархию, на основании
которой расставляются скобки [5].
34
35. Расстановка скобок
Каждая подформула окружается скобками.Скобки можно не ставить, если они внешние.
x y x y.
Отрицание связывает сильнее всех.
x y x y.
Конъюнкция связывает сильнее остальных
x y z x z y
x y z x z y.
35
36. Элементарной конъюнкцией [1-3] называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не
болееодного раза.
1, x , x y , x y z .
36
37.
Дизъюнктивной нормальной формой(ДНФ) [1-3] называется дизъюнкция
элементарных конъюнкций.
x x y x y z.
37
38.
Дизъюнктивная форма будетсовершенной (СДНФ), если каждая
элементарная конъюнкция содержит
все наименования переменных [1-3].
x y z x y z x y z x y z.
38
39. Элементарной дизъюнкцией [1-3] называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не
болееодного раза.
0, x, x y, x y z.
39
40.
Конъюнктивной нормальной формой(KНФ) [1-3] называется конъюнкция
элементарных дизъюнкций.
x x y x y z .
40
41.
Конъюнктивная форма будетсовершенной (СКНФ), если каждая
элементарная дизъюнкция содержит
все наименования переменных [1-3].
x y z x y z x y z .
41
42. Разложение функции по переменным
Введем обозначениеx x , x x.
0
1
Замечание:
1, x
x
0, x
42
43. Разложение функции по переменным
Доказательство:x 0, 0, x 0 0 1,
0
x 1, 1, x 1 1,
1
1
0
x 0, 1, x 0 0,
x 1, 0, x 1 1 0.
43
44. Теорема о разложении функции по переменным
Всякая логическая функция [1-3]y f x1 , x2 , ..., xn
может быть разложена по переменным
x1 , x2 , ..., xm , m n.
44
45. Разложение функции по переменным
то есть представлена в виде:f x1 , x2 , ... , xm , ... , xn
x x
1
1
2
2
m
... xm
1 2 ... m
f 1 , 2 , ... , m , xm 1 , ... , xn .
45
46. Разложение функции по переменным
Дизъюнкция в правой части равенстваберется по всем наборам параметров.
1 , 2 , ... , m 0,1 .
Всего частей разложения будет
m
2 .
Рассмотрим разложение по одной
переменной и по всем переменным.
46
47. Разложении по одной переменной
При m = 1 в разложении будет ровно 2конъюнкции, соединенные дизъюнкцией.
f x, y, z x 0 f 0, y, z x1 f 1, y, z
x f 0, y, z x f 1, y, z .
47
48. Пример 1:
Разложить по переменной х функцию,заданную формулой.
f x, y, z x z x y .
48
49. Пример 1:
f x , y , z x z x yx f 0, y , z x f 1, y , z
x 0 z 0 y x 1 z 1 y
x 1 z y x 0 z 1
x z y x z 1
49
50. Пример 1:
yz
z y
0
0
0
0
1
1
1
0
1
1
1
1
50
51. Пример 1:
x z y x z 1x y z x.
51
52. Пример 2:
Разложить по переменной х функцию,заданную вектор-столбцом
f x, y, z 01101110 .
Т
52
53. Пример 2:
f x, y , z0
x f 0, y, z x f 1, y, z 0
y
z
F(x,y,z)
0
0
0
0
1
1
x 0110 x 1110 0
1
0
1
1
1
0
x y z x y z .
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
x
T
T
0
53
54. Разложении по всем переменным
При m = n в разложении будет ровностолько частей, сколько единичных
наборов у функции. Каждая часть
соответствует одному единичному
набору.
54
55. Разложении по всем переменным
То есть для всех наборовтаких что:
1 2 3
,
f 1 , 2 , 3 1
f x, y , z
x y z
1 2 3
f 1 , 2 , 3 1
55
56. Правило построения СДНФ из вектор-столбца
Функция заданах
у
F(x,y)
таблицей
0
0
1
1. Выбрать все
0
1
0
единичные
1
0
1
1
1
1
наборы значений
аргументов.
56
57. Правило построения СДНФ из вектор-столбца
2. Каждомуединичному
х
набору
0 0
1
сопоставить
0 1
0
элементарную
1
0
1
x y
1 1
1
x y
конъюнкцию всех
у
F(x,y)
x y
переменных.
57
58. Правило построения СДНФ из вектор-столбца
так чтобых
переменная в
0 0
1
конъюнкции была
0 1
0
с отрицанием,
1
0
1
xx yy
1 1
1
x yy
если в наборе она
у
F(x,y)
x y
равна 0.
58
59. Правило построения СДНФ из вектор-столбца
3. Соединить полученныеконъюнкции знаком дизъюнкции
x y x y x y.
59
60. Лекция 3
Булева алгебра61.
Булева алгебраБулевы операции – это конъюнкция (˄),
дизъюнкция (˅) и отрицание (¬).
Булева алгебра – это множество
логических функций с введенными на
нем булевыми операциями [1-3].
А P2 , , , .
61
62.
Булева алгебраФормулы, представляющие одну и ту
же функцию называются
равносильными (эквивалентными).
62
63. Основные свойства булевых операций
Закон коммутативности1 x y y x , 2 x y y x ,
Закон ассоциативности
3 x y z x y z ,
4 x y z x y z ,
63
64. Основные свойства булевых операций
Закон дистрибутивности5 x y z x z y z ,
6 x y z x z y z ,
Закон де Моргана
7 x y x y ,
8 x y x y ,
64
65. Основные свойства булевых операций
Закон уничтожения кратности9 x x x ,
10 x x x ,
Закон исключенного третьего
11 x x 1,
Закон противоречия
12 x x 0,
65
66. Основные свойства булевых операций
Закон поглощения13 x xy x ,
14 x x y x ,
Закон двойного отрицания
15 x x ,
66
67. Основные свойства булевых операций
Свойства констант16 x 0 x ,
17 x 0 0,
18 x 1 1,
19 x 1 x ,
20 0 1 1,
21 0 1 0.
67
68.
Основные эквивалентностиЗакон простого склеивания
22 xy xy x,
23 x y x y x,
Закон расщепления
24 x xy xy,
25 x x y x y ,
68
69.
Основные эквивалентностиПервый закон обобщенного склеивания
26 xz yz xy xz yz ,
Второй закон обобщенного склеивания
27 x xy x y.
69
70. Основные эквивалентности
Эквивалентность28 x ~ x 1,
29 x ~ x 0,
30 x ~ 1 x ,
31 x ~ 0 x .
70
71. Основные эквивалентности
Сложение по модулю 232 x x 0,
33 x x 1,
34 x 1 x ,
35 x 0 x.
71
72. Основные эквивалентности
Импликация36 x x 1, 39 x 0 x ,
37 x x x , 40 x 1 1,
38 x x x , 41 0 x 1,
42 1 x x.
72
73. Утверждение о единственности СДНФ логической функции
СДНФ любой логической функцииединственна с точностью до порядка
элементарных конъюнкций и порядка
элементов в конъюнкциях.
Единственная логическая функция, не
имеющая СДНФ, функция – константа 0.
73
74. Теорема о преобразовании равносильных формул друг в друга
Пусть F и1
F2 равносильные формулы.
Тогда существует последовательность
эквивалентных преобразований,
переводящих одну эквивалентную
формулу в другую.
74
75. Теорема о преобразовании равносильных формул друг в друга
Доказательство:Так как формулы F1 и F2 равносильны,
то они представляют одну функцию f
.
У каждой функции единственна СДНФ.
Приведем
F1 и F2 к СДНФ.
F1 СДНФ ; F2 СДНФ .
75
76. Теорема о преобразовании равносильных формул друг в друга
Доказательство:Обратим второе преобразование.
F1 СДНФ F2 .
Получим последовательность
преобразований, переводящих
F1 в F2 .
76
77. Теорема о представимости логической функции булевой формулой
Любая логическая функция представимабулевой формулой.
Доказательство: у каждой функции
существует СДНФ – булева формула.
Функция константа 0 может быть выражена
булевой формулой вида:
x x 0.
77
78. Лекция 4
Преобразованиевыражений
79.
Преобразование выраженийЛюбую формулу можно преобразовать к
ДНФ [1-3].
1. Заменить все знаки функций на знаки
булевых функций (конъюнкция (˄),
дизъюнкция (˅) и отрицание (¬)), используя
тождества.
79
80.
Преобразование выражений2. По закону де Моргана и двойного
отрицания опустить отрицание до
переменных.
3. По закону дистрибутивности раскрыть
скобки.
80
81.
Преобразование выражений4. Уменьшить число элементов в
конъюнкциях, пользуясь законом
уничтожения кратности, свойствами
констант.
81
82.
Преобразование выражений5. Уменьшить число конъюнкций, пользуясь
законами поглощения, склеивания,
уничтожения кратности, свойствами
констант.
Получим ДНФ.
82
83. Пример 1:
f x , y , z x yz yz yz xyzx yz yz yz x y z
x yz yz yz x y z
x y x zy x y y z
84. Пример 1:
x yz yz yz x y zx y z y z x y z
xy xz yz yz yz x y z
x
x yxy
x y x
85.
xy xz yz yz yz x y zx xy x закон поглощения
xy xz x y z
x xy x y закон обощенного
склеивания
y x x y z 1
86. Пример 2:
f x , y , z x z xy xyz x zx z xy x yz x z
xz xy xyz x z
xy x z
x xy x
87. Пример 2:
xy x zy x z.
x xy x y
88. Пример 3:
f x , y , z xy x yz x yxy x yz x y
x y x y z x y
89. Пример 3:
x y x y z x yx x x y x z xy yy yz x y
x y x z xy yz x y
x x yx z0 xx z0 yx z
90. Пример 3:
x y x z xy yz x yx y yz x z xy x y
x y yz xy x y
xz yz xy xz yz
91. Пример 3:
x y yz xy x yx y x y yz x y xy x y
x y x z 0 0 x y.
x x x
92. Пример 4:
f x , y , z xyz x y x xy zxyz x y x xy z
xyz x y x xy z
xyz x y x y z
93. Пример 4:
xyz x y x y zxyz x y xz yz
xyz x y yz
xyz yz x y
94. Пример 4:
y xz z x yy x z x y
xy yz x y .
95.
Пример 5:F ( x , y , z ) xy x yz x y
8
xy x yz x y
15
x y x y z x y
5
x y x y z x y
95
96.
Пример 5:12
x x x y x z xy yy yz x y
1,3
x y x z xy yz x y
26
x y yz x z xy x y
3
x y yz xy x y
96
97.
Пример 5:5
x y yz xy x y
10 ,12
x y x y yz x y xy x y
16 ,17
x y x z 0 0 x y.
97
98. Переход от ДНФ к КНФ [1]
1. Пусть функция f задана в виде ДНФ.F k1 k2 ... kn
Здесь k1 , k 2 , ..., k n –
элементарные конъюнкции.
98
99. Переход от ДНФ к КНФ
2. Применим закон двойногоотрицания
F F.
3. Приведем к ДНФ
F.
F k1 k2 ... kn k1 k2 ... kn
d1 d 2 ... d n k1 k2 ... kn
Здесь d1 , d 2 , ..., d n – элементарные
дизъюнкции.
99
100. Переход от ДНФ к КНФ
4. Возьмем второе отрицание над F.Во время преобразования не будем раскрывать
скобки – остановимся на формуле, имеющей вид
конъюнкции элементарных дизъюнкций – КНФ.
F F k1 k2 ... k n
k1 k2 ... kn
d1 d 2 ... d n .
100
101. Правило построения СКНФ из вектор-столбца
Функция заданах
у
F(x,y)
таблицей [1-3].
0
0
0
1. Выбрать все
0
1
1
нулевые наборы
1
0
0
1
1
0
значений
аргументов.
101
102. Правило построения СКНФ из вектор-столбца
2. Каждомух
у
F(x,y)
x y
нулевому набору
0 0
0
сопоставить
0 1
1
элементарную
1
0
0
x y
1 1
0
x y
дизъюнкцию всех
переменных
102
103. Правило построения СКНФ из вектор-столбца
так чтобых
переменная в
0 0
0
дизъюнкции была
0 1
1
с отрицанием,
1
если в наборе она
равна 1.
у
F(x,y)
x y
0
0
x y
1 1
0
x y
103
104. Правило построения СКНФ из вектор-столбца
3. Соединить полученные дизъюнкциизнаком конъюнкции
x y x y x y .
104
105. Пример 6:
Построить СДНФ иСКНФ функции,
заданной вектор-столбцом:
f 10100111 T
СДНФ f x y z x y z x y z
x y z x y z.
СКНФ f x y z x y z x y z .
105
106. Лекция 5
Импликанты107. ДНФ и импликанты
Функция f имплицирует функцию g,если f g 1 [1-3] .
Замечание: Если f g 1
,
то M f M g .
107
108. Импликант
Если f имплицирует g, и fпредставлена единственной
элементарной конъюнкцией, то f
называется импликантом g.
Если из импликанта нельзя удалить ни
одной переменной, то оно называется
простым импликантом.
108
109. Теорема (о мощности единичного множества функции, представимой единственной элементарной конъюнкции)
Если функцияf x1 , x2 , ... , xn
представима единственной
элементарной конъюнкцией
– всех n переменных [1] то M f 1 ;
– m < n переменных, то
Mf 2
n m
.
109
110. Пример 1:
Пустьf ( x, y , z ) xyz .
Она принимает значение 1 тогда и
только тогда, когда x = 1, y = 1, z = 1.
Значит M f 111 .
110
111. Пример 2:
Пустьf ( x, y , z ) yz.
Она принимает значение 1 тогда и
только тогда, когда y = 0, z = 1. Значит,
чему равняется переменная х – неважно,
и она может принимать любые
значения. Поэтому M f 001,101 .
111
112. Утверждение 1
Утверждение 1Представление функции в виде ДНФ
соответствует представлению ее
единичного множества в виде
объединения единичных множеств,
входящих в эту ДНФ элементарных
конъюнкций.
112
113. Пример 3:
Пусть функция представлена своей ДНФ.f ( x , y , z ) xyz y z x y .
Тогда ее единичное множество может
быть представлено в виде:
M f M xyz M y z M x y
101 000, 100 000, 001 .
Получилось, что M f 000, 001, 100, 101 .
113
114. Утверждение 2
Утверждение 2Любая конъюнкция ДНФ функции
является импликантом данной функции.
114
115. Утверждение 3
Утверждение 3Если конъюнкция ДНФ функции не
является простым импликантом, то
можно найти соответствующий ей
простой импликант (или импликанты)
и заменить им (или их дизъюнкцией)
непростой импликант.
115
116. Определение
ДНФ, состоящая только из простыхимпликантов, называется
сокращенной.
.
116
117. Пример 4:
Пусть функция представлена своейДНФ:
f ( x, y, z ) x xyz.
Тогда ее единичное множество имеет
вид:
M f M x M xyz 000, 001, 010, 011 101
000, 001, 010, 011, 101 .
117
118. Пример 4:
Очевидно, чтоx
– это простой
импликант. Он состоит из одной буквы,
и если ее вычеркнуть, получится
вырожденная конъюнкция
(конъюнкция не имеющая
переменных), что возможно только в
случае, если f 1 .
118
119. Пример 4:
Проверим, будет ли простым импликантk xy z .
Вычеркнем из него переменную х.
119
120. Пример 4:
Получим конъюнкциюk1 yz .
Ее единичное множество содержит 2
M
001
,
101
M
k
f ,
набора:
1
то есть k1 по-прежнему является
импликантом f.
Значит
k xyz
импликант.
– не простой
120
121. Сокращенная ДНФ
Сокращенная ДНФ – ДНФ, состоящаятолько из простых импликантов [1-3].
122. Пример 5:
Проверить импликанты данной ДНФ напростоту. Заменить простыми. Построить
сокращенную ДНФ.
f x, y, z xy xyz x y.
123. Пример 5:
Построить единичное множество функции,как объединение единичных множеств
элементарных конъюнкций, входящих в
f x, y , z xy xyz x у
M f M xy M xyz M x у
ДНФ:
110,111 101 000, 001
110,111,101, 000, 001 .
124. Пример 5:
M f 110,111,101, 000, 001 .k1 xy
вычеркнем х, получим k11 y
M y 010, 011,110,111 M f
Вывод : х вычеркивать нельзя.
125. Пример 5:
M f 110,111,101, 000, 001 .k1 xy
вычеркнем y, получим k12 x
M x 100,101,110,111 M f
k1 xy простой импликант.
126. Пример 5:
M f 110,111,101, 000, 001 .k2 xyz
вычеркнем x, получим k21 yz
M yz 001, 101, M f .
127. Пример 5:
M f 110,111,101, 000, 001 .k2 xyz
вычеркнем y , получим k22 xz
M xz 101, 111, M f .
128. Пример 5:
M f 110,111,101, 000, 001 .k2 xyz
вычеркнем z , получим k23 xy
M xy 100,101, M f
Вывод : z вычеркивать нельзя.
129. Пример 5:
Проверим,будет ли конъюнкцияиз 1 переменной импликантом
M x 100,101,110,111
M x 000, 001, 010, 011
M y 010, 011,110,111
M y 000, 001,100,101
M z 001, 011,101,111
M z 000, 010,100,110
130. Пример 5:
k2 xyzнепростой импликант
его можно заменить на
xz yz
131. Пример 5:
M f 110,111,101, 000, 001 .k3 x у
вычеркнем x , получим k31 у
M z 000, 001, 100, 101 M f
132. Пример 5:
M f 110,111,101, 000, 001 .k3 x у
вычеркнем у , получим k32 x
M z 000, 001, 010, 011 M f
k3 x у простой импликант.
133. Пример 5:
f x, y, z xy xyz x уxy xz yz x у
сокращенная ДНФ.
134. Пример 6:
Проверить импликанты данной ДНФна простоту. Заменить простыми.
Построить сокращенную ДНФ.
f ( x, y, z ) xyz xyz y z x y.
135. Пример 6:
Построить единичное множество функции,как объединение единичных множеств
элементарных конъюнкций, входящих в
ДНФ: f ( x , y , z ) xyz xyz y z x y
M f M xyz M xyz M y z M x y
111 101 000,100 000, 001
111,101, 000,100, 001 .
136. Пример 6:
M f 111,101, 000,100, 001 .k1 xyz
вычеркнем x, получим k11 yz
M yz 011,111 M f
Вывод : x вычеркивать нельзя
137. Пример 6:
M f 111,101, 000,100, 001 .k1 xyz
вычеркнем y, получим k12 xz
M xz 101,111 M f
138. Пример 6:
M f 111,101, 000,100, 001 .k1 xyz
вычеркнем z , получим k13 xy
M xy 110, 111 M f
Вывод : z вычеркивать нельзя.
139. Пример 6:
k1 xyz можно заменитьна простой импликант xz.
140. Пример 6:
M f 111,101, 000,100, 001 .k2 xyz
вычеркнем x, получим k21 yz
M yz 001,101 M f
прием, z не импликант,
а у простой импликант
141. Пример 6:
M f 111,101, 000,100, 001 .k2 xyz
вычеркнем y , получим k22 xz
M xz 101,111 M f
xz простой импликант.
142. Пример 6:
M f 111,101, 000,100, 001 .k2 xyz
вычеркнем z, получим k23 xy
M xy 100,101 M f
причем, х не импликант,
а у простой импликант.
143. Пример 6:
k2 xyz можно заменитьна дизъюнкцию
простых импликантов
xz y .
144. Пример 6:
M f 111,101, 000,100, 001 .Среди y z х у
простым импликантом
будет только у .
145. Пример 6:
ВЫВОД :f ( x, y, z ) xyz xyz y z x y
xz xz y y y xz y .
Это сокращенная ДНФ - сДНФ.
146. Лекция 6
МетодБлейка-Порецкого
147. Тупиковая ДНФ
Отношение покрытия междуединичными наборами и
импликантами ДНФ наглядно задается
таблицей покрытия [1-3].
147
148. Таблица покрытия
Строки таблицы соответствуют конъюнкциямДНФ, столбцы – элементам единичного
множества. На пересечении строки и столбца
ставится пометка, если данная конъюнкция
обращается в единицу данным набором
значений аргументов (набор покрывается
единичным множеством конъюнкции).
148
149. Пример 1:
Пусть ДНФ функции имеет вид:f ( x, y, z) y∨ yz.
Тогда ее единичное множество может быть
представлено в виде:
M f M y ∪ M yz 010, 011, 110, 111 .
Построим таблицу покрытия.
149
150. Пример 1:
yyz
010 011
110
111
*
*
*
*
*
*
Из таблицы видно, что вторая строчка –
лишняя, то есть если ее убрать, все элементы
единичного множества останутся покрыты.
150
151. Пример 1:
Значит, импликант yz – лишнийимпликант.
Таким образом, ДНФ можно упростить, убрав
лишний импликант.
f ( x, y, z ) y.
Эта ДНФ является тупиковой, так как
оставшийся импликант – простой.
Так бывает не всегда.
151
152. Тупиковая ДНФ
Сокращенная ДНФ, изкоторой удалены все лишние
импликанты, называется
тупиковой [1-3].
152
153. Замечание 1
Чтобы с помощью таблицы покрытияполучить тупиковую ДНФ, необходимо
сначала получить сокращенную ДНФ
(сДНФ) и именно ее простые
импликанты помещать в таблицу
покрытия.
153
154. Замечание 2
У функции может быть несколькотупиковых ДНФ.
Чтобы найти их необходимо построить
сокращенную ДНФ, содержащую все
простые импликанты данной функции.
154
155. Метод Блейка-Порецкого –
метод получения сокращенной ДНФ,содержащей все простые импликанты.
Пусть дана СДНФ функции.
1. Перенумеруем элементарные конъюнкции.
2. Осуществим попарно склеивание каждой
конъюнкции с каждой, если это возможно.
Под полученными конъюнкциями будем
фиксировать номера.
155
156. Метод Блейка-Порецкого
3. Допишем к списку полученныхконъюнкций те, которые не участвовали в
склеивании (их номера не фиксировались).
4. Вернемся к п.1.
В результате получим сокращенную ДНФ,
содержащую все простые импликанты.
156
157. Пример 2:
Дана СДНФ вида:f ( x, y, z) x y z x yz xy z xyz xyz.
Получить с помощью метода БлейкаПорецкого сокращенную ДНФ,
содержащую все простые импликанты.
157
158. Метод Блейка-Порецкого
П. 1.xy xy x
f ( x , y , z ) x y z x yz xy z xyz xyz
4
5
1
2
3
П. 2, 3.
П.4.
f ( x, y, z ) = х y∨ y z∨ x z ∨ x y
1, 2 1, 3 3,4 4,5
f ( x, y, z ) = х y∨ y z∨ x z ∨ x y
1 2 3 4
158
159. Метод Блейка-Порецкого
Так как больше склеивания произвестинельзя, сокращенная ДНФ имеет вид:
f ( x, y, z) x y∨ y z ∨ xz ∨ x y.
Построим таблицу покрытия:
159
160. Таблица покрытия
000xy
yz
xz
xy
001
∨ ∨
∨
100
110
111
∨
∨ ∨
∨ ∨
160
161. Таблица покрытия
000 001 100 110 111xy
yz
xz
xy
∨ ∨
∨
∨
∨ ∨
∨ ∨
161
162. Таблица покрытия
000xy
yz
xz
xy
001
∨ ∨
∨
100
110
111
∨
∨ ∨
∨ ∨
F1( x, y, z) x y xz x y.
162
163. Таблица покрытия
000xy
yz
xz
xy
001
∨ ∨
∨
100
110
111
∨
∨ ∨
∨ ∨
F2 ( x, y, z) x y y z x y.
163
164. Пример 3:
Дана СДНФ вида:f ( x, y, z) x y z xyz xyz xyz xyz.
Получить с помощью метода БлейкаПорецкого сокращенную ДНФ,
содержащую все простые импликанты.
164
165. Метод Блейка-Порецкого
П. 1.Метод Блейка-Порецкого
f ( x, y, z ) = x y z∨ xyz∨ x yz∨ xyz∨ xyz
1
2
3
4
5
П. 2, 3.
= x z ∨ y z∨ x y ∨ x y z
2,5 3,5 4,5 1
П.4.
= x z∨ yz∨ xy∨ x y z
1 2 3 4
165
166. Метод Блейка-Порецкого
Так как больше склеивания произвестинельзя, сокращенная ДНФ имеет вид:
f ( x, y, z) x y yz xz x y z.
Построим таблицу покрытия:
166
167. Таблица покрытия
000101
xy
∨
yz
xz
x yz ∨
011
∨
110
111
∨
∨
∨
∨
167
168. Таблица покрытия
000 101 011 110 111∨
xy
∨
yz
xz
x yz ∨
∨
∨
∨
∨
ТДНФ f ( x, y, z) x y∨ yz∨ xz∨ x y z.
168
169. Пример 4:
Дана СДНФ вида:f ( x, y, z) x y z∨ xyz∨ xyz∨ xyz ∨ xyz.
Получить с помощью метода БлейкаПорецкого сокращенную ДНФ,
содержащую все простые импликанты.
169
170. Метод Блейка-Порецкого
П. 1.Метод Блейка-Порецкого
f ( x, y, z ) = x y z∨ xyz∨ x yz∨ xyz∨ xyz
1
2
3
4
5
П. 2, 3.
f ( x, y, z ) = y z∨ x z∨ x z ∨ y z ∨ x y =
1,2 1,3 2,5 3,5 4,5
П.4.
f ( x, y, z ) = y z∨ x z∨ x z ∨ y z ∨ x y =
1 2 3 4 5
170
171. Метод Блейка-Порецкого
П. 1.Метод Блейка-Порецкого
f ( x, y, z ) = y z∨ x z∨ x z ∨ y z ∨ x y =
1 2 3 4 5
П. 2, 3.
П.4.
f ( x, y, z ) = z ∨ z ∨ xy =
1,4 2,3 5
f ( x, y, z ) = z∨ xy
1 2
171
172. Метод Блейка-Порецкого
Так как больше склеивания произвестинельзя, сокращенная ДНФ имеет вид:
f ( x, y, z) z∨ xy.
Построим таблицу покрытия:
172
173. Таблица покрытия
001z
xy
101
011
∨ ∨
∨
110
111
∨
∨
∨
173
174. Таблица покрытия
001 101 011 110 111z
∨
xy
ТДНФ
∨
∨
∨
∨ ∨
f ( x, y, z) z∨ xy.
174
175. Лекция 7
Двойственность176. Двойственная функция
Функция*
f ( x1 , x2 ,
, xn ) f ( x1 , x2 ,
, xn )
называется двойственной
функцией [1-3] к функции
*
f ( x1 , x2 ,
, xn ) f ( x1 , x2 ,
, xn )
176
177. Замечание 1
У двойственной функции напротивоположных наборах принимаются
противоположные значения:
если
f (0,0,1) 1,
то
f (1,1,0) 0.
*
177
178. Самодвойственная функция
Функция называетсяf ( x1 , x2 ,
, xn )
самодвойственной [1-3],
если
f ( x1 , x2 , , xn ) f ( x1 , x2 , , xn )
*
178
179. Пример 1:
Пустьf x, y x y – дизъюнкция.
Тогда, двойственной к ней является
конъюнкция:
f x, y f x , y x y xy
179
180. Пример 2:
Пустьf x, y xy – конъюнкция
Тогда, двойственной к ней является
дизъюнкция:
f x, y f x , y x y x y
180
181. Пример 3:
Пустьf x x
– тождество.
Тогда, двойственной к ней является:
f x f x x x
181
182. Пример 4:
Пустьf x x
- отрицание.
Тогда, двойственной к ней является:
f x f x x x
182
183. Замечание 2
Тождество и отрицание –самодвойственные функции.
183
184. Пример 5:
Пустьf x 0 – константа 0.
Ее переменная x – фиктивна, в формуле
отсутствует.
Тогда, двойственной к ней является:
f x f x 0 1.
184
185. Пример 6:
Пустьf x 1 – константа 1.
Ее переменная x – фиктивна, в формуле
отсутствует.
Тогда, двойственной к ней является:
f x f x 1 0.
185
186. Замечание 3
Отношение двойственностисимметрично.
Если f двойственна к g,
то и g двойственна к f.
186
187. Пример 7:
Найти двойственную для функции:f x, y, z xy xz yz.
Решение:
f x, y,z x y x z y z
x y x z y z
x y x z y z
187
188. Пример 7:
x y x z y zx yz y z xy xz yz yz
xy xz yz.
f x1 ,x2 , ,xn f
*
x1 ,x2 ,
,xn
Данная функция самодвойственна.
188
189. Замечание 4
Вектор-столбец самодвойственнойфункции антисимметричен
относительно своей середины.
189
190. Пример 7:
F xy xz yz.x
y
z
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
F(x, y, z)
0 1
0 1
0 1
1 0
0
1
1
1
190
191. Принцип двойственности
Если в формуле F, представляющейфункцию f все знаки функций заменить
на знаки двойственных функций,
то получится формула F ,
представляющая функцию f
двойственную к f.
191
192. Принцип двойственности для Булевой алгебры
Если в формуле F, представляющейфункцию f все конъюнкции заменить
на дизъюнкции, дизъюнкции
на конъюнкции, 1 на 0 и 0 на 1,
то получится формула F ,
представляющая функцию f
двойственную к f.
192
193. Пример 8:
Воспользуемся принципом двойственности.f ( x , y , z ) xy xz yz
f ( x, y,z ) x y x z y z
x y x z y z
x y x z y z
x y z xyz
193
194. Лекция 8
Алгебра Жегалкина195. Алгебра Жегалкина
Алгеброй Жегалкина [1-3]называется алгебра вида
AG P2 , ,
В алгебре Жегалкина действуют
тождества:
195
196. Тождества алгебры Жегалкина
1) коммутативность сложения по модулю 2:х у у х
2) ассоциативность сложения по модулю 2:
( х у) z х ( y z )
3) дистрибутивность конъюнкции по
отношению к сложению по модулю 2:
( x y) z xz yz
4) свойства констант:
x x 0, x 0 x
196
197. Формулы перехода
От любой булевой формулы можноперейти к формуле алгебры Жегалкина,
используя тождества:
x x 1
x y xy x y
x y x y x y 1 x 1 y 1 1
xy x y 1 1 xy x y
197
198. Полином Жегалкина
Полином Жегалкина – это формула алгебрыЖегалкина, имеющая вид суммы по модулю 2
элементарных конъюнкций различного
количества переменных без отрицаний [1-3].
xyz⊕xy⊕xz ⊕yz ⊕x⊕y ⊕z ⊕1
198
199. Линейная функция
Линейной функцией называется функция,полином Жегалкина которой имеет вид [1-3] :
f ( x1 , x2 , ..., xn ) 1x1 2 x2 ... n xn
1 , 2 , ..., n , 0, 1
Примеры линейных функций от 3-х
переменных:
1) x ⊕y ⊕z ⊕1;
2) x ⊕y ⊕z;
3) x y;
4) z ⊕1.
199
200. Утверждение 1
Утверждение 1Если
f1 f 2 0 ,,
–
то
f1 f 2 f1 f 2 .
200
201. Утверждение 2
Утверждение 2Если формула F – СДНФ, то при
переходе к формуле алгебры Жегалкина
достаточно заменить символы
дизъюнкции (∨ ) на символ сложения по
модулю 2 (⊕).
201
202. Пример 1:
f ( x, y, z) xy z xy z xy zx y 1 z 1 x y 1 z 1
= x(yz ⊕y ⊕z ⊕1)⊕xy⊕x ⊕z ⊕1 =
= xyz⊕xy⊕xz⊕x ⊕xy⊕x ⊕z ⊕1 =
x y xy x y
=
xyz
⊕
xz
⊕
z
⊕
1
.
=
0
( x ⊕xx⊕
y) z x=
xz
x ⊕
1 yz
202
203. Пример 2: Дана СДНФ:
f ( x, y, z ) = xyz ∨ xyz ∨ xyz == xyz⊕xyz ⊕xyz =
= xyz⊕x(y ⊕1)z ⊕xy(z ⊕1) =
xyz xyz xz xyz xy
f1 f(2 x=⊕
0
,
f
∨
f
=
f
⊕
f
2xz
xyzy
xy⊕
.1 yz 2
)1zxz=
x⊕
x xx= 01
203
204. Пример 3:
f ( x, y, z ) x y x z y zxy x y x z x z yz y z
0 0 xyz 0 0 xz xyz xy yz
yz y z xyz xz xyz xy yz
yz y z
x
(xx
yyx) zxy
xzx
yz y
0
205. Продолжим раскрывать скобки
xyz xz xyz xy yz yz y z0 xyz 0 0 xyz 0 0 x yz 0
x yz x y x yz 0 yz 0
xyz xyz x yz x yz x y x yz yz
x yz x y yz
15 xслагаемых
x 0
206. Избавимся от отрицания
x yz x y yzx 1 yz x 1 y yz
xyz yz xy y yz
xyz xy y L
x x 1
207. Пример 4: Дана СДНФ:
f ( x, y, z) xyz xyz x y z x y zxyz x yz x y z x y z
xyz x 1 yz
x 1 y z 1 x 1 y 1 z 1
f1 f 2 x0, тоxf1
1
f 2 f1 f 2
208. Раскроем скобки и приведем подобные
xyz x 1 yzx 1 y z 1 x 1 y 1 z 1
xyz xyz yz
xyz xy yz y
xyz xy xz yz x y z 1
xz yz x z 1 L
209. Пример 5: Дана ДНФ:
f x, y, z xy yz xy xyzxy yz xy xyz
x yz x y yz xy x yz
x yz x y yz xy x yz
x yz x y yz xy x yz
xyz xyz xyz xyz xy yz xy xyz
y zxy
x
xz x yzy
210. Избавимся от отрицания
xy yz xy xyzx 1 y y z 1
x y 1 x 1 y z 1
xy y yz y
xy x xyz xy yz y
xyz xy yz x y L
x x 1
211. Пример 6: Дана булева формула:
f ( x , y , z ) x y xy yzx y xy yz 1
x y 1 xy yz 1
x x 1
212. Привести к полиному Жегалкина булеву формулу
x y 1 xy yz 1x y xy x y
xy x y 1 xy yz 1
xyz xy xyz yz xy yz 1
1 L
213. Теорема (о существовании и единственности полинома Жегалкина логической функции)
У каждой логической функциисуществует и единственен полином
Жегалкина [1-3].
213
214. Доказательство:
1. Существование полинома уже доказано.2. Докажем единственность.
Для этого установим взаимно
однозначное соответствие между
полиномами и логическими функциями
от n переменных.
214
215. Доказательство:
Полином состоит из слагаемых –конъюнкций переменных без отрицаний.
Сколько может быть различных
слагаемых?
Столько, сколькими способами можно
составить подмножеств из множества
переменных.
215
216.
Множество переменных имеет вид:U={x1, x2, x3, …, xn}.
Тогда его подмножеств будет 2n [5].
1; конъюнкция без переменных
{x1} x1 ;
{x1, x2} x1x2;
{x1, x2, x3} x1x2x3;…
{x1, x2, x3, …, xn} x1x2x3…xn.
216
217. Доказательство:
.Доказательство:
Полином от полинома отличается составом
слагаемых.
Значит, сколько подмножеств множества
слагаемых можно образовать, столько и
будет полиномов.
Подмножеств у множества с мощностью 2n,
2п
будет 2 .
217
218.
0; полином без слагаемых{x1} x1
полином с одним слагаемым ;
{x1, x1x2} x1 x1x2
полином с 2 слагаемыми ;
{x1, x1x2, x1x2x3}
x1 x1x2 x1x2x3
полином с 3 слагаемыми ; и так далее.
218
219. Доказательство:
Таким образом, полиномов от nпеременных столько же, сколько и
2п
функций от n переменных – 2 .
Значит, между этими множествами
можно установить взаимно однозначное
соответствие.
219
220. Лекция 9
Замкнутые классы221. Замкнутый класс
Система функций называетсязамкнутым классом, если любая
суперпозиция функций системы
снова принадлежит системе [1-3].
221
222. Пример 1:
Множество всех конъюнкций K1 –замкнутый класс.
f x, y xy K1 , g x,z xz K1 ,
h x, y,t xyt K1 .
w x, y,z,t f g x,z ,h x, y,t
xz xyt xzxyt xyzt K1
222
223. Пример 2:
Множество всех дизъюнкций K2 –замкнутый класс.
f x,z x z K 2 , g y,z y z K 2 ,
h y,z,t y z t K 2 .
v x, y,z h y,g y,z , f x,z
y y z x z y y z x z
x y z K2
223
224. Пример 3:
Множество всех полиномов Жегалкина K3– замкнутый класс.
f x,z x z 1 K3 , g y,z y z K3 ,
h x,z,t x z t K3 .
w x, y,z,t f h x,z,t ,g y,z
x z t y z 1
x y z z t 1
x y t 1 K3
224
225. Замыкание
Замыканием сиcтемы функцийназывается система [ ], состоящая из
всех функций системы и всех
суперпозиций функций системы [1-3].
225
226. Функционально полные системы
Система функций называетсяфункционально полной (ФП), если через
суперпозиции функций этой системы
можно выразить любую логическую
функцию [1-3].
226
227. Замечание 1
Если система функций являетсязамкнутым классом,
то есть = K,
тогда она равна своему
замыканию:
K K
227
228. Замечание 2
Если система функций являетсяфункционально полной,
тогда ее замыкание равно всему
множеству логических функций:
P2
228
229. Пример 4:
Пусть система 0, , –
множество булевых операций
(базис Буля).
0 – ФП, так как любая логическая
функция может быть выражена Булевой
формулой (БФ).
229
230. Пример 5:
Система 0 является избыточной.Дизъюнкцию можно выразить через
конъюнкцию и отрицание:
x y x y
Конъюнкцию можно выразить через
дизъюнкцию и отрицание:
x y x y
230
231. Пример 5:
Откуда:1 , ФП
2 , ФП
231
232. Замечание 3
За неизбыточность системыприходится платить
избыточностью формул.
232
233. Пример 6:
Пусть булева формула имеет вид:F0 x, y, z xy xz
Тогда, в системе 1 она принимает
вид:
F1 x, y, z xy xz xy xz
233
234. Пример 7:
F0 x, y, z xy xzТогда, в системе 2 она принимает
вид:
F2 x, y, z x y x z
x y x z
234
235. Пример 8:
Система4
– функционально полна.
Это следует из того, что через штрих
Шеффера можно выразить функции ФП
системы:
1 , .
235
236. Продолжение примера 8
Отрицание выразим по формуле:x xx
Конъюнкцию выразим по формуле:
x y x y x y x y .
236
237. Продолжение примера 8
Убедимся в истинности равенства:x xx
0 1, 0 0 1
1 0, 11 0.
237
238. Пример 9:
Система4
– функционально полна.
Это следует из того, что через стрелку
Пирса можно выразить функции ФП
системы:
2 , .
238
239. Продолжение примера 9
Отрицание выразим по формуле:x x x
Дизъюнкцию выразим по формуле:
x y x y x y x y .
239
240. Продолжение примера 9
Убедимся в истинности равенства:x x x
0 1, 0 0 1
1 0, 1 1 0.
240
241. Теорема 1
Если через функции системы можновыразить функции булева базиса
0 , , ,
то система – функциональна полна [1-3].
Тогда говорят, что система – сводится к
системе 0:
0.
241
242. Следствие
1 , 0 , ,2 , 0 , ,
3
1 ,
4 2 ,
242
243. Теорема 2
Если через функции системы можновыразить функции некоторой
функционально полной системы
f1 , f 2 , ..., f k ,
то система – функциональна полна [1-3].
.
243
244. Следствие
Таким образом, доказательствофункциональной полноты произвольной
системы функций можно строить путем
сведения ее к некоторой системе,
функциональная полнота которой
доказана.
244
245. Функциональная полнота в слабом смысле
Система функций называетсяфункционально полной в слабом
смысле (сФП),
если она будет функционально полной
после добавления констант 0 и 1 [1-3].
0,1 ФП.
245
246. Функциональная полнота в слабом смысле
Система функций, сФП
Среди функций, образующей AG, нет
константы 1.
Но ровно половина всех полиномов
содержит слагаемое 1.
5 , ,1 ФП.
246
247. Лекция 10
Функционально полныесистемы
248.
Предполные классыФункционально полной называется
такая система функций Σ, через
функции которой можно выразить
любую логическую функцию [3–5].
248
249.
Предполные классыНапример,
, , .
0
Эта система функционально полна,
так как любая функция имеет булеву
формулу.
249
250.
Теорема 1Произвольная
система
Σ′
будет
функционально полной, если она сводится
к функционально полной системе Σо [1-3].
Это означает, что через функции системы
Σ′ можно выразить все функции системы
Σо.
250
251.
Функцияy f x1 , x2 , ..., xn
называется
сохраняющей 0 [1-3], если
f 0, 0, ..., 0 0.
Функция
y f x1 , x2 , ..., xn
называется
сохраняющей 1 [1-3], если
f 1,1, ...,1 1.
251
252.
Функция называется монотонной [1-3],если для любых двух наборов значений
аргументов σ и τ, таких что σ ≤ τ,
выполняется:
f(σ) ≤ f(τ).
252
253.
Утверждение 1Класс Т0 – класс функций, сохраняющих 0,
замкнут.
Утверждение 2
Класс Т1 – класс функций, сохраняющих 1,
замкнут.
253
254.
Утверждение 3Класс S – класс самодвойственных функций,
замкнут.
Утверждение 4
Класс L – класс линейных функций, замкнут.
254
255.
Теорема о булевой формулемонотонной функции
У каждой булевой формулы, отличной от 0 и
1,
существует
булева
формула
без
отрицаний.
Каждая булева формула без отрицаний
описывает монотонную функцию, отличную
от 0 и 1 [1-3].
255
256.
ЗамечаниеЧтобы проверить, есть ли у данной функции
булева формула без отрицаний, достаточно
построить ее сокращенную ДНФ. Если она
содержит
отрицания,
значит,
булевой
формулы без отрицаний у этой функции не
существует.
Следовательно,
она
немонотонна.
256
257.
Утверждение 5. Класс М – классмонотонных функций замкнут.
Очевидно, что подстановка булевой
формулы без отрицаний в булеву формулу
без отрицаний даст булеву формулу без
отрицаний.
257
258.
Лемма 1Если функция
немонотонна,
y = f (x1, x 2, ..., xn) –
то
подстановкой
n-1
константы из нее можно получить
отрицание [1-3].
258
259.
Доказательствоy
=
f
(
x
1, x 2, ..., xn )
Пусть функция
– немонотонна.
Тогда существуют два набора аргументов
σ и τ, таких что σ ≤ τ, при этом f(σ) > f(τ).
259
260.
Наборыσ = (σ1, σ2, …, σn), τ = (τ1, τ2, …, τn),
Причем
f(σ) = 1, а f(τ) = 0.
Образуем
цепочку
соседних
наборов,
переводящих σ в τ:
σ = δ1 ≤ δ2 ≤ … δk-1 ≤ δk = τ.
260
261.
Среди этих наборов есть такие два соседнихнабора
δi ≤ δi+1,
которые отличаются лишь в одной (i-ой)
координате
δj i = 0 и δj i+1 = 1.
261
262.
Но при этом f(δi) = 1, а f(δi+1) = 0. Остальныекоординаты этих наборов одинаковы.
Если подставить значения остальных
координат вместо n – 1 переменной функции
y = f (x1, x 2, ..., xn) , то функция оставшейся
одной переменной является отрицанием:
g(x j ) x j.
262
263.
Пример 1:Пусть немонотонная функция f(x, y, z) задана
таблицей.
Пользуясь леммой 1 получить из нее
отрицание, заменив две переменные
константами.
263
264.
Решение:Таблица функции имеет вид:
264
265.
Пусть σ = (0, 0, 0) ≤ τ = (1, 1, 1), приэтом f(0, 0, 0) = 1, а f(1, 1, 1) = 0.
Образуем цепочку соседних наборов,
переводящих σ в τ:
σ = (0, 0, 0) ≤ (0, 0, 1) ≤ (1, 0, 1) ≤ (1, 1, 1) = τ
265
266.
Заметим, что:f(0, 0, 0) = 1,
f(0, 0, 1) = 1,
f(1, 0, 1) = 0,
f(1, 1, 1) = 0.
266
267.
То есть наборы (0, 0, 1) ≤ (1, 0, 1) такие,что при переходе от меньшего к
большему значение функции меняется с
большего на меньшее.
Обратим внимание, что одинаковые
значения в этих наборах имеют
переменные y = 0 и z = 1.
267
268.
Заменим эти переменные в спискеаргументов функции f(x, y, z) на
соответствующие константы.
Получим функцию:
g x f x, 0, 1 x .
268
269.
Убедимся в том, что полученная функциядействительно является отрицанием.
Построим таблицу функции g(x).
Для этого выберем в таблице функции
f(x, y, z) только те строки, где y = 0 и z = 1.
269
270.
270271.
Получим таблицу видаОчевидно, что
g x x.
271
272.
Лемма 2Если функция y f ( x1 , x2 , ... , xn )
–
нелинейна, то подстановкой n – 2 констант
и используя отрицание из нее можно
получить дизъюнкцию и конъюнкцию [1-3].
272
273.
ДоказательствоПусть функция
y f ( x1 , x2 , ... , xn ) –
нелинейна.
Тогда ее полином Жегалкина содержит
конъюнкцию нескольких переменных.
273
274.
ДоказательствоВыберем одну из самых коротких.
Обозначим ее, подставим вместо
переменных
k xi1 xi2 ... xim
единицу, а переменные, не вошедшие в
конъюнкцию, xi3 , xi4 , ..., xim
положим равными 0.
274
275.
Заменимxi1 переменную на x,
а переменную xi2 на y.
Тогда полином Жегалкина такой
функции примет вид:
xy x y
275
276.
В зависимости от вида функцииy f ( x1 , x2 , ... , xn )
параметры α, β и γ могут принимать
различные значения. Покажем, что в каждом
случае суперпозиция полученной функции и
отрицания будет являться конъюнкцией или
дизъюнкцией переменных x и y.
276
277.
277278.
Пример 2Пусть полином Жегалкина функции имеет
вид:
f x, y, z, t xyzt xyz xzt x y z 1
Выберем одну из самых коротких
конъюнкций нескольких переменных.
k xzt.
278
279.
Заменим в конъюнкцииk xzt
переменную t на 1, а переменную у, не
вошедшую в эту конъюнкцию на 0. Тогда
f x, 0, z,1
x 0 z 1 x 0 z xz 1 x 0 z 1
xz x z 1 x z h x, z .
Тогда дизъюнкция получается как суперпозиция
h и отрицания:
x z h x, z .
279
280. Теорема 1 (о слабой функциональной полноте)
Для того чтобы система функций Σ былаполной в слабом смысле необходимо и
достаточно, чтобы она содержала хотя бы
одну нелинейную функцию и хотя бы одну
немонотонную функцию [1-3].
280
281.
Лемма 3Если функция
y f ( x1 , x2 , ... , xn )
–
несамодвойственна,
то подстановкой отрицания из нее можно
получить константы 0 и 1.
281
282. Теорема Поста
Для того чтобы система функций былафункционально полна (в сильном смысле) [1-3],
необходимо и достаточно, чтобы она содержала:
• хотя бы одну немонотонную,
• хотя бы одну нелинейную,
• хотя бы одну несамодвойственную,
• хотя бы одну не сохраняющую 0,
• хотя бы одну не сохраняющую 1.
282
283. Почему классы M, S, L, T0 и T1 называются предполными?
Построим таблицу, где на пересечении строки истолбца укажем функции, которые принадлежат
одному классу и не принадлежат другому.
T0
T1
T0
M
0
T1
1
M
1
0
S
x
x
x
x
L
S
x y
x~ y
x
x
L
x y
xy
xy
x y
x y
xy
m(x,y,z)
x y
283
284. Почему классы M, S, L, T0 и T1 называются предполными?
Очевидно, что ни один класс не входитцеликом в другой класс.
Поэтому в ФПС должны присутствовать
представители всех предполных классов: не
сохраняющих 0, не сохраняющих 1, не
монотонных, не самодвойственных, не
линейных.
284
285. Пример 3:
Построить таблицу Поста и сделать вывод офункциональной полноте системы
Σ , , .
Переобозначим функции.
f1 x , y x y , f 2 x , y x y , f3 x , y x .
285
286. Пример 3:
Построить таблицы заданных функций.f1 x , y x y , f 2 x , y x y , f x , y x .
x
y
f1 x , y
f2 x , y
f3 x , y
0
0
0
0
1
0
1
0
1
1
1
0
0
1
0
1
1
1
1
0
286
287. Пример 3:
Проверим напринадлежность
классам Т0 и Т1.
f1(0, 0) = 0 f1 x , y Т 0
f2(0, 0) = 0 f 2 x , y Т 0
f3(0, 0) = 1 f3 x , y Т 0
f1(1, 1) = 1 f1 x , y Т1
f2(1, 1) = 1 f 2 x , y Т1
f3(1, 1) = 0 f3 x , y Т1
287
288. Пример 3:
Проверим напринадлежность
классу S.
f1(0, 1) = f1(1, 0) f1 x , y S
f2(0, 1) = f2(1, 0) f 2 x , y S
f3(0, 0) ≠ f3(1, 1),
f3 x , y S
f3(0, 1) ≠ f3(1, 0)
288
289. Пример 3:
Проверим напринадлежность
классу М. Построим
булеву формулу
без отрицаний
или найдем наборы, где нарушена монотонность.
f1(x, y) = xy – б.ф. без отрицаний f1 x , y М
f2(x, y) = x˅y – б.ф. без отрицаний f 2 x , y М
0,0 1,1 & f3 0,0 f3 1,1 f3 x , y M
289
290. Пример 3:
Проверим напринадлежность
классу L. Построим
полином Жегалкина.
f1(x, y) = xy – есть конъюнкция 2-х
переменных f1 x , y L
f 2 x , y x y xy x y – есть конъюнкция
2-х переменных
f 2 x , y L
f3 x , y x x 1 – нет конъюнкции 2-х
переменных f3 x , y L
290
291. Пример 3:
Построим таблицу Поста.f1 x , y
f2 x , y
f3 x , y
T0
T1
S
M
L
Система удовлетворяет теореме Поста. Она
является функционально полной.
291
292. Пример 4:
Построить таблицу Поста и сделать вывод офункциональной полноте системы
Σ , .
Переобозначим функции.
f1 x , y x y , f 2 x , y x y .
292
293. Пример 4:
Построить таблицы заданных функций.f1 x , y x y , f 2 x , y x y .
x
y f1 x , y
0
0
0
1
0
1
1
1
1
0
1
0
1
1
0
1
f2 x , y
293
294. Пример 4:
Проверим напринадлежность
классам Т0 и Т1.
f1(0, 0) = 0 f1 x , y Т 0
f2(0, 0) = 1 f 2 x , y Т 0
f1(1, 1) = 0 f1 x , y Т1
f2(1, 1) = 1 f 2 x , y Т1
0
294
295. Пример 4
Проверим напринадлежность
классу S.
f1(0, 1) = f1(1, 0) f1 x , y S
f2(0, 1) = f2(1, 0) f 2 x , y S
295
296. Пример 4:
Проверим напринадлежность
классу М. Построим
булеву формулу
без отрицаний
или найдем наборы,
где нарушена монотонность.
1,0 1,1 & f1 1,0 f1 1,1 f1 x , y M
0,0 1,0 & f 2 0,0 f 2 1,0 f 2 x , y M
296
297. Пример 4:
Проверим напринадлежность классу L.
Построим
полином Жегалкина.
f1 x , y x y – нет конъюнкции 2-х
переменных
f1 x , y L
f 2 x , y x y x y x y xy x 1
– есть конъюнкция 2-х переменных
f 2 x , y L
297
298. Пример 4:
Построим таблицу Поста.f1 x , y
f2 x , y
T0
T1
S
M
L
Система удовлетворяет теореме Поста. Она
является функционально полной.
298
299. Пример 5:
Система Σ = {f} состоит из однойлогической функции, заданной своим вектор-
столбцом. Построить таблицу Поста и
сделать вывод о функциональной полноте
данной системы.
T
f 10100111
299
300. Пример 5:
Построим таблицуданной функции.
f 10100111
T
x
y
z
f x , y , z
0
0
0
1
0
0
1
0
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1 300
301. Пример 5:
Проверим напринадлежность
классам Т0 и Т1.
f(0, 0, 0) = 1 f x , y , z Т 0
f(1, 1, 1) = 1 f x , y , z Т1
0
301
302. Пример 5:
Проверим напринадлежность
классу S.
f(0, 0, 0) = f(1, 1, 1) f x , y S
302
303. Пример 5:
Проверим напринадлежность классу М.
Найдем сДНФ и проверим ее
на наличие отрицаний
или найдем наборы,
где нарушена монотонность.
0,0,0 0,1,1 & f1 0,0,0 f1 0,1,1
f x , y , z M
f x , y , z x y z xyz xyz xyz xyz
1
2
3
4
5
f x , y , z x z yz xz xy сДНФ с отриц.
45
12
24
35
f x , y , z M303
304. Пример 5:
Проверим напринадлежность классу L.
Построим полином Жегалкина.
f x , y , z x y z x yz xyz xyz xyz
x 1 y 1 z 1
x 1 y z 1 x y 1 z
xy z 1 xyz
xyz xy xz yz x y z 1
– есть конъюнкция
xyz xy yz y
2-х переменных
xyz xz xyz xy xyz
f 2 x , y L 304
xyz xy x z 1
305. Пример 5:
Построим таблицу Поста.f x , y , z
T0
T1
S
M
L
1. Система не является ФП.
2. Система является сФП (есть немонотонная
и нелинейная функции).
3. ФП будет система Σ ᴗ {0}.
305
306. Лекция 11
Логикавысказываний
307. Высказывание
Высказывание – это утверждение илиповествовательное предложение, которое
может быть либо истинным, либо
ложным [1, 3-4].
Значением истинного высказывания
является «И» – истина, ложного «Л» –
«ложь».
307
308. Высказывание
Повелительные («Войдите,пожалуйста»), вопросительные
(«Который час?») и бессмысленные
предложения («Сумма пяти и
восемнадцати»), в которых ничего не
утверждается, не являются
высказываниями.
308
309. Высказывание
Не будет высказыванием утверждение,истинность или ложность которого
нельзя определить однозначно.
Например: «Музыка Вагнера очень
мелодична», «Картины Пикассо
слишком абстрактны».
309
310. Логика высказываний
Предметом логики высказываний являетсяанализ различных логических связей и
методы построения на их основе правильных
логических рассуждений [1, 3-4].
Способы построения новых высказываний
из заданных с помощью логических связок и
определение истинности высказываний,
изучаются в логике высказываний.
310
311. Логика высказываний
Основные логические связки это связки:и, или, не, если … то…, которые в логике
высказываний имеют специальные названия
и обозначения. Иногда к ним добавляют еще
две связки либо …, либо …(или …, или …);
если, и только если (тогда и только тогда).
Для одной и той же связки в разных источниках используются разные
названия и обозначения, которые приведены в таблице 1.
311
312.
СвязкаНазвание
Обозначение
Высказывание,
полученное
с помощью связки
Математическая
запись
А В
А В
А В, АВ
А В
и
конъюнкция
(или логическое
умножение)
АиВ
или
не
дизъюнкция
А или В
отрицание,
инверсия
импликация
не А
если А, то В
(А влечет В)
исключающее
«или»,
неравнозначность
эквивалентность,
равнозначность
либо А, либо В
если …,
то …
либо …,
либо …
если и
только
если
А,
A
A B,
A B
А В
А В
~, А, если и только А В
если В
А ~ В,
А 312
В
313. Логика высказываний
В последней колонке табл. 1 записаныформулы, или выражения логики
высказываний. С помощью букв А, В, С,
... обозначающих высказывания, связок
и скобок можно построить
разнообразные формулы.
313
314. Логика высказываний
A – светит солнце, В – идет дождь,АВ – светит солнце и идет дождь.
С – контакт замкнут, D – лампа горит,
С D – если контакт замкнут, то лампа горит.
Истинными или ложными будут составные
высказывания, зависит от истинности простых
высказываний, входящих в формулу.
314
315. Логика высказываний
A – Марс – спутник Земли, В – Лондон –столица Англии,
АВ – Марс – спутник Земли и Лондон –
столица Англии, ложное высказывание;
А В – Марс – спутник Земли или Лондон –
столица Англии, истинное;
А В – если Марс – спутник Земли , то
Лондон – столица Англии, истинное.
315
316. Алгебра высказываний
Исследование свойств таких формул испособов установления их истинности и
является основным предметом логики
высказываний.
Существуют два подхода к построению
логики высказываний, которые образуют два
варианта этой логики: алгебру логики и
исчисление высказываний.
316
317. Алгебра высказываний
Алгебра высказываний рассматриваетлогические формулы как алгебраические
выражения, связывающие высказывания,
которые можно преобразовать по
определенным правилам. Знаки операций
обозначают логические операции (логические
связки).
317
318. Алгебра высказываний
В формулах алгебры логики переменные – этовысказывания. Они принимают только два
значения – ложь и истина, которые
обозначаются либо 0 и 1, либо Л и И, либо
false и true.
Каждая формула задает логическую функцию,
которая сама может принимать только два
логических значения.
318
319. Алгебра высказываний
Таблица логических функцийодной переменной
Константа 0: Тождество: Отрицание: Константа 1:
x f (x) = 0 f ( x) = x f ( x) = x f (x) = 1
0
0
0
1
1
1
0
1
0
1
319
320. Таблица функций двух переменных и основные логические связки
x1 x2Импликация
Эквивалентность
(равнозначность)
Стрелка Пирса
(НЕ – ИЛИ)
x1 x 2
Конъюнкция
x 1 ∨ x 2 x 1 ∧ x 2 x 1 → x2 x 1 ~ x 2 x 1 x2 x 1 x2
Дизъюнкция
Неравнозначность
(сложение по модулю
2)
Штрих Шеффера
(НЕ – И)
Таблица функций двух переменных
и основные логические связки
0
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
0
1
0
1
0
0
0
1
1
0
320
1
1
1
1
1
1
0
0
0
321. Алгебра высказываний
Интерпретацией [1, 3-4] формулылогики высказываний называется набор
значений высказываний,
входящих в нее.
321
322. Алгебра высказываний
Формула F называется тождественноистинной [1, 3-4] или тавтологией,
если она принимает значение «истина»
независимо от значений входящих в нее
высказывательных переменных, (на всех
интерпертациях).
322
323. Алгебра высказываний
Формула F называется тождественноложной [1, 3-4] или противоречивой,
если она принимает значение «ложь»
независимо от значений входящих в нее
высказывательных переменных, (на всех
интерпертациях).
323
324. Алгебра высказываний
Формула F называется выполнимой, еслипри некоторых интерпретациях она
принимает значение «истина».
Интерпретация, при которой формула
принимает значение «истина», называется
моделью формулы F.
324
325. Исчисление высказываний
Пусть интерпретация определена на всехвысказывательных переменных,
встречающихся в формулах множества .
Говорят, что выполняет или
модель , если каждая формула из
множества принимает значение
«истина», при интерпретации [1, 3-4].
325
326. Исчисление высказываний
Говорят, что выполнимо, если имеетмодель.
Если не выполнимо, то пишут:
=.
326
327. Исчисление высказываний
Пусть – множество формул логикивысказываний, F – произвольная формула.
Говорят, что множество логически
влечет формулу F, если любая модель
являются моделью для F [1, 3-4].
Обозначается:
= F.
327
328. Исчисление высказываний
Утверждение того, что некотороевысказывание (заключение) следует из
других высказываний (посылок),
называется аргументом [1, 3-4].
328
329. Аргумент
H1H2
...
гипотезы
Hn
∴ G заключение
329
330. Исчисление высказываний
Аргумент называется правильным, еслииз множества гипотез логически следует
заключение аргумента.
330
331. Пример 1.1
Проверить истинность, выполнимостьили ложность формулы.
F = ( A B ) A.
Построим
таблицу
истинности
и
убедимся в наличии моделей формулы F.
331
332. Пример 1.1
Напомним, интерпретация модель F,если значение функции на
интерпретации равен Истине.
332
333. Пример 1.1 F = (A B) A
Пример 1.1F = (A B) A
Моделью F является интерпретация (набор
значений аргументов) = (0, 1).
333
334. Пример 1.1
Так как у F есть модель, значит она неявляется тождественно ложной
(противоречивой).
Так как не все интерпретации F являются ее
моделями, значит она не является
тождественно истинной (тавтологией).
F является выполнимой.
334
335. Пример 1.2
Проверить истинность, выполнимостьили ложность формулы.
F = (A B) (A│B).
Построим
таблицу
истинности
и
убедимся в наличии моделей формулы F.
335
336. Пример 1.2 F = (A B) (A│B)
Пример 1.2 F = (A B) (A│B)А В А В
А│В
F
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
1
0
1
Все интерпретации F является ее моделями.
336
337. Пример 1.2
Так как все интерпретации F являютсяее моделями, значит она является
тождественно истинной (тавтологией).
337
338. Пример 2.1
Проверить, выполнимо ли множество Г.Г = {A B, A B}.
Надо проверить, найдется ли такая
интерпретация , которая является моделью
разу для всех формул множества Г.
Построим таблицу для всех функций из Г.
338
339. Пример 2.1 Г = {AB, AB}
Пример 2.1А В
Г = {A B, A B}
А В
А В
0
0
1
1
0
1
1
0
1
0
0
0
1
1
1
0
= (0,0) является моделью всех формул Г.
Значит Г – выполнимо
339
340. Пример 2.2
Проверить, выполнимо ли множество Г.Г = {A B, A B, А В}.
Надо проверить, найдется ли такая
интерпретация , которая является моделью
сразу для всех формул множества Г.
Построим таблицу для всех функций из Г.
340
341. Пример 2.2 Г = {A B, A B, А В}
Пример 2.2 Г = {A B, A B, А В}А В A B
A B
А В
0
0
1
1
0
0
1
1
0
1
1
0
1
0
1
1
1
0
1
1
Г не имеет моделей. Значит Г не выполнимо: Г
341
342. Пример 3.1
Проверить, будет ли из множества формул Глогически следовать функция F.
Г = { A B, А В}, F = A B
Надо проверить, будет ли всякая модель
множества Г моделью формулы F.
Построим таблицу для функций Г и F .
342
343. Пример 3.1 Г={AB, АВ}, F=AB
Пример 3.1 Г={ A B, А В}, F=A BА В A B
А В
A B
0 0
0
1
0
0 1
1
1
1
1 0
1
0
1
1 1
0
1
1
Модель Г ( = 01) является моделью F.
Значит из Г логически следует F. Г F.
343
344. Пример 4.1
Проверить правильность аргумента.Если Джон коммунист, то Джон атеист.
Джон атеист. Значит Джон коммунист.
А – Джон коммунист;
В – Джон атеист.
Составим аргумент.
344
345. Пример 4.1
А ВВ_
А
Здесь Г={А В, В} – множество
посылок,
F = A – заключение.
345
346. Пример 4.1
Чтобы проверить правильность аргумента,необходимо убедиться в том, что из множества
посылок логически следует заключение: Г F.
В нашем случае:
{А В, В} А
346
347. Пример 4.1
А В A B0 0
1
0 1
1
1 0
0
1 1
1
В
0
1
0
1
A
0
0
1
1
= 11 является моделью Г и F. = 01 является
моделью Г и не является моделью F.
347
348. Пример 4.1
Таким образом, из множества посылокГ не следует логически заключение F.
Это означает, что аргумент неверный.
348
349. Лекция 12
Логикапредикатов
350. Предикаты
Предикат – это функция вида [1, 3-4]Р(х1, х2, …, хn) = y,
Здесь х1, х2, …, хn – предметные
переменные; y – значение предиката.
350
351. Предикаты
x1 M 1 , x2 M 2 , ..., xn M nгде M 1 , M 2 , ..., M n
предметные множества [1, 3-4],
M 1 M 2 ... M n
поле предиката [1, 3-4].
351
352. Предикаты
Переменная y – может приниматьзначения из множества
В ={0, 1}.
Здесь 0 – «нет», «ложь»;
1 – «да», «истина».
352
353. Предикаты
Например:1) на множестве N задан предикат Р(х) –
«х является четным числом».
Тогда Р(1) = 0, Р(2) = 1;
2) на множестве N×N задан предикат
Q(x,y) – «x ≤ y».
Тогда Q(1,1) = 1; Q(1,2) = 1; Q(3,2) = 0.
353
354. Предикаты
Подмножество I множества Мназывается областью истинности [1, 3-4]
предиката Р, если наборы значений
предметных переменных из множества I
обращают предикат P в 1.
354
355. Предикаты
Например:для предиката Q(x,y) область истинности
I – множество всех точек плоскости с
натуральными координатами, лежащие
на диагонали первого координатного
угла и выше.
355
356. Предикаты
Рис. 1. Область истинности356
357. Предикаты
Над предикатами можно совершатьзнакомые нам логические операции:
конъюнкцию, дизъюнкцию, отрицание,
импликацию, и т. д.
Например: Р(х,у) – «х<y», R(x,y) – «x=y».
Тогда ⌐ Р(х,у) – «х≥у»,
Р(х,у)˅ R(x,y) – «х≤у» и т. д.
357
358. Предикаты
При этом область истинностиполученных предикатов изменяется по
тем же правилам:
I P I P ;
I P R I P I R ;
и так далее.
358
359. Предикаты
Однако в логике предикатов естьоперация, которая отсутствуют в логике
высказываний.
Квантификация или квантирование.
359
360. Предикаты
В результате этой операции напеременную предиката навешивается
квантор (переменная связывается
квантором). Переменная при этом
становится связанной. Переменная, не
связанная называется свободной [1, 3-4].
360
361. Предикаты
361362. Предикаты
Предикатная формула:xP x
истинна тогда и только тогда, когда
предикат Р(х) = 1 при любом х,
ложна тогда и только тогда, когда
найдется х, при котором предикат Р(х)=0.
362
363. Предикаты
Предикатная формула:xP x
истинна тогда и только тогда, когда
найдется х, при котором предикат
Р(х) = 1, ложна тогда и только тогда,
когда предикат Р(х) = 0 при любом х.
363
364. Замечание
Когда в предикате Р(х) переменная хсвязывается квантором, она перестает
влиять на значение предиката и
предикат становится высказыванием,
принимающим фиксированное значение
Истина или Ложь.
364
365. Предикаты
Например: Р(х) – «х является четнымчислом» на множестве N .
0.
Тогда xP x
так как есть х = 3, при котором Р(3)=0.
Тогда
xP x 1.
так как есть х = 2, при котором Р(2)=1.
365
366. Предикаты
Если предикат имеет более 1переменной, то ее квантификация
приводит к уменьшению числа
переменных на 1.
Пример 1. Предикат Q(x,y) – «x ≤ y» на
множестве N×N. Квантифицируем его.
366
367. Пример 1
xQ x, y R( y )новый предикат от одной переменной у
– «любое натуральное число х меньше
либо равно у».
При у = 1 это не так (любой х ≤ 1) ,
xQ x,1 R(1) 0,
При у = 2 это не так (любой х ≤ 2),
xQ x,2 R(2) 0, ...
367
368. Пример 1
Таким образом, предикатR( y) xQ x, y 0,
то есть является функцией-константой.
368
369. Пример 1
xQ x, y W ( y )новый предикат от одной переменной у
– «найдется натуральное число х
меньше либо равно у».
При у = 1 это так (найдется х ≤ 1) ,
xQ x,1 W (1) 1,
При у = 2 это так (найдется х ≤ 2),
xQ x,2 W (2) 1, ...
369
370. Пример 1
Таким образом, предикатW( y) xQ x, y 1
то есть тоже является функцией –
константой.
370
371. Пример 1
yQ x, y V ( x)новый предикат от одной переменной x –
«натуральное число х меньше либо равен
любого натурального числа у».
При х = 1 это так (верно, что любой y ≥ 1) ,
yQ 1, y V (1) 1,
При x = 2 это не так (неверно, что любой y ≥ 2)
yQ 2, y V (2) 0,...
371
372. Пример 1
Таким образом, предикат1, x 1,
V ( x) yQ x, y
0, x 1.
то есть не является функцией – константой.
372
373. Пример 1
yQ x, y U ( x)Новый предикат от одной переменной х
«натуральное число х меньше либо равно
некоторому числу у».
При х = 1 это так (найдется число, которому
меньше или равна 1)
yQ 1, y U (1) 1,
При х = 2 это так (найдется число, которому меньше
или равна 2)
yQ 2, y U (2) 1, ...
373
374. Пример 1
Таким образом, предикатU ( x) yQ x, y 1,
то есть является функцией-константой.
374
375. Пример 1
Кванторы можно навесить на всепеременные предиката. Тогда предикат
станет высказыванием.
375
376. Пример 1
x yQ x, y 0так как неверно то, что любой
натуральный х меньше либо равен
любому натурального у.
Например, при х = 5, у = 2.
376
377. Пример 1
x yQ x, y 1так как верно то, что любой натуральный
х меньше либо равен некоторого
натурального у.
Например, при х = 1, у = 1;
при х = 2, у = 2, …
377
378. Пример 1
y xQ x, y 0так как неверно то, что найдется такой
натуральный у, который будет больше
либо равен любого натурального х.
Это связано с тем, что натуральное
множество не ограничено сверху.
378
379. Пример 1
x yQ x, y 1так как верно то, что найдется такой
натуральный х, который будет меньше
либо равен любого натурального у.
Этот х = 1. Если бы неравенство было
строгое, высказывание было бы ложным.
379
380. Пример 1
y xQ x, y 1так как верно то, что любой натуральный
у, больше либо равен некоторому
натуральному х.
Например, у = 1, х = 1; у = 2, х = 2,…
380
381. Пример 1
x yQ x, y 1так как верно то, что найдутся такие
натуральные х и у, что х меньше либо
равен этому у.
Например, х = 3, у = 7.
381
382. Пример 2
Дан предикатQ(x,y) – «x является делителем y»,
заданный на множестве N×N.
Навесим кванторы сначала на одну
переменную предиката, затем на обе
переменные.
382
383. Пример 2
xQ x, y R( y )новый предикат от одной переменной у
– «любое натуральное число х является
делителем натурального числа у».
При у = 1 это не так (любой х не делитель 1),
xQ x,1 R(1) 0,
При у = 2 это не так (любой х не делитель 2),
xQ x,2 R(2) 0, ...
383
384. Пример 2
Таким образом, предикатR( y) xQ x, y 0,
то есть является функцией-константой.
384
385. Пример 2
xQ x, y W ( y )новый предикат от одной переменной у
– «найдется натуральное число х,
которое является делителем у».
При у = 1 это так (найдется делитель х = 1),
xQ x,1 W (1) 1,
При у = 2 это так (найдется делитель х = 2),
xQ x,2 W (2) 1, ...
385
386. Пример 2
Таким образом, предикатW ( y) xQ x, y 1 , ,
то есть тоже является функцией –
константой.
386
387. Пример 2
yQ x, y V ( x)новый предикат от одной переменной x –
«натуральное число х делитель любого
натурального числа у».
При х = 1 это так (1 – делитель любого у) ,
yQ 1, y V (1) 1,
При x = 2 это не так (2 – не делитель любого у),
yQ 2, y V (2) 0,...
387
388. Пример 2
Таким образом, предикат1, x 1,
V ( x) yQ x, y
0, x 1.
то есть не является функцией-константой.
388
389. Пример 2
yQ x, y U ( x)новый предикат от одной переменной x
– «натуральное число х делитель
некоторого натурального числа у».
При х = 1 это так (1 – делитель некоторого у) ,
yQ 1, y V (1) 1,
При x = 2 это так (2 – делитель некоторог у),
yQ 2, y V (2) 1,...
389
390. Пример 2
Таким образом, предикатU ( x) yQ x, y 1 ,
то есть является функцией – константой.
390
391. Пример 2
Кванторы можно навесить на всепеременные предиката. Тогда предикат
станет высказыванием.
391
392. Пример 2
x yQ x, y 0так как неверно то, что любой
натуральный х является делителем
любого натурального у.
Например, при х = 5, у = 2.
392
393. Пример 2
x yQ x, y 1так как верно то, что любой натуральный
х является делителем некоторого
натурального у.
Например, при х = 1, у = 1;
при х = 2, у = 2, …
393
394. Пример 2
y xQ x, y 0так как неверно то, что найдется такой
натуральный у, который будет
делиться на любой натуральный х.
Это связано с тем, что натуральное
множество не ограничено сверху.
394
395. Пример 2
x yQ x, y 1так как верно то, что найдется такой
натуральный х, который будет
делителем любого натурального у.
Этот х = 1. Если бы неравенство было
строгое, высказывание было бы ложным.
395
396. Пример 2
y xQ x, y 1,так как верно то, что любой натуральный
у, делится на некоторый натуральный х.
Например, у = 1, х = 1; у = 2, х = 2,…
396
397. Пример 2
x yQ x, y 1,так как верно то, что найдутся такие
натуральные х и у, что х является
делителем этого у.
Например, х = 2, у = 4.
397
398. Пример 3
Дан предикатQ(x,y) – «x является родителем y»,
заданный на множестве L×L, где L –
множество людей. Навесим кванторы
сначала на одну переменную предиката,
затем на обе переменные.
398
399. Пример 3
xQ x, y R( y )новый предикат от одной переменной у
– «любой человек х является родителем
человека у».
Это неверно, так как у человека у только
двое родителей – мать и отец.
399
400. Пример 3
Таким образом, предикатR( y) xQ x, y 0,
то есть является функцией-константой.
400
401. Пример 3
xQ x, y W ( y )новый предикат от одной переменной у
– «найдется такой человек х, который
является родителем у».
Это верно, так как если человек рожден,
у него есть (были) родители.
401
402. Пример 3
Таким образом, предикатW ( y) xQ x, y 1 ,
то есть тоже является функцией –
константой.
402
403. Пример 3
yQ x, y V ( x)новый предикат от одной переменной x –
«человек х родитель любого человека у».
Это не так, так как у любого человека
ограниченное количество детей.
403
404. Пример 3
Таким образом, предикатV ( x) yQ x, y 0 ,
то есть является функцией-константой.
404
405. Пример 3
yQ x, y U ( x)новый предикат от одной переменной x
– «человек х является родителем
некоторого человека у».
Это верно, если у человека х есть дети,
и неверно, если у человека х нет детей.
405
406. Пример 3
Таким образом, предикат1,если у х есть дети
U ( x) yQ x, y
0,если у х нет детей
то есть не является функцией –
константой.
406
407. Пример 3
Кванторы можно навесить на всепеременные предиката. Тогда предикат
станет высказыванием.
407
408. Пример 3
x yQ x, y 0 ,так как неверно то, что любой человек х
является родителем любого человека у.
408
409. Пример 3
x yQ x, y 0 ,так как верно то, что любой человек х
является родителем некоторого
человека у.
Не у каждого человека есть дети.
409
410. Пример 3
y xQ x, y 0 ,так как неверно то, что найдется такой
человек у, который будет родителем
любой человек х.
Это связано с тем, что натуральное
множество не ограничено сверху.
410
411. Пример 3
x yQ x, y 0 ,так как неверно то, что найдется такой
человек х, который будет родителем
любого человека у.
411
412. Пример 3
y xQ x, y 1 ,так как верно то, что у любого человека у,
имеется (имелся когда-то) родитель х.
412
413. Пример 3
x yQ x, y 1,так как верно то, что найдутся такие два
человека х и у такие, что человек х
является родителем человека у.
413
414. Логика предикатов
Равносильные предикатные формулы– те, у которых область истинности
совпадает.
414
415. Логика предикатов
Интерпретация [1, 3-4] – этосопоставление каждому предикатному
символу в формуле определенного
предиката.
415
416. Логика предикатов
Пусть формулы F и G содержат одно итоже множество свободных переменных.
Формулы F и G равносильны в данной
интерпретации – если они выражают
один и тот же предикат [1, 3-4].
416
417. Логика предикатов
Например:P x, y : x y; Q x, y : x y.
Тогда предикатные формулы:
F P x, y и G Q x, y
являются равносильными в данной
интерпретации, так как
P x, y Q x, y .
При других интерпретациях предикатов P и Q
формулы могут не быть равносильными.
417
418. Логика предикатов
Формулы F и G равносильны намножестве М – если они равносильны
во всех интерпретациях на этом
множестве [1, 3-4].
418
419. Логика предикатов
Например: F xP x , G xP xРавносильны в любой интерпретации на
множестве М, если М состоит из одного
элемента. Если
a M : P a 0, xP x 0 и xP x 0.
Если
a M : P a 1, xP x 1 и xP x 1.
На другом множестве формулы F и G могут не быть
419
равносильными.
420. Логика предикатов
Формулы F и G равносильны в логикепредикатов – если они равносильны на
всех множествах [1, 3-4].
420
421. Логика предикатов
Например:F P x P x ,
G P x P x .
Тогда F и G равносильны на любых
множествах и при любых интерпретациях
предиката P(x).
F G
421
422. Равносильные формулы
Для предикатных формул сохраняютсявсе равносильности (эквивалентности)
алгебры логики. Например, закон де
Моргана:
P x Q x P x Q x
P x Q x P x Q x
422
423. Свойства операций над предикатами
Перенос квантора через отрицаниеxP x x P x
1
xP x x P x
2
Здесь и далее, знак равносильности ≡ заменен
знаком равенства.
423
424. Свойства операций над предикатами
Вынос квантора за скобкиxP x Q x P x Q 3
xP x Q x P x Q 4
424
425. Свойства операций над предикатами
Вынос квантора за скобкиxP x Q x P x Q 5
xP x Q x P x Q 6
425
426. Свойства операций над предикатами
Закон коммутативности дляодноименных кванторов:
x yP x, y y xP x, y 7
x yP x, y y xP x, y 8
426
427. Свойства операций над предикатами
Коммутативность дает возможностьиспользовать более краткую запись:
x y zP x, y,z x, y, zP x, y,z 9
x y zP x, y, z x, y, zP x, y, z 10
427
428. Равносильные формулы
Проверить равносильность формулы в логикепредикатов не так просто, как в логике
высказываний. Высказывание может
принимать значения 0 и 1. Формула с 2
высказываниями содержит 2² возможных
значений, и так далее.
Предикат имеет бесконечное множество
интерпретаций.
428
429. Истинность в логике предикатов
Предикатная формула F называетсявыполнимой (непротиворечивой), если
существует интерпретация входящих в
нее предикатов, в которой F принимает
значение истина. То есть ее область
истинности не пуста [1, 3-4].
429
430. Истинность в логике предикатов
Предикатная формула F называетсятождественно истинной
(общезначимой) [1, 3-4], если при любой
интерпретации входящих в нее
предикатов, область истинности
совпадает с областью определения.
430
431. Истинность в логике предикатов
Предикатная формула F называетсятождественно ложной
(противоречивой) [1, 3-4], если при
любой интерпретация входящих в нее
предикатов, область истинности пуста.
431
432. Истинность в логике предикатов
Например:F P x P x 1
Тождественно истинная формула.
G P x P x 0
Тождественно ложная формула.
432
433. Истинность в логике предикатов
Замечание 1Формула F – общезначима тогда и только
тогда, когда ¬F – противоречива.
Замечание 2
Формула F – выполнима тогда и только тогда,
когда ¬F – не является общезначимой.
433
434. Истинность в логике предикатов
Замечание 3Если F и G – равносильные формулы в
логике предикатов, то формула
W=F~G
общезначима и выполняется равенство:
I F IG .
434
435. Истинность в логике предикатов
Замечание 4Если формула
W=F→G
общезначима, то выполняется:
I F IG .
435
436. Истинность в логике предикатов
Замечание 5Если y не входит в формулу P(x), то
следующие формулы являются
общезначимыми:
xP x P y ;
P y xP x .
436
437. Истинность в логике предикатов
Квантор общности являетсяобобщением конъюнкции, поэтому
справедлива формула:
x P x Q x
11
xP x xQ x .
437
438. Истинность в логике предикатов
Квантор существования являетсяобобщением дизъюнкции, поэтому
справедлива формула:
x P x Q x
12
xP x xQ x .
438
439. Истинность в логике предикатов
Замечание 6Если в формулах (11) и (12) поменять
местами кванторы, то получаются
выражения, истинные лишь в одну
сторону:
x P x Q x
13
xP x xQ x .
439
440. Истинность в логике предикатов
xP x xQ x14
x P x Q x .
В таких случаях говорят, что левая
часть утверждения более сильная, чем
правая.
440
441. Истинность в логике предикатов
В таком случае, надо воспользоватьсяправилом:
xP x yP y zP z tP t ...
xP x yP y zP z tP t ...
То есть, если переменная связана квантором,
то неважно, как она называется.
441
442. Истинность в логике предикатов
В выражениях (13) и (14) надо сделать заменупеременной, после чего воспользоваться
формулами (4) и (5):
xP x xQ x
xP x yQ y
x y P x Q y .
15
442
443. Истинность в логике предикатов
xP x xQ xxP x yQ y
x y P x Q y .
16
443
444. Истинность в логике предикатов
Префиксной нормальной формой (ПНФ)называется формула, имеющая вид [1, 3-4] :
Q1 x1Q2 x2 ...Qn xn F ,
где Q1 , Q2 ,...Qn кванторы,
F – предикатная формула, имеющая вид
ДНФ.
444
445. Пример 4
Получить префиксную нормальную формупредикатной формулы:
x yP1 x , y x yP2 x , y
x yP1 x , y x yP2 x , y
x yP1 x , y x yP2 x, y
x u yP1 x , y yP2 u , y
x u y P1 x , y P2 u , y .
x y x y
xP x xP x
xP x xP x
xP x xQ x
x y P x Q y
xP x xQ x
x P x Q x
445
446. Пример 5
Получить префиксную нормальную формупредикатной формулы:
x yP1 x , y xP2 x y zP3 y , z
x yP1 x , y P2 x y zP3 y , z
x yP1 x , y P2 x y zP3 y , z
x yP1 x , y P2 x y zP3 y , z
x yP1 x, y P2 x y zP3 y , z
x y P1 x , y P2 x y zP3 y , z
446
447. Пример 5
x y P1 x, y P2 x y zP3 y , zx y P1 x , y P2 x zP3 y , z
x y z P1 x, y P2 x P3 y , z .
447
448. Лекция 13
Переключательные икомбинационные схемы
449. Схемы переключателей
Релейно-контактные схемы (илипереключательные схемы) широко
используются в технике автоматического
управления [1, 4].
449
450. Схемы переключателей
Под переключательной схемой понимаютсхематическое изображение некоторого
устройства, состоящее из следующих
элементов: 1) переключателей (ключей);
2) соединяющих их проводников;
3) входов в схему и выходов из нее
(полюсов).
450
451. Схемы переключателей
Простейшая схема содержит одинпереключатель Р и имеет один вход и
один выход. Переключателю Р ставится в
соответствие истинное высказывание Р,
гласящее «переключатель Р замкнут», что
соответствует ситуации: «ток идет».
451
452. Схемы переключателей
Простейшая схема содержит одинпереключатель Р и имеет один вход и один
выход. Переключателю Р ставится в
соответствие истинное высказывание Р,
гласящее «переключатель Р замкнут».
Замкнутый переключатель Р приведен на
рис.1.
452
453. Схемы переключателей
Рис.1. Замкнутый переключатель Р453
454. Схемы переключателей
Переключателю Р ставится всоответствие истинное высказывание:
«переключатель Р разомкнут» или
«переключатель Р замкнут».
Разомкнутый переключатель Р
приведен на рис. 2.
454
455. Схемы переключателей
Рис.2. Разомкнутый переключатель РТаким образом, когда Р замкнут,
Р – разомкнут и наоборот.
455
456. Схемы переключателей
Если высказывание Р истинно, топереключатель Р замкнут – схема
пропускает ток,
если высказывание Р ложно, то
переключатель Р разомкнут – схема
не пропускает ток.
456
457. Схемы переключателей
Следовательно, любому высказываниюможет быть поставлена в соответствие
переключательная схема с двумя
полюсами (двухполюсная схема).
457
458. Схемы переключателей
Конъюнкции высказываний А и Всоответствует последовательное
соединение переключателей А и В (рис.3):
Рис. 3. Последовательное соединение
переключателей А и В
458
459. Схемы переключателей
Дизъюнкции высказываний А и Всоответствует параллельное соединение
переключателей А и В (рис.4):
Рис.4. Параллельное соединение
переключателей А и В
459
460. Схемы переключателей
На рисунке 5 приведена схема, содержащаяпереключатели А и А, В и В, С и С.
Рис. 5. Схема переключателей параллельнопоследовательными соединениями
460
461. Схемы переключателей
Для простоты изображения, далее на схемахпереключателей ключи (переключатели) будем
обозначать прямоугольниками, подписывая,
какого вида этот ключ: Р или Р (рис. 6).
Рис. 6. Схема переключателей с простым
обозначением ключей
461
462. Схемы переключателей
Тогда схема на рис. 5 приобретет новый, болеепростой вид (см. рис. 7):
Рис. 7. Упрощенное изображение схемы
переключателей рисунка 5
462
463. Схемы переключателей
Так как любая формула логикивысказываний может быть записана в виде
ДНФ или КНФ, то ясно, что любой
формуле можно сопоставить схему
переключателей. Причем, упрощение
формулы ведет к упрощению схемы.
463
464. Схемы переключателей
Упростим схему переключателей,приведенную на рисунке 7.
Построим булеву формулу,
соответствующую данной схеме.
464
465. Пример 1
Данной части схемысоответствует подформула:
А В АВ
465
466. Пример 1
Данной части схемысоответствует подформула:
А В АВ
466
467. Пример 1
Данной части схемысоответствует подформула:
С А В С АВ
467
468. Пример 1
Данной части схемысоответствует подформула:
С С А В С С АВ
468
469. Пример 1
Всей схеме соответствует формула:А В С С А В
АВ С С АВ
469
470. Пример 1
Упростим полученную булеву формулу.АВ С С АВ АВ СС САВ
АВ САВ
Построим соответствующую схему
переключателей.
470
471. Пример 1
АВ САВ471
472. Комбинационные схемы
Комбинационные элементы – электронныекомпоненты [1, 4], техническая реализация
которых может быть основана на
использовании различных физических
явлений: магнитных, явлений в
полупроводниках и т. д. Они являются
основными компонентами компьютеров.
472
473. Комбинационные схемы
Все комбинационные элементы имеют одинили более входов и один выход [1, 4].
Каждый вход может принимать одно из двух
значений (обычно низкое или высокое
напряжение).
Наиболее важные типы комбинационных
элементов приведены в таблице 1.
473
474. Комбинационные схемы
Таблица 1Основные типы комбинационных
элементов
Элемент Конъюнкция Дизъюнкция Отрицание
х у
х у
х
Обозначения
474
475. Комбинационные схемы
Так как комбинационный элемент НЕ имеет,в отличие от других, только 1 вход, иногда
его обозначают иначе, чем остальные
элементы (см. рис.9):
Рис. 9. Обозначение элемента НЕ
475
476. Комбинационные схемы
Различные комбинационные элементы могутбыть связаны друг с другом в цепи так, что
выход одних является входом других.
Такие цепи называются комбинационными
схемами (логическими сетями).
476
477. Комбинационные схемы
Так как штрих Шеффера и стрелка Пирсаявляются функционально полными
системами, возможно описание выходов
комбинационных схем с помощью каждого
из этих элементов.
477
478. Комбинационные схемы
Штрих Шеффера (ШШ) – отрицаниеконъюнкции. Тогда его логическая
схема имеет вид (см. рис.10):
Рис. 10. Логическая схема ШШ
478
479. Пример 2
Записать формулу, соответствующуюлогической схеме, приведенной на рисунке 11.
Рис.11. Логическая схема
479
480. Пример 2
Данной части схемысоответствует подформула:
xy
480
481. Пример 2
Данной части схемысоответствует подформула:
x z
481
482. Пример 2
Всей схеме соответствует формулаf x, y, z xy x z
482
483. Пример 2
Иногда подформулы пишут на схеме.Получается скелет формулы.
xy
xy
f ( x, y, z )
x z
483
484.
484485.
Учебное изданиеГУТОВА
Светлана Геннадьевна
КАГАН
Елена Сергеевна
НОСЕЛЬЦЕВА
Марина Александровна
ДИСКРЕТНАЯ МАТЕМАТИКА
Курс лекций
485










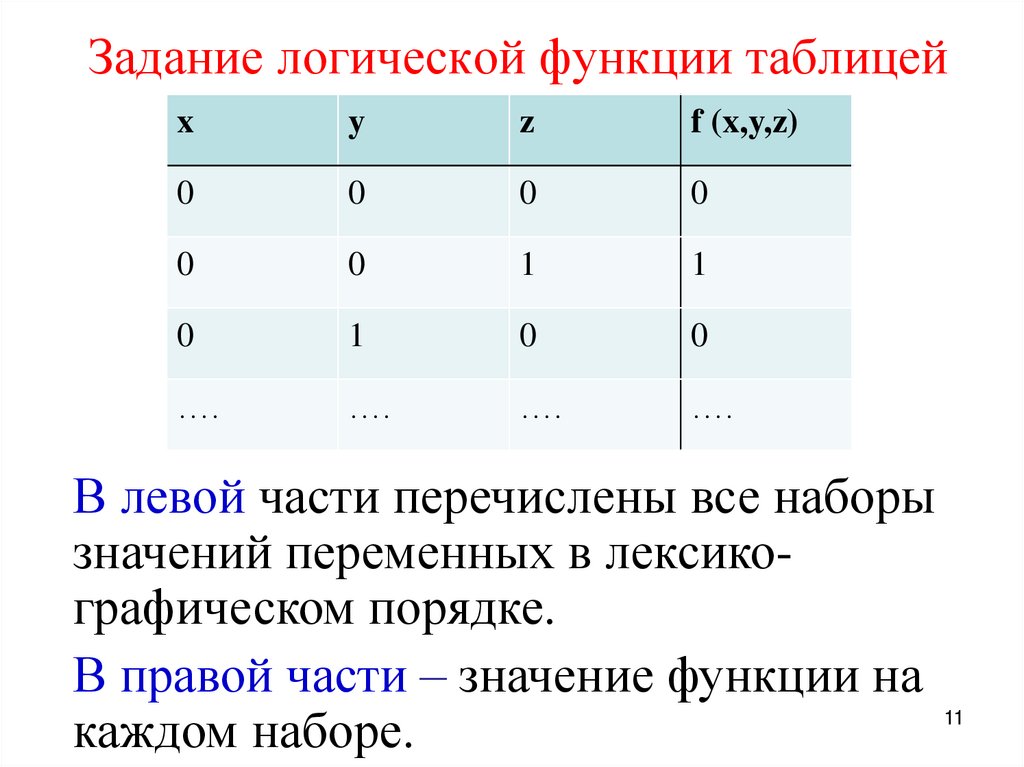







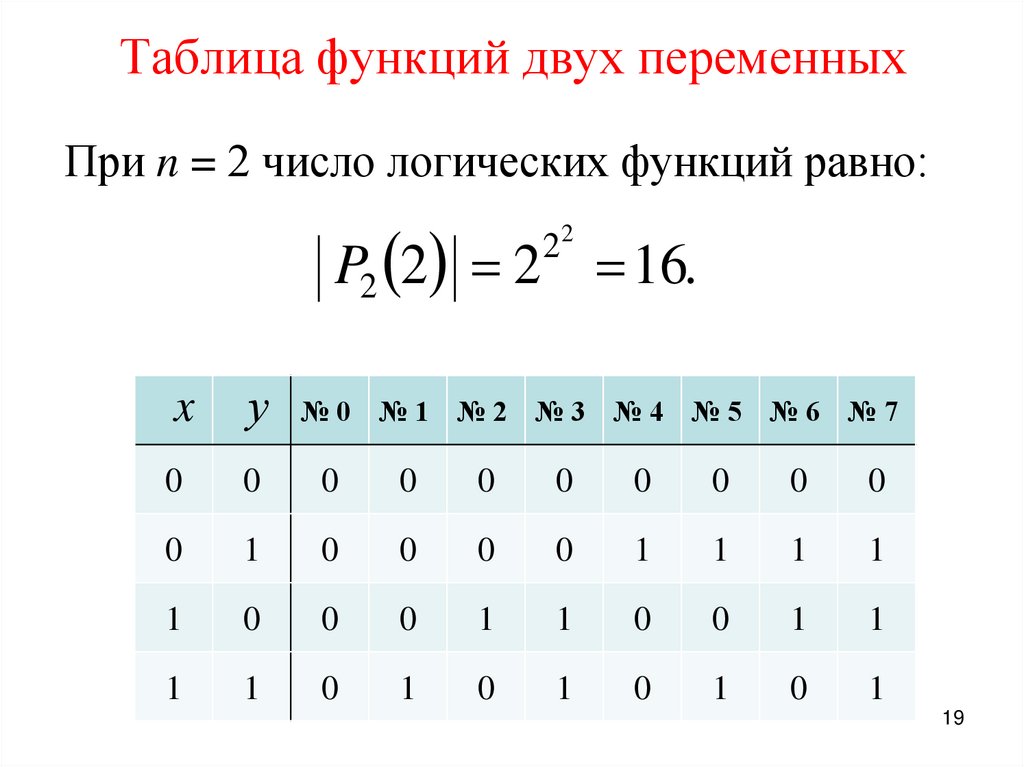
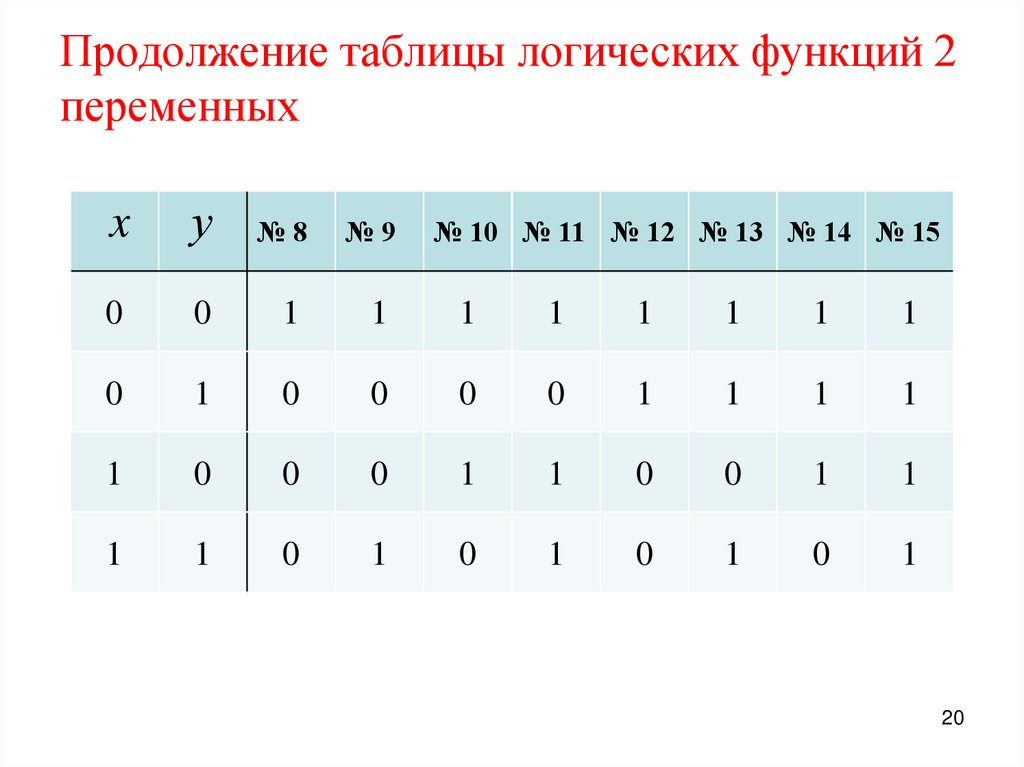
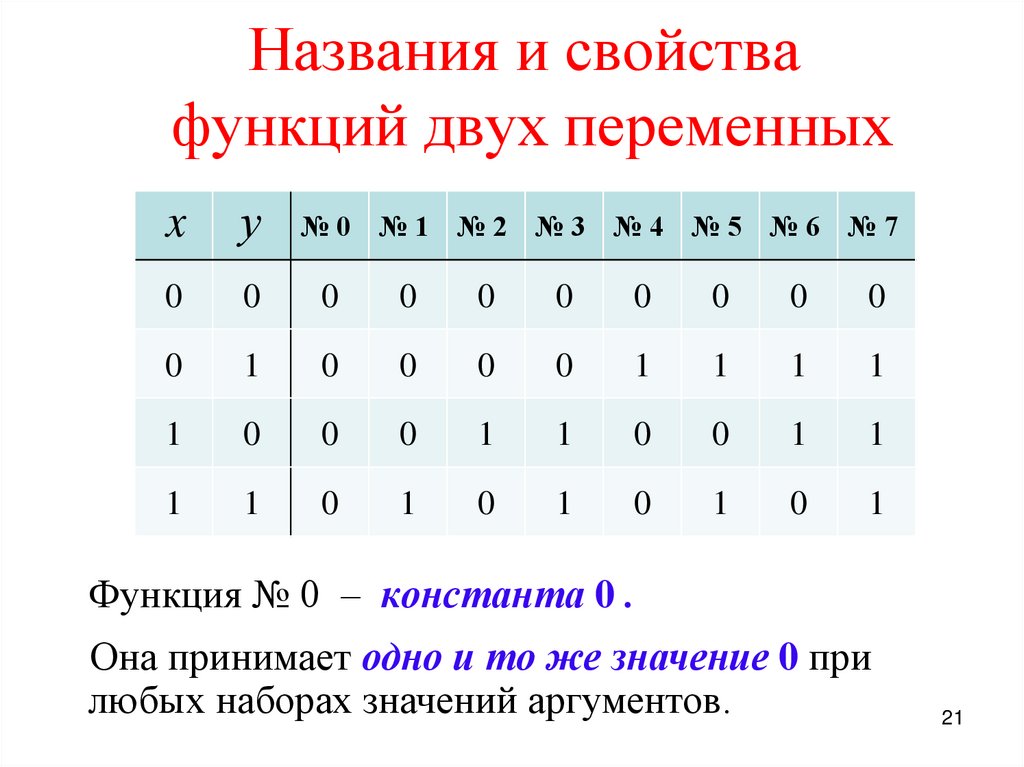
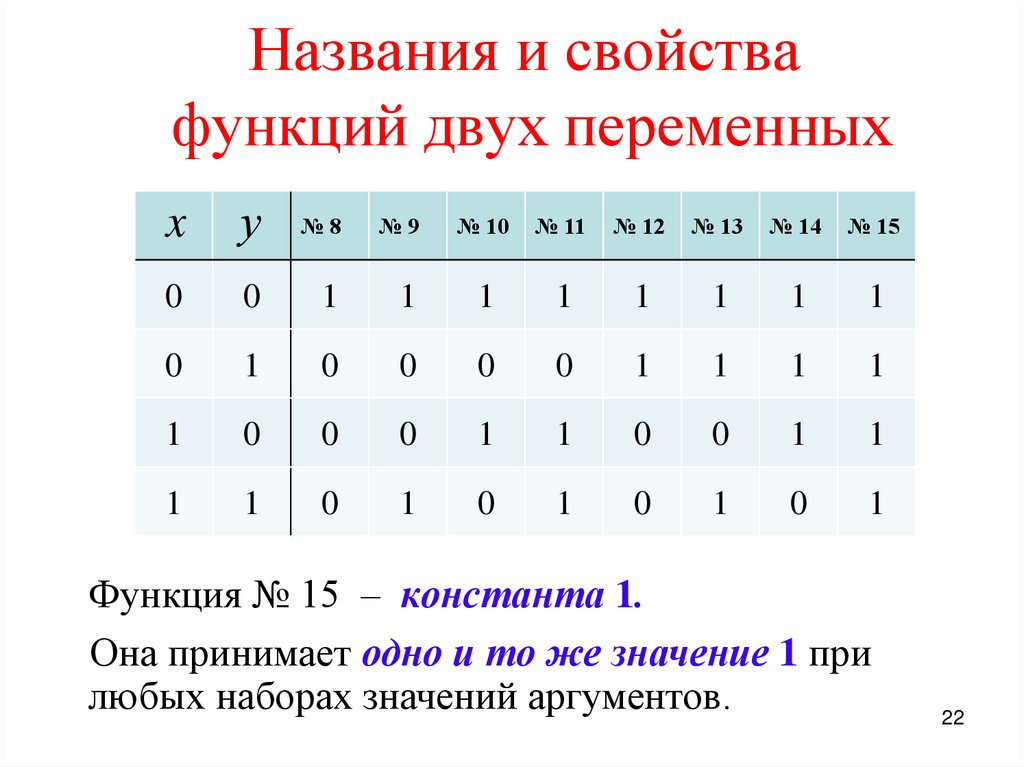

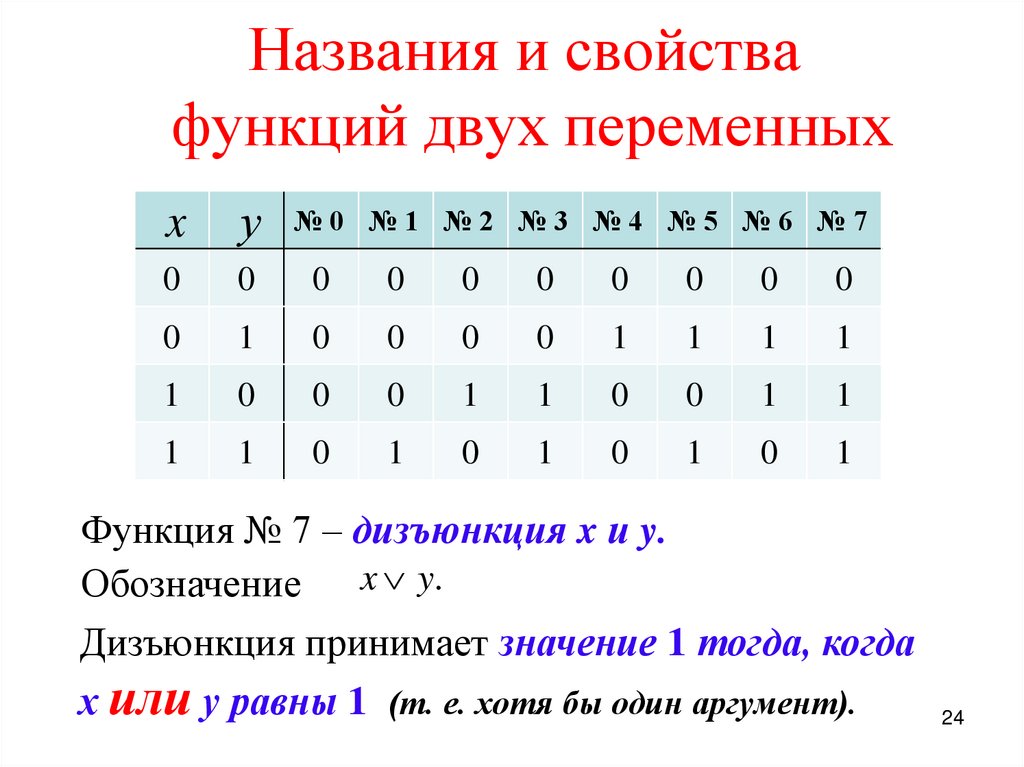

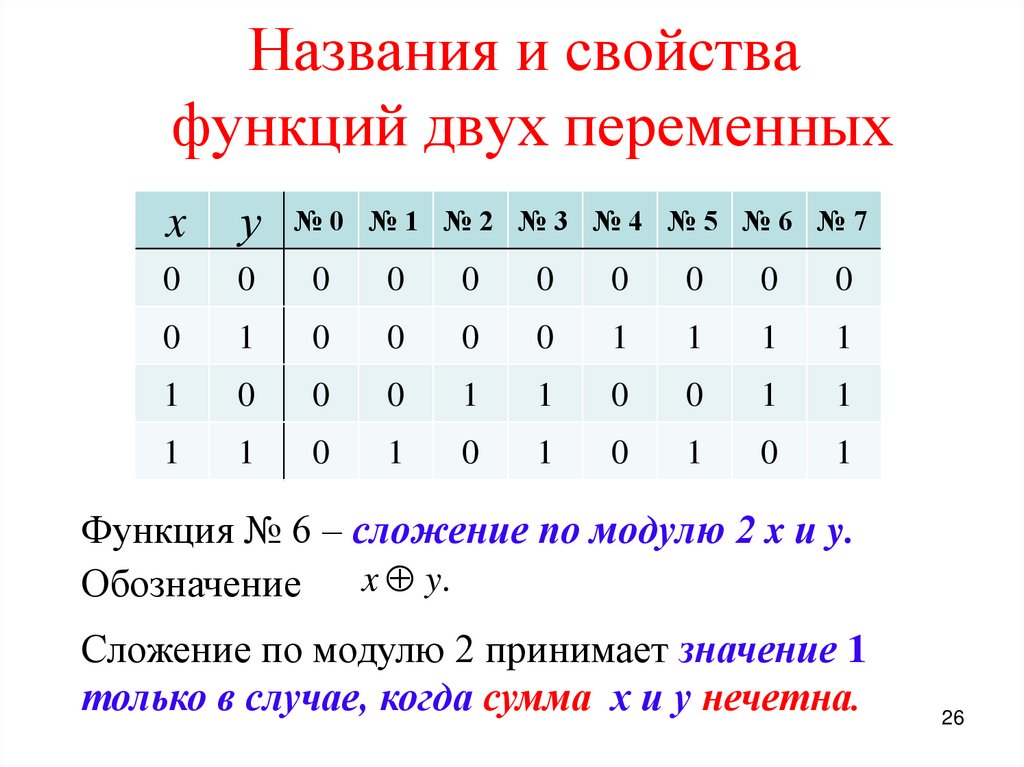
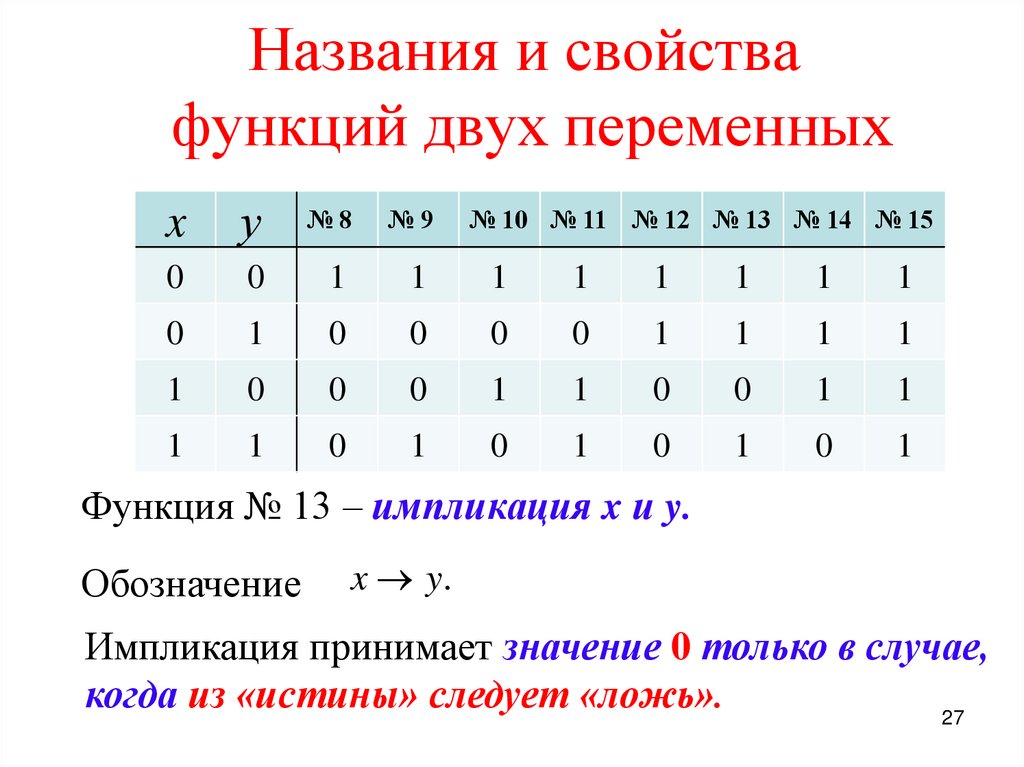
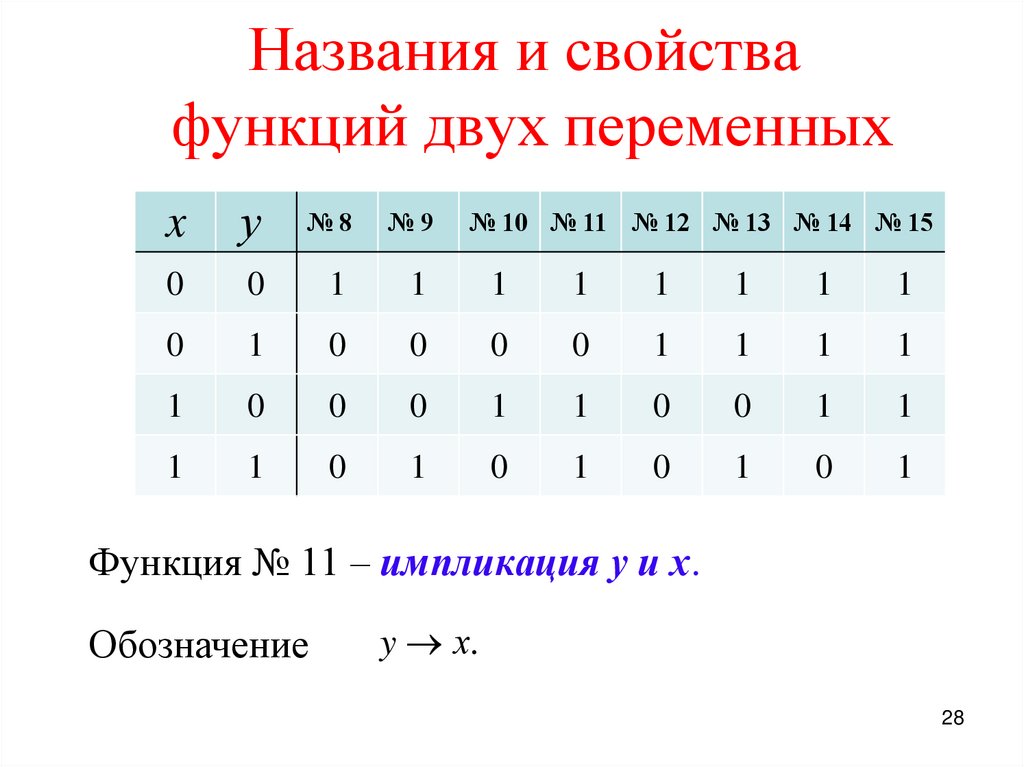







![Элементарной конъюнкцией [1-3] называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не Элементарной конъюнкцией [1-3] называется конъюнкция переменных или их отрицаний, в которой каждая переменная встречается не](https://cf5.ppt-online.org/files5/slide/x/XKRPWfHhBNzZkTgIsO1d8w4DySEicJtq63QMo5/slide-35.jpg)


![Элементарной дизъюнкцией [1-3] называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не Элементарной дизъюнкцией [1-3] называется дизъюнкция переменных или их отрицаний, в которой каждая переменная встречается не](https://cf5.ppt-online.org/files5/slide/x/XKRPWfHhBNzZkTgIsO1d8w4DySEicJtq63QMo5/slide-38.jpg)









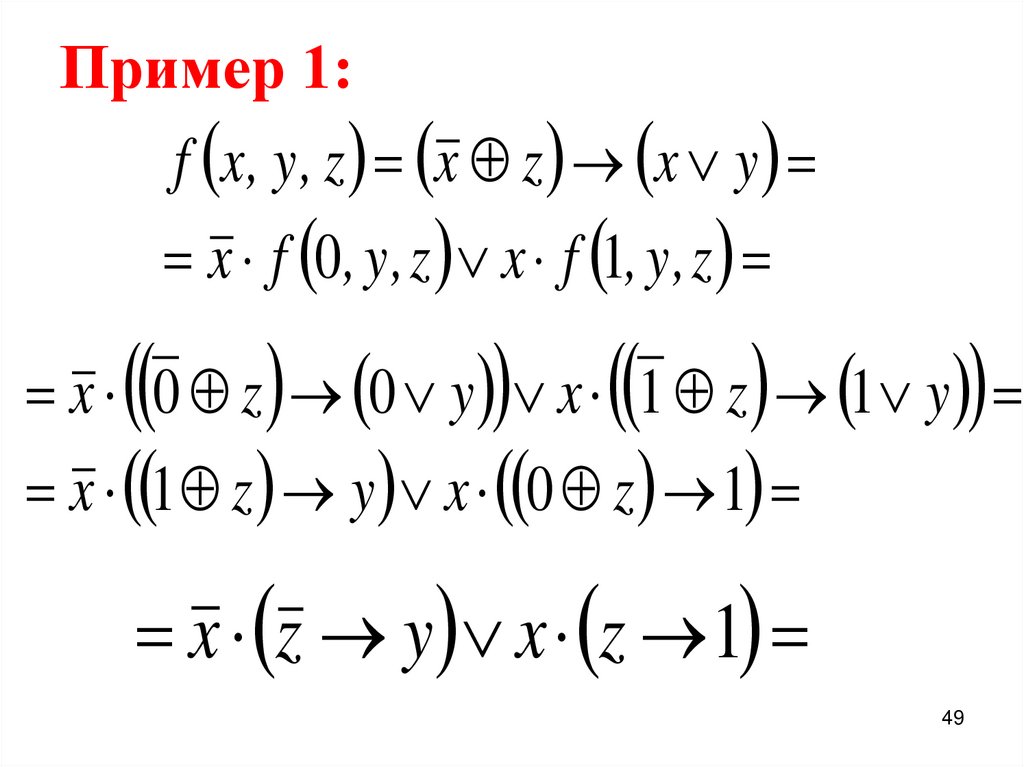
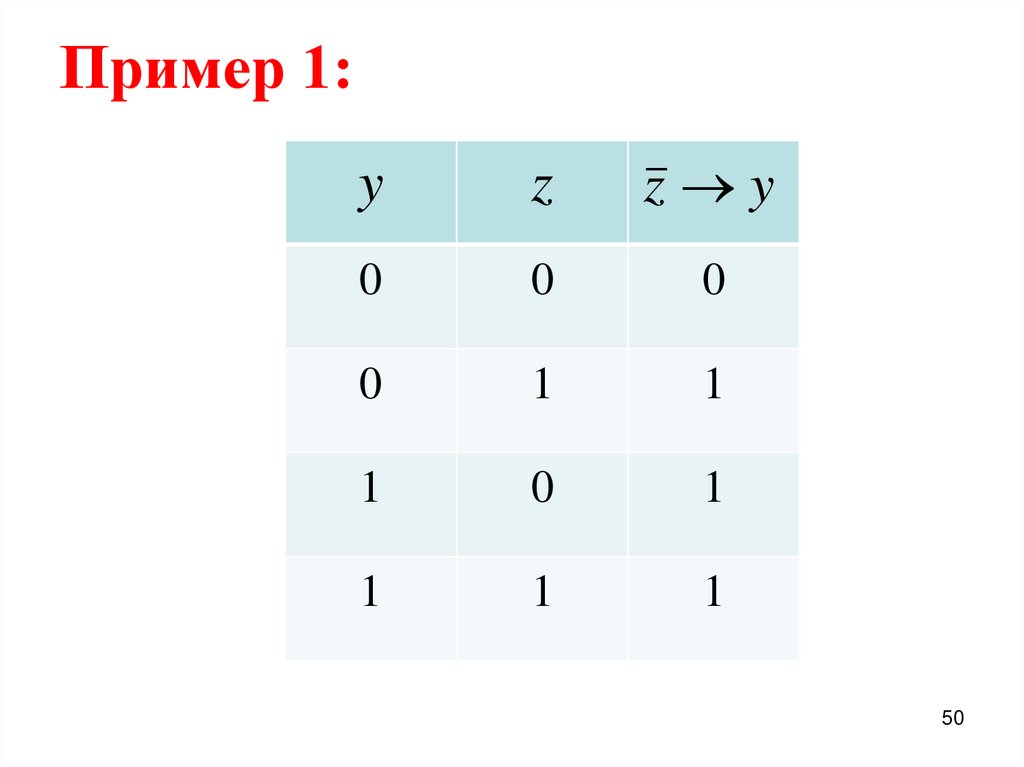
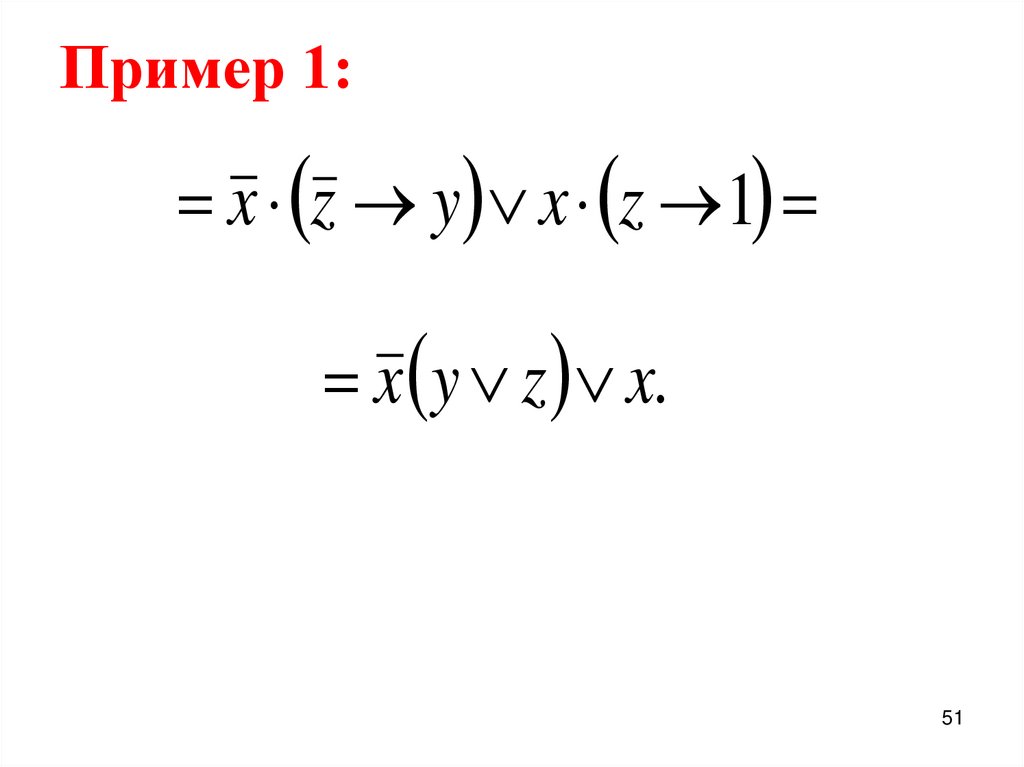




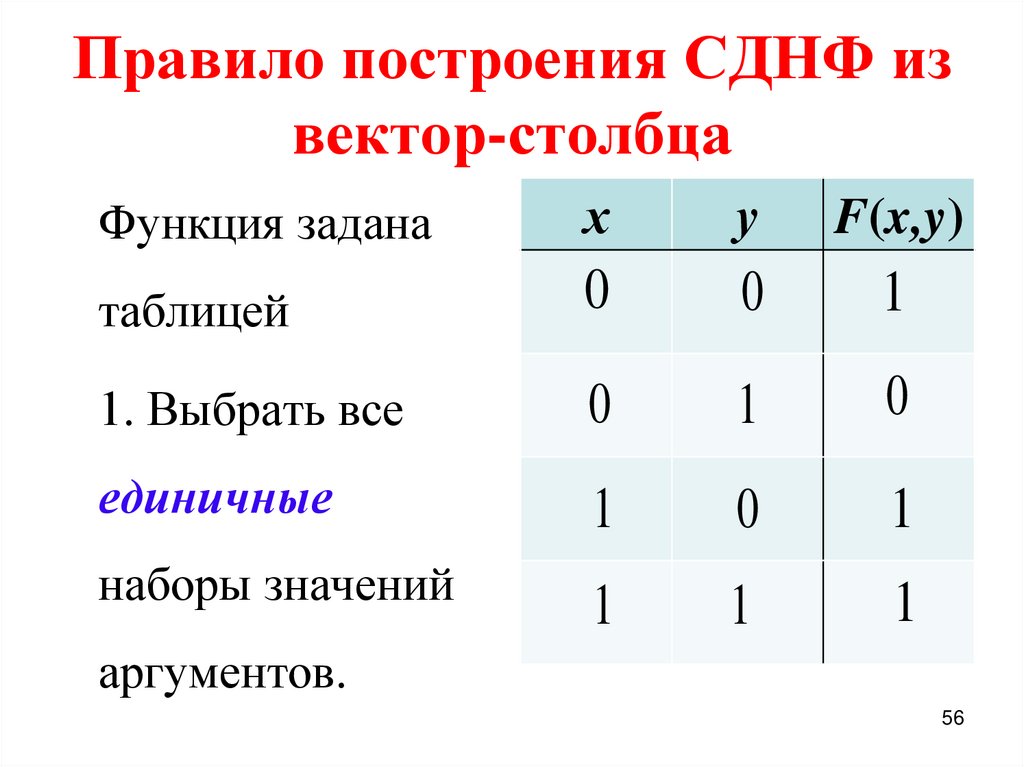
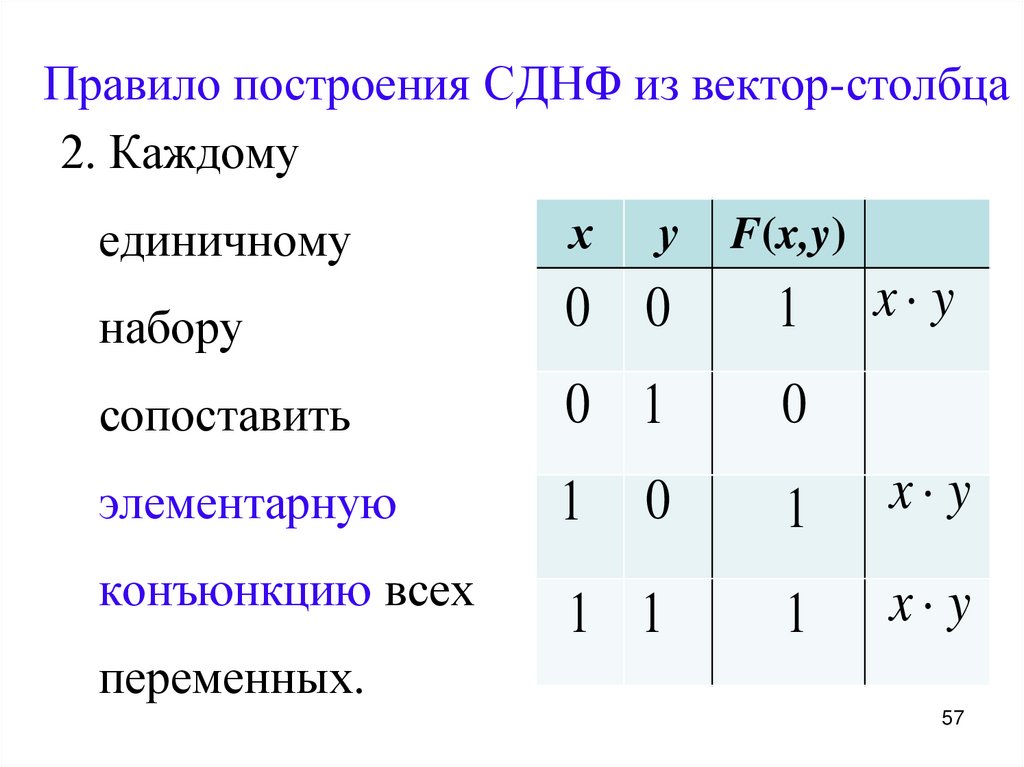
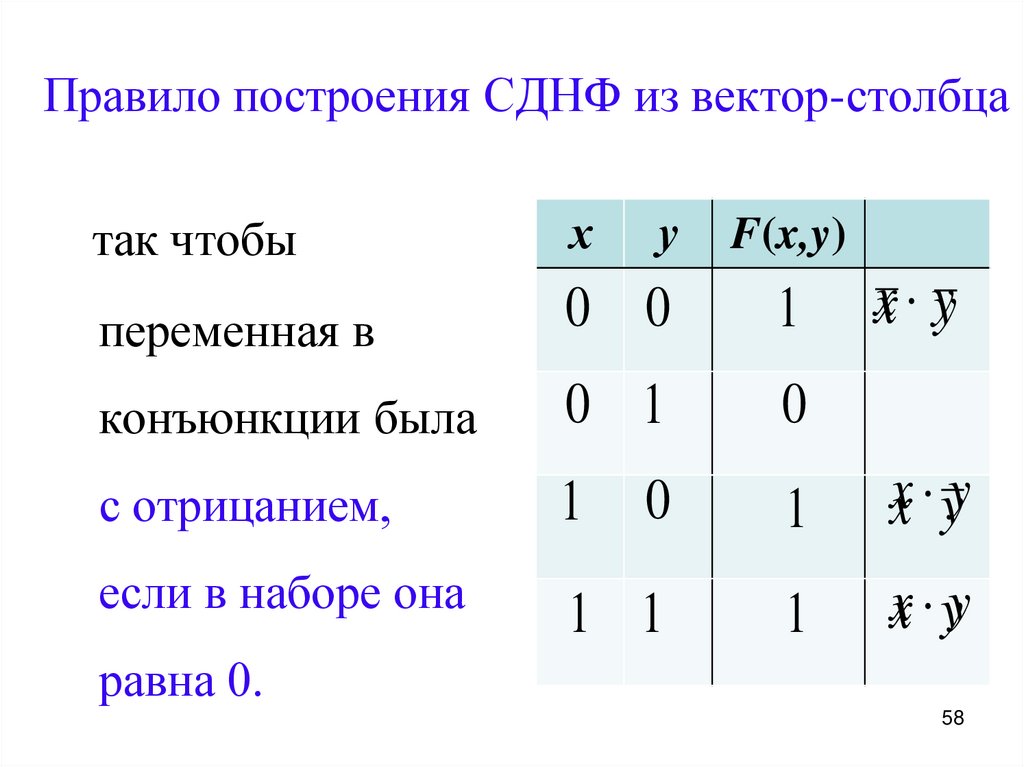
























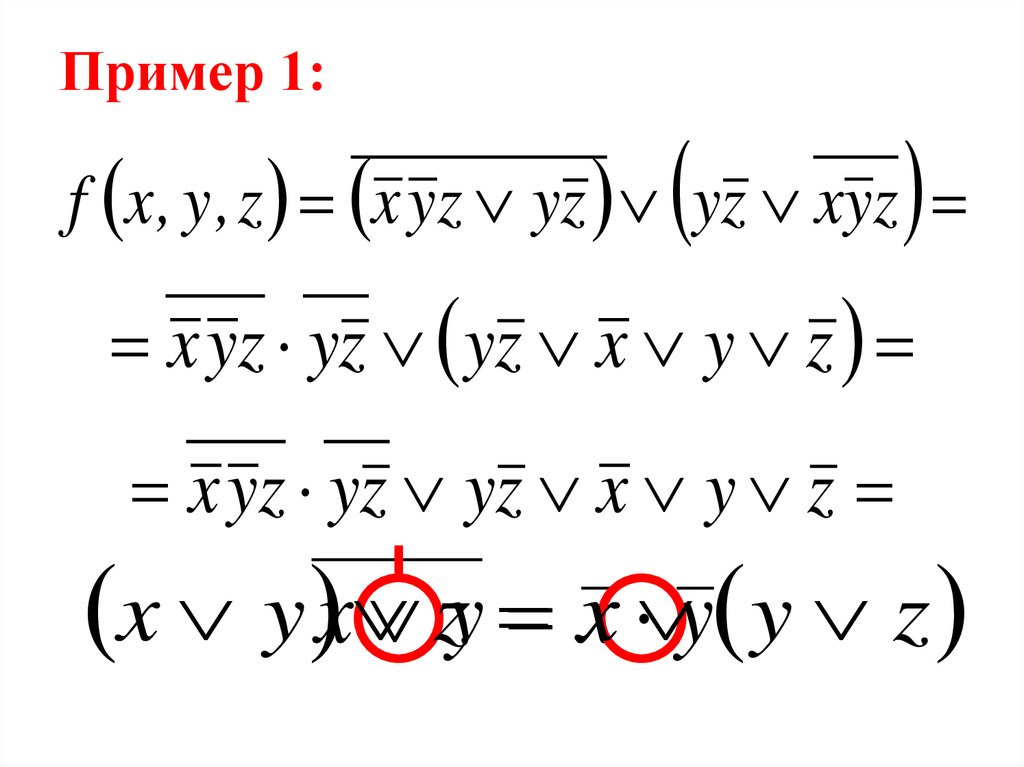




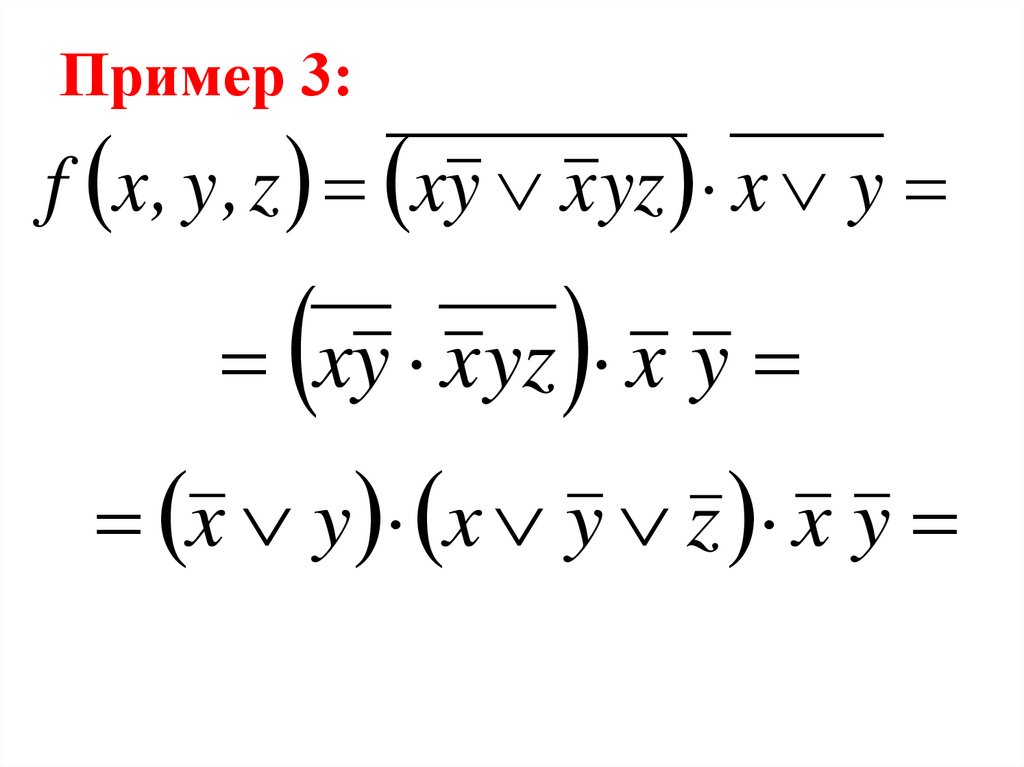



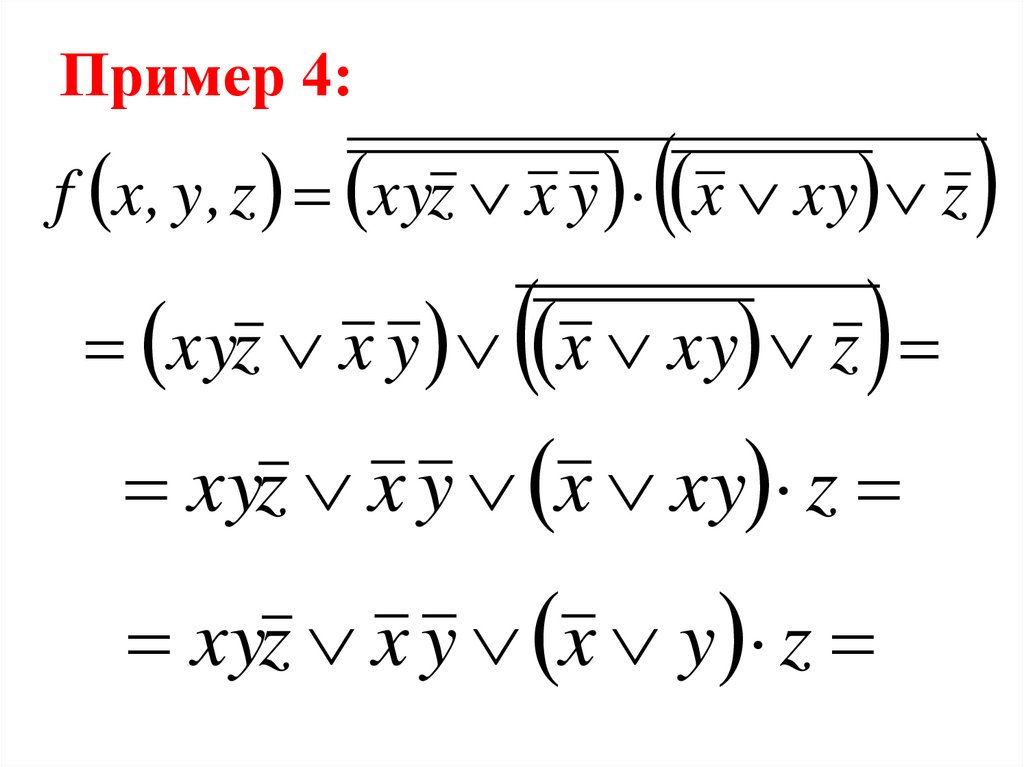
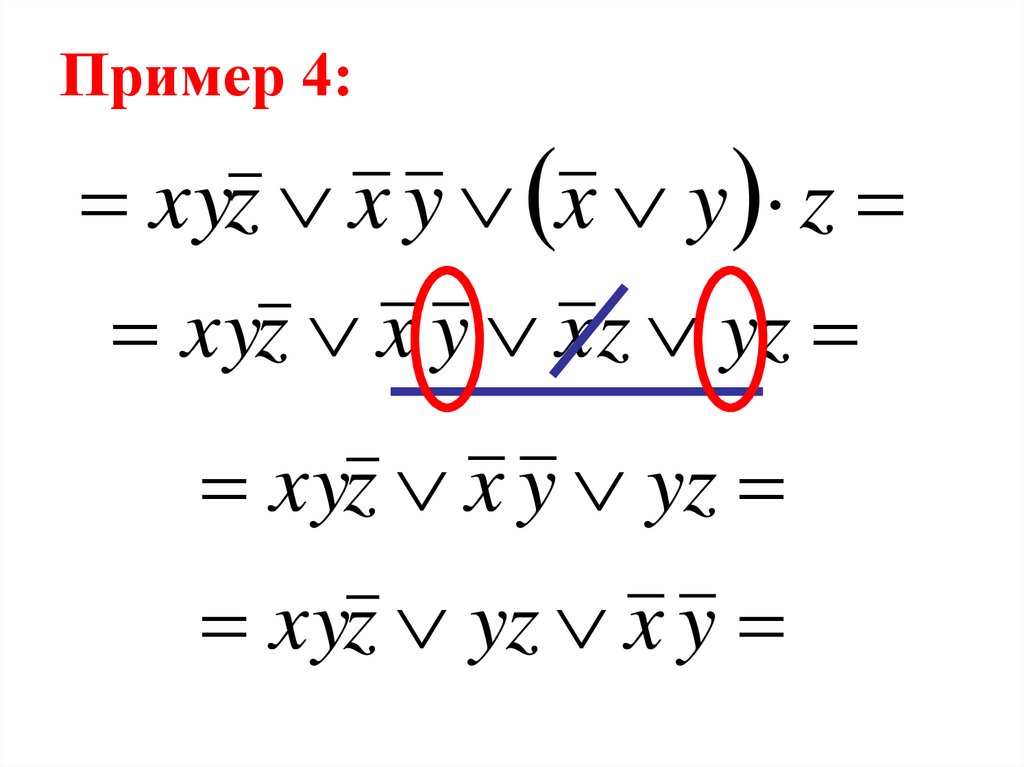
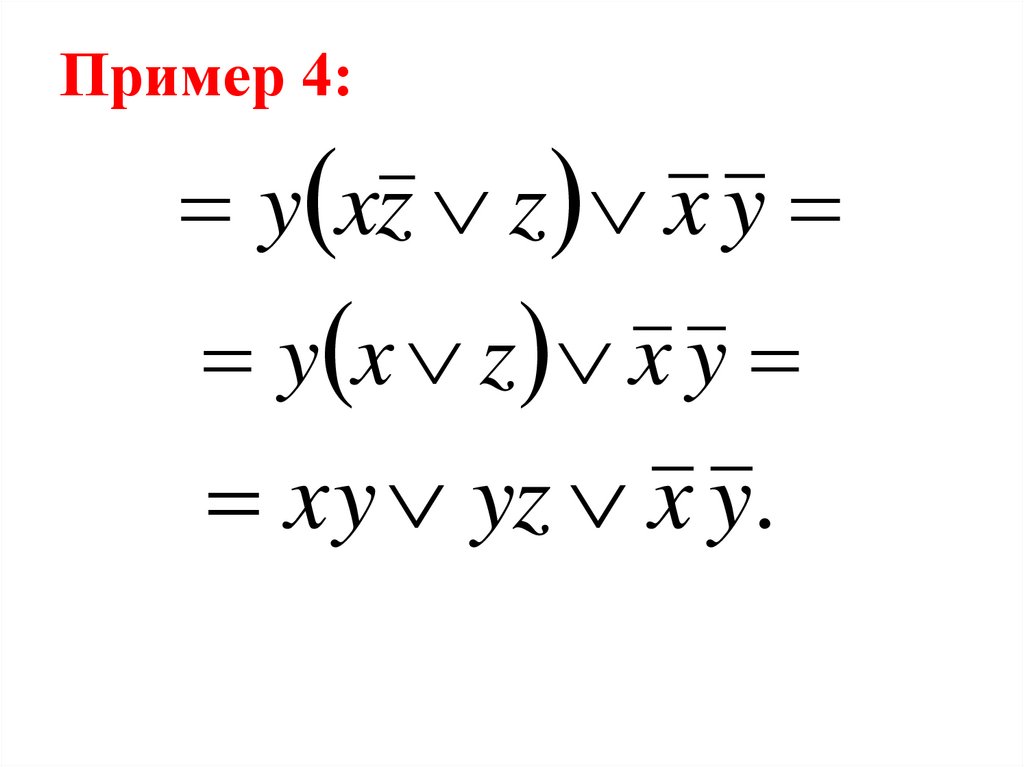



![Переход от ДНФ к КНФ [1] Переход от ДНФ к КНФ [1]](https://cf5.ppt-online.org/files5/slide/x/XKRPWfHhBNzZkTgIsO1d8w4DySEicJtq63QMo5/slide-97.jpg)


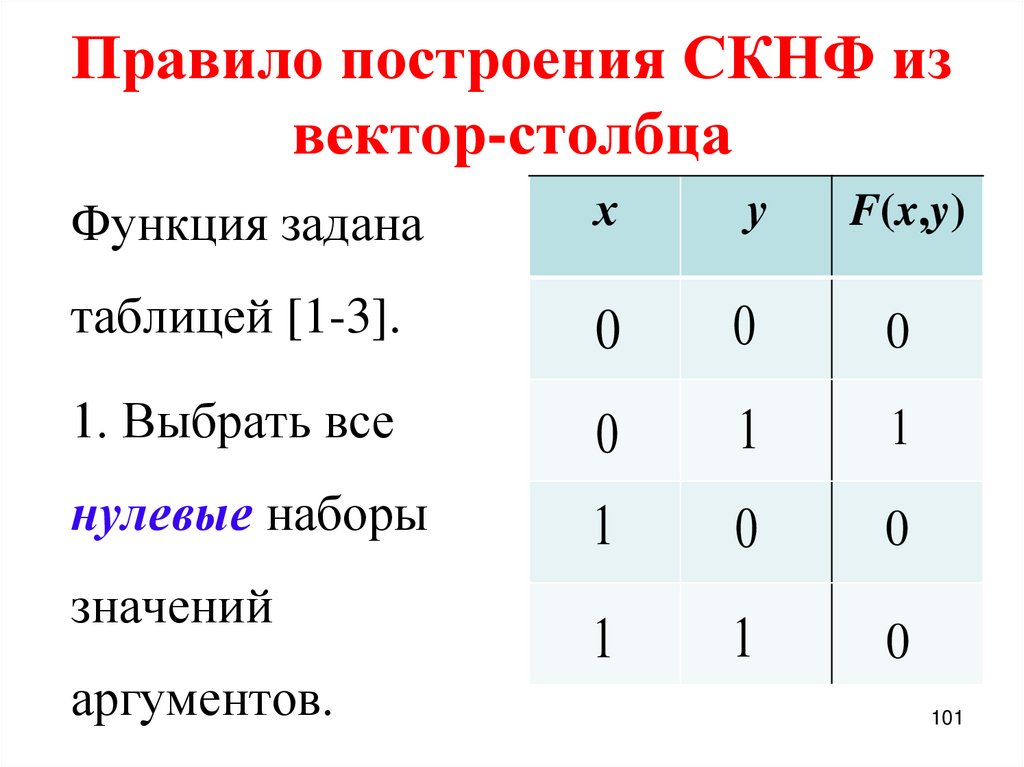
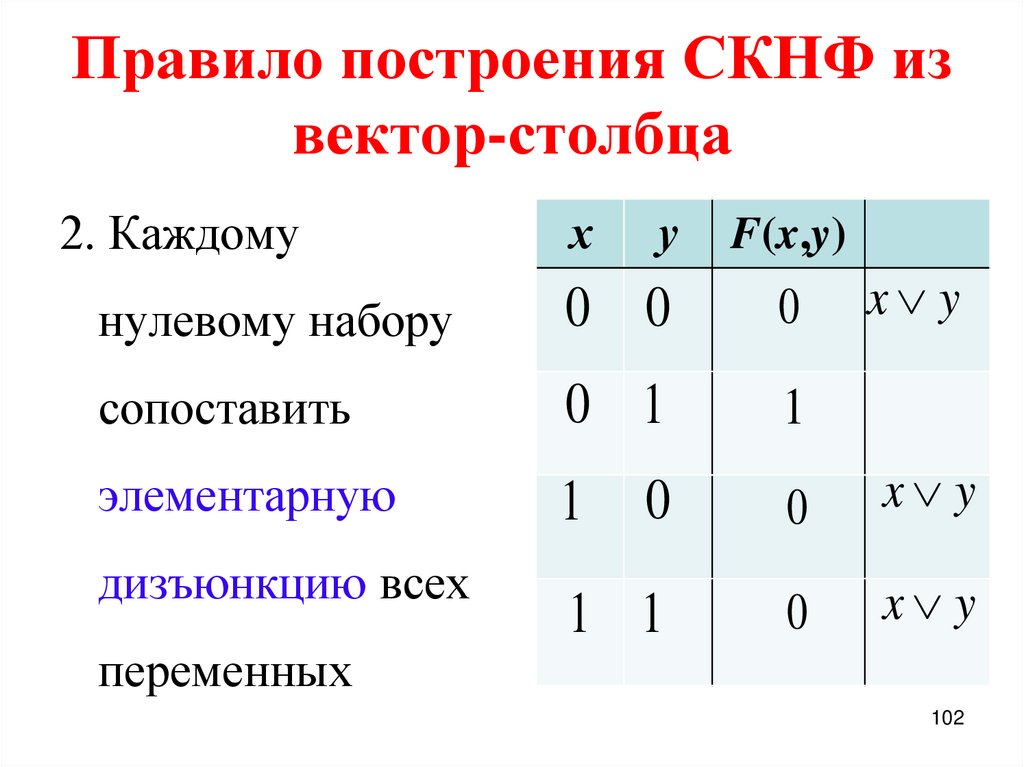
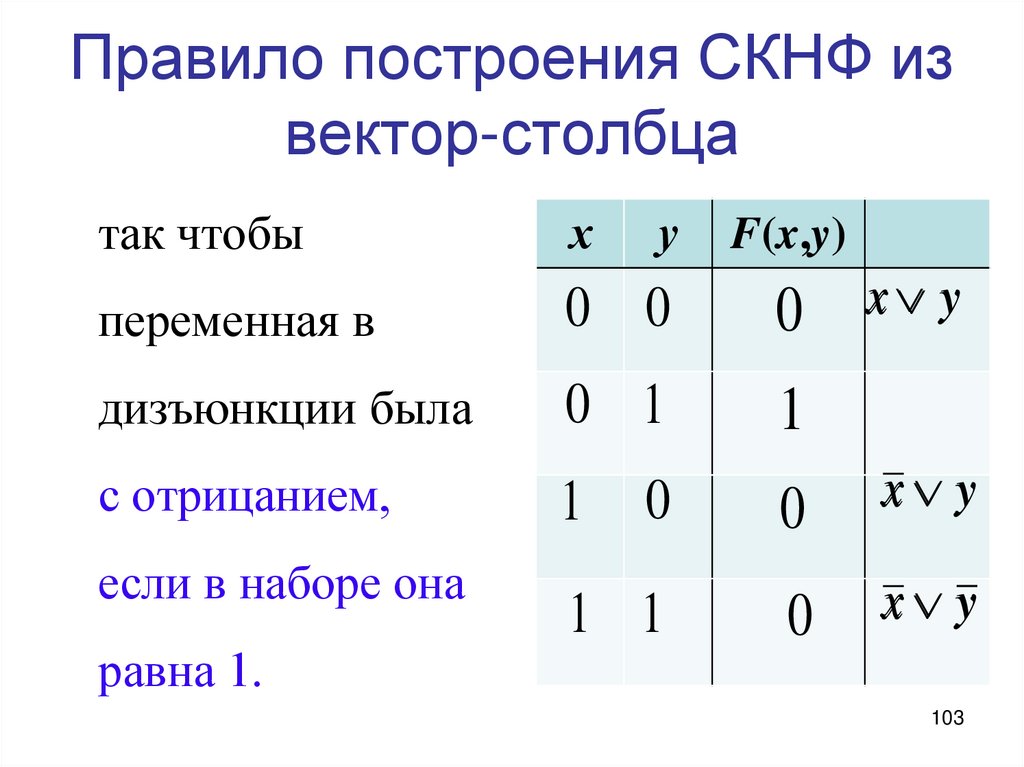































































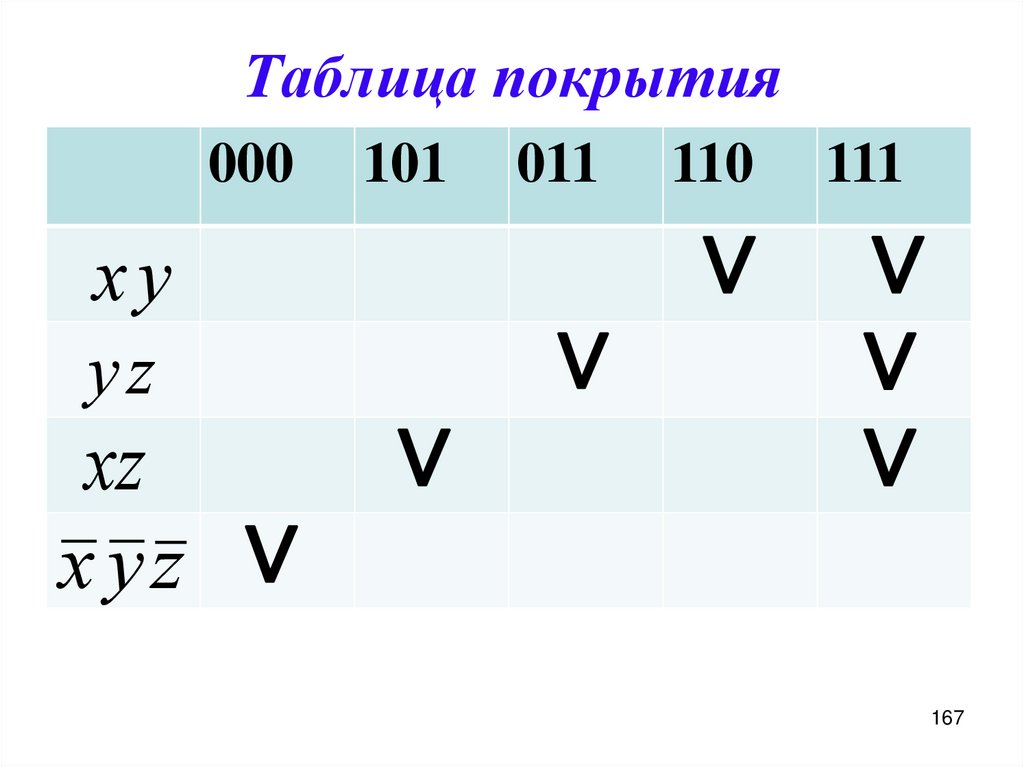





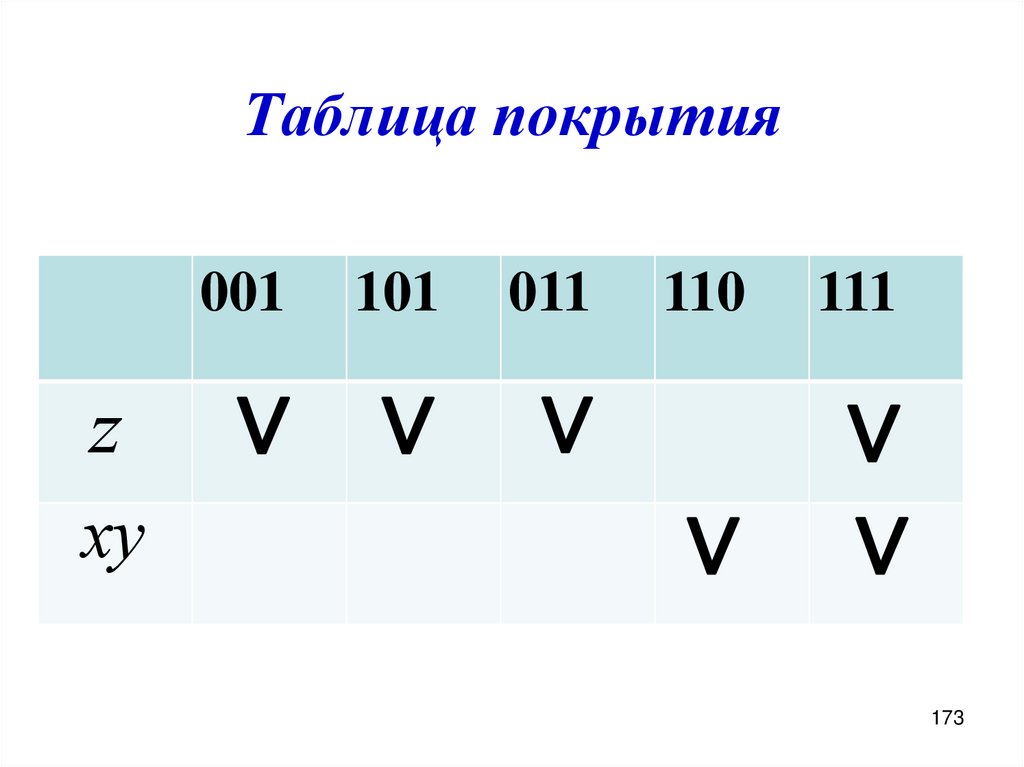
















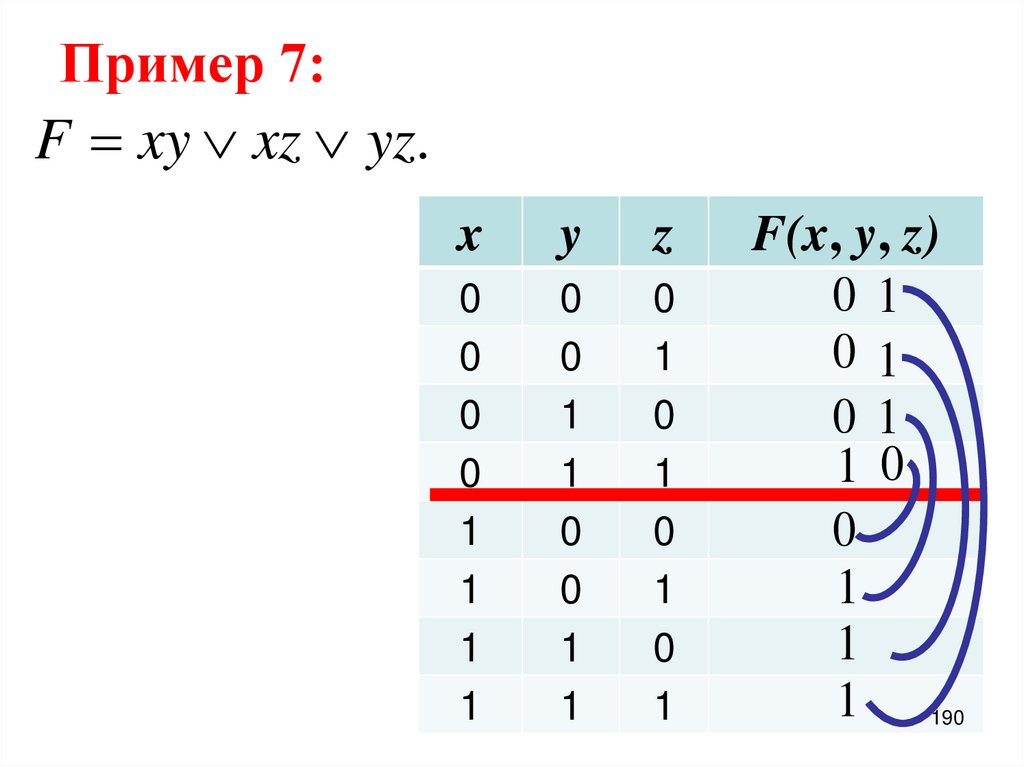









































































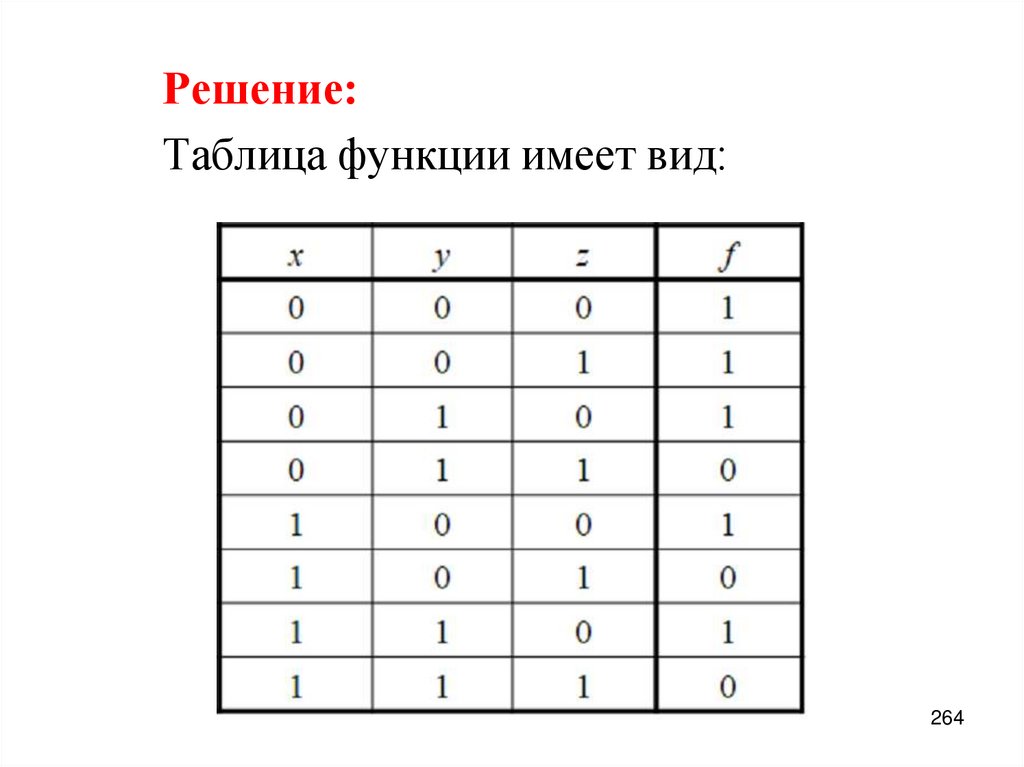





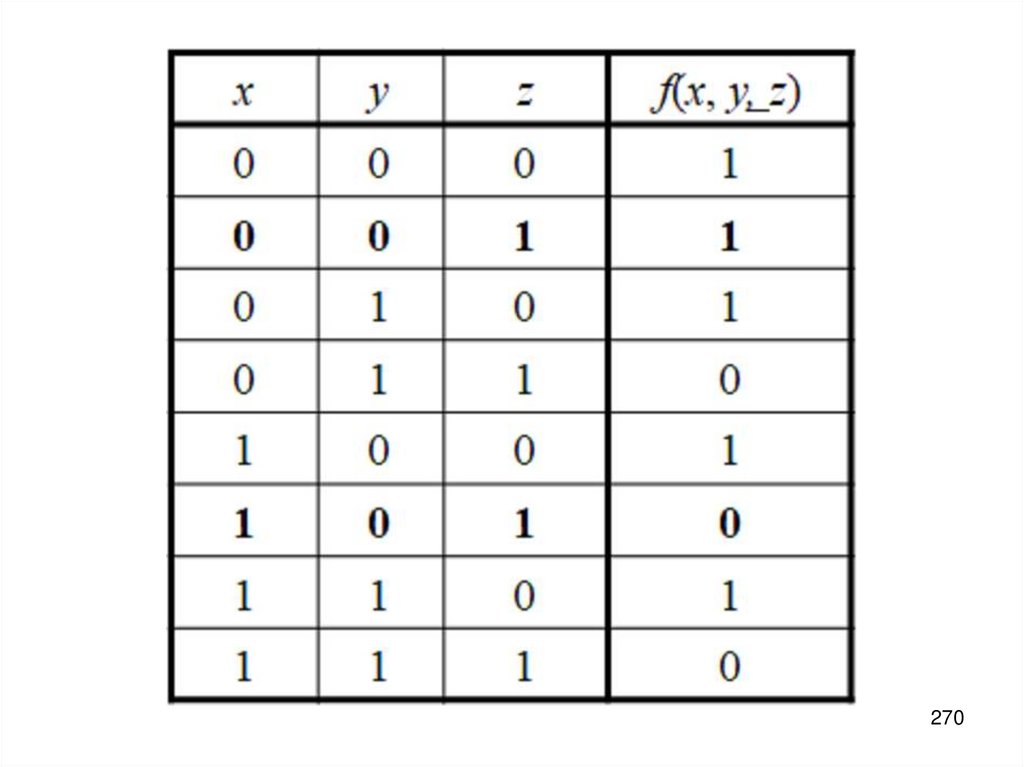






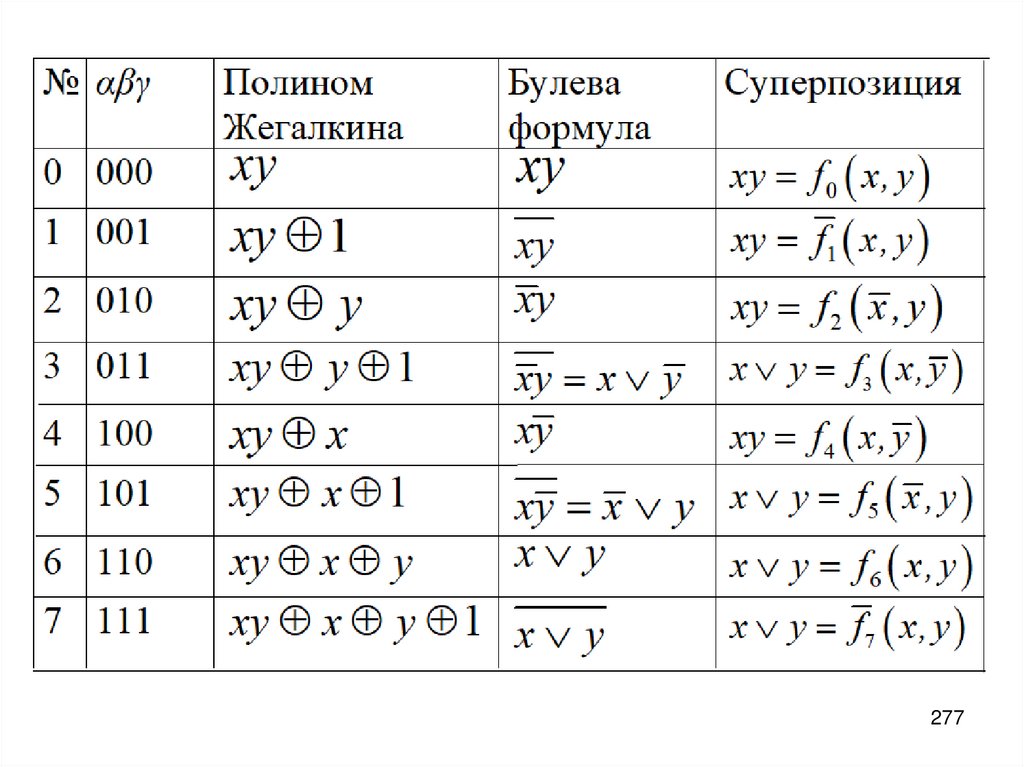






















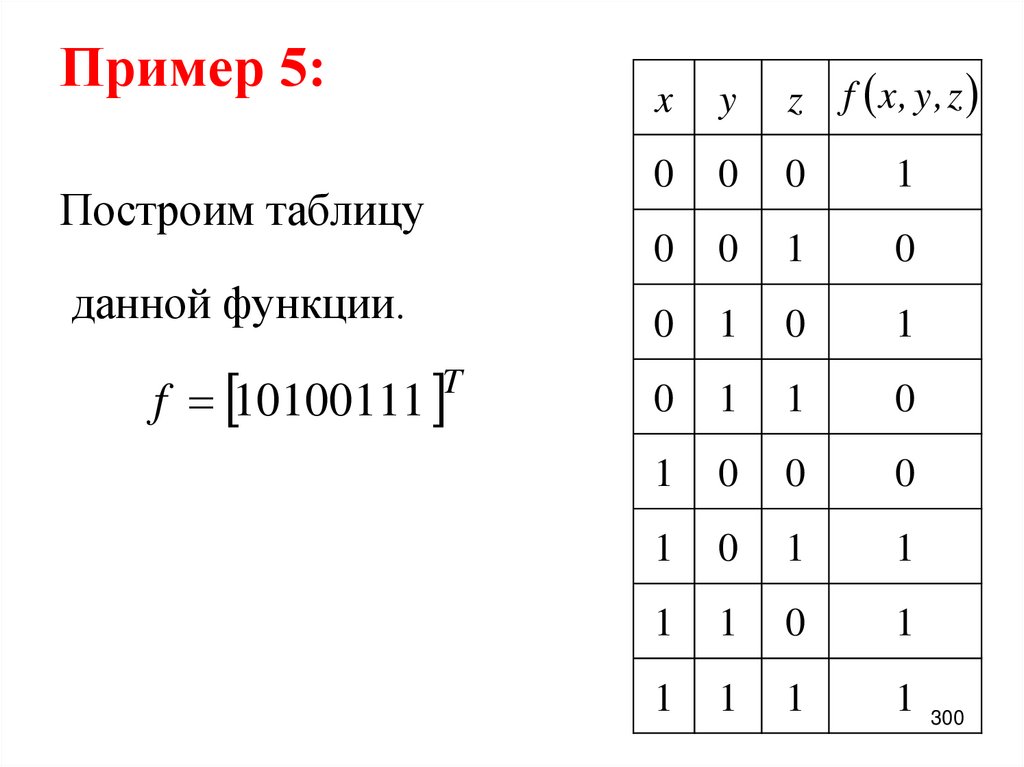











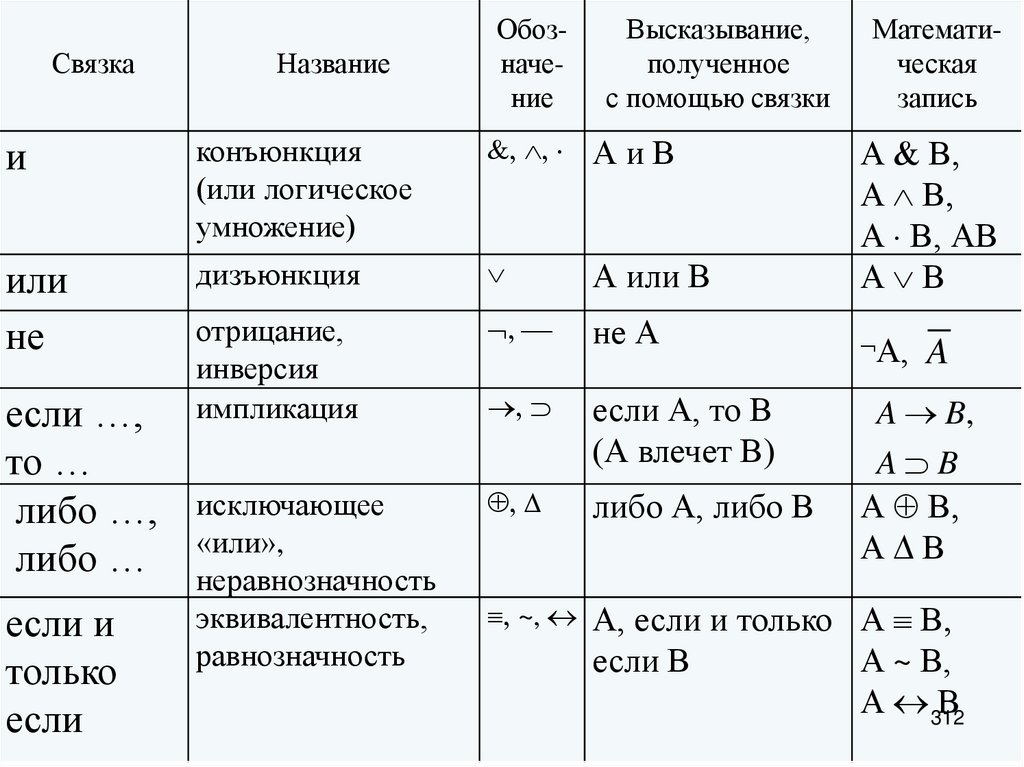


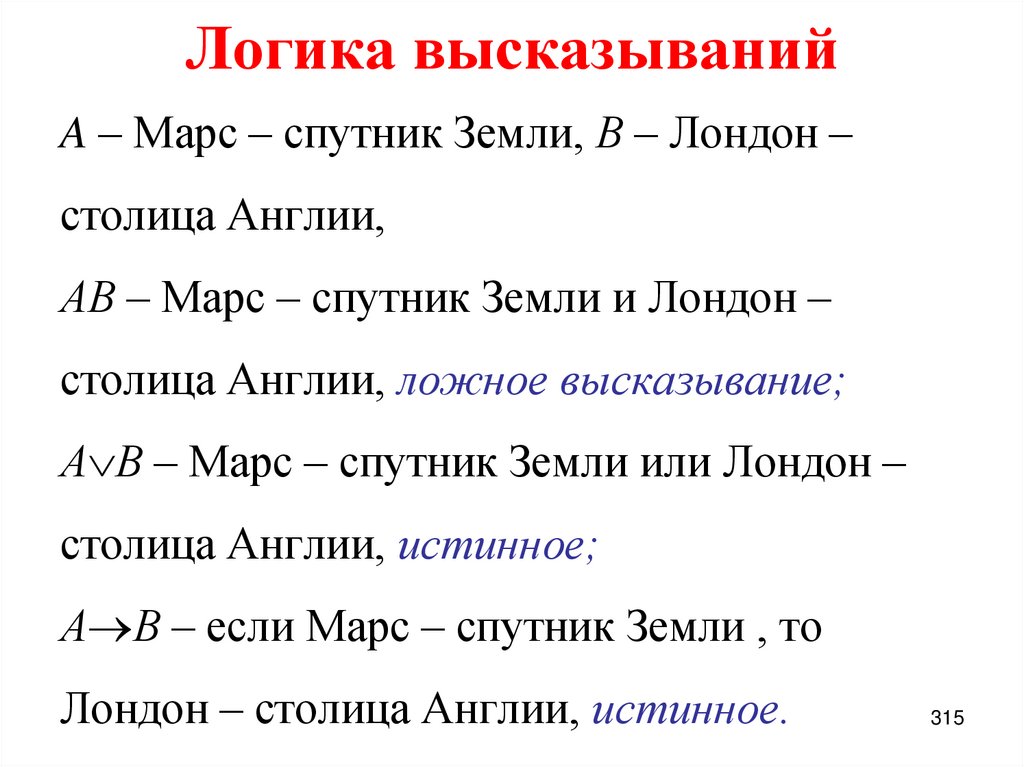



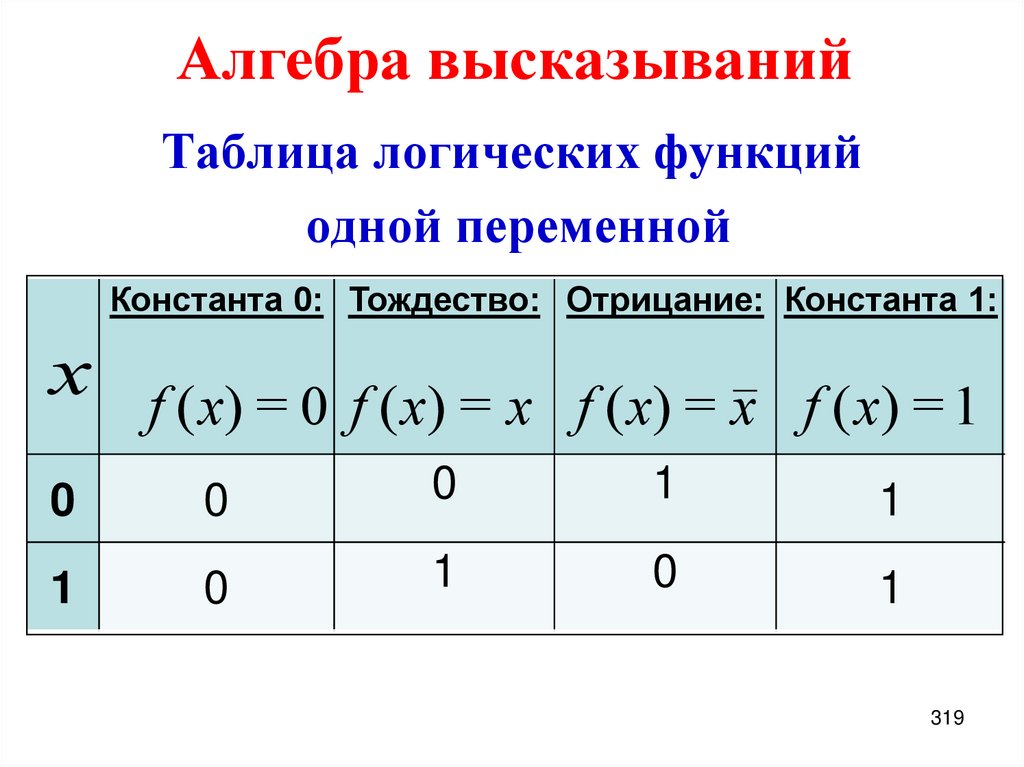









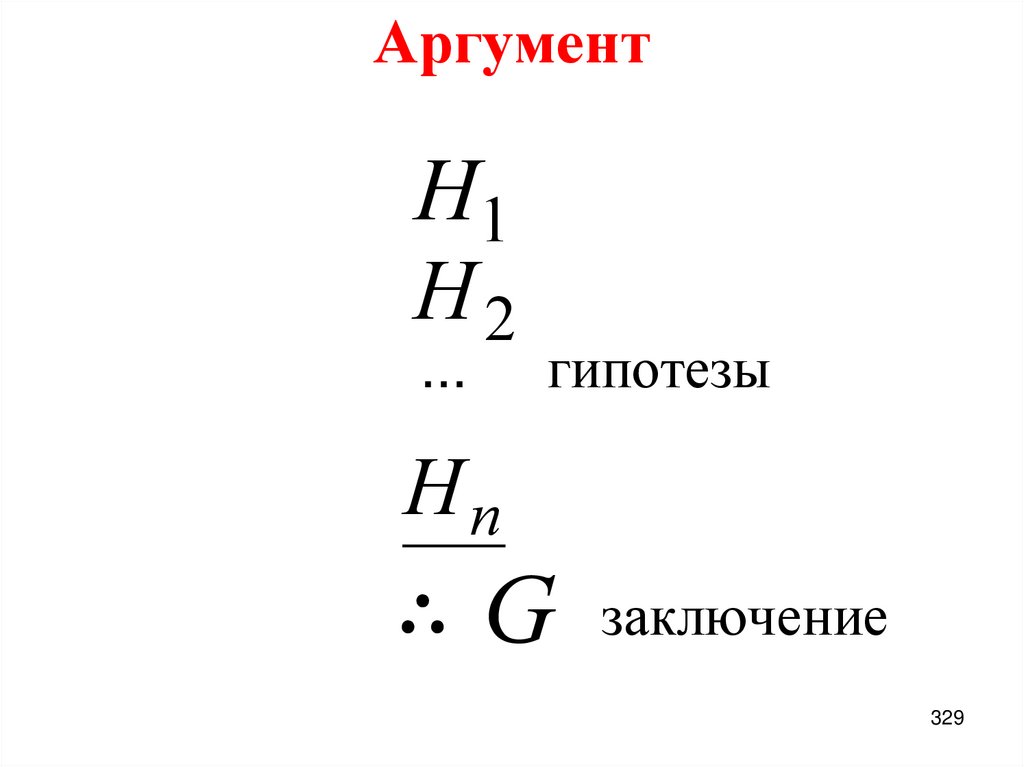



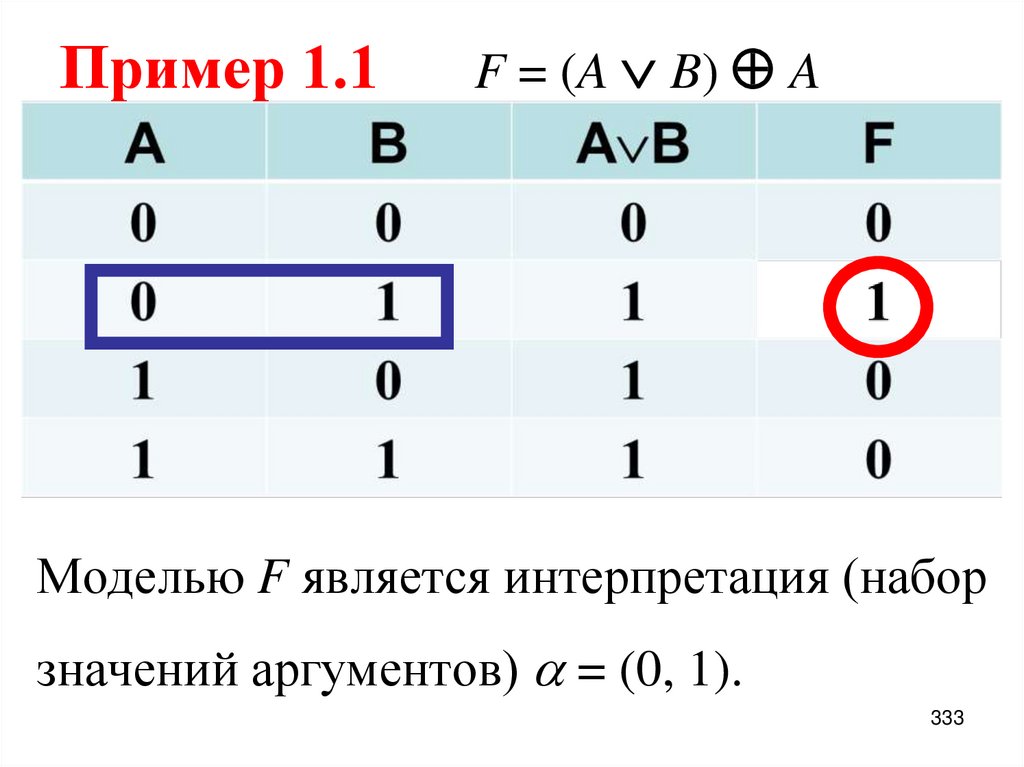


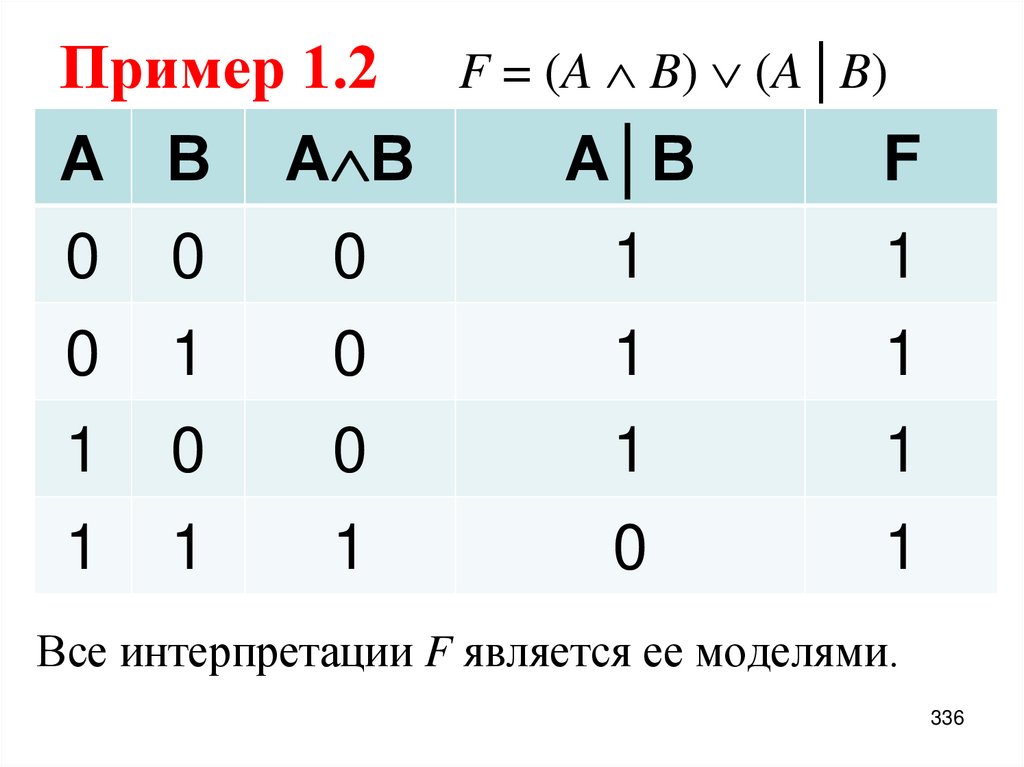


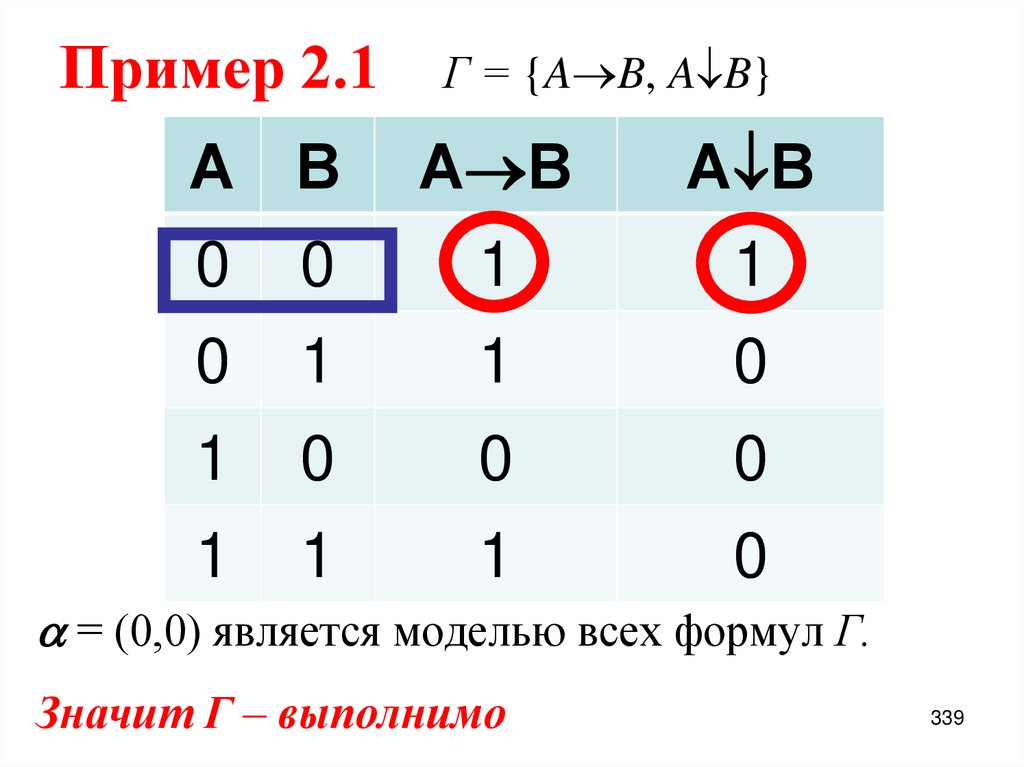

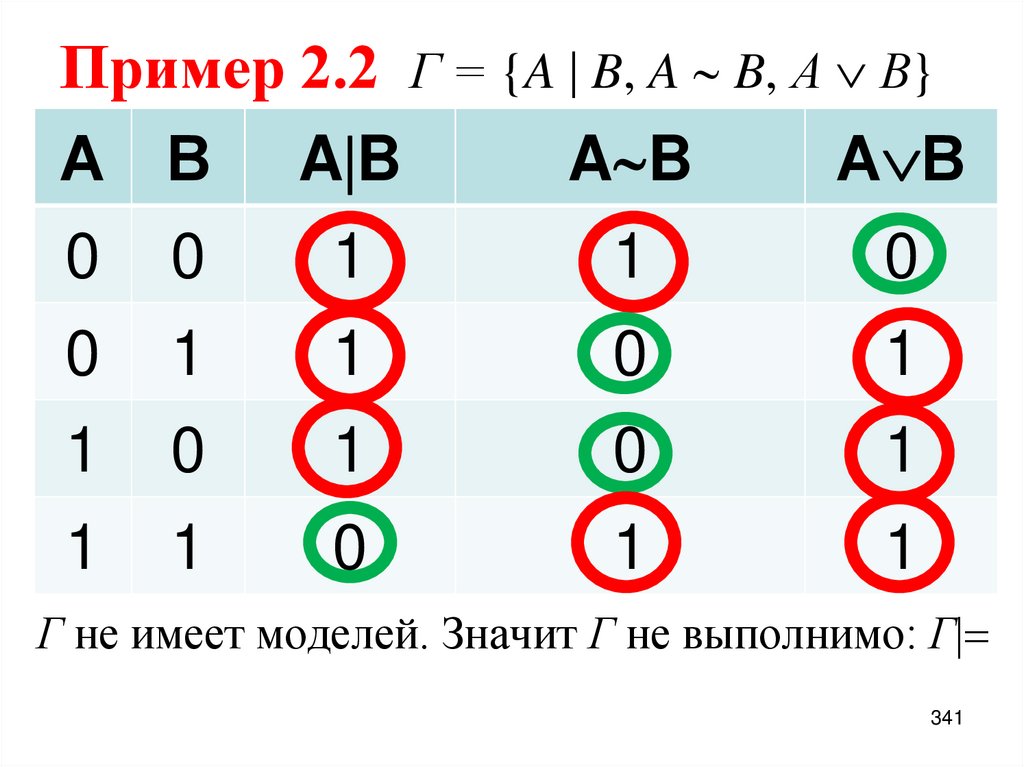





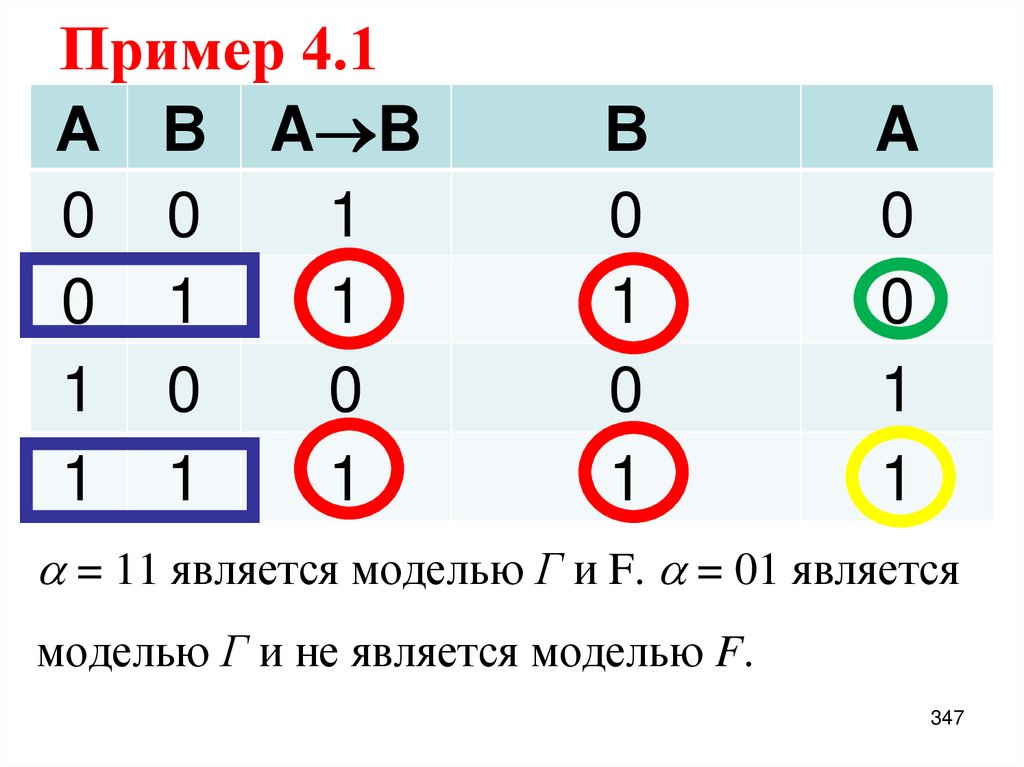








































































































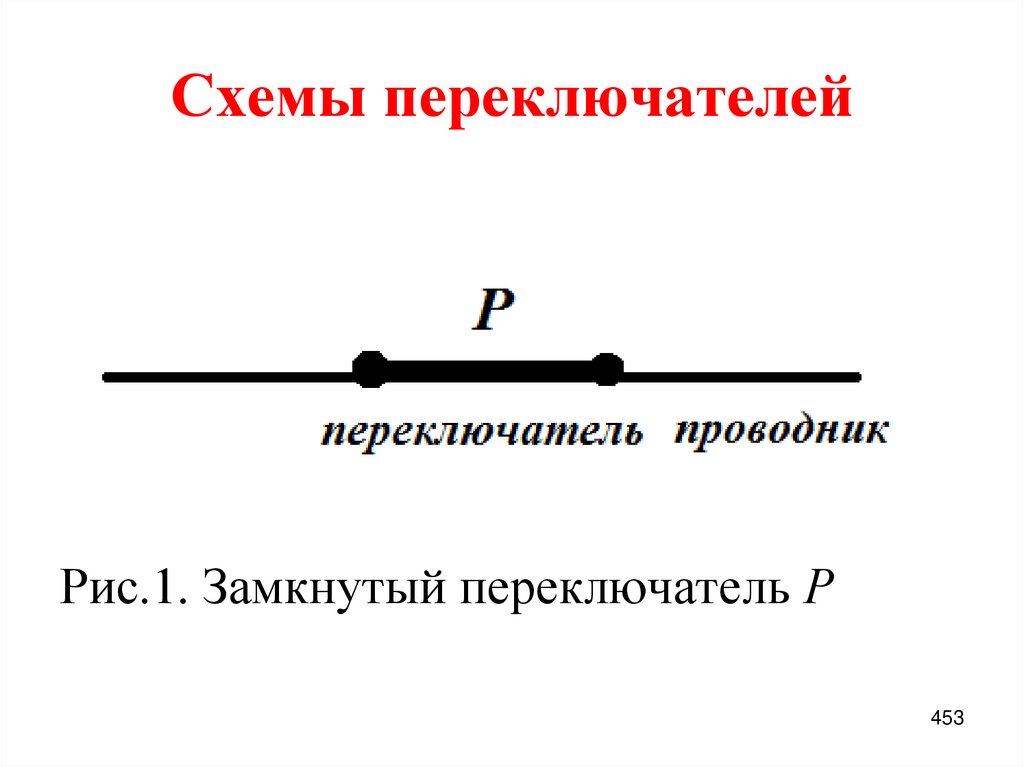

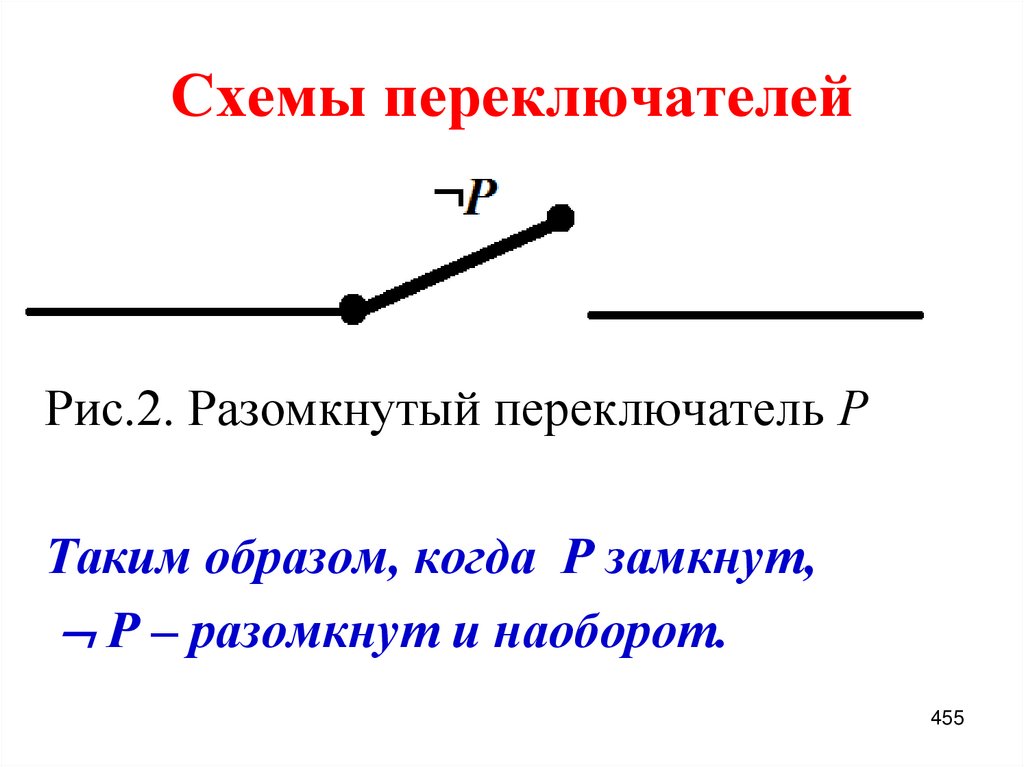


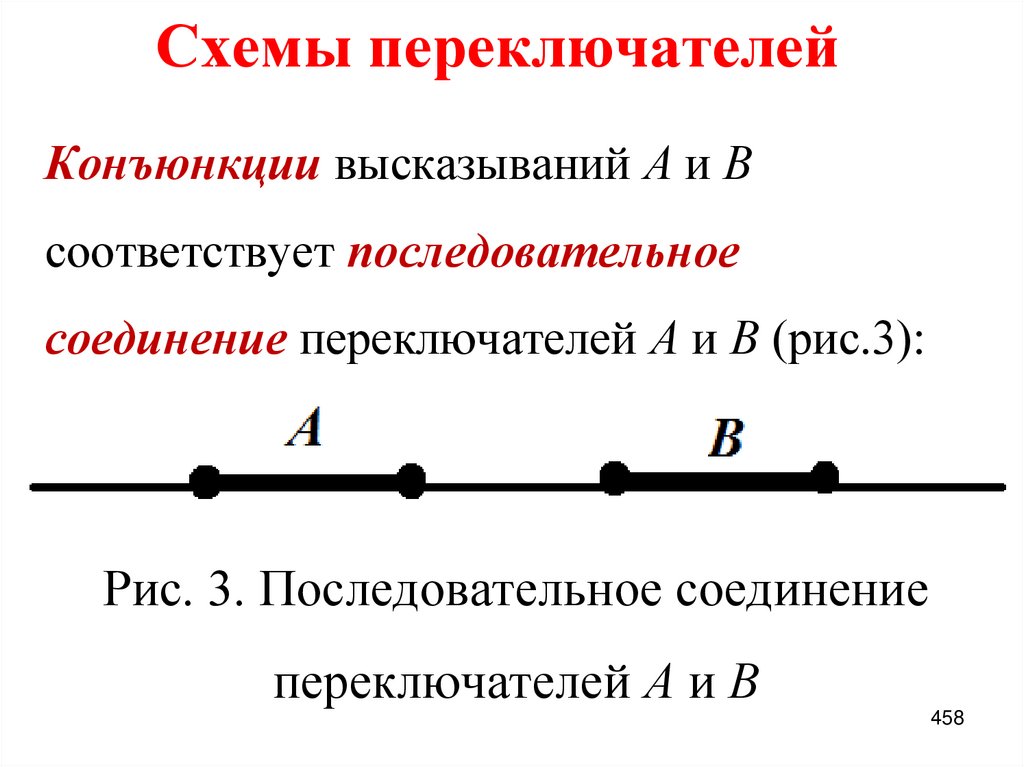
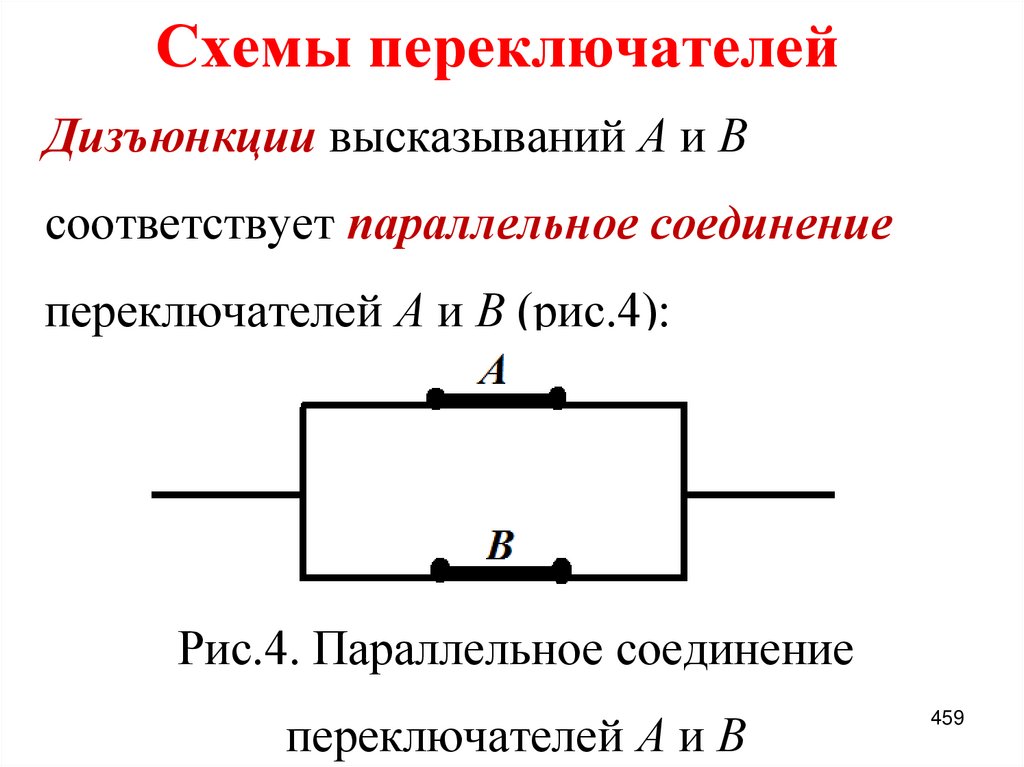
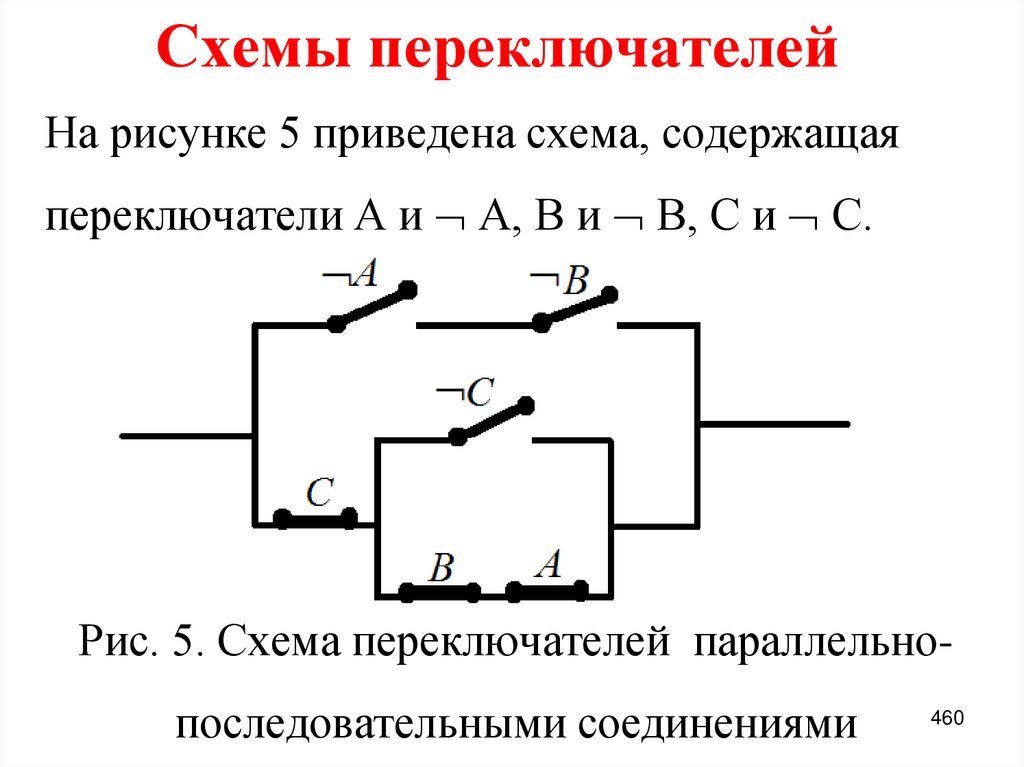
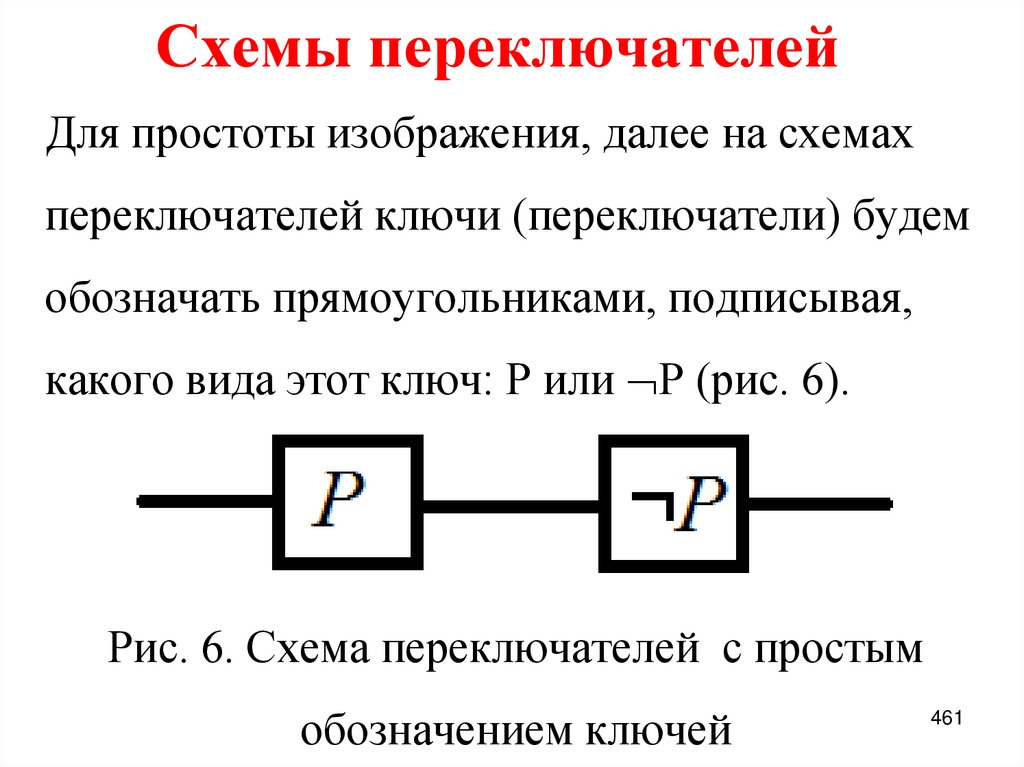
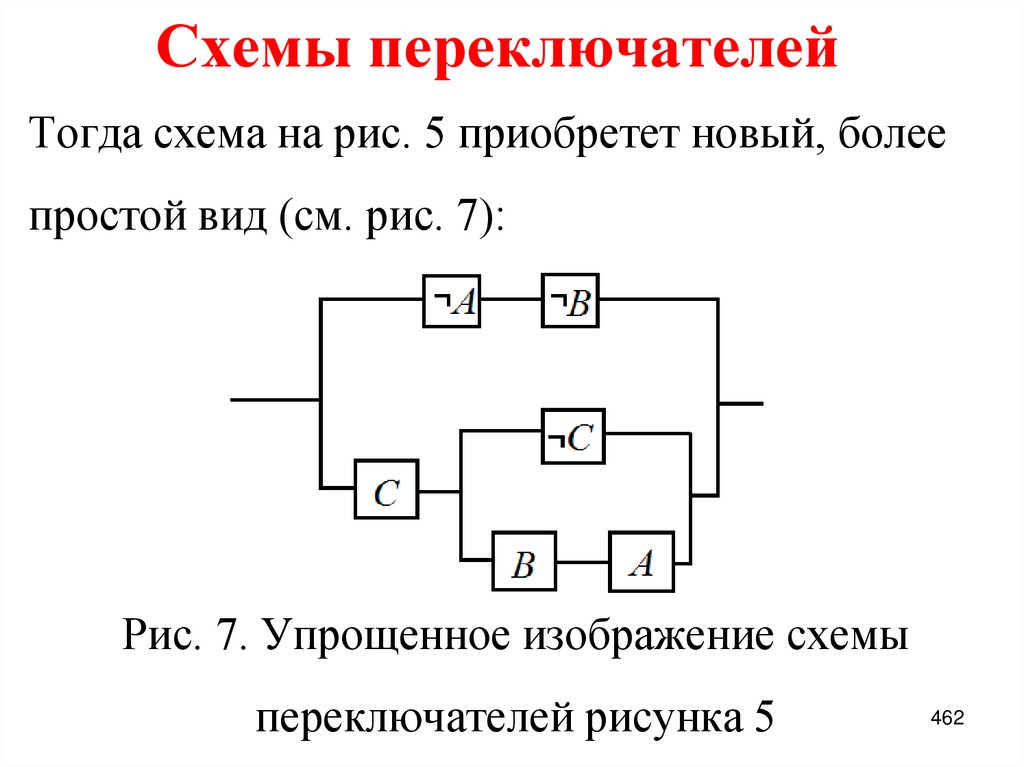


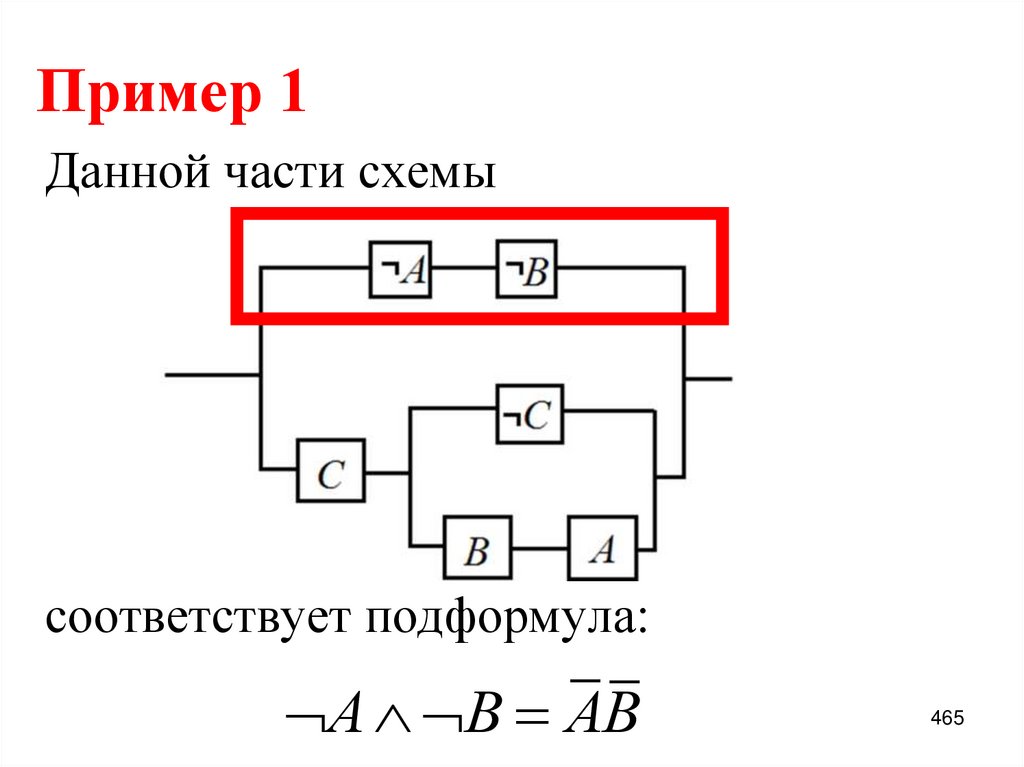
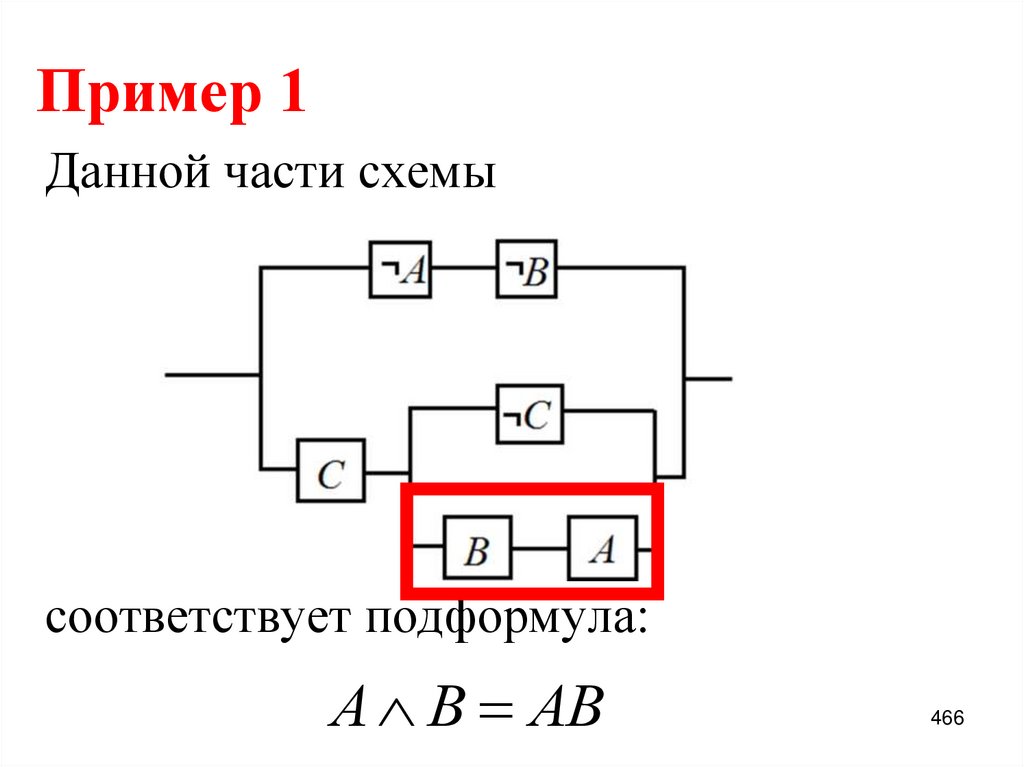
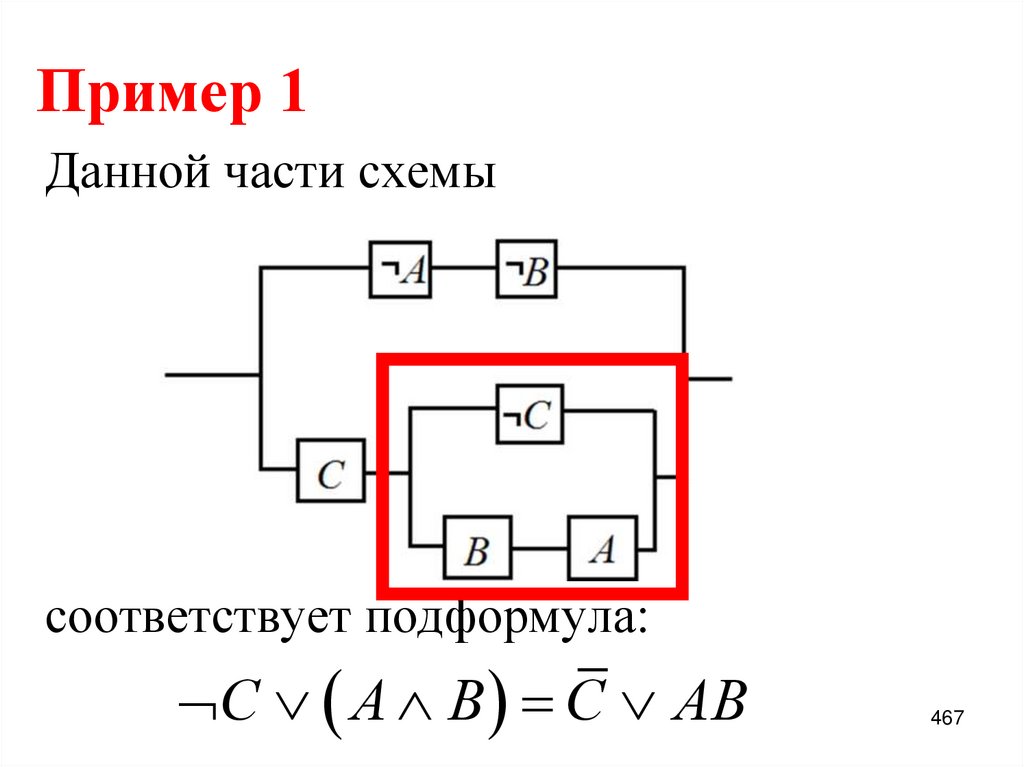
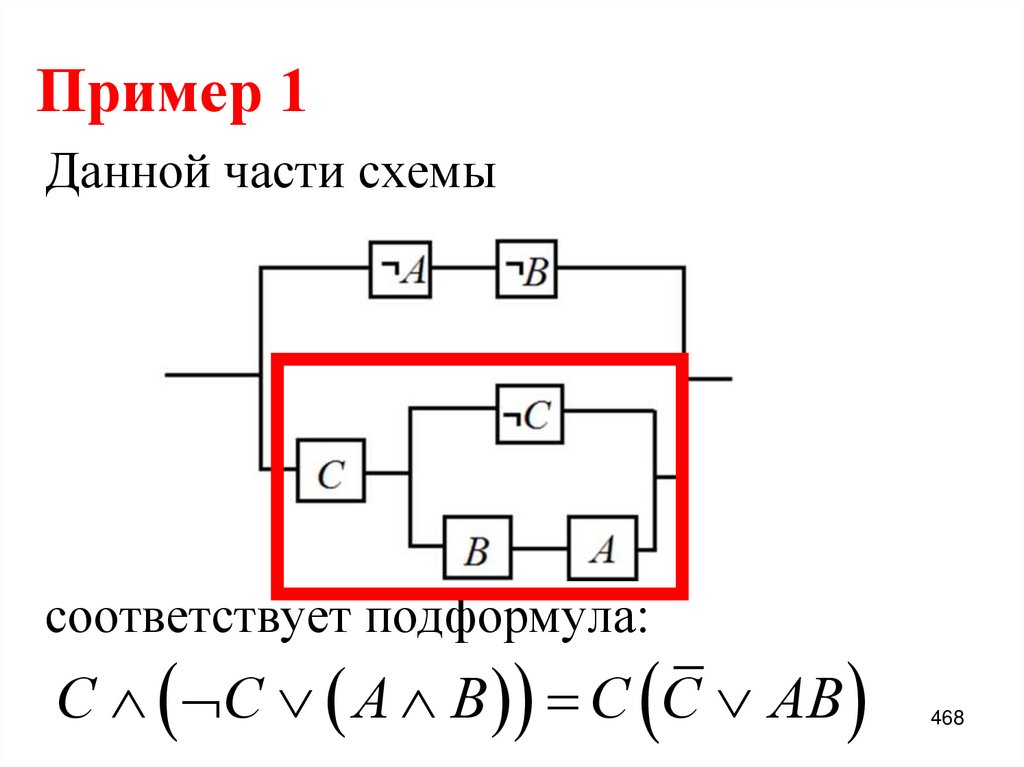
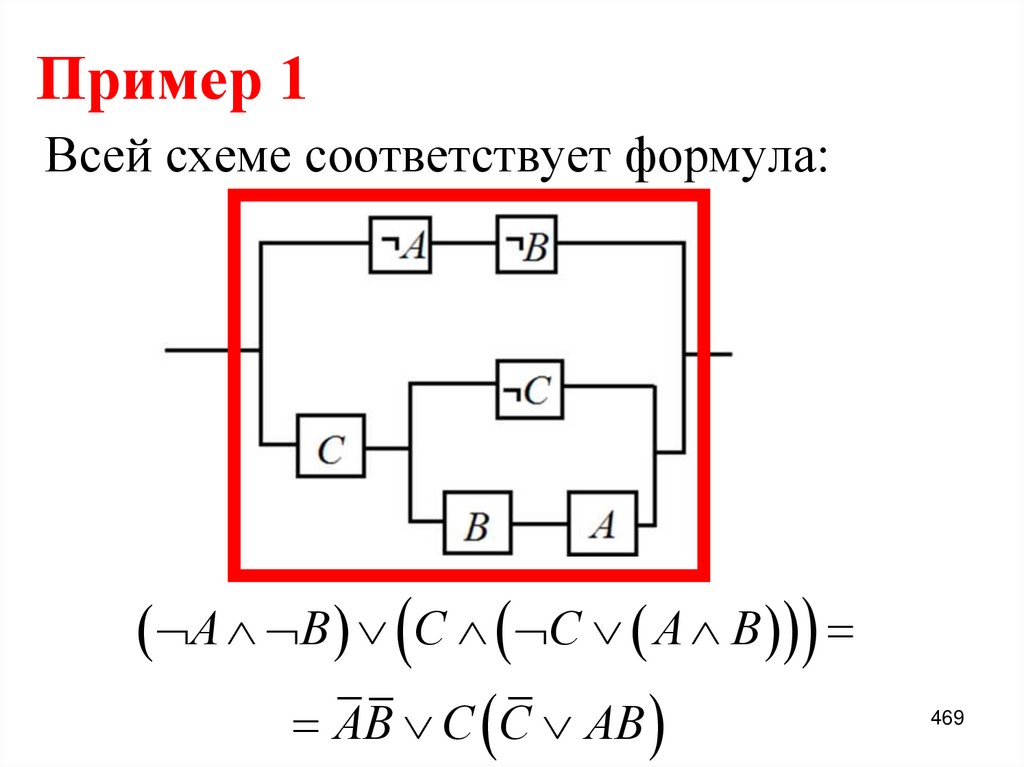

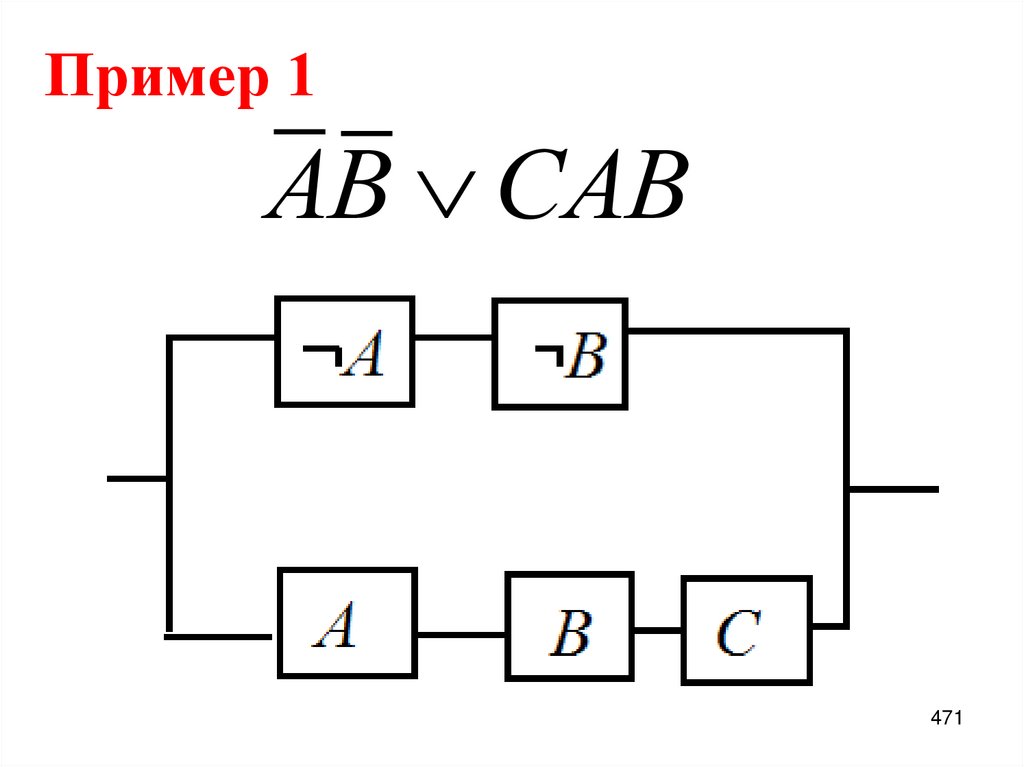


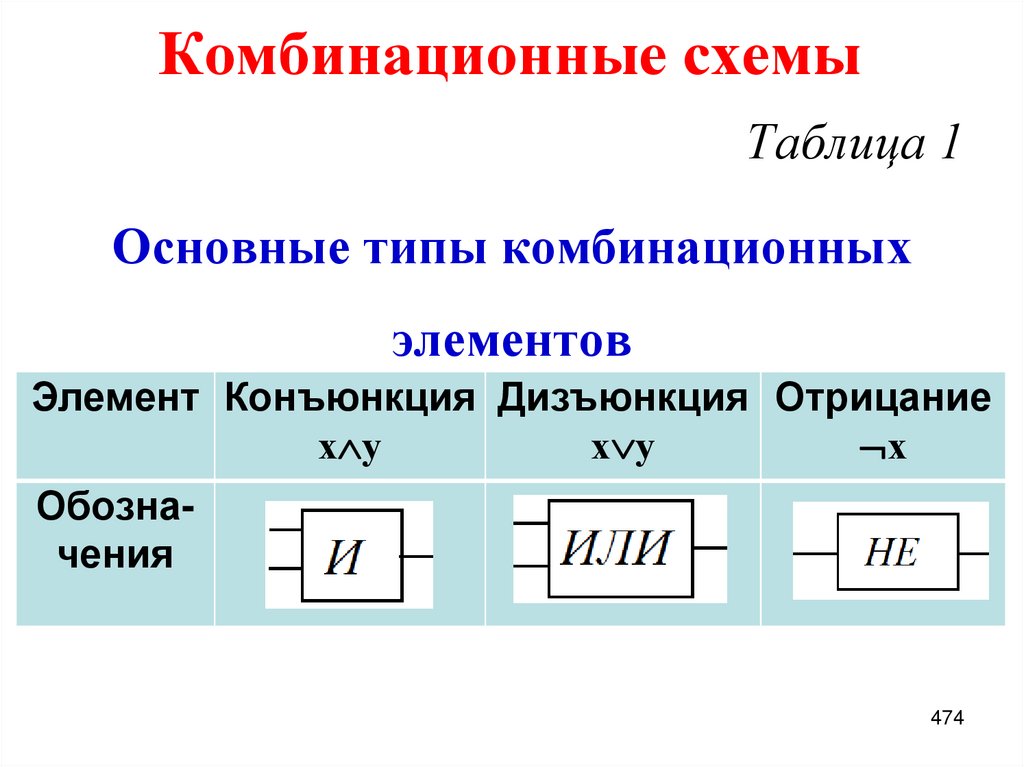


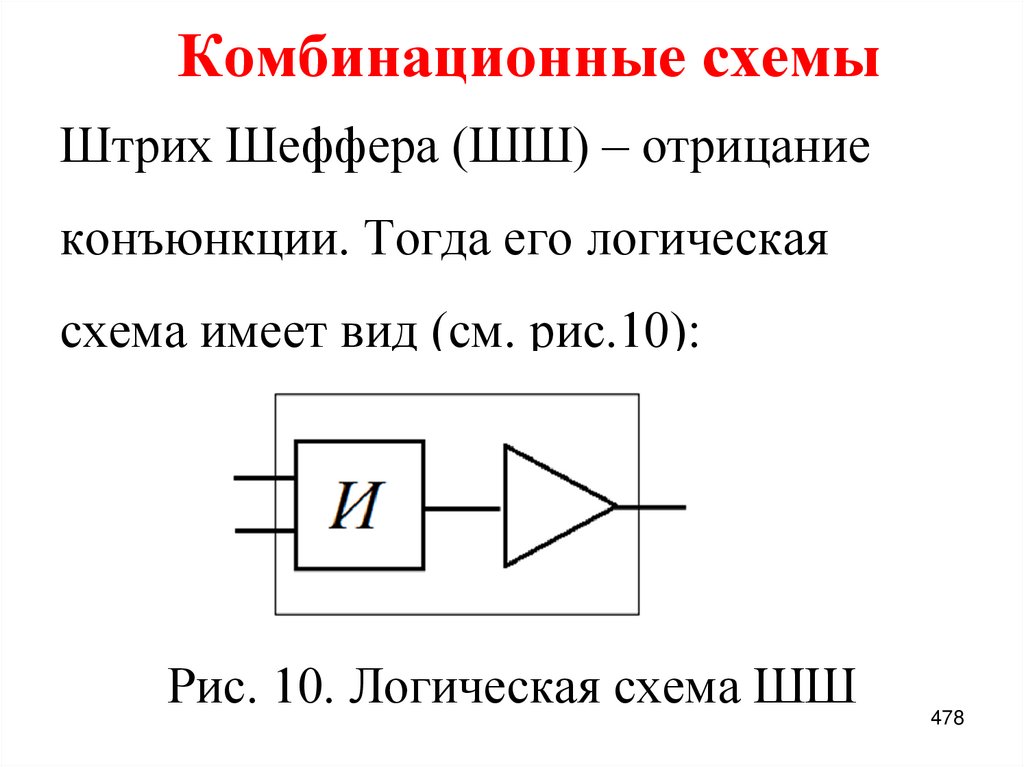
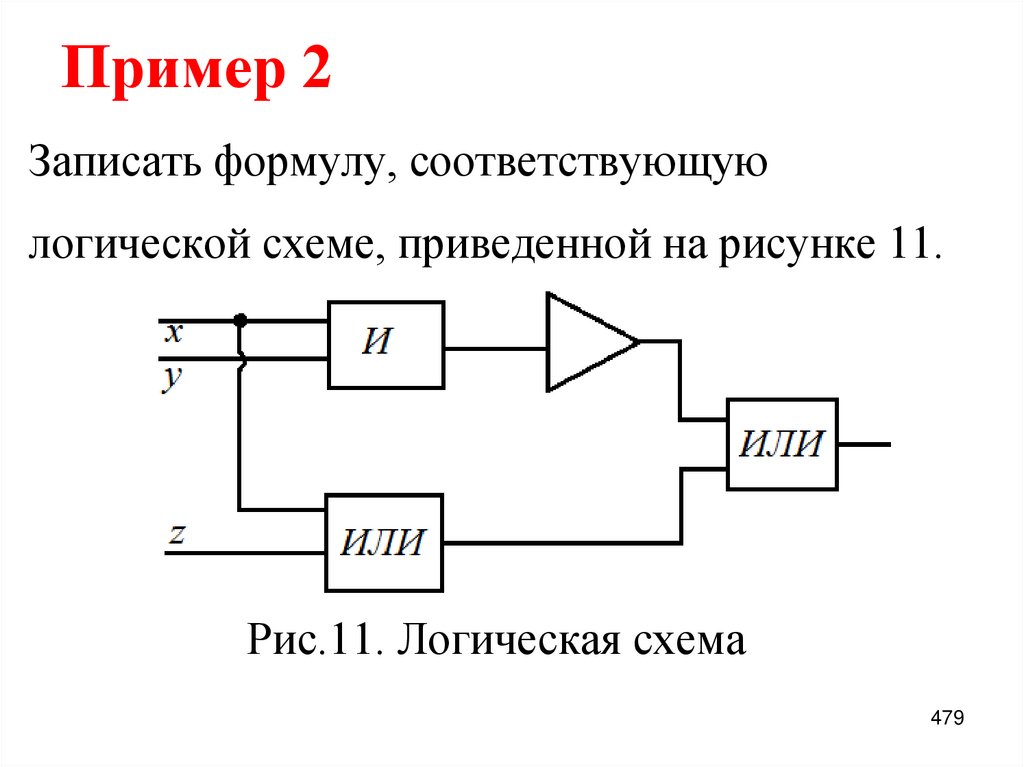
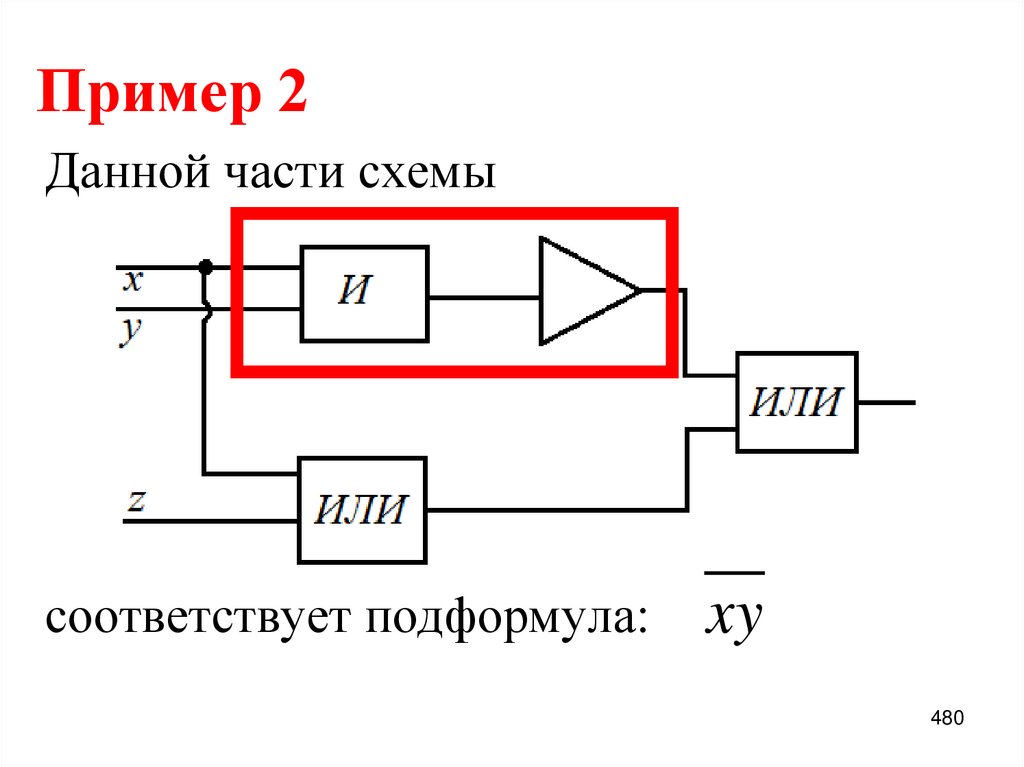
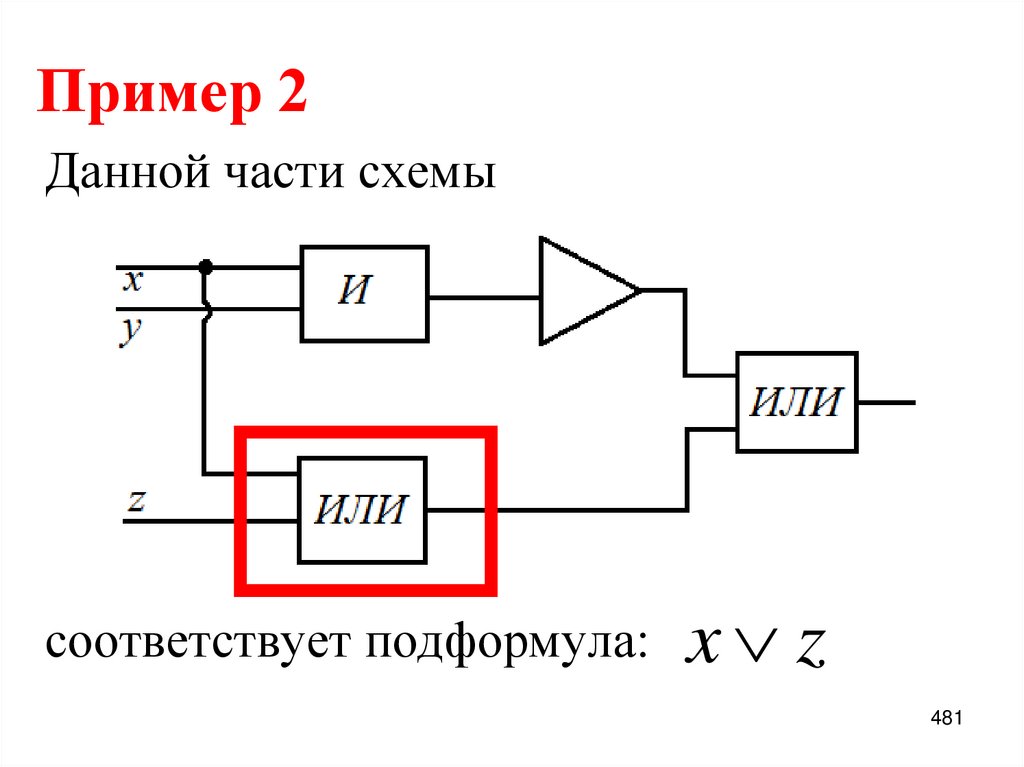
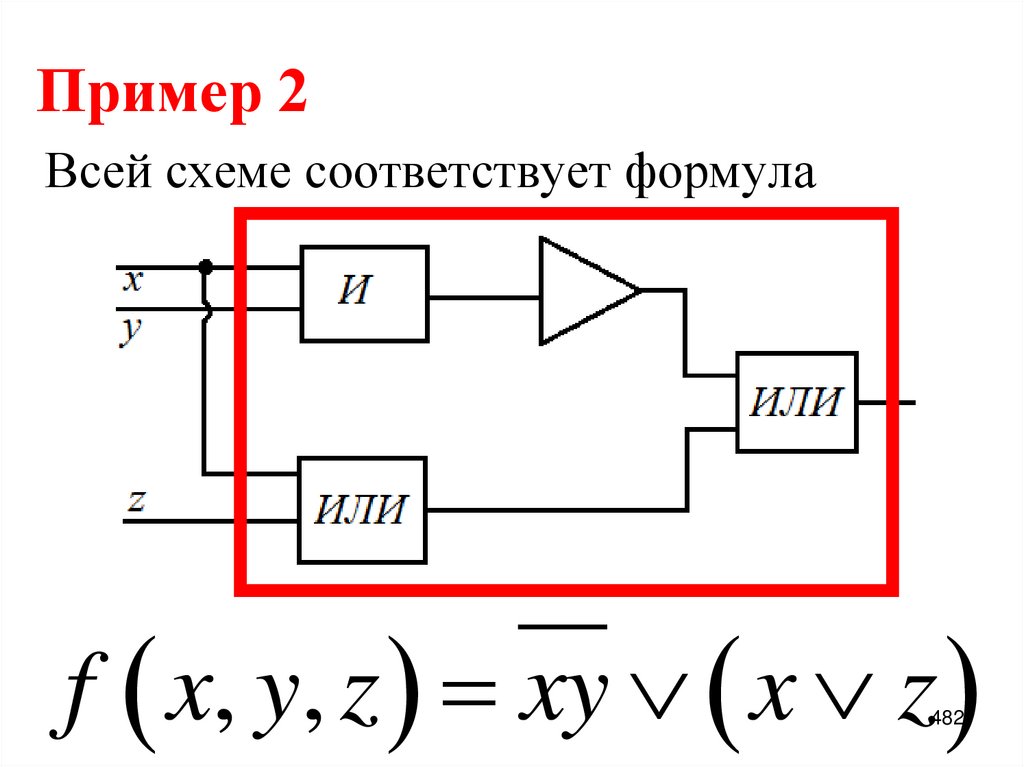
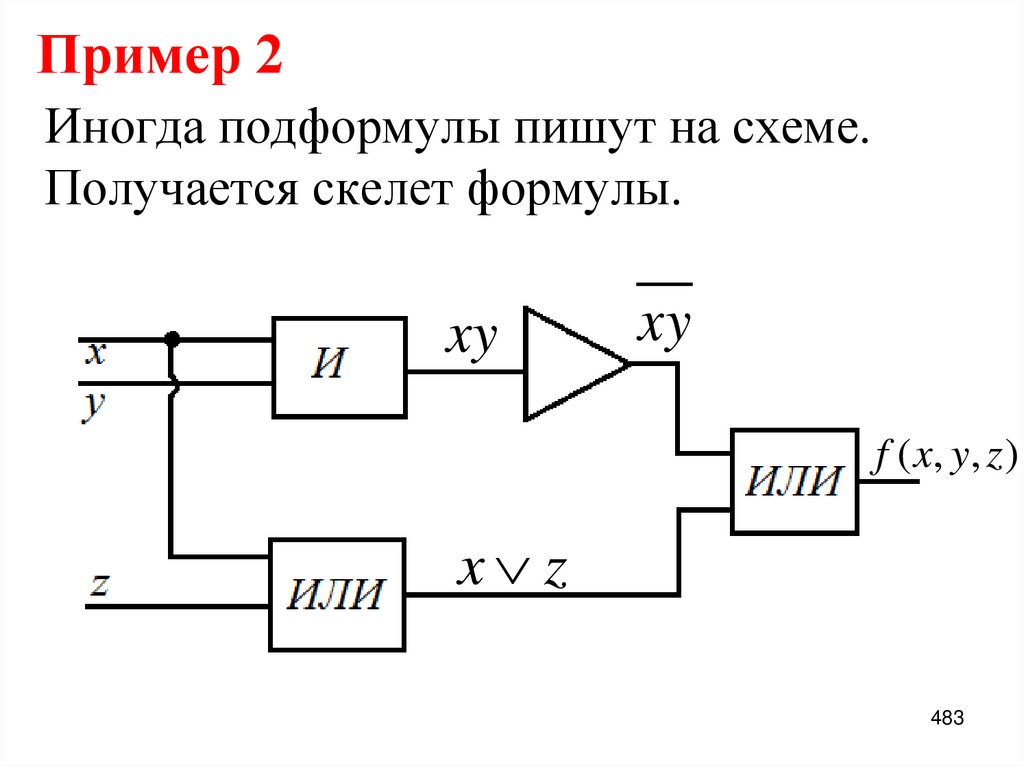


 mathematics
mathematics








