Similar presentations:
Приложения двойного интеграла. Вычисление площади плоской фигуры. Вычисление объема тела. (Семинар 30)
1. Семинар 30
Приложения двойного интеграла.Вычисление площади плоской
фигуры. Вычисление объема тела
2.
Площадь плоской фигуры, ограниченной областью D, находится по формулеS
dxdy
D
Если область D определена, например, неравенствами a x b, 1 ( x) y 2 ( x)
то S
b
2 ( x)
a
1 ( x)
dxdy dx dy
D
Если область D в полярных координатах определена
неравенствами
( )
, 1 ( ) 2 ( ) , то S d d d d
2
D
1 ( )
Объем цилиндрического тела, ограниченного сверху непрерывной
поверхностью z=f(x,y), снизу плоскостью z=0 и сбоку прямой
цилиндрической поверхностью, вырезающей на плоскости OXY область D.
вычисляется по формуле: V f ( x, y)dxdy
D
3.
Примеры с решениями2
1.Вычислить площадь фигуры, ограниченной линиями x 4 y y , x y 6
Решение. Найдем координаты точек пересечения заданных линий, решая
систему уравнений x 4 y y 2 , x y 6. В результате получим A(4;2), B(3;3).
3
Таким образом, S dxdy dy
D
2
4y y2
3
dx x
6 y
4y y
6 y
2
3
5
1
1
dy ( y 2 5 y 6)dy y 2 y 2 6 y
2
3
2 6
2
3
2
2. Найти площадь, ограниченную лемнискатой ( x 2 y 2 ) 2 2a 2 xy
Решение. Полагая x cos , y sin , преобразуем уравнение кривой к
полярным координатам.
2
2
В результате получим а sin 2 . Очевидно, что изменению угла от 0
до соответствует четверть искомой площади. Следовательно,
4
/4
S 4 d d 4 d
D
0
a sin 2
/4
2
d
2
0
0
a sin 2
0
/4
/4
d 2a 2 sin 2 d a 2 cos 2
0
0
a2
4.
3. Найти объем тела, ограниченного поверхностями y 1 x , z 3x, y 5, z 0и расположенного в первом октанте.
Решение. Тело, объем которого надо вычислить, ограничено сверху
плоскостью z=3x, сбоку – параболическим цилиндром y 1 x 2 и
плоскостью y=5.
Следовательно, это – цилиндрическое тело. Область D ограничена
2
y
1
x
параболой
и прямыми y=5,x=0. Таким образом, имеем
2
5
2
1
V 3xdxdy 3 xdx dy 3 x y dx 3 (4 x x 2 )dx 3 2 x 2 x 4 12
4 0
D
0
0
0
1 x 2
1 x 2
2
5
2
2
4. Вычислить объем тела, ограниченного цилиндрическими поверхностями
x 2 и плоскостью z=0
2
z 4 y ,y
2
5.
zy
(-2,2)
y
(2,2)
x2
y
2
X
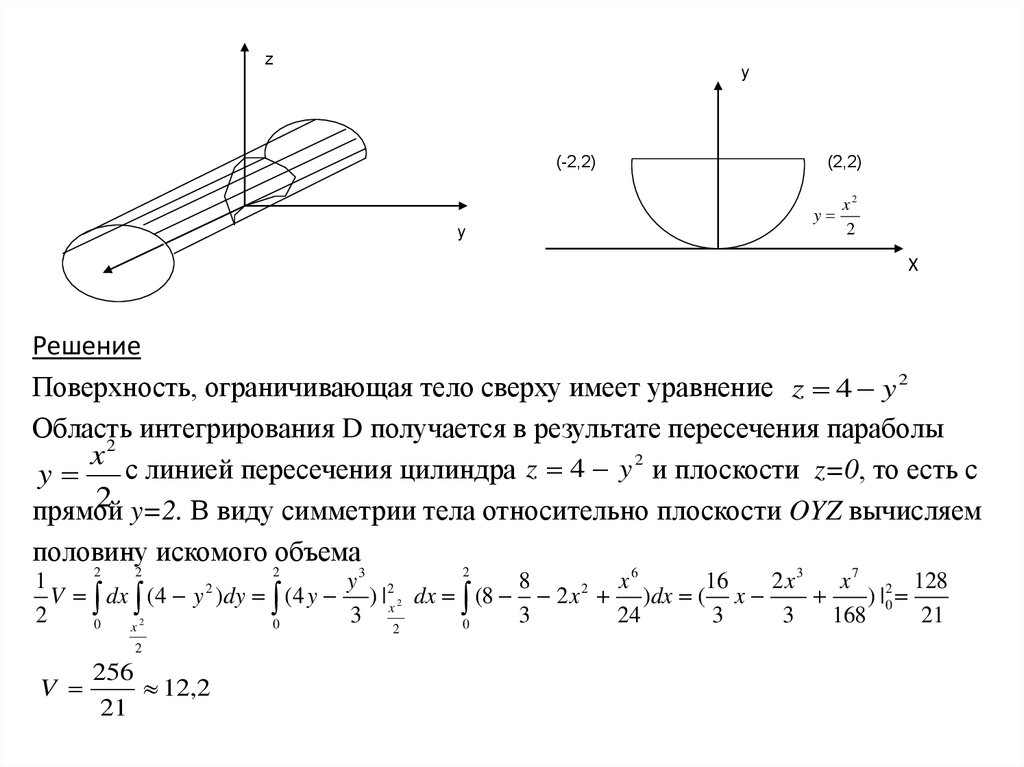
Решение
Поверхность, ограничивающая тело сверху имеет уравнение z 4 y 2
Область
интегрирования D получается в результате пересечения параболы
2
x с линией пересечения цилиндра z 4 y 2 и плоскости z=0, то есть с
y
2 y=2. В виду симметрии тела относительно плоскости OYZ вычисляем
прямой
половину искомого объема
2
2
2
2
1
y3 2
8
x6
16
2x3
x 7 2 128
2
2
V dx (4 y )dy (4 y ) | x 2 dx (8 2 x )dx ( x
) |0
2
3 2
3
24
3
3
168
21
0
0
0
x2
2
V
256
12,2
21
6.
4. Вычислить объем тела, ограниченного поверхностью z 1 4 x y иплоскостью OXY.
Заданное тело – сегмент эллиптического параболоида, расположенного над
плоскостью OXY. Параболоид пересекается с плоскостью OXY по эллипсу .
Следовательно, необходимо вычислить объем тела, имеющего своим
основанием внутреннюю часть указанного эллипса и ограниченного
параболоидом. В силу симметрии относительно плоскостей OXZ и OYZ
можно вычислить объем четвертой его части, заключенной в первом
2
2
октанте. Область интегрирования 4 x y 1, x 9, y 0
2
Интегрируем сначала по у, затем по х
1
1
2
1
V dx
4
0
V
1 4 x
4
2
22
2 1
1 3
2 2
4
(
1
4
x
y
)
dy
(
1
4
x
)
dx
{
2
x
sin
t
}
cos
t
dt
0
3 0
3 2 0
3 16
16
2
3
2
2
7.
Примеры для самостоятельного решения1. Вычислить площадь, ограниченную линиями
2
2
2
2
2
a) x y 2 y, x y 0; b) y 2 x, y 4 x 4; c) y 4 x x , y 2 x (вне параболы)
d) 3 y 2 25x,5x 2 9 y; e)y 2 2 y 3x 1 0,3x 3 y 7 0; f) (2 cos ), 2
(вне кардиоиды); g) 2(1 cos ), 2 cos ;
2. Вычислить объем тела, ограниченного поверхностями:
a) x 2 y 2 8, x 0, y 0, z 0, x y z 4
b) x 2 y 2 , y 0, z 0, x 2 y z 4
c) x 2 4 y 2 z 1, z 0
d) z x 2 y 2 , y x 2 , y 1, z 0
e) z 4 x 2 ,2 x y 4, x 0, y 0, z 0






 mathematics
mathematics








