Similar presentations:
Двойной интеграл. Основные понятия
1.
§29. Двойной интегралп.1. Определение.
Пусть
D — замкнутая область плоскости Oxy;
z f ( x, y ) — непрерывная функция,
заданная в D.
y
Разобьем область D:
n
i i 1
{D } :
Di D j , i j;
D
O
n
x i 1
Di D.
2.
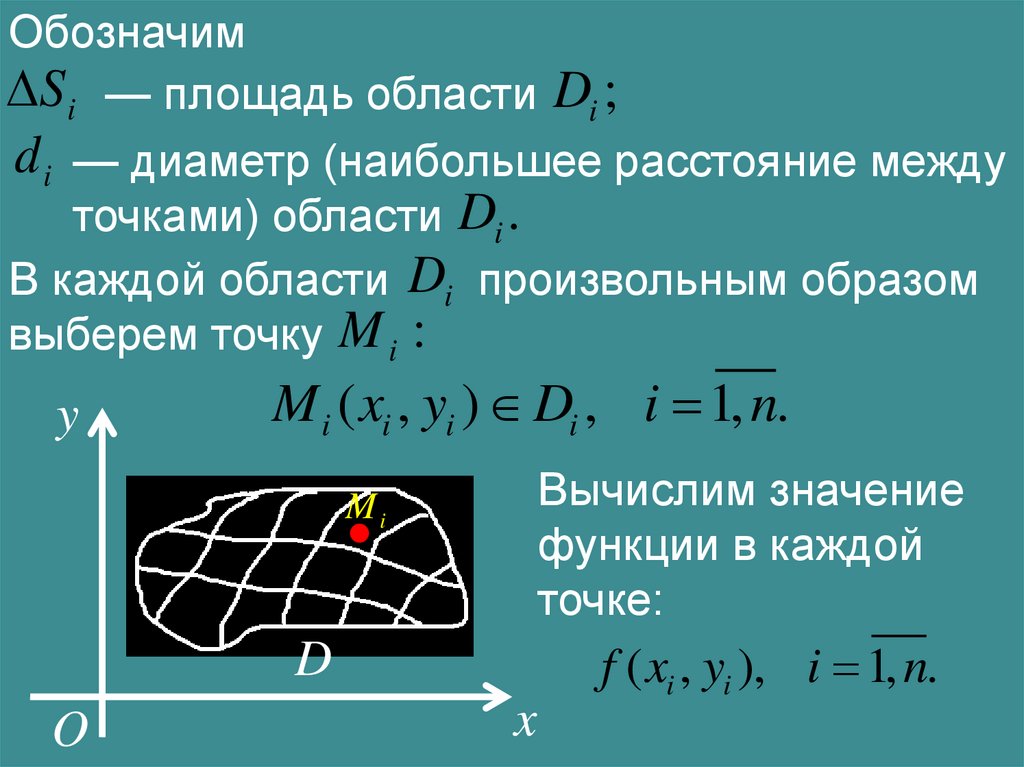
ОбозначимS i — площадь области Di ;
d i — диаметр (наибольшее расстояние между
точками) области Di .
В каждой области Di произвольным образом
выберем точку M i :
y
M i ( xi , yi ) Di , i 1, n.
Вычислим значение
функции в каждой
точке:
Mi
D
O
x
f ( xi , yi ), i 1, n.
3.
Составим интегральную сумму:f ( x1 , y1 ) S1 f ( x2 , y2 ) S 2 ... f ( xn , yn ) S n
n
f ( xi , yi ) Si .
i 1
Пусть
max di 0
при n .
4.
Если существует пределn
lim f ( xi , yi ) Si ,
n
i 1
причем этот предел не зависит ни от способа
разбиения области D, ни от выбора точек M i ,
то он называется двойным интегралом от
функции z f ( x, y ) по области D.
n
f ( x, y)dxdy lim f ( x , y ) S .
D
n
i 1
i
i
i
D — область интегрирования;
z f ( x, y ) — интегрируемая в D функция.
5.
Теорема 1. (Достаточное условиеинтегрируемости.)
Если функция z f ( x, y ) непрерывна в
замкнутой области D, то она интегрируема в
этой области.
Замечание 1.
Достаточное условие не является
необходимым.
Замечание 2.
Если двойной интеграл существует, то область
D можно разбивать прямыми, параллельными
осям координат.
6.
Геометрический смысл двойного интегралаПусть
f ( x, y ) 0, ( x, y ) D.
Рассмотрим тело ограниченное поверхностью
z f ( x, y ) 0,
областью D и цилиндрической поверхностью с
образующими, параллельными оси Oz, и
границей области D в качестве
направляющей.
Определим и найдем его объем.
7.
zz f ( x, y )
y
D
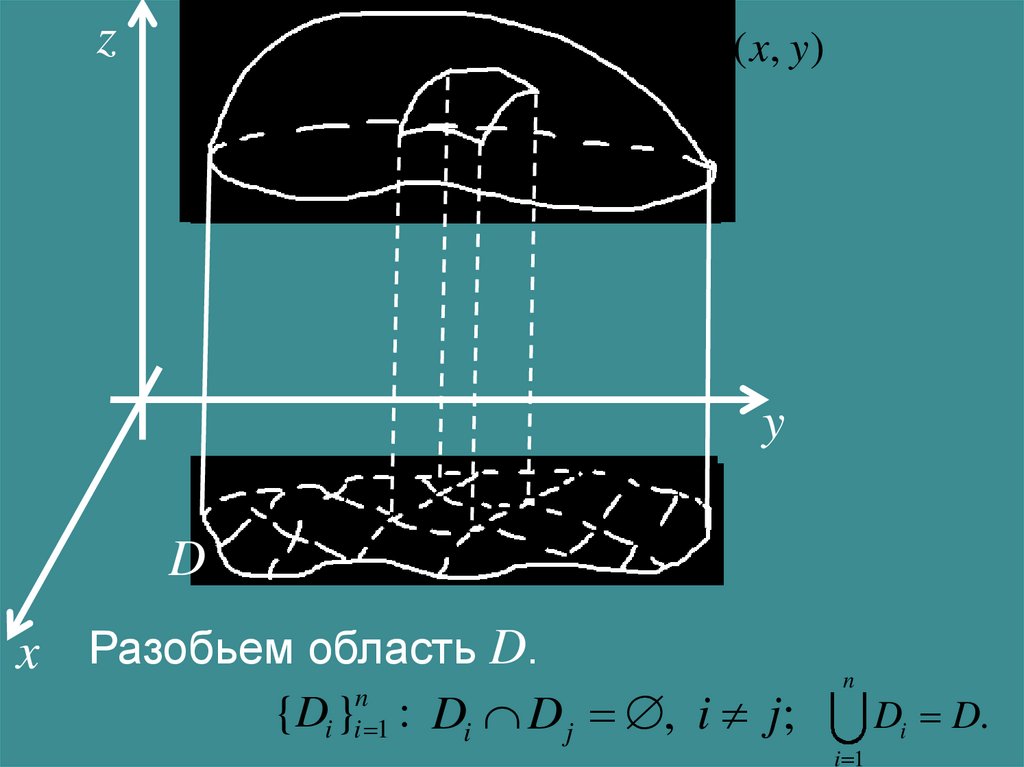
x Разобьем область D.
{D } : Di D j , i j;
n
i i 1
n
i 1
Di D.
8.
Все тело разобьется на цилиндрическиестолбики при этом
n
V Vi .
i 1
Пусть
M i ( xi , yi ) Di , i 1, n.
9.
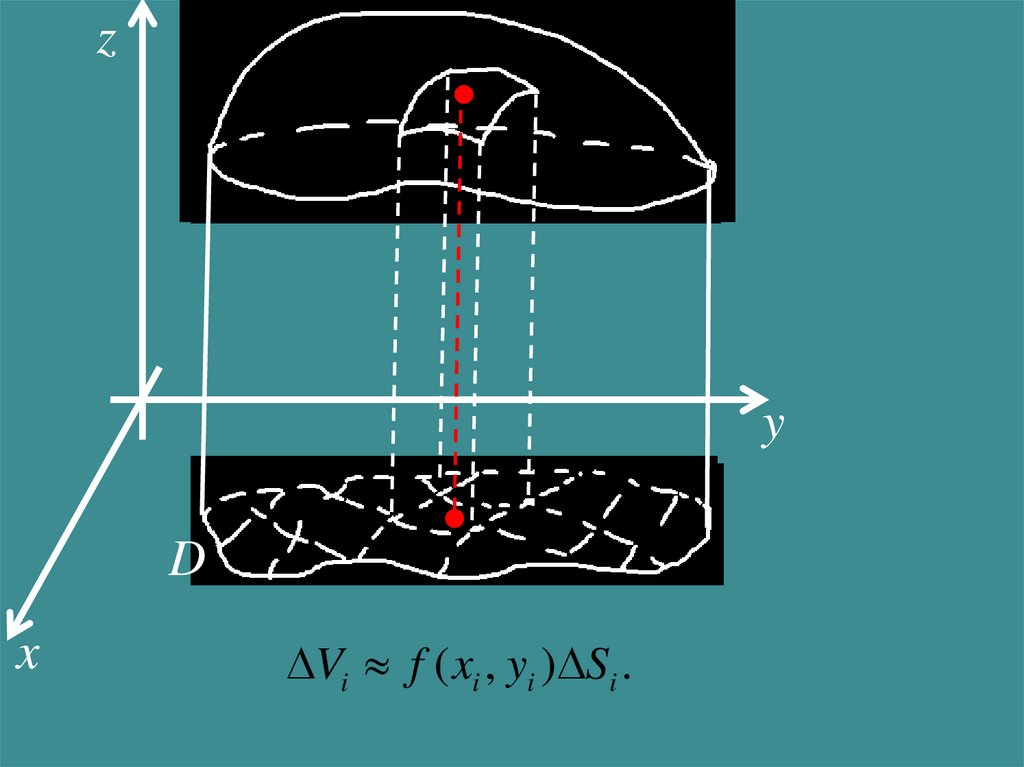
zf ( xi , yi )
y
D
x
Vi f ( xi , yi ) Si .
10.
Поэтомуn
V f ( xi , yi ) Si .
i 1
С уменьшением S i точность приближения
тела ступенчатой фигурой увеличивается.
За точное значение объема V принимается
предел суммы, когда n неограниченно
возрастает так, что Si 0.
n
V lim f ( xi , yi ) Si .
n
i 1
Учитывая определение двойного интеграла
V f ( x, y )dxdy.
D
11.
Величина двойного интеграла отнеотрицательной функции равна объему
цилиндрического тела.
12.
п.2. Свойства двойного интеграла.1.
k f ( x, y)dxdy k f ( x, y)dxdy, k const.
D
D
2.
( f ( x, y) g ( x, y))dxdy f ( x, y)dxdy g ( x, y)dxdy.
D
3.
D
D
f ( x, y)dxdy f ( x, y)dxdy f ( x, y)dxdy,
D
D1
D1 D2 , D1 D2 D.
D2
D1
D2
D
13.
4. f ( x, y ) 0, ( x, y ) Df ( x, y)dxdy 0.
D
5. f ( x) g ( x), ( x, y ) D
f ( x, y)dxdy g ( x, y)dxdy.
D
6.
D
dxdy S .
D
D
14.
7. m f ( x, y ) M , ( x, y ) DmS D f ( x, y)dxdy MS D .
D
8.
Теорема 1. (О среднем значении двойного
интеграла)
Пусть
функция z f ( x, y ) непрерывна в замкнутой
области D.
Тогда
существует точка ( x0 , y0 ) D такая, что
f
(
x
,
y
)
dxdy
f
(
x
,
y
)
S
.
0
0
D
D
15.
п.3. Вычисление двойного интеграла.Пусть
Тогда
f ( x, y ) 0, ( x, y ) D.
f ( x, y)dxdy V .
D
Вычислим объем тела, используя свойства
определенного интеграла.
(1)
16.
1) Пусть область D ограничена линиямиx a, x b, y 1 ( x), y 2 ( x)
причем
y
1 ( x) 2 ( x), x [a, b].
y 2 ( x)
В этом случае
D область D
называется
правильной в
A
y 1 ( x)
направлении оси
b x Oy.
B
O a
Проведем прямую, перпендикулярную оси Ox.
Получим точки: A( x, ( x)), B ( x, ( x)).
1
2
17.
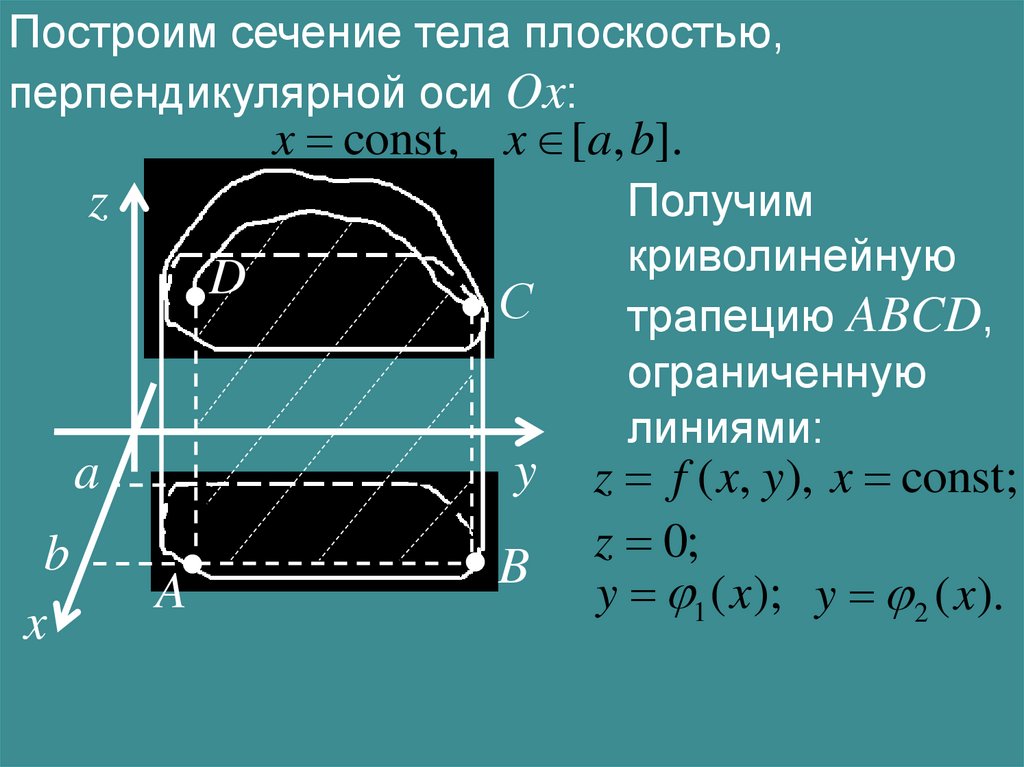
Построим сечение тела плоскостью,перпендикулярной оси Ox:
x const, x [a, b].
z
D
y
a
b
x
С
A
B
Получим
криволинейную
трапецию ABCD,
ограниченную
линиями:
z f ( x, y), x const;
z 0;
y 1 ( x ); y 2 ( x).
18.
Учитывая свойства определенного интеграла(п.1 §24):
2 ( x )
S ABCD S ( x)
f ( x, y )dy.
1 ( x)
Тогда объем тела равен (п.3 §24):
2 ( x )
V S ( x)dx f ( x, y )dy dx.
a
a 1 ( x )
b
b
(2)
19.
Приравнивая полученные результаты(формулы (1) и (2)), получаем:
2 ( x )
D f ( x, y)dxdy a ( x) f ( x, y)dy dx
1
b
или
b
2 ( x )
a
1 ( x)
f ( x, y)dxdy dx f ( x, y)dy.
D
повторный интеграл
20.
2) Пусть область D ограничена линиямиy c, y d , x 1 ( y ), x 2 ( y )
причем
1 ( y ) 2 ( y ), y [c, d ].
Аналогичным образом можно получить:
d
2 ( y)
c
1( y)
f ( x, y)dxdy dy f ( x, y)dx.
D
21.
Замечание.Полученные формулы справедливы и без
ограничения
f ( x, y ) 0, ( x, y ) D.
22.
Пример. Вычислить( x 2 y)dxdy,
D
где
D:
y x 2 , y 0, x y 2 0.
Решение. Построим область D.
y
0 y 1;
y x 2 y.
1
D
1
2
x
23.
12 y
D
0
y
2 y
2 y
2 y
y
y
y
( x 2 y)dxdy dy ( x 2 y)dx.
( x 2 y)dx xdx 2 ydx
2 y
2 y
2 y
x2
xdx 2 y dx 2 xy
2
y
y
y
(2 y )
y
2
4y 2y 2y ;
2
2
2
3
2
24.
3(2 y ) 2
y
2
2
4
y
2
y
2
y
dy
0 2
2
1
1
5
3
2
2
( y 2)3
y
y
y
2
2 y 2 2 1, 45.
5
3
3
4
2 0
25.
D1 :y
0 y x2 ;
D
1 D
D2 :
D2
1
1
0 x 1;
x
2
1 x 2;
0 y 2 x.
( x 2 y)dxdy ( x 2 y)dxdy ( x 2 y)dxdy.
D
D1
D2
26.
1x2
0
0
( x 2 y)dxdy dx ( x 2 y)dy
D1
1
x
x
xy y dx ( x x )dx
0
4 5 0
0
0
1
2
x
2
1
4
3
5
4
1 1 9
.
4 5 20
27.
22 x
1
0
( x 2 y)dxdy dx ( x 2 y)dy
D2
2
xy y
2
1
2 x
0
2
dx (2 x x (2 x) )dx
2
2
1
2
2 x ( x 2)
8 1 1
x
4 1 1.
3
3 1
3 3 3
3
3
9
D ( x 2 y)dxdy 20 1 1, 45.









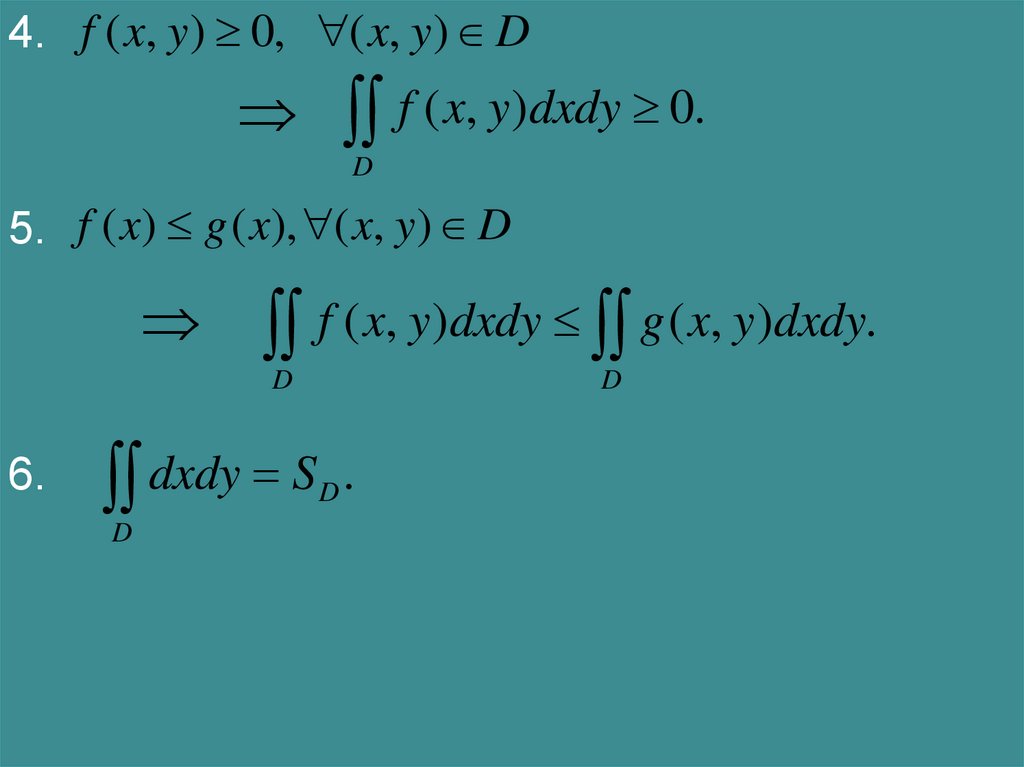








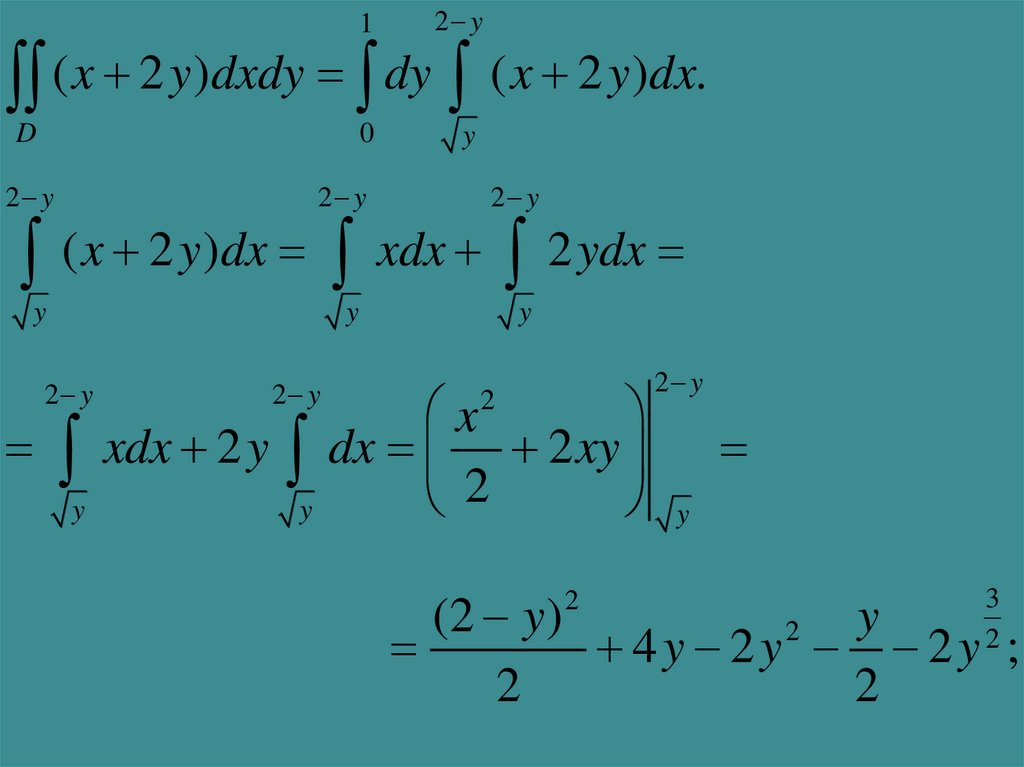
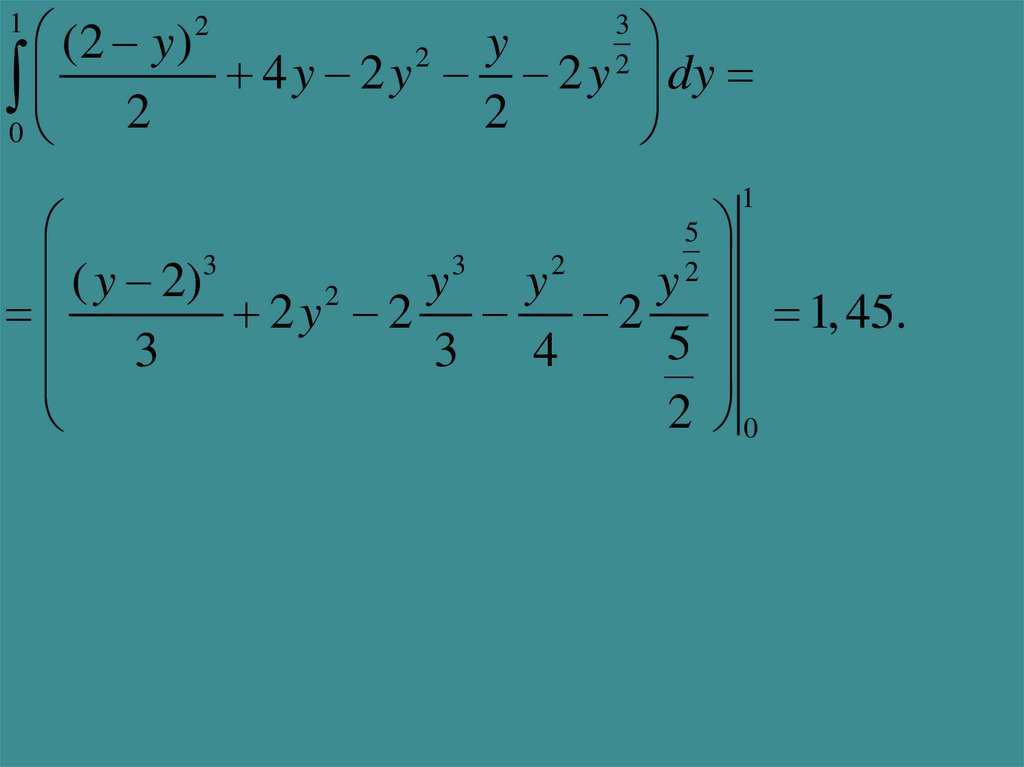
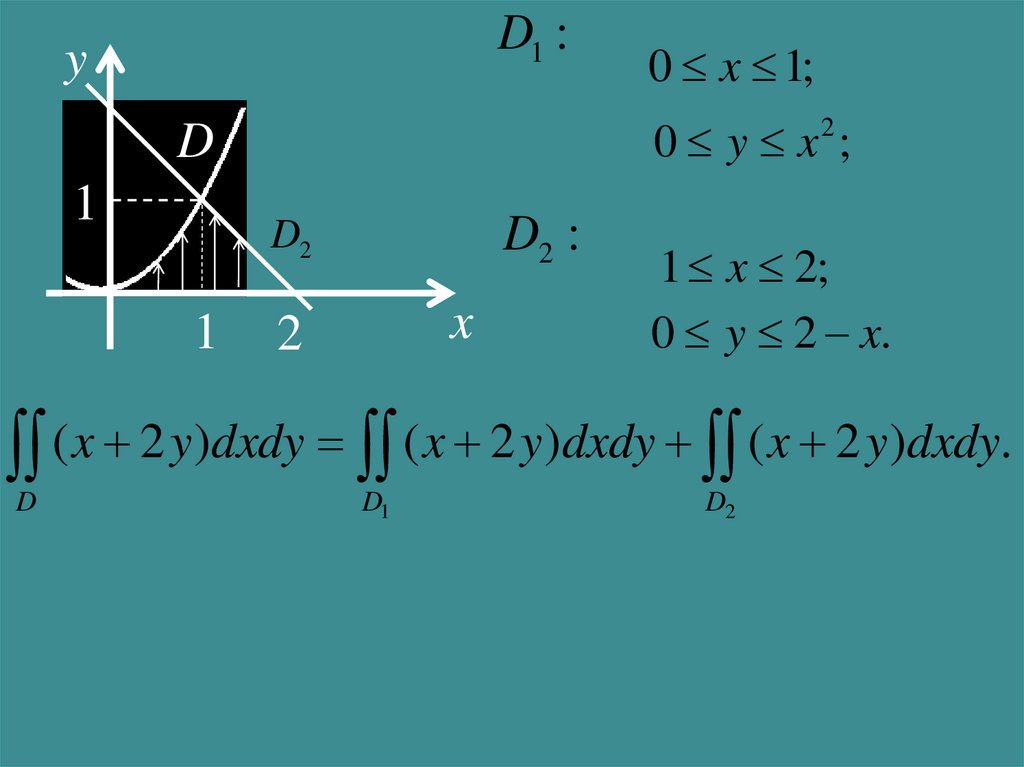
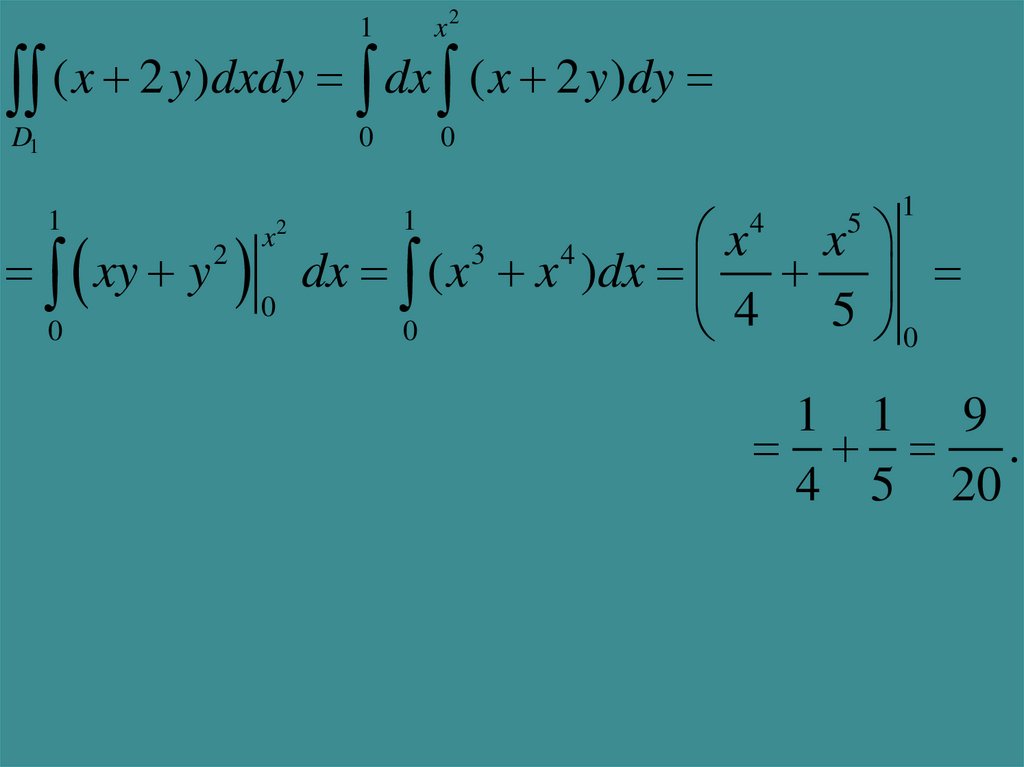
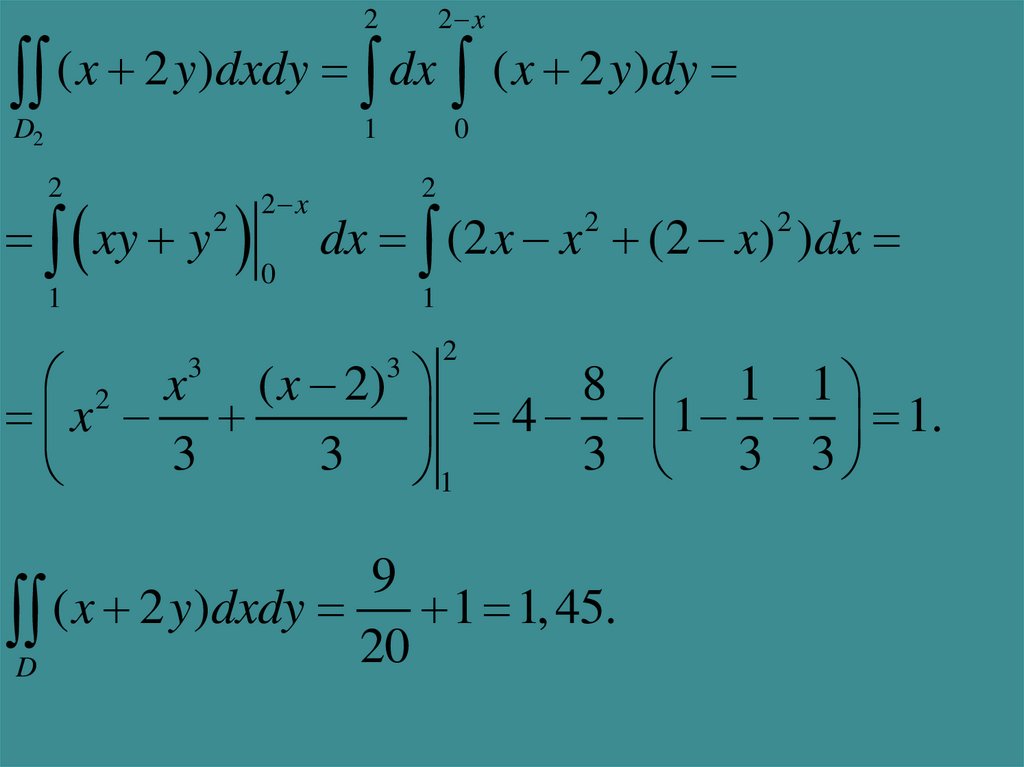
 mathematics
mathematics








