Similar presentations:
Двойные интегралы. Лекция №8
1. ДВОЙНОЙ ИНТЕГРАЛ: ОПРЕДЕЛЕНИЕ, ГЕОМЕТРИЧЕСКИЙ СМЫСЛ, ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ, СВОЙСТВА, ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ.
Лекция №82.
Двойные интегралыРассмотрим на плоскости некоторую замкнутую кривую, уравнение которой
f(x, y) = 0.
y
0
x
Совокупность всех точек, лежащих внутри кривой и на самой кривой назовем
замкнутой областью . Если выбрать точки области без учета точек, лежащих на кривой,
область будет называется незамкнутой область .
С геометрической точки зрения - площадь фигуры, ограниченной контуром
3.
Определение 1. Сумма видаDk
( Pk , S k ) f ( P1) S 1 ... f ( P n) S n
называется двойной интегральной суммой
Рис. 1
для функции z f (P )
D R
Число d max S k
k 1,n
2
называется
диаметром разбиения области D
.
в области
4.
Определение 2. Если существует конечный пределдвойных интегральных сумм
( Pk , S k ) f ( P1) S1 ... f ( Pn) S n
при стремлении диаметра разбиения к нулю и этот
предел не зависит ни от способа разбиения области D
на части,
ни от выбора в них промежуточных точек Р1 ,..., Рп
то этот предел называется
двойным интегралом от функции по области
D R 2 , а сама функция называется
интегрируемой в области D .
Для двойного интеграла используется f ( x; y )dxdy
D
следующее обозначение:
5. Достаточное условие существования двойного интеграла
Теорема. Если функция z f ( x, y )непрерывна в
2
замкнутой области D R , то она интегрируема на этой
области и существует ее двойной интеграл по области D .
f ( x; y)dxdy lim P , S
D
d 0
k
k
6.
Следовательно, двойная интегральная сумма( Pk , S k ) f ( P1) S 1 ... f ( P n) S n
,
как сумма объемов указанных элементарных цилиндров,
равна объему
V n некоторого ступенчатого
цилиндрического тела.
Тогда предел
f ( x; y)dxdy lim P , S
D
d 0
k
совпадает с объемом цилиндрической области.
k
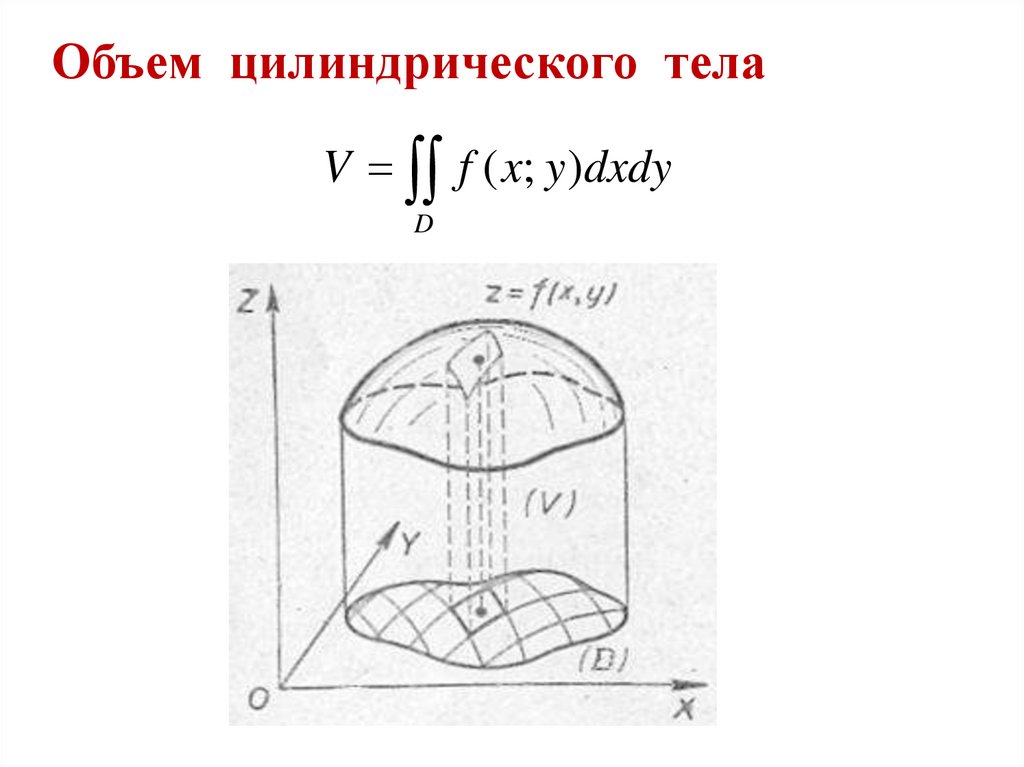
7. Объем цилиндрического тела
V f ( x; y )dxdyD
8.
Замечание 1. Если непрерывная функция z f (P )не сохраняет знак в области D ,
то двойной интеграл
f ( x; y )dxdy
D
с геометрической точки зрения интерпретируют
как алгебраическую сумму объемов, учитываемых
со знаком + или в зависимости от того,
лежит ли поверхность
выше или ниже,
z f ( x, y )
соответственно, плоскости
.
Oxy
9.
Условия существования двойного интегралаСформулируем достаточные условия существования двойного
интеграла.
Теорема. Если функция f(x, y) непрерывна в замкнутой области , то
двойной интеграл f ( x, y )d существует.
Теорема. Если функция f(x, y) ограничена в замкнутой области и
непрерывна в ней всюду, кроме конечного числа кусочно – гладких линий, то
двойной интеграл f ( x, y )d существует.
10.
Свойства двойного интеграла1)
f1 ( x, y) f 2 ( x, y) f3 ( x, y) dydx f1 ( x, y )dydx f 2 ( x, y )dydx f 3 ( x, y )dydx
2)
kf ( x, y)dydx k f ( x, y )dydx .
3) Если = 1 + 2, то
f ( x, y)dydx f ( x, y)dydx f ( x, y)dydx .
1
2
4) Теорема о среднем. Двойной интеграл от функции f(x, y) равен
произведению значения этой функции в некоторой точке области
интегрирования на площадь области интегрирования.
f ( x, y)dydx f ( x , y ) S .
0
0
5) Если f(x, y) 0 в области , то
f ( x, y)dydx 0 .
6) Если f1(x, y) f2(x, y), то
f ( x, y)dydx f ( x, y)dydx .
1
7)
f ( x, y)dydx
f ( x, y ) dydx .
2
11. Геометрический смысл двойного интеграла
Свойство 5.dxdy S
D
, где S D площадь D.
D
Свойство 6.
Объем цилиндрического
тела
V f ( x; y )dxdy
D
12. Теорема о среднем значении
Теорема. Если функция z f ( x, y )непрерывна в замкнутой области D R 2,
тогда найдется хотя бы одна точка,
в которой выполняется следующее равенство: P0 ( x0 , y0 ) D,
f ( x; y)dxdy f ( P ) S
0
D
D
.
13.
Доказательство: По свойству непрерывной функции в замкнутой области,функция z f ( x; y) в области D достигает своих наименьшего (m) и
наибольшего (M) значений. Значит:
m f(x;y) M для ( x; y ) D .
Тогда для всех ( xi ; yi ) D можно записать
m f ( xi ; yi ) M ,
где i 1; n.
Умножая последнее неравенство на Si 0 , получим:
m Si f ( xi ; yi ) Si M Si .
Суммируем все n неравенств ( i 1; n ):
n
n
n
i 1
i 1
i 1
m Si f ( xi ; yi ) Si M Si .
14.
Вынесем m и М за знаки сумм (как постоянные величины) и перейдёмк пределам при n и max Si 0 (стягиваясь в точку):
m lim
n
Si
n i 1
max Si 0
n
lim f ( xi ; yi ) S i M lim
n i 1
max Si 0
n
Si .
n i 1
max Si 0
Ссылаемся на определение двойного интеграла и получаем:
m ds f ( x; y )ds M ds
D
D
D
m S D f ( x; y )ds M S D .
D
Разделим последнее неравенство на S D , где S D 0 . Тогда
m
f ( x; y )ds
D
SD
M.
По свойству непрерывной функции в замкнутой области, функция
z f ( x; y) в области D принимает все промежуточные значения между
наименьшим (m) и наибольшим (М) значениями. Следовательно,
существует точка ( x0 ; y0 ) D , в которой:
f ( x; y)ds
f ( x0 ; y 0 ) D
, умножаем на S D f ( x; y )dS f ( x0 ; y0 ) S D
SD
D
Теорема доказана.
15.
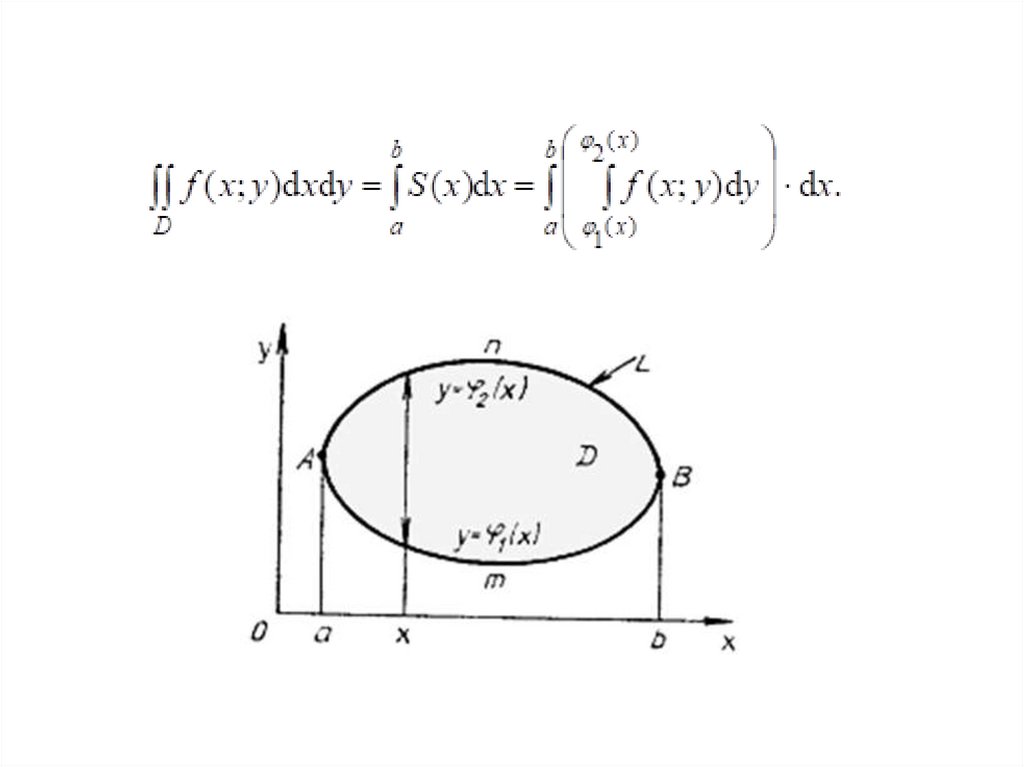
Вычисление двойного интеграла в декартовых координатахОпределение 1. Замкнутая область D называется правильной в направлении
оси 0y (или 0x), если любая прямая, проходящая через внутреннюю точку
области D и параллельная оси 0y (или 0x), пересекает границу области D
только в двух точках
(На рисунках: а – D правильная в направлении 0y; б – D правильная в
направлении 0x; в – D правильная в направлении 0x, но неправильная в
направлении 0y; г – D правильная в направлении 0y, но неправильная в
направлении 0x).
16.
17.
18.
Если f ( x; y) f1( x) f 2 ( y) и область D – прямоугольник: a x b , c y d , тодвойной интеграл от f1 ( x) f 2 ( y) по такой области D равен произведению
определённых интегралов:
b
d
a
c
f1 ( x) f 2 ( y)dxdy f1 ( x)dx f 2 ( y)dy
D
a x b
.
D :
c y d
19.
Пример 1. Вычислить повторный интеграл:1
2 x
x
2
0
2
1
2 2 x
y
xy
d
y
x
2 dx
0
x
0
x
2
1
4 4x x 2 x5
x 2
dx
x
dx x
2
2
2
0
dx
1
2 x
2
2
1
1
1
1
x3 x5
2x3
x4
x6
2
2
dx x
2 x 2 x
0
2
2
3
8
12
0
0
0
0
2 1 1 24 16 3 2 27 18 9 3
1
.
3 8 12
24
24
24 8
1
1
2 x
0
x2
3
8
Ответ: dx xydy .
20.
Пример 2. Расставить пределы интегрирования в различном порядке:f ( x; y )dxdy , если область D ограничена линиями: y = 2x; y = x; x = 1.
D
1) Чертёж области D
2) Область D правильная в направлении оси 0y для x [0;1] .
Нижняя граница D: y = x; верхняя граница D: y = 2x. Поэтому:
1
2x
0
x
f ( x; y)dxdy dx f ( x; y)dy
D
21.
3) Область D правильная в направлении оси 0х, но для y 0;1 левая границаD: x y ; правая граница D: x y , а для y 1;2 левая граница D: x y ;
2
2
правая граница D: x 1 . Поэтому область D в этом случае разбиваем на две
области прямой y=1: D1 y 0;1 и D2 y 1;2 , интеграл по области D
представляем суммой по областям D1 и D2 :
1
y
2
1
0
y
2
1
y
2
f ( x; y)dxdy dy f ( x; y)dx dy f ( x; y)dx
D
Ответ:
1
2x
1
y
2
1
0
x
0
y
2
1
y
2
f ( x; y)dxdy dx f ( x; y)dy dy f ( x; y)dx dy f ( x; y)dx
D
22.
Пример 3. Изменить порядок интегрирования:1
1 x
0
1 x
dx f ( x; y)dy.
Чертёж области D: 0 x 1 , нижняя граница области D: y 1 x ,
верхняя граница y 1 x
23.
Чтобы изменить порядок интегрирования, надо внешний интегралвзять по y, а внутренний – по x. Область D в направлении оси 0x правильная,
но для y 0;1 левая граница области D: х = 1 – у, правая граница х = 1, а
для y 1;2 левая граница D: х = у – 1, правая – та же, x 1. Поэтому область
D разбиваем на две области прямой y = 1: D1 y 0;1 и D2 y 1;2 и интеграл
по области D представляем в виде суммы интегралов по областям D1 и D2 :
1
1 x
0
1 x
dx f ( x; y)dy f ( x; y)dxdy f ( x; y)dxdy
D1
D2
1
1
2
1
0
1 y
1
y 1
dy
f ( x; y)dx dy f ( x; y)dx
1
1 x
1
1
2
1
0
1 x
0
1 y
1
y 1
Ответ: dx f ( x; y )dy dy f ( x; y )dx dy f ( x; y )dx.














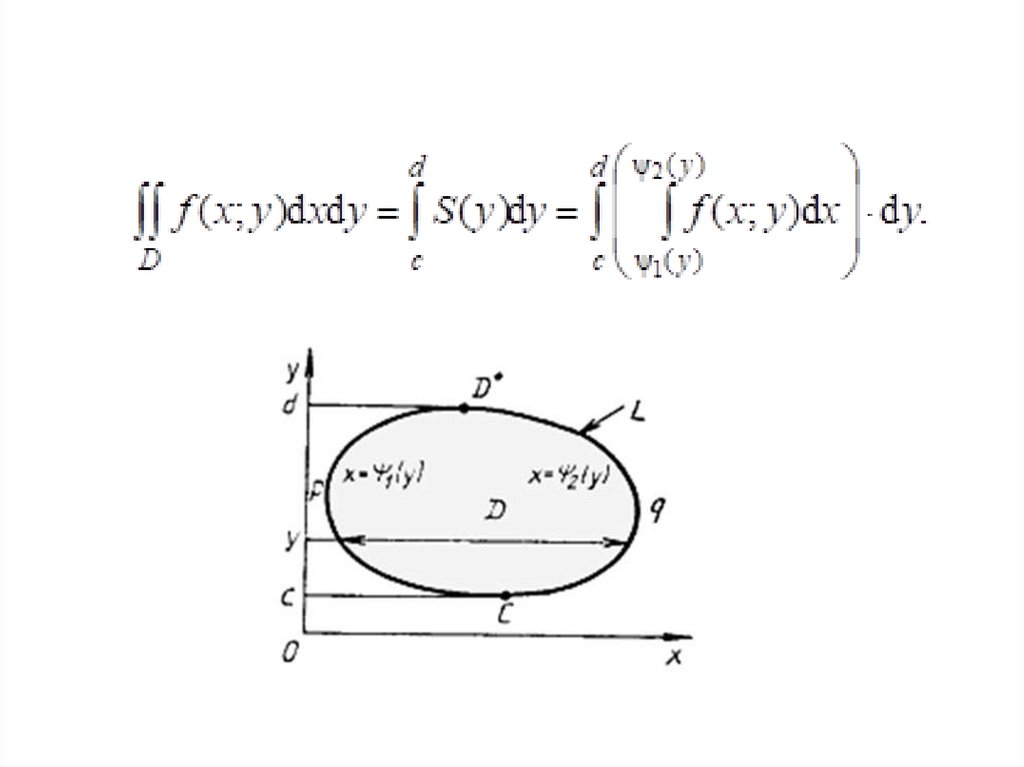






 mathematics
mathematics








