Similar presentations:
Двойные интегралы
1. 6B07102 Машиностроение 6B07107 Химическая технология неорганических веществ 6B07305 Инженерные системы и сети 6B11301
Дисциплина: «Математика 2»Слайд-лекция «Двойные интегралы»
6B07102 МАШИНОСТРОЕНИЕ
6B07107 ХИМИЧЕСКАЯ ТЕХНОЛОГИЯ НЕОРГАНИЧЕСКИХ ВЕЩЕСТВ
6B07305 ИНЖЕНЕРНЫЕ СИСТЕМЫ И СЕТИ
6B11301 ОРГАНИЗАЦИЯ ПЕРЕВОЗОК, ДВИЖЕНИЯ И ЭКСПЛУАТАЦИЯ ТРАНСПОРТА
6B07202 МЕТАЛЛУРГИЯ
6B07205 МЕТАЛЛУРГИЯ
6B07110 ТЕХНОЛОГИЧЕСКИЕ МАШИНЫ И ОБОРУДОВАНИЕ (ПО ОТРАСЛЯМ)
6B07103 ТРАНСПОРТ, ТРАНСПОРТНАЯ ТЕХНИКА И ТЕХНОЛОГИИ
6B07302 СТРОИТЕЛЬСТВО
6B07501 СТАНДАРТИЗАЦИЯ, СЕРТИФИКАЦИЯ И МЕТРОЛОГИЯ (ПО ОТРАСЛЯМ)
.
2.
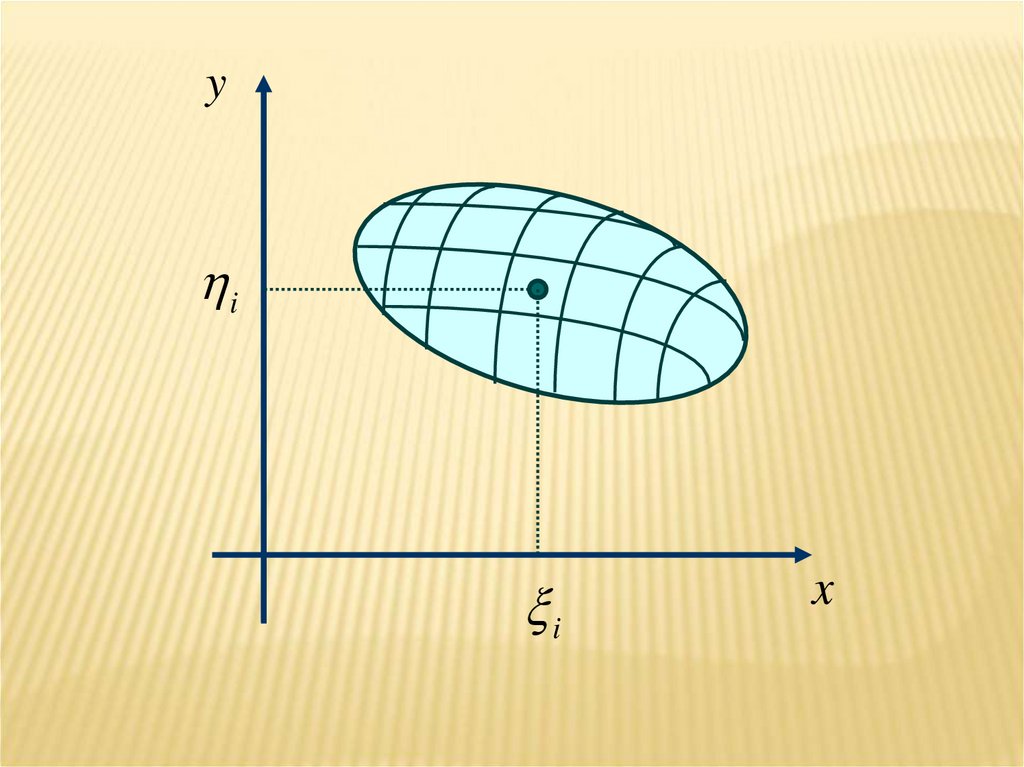
Пусть D – замкнутая и ограниченная область наплоскости
XOY
и
в
ней
определена
произвольная ограниченная функция z=f(x,y).
Разобьем область D сетью кривых на n
произвольных частей Di с площадями ΔSi.
В каждой из областей Di выберем точку (ξi,ηi).
3.
yi
i
x
4.
Сумму видаn
f ( i , i ) S i
i 1
называют интегральной суммой
для функции z=f(x,y) в области D.
1
5.
Интегральная сумма зависит от способаразбиения отрезка и выбора точек (ξi, ηi).
Диаметром d области D называется наибольшее
расстояние между граничными точками этой
области.
Пусть max d – наибольший из всех диаметров
частичных областей. Тогда
6.
Еслисуществует
конечный
предел
интегральной суммы при max d 0
не зависящий от способа разбиения
области D и выбора точек (ξi, ηi), то он
называется двойным интегралом от
функции z=f(x,у) по области D.
n
lim
max d 0
f ( , ) S f ( x, y)dS
i 1
i
i
i
D
7.
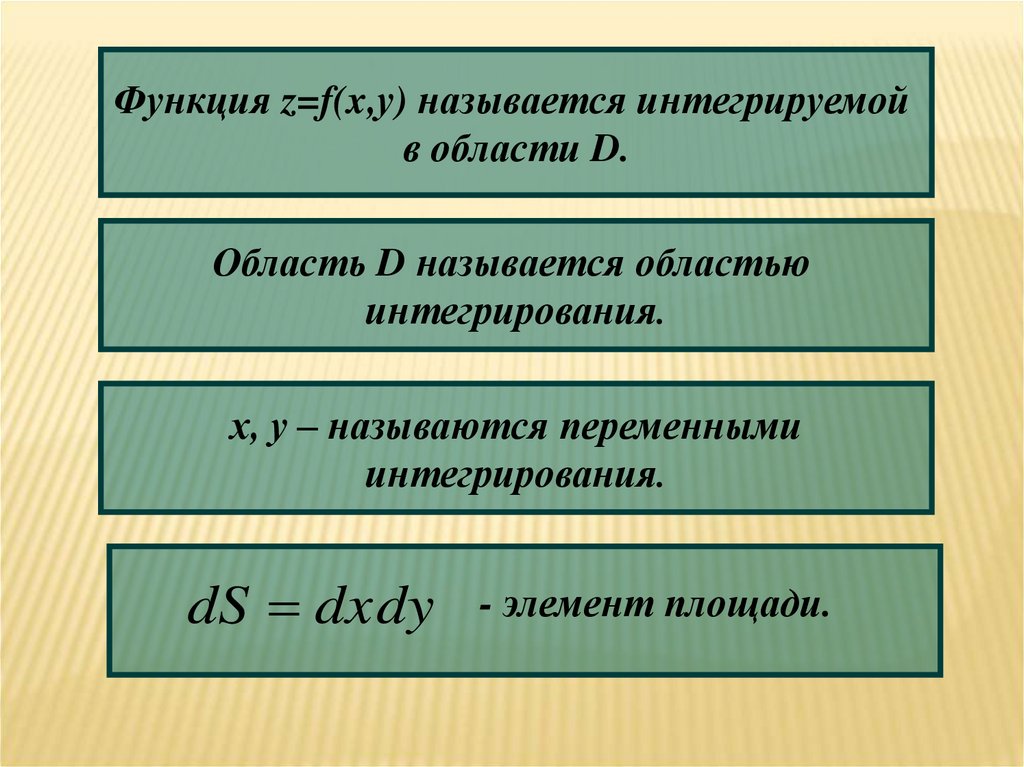
Функция z=f(x,у) называется интегрируемойв области D.
Область D называется областью
интегрирования.
х, у – называются переменными
интегрирования.
dS dxdy
- элемент площади.
8.
Если функция f(x,y) непрерывнав замкнутой ограниченной
области, то она интегрируема
в этой области.
9.
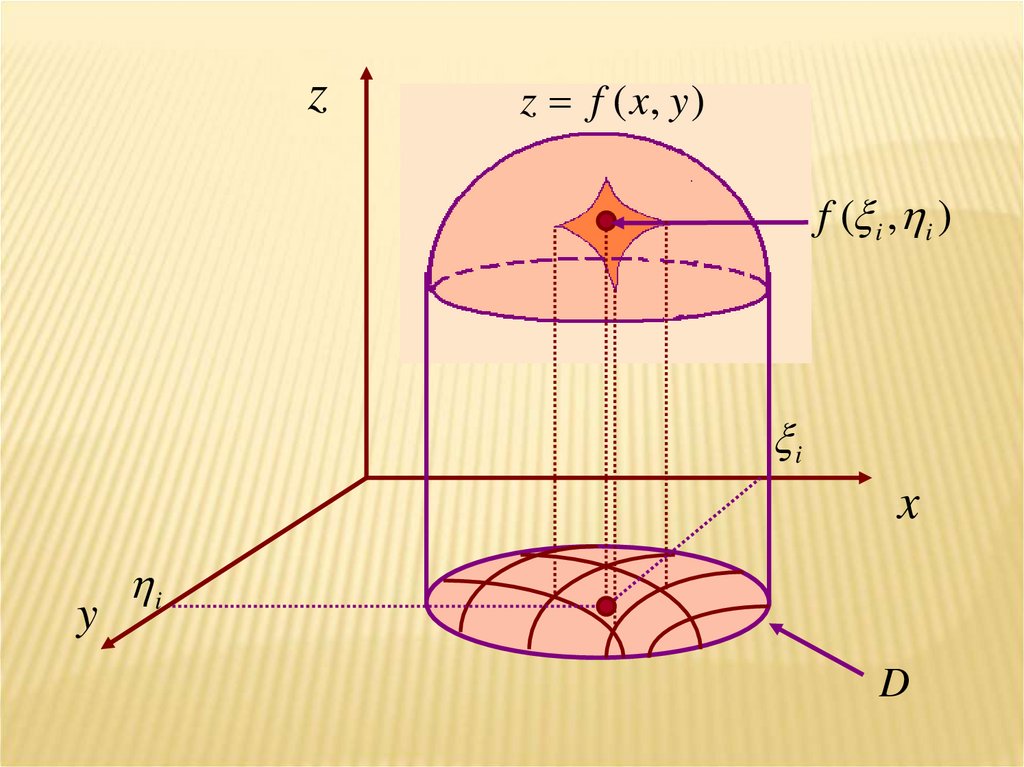
Рассмотрим геометрическое тело, ограниченноесверху поверхностью, задаваемой непрерывной и
неотрицательной функцией z=f(x,y), снизу –
ограниченной областью D, с боков –
цилиндрической поверхностью, у которой
направляющей является граница области D,
причем образующие параллельны оси z.
10.
zz f ( x, y )
f ( i , i )
i
x
y
i
D
11.
Это тело называется криволинейным цилиндром.Интегральная сумма (1) будет суммой объемов
прямых цилиндров с площадями оснований S i
и высотами f ( i , i )
Эта сумма приближенно будет равна объему всего
тела:
n
V f ( i , i ) S i
i 1
Поскольку функция f(x,y) интегрируема, то предел
этой интегральной суммы существует и будет
равен двойному интегралу:
12.
V f ( x, y)dxdyD
Двойной интеграл по области D от
непрерывной неотрицательной функции
равен объему криволинейного цилиндра
с основанием D.
13.
Пусть функция f(x,y) непрерывна в некоторойзамкнутой ограниченной области D, и существует
f ( x, y)dxdy
D
Предположим, что возможен переход к новым
переменным:
( x, y ) (u, v)
14.
x x (u , v )y y (u , v )
u u ( x, y )
v v ( x, y )
15.
Пусть преобразование x=x(u,v), y=y(u,v)переводит замкнутую ограниченную
область
D
в
замкнутую
ограниченную область D* и является
взаимно однозначным.
Если функции x(u,v), y(u,v) имеют в D*
непрерывные частные производные,
и выражение
16.
x( xy)
u
y
(uv )
u
x
v 0
y
v
то имеет место
17.
( xy)D f ( x, y)dxdy f x(u, v), y(u, v) (uv) dudv
D
18.
x( xy)
u
y
(uv )
u
x
v
y
v
19.
1Вычислить двойной интеграл
sin( x y) dxdy
D
где область D ограничена линиями
x y,
x y
2
,
y 0
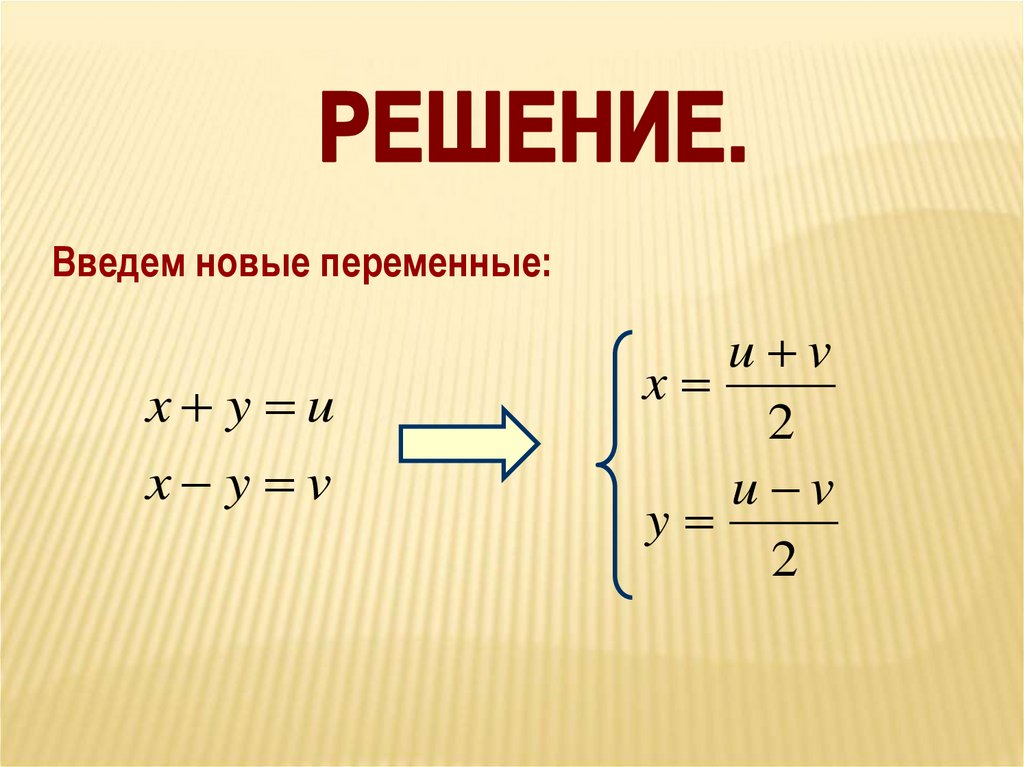
20.
Введем новые переменные:x y u
x y v
u v
x
2
u v
y
2
21.
Тогда прямая x y2
u
переходит в прямую
2
Прямая
x y переходит в прямую
v 0
Прямая
y 0 переходит в прямую
v u
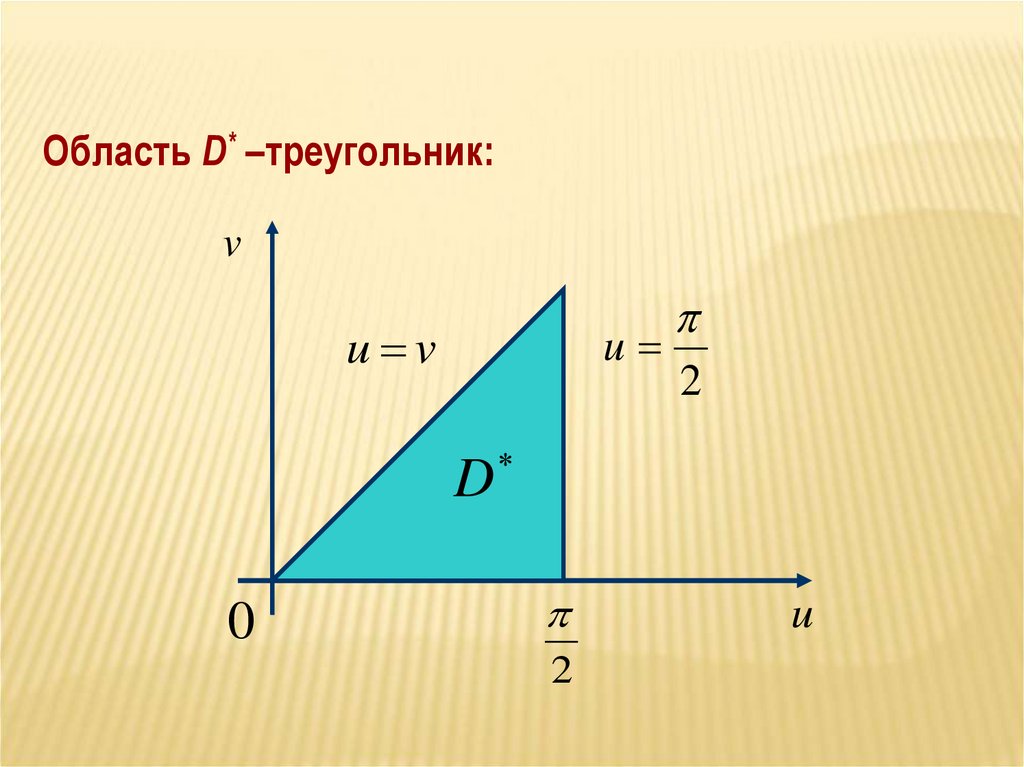
22.
Область D* –треугольник:v
u
2
u v
D
0
2
u
23.
Найдем якобиан:x 1
u 2
x 1
v 2
1
( xy)
2
1
(uv)
2
y 1
u 2
1
2 1
1
2
2
( xy) 1
(uv) 2
y
1
v
2
24.
2u
1
1
D sin( x y) dxdy 2 sin ududv 2 0 du 0 sin udv
D
1 2
1 2
u
du sin u v 0 du sin u u
2 0
2 0
2
1
1
1
1
2
2
u cos u 0 cos udu sin u 0
2
2 0
2
2
0
25.
Изгеометрического
смысла
двойного
интеграла следует, что любой двойной
интеграл задает объем тела, ограниченного
сверху графиком подынтегральной функции,
снизу – областью D, с боков – цилиндрической
поверхностью с направляющими по границе
области D.
26.
Вычислить объем тела,ограниченного поверхностями
z x y,
x y a, (a 0)
z 0
27.
Посколькуподынтегральная
функция
должна быть не отрицательна, то область
интегрирования ограничена на плоскости
ХОУ
прямоугольным
равнобедренным
треугольником с катетами, равными а.
y
a
D
0
a
x
28.
a xa
a
1
2 a x
D x y dxdy 0 dx 0 x ydy 2 0 dx x y 0
a
a
1
1
2
dx x (a x) dx ( x 3 2a x 2 a 2 x)
20
20
a
1 x
2ax
a x
a4
(куб .ед.)
2 4
3
2 0 24
4
3
2
2
29.
Площадь некоторой области D может бытьнайдена по формуле:
dxdy S
D
D
30.
Вычислить площадь фигуры,ограниченной линиями:
y ln x,
x y 1,
y 1
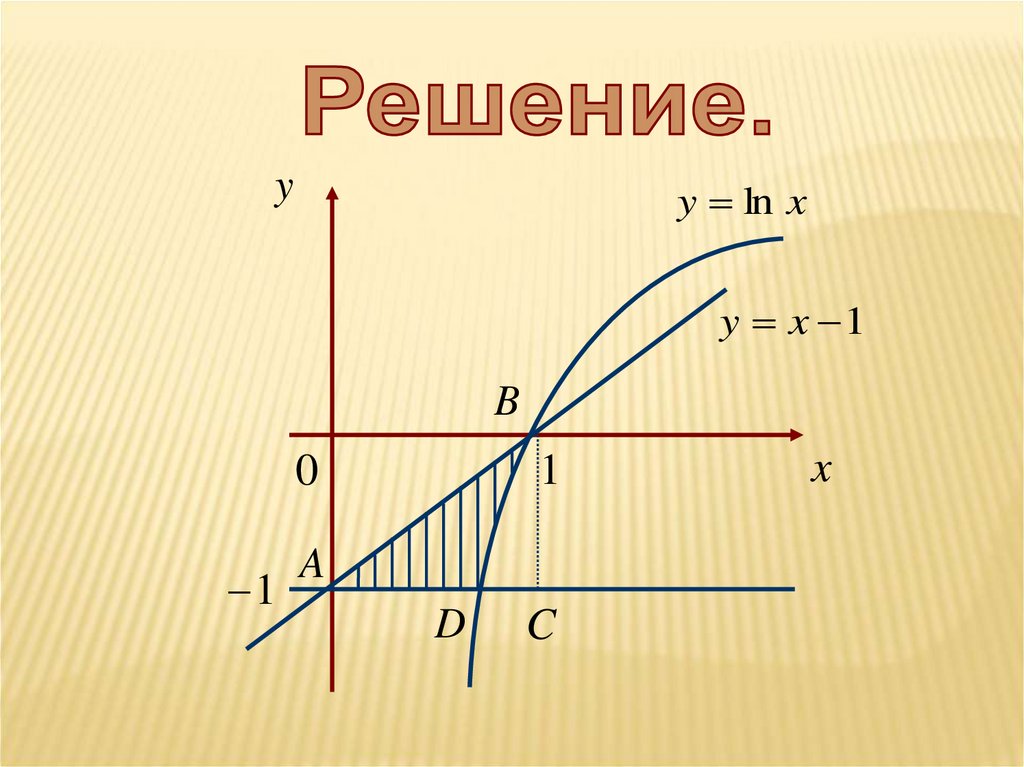
31.
yy ln x
y x 1
B
1
0
1
A
D
C
x
32.
S ABD S ABC S BCDS ABC -площадь прямоугольного треугольника,
катеты которого равны 1.
1
S ABC
2
S BCD -ограничена снизу прямой y=-1 при
1
x 1
e
-сверху кривой y=lnx и справа прямой
x=1.
33.
1ln x
1
1
S ABD dxdy dx dy
2 BCD
2 1
1
e
1
1
e
e
1
1
ln x
dx y 1 dx ln x 1
2 1
2 1
ln x 1 u
1
du dx
x
dx dv
x v
34.
11
1
1 1
1
1
x ln x 1 x dx e x 1
e
e
2
x
2 e
1
e
1
1 1 1
1 1 кв.ед.
2
e 2 e






















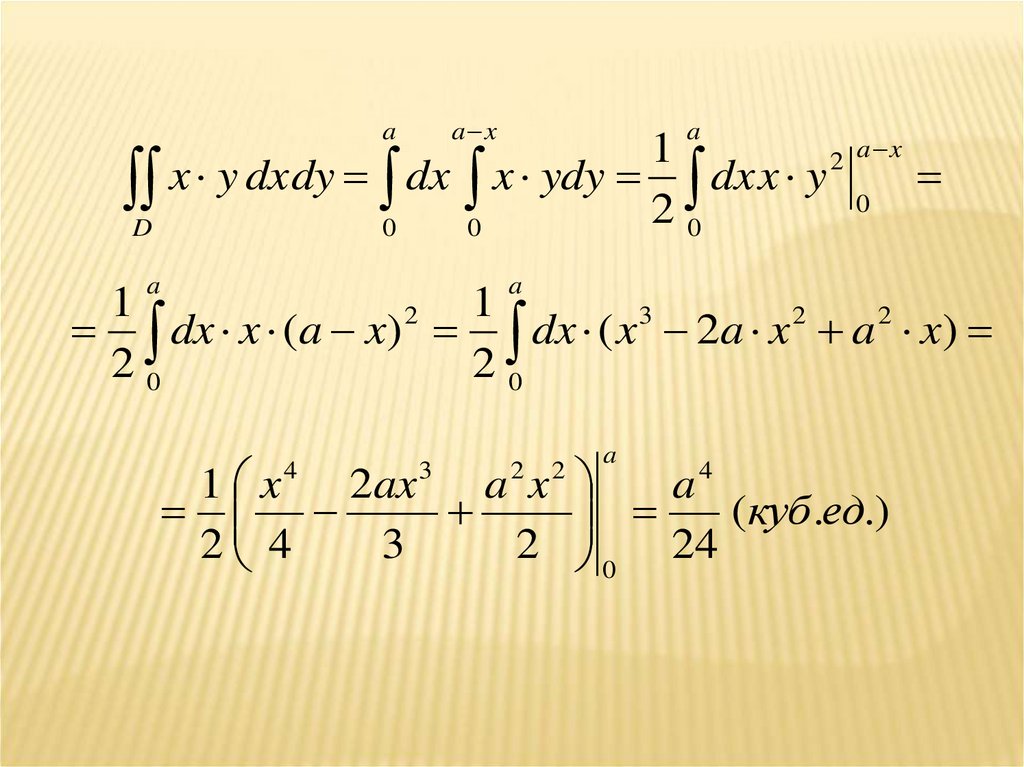



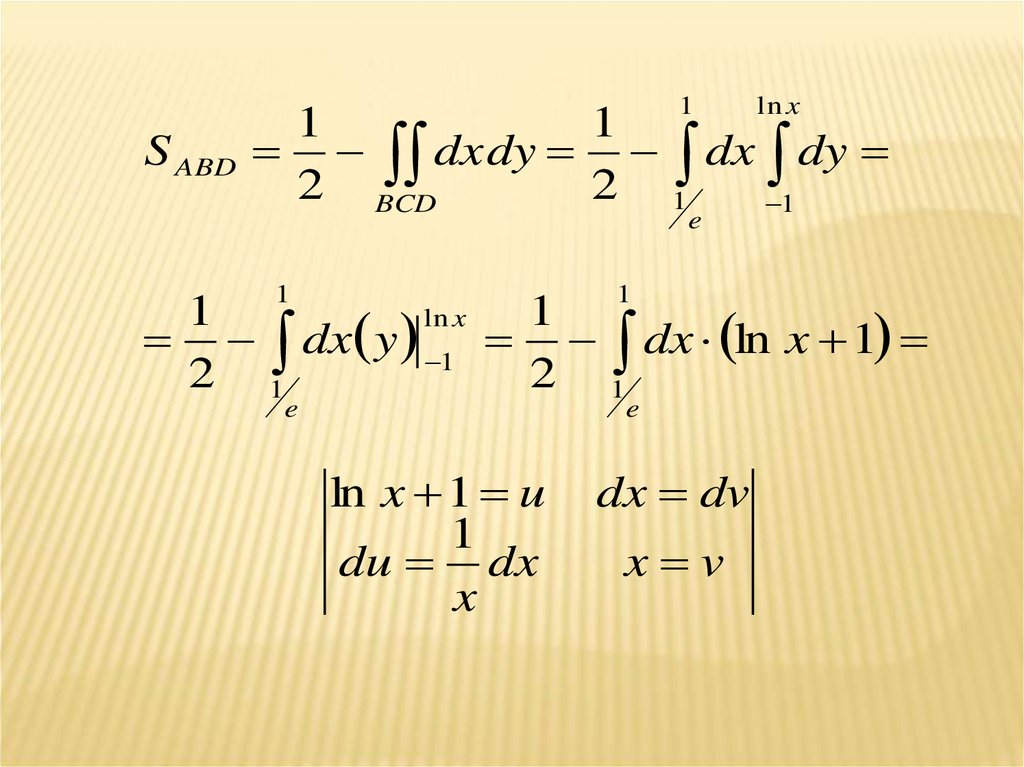
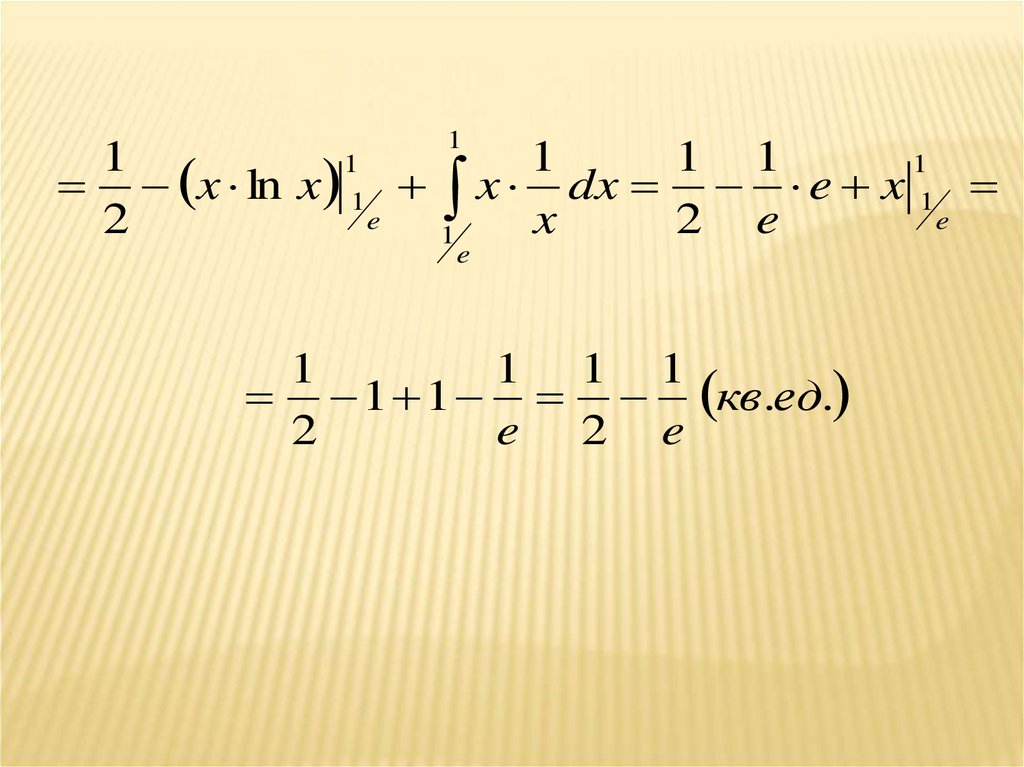
 mathematics
mathematics








