Similar presentations:
Объем цилиндрического тела. Двойной интеграл. (Лекция 2.1)
1. Лекция 2.1 9 ДВОЙНЫЕ ИНТЕГРАЛЫ. 9.1 Объем цилиндрического тела. Двойной интеграл.
zy
D
z = z ( x, y ) ³ 0
x
Цилиндрическим телом называется тело,
ограниченное замкнутой областью D плоскости Oxy,
поверхностью z=z(x,y), где z=z(x,y) непрерывна и
неотрицательна в области D и цилиндрической
поверхностью с образующей параллельной оси Oz и
направляющей – границей области D.
2. Разобьем область D на n произвольных частичных областей (k(1,…,n)).
Разобьем область D на n произвольных частичныхобластей Ds k (k (1,…,n)).
Ds k
y
( xk , yk )
D
x
Выберем в каждой из частичных областей произвольную точку с
(
)
координатами xk , yk . Объем цилиндрического тела между
опорной плоскостью Oxy и поверхностью z=z(x,y) над частичной
областью Ds k равен DVk » z xk , yk Ds k
. Объем всего
цилиндрического тела равен
(
n
n
k =1
k =1
)
V = å DVk » å z ( xk , yk ) Dsk
3.
Устремим наибольший диаметр частичных областей
max diam ( Dsk ) ® 0 , n ® ¥
Ds k
и рассмотрим предел интегральной суммы
к нулю, при этом
n
lim
max diam( Dsk
n®¥
z ( xk , yk ) Dsk
å
) ®0
k =1
Если этот предел существует, то очевидно, что
V=
n
lim
max diam( Dsk
n®¥
z ( xk , yk ) Dsk
å
) ®0
k =1
4. Определение.
Двойным интегралом от функции z=z(x,y) по области Dназывается предел, к которому стремится интегральная
сумма при стремлении к нулю наибольшего диаметра
частичных областей
n
lim
max diam( Dsk
n ®¥
z ( xk , yk ) Dsk = òò z ( x, y ) d s
å
) ®0
k =1
D
z ( x, y ) ds
– подынтегральное выражение;
z(x,y) – подынтегральная функция;
ds - элемент (дифференциал) площади;
D – область интегрирования.
Таким образом, V = z ( x, y ) d s
òò
D
5. Теорема существования двойного интеграла.
Если z(x,y) непрерывна в замкнутойограниченной области D, то ее интегральная
сумма стремится к пределу при стремлении к
нулю наибольшего диаметра частичных
областей. Этот предел не зависит от способа
разбиения области на частичные области Ds k
и выбора в них точек ( xk , yk ) .
6. 9.2 Свойства двойных интегралов.
1)D
òò ( z1 ( x, y ) ± ... ± zn ( x, y ) ) d s = òò z1 ( x, y ) d s ± ... ± òò zn ( x, y ) d s
2)
D
òò cz ( x, y ) d s = c òò z ( x, y ) d s
D
D
D
3) D = D1 U D2 , D1 I D2 = Æ .
Тогда
òò z ( x, y ) d s = òò z ( x, y ) d s + òò z ( x, y ) d s
D
D1
D2
7. Свойства двойных интегралов.
4) Если (x,y) D z1 ( x, y ) ³ z2 ( x, y )то
òò z1 ( x, y ) d s ³ òò z2 ( x, y ) d s
D
D
D
5) Если m = zвнаим
, M = zвнаиб
mS £ òò z ( x, y ) d s £ MS
то
D
6)
z ( x, y ) d s = z ( x, h) S , ( x, h) D
òò
D
D
z ( x, h )
,
, где S = òò d s .
D
- среднее значение z в области D.
8. 9.3 Вычисление двойных интегралов.
Разобьем область D с помощью линий,параллельных осям координат
с шагом dx и dy соответственно.
Тогда d s = dxdyи, следовательно,
y
ds
D
òò z ( x, y ) d s = òò z ( x, y ) dxdy.
D
D
При вычислении двойного интеграла будем использовать
b
формулу
V = ò S ( x ) dx,
(9.1)
a
где
- площадь поперечного
сечения тела плоскостью
S ( x)
x=const.
Предположим, что любая прямая, параллельная осям Ox или
Oy, пересекает границу области D не более чем в двух точках.
x
9.
yE
d
y = y2 ( x )
B
A
c
a
z = z ( x, y )
y
z
C
y = y1 ( x )
b
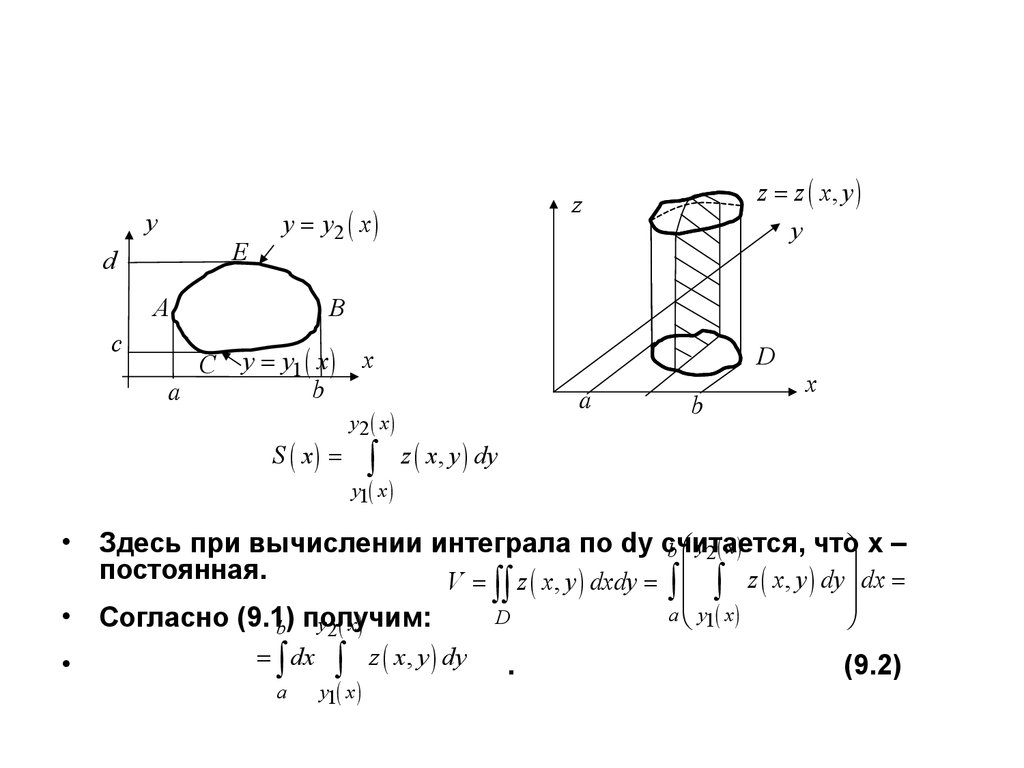
S ( x) =
D
x
a
y2 ( x )
b
x
ò z ( x, y ) dy
y1( x )
• Здесь при вычислении интеграла по dy считается,
чтоö x –
b æ y2 ( x )
постоянная.
z ( x, y ) dy ÷ dx =
V = z ( x, y ) dxdy = ç
• Согласно (9.1)
y2 ( x )
b получим:
= ò dx
a
ò z ( x, y ) dy
y1( x )
òò
D
.
òç ò
a è y1( x )
÷
ø
(9.2)
10.
• Изменив порядок интегрирования, аналогичнополучим
d
x2 ( y )
c
x1( y )
òò z ( x, y ) dxdy = ò dy ò z ( x, y ) dx
D
.
(9.3)
• Правые части формул (9.2) и(9.3) называются
повторными (или двухкратными) интегралами.
• Процесс расстановки пределов интегрирования
называется приведением двойного интеграла к
повторному.
11. Примеры:
1)y
d
D
c
x
a
b
b
d
d
b
a
c
c
a
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy = ò dy ò z ( x, y ) dx
D
12. 2)
yy=x
a
y=0
x=a
x
a
a
x
a
a
0
0
0
y
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy = ò dy ò z ( x, y ) dx
D
13. 3)
y1
y = x2
x+ y =2
y=0
x
2
1
1
x2
2
2- x
1
2- y
0
0
1
0
0
y
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy + ò dx ò z ( x, y ) dy = ò dy ò z ( x, y ) dx
D
14. 4)
yy = y2 ( x )
y = y1 ( x )
a
b
x
b
y2 ( x )
a
y1( x )
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy
D
15. 5)
yd
c
.
x = x1 ( y )
x = x2 ( y )
x
d
x2 ( y )
c
x1( y )
òò z ( x, y ) dxdy = ò dy ò z ( x, y ) dx
D
16. 6)
yD1
D = D1 + D2 + D3
D2
D3
x
òò z ( x, y ) dxdy =
D
= òò z ( x, y ) dxdy +
D1
òò z ( x, y ) dxdy + òò z ( x, y ) dxdy
D2
D3















 mathematics
mathematics








